Адиабатным
называют процесс, в котором отсутствует
обмен энергией в форме теплоты (теплообмен)
между системой и внешней средой.
Адиабатный процесс подчиняется условию:
dQ=0.
Практически
адиабатный процесс осуществляется при
достаточно быстром расширении или
сжатии газа. Условие адиабатности будет
выполнено, если процесс протекает так
быстро, что теплообмен между газом и
внешней средой не успевает произойти.
Из
первого начала термодинамики (1), следует,
что в адиабатическом процессе
dА=
— dU, (17)
т.е.
работа совершается системой за счет
убыли ее внутренней энергии.
Из
(8) следует, что в адиабатном процессе
,
(18)
из
(17) и (18) видно, что при адиабатном
расширении dV>0,
dА=pdV>0
, тогда dT<0
, т.е. газ, охлаждается, а при адиабатном
сжатии dV<0,
dА=pdV<0
и dT>0,
т.е.
газ нагревается.
Найдем уравнение
адиабаты для идеального газа, т.е.
уравнение, связывающее параметры
состояния идеального газа, например, р
и V при адиабатном процессе. Для этого
перепишем уравнение (17) в форме:
,
а
величину
найдем из уравнения состояния газа (10)
путем
дифференцирования
этого уравнения по всем переменным:
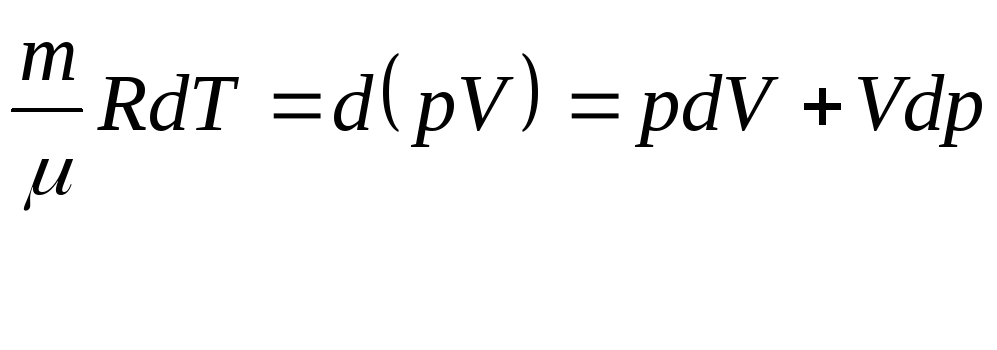
Таким
образом,
,
или, учитывая уравнение Майера (14),
получим:
Разделив
обе части этого уравнения на
получим:
где:
—
безразмерная величина, называемаяпоказателем
адиабаты.
Пренебрегая зависимостью Cv
от температуры, можно считать, что для
данного газа g=const
.
Так
как и
,
то
написанное выше уравнение можно
представить в виде:
,
или
откуда следует, что
pVg
= const
(19)
Уравнение
(19) называют формулой
Пуассона.
В адиабатном
процессе изменяются все параметры
состояния: объем, давление и температура.
Соотношение между
давлением и температурой, а также между
объемом и температурой идеального газа
в адиабатном процессе легко получить
из (19) и уравнения Менделеева- Клапейрона
(10):
;
Линию,
изображающую адиабатный процесс на
диаграмме состояния, называют адиабатой.
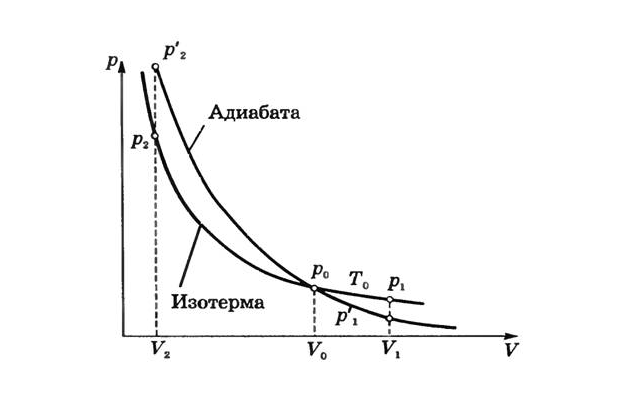
На рис. 3 сплошной линией показан вид
адиабаты. Для сравнения на том же рисунке
пунктирной линией изображена изотерма,
соответствующая температуре газа в
состоянии 1. Так как для любого идеального
газа показатель адиабаты g>1,
то на диаграмме адиабата идет круче,
чем изотерма. Объясняется это тем, что
при адиабатном сжатии (процесс 1-3)
увеличение давления обусловлено не
только уменьшением объема газа, как при
изотермическом сжатии, но также еще и
увеличением температуры.
При адиабатном
расширении температура газа уменьшается,
поэтому давление газа падает быстрее,
чем при изотермическом расширении
(процесс 1-2).
Описание установки и принципа измерений.
Определение
отношения Сp/Сv
для воздуха основано на осуществлении
адиабатного расширения и использовании
для этого процесса формулы Пуассона
(19) pVg
= const: где
g
= Ср/Cv.
Экспериментальная
установка для определения g
методом Клемана-Дезорма состоит из
стеклянного баллона А (рис. 4), который
соединяется, с одной стороны, с U-образным
манометром М, с другой стороны, посредством
трехходового крана К — либо с атмосферой,
либо с насосом. Манометр М, наполненный
какой-либо жидкостью (керосином,
подкрашенной водой и т.д.), позволяет по
разнице уровней h жидкостей в левом и
правом коленах измерить в баллоне
давление р, избыточное над атмосферным:
р=rg
h , где r
— плотность жидкости (чем меньше r,
тем заметнее разность уровней h ). Баллон
А обшит темным материалом для уменьшения
теплообмена с окружающей средой путем
излучения.
Для
осуществления адиабатного расширения
предварительно в баллон А накачивают
воздух, для чего трехходовой кран К
соединяют с насосом и после накачивания
кран К перекрывают. Манометр М в момент
закрытия крана показывает некоторую
разницу уровней жидкости, которая в
течение нескольких последующих минут
изменяется. Это объясняется тем, что
процесс нагнетания воздуха подобен
адиабатному сжатию, вследствие чего
воздух в баллоне нагревается, а затем
после закрытия крана, он постепенно
изохорически охлаждается от окружающей
среды до комнатной температуры. В
результате давление в баллоне,
превосходящее атмосферное, начинает
уменьшаться, поэтому изменяется и
разность уровней жидкости в манометре.
Когда температура в баллоне сравняется
с комнатной, разность уровней в манометре
остается постоянной, равной величине
Н, а давление в баллоне станет равным
ратм
+ r
g H.
Затем
осуществляется адиабатное расширение
воздуха, для чего краном К соединяют
баллон с атмосферой на очень короткое
время, при этом уровни жидкости в
манометре моментально сравниваются.
Предварительно сжатый воздух быстро
выходит из баллона, т.е. резко адиабатно
расширяется и поэтому охлаждается, а
затем медленно (в течение 2-3 минут) воздух
в баллоне изохорически нагревается,
вследствие чего давление в нем
увеличивается и разность уровней
жидкостей в манометре снова начинает
изменяться до тех пор, пока воздух в
баллоне не нагреется до, комнатной
температуры. Тогда манометр покажет
разницу уровней h, давление, избыточное
над атмосферным, будет равно r
g h, а давление в баллоне будет ратм
+ r
g h.
Докажем,
что величину g
= Ср/Cv
, легко вычислить по измеренным величинам
Н и h.
Представим
графически процессы, происходящие с
воздухом в баллоне (рис. 5). Построение
графика начнем с того момента времени,
когда предварительно накачанный в
баллон воздух охладился до комнатной
температуры Т1
(состояние
1 на рис. 5), а давление р1
стало
равным
ратм
+ r
g
H
= р0
+ r
g
H.
Из
состояния 1 (р1,
V1,
T1)
воздух, адиабатно расширяясь, переходит
в состояние 2, при этом давление
сравнивается с атмосферным р0,
а температура понижается и становится
равной Т2Т1.
Затем,
при закрытом кране, т.е. при неизменном
объеме воздух в баллоне изохорически
нагревается (процесс 2-3) до комнатной
Т1
температуры, а давление при этом
становится равным р2
=
р0
+ r
g h.
Следует
заметить, что в процессе 1-2 воздух выходит
из баллона, поэтому масса воздуха в
баллоне изменяется. Чтобы в дальнейшем
иметь возможность воспользоваться
газовыми законами, справедливыми для
постоянной массы газа, будем состояние
1 относить к объему V1
ТОлько
той части массы газа в баллоне объемом
V2 ,
которая после расширения до состояния
2 примет значение, равное объему баллона
V2
, т.е. V1
<
V2.
Точки
1 и 3, имеющие одинаковую температуру
Т1,
теоретически расположены на изотерме,
поэтому по закону Бойля-Мариотта можно
записать:
р1V1
= р2V2
,
(20)
Точки 1 и 2 лежат
на адиабате, следовательно по формуле
Пуассона (19) параметры этих состояний
связаны соотношением:
,
(21)
Если
уравнение (20) возвести в степень
и разделить на уравнение (21), то получим:
или
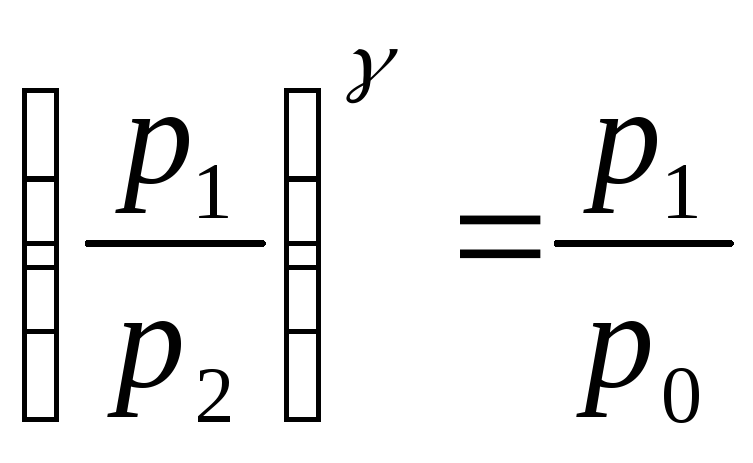
Логарифмируя (22),
находим:
,
(23)
Подставляя
в (23) значение р1
= р0
+r
g H и р2
= р0
+ r
g h получим:
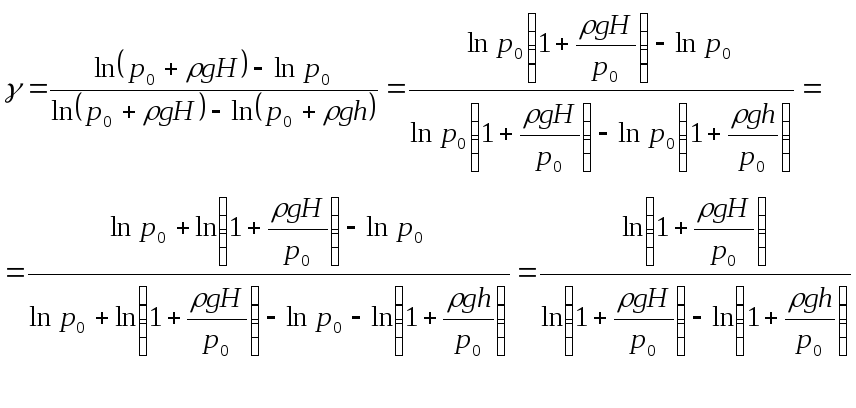
(24)
Так
как давление r
g H<<
р0
и r
g h <<
р0
то
<<1
и<<1,
поэтому воспользуемся разложением в
ряд вида:
.
Если в этом разложении x<<1 ,
то можно
пренебречь членами второго порядка,
тогда ln(1+x) »
x. Аналогично полученному можно написать,
что
и
.
Таким образом выражение (24) преобразуется
к виду:
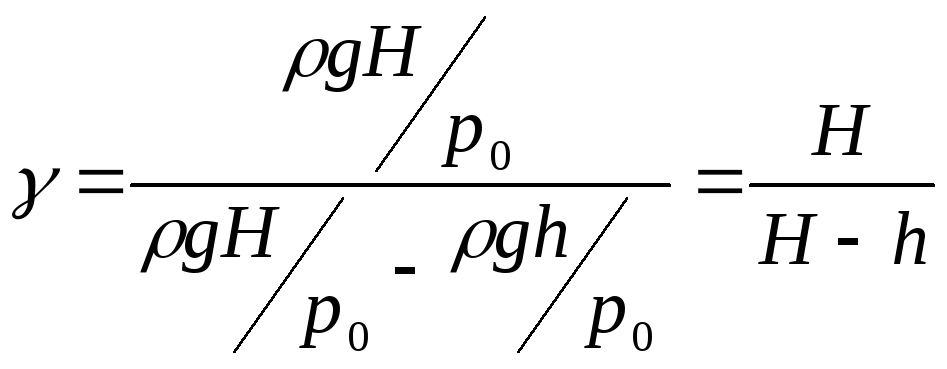
(25)
Уточним
в формуле (25) величину h . Осуществляя
практически адиабатное расширение
(процесс. 1-2 рис. 5), мы не можем закрыть
кран точно в момент окончания этого
процесса. Однако, если кран закрыть
несколько позже окончания адиабатного
процесса, то газ еще некоторое время
будет продолжать расширяться при
постоянном атмосферном давлении, т.е.
изобарически (процесс 2-2¢
на рис. 5), и в опыте вместо значения h мы
всегда будем получать значение h¢,
соответствующее отрезку 2¢-3¢,
причем h¢
тем сильнее будет отличаться от h , чем
больше будет это время запаздывания. С
учетом сказанного выше, формула (25) дает
несколько заниженное значение величины
.
Однако,
величину h=hист,
соответствующую моменту окончания
адиабатного расширения, можно точнее
определить следующим образом.
Опыт
показывает, что величины h¢
и t связаны соотношением:
ln
h¢
= ln hист
— At, (26)
где
А- константа, зависящая от параметров
установки; t — время изобарического
расширения (время открытия крана); hист
— разность уровней жидкости
в манометре
в момент времени t =0, т.е. разность
уровней, которую мы должны были бы
получить, если бы смогли закрыть кран
сразу после адиабатного расширения.
Величину
hист
легко определить, если зависимость ln
h¢
от времени t (26) представить графически
(рис. 6). Получив по экспериментальным
данным прямую АВ, можно ее продолжить
до пересечения с осью ординат и в т. С
пересечения прямой с осью координат
(т.е. в точке, соответствующей t=0)
прочесть значение ln hист
,а затем определить величину hист.
Подставив в (25) значение hист
вместо h получим более точное значение
:
(27)
Соседние файлы в папке Механика
- #
- #
- #
- #
- #
- #
- #
- #
- #
This article is about adiabatic processes in thermodynamics. For the adiabatic theorem in quantum mechanics, see adiabatic theorem.
In thermodynamics, an adiabatic process (Greek: adiábatos, «impassable») is a type of thermodynamic process that occurs without transferring heat or mass between the thermodynamic system and its environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as work.[1][2] As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics.
Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient «adiabatic approximation».[3] For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of flame temperature by assuming combustion loses no heat to its surroundings.
In meteorology and oceanography, adiabatic cooling produces condensation of moisture or salinity, oversaturating the parcel. Therefore, the excess must be removed. There, the process becomes a pseudo-adiabatic process whereby the liquid water or salt that condenses is assumed to be removed upon formation by idealized instantaneous precipitation. The pseudoadiabatic process is only defined for expansion because a compressed parcel becomes warmer and remains undersaturated.[4]
Description[edit]
A process without transfer of heat to or from a system, so that Q = 0, is called adiabatic, and such a system is said to be adiabatically isolated.[5][6] The simplifying assumption frequently made is that a process is adiabatic. For example, the compression of a gas within a cylinder of an engine is assumed to occur so rapidly that on the time scale of the compression process, little of the system’s energy can be transferred out as heat to the surroundings. Even though the cylinders are not insulated and are quite conductive, that process is idealized to be adiabatic. The same can be said to be true for the expansion process of such a system.
The assumption of adiabatic isolation is useful and often combined with other such idealizations to calculate a good first approximation of a system’s behaviour. For example, according to Laplace, when sound travels in a gas, there is no time for heat conduction in the medium, and so the propagation of sound is adiabatic. For such an adiabatic process, the modulus of elasticity (Young’s modulus) can be expressed as E = γP, where γ is the ratio of specific heats at constant pressure and at constant volume (γ = Cp/Cv) and P is the pressure of the gas.
Various applications of the adiabatic assumption[edit]
For a closed system, one may write the first law of thermodynamics as ΔU = Q − W, where ΔU denotes the change of the system’s internal energy, Q the quantity of energy added to it as heat, and W the work done by the system on its surroundings.
- If the system has such rigid walls that work cannot be transferred in or out (W = 0), and the walls are not adiabatic and energy is added in the form of heat (Q > 0), and there is no phase change, then the temperature of the system will rise.
- If the system has such rigid walls that pressure–volume work cannot be done, but the walls are adiabatic (Q = 0), and energy is added as isochoric (constant volume) work in the form of friction or the stirring of a viscous fluid within the system (W < 0), and there is no phase change, then the temperature of the system will rise.
- If the system walls are adiabatic (Q = 0) but not rigid (W ≠ 0), and, in a fictive idealized process, energy is added to the system in the form of frictionless, non-viscous pressure–volume work (W < 0), and there is no phase change, then the temperature of the system will rise. Such a process is called an isentropic process and is said to be «reversible». Ideally, if the process were reversed the energy could be recovered entirely as work done by the system. If the system contains a compressible gas and is reduced in volume, the uncertainty of the position of the gas is reduced, and seemingly would reduce the entropy of the system, but the temperature of the system will rise as the process is isentropic (ΔS = 0). Should the work be added in such a way that friction or viscous forces are operating within the system, then the process is not isentropic, and if there is no phase change, then the temperature of the system will rise, the process is said to be «irreversible», and the work added to the system is not entirely recoverable in the form of work.
- If the walls of a system are not adiabatic, and energy is transferred in as heat, entropy is transferred into the system with the heat. Such a process is neither adiabatic nor isentropic, having Q > 0, and ΔS > 0 according to the second law of thermodynamics.
Naturally occurring adiabatic processes are irreversible (entropy is produced).
The transfer of energy as work into an adiabatically isolated system can be imagined as being of two idealized extreme kinds. In one such kind, no entropy is produced within the system (no friction, viscous dissipation, etc.), and the work is only pressure-volume work (denoted by P dV). In nature, this ideal kind occurs only approximately because it demands an infinitely slow process and no sources of dissipation.
The other extreme kind of work is isochoric work (dV = 0), for which energy is added as work solely through friction or viscous dissipation within the system. A stirrer that transfers energy to a viscous fluid of an adiabatically isolated system with rigid walls, without phase change, will cause a rise in temperature of the fluid, but that work is not recoverable. Isochoric work is irreversible.[7] The second law of thermodynamics observes that a natural process, of transfer of energy as work, always consists at least of isochoric work and often both of these extreme kinds of work. Every natural process, adiabatic or not, is irreversible, with ΔS > 0, as friction or viscosity are always present to some extent.
Adiabatic heating and cooling[edit]
The adiabatic compression of a gas causes a rise in temperature of the gas. Adiabatic expansion against pressure, or a spring, causes a drop in temperature. In contrast, free expansion is an isothermal process for an ideal gas.
Adiabatic heating occurs when the pressure of a gas is increased by work done on it by its surroundings, e.g., a piston compressing a gas contained within a cylinder and raising the temperature where in many practical situations heat conduction through walls can be slow compared with the compression time. This finds practical application in diesel engines which rely on the lack of heat dissipation during the compression stroke to elevate the fuel vapor temperature sufficiently to ignite it.
Adiabatic heating occurs in the Earth’s atmosphere when an air mass descends, for example, in a Katabatic wind, Foehn wind, or Chinook wind flowing downhill over a mountain range. When a parcel of air descends, the pressure on the parcel increases. Because of this increase in pressure, the parcel’s volume decreases and its temperature increases as work is done on the parcel of air, thus increasing its internal energy, which manifests itself by a rise in the temperature of that mass of air. The parcel of air can only slowly dissipate the energy by conduction or radiation (heat), and to a first approximation it can be considered adiabatically isolated and the process an adiabatic process.
Adiabatic cooling occurs when the pressure on an adiabatically isolated system is decreased, allowing it to expand, thus causing it to do work on its surroundings. When the pressure applied on a parcel of gas is reduced, the gas in the parcel is allowed to expand; as the volume increases, the temperature falls as its internal energy decreases. Adiabatic cooling occurs in the Earth’s atmosphere with orographic lifting and lee waves, and this can form pilei or lenticular clouds.
Due in part to adiabatic cooling in mountainous areas, snowfall infrequently occurs in some parts of the Sahara desert.[8]
Adiabatic cooling does not have to involve a fluid. One technique used to reach very low temperatures (thousandths and even millionths of a degree above absolute zero) is via adiabatic demagnetisation, where the change in magnetic field on a magnetic material is used to provide adiabatic cooling. Also, the contents of an expanding universe can be described (to first order) as an adiabatically cooling fluid. (See heat death of the universe.)
Rising magma also undergoes adiabatic cooling before eruption, particularly significant in the case of magmas that rise quickly from great depths such as kimberlites.[9]
In the Earth’s convecting mantle (the asthenosphere) beneath the lithosphere, the mantle temperature is approximately an adiabat. The slight decrease in temperature with shallowing depth is due to the decrease in pressure the shallower the material is in the Earth.[10]
Such temperature changes can be quantified using the ideal gas law, or the hydrostatic equation for atmospheric processes.
In practice, no process is truly adiabatic. Many processes rely on a large difference in time scales of the process of interest and the rate of heat dissipation across a system boundary, and thus are approximated by using an adiabatic assumption. There is always some heat loss, as no perfect insulators exist.
Ideal gas (reversible process)[edit]
For a simple substance, during an adiabatic process in which the volume increases, the internal energy of the working substance must decrease
The mathematical equation for an ideal gas undergoing a reversible (i.e., no entropy generation) adiabatic process can be represented by the polytropic process equation[3]
where P is pressure, V is volume, and γ is the adiabatic index or heat capacity ratio defined as
Here CP is the specific heat for constant pressure, CV is the specific heat for constant volume, and f is the number of degrees of freedom (3 for a monatomic gas, 5 for a diatomic gas or a gas of linear molecules such as carbon dioxide).
For a monatomic ideal gas, γ = 5/3, and for a diatomic gas (such as nitrogen and oxygen, the main components of air), γ = 7/5.[11] Note that the above formula is only applicable to classical ideal gases (that is, gases far above absolute zero temperature) and not Bose–Einstein or Fermi gases.
One can also use the ideal gas law to rewrite the above relationship between P and V as [3]
where T is the absolute or thermodynamic temperature.
Example of adiabatic compression[edit]
The compression stroke in a gasoline engine can be used as an example of adiabatic compression. The model assumptions are: the uncompressed volume of the cylinder is one litre (1 L = 1000 cm3 = 0.001 m3); the gas within is the air consisting of molecular nitrogen and oxygen only (thus a diatomic gas with 5 degrees of freedom, and so γ = 7/5); the compression ratio of the engine is 10:1 (that is, the 1 L volume of uncompressed gas is reduced to 0.1 L by the piston); and the uncompressed gas is at approximately room temperature and pressure (a warm room temperature of ~27 °C, or 300 K, and a pressure of 1 bar = 100 kPa, i.e. typical sea-level atmospheric pressure).
so the adiabatic constant for this example is about 6.31 Pa m4.2.
The gas is now compressed to a 0.1 L (0.0001 m3) volume, which we assume happens quickly enough that no heat enters or leaves the gas through the walls. The adiabatic constant remains the same, but with the resulting pressure unknown
We can now solve for the final pressure[12]
or 25.1 bar. This pressure increase is more than a simple 10:1 compression ratio would indicate; this is because the gas is not only compressed, but the work done to compress the gas also increases its internal energy, which manifests itself by a rise in the gas temperature and an additional rise in pressure above what would result from a simplistic calculation of 10 times the original pressure.
We can solve for the temperature of the compressed gas in the engine cylinder as well, using the ideal gas law, PV = nRT (n is amount of gas in moles and R the gas constant for that gas). Our initial conditions being 100 kPa of pressure, 1 L volume, and 300 K of temperature, our experimental constant (nR) is:
We know the compressed gas has V = 0.1 L and P = 2.51×106 Pa, so we can solve for temperature:
That is a final temperature of 753 K, or 479 °C, or 896 °F, well above the ignition point of many fuels. This is why a high-compression engine requires fuels specially formulated to not self-ignite (which would cause engine knocking when operated under these conditions of temperature and pressure), or that a supercharger with an intercooler to provide a pressure boost but with a lower temperature rise would be advantageous. A diesel engine operates under even more extreme conditions, with compression ratios of 16:1 or more being typical, in order to provide a very high gas temperature, which ensures immediate ignition of the injected fuel.
Adiabatic free expansion of a gas[edit]
For an adiabatic free expansion of an ideal gas, the gas is contained in an insulated container and then allowed to expand in a vacuum. Because there is no external pressure for the gas to expand against, the work done by or on the system is zero. Since this process does not involve any heat transfer or work, the first law of thermodynamics then implies that the net internal energy change of the system is zero. For an ideal gas, the temperature remains constant because the internal energy only depends on temperature in that case. Since at constant temperature, the entropy is proportional to the volume, the entropy increases in this case, therefore this process is irreversible.
Derivation of P–V relation for adiabatic heating and cooling[edit]
The definition of an adiabatic process is that heat transfer to the system is zero, δQ = 0. Then, according to the first law of thermodynamics,
-
(a1)
where dU is the change in the internal energy of the system and δW is work done by the system. Any work (δW) done must be done at the expense of internal energy U, since no heat δQ is being supplied from the surroundings. Pressure–volume work δW done by the system is defined as
-
(a2)
However, P does not remain constant during an adiabatic process but instead changes along with V.
It is desired to know how the values of dP and dV relate to each other as the adiabatic process proceeds. For an ideal gas (recall ideal gas law PV = nRT) the internal energy is given by
-
(a3)
where α is the number of degrees of freedom divided by 2, R is the universal gas constant and n is the number of moles in the system (a constant).
Differentiating equation (a3) yields
-
(a4)
Equation (a4) is often expressed as dU = nCV dT because CV = αR.
Now substitute equations (a2) and (a4) into equation (a1) to obtain
factorize −P dV:
and divide both sides by PV:
After integrating the left and right sides from V0 to V and from P0 to P and changing the sides respectively,
Exponentiate both sides, substitute α + 1/α with γ, the heat capacity ratio
and eliminate the negative sign to obtain
Therefore,
and
-
(b1)
At the same time, the work done by the pressure–volume changes as a result from this process, is equal to
-
(b2)
Since we require the process to be adiabatic, the following equation needs to be true
-
(b3)
By the previous derivation,
-
(b4)
Rearranging (b4) gives
Substituting this into (b2) gives
Integrating we obtain the expression for work,
Substituting γ = α + 1/α in second term,
Rearranging,
Using the ideal gas law and assuming a constant molar quantity (as often happens in practical cases),
By the continuous formula,
or
Substituting into the previous expression for W,
Substituting this expression and (b1) in (b3) gives
Simplifying,
Derivation of discrete formula and work expression[edit]
The change in internal energy of a system, measured from state 1 to state 2, is equal to
At the same time, the work done by the pressure–volume changes as a result from this process, is equal to
-
(c2)
Since we require the process to be adiabatic, the following equation needs to be true
-
(c3)
By the previous derivation,
-
(c4)
Rearranging (c4) gives
Substituting this into (c2) gives
Integrating we obtain the expression for work,
Substituting γ = α + 1/α in second term,
Rearranging,
Using the ideal gas law and assuming a constant molar quantity (as often happens in practical cases),
By the continuous formula,
or
Substituting into the previous expression for W,
Substituting this expression and (c1) in (c3) gives
Simplifying,
Graphing adiabats[edit]
An adiabat is a curve of constant entropy in a diagram. Some properties of adiabats on a P–V diagram are indicated. These properties may be read from the classical behaviour of ideal gases, except in the region where PV becomes small (low temperature), where quantum effects become important.
- Every adiabat asymptotically approaches both the V axis and the P axis (just like isotherms).
- Each adiabat intersects each isotherm exactly once.
- An adiabat looks similar to an isotherm, except that during an expansion, an adiabat loses more pressure than an isotherm, so it has a steeper inclination (more vertical).
- If isotherms are concave towards the north-east direction (45°), then adiabats are concave towards the east north-east (31°).
- If adiabats and isotherms are graphed at regular intervals of entropy and temperature, respectively (like altitude on a contour map), then as the eye moves towards the axes (towards the south-west), it sees the density of isotherms stay constant, but it sees the density of adiabats grow. The exception is very near absolute zero, where the density of adiabats drops sharply and they become rare (see Nernst’s theorem).[clarification needed]
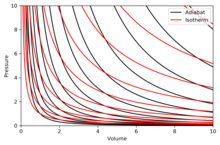
The right diagram is a P–V diagram with a superposition of adiabats and isotherms:
The isotherms are the red curves and the adiabats are the black curves.
The adiabats are isentropic.
Volume is the horizontal axis and pressure is the vertical axis.
Etymology[edit]
The term adiabatic () is an anglicization of the Greek term ἀδιάβατος «impassable» (used by Xenophon of rivers).
It is used in the thermodynamic sense by Rankine (1866),[13][14] and adopted by Maxwell in 1871 (explicitly attributing the term to Rankine).[15]
The etymological origin corresponds here to an impossibility of transfer of energy as heat and of transfer of matter across the wall.
The Greek word ἀδιάβατος is formed from privative ἀ- («not») and διαβατός, «passable», in turn deriving from διά («through»), and βαῖνειν («to walk, go, come»).[16]
Conceptual significance in thermodynamic theory[edit]
The adiabatic process has been important for thermodynamics since its early days. It was important in the work of Joule because it provided a way of nearly directly relating quantities of heat and work.
Energy can enter or leave a thermodynamic system enclosed by walls that prevent mass transfer only as heat or work. Therefore, a quantity of work in such a system can be related almost directly to an equivalent quantity of heat in a cycle of two limbs. The first limb is an isochoric adiabatic work process increasing the system’s internal energy; the second, an isochoric and workless heat transfer returning the system to its original state. Accordingly, Rankine measured quantity of heat in units of work, rather than as a calorimetric quantity .[17] In 1854, Rankine used a quantity that he called «the thermodynamic function» that later was called entropy, and at that time he wrote also of the «curve of no transmission of heat»,[18] which he later called an adiabatic curve.[13] Besides its two isothermal limbs, Carnot’s cycle has two adiabatic limbs.
For the foundations of thermodynamics, the conceptual importance of this was emphasized by Bryan,[19] by Carathéodory,[1] and by Born.[20] The reason is that calorimetry presupposes a type of temperature as already defined before the statement of the first law of thermodynamics, such as one based on empirical scales. Such a presupposition involves making the distinction between empirical temperature and absolute temperature. Rather, the definition of absolute thermodynamic temperature is best left till the second law is available as a conceptual basis.[21]
In the eighteenth century, the law of conservation of energy was not yet fully formulated or established, and the nature of heat was debated. One approach to these problems was to regard heat, measured by calorimetry, as a primary substance that is conserved in quantity. By the middle of the nineteenth century, it was recognized as a form of energy, and the law of conservation of energy was thereby also recognized. The view that eventually established itself, and is currently regarded as right, is that the law of conservation of energy is a primary axiom, and that heat is to be analyzed as consequential. In this light, heat cannot be a component of the total energy of a single body because it is not a state variable but, rather, a variable that describes a transfer between two bodies. The adiabatic process is important because it is a logical ingredient of this current view.[21]
Divergent usages of the word adiabatic[edit]
This present article is written from the viewpoint of macroscopic thermodynamics, and the word adiabatic is used in this article in the traditional way of thermodynamics, introduced by Rankine. It is pointed out in the present article that, for example, if a compression of a gas is rapid, then there is little time for heat transfer to occur, even when the gas is not adiabatically isolated by a definite wall. In this sense, a rapid compression of a gas is sometimes approximately or loosely said to be adiabatic, though often far from isentropic, even when the gas is not adiabatically isolated by a definite wall.
Quantum mechanics and quantum statistical mechanics, however, use the word adiabatic in a very different sense, one that can at times seem almost opposite to the classical thermodynamic sense. In quantum theory, the word adiabatic can mean something perhaps near isentropic, or perhaps near quasi-static, but the usage of the word is very different between the two disciplines.
On the one hand, in quantum theory, if a perturbative element of compressive work is done almost infinitely slowly (that is to say quasi-statically), it is said to have been done adiabatically. The idea is that the shapes of the eigenfunctions change slowly and continuously, so that no quantum jump is triggered, and the change is virtually reversible. While the occupation numbers are unchanged, nevertheless there is change in the energy levels of one-to-one corresponding, pre- and post-compression, eigenstates. Thus a perturbative element of work has been done without heat transfer and without introduction of random change within the system. For example, Max Born writes «Actually, it is usually the ‘adiabatic’ case with which we have to do: i.e. the limiting case where the external force (or the reaction of the parts of the system on each other) acts very slowly. In this case, to a very high approximation
that is, there is no probability for a transition, and the system is in the initial state after cessation of the perturbation. Such a slow perturbation is therefore reversible, as it is classically.»[22]
On the other hand, in quantum theory, if a perturbative element of compressive work is done rapidly, it changes the occupation numbers and energies of the eigenstates in proportion to the transition moment integral and in accordance with time-dependent perturbation theory, as well as perturbing the functional form of the eigenstates themselves. In that theory, such a rapid change is said not to be adiabatic, and the contrary word diabatic is applied to it.
Recent research[23] suggests that the power absorbed from the perturbation corresponds to the rate of these non-adiabatic transitions. This corresponds to the classical process of energy transfer in the form of heat, but with the relative time scales reversed in the quantum case. Quantum adiabatic processes occur over relatively long time scales, while classical adiabatic processes occur over relatively short time scales. It should also be noted that the concept of ‘heat’ (in reference to the quantity of thermal energy transferred) breaks down at the quantum level, and the specific form of energy (typically electromagnetic) must be considered instead. The small or negligible absorption of energy from the perturbation in a quantum adiabatic process provides a good justification for identifying it as the quantum analogue of adiabatic processes in classical thermodynamics, and for the reuse of the term.
Furthermore, in atmospheric thermodynamics, a diabatic process is one in which heat is exchanged.[24]
In classical thermodynamics, such a rapid change would still be called adiabatic because the system is adiabatically isolated, and there is no transfer of energy as heat. The strong irreversibility of the change, due to viscosity or other entropy production, does not impinge on this classical usage.
Thus for a mass of gas, in macroscopic thermodynamics, words are so used that a compression is sometimes loosely or approximately said to be adiabatic if it is rapid enough to avoid significant heat transfer, even if the system is not adiabatically isolated. But in quantum statistical theory, a compression is not called adiabatic if it is rapid, even if the system is adiabatically isolated in the classical thermodynamic sense of the term. The words are used differently in the two disciplines, as stated just above.
See also[edit]
- Fire piston
- Heat burst
- Related physics topics
- First law of thermodynamics
- Entropy (classical thermodynamics)
- Adiabatic conductivity
- Adiabatic lapse rate
- Total air temperature
- Magnetic refrigeration
- Berry phase
- Related thermodynamic processes
- Cyclic process
- Isobaric process
- Isenthalpic process
- Isentropic process
- Isochoric process
- Isothermal process
- Polytropic process
- Quasistatic process
References[edit]
- ^ a b Carathéodory, C. (1909). «Untersuchungen über die Grundlagen der Thermodynamik». Mathematische Annalen. 67 (3): 355–386. doi:10.1007/BF01450409. S2CID 118230148.. A translation may be found here Archived 2019-10-12 at the Wayback Machine. Also a mostly reliable translation is to be found in Kestin, J. (1976). The Second Law of Thermodynamics. Stroudsburg, PA: Dowden, Hutchinson & Ross.
- ^ Bailyn, M. (1994). A Survey of Thermodynamics. New York, NY: American Institute of Physics Press. p. 21. ISBN 0-88318-797-3.
- ^ a b c Bailyn, M. (1994), pp. 52–53.
- ^ «pseudoadiabatic process». American Meteorological Society. Retrieved November 3, 2018.
- ^ Tisza, L. (1966). Generalized Thermodynamics. Cambridge, MA: MIT Press. p. 48.
(adiabatic partitions inhibit the transfer of heat and mass)
- ^ Münster, A. (1970), p. 48: «mass is an adiabatically inhibited variable.»
- ^ Münster, A. (1970). Classical Thermodynamics. Translated by Halberstadt, E. S. London: Wiley–Interscience. p. 45. ISBN 0-471-62430-6.
- ^ Knight, Jasper (31 January 2022). «Snowfall in the Sahara desert: an unusual weather phenomenon». The Conversation. Retrieved 3 March 2022.
- ^ Kavanagh, J. L.; Sparks, R. S. J. (2009). «Temperature changes in ascending kimberlite magmas». Earth and Planetary Science Letters. Elsevier. 286 (3–4): 404–413. Bibcode:2009E&PSL.286..404K. doi:10.1016/j.epsl.2009.07.011. Retrieved 18 February 2012.
- ^ Turcotte and Schubert (2002). Geodynamics. Cambridge: Cambridge University Press. pp. 185. ISBN 0-521-66624-4.
- ^ Adiabatic Processes.
- ^ Atkins, Peter; de Paula, Giulio (2006). Atkins’ Physical Chemistry (8th ed.). W.H.Freeman. p. 48. ISBN 0-7167-8759-8.
- ^ a b Rankine, W.J.McQ. (1866). On the theory of explosive gas engines, The Engineer, July 27, 1866; at page 467 of the reprint in Miscellaneous Scientific Papers, edited by W.J. Millar, 1881, Charles Griffin, London.
- ^ Partington, J. R. (1949), An Advanced Treatise on Physical Chemistry., vol. 1, Fundamental Principles. The Properties of Gases, London: Longmans, Green and Co., p. 122
- ^
Maxwell, J. C. (1871), Theory of Heat (first ed.), London: Longmans, Green and Co., p. 129 - ^ Liddell, H.G., Scott, R. (1940). A Greek-English Lexicon, Clarendon Press, Oxford UK.
- ^ Rankine, W.J.McQ. (1854). «On the geometrical representation of the expansive action of heat, and theory of thermodynamic engines». Proc. R. Soc. 144: 115–175. Miscellaneous Scientific Papers p. 339
- ^ Rankine, W.J.McQ. (1854). «On the geometrical representation of the expansive action of heat, and theory of thermodynamic engines». Proc. R. Soc. 144: 115–175. Miscellaneous Scientific Papers p. 341.
- ^ Bryan, G. H. (1907). Thermodynamics. An Introductory Treatise dealing mainly with First Principles and their Direct Applications. Leipzig: B. G. Teubner.
- ^ Born, M. (1949). «Natural Philosophy of Cause and Chance». London: Oxford University Press.
- ^ a b Bailyn, M. (1994). «Chapter 3». A Survey of Thermodynamics. New York, NY: American Institute of Physics. ISBN 0-88318-797-3.
- ^ Born, M. (1927). «Physical aspects of quantum mechanics». Nature. 119 (2992): 354–357. Bibcode:1927Natur.119..354B. doi:10.1038/119354a0. (Translation by Robert Oppenheimer.)
- ^ Mandal, Anirban; Hunt, Katharine L. C. (2020-03-14). «Variance of the energy of a quantum system in a time-dependent perturbation: Determination by nonadiabatic transition probabilities». The Journal of Chemical Physics. 152 (10): 104110. Bibcode:2020JChPh.152j4110M. doi:10.1063/1.5140009. ISSN 0021-9606. PMID 32171229. S2CID 212731108.
- ^ «diabatic process». American Meteorological Society. Retrieved 24 November 2020.
- General
- Silbey, Robert J.; et al. (2004). Physical chemistry. Hoboken: Wiley. p. 55. ISBN 978-0-471-21504-2.
- Nave, Carl Rod. «Adiabatic Processes». HyperPhysics.
- Thorngren, Dr. Jane R.. «Adiabatic Processes». Daphne – A Palomar College Web Server., 21 July 1995.Archived 2011-05-09 at the Wayback Machine.
External links[edit]
Look up adiabatic in Wiktionary, the free dictionary.
Media related to Adiabatic processes at Wikimedia Commons
- Article in HyperPhysics Encyclopaedia
Адиабатный процесс

4.7
Средняя оценка: 4.7
Всего получено оценок: 149.
4.7
Средняя оценка: 4.7
Всего получено оценок: 149.
Среди различных явлений, происходящих с газами, важную роль играет адиабатный процесс. Он широко используется в технике и часто встречается в Природе. Рассмотрим его суть более подробно.
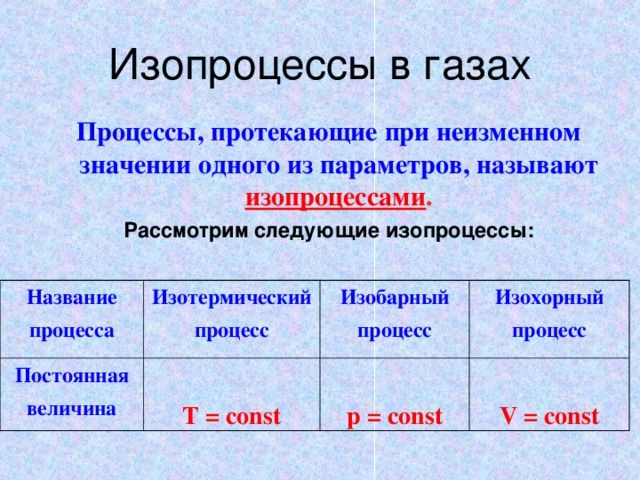
Адиабатный процесс
При изучении законов газовых процессов (изопроцессов) для изменения внутренней энергии газа используется обмен теплом с внешними источниками. Например, в изохорическом процессе, когда объем газа не меняется, увеличение внутренней его энергии возможно за счет внешнего нагрева. Обмен теплом также происходит и в изобарическом и изотермическом процессах.
Однако, состояние газа и его внутренняя энергия могут меняться и без теплового обмена с внешними источниками. Такой процесс, для которого количество подведенного тепла равно нулю ($Q=0$), называется адиабатным.
Для того, чтобы газовый процесс был приближен к адиабатному в реальных условиях, существует два способа (и их комбинация). Во-первых, можно окружить систему толстой теплоизолирующей оболочкой, сильно замедляющей обмен теплом. Во-вторых, процесс можно проводить очень быстро, при этом теплообмен просто не успеет произойти.
На первый взгляд, может показаться, что если к системе не подводится тепло, то она не может совершать работу. Однако, это не так. Согласно Первому Закону термодинамики, изменение внутренней энергии системы равно сумме работы внешних сил и количества тепла переданного системе:
$$ΔU=A+Q$$
А это значит, что в адиабатном процессе совершение работы возможно. Но вся эта работа будет произведена за счет изменения внутренней энергии газа.
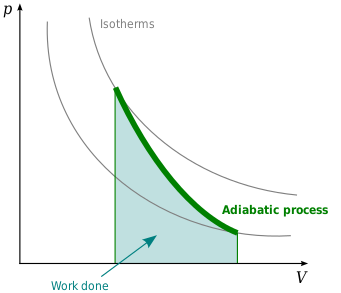
График адиабаты
Характеристикой внутренней энергии газа является его температура. То есть, если в адиабатном процессе производится работа, то это происходит с обязательным изменением температуры. Например, если работа положительна, и внешние силы сжимают газ, то его температура увеличится, газ нагреется.
Отсюда следует, что давление газа при сжатии в адиабатном процессе будет расти быстрее, чем в изотермическом. В адиабатном процессе давление будет повышаться не только за счет уменьшения объема, но и за счет увеличения температуры. То есть, график адиабаты в координатах $p-V$ внешне будет похож на график изотермы, но пройдет более круто.
Можно вывести математические уравнения данных процессов:
- Изотерма: $pV=const$;
- Адиабата: $pV^gamma=const$.
Параметр $gamma$ в формуле адиабатного процесса называется показателем адиабаты. Для реальных газов в нормальных условиях показатели адиабаты несколько больше единицы, и равны:
|
Газ |
Показатель |
|
Пропан |
1.13 |
|
Метан |
1.32 |
|
Воздух |
1.40 |
|
Аргон |
1.67 |
Фактически, изотерму можно представить адиабатой, с показателем адиабаты $gamma=1$.
Адиабатные процессы в Природе и технике
Поскольку при быстром сжатии и расширении газа теплообмен очень невелик, адиабатные процессы широко используются в технике, и играют большую роль в атмосферных явлениях в Природе.
Например, в двигателях внутреннего сгорания горючая смесь после впуска в цилиндр в течение короткого времени сжимается, а затем, после воспламенения смеси в течении короткого времени расширяется. Таким образом, такты сжатия и рабочего хода в двигателях являются хорошими примерами адиабатного процесса.
Значительный нагрев газа при адиабатном процессе используется в дизельных двигателях. В этих двигателях нет систем для поджигания сжатой топливовоздушной смеси. В дизеле происходит сжатие атмосферного воздуха, сильнее, чем в бензиновом карбюраторном двигателе. А в конце сжатия топливо впрыскивается в цилиндр с помощью специальной форсунки. В этот момент воздух имеет температуру, достаточную для самовоспламенения впрыснутой горючей смеси, температура сгоревшей топливовоздушной смеси резко возрастает, смесь расширяется, толкая поршень и совершая полезную работу.
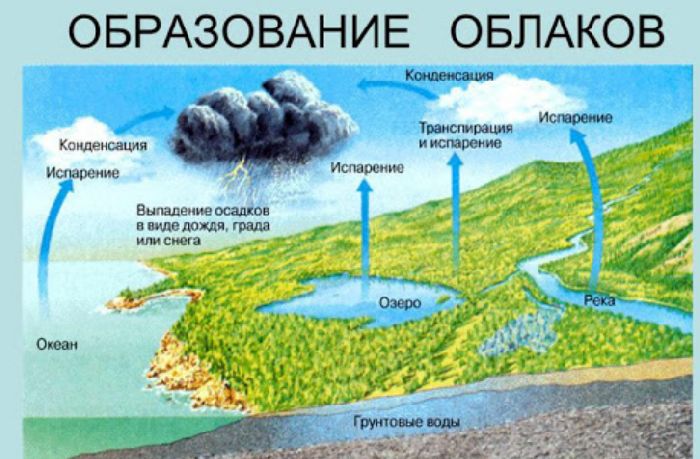
Природные адиабатные процессы играют значительную роль в формировании погоды. Нагретые массы воздуха быстро поднимаются вверх и расширяются. В результате их температура падает ниже точки росы, и влага, содержащаяся в воздухе, конденсируется в облака. Однако, при снижении снова происходит адиабатное сжатие, температура повышается, и облачные капли у нижней границы облаков снова превращаются в пар.
Что мы узнали?
Адиабатный процесс – это газовый процесс, при котором не происходит теплообмена с внешней средой. Работа при адиабатном процессе может быть совершена только за счет изменения внутренней энергии. На графике $p-V$ график адиабаты похож на график изотермы, но пройдет более круто.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 149.
А какая ваша оценка?
Процесс, происходящий без теплообмена с окружающей средой, называется адиабатическим.
Характеристика процесса:
δQ=0δQ = 0.
Применив к адиабатическому процессу первый принцип термодинамики, получим:
δQ+δA=0.δQ+δΑ = 0.
Откуда
δA=−dUδΑ = -dU,
то есть в адиабатическом процессе работа выполняется только благодаря внутренней энергии системы.
Для идеального газа
δA=−СVdt,δΑ=-СVdt,
то есть когда газ выполняет работу против внешних сил в процессе адиабатического расширения, то температура газа снижается. Напротив, в процессе адиабатического сжатия, когда работа выполняется над газом, его температура повышается.
Примеры адиабатических процессов
Очевидно, чтобы исключить теплообмен и осуществить адиабатический процесс, надо было бы термодинамическую систему окружить нетеплопроводной стенкой. В природе таких стенок не существует, но могут создаваться подобные условия, в которых происходят процессы, очень близкие к адиабатическим.
Адиабатические процессы играют важную роль в природе и технике.
То, что в атмосфере верхние слои холоднее от более низких вопреки действию конвекции, а также образование облаков и туманов, можно объяснить, процессами адиабатического расширения воздуха в атмосфере.
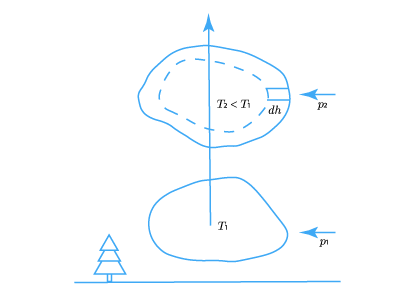
Огромные массы воздуха, нагреваясь у поверхности Земли и поднимаясь вверх, попадают в область все более низких давлений и расширяются:
Этот процесс адиабатический, поскольку из-за плохой теплопроводности воздуха теплообменом можно пренебречь. Выполняя работу расширения против внешнего давления, воздух охлаждается, а водяной пар превращается в насыщенный и конденсируется.
Сгущения и разрежения, возникающие в звуковых волнах в газах — это тоже, по сути, процессы адиабатического сжатия и расширения газа. Поскольку звук имеет большую скорость (в воздухе — 340 м / с), процессы здесь происходят так быстро, что за это короткое время теплообменом можно пренебречь.
Все процессы, происходящие очень быстро, приближаются к адиабатическим.
В таких условиях, в частности, осуществляются адиабатические процессы в некоторых тепловых машинах.
Адиабатическое сжатие воздуха и нагрев его вследствие этого хорошо наблюдаются даже в ручных насосах при накачивании велосипедной камеры.
Уравнение Пуассона
В адиабатическом процессе одновременно изменяются все три параметра газа: V,р,Т,V, р, Т, зависимость между которыми выражает уравнение Клапейрона-Менделеева. Дополнительно для адиабатического процесса подтверждается уравнение Пуассона, которое выражает зависимость между давлением и объемом газа в этом процессе. Чтобы найти его, применим к адиабатическому процессу идеального газа первый принцип термодинамики:
0=CVdT+pdV0={{C}_{V}}dT+pdV
Исключив из этого выражения dTdT по уравнению Клапейрона-Менделеева
pV=RT,pV = RT,
то есть
dT=1R(pdV+Vdp)dT=frac{1}{R}(pdV+Vdp)
получим
CVR(pdV+Vdp)+pdV=0frac{{{C}_{V}}}{R}(pdV+Vdp)+pdV=0
Подставив из уравнения Майера R=CP−CVR = CP-CV, поделим числитель и знаменатель дроби перед скобками на CVCV и обозначим CP/CV−γCP/CV — γ.
После этого получим
1γ−1(pdV+Vdp)+pdV=0frac{1}{gamma -1}(pdV+Vdp)+pdV=0
откуда
Vdp+γpdV=0.Vdp + γpdV = 0.
Если почленно разделить это выражение на произведение pV, то получим
dpp+γdVV=0frac{dp}{p}+gamma frac{dV}{V}=0
Проинтегрировав это уравнение, получим
lnp+γlnV=lnС,lnp + γlnV = lnС,
где СС — постоянная интегрирования.
Если пропотенциировать последнее выражение, то получим уравнение Пуассона
pVγ=const,pVγ = const,
где γγ зависит от природы газа (для воздуха γ=1,42γ = 1,42).
Графическое изображение адиабатического процесса
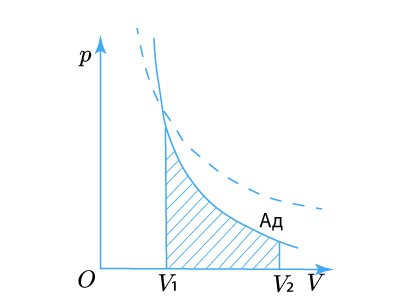
Графически на диаграмме p, V адиабатический процесс изображается кривой, которая называется адиабата:
Поэтому уравнение Пуассона иначе называют уравнением адиабаты. По сравнению с изотермой (пунктир на графике) адиабата является гиперболой высшего порядка, она круче изотермы.
Графически работа газа в адиабатическом процессе определяется площадью подграфика (заштрихованная область на графике) так же, как и в других процессах.
Приведем еще некоторые другие формулы для вычисления работы газа в адиабатическом процессе.
По первому принципу термодинамики для адиабатического процесса идеального газа имеем
dA=−CVdT;dA = -CVdT;
A=CV(T1−T2).A = CV(T1-T2).
Если по уравнению Клайпейрона-Менделеева определить температуру и подставить ее значение в выражение, то получим
A=CVR(p1V1−p2V2)=1γ−1(p1V1−p2V2)A=frac{{{C}_{V}}}{R}({{p}_{1}}{{V}_{1}}-{{p}_{2}}{{V}_{2}})=frac{1}{gamma -1}({{p}_{1}}{{V}_{1}}-{{p}_{2}}{{V}_{2}})
Если проинтегрировать выражение элементарной работы газа, сводя при этом его к одной переменной исключением давления по уравнению Пуассона, то получим
A=∫V1V2pdV=∫V1V2p1V1γdVVγ=p1V1γ−1[1−(V2V1)1−γ]A=intlimits_{{{V}_{1}}}^{{{V}_{2}}}{pdV=}intlimits_{{{V}_{1}}}^{{{V}_{2}}}{frac{{{p}_{1}}{{V}_{1}}^{gamma }dV}{{{V}^{gamma }}}=frac{{{p}_{1}}{{V}_{1}}}{gamma -1}left[ 1-{{left( frac{{{V}_{2}}}{{{V}_{1}}} right)}^{1-gamma }} right]}
Тест по теме «Адиабатический процесс»
Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023