Как найти циклическая частота переменного тока

Период, частота, амплитуда и фаза переменного тока

Период и частота переменного тока

Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.

Период выражают в секундах и обозначают буквой Т.

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

1 мс =0,001сек =10^-3сек.

1 мкс=0,001 мс = 0,000001сек =10^-6сек.

1000 мкс = 1 мс.

Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.

Частота обозначается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 Гц = 10³ Гц = 1 кГц;

1000 000 Гц = 10⁶ Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10⁹ Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2. Радиан.

Тогда,

1рад = 360°/2

Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.

Итак,

?= 6,28*f = 2f

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Переменный электрический ток

Переменный ток (AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

DC — Direct Current — постоянный ток, не меняющий своей величины и направления.

В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.

Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.

Термины AC и DC применимы как для тока, так и для напряжения.

Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:

Период T — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.

Частота f — величина, обратная периоду, равная количеству периодов за одну секунду.

Один период в секунду это один герц (1 Hz). Частота f = 1/T

Циклическая частота ω — угловая частота, равная количеству периодов за 2π секунд.

ω = 2πf = 2π/T

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°

Начальная фаза ψ — величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.

Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.

Мгновенное значение — величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.

i = i(t); u = u(t)

Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:

i = I_ampsin(ωt); u = U_ampsin(ωt)

С учётом начальной фазы:

i = I_ampsin(ωt + ψ); u = U_ampsin(ωt + ψ)

Здесь I_amp и U_amp — амплитудные значения тока и напряжения.

Амплитудное значение — максимальное по модулю мгновенное значение за период.

I_amp = max|i(t)|; U_amp = max|u(t)|

Может быть положительным и отрицательным в зависимости от положения относительно нуля.

Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) — максимальное отклонение от нулевого значения.

Среднее значение (avg) — определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.

Средневыпрямленное значение — среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой I_amp (U_amp)
среднеквадратичное значение определится из расчёта:

Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов.
Является объективным количественным показателем для любой формы тока.

В активной нагрузке переменный ток совершает такую же работу за время периода,
что и равный по величине его среднеквадратичному значению постоянный ток.

Коэффициент амплитуды и коэффициент формы

Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой
амплитудное, среднеквадратичное и средневыпрямленное значения.

Коэффициент амплитуды — отношение амплитудного значения к среднеквадратичному.

Для синусоидального тока и напряжения коэффициент амплитуды K_A = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды K_A = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды K_A = 1

Коэффициент формы — отношение среднеквадратичного значения к средневыпрямленному.

Для переменного синусоидального тока или напряжения коэффициент формы K_Ф ≈ 1.111
Для тока и напряжения треугольной или пилообразной формы K_Ф ≈ 1.155
Для переменного тока и напряжения прямоугольной формы K_Ф = 1

Замечания и предложения принимаются и приветствуются!

Источник

Период и частота переменного тока

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.

Период выражают в секундах и обозначают буквой Т.

1 мс =0,001сек =10-3сек.

1 мкс=0,001 мс = 0,000001сек =10-6сек.

1000 мкс = 1 мс.

Частота обозначается буквой f и выражается в периодах в секунду или в герцах.

1000 Гц = 103 Гц = 1 кГц;

1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Что такое переменное напряжение?

Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.

Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид

где Т – период.

Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда

Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже

Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.

Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением

где Um – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла),

φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.

Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.

Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.

Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда

В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.

Угловая (циклическая) частота переменного тока.

Рисунок 2. Радиан.

Тогда,

1рад = 360°/2

Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.

Итак,

?= 6,28*f = 2f

Токи высокой частоты

ТВЧ – такова их аббревиатура, используются для плавки металлов, закалки поверхности металлических изделий. ТВЧ – это токи, имеющие частоту более 10 кГц. В индукционных печах используют ТВЧ, помещая проводник внутрь обмотки, через которую пропускают ТВЧ. Под их воздействием возникающие в проводнике вихревые токи разогревают его. Регулируя силу ТВЧ, контролируют температуру и скорость нагрева.

Интересно. Расплавляемый металл может быть подвешен в вакууме с помощью магнитного поля. Для него не нужен тигель (специальный ковш для нагрева). Так получают очень чистые вещества.

Плюсы использования ТВЧ в разных случаях:

быстрый нагрев при ковке и прокате металла;
оптимальный температурный режим для пайки или сварки деталей;
расплав даже очень тугоплавких сплавов;
приготовление пищи в микроволновых печах;
дарсонвализация в медицине.

Получают ТВЧ с помощью установок, включающих в свой состав колебательный контур, или электромашинных генераторов. У статора и ротора генераторов на сторонах, обращённых друг другу, нанесены зубцы. Их взаимное движение порождает пульсацию магнитного поля. Частота на выходе тем больше, чем больше произведение числа зубцов ротора на частоту его вращения.

Фаза переменного тока.

Рисунок 3. Фаза переменного тока.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Взаимосвязь частоты и работы электрооборудования

Частота тока – это один из параметров электроэнергии, который влияет на стабильную работу электроустановок и оборудования. При поставке энергии потребителю этот параметр строго контролируется, так же, как и напряжение.

Нить взаимосвязи выражается формулой номинального количества оборотов в минуту для вращающихся машин. КПД (коэффициент полезного действия) заложен в самой конструкции агрегатов. Он максимален при:

n = 60f/p,

где:

n – количество об./мин.;
f – частота;
p – количество пар полюсов.

Количество оборотов турбины генераторов напрямую связано с частотой вырабатываемого переменного тока, полученная частота отвечает за оптимальный режим вращения электродвигателя потребителя. При снижении частоты в сети обороты машины снижаются автоматически. Происходит перегрузка на валу, и страдает двигатель.

В то же время технологическая линия, в которую он передаёт энергию вращения, также терпит изменения в работе:

изменяется скорость движения конвейера, что влечёт за собой сбой технологического процесса и брак в итоге;
снижаются мощность и частота вращения насосов, вентиляторов, что приводит к нестабильной работе систем, в которых они установлены;
снижение частоты в энергосистеме на 1% приводит к падению общей мощности на нагрузке до 2%.

Для контроля этого важного электрического параметра применяют частотомеры.

Внимание! Снижение частоты на 10-15% вызывает падение производительности механизмов даже на самой электростанции до нуля. При частоте тока в сети 50 Гц (критической величиной являются 45 Гц) происходит лавинный спад.

Как можно получить переменный электрический ток дома

Предположим, что мы имеем некоторую конструкцию, которая способна проводить переменный электрический ток. Что будет, если она попадет под влияние силового поля?

Если следовать формулам, которые мы привели выше, при вращении через данную конструкцию будет протекать переменный ток определённой напряженности.

Если конструкция будет оборачиваться равномерно, то на ее концах образуется цепь переменного электротока. Она будет иметь форму синусоиды.

Весь этот процесс объясняется тем, что через конструкцию в разных ее положениях проходит большое число различных силовых потоков.

Если конструкция вращается, то значение электродвижущей силы не будет распределяться равномерно, а будет коррелировать от положения осей конструкции.

Во время получения оборачиваемости токопроводящей конструкции от количества оборотов за определенное время будет зависеть, как частота переменного электротока, так и значение движущей силы на концах изделия.

Для того, чтобы движущая сила достигла некоторого значения при стабильной частоте, на проводнике добавляют количество намоток. Из-за этого проводимая конструкция превращается в катушку.

В промышленности цепь переменного электротока образовывается по такому же принципу.Сейчас можно встретить множество электрических станций, которые применяют генераторы с таким электрическим током.

Чаще всего применяют синхронные движки, которые удобно регулировать по частоте и величине электродвижущей силы переменного тока. Кроме этого, они устойчивы к вспышкам перегрузок в электрической сети.

На электрических станциях широкую популярность приобрели генераторы из трех фаз.

Этот вариант был выбран с точки зрения экономичности и технических характеристик, которые необходимы для получения движущегося силового поля.

А без него не будет работать ни один электрический двигатель, которые и лежат в основе работы любого электрического производства в нашей стране.

Подвижную часть любого двигателя (ротор)приводят в действие определенные силы. Количество полюсов может быть совершенно разным, при этом.

Например, если движущаяся часть оборачивается со скоростью 3000 оборотов в минуту, то, чтобы допиться величины переменного электротока с частотой около 50 Гц, необходим генератор с двойной полярностью.

Если же количество оборот сокращается в два раза, число полюсов возрастает с обратной пропорциональностью.

На движимой части двигателя (роторе) расположена намотка возбуждения, по которой поступает электроток от генератора-побудителя. Ток может поступать и от полупроводникового побудителя при помощи механизма со специальными щетками.

В отличие от коллекторных двигателей, щетки находятся на кольцах. Это обеспечивает изменение силового поля намоток по величине – во время регулирования электротока побудителя. При этом силовое поле катушки остается неизменным по знаку и направлению.

Исходя из этого принципа работы, выбираются предпочтительные условия для поддержания функционирования генератора с переменным электрическим током.

Как мы видим, переменный электроток для масштабных производств образовывается при помощи явления электромагнитной индукции.

Пример рассмотрен на основе генераторов с тремя фазами.В домашних условиях можно также применять и генераторы с одной фазой.

Для ремонтных работ чаще всего используют трехфазные механизмы. Это объясняется тем, что основные строительные приборы питаются от трехфазной сети.Это, например, бетономешалки, циркулярные пилы, некоторые модели сварочных приборов.

Обращаем ваше внимание, что для получения электротока подходят только синхронные генераторы. Асинхронные двигатели – не выдерживают большой нагрузки. Их чаще всего покупают для получения электрического обеспечения дач или коттеджей.

Источник

Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.

Определение

Переменный ток — вынужденные электромагнитные колебания.

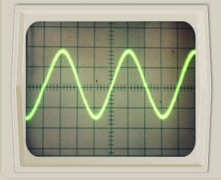
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:

Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.

Определение

Частота переменного тока — это количество колебаний за 1 с.

Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.

Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.

Внимание!

При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙10⁸ м/с).

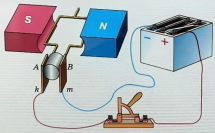
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).

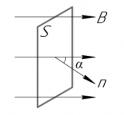
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.

Численно магнитный поток определяется формулой:

Φ=BScosα

При равномерном вращении рамки угол α увеличивается пропорционально времени:

α=2πnt

где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:

Φ=BScos2πnt

Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:

ω=2πn

Следовательно:

Φ=BScosωt

Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:

e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt

εmax — амплитуда ЭДС индукции, равная:

εmax=BSω

Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:

u=Umaxsinωt

u=Umaxcosωt

где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).

Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:

i=Imaxsin(ωt+φс)

где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.

u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).

Активное сопротивление в цепи переменного тока

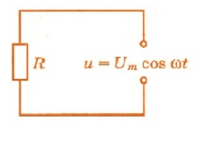
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).

Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.

Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:

u=Umaxcosωt

Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:

i=uR=UmaxcosωtR=Imaxcosωt

В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:

Imax=UmaxR

Мощность в цепи с резистором

В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.

Определение

Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.

Мощность постоянного тока определяется формулой:

P=I2R

Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:

p=i2R

Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:

p=(Imaxcosωt)2R

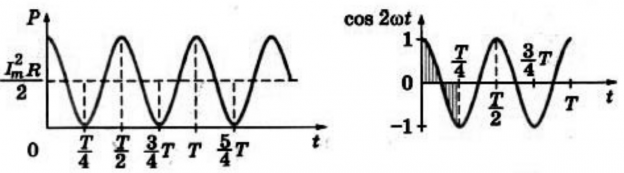
Вспомним из курса математики:

cos2α=1+cos2α2

Отсюда:

p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt

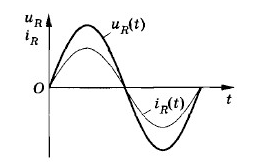
График зависимости мгновенной мощности от времени:

На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.

Средняя мощность −p равна:

−p=I2maxR2=−i2R

Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.

p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)

Действующие значения силы тока и напряжения

Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:

−i2=I2max2

Определение

Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.

I=√−i2=Imax√2

Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.

Аналогично определяется действующее значение напряжения U:

U=√−u2=Umax√2

Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:

P=I2R=UI

Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.

P=I2R

I=Imax√2

P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠

Задание EF22720

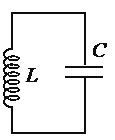
В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону U_C = U₀cos ωt, где U₀ = 5 В, ω = 1000π с^–1. Определите период колебаний напряжения на конденсаторе.

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу Томсона.

3.Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.

• Амплитуда напряжения: U0=5 В.

• Циклическая частота колебаний: ω = 1000π с^–1.

Запишем формулу Томсона:

T=2πω=2π1000π=21000=0,002 (с)

Ответ: 0,002

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18735

В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Описать, что происходит в момент замыкания и размыкания цепи.

3.Выполнить решение задачи в общем виде.

4.Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

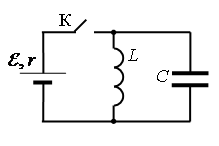
• ЭДС источника тока: ε=5 В.

• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.

• Сопротивление ЭДС источника тока: r = 2 Ом.

• Индуктивность катушки: L = 1 мГн.

1 мГн = 10^–3Гн

Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:

I0=εr

Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.

После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:

u=−UCmaxsinωt

Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.

Циклическую частоту выразим из формулы Томсона:

ω=2πT=1√LC

Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:

W=Li22+Cu22=CU2Cmax2=LI202

Выразим максимальное напряжение на конденсаторе:

CU2Cmax=LI20

UCmax=I0√LC

Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:

UCmax=ε=I0r=I0√LC

Отсюда:

√LC=r

C=Lr2

Период колебаний в контуре определим через формулу Томсона:

T=2π√LC=2π√LLr2=2πLr

Вспомним зависимость напряжения от времени:

u=−UCmaxsinωt

Подставим известные данные для искомого момента времени:

5=−5sinωt

Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:

t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)

Ответ: 7,85

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18116

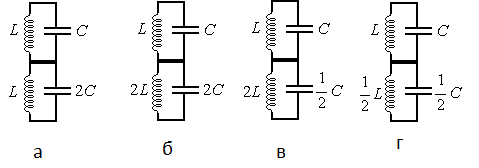
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?

Алгоритм решения

Выделить цель эксперимента.
Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
Выбрать верную пару контуров

Решение

Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18656

На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.

Алгоритм решения

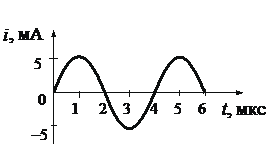
1.Записать исходные данные (определить по графику начальный период колебаний).

2.Перевести единицы измерения величин в СИ.

3.Записать формулу Томсона.

4.Выполнить решение в общем виде.

5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.

Решение

Запишем исходные данные:

• Период колебаний (определяем по графику): T = 4 мкс.

• Емкость конденсатора в первом опыте: C₁ = 4C.

• Емкость конденсатора во втором опыте: C₂ = C.

4 мкс = 4∙10^–6 с

Запишем формулу Томсона:

T=2π√LC

Применим формулу для обоих опытов и получим:

T1=2π√L4C=4π√LC

T2=2π√LC

Поделим первый период на второй:

T1T2=4π√LC2π√LC=2

Отсюда:

T2=T12=4·10−62=2·10−6 (с)=2 (мкс)

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 5.6k

Источник

Как определить частоту переменного тока

Содержание

1 Что такое частота
2 Как определяется
- 2.1 Измерение частоты
- 2.2 Расчёт частоты тока
3 Заключение
4 Видео по теме

В силу различных преимуществ большинство энергетических систем — от общегосударственных до бытовых, функционируют на переменном токе. Однако мало кто считается с тем, что кроме параметров напряжения и тока системы, важную роль играет также частота тока. Например, в функционале популярных мультитестеров измерение частоты переменного тока отсутствует. Между тем значения этой величины, которые выходят за требуемые пределы, грозят тяжёлыми последствиями. Мгновенно происходит разбалансированность системы энергоснабжения с неминуемыми катастрофическими последствиями для целых регионов.

Графическое отображение переменного тока

Что такое частота

Производство электроэнергии в подавляющем большинстве ситуаций называют контролируемым. Эту работу проделывают генераторы, преобразующие механическую энергию ротора турбины в электрическую. Как показано на схеме, на поверхности ротора имеется обмотка из медной проволоки, поэтому он представляет собой непрерывно вращающийся электромагнит.

Схематическое изображение генератора

Во время вращения ротора, созданное вокруг него магнитное поле, наводит электрический ток. Его направление периодически изменяется на противоположное, поскольку месторасположение полюсов электромагнита чередуется после каждого оборота ротора. Соответственно, ток тоже меняет своё направление два раза за цикл вращения.

Следствием и мерой скорости этих изменений является частота, которая измеряется количеством изменений месторасположения полюсов в секунду. Единица частоты получила наименование герц и обозначается двумя буквами — Гц. Таким образом, можно сказать, что генератор, который снабжён парой магнитных полюсов, вращающихся с угловой скоростью 3000 мин^-1, будет производить ток частотой 50 Гц.

Мощность переменного тока изменяется по синусоидальному закону с чередованием положительных и отрицательных полюсов. При переходе каждого цикла из положительной области в отрицательную происходит соответствующее перемещение электронов. В конечном счете, эти циклы создают электрический нагрев или рассеивание мощности. Независимо от направления движения тока (т. е., положительного или отрицательного), если силы тока (напряжения) достаточно для удовлетворения требований электрического устройства, оно будет работать.

Синусоида переменного тока

Таким образом, количество полных циклов за секунду, когда переменный ток переходит от положительного полюса к отрицательному, называется частотой, а сам временной отрезок называется периодом. С точки зрения электрического тока частотой принято считать количество повторений синусоиды, а другими словами — это полное колебание, состоящее из положительной и отрицательной составляющих. Следовательно, частота и период связаны между собой обратно пропорциональной зависимостью:

Определение частоты

Частота и период переменного тока варьируются в зависимости от страны, причём не обязательно привязываются к местному стандарту напряжения. Например, в США, Канаде и других странах со стандартным линейным напряжением 110…120 В эталоном частоты является 60 Гц. В большинстве стран, где значения переменного напряжения равняются 220…240 В (в том числе и в нашей стране), за стандартную частоту принято 50 Гц, однако Южная Корея, Филиппины и многие страны Карибского бассейна используют 220…240 В с частотой 60 Гц. А есть ещё и Япония, где напряжение в сети достигает 100 В, но стандартная частота переменного тока в разных районах составляет 50 и 60 Гц.

Большинство электронных устройств могут работать, потребляя переменный ток, если его частота 50 или 60 Гц. Но, для электроприборов, использующих довольно мощные приводы, рассчитанные на конкретную частоту (холодильники, морозильники, стиральные и сушильные машины), разница в 10 Гц уже значительна. В первую очередь это касается устройств, включающихся периодически. Их электромоторам приходится вращаться то быстрее, то медленнее, что отрицательно сказывается на их долговечности. В таких случаях необходимо использовать преобразователи частоты или трансформаторы напряжения.

Внешний вид преобразователя частоты

Как определяется

Существует два способа установить, чему равна частота и амплитуда переменного тока — применять специальные приборы либо воспользоваться результатами расчётов.

Измерение частоты

Для измерения частоты переменного тока используется принцип механического резонанса. Он является достаточно простым, хотя и не очень точным. Основывается на том факте, что для каждого физического объекта, обладающего упругими свойствами, существует определенное значение частоты, при которой он начинает вибрировать.

Примером подобного устройства является камертон. Если по нему ударить, он будет довольно продолжительное время вибрировать со звуком, зависящим от его длины. Чем длиннее камертон, тем ниже будет резонансная частота и наоборот.

Если представить себе ряд камертонов с постепенно увеличивающимися размерами, установленными на общем основании, то это основание станет вибрировать с частотой измеряемого напряжения или тока. Для этого устройство следует снабдить электромагнитом.

Измерения частоты тока выполняются с помощью набора «камертонов», в качестве которых используются полоски листового металла. Это устройство называется частотомером вибрирующего геркона.

Схема вибрационного частотомера

Используя частотомер, можно наглядно увидеть, как концы всех полосок встряхиваются в зависимости от того, как меняется величина переменного напряжения, приложенного к катушке. Тот из лепестков, который будет ближе всего к резонансной частоте переменного тока, станет вибрировать наиболее интенсивно.

Особой точностью вибрационные частотомеры не отличаются, зато характеризуются простотой своего изготовления. Их применяют в небольших электроремонтных мастерских, а также в быту с целью калибровки частоты вращения двигателя.

Хотя подобный прибор будет иметь малую точность, этого нельзя сказать о самом принципе измерения. Заменив механический резонатор на электрический, можно получить частотомер на основе катушки индуктивности и параллельно включённого конденсатора. Вместе они образуют колебательный контур.

Один или оба компонента этого контура могут быть регулируемыми. В цепь включается измерительный блок, который показывает максимальную амплитуду напряжения на конденсаторе и катушке. Ручки регулировки предварительно откалибровываются, чтобы иметь возможность выставлять резонансную частоту для любого варианта настройки. Частота считывается после настройки устройства на максимальное показание шкалы измерителя.

Схема электрического частотомера

Фактически частотомер реализует схему настраиваемого фильтра, после чего отсчёт показаний происходит как в мостовой схеме (она вначале балансируется для условного нулевого состояния, после чего выполняется отсчёт). До тех пор, пока катушка и/или конденсатор смогут перехватывать достаточное поле магнитного или электрического рассеивания от тестируемой цепи, устройство будет сохранять свою работоспособность.

Метод не требует прямого подключения к цепи, поэтому часто применяется в бытовых условиях. Наиболее точные результаты дают электронные частотомеры.

Внешний вид электронного частотомера

Расчёт частоты тока

Для расчёта требуется знать период или временной отрезок, в течение которого значение переменного тока повторяется и образует одну полную волну. Между периодом и частотой переменного тока имеется зависимость, которую отражает следующая формула:

Определение частоты электротока

Если известно значение циклической частоты ɷ и амплитуда А, то по схожей зависимости можно вычислить силу тока I:

Определение силы электротока

Определение угловой частоты выполняется с помощью такого уравнения:

Формула угловой скорости

Заключение

Учитывая тенденцию к постепенному уменьшению производства электроэнергии с использованием традиционных видов топлива, всё чаще возникают вопросы оптимального управления частотными параметрами систем энергетики. Идеальным выходом их положения считают такой, при котором данные функции будут реализованы вследствие применения более стабильных и доступных форм генерации. К ним стоит отнести атомную энергетику, использование энергии солнца и ветра.

Видео по теме

Источник

Период, частота, амплитуда и фаза переменного тока

Период и частота переменного тока

Амплитуда переменного тока

Угловая (циклическая) частота переменного тока.

Фаза переменного тока.

Похожие материалы:

Добавить комментарий

Переменный электрический ток

Параметры переменного тока и напряжения

Коэффициент амплитуды и коэффициент формы

Период и частота переменного тока

Что такое переменное напряжение?

Угловая (циклическая) частота переменного тока.

Токи высокой частоты

Фаза переменного тока.

Похожие материалы:

Комментарии

Взаимосвязь частоты и работы электрооборудования

Как можно получить переменный электрический ток дома

Активное сопротивление в цепи переменного тока

Мощность в цепи с резистором

Действующие значения силы тока и напряжения

Как определить частоту переменного тока

Что такое частота

Как определяется

Измерение частоты

Расчёт частоты тока

Заключение

Видео по теме

Не пропустите также: