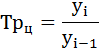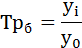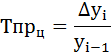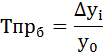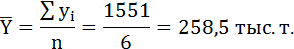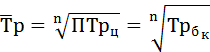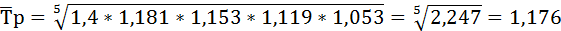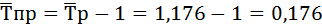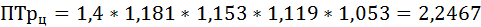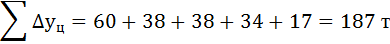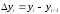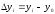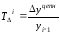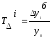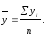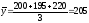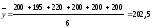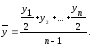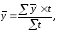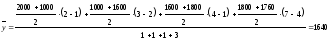Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Добыча нефти характеризуется следующими данными:
| Годы | Добыча нефти, тыс. т |
|---|---|
| 1-ый | 150 |
| 2-ой | 210 |
| 3-ий | 248 |
| 4-ый | 286 |
| 5-ый | 320 |
| 6-ой | 337 |
Произвести анализ ряда динамики по:
1) показателям, характеризующим рост добычи нефти (на цепной и базисной основе): абсолютный прирост, темпы роста и прироста (по годам к базисному году); результаты расчетов изложить в табличной форме;
2) средний уровень и среднегодовой темп ряда динамики;
3) показать взаимосвязь между цепными и базисными показателями.
Сделайте выводы.
Решение:
Абсолютный прирост цепной (Δyц) – это разность между текущим уровнем ряда и предыдущим:
Δyц =yi – yi-1
Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:
Δyц 2-й год = y2 – y1 =
= 210 – 150 = 60 тыс. т.
В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:
Δyц 3-й год = 248 – 210 = 38 тыс. т.
Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.
Абсолютный прирост базисный (Δyб) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:
Δyб = yi – y0
Так как в задании не указано, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год.
Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:
Δyб = 210 – 150 = 60 тыс. т
в 3-ем году базисный абсолютный прирост равен:
Δyб = y3 – y2 = 248 – 150 = 98 тыс. т и т.д (гр. 3 расчётной таблицы).
Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.
Цепной темп роста исчисляют отношением текущего уровня к предыдущему:
(гр. 5 расчётной таблицы);
базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:
(гр. 4 расчётной таблицы).
Темп прироста (Тпр) так же может быть цепной или базисный.
Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:
Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:
Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:
Тпр= Тр – 1;
или как разность между темпами роста и 100%, если темпы роста выражены в процентах:
Тпр= Тр – 100% (гр. 6 и 7 расчётной таблицы).
Расчётная таблица
| Годы | Добыча нефти, тыс. т | Абсолютный прирост базисный, тыс. т | Абсолютный прирост цепной, тыс. т | Темп роста базисный, % | Темп роста цепной, % | Темп прироста базисный, % | Темп прироста цепной, % |
|---|---|---|---|---|---|---|---|
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1-ый | 150 | 0 | — | 100,00 | — | — | — |
| 2-ой | 210 | 60 | 60 | 140,00 | 140,0 | 40,00 | 40,0 |
| 3-ий | 248 | 98 | 38 | 165,33 | 118,1 | 65,33 | 18,1 |
| 4-ый | 286 | 136 | 38 | 190,67 | 115,3 | 90,67 | 15,3 |
| 5-ый | 320 | 170 | 34 | 213,33 | 111,9 | 113,33 | 11,9 |
| 6-ой | 337 | 187 | 17 | 224,67 | 105,3 | 124,67 | 5,3 |
Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.
2) Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:
Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрической
где ПТр – произведение цепных темпов роста (в коэффициентах),
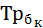
n – число темпов.
Среднегодовой темп прироста ряда динамики:
Добыча нефти ежегодно возрастала в среднем на 17,6%.
3) Между цепными и базисными темпами роста имеется взаимосвязь:
произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.
Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:
Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала на 17,6%.
Показатели ряда динамики
Примеры решения задач
Задача 1
По АО
«Керамик» имеются данные о производстве кирпича за год. Рассчитайте все
недостающие в таблице уровни ряда и цепные показатели анализа динамики.
Рассчитайте средний уровень ряда, средние абсолютный прирост и темп роста.
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели | |||
| абсолютный | темп роста, % | темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | ||||
| Февраль | 100 | ||||
| Март | 80 | ||||
| Апрель | -30 | ||||
| Май | 250 | ||||
| Июнь | -30 | ||||
| Июль | |||||
| Август | 300 | 5,0 | |||
| Сентябрь | 150 | ||||
| Октябрь | 80 | ||||
| Ноябрь | -60 | ||||
| Декабрь | 300 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Формулы цепных показателей динамики
Абсолютный цепной прирост можно
найти по формуле:
-уровень ряда;
-предыдущий
уровень ряда
Цепной темп роста:
Темп прироста:
Абсолютное
содержание 1% прироста:
Расчет недостающих уровней ряда динамики
Исходя из формул, заполним
недостающие показатели:
Февраль:
Март:
Апрель:
Май:
Июнь:
Июль:
Август:
Сентябрь:
Октябрь:
Ноябрь:
Декабрь:
Вычисление цепных показателей динамики
|
Абсолютные приросты цепные: |
Темпы роста цепные: |
|
Темпы прироста цепные: |
Абсолютное содержание 1% прироста: |
Показатели динамики производства кирпича
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели |
|||
| абсолютный |
темп роста, % |
темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | —- | 100 | —- | —— |
| Февраль | 900 | 450 | 200 | 100 | 4.5 |
| Март | 720 | -180 | 80.0 | -20.0 | 9,0 |
| Апрель | 690 | -30 | 95.8 | -4.2 | 7.2 |
| Май | 1725 | 1035 | 250.0 | 150.0 | 6.9 |
| Июнь | 1208 | -517 | 70.0 | -30.0 | 17.25 |
| Июль | 500 | -708 | 41.4 | -58.6 | 12.08 |
| Август | 800 | 300 | 160.0 | 60.0 | 5,0 |
| Сентябрь | 1200 | 400 | 150.0 | 50.0 | 8,0 |
| Октябрь | 2160 | 960 | 180.0 | 80.0 | 12,0 |
| Ноябрь | 2100 | -60 | 97.2 | -2.8 | 21.6 |
| Декабрь | 6300 | 4200 | 300 | 200 | 21,0 |
Расчет средних уровней ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Вывод к задаче
Среднемесячный
показатель производства составил 1562,8 тыс.р. В среднем за месяц показатель
увеличивался на 531,8 тыс.р. или на 27,1% в относительном выражении.
Задача 2
Для
изучения динамики товаропотока рассчитайте:
- Абсолютные и относительные показатели динамики по годам периода (абсолютные
приросты – базисные и цепные; темпы роста – базисные и цепные). - Динамические средние за период в целом – среднегодовой уровень ряда,
среднегодовой абсолютный прирост, среднегодовой темп роста. Объясните их смысл. - Выполните прогнозы уровня ряда на следующий год, используя среднегодовой
абсолютный прирост и среднегодовой темп роста. Сделайте выводы о развитии
изучаемого процесса. - Постройте график динамики изучаемого процесса.
Динамика
экспорта РФ в Португалию, млрд. долл. США
| Годы | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Экспорт | 0.62 | 1.14 | 1.38 | 1.25 | 0.21 | 0.13 | 0.20 |
Решение
1)
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики экспорта 2004-2010 гг.
| Годы |
Экспорт, млрд.долл |
Абсолютные приросты, млрд.долл |
Темпы роста, % |
Темпы прироста, % |
|||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2004 | 0.62 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2005 | 1.14 | 0.52 | 0.52 | 183.9 | 183.9 | 83.9 | 83.9 |
| 2006 | 1.38 | 0.24 | 0.76 | 121.1 | 222.6 | 21.1 | 122.6 |
| 2007 | 1.25 | -0.13 | 0.63 | 90.6 | 201.6 | -9.4 | 101.6 |
| 2008 | 0.21 | -1.04 | -0.41 | 16.8 | 33.9 | -83.2 | -66.1 |
| 2009 | 0.13 | -0.08 | -0.49 | 61.9 | 21.0 | -38.1 | -79.0 |
| 2010 | 0.20 | 0.07 | -0.42 | 153.8 | 32.3 | 53.8 | -67.7 |
2)
Средний уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Таким
образом в среднем за исследуемый период экспорт
составлял 0,704 млрд. долл. в год. В среднем показатель уменьшался на 0,07 млрд.долл. в год или на 17,2% в
относительном выражении.
3)
Прогноз на 2011 год с помощью среднего абсолютного прироста:
Прогноз
на 2011 год с помощью среднегодового темпа роста:
На
2011 год показатель, прогнозируемый с помощью среднего
абсолютного прироста составил 0,13 млрд. долл., а с помощью
среднегодового темпа роста – 0,166 млрд. долл.
4)
График динамики экспорта 2004-2010 гг.
![Определить базисным и цепным способами абсолютный прирост [18.05.13]](https://studrb.ru/files/works_screen/1/44/43.png)
Тема: Определить базисным и цепным способами абсолютный прирост
Раздел: Бесплатные рефераты по статистике
Тип: Задача | Размер: 12.01K | Скачано: 233 | Добавлен 18.05.13 в 22:51 | Рейтинг: 0 | Еще Задачи
Задача
Имеются следующие данные:
|
Год |
Наличие в городе Архангельске цветочных клумб |
|
1990 |
16226 |
|
1991 |
17159 |
|
1992 |
15833 |
|
1993 |
11455 |
|
1994 |
12668 |
|
1995 |
13126 |
|
1996 |
14553 |
|
1997 |
14120 |
|
1998 |
15663 |
|
1999 |
17290 |
|
2000 |
18115 |
|
2001 |
19220 |
Определить базисным и цепным способами:
- Абсолютный прирост;
- Темп роста (%);
- Темп прироста (%);
- Среднегодовой темп роста.
Привести расчёты всех показателей, результаты расчётов свести в таблицу. Сделать выводы, описав в них каждый показатель таблицы в сравнении с предыдущим и базисным показателем. Результатом данной работы является подробный вывод.
Вычисления
- Абсолютный прирост (снижение) (Апр)
- Абсолютный прирост (снижение) «цепным» способом.
Если определять абсолютный прирост (снижение) наличия в городе Архангельске цветочных клумб каждый раз к предыдущему году, то он составит:
В 1991 году: 17159 – 16226 = 933 единицы.
В 1992 году: 15833 – 17159 = — 1326 единиц.
В 1993 году: 11455 – 15833 = — 4378 единиц.
В 1994 году: 12668 – 11455 = 1213 единиц.
В 1995 году: 13126 – 12668 = 458 единицы.
В 1996 году: 14553 – 13126 = 1427 единиц.
В 1997 году: 14120 – 14553 = — 433 единицы.
В 1998 году: 15663 – 14120 = 1543 единиц.
В 1999 году: 17290 – 15663 = 1627 единиц.
В 2000 году: 18115 – 17290 = 825 единиц
В 2001 году: 19220 – 18115 = 1105 единиц.
- Абсолютный прирост (снижение) «базисным» способом.
Если 1990 год принять за базу сравнения, то по отношению к нему абсолютный прирост (снижение) наличия в городе Архангельске цветочных клумб в последующие годы будет составлять:
В 1991 году: 17159– 16226 = 933 единицы.
В 1992 году: 15833 – 16226 = — 393единиц.
В 1993 году: 11455 – 16226 = — 4771 единиц.
В 1994 году: 12668 – 16226 = 3558 единиц.
В 1995 году: 13126 – 16226 = — 3100 единицы.
В 1996 году: 14553 – 16226 = — 1673 единиц.
В 1997 году: 14120 – 16226 = — 2106 единицы.
В 1998 году: 15663 – 16226 = — 563 единиц.
В 1999 году: 17290 – 16226 = 1064 единиц.
В 2000 году: 18115 – 16226 = 1889 единиц
В 2001 году: 19220 – 16226 = 2994 единиц.
- Темп роста (снижения) (Тр)
- Темп роста (снижения) «цепным» способом.
Если определять темп роста (снижения) наличия в городе Архангельске цветочных клумб каждый раз к предыдущему году, то он составит:
В 1991 году: 17159 / 16226 * 100% = 105,7(%)
В 1992 году: 15833 / 17159 * 100% = 92,3 (%)
В 1993 году: 11455 / 15833 * 100% = 72,3 (%)
В 1994 году: 12668 / 11455 * 100% = 110,6 (%)
В 1995 году: 13126 / 12668 * 100% = 103,6 (%)
В 1996 году: 14553 / 13126 * 100% = 110,8 (%)
В 1997 году: 14120 / 14553 * 100% = 97,0 (%)
В 1998 году: 15663 / 14120 * 100% = 110,9 (%)
В 1999 году: 17290 / 15663 * 100% = 110,4 (%)
В 2000 году: 18115 / 17290 * 100% = 104,8 (%)
В 2001 году: 19220 / 18115 * 100% = 106,1 (%)
- Темп роста (снижения) «базисным» способом.
Если 1990 год принять за базу сравнения, то по отношению к нему темп роста (снижения) наличия в городе Архангельске цветочных клумб в последующие годы будет составлять:
В 1991 году: 17159 / 16226 * 100% = 105,7(%)
В 1992 году: 15833 / 16226 * 100% = 97,6 (%)
В 1993 году: 11455 / 16226 * 100% = 70,6 (%)
В 1994 году: 12668 / 16226 * 100% = 78,0 (%)
В 1995 году: 13126 / 16226 * 100% = 80,9 (%)
В 1996 году: 14553 / 16226 * 100% = 89,7 (%)
В 1997 году: 14120 / 16226 * 100% = 87,0 (%)
В 1998 году: 15663 / 16226 * 100% = 96,5 (%)
В 1999 году: 17290 / 16226 * 100% = 106,5 (%)
В 2000 году: 18115 / 16226 * 100% = 111,6 (%)
В 2001 году: 19220 / 16226 * 100% = 118,5 (%)
- Темп прироста (снижения) (Тпр)
- Темп прироста (понижения) «цепным» способом.
Если определять темп прироста (снижения) наличия в городе Архангельске цветочных клумб каждый раз к предыдущему году, то он составит:
В 1991 году: (17159 – 16226) / 16226 * 100% = 5,8(%)
В 1992 году: (15833 – 17159) / 17159 * 100% = — 7,7(%)
В 1993 году: (11455 – 15833) / 15833 * 100% = — 27,7(%)
В 1994 году: (12668 – 11455) / 11455 * 100% = 10,6(%)
В 1995 году: (13126 – 12668) / 12668 * 100% = 3,6(%)
В 1996 году: (14553 – 13126) / 13126 * 100% = 10,9(%)
В 1997 году: (14120– 14553) / 14553 * 100% = -3,0(%)
В 1998 году: (15663 – 14120) / 14120 * 100% = 10,9(%)
В 1999 году: (17290 – 15663) / 15663 * 100% = 10,4(%)
В 2000 году: (18115 – 17290) / 17290 * 100% = 4,8(%)
В 2001 году: (19220 – 18115) / 18115 * 100% = 6,1(%)
- Темп прироста (снижения) «базисным» способом.
Если 1990 год принять за базу сравнения, то по отношению к нему темп прироста (понижения) наличия в городе Архангельске цветочных клумб в последующие годы будет:
В 1991 году: (17159 – 16226) / 16226 * 100% = 5,8(%)
В 1992 году: (15833 – 16226) / 16226 * 100% = — 2,4(%)
В 1993 году: (11455 – 16226) / 16226 * 100% = — 29,4(%)
В 1994 году: (12668 – 16226) / 16226 * 100% = — 21,9(%)
В 1995 году: (13126 – 16226) / 16226 * 100% = — 19,1(%)
В 1996 году: (14553 – 16226) / 16226 * 100% = — 10,3(%)
В 1997 году: (14120– 16226) / 16226 * 100% = — 13,0(%)
В 1998 году: (15663 – 16226) / 16226 * 100% = — 3,5(%)
В 1999 году: (17290 – 16226) / 16226 * 100% = 6,6(%)
В 2000 году: (18115 – 16226) / 16226 * 100% = 11,6(%)
В 2001 году: (19220 – 16226) / 16226 * 100% = 18,5(%)
Среднегодовой темп роста (Тр)
- Среднегодовой темп роста, определяемый «цепным» способом составит:
1,057*0,923*0,723*1,106*1,036*1,108*0,970*1,109*1,104*1,048*1,061 = 1,183
- Среднегодовой темп роста, определяемый «базисным» способом составит:
1,057*0,976*0,706*0,780*0,809*0,897*0,870*0,965*1,065*1,116*1,185 = 0,487
Динамика показателей абсолютного прироста (снижения), темпа роста (снижения), темпа прироста (понижения) наличия в городе Архангельске цветочных клумб в период с 1990 по 2001 год, исчисленных «цепным» и «базисным» способами
|
№ п/п |
Год |
Наличие в городе Архангельске цветочных клумб, единиц |
Абсолютный прирост (снижение) Наличия в городе Архангельске цветочных клумб, единиц |
Темп роста (снижения) Наличия в городе Архангельске цветочных клумб, % |
Темп прироста (понижения) наличия в городе Архангельске цветочных клумб, % |
|||
|
Цепной способ |
Базисный способ |
Цепной способ |
Базисный способ |
Цепной способ |
Базисный способ |
|||
|
1 |
1990 |
16226 |
100,0 |
100,0 |
||||
|
2 |
1991 |
17159 |
933 |
933 |
105,7 |
105,7 |
5,8 |
5,8 |
|
3 |
1992 |
15833 |
— 1326 |
— 393 |
92,3 |
97,6 |
— 7,7 |
— 2,4 |
|
4 |
1993 |
11455 |
— 4378 |
— 4771 |
72,3 |
70,6 |
— 27,7 |
— 29,4 |
|
5 |
1994 |
12668 |
1213 |
3558 |
110,6 |
78,0 |
10,6 |
— 21,9 |
|
6 |
1995 |
13126 |
458 |
— 3100 |
103,6 |
80,9 |
3,6 |
— 19,1 |
|
7 |
1996 |
14553 |
1427 |
— 1673 |
110,8 |
89,7 |
10,9 |
— 10,3 |
|
8 |
1997 |
14120 |
— 433 |
— 2106 |
97,0 |
87,0 |
— 3,0 |
— 13,0 |
|
9 |
1998 |
15663 |
1543 |
— 563 |
110,9 |
96,5 |
10,9 |
— 3,5 |
|
10 |
1999 |
17290 |
1627 |
1064 |
110,4 |
106,5 |
10,4 |
6,6 |
|
11 |
2000 |
18115 |
825 |
1889 |
104,8 |
111,6 |
4,8 |
11,6 |
|
12 |
2001 |
19220 |
1105 |
2994 |
106,1 |
118,5 |
6,1 |
18,5 |
Выводы
В 1990 году наличие в городе Архангельске цветочных клумб составило 16226.
В 1991 году наличие в городе Архангельске цветочных клумб составило 17159 еденицы. Абсолютный прирост наличия в городе Архангельске цветочных клумб по сравнению с 1990 годом составил 933 единицы. Темп роста наличия в городе Архангельске цветочных клумб в 1991 году по сравнению с 1990 годом составил 105,7 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1991 году по сравнению с 1990 годом составил 5,8 процента.
В 1992 году наличие в городе Архангельске цветочных клумб составило 15833 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1991 составил 1326 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1990 годом составило 393 единицы. Темп снижения наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1991 составил 92,3 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1990 годом составило 97,6 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1991 составил 7,7 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1992 году по сравнению с 1990 годом составил 2,4 процента.
В 1993 году наличие в городе Архангельске цветочных клумб составило 11455 единиц. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1992 составило 4378 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1990 годом составил 4771 единиц. Темп снижения наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1992 составил 72,3 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1990 годом составил 70,6 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1992 составил 27,7 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1993 году по сравнению с 1990 годом составил 29,4 процента.
В 1994 году наличия в городе Архангельске цветочных клумб составило 12668 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1993 составило 1213 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1990 годом составил 3558 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1993 составил 110,6 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1990 годом составил 78,0 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1993 составил 10,6 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1994 году по сравнению с 1990 годом составил 21,9 процента.
В 1995 году наличие в городе Архангельске цветочных клумб составило 13126 единиц. Абсолютный рост наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1994 составило 458 единиц. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1990 годом составил 3100 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1994 составил 103,6 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1990 годом составил 80,9 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1994 составил 3,6 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1995 году по сравнению с 1990 годом составил 19,1 процента.
В 1996 году наличие в городе Архангельске цветочных клумб составило 14553 единицы. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1995 составил 1427 единиц. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1990 годом составил 1673 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1995 составил 110,8 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1990 годом составил 89,7 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1995 составил 10,9 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1996 году по сравнению с 1990 годом составил 10,3 процента.
В 1997 году наличие в городе Архангельске цветочных клумб составило 14120 единиц. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1996 составил 433 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1990 годом составил 2106 единиц. Темп снижения наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1996 составил 97,0 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1990 годом составил 87,0 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1996 составил 3,0 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1997 году по сравнению с 1990 годом составил 13,0 процента.
В 1998 году наличие в городе Архангельске цветочных клумб составило 15663 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1997 составил 1543 единицы. Абсолютное снижение наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1990 годом составил 563 единицы. Темп роста наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1997 составил 110,9 процента. Темп снижения наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1990 годом составил 96,5 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1997 составил 10,9 процента. Темп понижения наличия в городе Архангельске цветочных клумб в 1998 году по сравнению с 1990 годом составил 3,5 процента.
В 1999 году наличие в городе Архангельске цветочных клумб составило 17290 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1998 составил 1627 единицы. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1990 годом составил 1064 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1998 составил 110,4 процента. Темп роста наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1990 годом составил 106,5 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1998 составил 10,4 процента. Темп роста наличия в городе Архангельске цветочных клумб в 1999 году по сравнению с 1990 годом составил 6,6 процента.
В 2000 году наличие в городе Архангельске цветочных клумб составило 18115 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1999 составил 825 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1990 годом составил 1889 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1999 составил 104,8 процента. Темп роста наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1990 годом составил 111,6 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1999 составил 4,8 процента. Темп роста наличия в городе Архангельске цветочных клумб в 2000 году по сравнению с 1990 годом составил 11,6 процента.
В 2001 году наличие в городе Архангельске цветочных клумб составило 19220 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 2000 составил 1105 единиц. Абсолютный прирост наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 1990 годом составил 2994 единиц. Темп роста наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 2000 составил 106,1 процента. Темп роста наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 1990 годом составил 118,5 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 2000 составил 6,1 процента. Темп прироста наличия в городе Архангельске цветочных клумб в 2001 году по сравнению с 1990 годом составил 18,5 процента.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Бесплатная оценка
0
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Добавить работу
Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
Похожие работы
- Решение задач по статистике для каждой темы
- Задачи по статистике с расчетами
- Задача с решением по статистике
- Определить цепным и базисным способами
- Контрольные задачи по Статистике
- Задачи по статистике с расчетами (6 задач)
- Задачи по статистике на экзамен с решением
- Расчетно-графическая работа по статистике
- Примеры решения задач по статистике
- Решение задачи по статистике с пояснением
- Типовые экзаменационные задачи по статистике
- Задачи по статистике с решением (5 задач)
- Решение задач по статистике (4 задачи)
- Решение задач по статистике в Excele
- Решение задач по статистике с подробным описанием решения
- Решение задач по статистике (5 задач)
- Решение задач по статистике (2 задачи)
- Решение задач по Статистике
- Задачи к экзаменационным билетам по статистике
- Задачи по статистике с решением и выводом
Темпы
роста − это
отношение уровней ряда одного периода
к другому.
Темпы
роста могут быть вычислены как базисные,
когда все уровни ряда относятся к уровню
одного и того же периода, принятому за
базу:
Тр=
yi/y0
− базисный
темп роста
и
как цепные,- это отношение каждого уровня
ряда к уровню предыдущего периода:
Тр=
yi/yi-1
− цепной темп роста.
Темпы
роста могут быть выражены коэффициентом
или процентом.
Базисные
темпы роста характеризуют непрерывную
линию развития, а цепные − интенсивность
развития в каждом отдельном периоде,
причём произведение цепных темпов равно
темпу базисному. А частное от деления
базисных темпов равно промежуточному
цепному.
8.3 Прирост и темп прироста. Абсолютное значение 1% прироста.
Различают
понятие абсолютного и относительного
прироста. Абсолютный прирост вычисляют
как разность уровней ряда и выражают в
единицах измерения показателей ряда.
Если
из последующего уровня вычитается
предыдущий, то мы имеем цепной абсолютный
прирост:
Если
из каждого уровня вычитается один и тот
же уровень − базисный, то это базисный
абсолютный прирост:
Между
цепными и базисными абсолютными
приростами существует следующая
взаимосвязь: сумма последовательных
цепных приростов равна соответствующему
базисному приросту, характеризующему
общий прирост за весь соответствующий
период времени.
Относительную
оценку
значения абсолютного прироста по
сравнению с первоначальным уровнем
дают показатели темпа прироста (Т∆i).
Его определяют двумя способами:
-
Как
отношение абсолютного прироста (цепного)
к предыдущему уровню:
Это
цепной темп прироста.
Как
отношение базисного абсолютного прироста
к базисному уровню:
Это
базисный темп прироста.
2
Как разницу между темпом роста и единицей,
если темп роста выражен коэффициентом:
Т∆
= Тр-1,
или
Т∆
= Тр—
100, если темп роста выражен в процентах.
Темп
прироста
показывает, на сколько процентов
увеличились размеры явления за изучаемый
период. Если темп прироста имеет знак
минус, то говорят о темпах снижения.
Абсолютное
значение 1-го процента прироста
равно отношению абсолютного прироста
(цепного) к цепному темпу прироста,
выраженному в процентах:
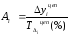
Этот
показатель можно также вычислить как
одну сотую часть предыдущего уровня:
Аi
= 0,01хУi;
8.4 Вычисление средних показателей динамики
Средний
уровень ряда
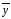
Средняя
хронологическая
− это средняя величина из показателей,
изменяющихся во времени.
В
интервальном ряду с равными интервалами
средний уровень ряда определяется по
формуле простой средней арифметической.
Средний
уровень ряда в интервальном ряду динамики
требует, чтобы было указано, за какой
период времени он вычислен (среднемесячный,
среднегодовой и т.д.).
Пример
1 Имеются
следующие данные о товарообороте,
ден.ед.:
|
Месяц |
январь |
февраль |
март |
|
Товарооборот |
200 |
195 |
220 |
Вычислить среднемесячный товарооборот
за первый квартал.
Т.к. нам дан интервальный ряд с равными
интервалами, применим формулу простой
средней арифметической:
Если
интервальный ряд имеет разные интервалы,
то его вначале нужно привести к ряду с
равными интервалами, а затем можно будет
использовать формулу простой средней
арифметической.
Пример
2 Имеются
следующие данные о товарообороте,
ден.ед.:
|
Месяц |
январь |
февраль |
март |
2-ой |
|
Товарооборот |
200 |
200 |
200 |
600 |
Будем считать, что во втором квартале
товарооборот распределялся по месяцам
равномерно, тогда среднемесячный
товарооборот за 1-ое полугодие:
Так
как показатели моментных рядов не
обладают свойством суммарности, то
среднюю нельзя вычислить, применяя
формулу простой средней арифметической,
в связи с тем, что остатки менялись
непрерывно в течение месяца, а данные
приводятся на определённый день.
Поэтому мы воспользуемся приближенным
методом, основанным на предположении,
что изучаемое явление менялось равномерно
в течение каждого месяца. Чем короче
будет интервал ряда, тем меньше ошибка
будет допущена при использовании этого
допущения.
Получим
формулу :
Эта
формула применяется для вычисления
среднего
уровня в моментных рядах с равными
интервалами.
Пример
3 Имеются
данные об остатках строительных
материалов на начало месяца, ден. ед.:
|
На |
1.01 |
1.02 |
1.03 |
1.04 |
|
Остатки |
2000 |
1000 |
1600 |
1800 |
Определить средний остаток за 1-й квартал.
Решение.
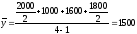
Если
интервалы в моментных рядах не равны,
то средний уровень ряда вычисляется по
формуле:
где
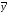
средний уровень в интервалах между
датами,
t
— период времени (интервал ряда)
Пример 4Имеются данные об остатках
сырья и материалов, ден. ед
|
На |
01.01 |
01.02 |
01.03 |
01.04 |
01.07 |
|
Остатки |
2000 |
1000 |
1600 |
1800 |
1760 |
Найти
среднемесячные остатки сырья и материалов
за первое полугодие.
Применяем
формулу:
Средний
абсолютный прирост вычисляется
двумя способами:
1
Как средняя арифметическая простая
годовых (цепных) приростов, т.е.
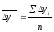
2 Как частное от деления базисного
прироста к числу периодов:
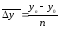
Расчет среднего абсолютного значения
1% приростаза несколько лет производится
по формуле простой средней арифметической:
При
вычислении среднегодового темпа роста
нельзя применять простую среднюю
арифметическую, т.к. сумма годовых темпов
не будет иметь смысла. В этом случае
применяют среднюю геометрическую, т.е.:
где
Трi
− годовые цепные темпы роста;
n
− число темпов.
Поскольку
произведение цепных темпов равно темпу
базисному, то средний темп роста может
быть рассчитан следующим образом:
Error: Reference source not found
При
расчёте по этой формуле не обязательно
знать годовые темпы роста. Величина
среднего темпа будет зависеть от
соотношения начального и конечного
уровня ряда.
Пример
5 Номинальная
заработная плата работников народного
хозяйства Республики Беларусь
характеризуется данными, представленными
в таблице 1.
Таблица
1 – Номинальная заработная плата
работников народного
хозяйства Республике Беларусь
|
Год |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
|
Размер |
558,9 |
1123,0 |
1189,2 |
2250,7 |
3347,5 |
4463,7 |
5582,2 |
7701,1 |
Для
анализа динамики заработной платы
определить:
-
среднегодовой
размер заработной платы за 8 лет; -
ежегодные
и базисные абсолютные приросты, темпы
роста и прироста заработной платы; -
абсолютное
значение 1% прироста; -
среднегодовой
абсолютный прирост; -
среднегодовой
темп роста и среднегодовой темп прироста; -
среднее
значение 1% прироста.
Результаты
представить в таблице, сделать выводы.
Решение
1
Среднегодовой размер заработной платы
определим по формуле средней арифметической
простой
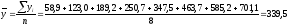
р.
2
Ежегодный (цепной) абсолютный прирост
(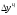
определим по формуле

где


в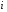
периоде и предшествующем ему.
Например,
для 2005 года
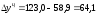
по сравнению с 2004 годом выросла на 64,1
тыс. р.; для 2006 года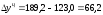
Базисный
абсолютный прирост (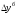
определим по формуле
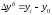
где
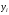
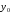
в
и базисном (2004 год) периоде.
Например,
для 2005 года
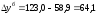
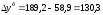
по сравнению с 2004 годом увеличилась на
130,3 тыс. р. и т. д.
Цепной
темп роста определим по формуле
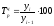
Например,
для 2005 года
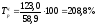
т. е. заработная плата в 2001 году по
сравнению с 2004 годом выросла на 108,8%; для
2006 года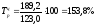
Базисный
темп роста определим по формуле
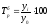
Например,
для 2001 года
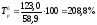
для 2002 года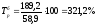
т. е. заработная плата в 2002 году по
сравнению с
2000 годом выросла на 221,2% и т. д.
Темп
прироста найдем по формуле
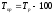
Так,
цепной темп прироста
за
2005 год: 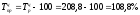
за
2006 год: 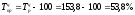
Базисный
темп прироста
за
2005 год: 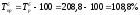
за
2006 год: 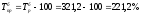
3
Абсолютное значение 1% прироста (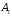
найдем по формуле

Этот
показатель можно также вычислить как
одну сотую часть предыдущего уровня:
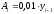
Например,
для 2005 года
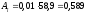
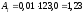
Расчеты
показателей по пунктам 1, 2, 3 оформим в
таблице 2
Таблица
2 – Показатели динамики заработной
платы за 2004-2011 гг.
|
Год |
Размер заработной тыс.р. |
Абсолютный |
Темп |
Темп |
Абсолютное |
|||
|
Цепной |
базисный |
цепной |
базисный |
цепной |
базисный |
|||
|
2004 |
58,9 |
— |
— |
— |
100 |
— |
— |
— |
|
2005 |
123,0 |
64,1 |
64,1 |
208,8 |
208,8 |
108,8 |
108,8 |
0,589 |
|
2006 |
189,2 |
66,2 |
130,3 |
153,8 |
321,2 |
53,8 |
221,2 |
1,23 |
|
2007 |
250,7 |
61,5 |
191,8 |
132,5 |
425,6 |
32,5 |
325,6 |
1,892 |
|
2008 |
347,5 |
96,8 |
288,6 |
138,6 |
590 |
38,6 |
490 |
2,507 |
|
2009 |
463,7 |
116,2 |
404,8 |
133,4 |
787,3 |
33,4 |
687,3 |
3,475 |
|
2010 |
582,2 |
118,5 |
523,3 |
125,6 |
988,5 |
25,6 |
888,5 |
4,637 |
|
2011 |
701,1 |
118,9 |
642,2 |
120,4 |
1190,3 |
20,4 |
1090,3 |
5,822 |
4
Среднегодовой абсолютный прирост
вычисляется двумя способами:
– как
средняя арифметическая простая годовых
(цепных) приростов, т.е.:
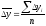
– как
частное от деления базисного прироста
к числу периодов
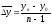
Так
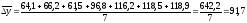
р.
или
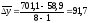
5
Среднегодовой темп роста найдем по
формуле
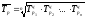
где

или

где

Так
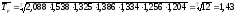
Либо
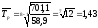
Среднегодовой
темп роста заработной платы за 2004-2011
гг. составляет 143%, следовательно,
среднегодовой прирост составит 43%.
6
Среднее значение 1% прироста рассчитаем
по формуле
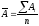
Так
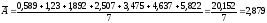
Таким
образом, на протяжении 2004-2011 гг. наблюдается
положительная динамика роста заработной
платы. Так, среднегодовой абсолютный
прирост составил 91,7 тыс. р. или 43%.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #