Как найти центробежную силу инерции - AvtoShod.ru

Пусть
диск равномерно вращается с угловой
скоростью 
(-const)
вокруг вертикальной оси, проходящей
через его центр. На диске, на разных
расстояниях от оси вращения на столбиках
подвешены шарики массой m
(рис. 5.6а). При вращении этой системы
шарики отклоняются от вертикали на
некоторый угол .

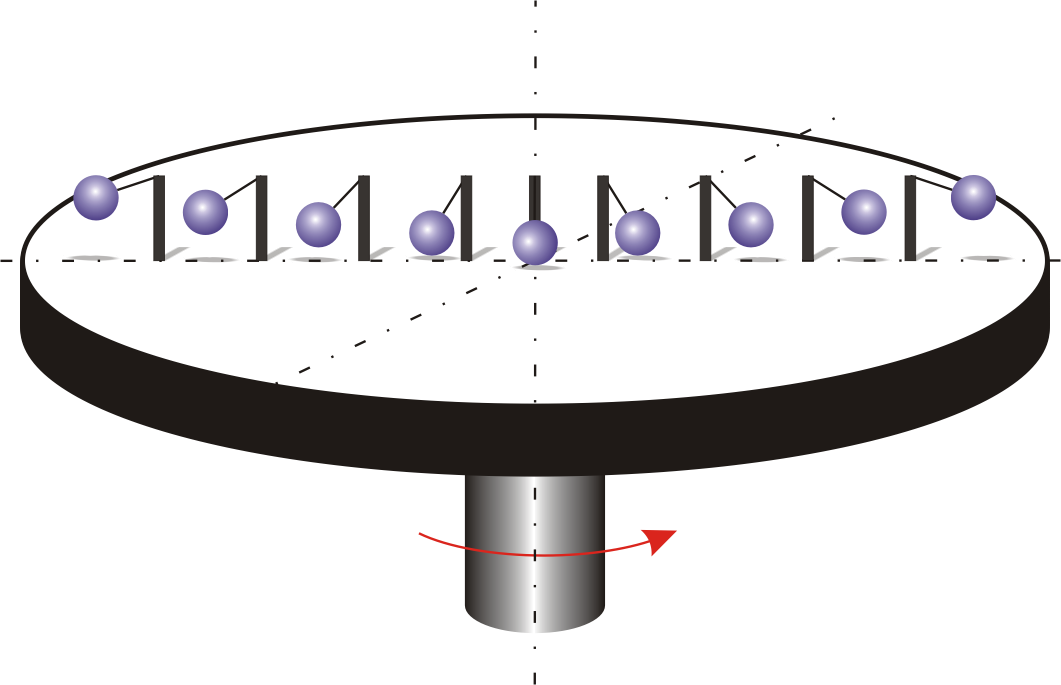
а б

Рис.
5.6. Положение
шариков на вращающемся диске

а
— положение шариков, помещенных на
различных расстояниях от оси вращения,

б
– силы, действующие на отдельный шарик

В
инерциальной системе отсчёта, связанной,
например с помещением, где установлен
диск, шарик равномерно вращается по
окружности радиусом R
(R
— расстояние
от центра вращающегося шарика до оси
вращения.) Следовательно, на него
действует сила, равная

и направленная перпендикулярно оси
вращения диска. Она является равнодействующей
силы тяжести

и силы натяжения нити
:
.
Когда движение шарика установится, то

(рис. 5.6б), откуда

т.е.
углы отклонения нитей маятников будут
тем больше, чем больше расстояние R
от центра шарика до оси вращения диска
и чем больше угловая скорость вращения
.

Относительность
системы отсчёта, связанной с вращающимся
диском, шарик покоится, что возможно,
если сила

уравновешивается равной и противоположно
направленной ей силой
,
которая является ничем иным, как силой
инерции, так как на шарик никакие другие
силы не действуют. Сила
,
называемая центробежной
силой инерции,
направлена по горизонтали от оси вращения
диска и равна

.
(5.12)

Действия
центробежных сил инерции подвергаются,
например, пассажиры в движущемся
транспорте на поворотах, летчики при
выполнении фигур высшего пилотажа,
центробежные силы используются во всех
центробежных механизмах: насосах,
сепараторах и т.д., где они достигают
огромных значений. При проектировании
быстро вращающихся деталей машин
(роторов, винтов самолетов и т.д.)
принимаются специальные меры для
уравновешивания центробежных сил
инерции.

Из
формулы (5.12) следует, что центробежная
сила инерции действует во вращающихся
системах на все тела, удаленные от оси
вращения на конечное расстояние,
независимо от того, покоятся ли они в
этой системе или движутся относительно
нее.

5.6.3. Сила Кориолиса

На
тело, движущееся во вращающейся системе
отсчета также действует сила инерции,
которую называют силой
Кориолиса
по имени открывшего ее французского
физика и инженера Гюстава
Гаспара Кориолиса (1792 – 1843).

Пусть
шарик массой m
движется с постоянной скоростью v
вдоль радиуса равномерно вращающегося
диска (v
– const,

– const,
v).
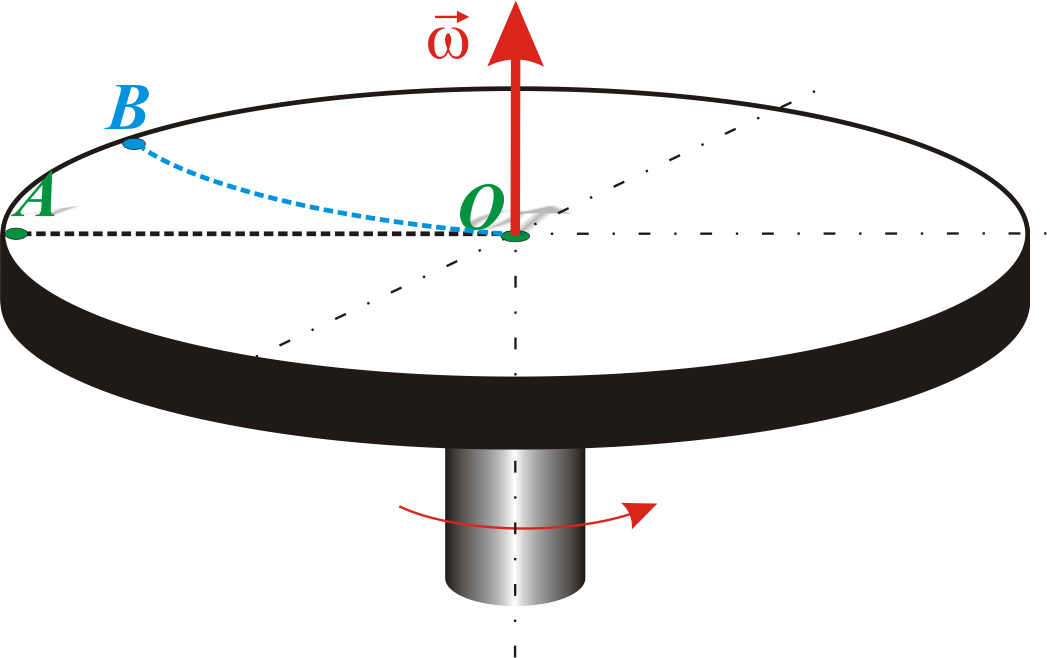
Если диск не вращается, то шарик,
направленный вдоль радиуса, движется
по радиальной прямой и попадает в точку
А (рис. 5.7), если же диск привести во
вращение в направлении, указанном
стрелкой, то шарик катится по кривой
ОВ, причем его скорость относительно
диска изменяет свое направление. Это
возможно лишь тогда, если на шарик
действует сила, перпендикулярная
скорости v.

Рис.
5.7.
Движение шарика на вращающемся диске

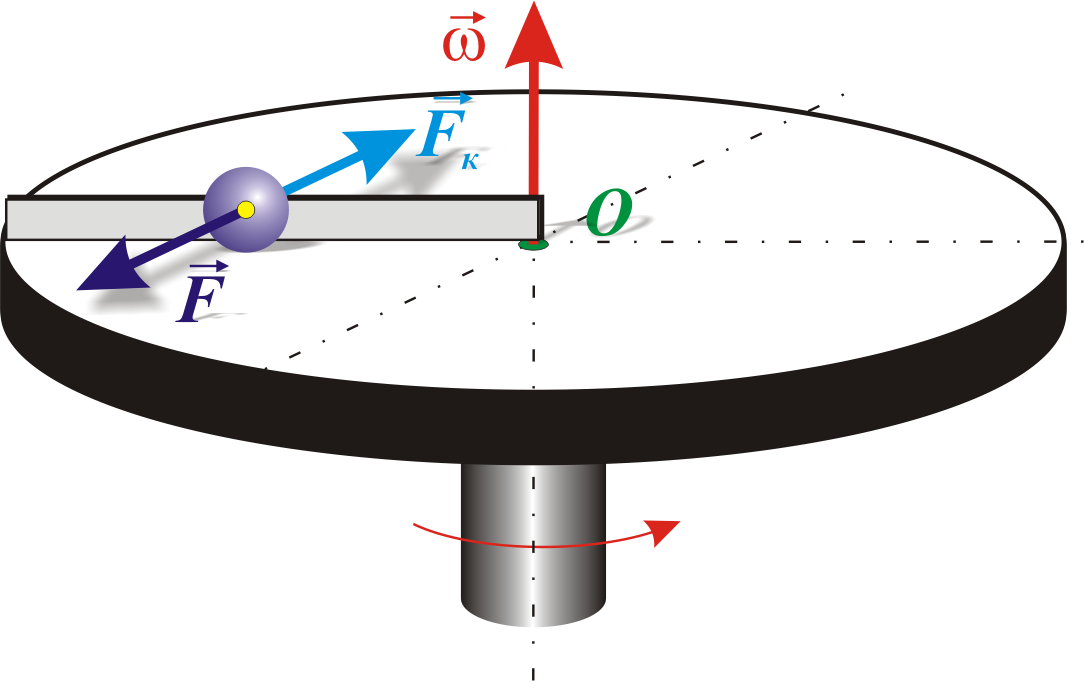
Для
того, чтобы заставить шарик катиться
по вращающемуся диску вдоль радиуса,
используем жестко укрепленный вдоль
радиуса диска стержень, на котором шарик
катится без трения равномерно и
прямолинейно со скоростью v
(рис. 5.8). При отклонении шарика стержень
действует на него с некоторой силой F.
Теперь относительно диска шарик движется
равномерно и прямолинейно, что можно
объяснить тем, сила F
уравновешивается приложенной к шарику
силой инерции F_К,
перпендикулярной скорости v.

Рис.
5.8.
Силы, действующие на шарик,

движущийся
на вращающемся диске

Эта сила и называется
силой Кориолиса:

.
(5.13)

Вектор

перпендикулярен векторам скорости тела

и угловой скорости вращения системы
отсчета

в соответствии с правилом правого винта.

Действием
этой силы объясняется ряд наблюдаемых
на Земле явлений. Например, тело, свободно
падая с вершины башни, движется не по
вертикали, а слегка отклоняется к
востоку. Это отклонение тем больше, чем
больше высота башни, и зависит от
географической широты места проведения
опыта. При прочих равных условиях
величина смещения максимальна на
экваторе и равна нулю на полюсах.
Рассмотрим случай падения на экваторе
с точки зрения неподвижного и подвижного
наблюдателей.

Для
неподвижного наблюдателя (как бы
смотрящего со стороны на Землю вместе
с башней) на свободно падающее тело
действует только сила тяготения к Земле
F.
Эта сила сообщает телу ускорение,
направленное к центру Земли. Следовательно,
сила F
не изменяет численного значения линейной
скорости тела в суточном сращении земли.
Иными словами, в процессе падения тело
сохраняет значение скорости, соответствующее
вершине башни v₁
(рис. 5.9). Линейная же скорость основания
башни v
меньше, чем скорость верхушки башни v₁:

где
R
– радиус Земли,

 – угловая
скорость ее суточного вращения.

Поэтому
точка приземления тела должна быть
несколько смещена к востоку (в направлении
вращения Земли) по сравнению с вершиной
башни.

Рис.
5.9.
Смещение
падающего с высоты h

тела
в направлении вращения Земли

Для
подвижного наблюдателя на тело, помимо
силы F
тяготения к Земле, действует центробежная
F_ц
и кориолисова F_K
cилы
инерции (рис. 5.10). Первые две силы
направлены радиально: F
— к центру
Земли, F_ц
— от центра Земли. Поэтому их равнодействующая
должна была бы вызвать строго вертикальное
падение тела. Однако кориолисова сила
инерции F_K
перпендикулярна
к скорости v
падения тела, поэтому вызывает искривление
его траектории и смещение точки
приземления к востоку.

Рис.
5.10. Силы,
действующие на тело падающее с высоты
h

во
вращающейся системе отсчета

Аналогичным
образом можно объяснить, почему реки,
текущие в меридиональном направлении,
всегда подмывают вполне определенный
берег: правый по течению – для рек
северного полушария Земли и левый –
для рек южного полушария. Например, реки
северного полушария, текущие с севера
на юг, подмывают западный берег.

С
точки зрения неподвижного наблюдателя
численные значения линейных скоростей
точек поверхности Земли в ее суточном
вращении зависят от географической
широты :

где
v₀
– линейная скорость точек экватора.
Поэтому частицы воды, перемещаясь с
севера на юг, должны увеличивать свою
линейную скорость v.
Так как эта скорость направлена с запада
на восток, то ее увеличение может
осуществляться только за счет
взаимодействия частиц воды с западным
берегом реки, который при этом подмыва-ется.

Для
подвижного наблюдателя на частицы воды,
движущиеся с севера на юг с относительной
скоростью v,
действуют кориолисовы силы инерции F_K,
которые направлены с востока на запад
(рис. 5.11). Поэтому частицы воды отклоняются
в том же направлении, подмывая западный
берег реки.

Рис.
5.11.
Направление силы Кориолиса для частиц
воды (для рек)

текущих
с севера на юг

Неинерциальность
земной системы отсчета легко обнаружить
на опыте с помощью маятника Фуко. Фуко
обнаружил, что плоскость качаний маятника
постепенно изменяет свою ориентацию
по отношению к земной системе отсчета,
это в свое время явилось одним из
доказательств вращения Земли. Если бы
не было силы Кориолиса, то плоскость
колебаний качающегося маятника оставалась
бы неизменной. Действие же сил Кориолиса
приводит к вращению плоскости колебания
вокруг вертикального направления.

Для
любого из тел, находящихся в неинерциальной
системе отсчета, силы инерции являются
внешними, следовательно, здесь нет
замкнутых систем. Это означает, что в
неинерциальных системах отсчета не
выполняются законы сохранения импульса,
энергии и момента импульса.

Силы
инерции, так же как и силы тяготения
пропорциональны массам тел. При некоторых
условиях силы инерции и силы тяготения
невозможно различить. Например, движение
тел в равноускоренном лифте происходит
точно так же, как и в неподвижном лифте,
висящем в однородном поле тяжести.
Никакой эксперимент, выполненный внутри
лифта, не может отделить однородное
поле тяготения от однородного поля сил
инерции. Аналогия между силами тяготения
и силами инерции лежит в основе принципа
эквивалентности гравитационных сил и
сил инерции (принципа
эквивалентности Эйнштейна).
Все физические явления в поле тяготения
происходят совершенно так же, как и в
соответствующем поле сил инерции, если
напряженность обоих полей в соответствующих
точках пространства совпадают, а прочие
начальные условия для рассматриваемых
тел одинаковы. Этот принцип является
основой общей теории относительности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Introduction

Centrifugal force is a term used to describe the apparent force that acts on an object moving in a circular path. It is often referred to as a «fictitious» force because it does not have a physical origin, but rather is a result of the object’s motion.

Despite its lack of a physical origin, the centrifugal force plays a crucial role in many aspects of our lives, from amusement park rides to the operation of centrifuges in laboratories. In this article, we will explore the principle behind centrifugal force, the formula used to calculate it, and its applications in various fields.

Principle of Centrifugal Force

The principle of centrifugal force is based on Newton’s laws of motion. According to Newton’s first law, an object in motion will continue to move in a straight line at a constant speed unless acted upon by an external force.

This means that an object moving in a circular path must be acted upon by an external force to maintain its circular motion. This external force is provided by the centripetal force, which acts towards the centre of the circular path.

The centrifugal force is the force that appears to act on an object moving in a circular path, in the opposite direction to the centripetal force.

It is a result of the object’s inertia, which tends to keep the object moving in a straight line rather than in a circular path. The centrifugal force is not a real force, but rather a mathematical construct that describes the motion of the object in the circular path.

Formula for Centrifugal Force

The formula used to calculate the centrifugal force is derived from the principle of centrifugal force. The centripetal force is given by the formula −

$$mathrm{F = mv^2/r}$$

Where F is the force acting on the object, m is the mass of the object, v is the velocity of the object, and r is the radius of the circular path. The centrifugal force is given by the formula −

$$mathrm{Fc = -mv^2/r}$$

Where Fc is the centrifugal force, m is the mass of the object, v is the velocity of the object, and r is the radius of the circular path.

The negative sign in the formula indicates that the centrifugal force acts in the opposite direction to the centripetal force, away from the centre of the circular path.

Applications of Centrifugal Force

The centrifugal force has many applications in various fields, including physics, engineering, and medicine. Here are some examples of its applications −

Centrifuges

Centrifuges are machines that use centrifugal force to separate substances based on their density. They are widely used in laboratories and industries to separate liquids and solids, such as blood samples and DNA strands.

A centrifuge works by spinning a container at high speeds, which generates centrifugal force that separates the substances based on their densities. The heavier substances are forced to the bottom of the container, while the lighter substances rise to the top.

Artificial Gravity

Centrifugal force can be used to simulate gravity in space stations and spacecraft. By rotating a spacecraft around its axis, centrifugal force can be generated that simulates the gravitational force experienced on Earth.

This can help to prevent the negative effects of prolonged weightlessness on the human body, such as muscle and bone loss. The concept of artificial gravity has been explored in science fiction for decades, and it may become a reality in the future as space travel becomes more commonplace.

Amusement Park Rides

Many amusement park rides, such as the Graviton and the Tilt-A-Whirl, use centrifugal force to create thrilling experiences for riders. In the Graviton, riders are strapped to the walls of a spinning cylinder, which generates centrifugal force that pins them to the walls.

In the Tilt-A-Whirl, riders sit in spinning cars that generate centrifugal force as they rotate around a central axis. These rides are popular because they provide a sense of weightlessness and disorientation, which many people find exhilarating.

Washing Machines

Washing machines use centrifugal force to remove excess water from clothes during the spin cycle. As the drum of the washing machine rotates, centrifugal force is generated that forces the water out of the clothes and towards the edges of the drum. This allows the clothes to dry faster and reduces the need for longer drying times.

Centrifugal Pumps

Centrifugal pumps are used to transport fluids in various industries, such as water treatment plants and oil refineries. These pumps work by spinning an impeller at high speeds, which generates centrifugal force that moves the fluid through the pump and towards its destination. Centrifugal pumps are efficient and reliable, and they are widely used in many different applications.

Racing Cars

Centrifugal force plays a crucial role in the performance of racing cars, particularly in corners. As a car goes around a corner, the tires generate a centripetal force that keeps the car on the track. At the same time, the centrifugal force generated by the car’s momentum tends to push it towards the outside of the corner. Skilled drivers use this balance between centripetal and centrifugal forces to maintain control of their cars and achieve faster lap times.

Conclusion

Centrifugal force is a concept that is widely used in many different fields, from amusement park rides to laboratory equipment. Although it is not a real force, it is a mathematical construct that describes the apparent force that acts on an object moving in a circular path.

The formula for centrifugal force is derived from the principle of centrifugal force, which states that an object in a circular path must be acted upon by an external force to maintain its circular motion. Understanding the principle and formula of centrifugal force is essential for many applications, from designing amusement park rides to developing centrifuges for laboratory use.

Источник

Классическая механика

$frac{mathrm{d}(m vec{v})}{mathrm{d}t} = vec{F}$
Второй закон Ньютона

История…

Фундаментальные понятия
Пространство · Время · Масса · Сила Энергия · Импульс

Формулировки
Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби

Разделы
Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика

Учёные
Галилей · Кеплер · Ньютон Эйлер · Лаплас · Д’Аламбер Лагранж · Гамильтон · Коши

См. также: Портал:Физика

Центробе́жная си́ла^[1] — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил.

Зачастую это бывает удобно. Например, когда вращается целиком вся лаборатория, может быть более удобным рассматривать все движения относительно нее, введя лишь дополнительно силы инерции, в том числе центробежную, действующие на все материальные точки, чем учитывать постоянное изменение положения каждой точки относительно инерциальной системы отсчета.

Часто, особенно в технической литературе, во вращающуюся с телом неинерциальную систему отсчёта переходят неявно, и говорят о проявлениях закона инерции как о центробежной силе, действующей со стороны движущегося по круговой траектории тела на вызывающие это вращение связи, и считают её по определению равной по модулю центростремительной силе и всегда направленной в противоположную ей сторону.

Однако в общем случае, когда мгновенный центр поворота тела по дуге окружности, которой аппроксимируется траектория в каждой её точке, может не совпадать с началом вектора силы, вызывающей движение, неверно называть действующую на связь силу силой центробежной. Ведь есть ещё составляющая силы связи, направленная по касательной к траектории, и эта составляющая будет изменять скорость движения тела по ней. Поэтому некоторые физики вообще избегают использовать термин «центробежная сила», как ненужный.^[2]

Содержание

1 Формулы
- 1.1 Вывод
2 Элементарное рассмотрение и мотивировка
- 2.1 Вращение с точки зрения инерциальной системы отсчета
- 2.2 Вращение с точки зрения неинерциальной системы отсчёта. Сила инерции
3 Центробежная сила как реальная сила
4 См. также
5 Примечания
6 Ссылки

Формулы[править | править вики-текст]

Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение этого понятия и может быть в некоторых случаях достаточно легко получено для релятивистской механики).

По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета.

Для материальной точки центробежная сила выражается формулой:

$vec{F}=-m left[ vec omega times left[ vec omega times vec R right] right] = m left( omega^2 vec R - left( vec omega cdot vec R right) vec omega right) ,$

где:

— центробежная сила приложенная к телу,

— масса тела,

— угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),

— радиус-вектор тела во вращающейся системе координат.

Эквивалентное выражение для центробежной силы можно записать как

$vec{F}= m omega^2 vec{R_0}$

если использовать обозначение $vec{R_0}$ для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.

Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело.

Вывод[править | править вики-текст]

Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью $vec {v}_n,$ а сама система движется поступательно с линейной скоростью $vec {v}_0$ в инерциальной системе координат и одновременно вращается с угловой скоростью

Тогда линейная скорость тела в инерциальной системе координат равна:

$vec v= vec {v}_0 + left[ vec omega times vec R right] + vec {v}_n,$

где vec R — радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:

$frac{d}{dt}vec v= frac{d}{dt}vec {v}_0 + frac{d}{dt}left[ vec omega times vec R right] +frac{d}{dt} vec {v}_n.$

Найдём значение каждого слагаемого в инерциальной системе координат:

$frac{d}{dt} vec {v}_0 = vec {a}_0 ,$

$frac{d}{dt} vec {v}_n = vec {a}_n + left[ vecomega times vec {v}_n right],$

$frac{d}{dt} left[ vecomega times vec R right] = left[ vec varepsilon times vec R right] + left[ vecomega times frac{d}{dt} vec R right] = left[ vec varepsilon times vec R right] + left[ vecomega times vec {v}_n right] + left[ vecomega times left[ vecomega times vec R right] right],$ где $vec {a}_n$ — линейное ускорение относительно системы, — угловое ускорение.

Таким образом, получаем:

$frac{d}{dt}vec v = vec a=vec {a}_0 + vec {a}_n + left[ vec varepsilon times vec R right] + 2left[ vec omega times vec {v}_n right]+ left[ vec omega times left[ vec omega times vec R right] right].$

Последнее слагаемое и будет центростремительным ускорением.

Раскрыв двойное векторное произведение и положив vec{R} перпендикулярным оси вращения, получим:

vec a_c = vec omega(vec omegavec R )-vec R vec omega^2=-vec R vec omega^2.

Элементарное рассмотрение и мотивировка[править | править вики-текст]

Вращение с точки зрения инерциальной системы отсчета[править | править вики-текст]

Рассмотрим спицу, вращающуюся вокруг перпендикулярной к ней вертикальной оси с угловой скоростью omega . Вместе со спицей вращается надетый на неё шарик, соединённый с осью пружиной.

Согласно второму закону Ньютона шарик займёт положение равновесия на таком расстоянии от центра диска, на котором сила натяжения пружины $F_mathrm{pr}$ оказывается равной произведению массы шарика на его ускорение^[3] :

$F_mathrm{pr} =-m omega^2 R =-m frac{v^2}{R}$

.^[4]

Связанная со спицей система отсчёта вращается по отношению к инерциальной системе. Относительно системы отсчёта, связанной со спицей, шарик покоится, хотя на него действует сила упругости пружины. Это не противоречит второму закону Ньютона, так как вращающаяся система отсчёта не является инерциальной и соотношение в ней не выполняется.

Вращение с точки зрения неинерциальной системы отсчёта. Сила инерции[править | править вики-текст]

Для практических целей, однако, удобнее считать, что второй закон Ньютона выполняется и с точки зрения вращающейся системы отсчёта, введя для этого формально силу инерции $F_mathrm{cf} = - F_mathrm{pr} = m omega^2 R$ ^[4], действующую на шарик вдоль радиуса от центра диска наряду с реальной силой $F_mathrm{pr}$ .

Силу инерции $F_mathrm{cf}$ , вводимую во вращающейся системе отсчёта, называют центробежной силой. Эта сила действует на тело во вращающейся системе отсчёта, независимо от того, покоится тело в этой системе или движется относительно неё со скоростью ’.

Следует иметь в виду, что для правильного описания движения тел во вращающихся системах отсчёта, кроме центробежной силы следует также вводить силу Кориолиса.

В литературе встречается и совсем другое понимание термина «центробежная сила». Так иногда называют реальную силу, приложенную не к совершающему вращательное движение телу, а действующую со стороны тела на ограничивающие его движение связи. В рассмотренном выше примере так называли бы силу, действующую со стороны шарика на пружину. (См., например, ниже ссылку на БСЭ.)

Центробежная сила как реальная сила[править | править вики-текст]

Центростремительная и центробежная силы при движении тел по круговым траекториям с общей осью вращения

Применяемый не к связям, а, наоборот, к поворачиваемому телу, как объекту своего воздействия, термин «центробежная сила» (букв. сила, приложенная к поворачивающемуся или вращающемуся материальному телу, заставляющая его бежать от мгновенного центра поворота), есть эвфемизм, основанный на ложном толковании первого закона (принципа Ньютона)^[5] в форме:

Всякое тело сопротивляется изменению своего состояния покоя или равномерного прямолинейного движения под действием внешней силы

Или ещё^[6]:

Всякое тело стремится сохранять состояние покоя или равномерного прямолинейного движения до тех пор, пока не подействует внешняя сила.

Отголоском этой традиции и является представление о некоей силе, как о материальном факторе, реализующем это сопротивление или стремление. О существовании такой силы уместно было бы говорить, если бы, например, вопреки действующим силам, движущееся тело сохраняло бы свою скорость, но это не так^[7].

Первый закон Ньютона, нередко называемый принципом и потому допускающим различия в словесной форме его выражения, сводится к утверждению, что природа вещей такова, что скорость движения материальной точки, как по величине, так и по направлению в некоторой системе отсчёта (сам Ньютон связывал её с эфиром, заполняющим всё пространство)^[5], остаётся постоянной, но начинает изменяться тотчас, как возникает на то причина, называемая силой.

Рассматриваемое тело с массой (точнее — инертной массой) приобретает отличающееся от нуля ускорение в тот же момент t = 0 , когда начинает действовать на него сила (Второй закон Ньютона:). Однако для достижения отличающейся от нуля скорости требуется некоторое время в соответствии с определением импульса силы: . Или, иначе, скорость тела не изменяется сама по себе, без причины, но она начинает изменяться тотчас, как на него начинает действовать сила^[8].

Использование термина «центробежная сила» правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле центробежная сила представляет собой один из членов в формулировке третьего закона Ньютона, антагониста центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект — изменение направление движения тела (материальной точки).

Оставаясь в инерциальной системе отсчёта, рассмотрим два небесных тела, например, компонента двойной звезды с массами одного порядка величины ${M_1}$ и ${M_2}$ , находящихся на расстоянии друг от друга. В принятой модели эти звёзды рассматриваются как материальные точки и есть расстояние между их центрами масс. В роли связи между этими телами выступает сила Всемирного тяготения ${F_G}: {G M_1 M_2 /R^2}$ , где — гравитационная постоянная. Это — единственная здесь действующая сила, она вызывает ускоренное движение тел навстречу друг другу.

Однако, в том случае, если каждое из этих тел совершает вращение вокруг общего центра масс с линейными скоростями ${v_1}$ = ${omega}_1$ ${R_1}$ и ${v_2}$ = ${omega_2}$ ${R_2}$ , то подобная динамическая система будет неограниченное время сохранять свою конфигурацию, если угловые скорости вращения этих тел будут равны: ${omega_1}$ = ${omega_2}$ = omega , а расстояния от центра вращения (центра масс) будут соотноситься, как: ${ M_1/M_2 }$ = ${R_2/R_1}$ , причём ${R_2} + {R_1} = R$ , что непосредственно следует из равенства действующих сил: ${F_1} = {M_1}{a_1}$ и ${F_2} = {M_2}{ a_2 }$ , где ускорения равняются соответственно: ${a_1 }$ = ${omega^2}{R_1}$ и ${a_2} = {omega^2}{ R_2}$ ^[9].

Центростремительные силы, вызывающие движение тел по круговым траекториям равны (по модулю): ${F_1}$ = ${F_2}$ $= {F_G}$ . При этом первая из них является центростремительной, а вторая — центробежной и наоборот: каждая из сил в соответствии с Третьим законом является и той, и другой.

Поэтому, строго говоря, использование каждого из обсуждаемых терминов излишне, поскольку они не обозначают никаких новых сил, являясь синонимами единственной силы — силы тяготения. То же самое справедливо и в отношении действия любой из упомянутых выше связей.

Однако, по мере изменения соотношения между рассматриваемыми массами, то есть всё более значительного расхождения в движении обладающих этими массами тел, разница в результатах действия каждой из рассматриваемых тел для наблюдателя становится всё более значительной.

В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел, и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.

См. также[править | править вики-текст]

Сила Кориолиса
Инерция

Примечания[править | править вики-текст]

↑ Вне контекста физики/механики/математики, например, в философии, публицистике или художественной литературе, а также иногда и в разговорной речи, слова центробежная сила могут нередко употребляться просто как обозначение некоего влияния, направленного прочь от некоторого «центра»; в таком употреблении это может быть никак не связано не только с каким-либо вращением, но и с понятием силы, как оно употребляется в физике.
↑ С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука».Главная редакция физико-математической литературы.
↑ Воспользуемся формулой центростремительного ускорения.
↑ ¹ ² Физическая энциклопедия, т.4 — М.:Большая Российская Энциклопедия стр.494 и стр.495
↑ ¹ ² Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
↑ Ключевым в этой формулировке является утверждение о наличии у предметов материального мира неких волевых качеств, что было в начале формирования научных представлений об окружающем мире весьма распространённым способом обобщения результатов наблюдения за явлениями природы и выяснения свойственных ей общих закономерностей . Примером такого анималистического представления о природе являлся бытовавший в натурфилософии принцип: «Природа боится пустоты», от которого пришлось отказаться после эксперимента Торричелли (Торричеллиева пустота)
↑ В связи с этим Максвелл заметил, что, с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, апеллируя к тому, что оно становится сладким не само по себе, а лишь после того, что в него положен сахар.
↑ С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
↑ При этом в каждый малый момент времени каждое из тел будет приближаться к центру на такое расстояние, какое равно разности расстояний между его траекторией и касательной в точке наблюдения. Иными словами, тела падают друг на друга, но всегда промахиваются.

Ссылки[править | править вики-текст]

«Центробежная сила» в Большой советской энциклопедии
Матвеев А. Н. Механика и теория относительности: Учебник для студентов вузов. — 3-е издание. — М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и образование», 2003. — с. 405—406

Источник

Во вращающейся системе отсчета наблюдатель испытывает на себе действие силы, уводящей его от оси вращения.

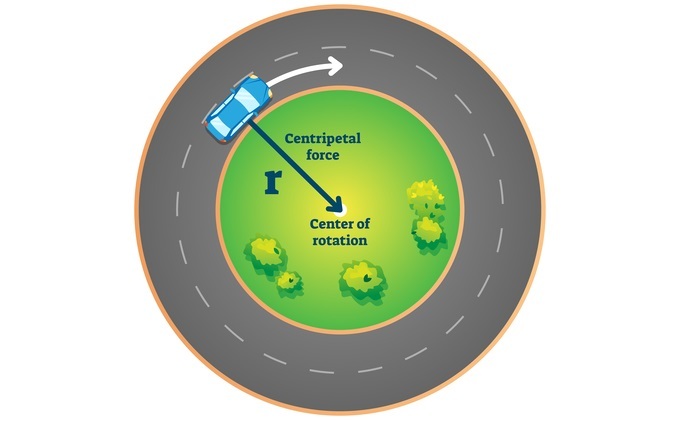
Вам, наверное, доводилось испытывать неприятные ощущения, когда машина, в которой вы едете, входила в крутой вираж. Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.)

Стороннему наблюдателю, однако, всё будет представляться иначе. Когда машина закладывает вираж, наблюдатель сочтет, что вы просто продолжаете прямолинейное движение, как это и делало бы любое тело, на которое не оказывает действия никакая внешняя сила; а автомобиль отклоняется от прямолинейной траектории. Такому наблюдателю покажется, что это не вас прижимает к дверце машины, а, наоборот, дверца машины начинает давить на вас.

Впрочем, никаких противоречий между этими двумя точками зрения нет. В обеих системах отсчета события описываются одинаково и для этого описания используются одни и те же уравнения. Единственным отличием будет интерпретация происходящего внешним и внутренним наблюдателем. В этом смысле центробежная сила напоминает силу Кориолиса (см. Эффект Кориолиса), которая также действует во вращающихся системах отсчета.

Поскольку не все наблюдатели видят действие этой силы, физики часто называют центробежную силу фиктивной силой или псевдосилой. Однако мне кажется, что такая интерпретация может вводить в заблуждение. В конце концов, едва ли можно назвать фиктивной силу, которая ощутимо придавливает вас к дверце автомобиля. Просто всё дело в том, что, продолжая двигаться по инерции, ваше тело стремится сохранить прямолинейное направление движения, в то время как автомобиль от него уклоняется и из-за этого давит на вас.

Чтобы проиллюстрировать эквивалентность двух описаний центробежной силы, давайте немного поупражняемся в математике. Тело, движущееся с постоянной скоростью по окружности, движется с ускорением, поскольку оно всё время меняет направление. Это ускорение равно v²/r, где v — скорость, а r — радиус окружности. Соответственно, наблюдатель, находящийся в движущейся по окружности системе отсчета, будет испытывать центробежную силу, равную mv²/r.

Теперь обобщим сказанное: любое тело, движущееся по криволинейной траектории, — будь то пассажир в машине на вираже, мяч на веревочке, который вы раскручиваете над головой, или Земля на орбите вокруг Солнца — испытывает на себе действие силы, которая обусловлена давлением дверцы автомобиля, натяжением веревки или гравитационным притяжением Солнца. Назовем эту силу F. С точки зрения того, кто находится во вращающейся системе отсчета, тело не движется. Это означает, что внутренняя сила F уравновешивается внешней центробежной силой:

F = mv²/r

Однако с точки зрения наблюдателя, находящегося вне вращающейся системы отсчета, тело (вы, мяч, Земля) движется равноускоренно под воздействием внешней силы. Согласно второму закону механики Ньютона, отношение между силой и ускорением в этом случае F = ma. Подставив в это уравнение формулу ускорения для тела, движущегося по окружности, получим:

F = ma = mv²/r

Но тем самым мы получили в точности уравнение для наблюдателя, находящегося во вращающейся системе отсчета. Значит, оба наблюдателя приходят к идентичным результатам относительно величины действующей силы, хотя и исходят из разных предпосылок.

Это очень важная иллюстрация того, что представляет собою механика как наука. Наблюдатели, находящиеся в различных системах отсчета, могут описывать происходящие явления совершенно по-разному. Однако, сколь бы принципиальными ни были различия в подходах к описанию наблюдаемых ими явлений, уравнения, их описывающие, окажутся идентичными. А это — не что иное, как принцип инвариантности законов природы, лежащий в основе теории относительности.

Источник

5.6.3. Сила Кориолиса

Introduction

Principle of Centrifugal Force

Formula for Centrifugal Force

Applications of Centrifugal Force

Centrifuges

Artificial Gravity

Amusement Park Rides

Washing Machines

Centrifugal Pumps

Racing Cars

Conclusion

Содержание

Формулы[править | править вики-текст]

Вывод[править | править вики-текст]

Элементарное рассмотрение и мотивировка[править | править вики-текст]

Вращение с точки зрения инерциальной системы отсчета[править | править вики-текст]

Вращение с точки зрения неинерциальной системы отсчёта. Сила инерции[править | править вики-текст]

Центробежная сила как реальная сила[править | править вики-текст]

См. также[править | править вики-текст]

Примечания[править | править вики-текст]

Ссылки[править | править вики-текст]

Не пропустите также: