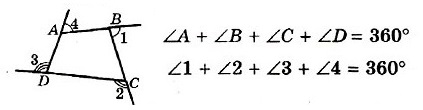Как найти центр выпуклого четырехугольника - AvtoShod.ru

Сообщения без ответов | Активные темы

Автор

Сообщение

Заголовок сообщения: Центр тяжести выпуклого четырехугольника

Добавлено: 15 ноя 2020, 21:06

Light & Truth

Зарегистрирован:
03 апр 2012, 19:13
Сообщений: 13534
Откуда: Москва
Cпасибо сказано: 1290
Спасибо получено:
3615 раз в 3174 сообщениях
Очков репутации: 678

Как чисто геометрически найти центр тяжести выпуклого четырехугольника?
Ни один метод, что в инете, мне не понравился.
Есть ли изящный способ?

Вернуться к началу

Avgust	Заголовок сообщения: Re: Центр тяжести выпуклого четырехугольника Добавлено: 15 ноя 2020, 23:30
	MihailM писал(а): Это самый известный. Поэтому и более-менее годен. Но изящества в нем мало. Все, как в поэзии. Пишут стихи многие, но шедевры появляются раз в сто лет. Думаю, что и в теме этой наверняка существует фантастически красивое построение.
Вернуться к началу

Li6-D	Заголовок сообщения: Re: Центр тяжести выпуклого четырехугольника Добавлено: 16 ноя 2020, 19:12
	Avgust писал(а): Способов много. Более-менее годен такой: Но многоделен, не очень красивый. Искомый центр тяжести четырехугольника ABCD симметричен точке пересечения отрезка S3S4 c диагональю четырехугольника BD относительно середины упомянутого отрезка. Как видите, точки S1 и S2 не нужны.
Вернуться к началу

	За это сообщение пользователю Li6-D «Спасибо» сказали: Avgust

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Центр тяжести в форуме Интегральное исчисление	Marina Mashtakova	0	432	17 дек 2013, 19:16
Интересный центр тяжести в форуме Размышления по поводу и без	Androoj	6	387	03 фев 2018, 11:15
Центр тяжести тела в форуме Интегральное исчисление	Shells	10	834	02 янв 2015, 17:36
Центр тяжести человека в форуме Геометрия	sfanter	4	526	15 июл 2014, 08:01
Центр тяжести отрезка в форуме Начала анализа и Другие разделы школьной математики	Gagarin	46	2271	17 июл 2015, 19:32
Центр тяжести сложной фигуры в форуме Механика	AK47samlab	7	481	17 фев 2016, 20:30
Центр тяжести сложной фигуры в форуме Механика	Shale	7	377	20 мар 2017, 12:03
Центр тяжести плоской, однородной фигуры в форуме Интегральное исчисление	Traktorsvolgi	1	226	09 май 2018, 11:43
Центр тяжести плоской однородной фигуры в форуме Интегральное исчисление	frynzik	1	302	18 май 2015, 22:17
Найти центр тяжести однородного тела в форуме Интегральное исчисление	KenDeR	0	96	22 ноя 2022, 19:12

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

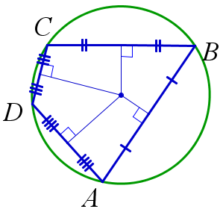
Содержание

Четырехугольник

Мнемоника

http://xn--b1aahabbrbr2bikfzb.xn--p1ai/podgotovka-k-zno/kak-podgotovitsya-k-zno-po-matematike-samostoyatelno/

для запоминания условий, для того чтобы можно было вписать или описать окружность в четырехугольнике, у меня в опорном конспекте (и отложилось, фактически само по себе, в голове): две картинки: дорожный знак «кирпич», на котором написано 180. И вторая картинка, это инопланетянин в квадратном шлеме с плюсами вместо ушей. Ну и чем более абсурдный образ, тем лучше. Я никогда не перепутаю эти условия потому что, например, знак «кирпич» — окружность снаружи, а надпись 180 – означает суму противоположных углов.

Окружность вписанная в четырехугольник

Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.

Наоборот: если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.

Доказательство на рисунке:

Центр вписанной окружности лежит на пересечении биссектрис углов четырехугольника.

Это следствие того факта, что: Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла.
Каждая точка биссектрисы угла равноудалена от его сторон.

Следствия:

Центр вписанной в многоугольник окружности лежит на пересечении биссектрис его углов.
Если в параллелограмм можно вписать окружность, то он является ромбом. Тогда центр окружности лежит на пересечении диагоналей.
Если в прямоугольник можно вписать окружность, то он является квадратом. Тогда центр окружности лежит на пересечении диагоналей.

Почему нельзя вписать окружность?

в отличие от треугольника, далеко не во всякий четырехугольник можно поместить окружность так, чтобы она касалась всех его сторон.

Треугольник всегда является описанным – потому что во всякий треугольник можно вписать окружность. Чем же четырехугольник-то хуже? И вот оказывается, что чем-то, да хуже.

Представь себе, например, длинный прямоугольник. Как вот в него, спрашивается, можно вписать окружность? Конечно, никак. И это лишь один из примеров четырехугольника, в которой НЕЛЬЗЯ вписать окружность.

Задача

Ответ

Окружность, описанная около четырехугольника

Около любого треугольника можно описать окружность (а сумма углов треугольника = 180 градусов). Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника

Если около выпуклого четырехугольника описана окружность, то сумма его противоположных углов равна ∠ϕ+∠γ=180∘.

И наоборот: Если сумма двух противоположных углов выпуклого четырехугольника равна ∠ϕ+∠γ=180∘, то около него можно описать окружность.

Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам.

Около выпуклого четырехугольника описана окружность ⇔ ∠α=∠β.

Площадь вписанного четырехугольника вычисляется по формуле

$$S = sqrt{(p-a)(p-b)(p-c)(p-d)}$$

где a, b, c, d – его стороны, p — полупериметр

Если около параллелограмма описана окружность, то он – прямоугольник
Если около ромба описана окружность, то он – квадрат
Если около трапеции описана окружность, то она равнобедренная.
И наоборот: около равнобедренной (и только равнобедренной) трапеции можно описать окружность

Задача 1

Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Ответ

Задача 2

Стороны AB, BC, CD, AD четырехугольника ABCD стягивают дуги описанной окружности, градусные меры которых равны соответственно 95^∘,49^∘,71^∘,145^∘. Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Решение

Задача 3

решить подготовительную задачу 2 при необходимости

Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB,BC,CD,DA, градусные величины которых относятся соответственно как 4:2:3:6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.

Решение

Центр тяжести

Центр тяжести системы материальных точек — обозначим через $m_k$ — массы точек, $x_k, y_k, z_k$ — координаты точек.

К каждой из точек приложен вектор величины $m_k$, все векторы параллельны и направлены в одну сторону.

Центр этих векторов есть точка с координатами
$$M_x = sum m_k x_k, M_y = sum m_k y_k, M_z = sum m_k z_k$$

Если все точки имеют одинаковую массу, то $M = sum m_k$ — масса всей системы, тогда

$$M_x = M sum x_k, M_y = M sum y_k, M_z = M sum z_k$$

Название «центр тяжести» выражает статическое свойство точки, имеющее местопри весьма ограничительных условиях: рассматриваемое тело должно быть сравнительно небольших размеров и находиться под действием силы тяжести на поверхности Земли. (это потому что вес пропорционален массе $p=mg$)

В математике и физике барицентр или геометрический центр области — это среднее арифметическое положений всех точек фигуры.

Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.

Центр масс (и центр тяжести в постоянном гравитационном поле) является средним арифметическим всех точек с учётом локальной плотности или удельного веса. Если физический объект имеет постоянную плотность, то его центр масс совпадает с барицентром фигуры той же формы.

Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.

Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильный многоугольник, правильный многогранник, цилиндр, прямоугольник, ромб, окружность, сфера, эллипс, эллипсоид, суперэллипс, суперэллипсоид, и т.д.) можно найти исходя исключительно из этого принципа.

Список центроидов — Википедия

В частности, барицентром параллелограмма является пересечение диагоналей. Вообще говоря, это неверно для других четырёхугольников.

Распределительное свойство центров тяжести

Если разделить систему материальных точек S на дне части S’ и S«, то ее центр тяжести есть в то же время центр тяжести двух масс М’ и М» систем S’ и S«, помещенных соответственно в центрах тяжести этих двух систем.

Центр тяжести четырехугольника

Центр тяжести площади треугольника лежит на любой его медиане на расстоянии двух третей ее длины от вершины.
Также он лежит на прямой Эйлера треугольника.
Центр масс сторон треугольника совпадает с центром вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера.

(1)

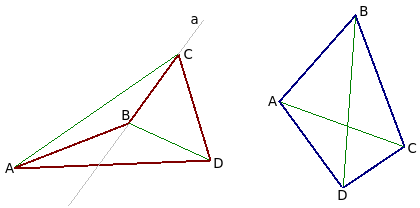
Центр тяжести площади четырехугольника определяется пересечением двух прямых, которые мы получаем, используя распределительное свойство центров тяжести.

Сначала делим четырехугольник диагональю на два треугольника. Центр тяжести четырехугольника лежит на прямой, соединяющей центры тяжести этих треугольников. Это первая искомая прямая.

Вторая искомая прямая получается аналогичным образом — разбивая четырехугольник на треугольники второй диагональю.

(2)

Центроид (барицентр или центр масс) произвольного четырёхугольника лежит в точке пересечения средних линий четырёхугольника и отрезка, соединяющего середины диагоналей, и делит все три отрезка пополам.

Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершины.

Метод отвеса

Барицентр однородной плоской фигуры, такой как на рисунке ниже, можно найти экспериментально с использованием отвеса и булавки. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке. Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр.

Метод балансировки

Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.

С помощью геометрического разложения

Барицентр плоской фигуры можно вычислить, разделив её на конечное число более простых фигур.

Рассмотрим пример. Фигуру на рисунке легко разделить на квадрат и треугольник с положительным знаком площади и круглое отверстие с отрицательным знаком площади.

Квадрат — пересечение диагоналей $(5, 5)$. Площадь 100.

Прямоугольный треугольник — отложить по трети катета от вершины прямого угла $(10+10/3,10/3) = (13.33; 3.33)$. Площадь 50.

Окружность — центр $(2.5; 12.5)$. Площадь $6.25pi = 19.63$

Средневзвешенное
$$x = frac {5cdot 100 + 13.33cdot 50 — 2.5 cdot 19.63}{100+50-19.63} approx 8.57$$

$$y = frac {5cdot 100 + 3.33cdot 50 — 12.5 cdot 19.63}{100+50-19.63} approx 3.23$$

Та же формула применима для любого трёхмерного объекта, только вместо площадей берут объёмы частей тела.

Центр тяжести объекта в форме буквы L

Делим на два прямоугольника, находим центры каждого из них как пересечение диагоналей, соединяем. Барицентр фигуры должен лежать на этом отрезке AB.

Делим фигуру на два прямоугольника другим способом. Находим барицентры этих двух прямоугольников. Проводим отрезок, соединяющий центры. Барицентр фигуры должен лежать на этом отрезке CD.

Барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.

Барицентр

это цетр масс двух и более тел, которые вращаются друг около друга.

Чем массивнее одно из двух тел, тем ближе к нему барицентр. Для системы Луна-Земля барицентр расположен примерно на расстоянии 4 671 км от центра Земли, радиус планеты 6 378 км.

Барицентрическая система отсчета

International Celestial Reference System (ICRS, Международная небесная система координат или Международная система астрономических координат) — с 1998 года стандартная небесная система координат.

Началом отсчёта является барицентр Солнечной системы. Координаты в этой системе максимально приближены к экваториальным эпохи J2000.0 (расхождение составляет доли секунды дуги)

Оси системы зафиксированы в пространстве относительно квазаров, которые считаются наиболее удалёнными объектами наблюдаемой Вселенной. Их предполагаемое собственное движение настолько мало, что им можно пренебречь. Внедрение системы обусловлено необходимостью повышения точности астрономических измерений до 0,05″.

Полученная система координат независима от вращения Земли.

Барицентрические координаты

Пусть дан треугольник ABC. Тогда любую точку P в плоскости треугольника можно представить как центр некоторых масс α, β, γ, помещенных в его вершины A, B, C.

Тройка чисел (α, β, γ) называется барицентрическими координатами точки P относительно треугольника.

Барицентрические координаты точки определены с точностью до ненулевого множителя: все тройки (kα, kβ, kγ) при любом k ≠ 0 задают одну и ту же точку P. Любые три числа с ненулевой суммой являются барицентрическими координатами некоторой точки. Иногда барицентрическими координатами называют ту из пропорциональных троек, у которой сумма чисел равна единице. Соответствие между такими тройками и точками плоскости взаимно-однозначно.

Если точка P лежит внутри треугольника ABC, то ее барицентрические координаты пропорциональны площадям треугольников PAB, PBC и PCA. Для точек вне треугольника это тоже верно, только нужно брать ориентированные площади.

Случай двух тел

Два тела взаимодействуют только друг с другом. Тела вращаются поэллиптической орбите пример двойные звезды.

Источник

Quadrilateral
Some types of quadrilaterals
Edges and vertices	4
Schläfli symbol	{4} (for square)
Area	various methods; see below
Internal angle (degrees)	90° (for square and rectangle)

In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning «side». It is also called a tetragon, derived from greek «tetra» meaning «four» and «gon» meaning «corner» or «angle», in analogy to other polygons (e.g. pentagon). Since «gon» means «angle», it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .^[1]

Quadrilaterals are either simple (not self-intersecting), or complex (self-intersecting, or crossed). Simple quadrilaterals are either convex or concave.

The interior angles of a simple (and planar) quadrilateral ABCD add up to 360 degrees of arc, that is^[1]

$angle A+angle B+angle C+angle D=360^{circ }.$

This is a special case of the n-gon interior angle sum formula: S = (n − 2) × 180°.^[2]

All non-self-crossing quadrilaterals tile the plane, by repeated rotation around the midpoints of their edges.^[3]

Simple quadrilaterals[edit]

Any quadrilateral that is not self-intersecting is a simple quadrilateral.

Convex quadrilateral[edit]

Euler diagram of some types of simple quadrilaterals. (UK) denotes British English and (US) denotes American English.

Convex quadrilaterals by symmetry, represented with a Hasse diagram.

In a convex quadrilateral all interior angles are less than 180°, and the two diagonals both lie inside the quadrilateral.

Irregular quadrilateral (British English) or trapezium (North American English): no sides are parallel. (In British English, this was once called a trapezoid. For more, see Trapezoid § Trapezium vs Trapezoid)
Trapezium (UK) or trapezoid (US): at least one pair of opposite sides are parallel. Trapezia (UK) and trapezoids (US) include parallelograms.
Isosceles trapezium (UK) or isosceles trapezoid (US): one pair of opposite sides are parallel and the base angles are equal in measure. Alternative definitions are a quadrilateral with an axis of symmetry bisecting one pair of opposite sides, or a trapezoid with diagonals of equal length.
Parallelogram: a quadrilateral with two pairs of parallel sides. Equivalent conditions are that opposite sides are of equal length; that opposite angles are equal; or that the diagonals bisect each other. Parallelograms include rhombi (including those rectangles called squares) and rhomboids (including those rectangles called oblongs). In other words, parallelograms include all rhombi and all rhomboids, and thus also include all rectangles.
Rhombus, rhomb:^[1] all four sides are of equal length (equilateral). An equivalent condition is that the diagonals perpendicularly bisect each other. Informally: «a pushed-over square» (but strictly including a square, too).
Rhomboid: a parallelogram in which adjacent sides are of unequal lengths, and some angles are oblique (equiv., having no right angles). Informally: «a pushed-over oblong». Not all references agree, some define a rhomboid as a parallelogram that is not a rhombus.^[4]
Rectangle: all four angles are right angles (equiangular). An equivalent condition is that the diagonals bisect each other, and are equal in length. Rectangles include squares and oblongs. Informally: «a box or oblong» (including a square).
Square (regular quadrilateral): all four sides are of equal length (equilateral), and all four angles are right angles. An equivalent condition is that opposite sides are parallel (a square is a parallelogram), and that the diagonals perpendicularly bisect each other and are of equal length. A quadrilateral is a square if and only if it is both a rhombus and a rectangle (i.e., four equal sides and four equal angles).
Oblong: longer than wide, or wider than long (i.e., a rectangle that is not a square).^[5]
Kite: two pairs of adjacent sides are of equal length. This implies that one diagonal divides the kite into congruent triangles, and so the angles between the two pairs of equal sides are equal in measure. It also implies that the diagonals are perpendicular. Kites include rhombi.

Tangential quadrilateral: the four sides are tangents to an inscribed circle. A convex quadrilateral is tangential if and only if opposite sides have equal sums.
Tangential trapezoid: a trapezoid where the four sides are tangents to an inscribed circle.
Cyclic quadrilateral: the four vertices lie on a circumscribed circle. A convex quadrilateral is cyclic if and only if opposite angles sum to 180°.
Right kite: a kite with two opposite right angles. It is a type of cyclic quadrilateral.
Harmonic quadrilateral: the products of the lengths of the opposing sides are equal. It is a type of cyclic quadrilateral.
Bicentric quadrilateral: it is both tangential and cyclic.
Orthodiagonal quadrilateral: the diagonals cross at right angles.
Equidiagonal quadrilateral: the diagonals are of equal length.
Ex-tangential quadrilateral: the four extensions of the sides are tangent to an excircle.
An equilic quadrilateral has two opposite equal sides that when extended, meet at 60°.
A Watt quadrilateral is a quadrilateral with a pair of opposite sides of equal length.^[6]
A quadric quadrilateral is a convex quadrilateral whose four vertices all lie on the perimeter of a square.^[7]
A diametric quadrilateral is a cyclic quadrilateral having one of its sides as a diameter of the circumcircle.^[8]
A Hjelmslev quadrilateral is a quadrilateral with two right angles at opposite vertices.^[9]

Concave quadrilaterals[edit]

In a concave quadrilateral, one interior angle is bigger than 180°, and one of the two diagonals lies outside the quadrilateral.

A dart (or arrowhead) is a concave quadrilateral with bilateral symmetry like a kite, but where one interior angle is reflex. See Kite.

Complex quadrilaterals[edit]

A self-intersecting quadrilateral is called variously a cross-quadrilateral, crossed quadrilateral, butterfly quadrilateral or bow-tie quadrilateral. In a crossed quadrilateral, the four «interior» angles on either side of the crossing (two acute and two reflex, all on the left or all on the right as the figure is traced out) add up to 720°.^[10]

Crossed trapezoid (US) or trapezium (Commonwealth):^[11] a crossed quadrilateral in which one pair of nonadjacent sides is parallel (like a trapezoid)
Antiparallelogram: a crossed quadrilateral in which each pair of nonadjacent sides have equal lengths (like a parallelogram)
Crossed rectangle: an antiparallelogram whose sides are two opposite sides and the two diagonals of a rectangle, hence having one pair of parallel opposite sides
Crossed square: a special case of a crossed rectangle where two of the sides intersect at right angles

Special line segments[edit]

The two diagonals of a convex quadrilateral are the line segments that connect opposite vertices.

The two bimedians of a convex quadrilateral are the line segments that connect the midpoints of opposite sides.^[12] They intersect at the «vertex centroid» of the quadrilateral (see § Remarkable points and lines in a convex quadrilateral below).

The four maltitudes of a convex quadrilateral are the perpendiculars to a side—through the midpoint of the opposite side.^[13]

Area of a convex quadrilateral[edit]

There are various general formulas for the area K of a convex quadrilateral ABCD with sides a = AB, b = BC, c = CD and d = DA.

Trigonometric formulas[edit]

The area can be expressed in trigonometric terms as^[14]

${displaystyle K={frac {pq}{2}}sin theta ,}$

where the lengths of the diagonals are p and q and the angle between them is θ.^[15] In the case of an orthodiagonal quadrilateral (e.g. rhombus, square, and kite), this formula reduces to ${displaystyle K={tfrac {pq}{2}}}$ since θ is 90°.

The area can be also expressed in terms of bimedians as^[16]

where the lengths of the bimedians are m and n and the angle between them is φ.

Bretschneider’s formula^[17]^[14] expresses the area in terms of the sides and two opposite angles:

${displaystyle {begin{aligned}K&={sqrt {(s-a)(s-b)(s-c)(s-d)-{tfrac {1}{2}}abcd;[1+cos(A+C)]}}\&={sqrt {(s-a)(s-b)(s-c)(s-d)-abcdleft[cos ^{2}left({frac {A+C}{2}}right)right]}}end{aligned}}}$

where the sides in sequence are a, b, c, d, where s is the semiperimeter, and A and C are two (in fact, any two) opposite angles. This reduces to Brahmagupta’s formula for the area of a cyclic quadrilateral—when A + C = 180° .

Another area formula in terms of the sides and angles, with angle C being between sides b and c, and A being between sides a and d, is

${displaystyle K={frac {ad}{2}}sin {A}+{frac {bc}{2}}sin {C}.}$

In the case of a cyclic quadrilateral, the latter formula becomes ${displaystyle K={frac {ad+bc}{2}}sin {A}.}$

In a parallelogram, where both pairs of opposite sides and angles are equal, this formula reduces to

Alternatively, we can write the area in terms of the sides and the intersection angle θ of the diagonals, as long θ is not 90°:^[18]

${displaystyle K={frac {left|tan theta right|}{4}}cdot left|a^{2}+c^{2}-b^{2}-d^{2}right|.}$

In the case of a parallelogram, the latter formula becomes ${displaystyle K={frac {left|tan theta right|}{2}}cdot left|a^{2}-b^{2}right|.}$

Another area formula including the sides a, b, c, d is^[16]

${displaystyle K={frac {sqrt {((a^{2}+c^{2})-2x^{2})((b^{2}+d^{2})-2x^{2})}}{2}}sin {varphi }}$

where x is the distance between the midpoints of the diagonals, and φ is the angle between the bimedians.

The last trigonometric area formula including the sides a, b, c, d and the angle α (between a and b) is:^[19]

${displaystyle K={frac {ab}{2}}sin {alpha }+{frac {sqrt {4c^{2}d^{2}-(c^{2}+d^{2}-a^{2}-b^{2}+2abcdot cos {alpha })^{2}}}{4}},}$

which can also be used for the area of a concave quadrilateral (having the concave part opposite to angle α), by just changing the first sign + to —.

Non-trigonometric formulas[edit]

The following two formulas express the area in terms of the sides a, b, c and d, the semiperimeter s, and the diagonals p, q:

$K={sqrt {(s-a)(s-b)(s-c)(s-d)-{tfrac {1}{4}}(ac+bd+pq)(ac+bd-pq)}},$

^[20]

${displaystyle K={frac {sqrt {4p^{2}q^{2}-left(a^{2}+c^{2}-b^{2}-d^{2}right)^{2}}}{4}}.}$

^[21]

The first reduces to Brahmagupta’s formula in the cyclic quadrilateral case, since then pq = ac + bd.

The area can also be expressed in terms of the bimedians m, n and the diagonals p, q:

${displaystyle K={frac {sqrt {(m+n+p)(m+n-p)(m+n+q)(m+n-q)}}{2}},}$

^[22]

${displaystyle K={frac {sqrt {p^{2}q^{2}-(m^{2}-n^{2})^{2}}}{2}}.}$

^[23]^{: Thm. 7}

In fact, any three of the four values m, n, p, and q suffice for determination of the area, since in any quadrilateral the four values are related by $p^{2}+q^{2}=2(m^{2}+n^{2}).$ ^[24]^{: p. 126} The corresponding expressions are:^[25]

${displaystyle K={frac {sqrt {[(m+n)^{2}-p^{2}]cdot [p^{2}-(m-n)^{2}]}}{2}},}$

if the lengths of two bimedians and one diagonal are given, and^[25]

${displaystyle K={frac {sqrt {[(p+q)^{2}-4m^{2}]cdot [4m^{2}-(p-q)^{2}]}}{4}},}$

if the lengths of two diagonals and one bimedian are given.

Vector formulas[edit]

The area of a quadrilateral ABCD can be calculated using vectors. Let vectors AC and BD form the diagonals from A to C and from B to D. The area of the quadrilateral is then

${displaystyle K={frac {|mathbf {AC} times mathbf {BD} |}{2}},}$

which is half the magnitude of the cross product of vectors AC and BD. In two-dimensional Euclidean space, expressing vector AC as a free vector in Cartesian space equal to (x₁,y₁) and BD as (x₂,y₂), this can be rewritten as:

${displaystyle K={frac {|x_{1}y_{2}-x_{2}y_{1}|}{2}}.}$

Diagonals[edit]

Properties of the diagonals in quadrilaterals[edit]

In the following table it is listed if the diagonals in some of the most basic quadrilaterals bisect each other, if their diagonals are perpendicular, and if their diagonals have equal length.^[26] The list applies to the most general cases, and excludes named subsets.

Quadrilateral	Bisecting diagonals	Perpendicular diagonals	Equal diagonals
Trapezoid	No	See note 1	No
Isosceles trapezoid	No	See note 1	Yes
Parallelogram	Yes	No	No
Kite	See note 2	Yes	See note 2
Rectangle	Yes	No	Yes
Rhombus	Yes	Yes	No
Square	Yes	Yes	Yes

Note 1: The most general trapezoids and isosceles trapezoids do not have perpendicular diagonals, but there are infinite numbers of (non-similar) trapezoids and isosceles trapezoids that do have perpendicular diagonals and are not any other named quadrilateral.

Note 2: In a kite, one diagonal bisects the other. The most general kite has unequal diagonals, but there is an infinite number of (non-similar) kites in which the diagonals are equal in length (and the kites are not any other named quadrilateral).

Lengths of the diagonals[edit]

The lengths of the diagonals in a convex quadrilateral ABCD can be calculated using the law of cosines on each triangle formed by one diagonal and two sides of the quadrilateral. Thus

$p={sqrt {a^{2}+b^{2}-2abcos {B}}}={sqrt {c^{2}+d^{2}-2cdcos {D}}}$

and

$q={sqrt {a^{2}+d^{2}-2adcos {A}}}={sqrt {b^{2}+c^{2}-2bccos {C}}}.$

Other, more symmetric formulas for the lengths of the diagonals, are^[27]

$p={sqrt {frac {(ac+bd)(ad+bc)-2abcd(cos {B}+cos {D})}{ab+cd}}}$

and

$q={sqrt {frac {(ab+cd)(ac+bd)-2abcd(cos {A}+cos {C})}{ad+bc}}}.$

Generalizations of the parallelogram law and Ptolemy’s theorem[edit]

In any convex quadrilateral ABCD, the sum of the squares of the four sides is equal to the sum of the squares of the two diagonals plus four times the square of the line segment connecting the midpoints of the diagonals. Thus

$a^{2}+b^{2}+c^{2}+d^{2}=p^{2}+q^{2}+4x^{2}$

where x is the distance between the midpoints of the diagonals.^[24]^: p.126 This is sometimes known as Euler’s quadrilateral theorem and is a generalization of the parallelogram law.

The German mathematician Carl Anton Bretschneider derived in 1842 the following generalization of Ptolemy’s theorem, regarding the product of the diagonals in a convex quadrilateral^[28]

$p^{2}q^{2}=a^{2}c^{2}+b^{2}d^{2}-2abcdcos {(A+C)}.$

This relation can be considered to be a law of cosines for a quadrilateral. In a cyclic quadrilateral, where A + C = 180°, it reduces to pq = ac + bd. Since cos (A + C) ≥ −1, it also gives a proof of Ptolemy’s inequality.

Other metric relations[edit]

If X and Y are the feet of the normals from B and D to the diagonal AC = p in a convex quadrilateral ABCD with sides a = AB, b = BC, c = CD, d = DA, then^[29]^: p.14

$XY={frac {|a^{2}+c^{2}-b^{2}-d^{2}|}{2p}}.$

In a convex quadrilateral ABCD with sides a = AB, b = BC, c = CD, d = DA, and where the diagonals intersect at E,

efgh(a+c+b+d)(a+c-b-d)=(agh+cef+beh+dfg)(agh+cef-beh-dfg)

where e = AE, f = BE, g = CE, and h = DE.^[30]

The shape and size of a convex quadrilateral are fully determined by the lengths of its sides in sequence and of one diagonal between two specified vertices. The two diagonals p, q and the four side lengths a, b, c, d of a quadrilateral are related^[14] by the Cayley-Menger determinant, as follows:

$det {begin{bmatrix}0&a^{2}&p^{2}&d^{2}&1\a^{2}&0&b^{2}&q^{2}&1\p^{2}&b^{2}&0&c^{2}&1\d^{2}&q^{2}&c^{2}&0&1\1&1&1&1&0end{bmatrix}}=0.$

Angle bisectors[edit]

The internal angle bisectors of a convex quadrilateral either form a cyclic quadrilateral^[24]^: p.127 (that is, the four intersection points of adjacent angle bisectors are concyclic) or they are concurrent. In the latter case the quadrilateral is a tangential quadrilateral.

In quadrilateral ABCD, if the angle bisectors of A and C meet on diagonal BD, then the angle bisectors of B and D meet on diagonal AC.^[31]

Bimedians[edit]

The Varignon parallelogram EFGH

The bimedians of a quadrilateral are the line segments connecting the midpoints of the opposite sides. The intersection of the bimedians is the centroid of the vertices of the quadrilateral.^[14]

The midpoints of the sides of any quadrilateral (convex, concave or crossed) are the vertices of a parallelogram called the Varignon parallelogram. It has the following properties:

Each pair of opposite sides of the Varignon parallelogram are parallel to a diagonal in the original quadrilateral.
A side of the Varignon parallelogram is half as long as the diagonal in the original quadrilateral it is parallel to.
The area of the Varignon parallelogram equals half the area of the original quadrilateral. This is true in convex, concave and crossed quadrilaterals provided the area of the latter is defined to be the difference of the areas of the two triangles it is composed of.^[32]
The perimeter of the Varignon parallelogram equals the sum of the diagonals of the original quadrilateral.
The diagonals of the Varignon parallelogram are the bimedians of the original quadrilateral.

The two bimedians in a quadrilateral and the line segment joining the midpoints of the diagonals in that quadrilateral are concurrent and are all bisected by their point of intersection.^[24]^: p.125

In a convex quadrilateral with sides a, b, c and d, the length of the bimedian that connects the midpoints of the sides a and c is

$m={tfrac {1}{2}}{sqrt {-a^{2}+b^{2}-c^{2}+d^{2}+p^{2}+q^{2}}}$

where p and q are the length of the diagonals.^[33] The length of the bimedian that connects the midpoints of the sides b and d is

$n={tfrac {1}{2}}{sqrt {a^{2}-b^{2}+c^{2}-d^{2}+p^{2}+q^{2}}}.$

Hence^[24]^: p.126

$displaystyle p^{2}+q^{2}=2(m^{2}+n^{2}).$

This is also a corollary to the parallelogram law applied in the Varignon parallelogram.

The lengths of the bimedians can also be expressed in terms of two opposite sides and the distance x between the midpoints of the diagonals. This is possible when using Euler’s quadrilateral theorem in the above formulas. Whence^[23]

$m={tfrac {1}{2}}{sqrt {2(b^{2}+d^{2})-4x^{2}}}$

and

$n={tfrac {1}{2}}{sqrt {2(a^{2}+c^{2})-4x^{2}}}.$

Note that the two opposite sides in these formulas are not the two that the bimedian connects.

In a convex quadrilateral, there is the following dual connection between the bimedians and the diagonals:^[29]

The two bimedians have equal length if and only if the two diagonals are perpendicular.
The two bimedians are perpendicular if and only if the two diagonals have equal length.

Trigonometric identities[edit]

The four angles of a simple quadrilateral ABCD satisfy the following identities:^[34]

$sin {A}+sin {B}+sin {C}+sin {D}=4sin {frac {A+B}{2}}sin {frac {A+C}{2}}sin {frac {A+D}{2}}$

and

${frac {tan {A}tan {B}-tan {C}tan {D}}{tan {A}tan {C}-tan {B}tan {D}}}={frac {tan {(A+C)}}{tan {(A+B)}}}.$

Also,^[35]

${frac {tan {A}+tan {B}+tan {C}+tan {D}}{cot {A}+cot {B}+cot {C}+cot {D}}}=tan {A}tan {B}tan {C}tan {D}.$

In the last two formulas, no angle is allowed to be a right angle, since tan 90° is not defined.

Let , , , be the sides of a convex quadrilateral, is the semiperimeter,
and and are opposite angles, then^[36]

${displaystyle adsin ^{2}{frac {A}{2}}+bccos ^{2}{frac {C}{2}}=(s-a)(s-d)}$

and

${displaystyle bcsin ^{2}{frac {C}{2}}+adcos ^{2}{frac {A}{2}}=(s-b)(s-c)}$

We can use these identities to derive the Bretschneider’s Formula.

Inequalities[edit]

Area[edit]

If a convex quadrilateral has the consecutive sides a, b, c, d and the diagonals p, q, then its area K satisfies^[37]

$Kleq {tfrac {1}{4}}(a+c)(b+d)$

with equality only for a rectangle.

$Kleq {tfrac {1}{4}}(a^{2}+b^{2}+c^{2}+d^{2})$

with equality only for a square.

$Kleq {tfrac {1}{4}}(p^{2}+q^{2})$

with equality only if the diagonals are perpendicular and equal.

$Kleq {tfrac {1}{2}}{sqrt {(a^{2}+c^{2})(b^{2}+d^{2})}}$

with equality only for a rectangle.^[16]

From Bretschneider’s formula it directly follows that the area of a quadrilateral satisfies

with equality if and only if the quadrilateral is cyclic or degenerate such that one side is equal to the sum of the other three (it has collapsed into a line segment, so the area is zero).

The area of any quadrilateral also satisfies the inequality^[38]

$displaystyle Kleq {tfrac {1}{2}}{sqrt[{3}]{(ab+cd)(ac+bd)(ad+bc)}}.$

Denoting the perimeter as L, we have^[38]^: p.114

$Kleq {tfrac {1}{16}}L^{2},$

with equality only in the case of a square.

The area of a convex quadrilateral also satisfies

$Kleq {tfrac {1}{2}}pq$

for diagonal lengths p and q, with equality if and only if the diagonals are perpendicular.

Let a, b, c, d be the lengths of the sides of a convex quadrilateral ABCD with the area K and diagonals AC = p, BD = q. Then^[39]

${displaystyle Kleq {frac {a^{2}+b^{2}+c^{2}+d^{2}+p^{2}+q^{2}+pq-ac-bd}{8}}}$

with equality only for a square.

Let a, b, c, d be the lengths of the sides of a convex quadrilateral ABCD with the area K, then the following inequality holds:^[40]

${displaystyle Kleq {frac {1}{3+{sqrt {3}}}}(ab+ac+ad+bc+bd+cd)-{frac {1}{2(1+{sqrt {3}})^{2}}}(a^{2}+b^{2}+c^{2}+d^{2})}$

with equality only for a square.

Diagonals and bimedians[edit]

A corollary to Euler’s quadrilateral theorem is the inequality

$a^{2}+b^{2}+c^{2}+d^{2}geq p^{2}+q^{2}$

where equality holds if and only if the quadrilateral is a parallelogram.

Euler also generalized Ptolemy’s theorem, which is an equality in a cyclic quadrilateral, into an inequality for a convex quadrilateral. It states that

where there is equality if and only if the quadrilateral is cyclic.^[24]^{: p.128–129} This is often called Ptolemy’s inequality.

In any convex quadrilateral the bimedians m, n and the diagonals p, q are related by the inequality

$pqleq m^{2}+n^{2},$

with equality holding if and only if the diagonals are equal.^[41]^: Prop.1 This follows directly from the quadrilateral identity ${displaystyle m^{2}+n^{2}={tfrac {1}{2}}(p^{2}+q^{2}).}$

Sides[edit]

The sides a, b, c, and d of any quadrilateral satisfy^[42]^{: p.228, #275}

$a^{2}+b^{2}+c^{2}>{frac {d^{2}}{3}}$

and^[42]^{: p.234, #466}

$a^{4}+b^{4}+c^{4}geq {frac {d^{4}}{27}}.$

Maximum and minimum properties[edit]

Among all quadrilaterals with a given perimeter, the one with the largest area is the square. This is called the isoperimetric theorem for quadrilaterals. It is a direct consequence of the area inequality^[38]^: p.114

$Kleq {tfrac {1}{16}}L^{2}$

where K is the area of a convex quadrilateral with perimeter L. Equality holds if and only if the quadrilateral is a square. The dual theorem states that of all quadrilaterals with a given area, the square has the shortest perimeter.

The quadrilateral with given side lengths that has the maximum area is the cyclic quadrilateral.^[43]

Of all convex quadrilaterals with given diagonals, the orthodiagonal quadrilateral has the largest area.^[38]^: p.119 This is a direct consequence of the fact that the area of a convex quadrilateral satisfies

$K={tfrac {1}{2}}pqsin {theta }leq {tfrac {1}{2}}pq,$

where θ is the angle between the diagonals p and q. Equality holds if and only if θ = 90°.

If P is an interior point in a convex quadrilateral ABCD, then

From this inequality it follows that the point inside a quadrilateral that minimizes the sum of distances to the vertices is the intersection of the diagonals. Hence that point is the Fermat point of a convex quadrilateral.^[44]^: p.120

Remarkable points and lines in a convex quadrilateral[edit]

The centre of a quadrilateral can be defined in several different ways. The «vertex centroid» comes from considering the quadrilateral as being empty but having equal masses at its vertices. The «side centroid» comes from considering the sides to have constant mass per unit length. The usual centre, called just centroid (centre of area) comes from considering the surface of the quadrilateral as having constant density. These three points are in general not all the same point.^[45]

The «vertex centroid» is the intersection of the two bimedians.^[46] As with any polygon, the x and y coordinates of the vertex centroid are the arithmetic means of the x and y coordinates of the vertices.

The «area centroid» of quadrilateral ABCD can be constructed in the following way. Let G_a, G_b, G_c, G_d be the centroids of triangles BCD, ACD, ABD, ABC respectively. Then the «area centroid» is the intersection of the lines G_aG_c and G_bG_d.^[47]

In a general convex quadrilateral ABCD, there are no natural analogies to the circumcenter and orthocenter of a triangle. But two such points can be constructed in the following way. Let O_a, O_b, O_c, O_d be the circumcenters of triangles BCD, ACD, ABD, ABC respectively; and denote by H_a, H_b, H_c, H_d the orthocenters in the same triangles. Then the intersection of the lines O_aO_c and O_bO_d is called the quasicircumcenter, and the intersection of the lines H_aH_c and H_bH_d is called the quasiorthocenter of the convex quadrilateral.^[47] These points can be used to define an Euler line of a quadrilateral. In a convex quadrilateral, the quasiorthocenter H, the «area centroid» G, and the quasicircumcenter O are collinear in this order, and HG = 2GO.^[47]

There can also be defined a quasinine-point center E as the intersection of the lines E_aE_c and E_bE_d, where E_a, E_b, E_c, E_d are the nine-point centers of triangles BCD, ACD, ABD, ABC respectively. Then E is the midpoint of OH.^[47]

Another remarkable line in a convex non-parallelogram quadrilateral is the Newton line, which connects the midpoints of the diagonals, the segment connecting these points being bisected by the vertex centroid. One more interesting line (in some sense dual to the Newton’s one) is the line connecting the point of intersection of diagonals with the vertex centroid. The line is remarkable by the fact that it contains the (area) centroid. The vertex centroid divides the segment connecting the intersection of diagonals and the (area) centroid in the ratio 3:1.^[48]

For any quadrilateral ABCD with points P and Q the intersections of AD and BC and AB and CD, respectively, the circles (PAB), (PCD), (QAD), and (QBC) pass through a common point M, called a Miquel point.^[49]

For a convex quadrilateral ABCD in which E is the point of intersection of the diagonals and F is the point of intersection of the extensions of sides BC and AD, let ω be a circle through E and F which meets CB internally at M and DA internally at N. Let CA meet ω again at L and let DB meet ω again at K. Then there holds: the straight lines NK and ML intersect at point P that is located on the side AB; the straight lines NL and KM intersect at point Q that is located on the side CD.
Points P and Q are called «Pascal points» formed by circle ω on sides AB and CD.
^[50]
^[51]
^[52]

Other properties of convex quadrilaterals[edit]

Let exterior squares be drawn on all sides of a quadrilateral. The segments connecting the centers of opposite squares are (a) equal in length, and (b) perpendicular. Thus these centers are the vertices of an orthodiagonal quadrilateral. This is called Van Aubel’s theorem.
For any simple quadrilateral with given edge lengths, there is a cyclic quadrilateral with the same edge lengths.^[43]
The four smaller triangles formed by the diagonals and sides of a convex quadrilateral have the property that the product of the areas of two opposite triangles equals the product of the areas of the other two triangles.^[53]

Taxonomy[edit]

A hierarchical taxonomy of quadrilaterals is illustrated by the figure to the right. Lower classes are special cases of higher classes they are connected to. Note that «trapezoid» here is referring to the North American definition (the British equivalent is a trapezium). Inclusive definitions are used throughout.

Skew quadrilaterals[edit]

A non-planar quadrilateral is called a skew quadrilateral. Formulas to compute its dihedral angles from the edge lengths and the angle between two adjacent edges were derived for work on the properties of molecules such as cyclobutane that contain a «puckered» ring of four atoms.^[54] Historically the term gauche quadrilateral was also used to mean a skew quadrilateral.^[55] A skew quadrilateral together with its diagonals form a (possibly non-regular) tetrahedron, and conversely every skew quadrilateral comes from a tetrahedron where a pair of opposite edges is removed.

References[edit]

^ ^a ^b ^c «Quadrilaterals — Square, Rectangle, Rhombus, Trapezoid, Parallelogram». Mathsisfun.com. Retrieved 2020-09-02.
^ «Sum of Angles in a Polygon». Cuemath. Retrieved 22 June 2022.
^ Martin, George Edward (1982), Transformation geometry, Undergraduate Texts in Mathematics, Springer-Verlag, Theorem 12.1, page 120, doi:10.1007/978-1-4612-5680-9, ISBN 0-387-90636-3, MR 0718119
^ «Archived copy» (PDF). Archived from the original (PDF) on May 14, 2014. Retrieved June 20, 2013.{{cite web}}: CS1 maint: archived copy as title (link)
^ «Rectangles Calculator». Cleavebooks.co.uk. Retrieved 1 March 2022.
^ Keady, G.; Scales, P.; Németh, S. Z. (2004). «Watt Linkages and Quadrilaterals». The Mathematical Gazette. 88 (513): 475–492. doi:10.1017/S0025557200176107. S2CID 125102050.
^ Jobbings, A. K. (1997). «Quadric Quadrilaterals». The Mathematical Gazette. 81 (491): 220–224. doi:10.2307/3619199. JSTOR 3619199. S2CID 250440553.
^ Beauregard, R. A. (2009). «Diametric Quadrilaterals with Two Equal Sides». College Mathematics Journal. 40 (1): 17–21. doi:10.1080/07468342.2009.11922331. S2CID 122206817.
^ Hartshorne, R. (2005). Geometry: Euclid and Beyond. Springer. pp. 429–430. ISBN 978-1-4419-3145-0.
^ «Stars: A Second Look» (PDF). Mysite.mweb.co.za. Archived from the original (PDF) on March 3, 2016. Retrieved March 1, 2022.
^ Butler, David (2016-04-06). «The crossed trapezium». Making Your Own Sense. Retrieved 2017-09-13.
^ E.W. Weisstein. «Bimedian». MathWorld – A Wolfram Web Resource.
^ E.W. Weisstein. «Maltitude». MathWorld – A Wolfram Web Resource.
^ ^a ^b ^c ^d Weisstein, Eric W. «Quadrilateral». mathworld.wolfram.com. Retrieved 2020-09-02.
^ Harries, J. «Area of a quadrilateral,» Mathematical Gazette 86, July 2002, 310–311.
^ ^a ^b ^c Josefsson, Martin (2013), «Five Proofs of an Area Characterization of Rectangles» (PDF), Forum Geometricorum, 13: 17–21.
^ R. A. Johnson, Advanced Euclidean Geometry, 2007, Dover Publ., p. 82.
^ Mitchell, Douglas W., «The area of a quadrilateral,» Mathematical Gazette 93, July 2009, 306–309.
^ https://www.mathcentre.ac.uk/resources/uploaded/mc-ty-triangleformulae-2009-1.pdf^{[bare URL PDF]}
^ J. L. Coolidge, «A historically interesting formula for the area of a quadrilateral», American Mathematical Monthly, 46 (1939) 345–347.
^ E.W. Weisstein. «Bretschneider’s formula». MathWorld – A Wolfram Web Resource.
^ Archibald, R. C., «The Area of a Quadrilateral», American Mathematical Monthly, 29 (1922) pp. 29–36.
^ ^a ^b Josefsson, Martin (2011), «The Area of a Bicentric Quadrilateral» (PDF), Forum Geometricorum, 11: 155–164.
^ ^a ^b ^c ^d ^e ^f Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
^ ^a ^b Josefsson, Martin (2016) ‘100.31 Heron-like formulas for quadrilaterals’, The Mathematical Gazette, 100 (549), pp. 505–508.
^ «Diagonals of Quadrilaterals — Perpendicular, Bisecting or Both». Math.okstate.edu. Retrieved 1 March 2022.
^ Rashid, M. A. & Ajibade, A. O., «Two conditions for a quadrilateral to be cyclic expressed in terms of the lengths of its sides», Int. J. Math. Educ. Sci. Technol., vol. 34 (2003) no. 5, pp. 739–799.
^ Andreescu, Titu & Andrica, Dorian, Complex Numbers from A to…Z, Birkhäuser, 2006, pp. 207–209.
^ ^a ^b Josefsson, Martin (2012), «Characterizations of Orthodiagonal Quadrilaterals» (PDF), Forum Geometricorum, 12: 13–25.
^ Hoehn, Larry (2011), «A New Formula Concerning the Diagonals and Sides of a Quadrilateral» (PDF), Forum Geometricorum, 11: 211–212.
^ Leversha, Gerry, «A property of the diagonals of a cyclic quadrilateral», Mathematical Gazette 93, March 2009, 116–118.
^ H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, MAA, 1967, pp. 52–53.
^ «Mateescu Constantin, Answer to Inequality Of Diagonal«.
^ C. V. Durell & A. Robson, Advanced Trigonometry, Dover, 2003, p. 267.
^ «Original Problems Proposed by Stanley Rabinowitz 1963–2005» (PDF). Mathpropress.com. Retrieved March 1, 2022.
^ «E. A. José García, Two Identities and their Consequences, MATINF, 6 (2020) 5-11». Matinf.upit.ro. Retrieved 1 March 2022.
^ O. Bottema, Geometric Inequalities, Wolters–Noordhoff Publishing, The Netherlands, 1969, pp. 129, 132.
^ ^a ^b ^c ^d Alsina, Claudi; Nelsen, Roger (2009), When Less is More: Visualizing Basic Inequalities, Mathematical Association of America, p. 68.
^ Dao Thanh Oai, Leonard Giugiuc, Problem 12033, American Mathematical Monthly, March 2018, p. 277
^ Leonard Mihai Giugiuc; Dao Thanh Oai; Kadir Altintas (2018). «An inequality related to the lengths and area of a convex quadrilateral» (PDF). International Journal of Geometry. 7: 81–86.
^ Josefsson, Martin (2014). «Properties of equidiagonal quadrilaterals». Forum Geometricorum. 14: 129–144.
^ ^a ^b «Inequalities proposed in Crux Mathematicorum (from vol. 1, no. 1 to vol. 4, no. 2 known as «Eureka»)» (PDF). Imomath.com. Retrieved March 1, 2022.
^ ^a ^b Peter, Thomas, «Maximizing the Area of a Quadrilateral», The College Mathematics Journal, Vol. 34, No. 4 (September 2003), pp. 315–316.
^ Alsina, Claudi; Nelsen, Roger (2010). Charming Proofs : A Journey Into Elegant Mathematics. Mathematical Association of America. pp. 114, 119, 120, 261. ISBN 978-0-88385-348-1.
^ «Two Centers of Mass of a Quadrilateral». Sites.math.washington.edu. Retrieved 1 March 2022.
^ Honsberger, Ross, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, Math. Assoc. Amer., 1995, pp. 35–41.
^ ^a ^b ^c ^d Myakishev, Alexei (2006), «On Two Remarkable Lines Related to a Quadrilateral» (PDF), Forum Geometricorum, 6: 289–295.
^ John Boris Miller. «Centroid of a quadrilateral» (PDF). Austmd.org.au. Retrieved March 1, 2022.
^ Chen, Evan (2016). Euclidean Geometry in Mathematical Olympiads. Washington, D.C.: Mathematical Association of America. p. 198. ISBN 9780883858394.
^ David, Fraivert (2019), «Pascal-points quadrilaterals inscribed in a cyclic quadrilateral», The Mathematical Gazette, 103 (557): 233–239, doi:10.1017/mag.2019.54, S2CID 233360695.
^ David, Fraivert (2019), «A Set of Rectangles Inscribed in an Orthodiagonal Quadrilateral and Defined by Pascal-Points Circles», Journal for Geometry and Graphics, 23: 5–27.
^ David, Fraivert (2017), «Properties of a Pascal points circle in a quadrilateral with perpendicular diagonals» (PDF), Forum Geometricorum, 17: 509–526.
^ Josefsson, Martin (2013). «Characterizations of Trapezoids» (PDF). Forum Geometricorum. 13: 23–35.
^ Barnett, M. P.; Capitani, J. F. (2006). «Modular chemical geometry and symbolic calculation». International Journal of Quantum Chemistry. 106 (1): 215–227. Bibcode:2006IJQC..106..215B. doi:10.1002/qua.20807.
^ Hamilton, William Rowan (1850). «On Some Results Obtained by the Quaternion Analysis Respecting the Inscription of «Gauche» Polygons in Surfaces of the Second Order» (PDF). Proceedings of the Royal Irish Academy. 4: 380–387.

External links[edit]

Wikimedia Commons has media related to Tetragons.

«Quadrangle, complete», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Quadrilaterals Formed by Perpendicular Bisectors, Projective Collinearity and Interactive Classification of Quadrilaterals from cut-the-knot
Definitions and examples of quadrilaterals and Definition and properties of tetragons from Mathopenref
A (dynamic) Hierarchical Quadrilateral Tree at Dynamic Geometry Sketches
An extended classification of quadrilaterals Archived 2019-12-30 at the Wayback Machine at Dynamic Math Learning Homepage Archived 2018-08-25 at the Wayback Machine
The role and function of a hierarchical classification of quadrilaterals by Michael de Villiers

Источник

Геометрия

Окружность и четырехугольник

Определение

Четырехугольник называется вписанным в окружность, если окружность проходит через все вершины четырехугольника.

Очевидно, что окружность, в которую вписан четырехугольник, является описанной около любого из треугольников, на которые разбивается четырехугольник какой-либо диагональю.

Определение

Четырехугольник называется описанным около окружности, если окружность касается всех сторон четырехугольника.

Свойства и признаки вписанных и описанных четырехугольников

Напомним, что сумма внутренних углов выпуклого -угольника находится по формуле . Для четырехугольника n=4 и сумма углов выпуклого четырехугольника равна . Обращаем внимание, что ь далее будут рассматриваться именно выпуклые четырехугольники.

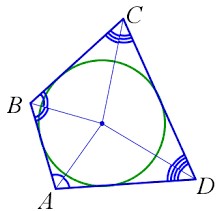
Теорема 1 (свойство и признак вписанного четырехугольника)

Если четырехугольник вписан в окружность, то сумма его противолежащих углов равна (свойство). И наоборот.
Если у четырехугольника сумма противолежащих углов равна , то около него можно описать окружность (признак).

Доказательство:

Пусть четырехугольник ABCD вписан в окружность (рис. 1). Тогда вписанные углы ABC и CDA , а также углы BCD и DAB опираются на дуги, дополняющие одна другую до окружности. А это и означает, что как , так и . Свойство вписанного четырехугольника доказано.

Рис. 1

Докажем признак вписанного четырехугольника.
Пусть у выпуклого четырехугольника ABCD сумма противолежащих углов и а значит, углов и равна . Через три вершины четырехугольника, например, через вершины проведем окружность (это можно сделать всегда). Тогда и четверая вершина принадлежит окружности так как в противном случае вершина лежала бы или внутри круга, ограниченного окружностью, или вне его. Следовательно, угол не измерялся бы половиной дуги ABC, и значит, сумма углов и не измерялась бы полусуммой дуг ABC и ADC и, таким образом, сумма углов и не равнялась бы Полученное противоречие и доказывает теорему.

Теорема доказана.

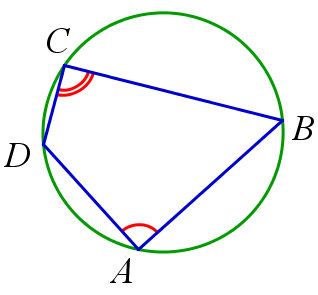
Теорема 2

Доказать, что если в выпуклом четырехугольнике ABCD углы ABD и ACD равны, то такой четырехугольник можно вписать в окружность. Верно и обратное.

Доказательство:

Пусть в четырехугольнике ABCD углы ABD и ACD равны. Проведем через точки A, B, C окружность и предположим, что вершина лежит, например, внутри круга (рис. 2), границей которого является проведенная окружность.

Рис. 2

Продолжим отрезки и до пересечения с окружностью в точках D_1 и D_2 соответственно.
Тогда $angle ABD = frac{1}{2} smile AD_2D_1$ , а $angle ACD = frac{1}{2} smile AD_2$ , что приводит к противоречию, так как по условию . Итак, точка должна лежать на окружности или находиться вне круга. Предположим, что она находится вне круга (рис. 3).

Рис. 3

Обозначим через D_1 и D_2 точки пересечения окружности с отрезками и соответственно. Тогда $angle ABD = frac{1}{2} smile AD_1$ , а $angle ACD = frac{1}{2} smile AD_1D_2$ , что, как и в первом случае, также вступает в противоречие с условием задачи. Вывод: точка является точкой окружности, описанной около четырехугольника ABCD .
Обратно, если четырехугольник ABCD вписан в окружность, то равенство углов ABD и ACD следует из того, что они являются вписанными углами, опирающимися на одну и ту же дугу.

Теорема доказана.

Замечание 1
Очевидно, что четырехугольник ABCD можно вписать в окружность и в случаях, когда или , или , или .

Теорема 3

Доказать, что если — точка пересечения диагоналей четырехугольника ABCD и , то около такого четырехугольника можно описать окружность. Верно и обратное.

Доказательство:

Пусть имеет место равенство , которое преобразуется в пропорцию $frac{AM}{BM} = frac{MD}{MC}$ . А тогда так как как вертикальные углы (рис. 4), то треугольники BMC и AMD подобны и, значит, .

Рис. 4

Последнее равенство и означает (замечание 1), что около четырехугольника ABCD можно описать окружность. Справедливость обратного утверждения очевидным образом следует из свойства хорд.

Теорема доказана.

Теорема 4 (Теорема Птолемея)

Если четырехугольник вписан в окружность, то сумма произведений его противолежащих сторон равна произведению его диагоналей.

Доказательство:

В четырехугольнике ABCD (рис. 5) построим угол ABE ( — точка диагонали ), равный углу DBC . Тогда треугольники ABE и DBC будут подобными, так как как вписанные углы, опирающиеся на одну и ту же дугу.

Рис. 5

Но в таком случае $frac{AB}{BD} = frac{AE}{DC}$ , т.е. Из подобия же треугольников BCE и ABD следует, что $frac{BC}{BD} = frac{EC}{AD}$ или Таким образом,, что и требовалось доказать.
Обратно. Пусть в четырехугольнике произведение его диагоналей равно сумме произведений его противолежащих сторон, то есть .
Через точки и проведем прямые так, чтобы в получившемся треугольнике ABK выполнялись равенства: , (рис. 6).

Рис. 6

Тогда по первому признаку подобия треугольников и, значит, $frac{AB}{AC} = frac{BK}{CD} = frac{AK}{AD}$ , откуда следует, что . Так как то по второму признаку подобия треугольников и, таким образом, $frac{KD}{BC} = frac{AD}{AC}$ , откуда . Но тогда или . Отсюда следует, что и, значит, точка принадлежит отрезку , откуда вытекает равенство . Полученное равенство углов означает, что точки , , и лежат на одной окружности (отрезок виден из точек и под одним углом), а это и требовалось доказать.

Теорема доказана.

Теорема 5 (свойство и признак описанного четырехугольника)

Если четырехугольник описан около окружности, то суммы его противолежащих сторон равны (свойство). И наоборот.
Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность (признак).

Доказательство:

Пусть четырехугольник ABCD описан около окружности и пусть , , , — точки касания окружности со сторонами четырехугольника (рис. 7). Тогда по свойству касательных имеем . Складывая полученные равенства, находим, что или .
Свойство описанного четырехугольника доказано.

Рис. 7

Докажем признак описанного четырехугольника.
Если четырехугольник ABCD ромб, то он является описанным около окружности с центром в точке пересечения его диагоналей.

Рассмотрим теперь случай, когда у выпуклого четырехугольника ABCD есть неравные соседние стороны. Допустим, что AB > BC , и, значит, AD > DC . Отложим на сторонах углов ABC и ADC отрезки BM = BC и DN=DC (рис. 8).

Рис. 8

Поскольку по условию имеем AM=AN , и поэтому треугольник AMN — равнобедренный с основанием . Треугольники CBM и CDN по построению также равнобедренные с основаниями и .
По свойству медианы равнобедренного треугольника медианы этих трех треугольников, проведенные к их основаниям, являются их высотами. Значит, прямые, содержащие эти медианы, — серединные перпендикуляры к сторонам треугольника CMN и поэтому пересекаются в одной точке .
Эти же медианы являются и биссектрисами равнобедренных треугольников AMN , CBM и CDN . Поэтому лучи , и — биссектрисы углов , и четырехугольника ABCD , которые образуют с его сторонами острые углы, так как по условию данный четырехугольник выпуклый. Значит, точка равноудалена от всех сторон четырехугольника ABCD , и поэтому он является описанным около окружности с центром в этой точке.
Теорема доказана.

Рассмотрим примеры.

Пример 1

В остроугольном треугольнике ABC проведены высоты $AA_{1}$ , $BB_{1}$ , $CC_{1}$ . Пусть — точка пересечения высот. Построить треугольник $A_{1}B_{1}C_{1}$ и перечислить все образовавшиеся четырехугольники, около которых можно описать окружность (рис. 9).

Рис. 9

Решение:
Рассмотрим четырёхугольник $BA_{1}HC_{1}$ : прямые углы $BA_{1}H$ и $BC_{1}H$ опираются на один и тот же отрезок , который и будет диаметром описанной окружности. Аналогично для четырёхугольников: $AC_{1}A_{1}C$ (диаметр ); $BC_{1}B_{1}C$ (диаметр ); $BA_{1}B_{1}A$ (диаметр ); $CA_{1}HB_{1}$ (диаметр ); $AB_{1}HC_{1}$ (диаметр ).

Ответ:

$BA_{1}HC_{1}$ , $CA_{1}HB_{1}$ , $AC_{1}HB_{1}$ , $AC_{1}A_{1}C$ , $BC_{1}B_{1}C$ , $BA_{1}B_{1}A$ .

Пример 2

В остроугольном треугольнике ABC проведены высоты $AA_{1}$ и $CC_{1}$ . Доказать, что треугольник $A_{1}BC_{1}$ подобен данному треугольнику ABC с коэффициентом подобия, равным cos B .

Решение:
На стороне треугольника ABC как на диаметре опишем полуокружность, которая пройдет через основания высот $A_{1}$ и $C_{1}$ (рис. 10).

Рис. 10

Так как четырехугольник $AC_{1}A_{1}C$ вписанный, то $angle BAC = 180^circ - angle C_{1}A_{1}C.$ Следовательно, $angle BAC = angle C_{1}A_{1}B$ и $triangle A_{1}BC_{1} sim triangle ABC$ . Так как стороны $A_{1}B$ и являются соответствующими сторонами в подобных треугольниках, то их отношение $A_{1}B : AB$ равно коэффициенту подобия. Но в прямоугольном треугольнике $ABA_{1}$ отношение сторон $A_{1}B : AB = cos B$ . Итак, $triangle A_{1}BC_{1} sim triangle ABC$ и . Что и требовалось доказать.

Пример 3

Доказать, что около параллелограмма можно описать окружность тогда и только тогда, когда параллелограмм является прямоугольником.

Решение:
Покажем, что если параллелограмм можно вписать в окружность, то такой параллелограмм будет прямоугольником.
Действительно, пусть параллелограмм ABCD вписан в окружность. Тогда по теореме 1 . Но в параллелограмме противолежащие углы равны, поэтому .
Аналогично показывается, что и , а это и доказывает требуемое. Обратное утверждение очевидно.

Пример 4

Доказать, что параллелограмм, в который можно вписать окружность, является ромбом.

Решение:
Так как в описанном около окружности четырехугольнике суммы противолежащих сторон равны (теорема 5), то в случае параллелограмма это условие равносильно равенству смежных сторон. Следовательно, такой параллелограмм — ромб. Что и требовалось доказать.

Следствие 1

Параллелограмм, в который можно вписать окружность и около которого можно описать окружность, является квадратом.

Пример 5

Доказать, что около трапеции можно описать окружность тогда и только тогда, когда она является равнобочной.

Решение:
Рассмотрим трапецию ABCD с параллельными сторонами и (рис. 11).

Рис. 11

Так как сумма внутренних односторонних углов при параллельных прямых равна , то
А поскольку около трапеции можно описать окружность тогда и только тогда, когда сумма ее противолежащих углов равна (теорема 1), то . Таким образом, . Но эти вписанные углы измеряются соответственно половинами дуг BCD и ABC . Поэтому, так как дуга у дуг BCD и ABC общая, то вписанные углы, опирающиеся на дуги и , равны. Но тогда равными будут и дуги и . Но равные дуги стягиваются равными хордами, что и требовалось доказать.

Пример 6

Доказать, что если выпуклый четырехугольник имеет ось симметрии, то либо около него можно описать окружность, либо в него можно вписать окружность.

Решение:
Если ось симметрии не проходит ни через одну вершину четырехугольника, он представляет собой равнобочную трапецию или прямоугольник и является вписанным.
Рассмотрим случай, когда ось симметрии выпуклого четырехугольника, например, ABCD проходит через его вершину, скажем, . Тогда очевидно, что эта ось будет проходить и через противолежащую вершине вершину . Но в таком случае вершина будет симметрична вершине и, значит, сторона окажется симметричной стороне , а сторона будет симметрична стороне . Поэтому AB=AD , BC=CD и, таким образом, . Полученное равенство означает, что четырехугольник ABCD является описанным около окружности и это есть или дельтоид (рис. 12), или ромб. Что и требовалось доказать.

Рис. 12

Пример 7

Трапеция описана около окружности. Доказать, что концы боковой стороны трапеции и центр окружности являются вершинами прямоугольного треугольника.

Решение:
Рассмотрим описанную трапецию с параллельными сторонами и (рис. 13).

Рис. 13

Так как сумма внутренних односторонних углов при параллельных прямых равна , то .
А поскольку лучи и , где — центр вписанной в трапецию окружности, являются биссектрисами углов BCD и CDA соответственно, то и, таким образом, в треугольнике DOC угол COD с вершиной является прямым.
Аналогично показывается, что треугольник BOA также является прямоугольным, а это и доказывает требуемое.

Пример 8

Равнобочная трапеция описана около окружности. Найти радиус окружности, если основания трапеции равны и .

Решение:
Пусть в описанной равнобочной трапеции ABCD основание AD = a , а основание (рис. 14).

Рис. 14

Тогда из равенства сторон и и того, что (теорема 5), следует, что $AB = CD = frac{(a + b)}{2}$ .
Пусть и — перпендикуляры к основанию . Очевидно, что и AE = FD , а значит, четырехугольник EBCF — прямоугольник, у которого . Поэтому $AE = frac{AD - EF}{2} = frac{a - b}{2}$ . Из прямоугольного же треугольника BEA находим $BE = sqrt{{AB^2} - {AE^2}} = sqrt{(frac{a+b}{2})^2 - (frac{a - b}{2})^2} = sqrt{ab}$ и, таким образом, радиус вписанной в трапецию окружности равен $frac{sqrt{ab}}{2}$

Ответ:

$dfrac{sqrt{ab}}{2}$

Пример 9

Около окружности описана равнобочная трапеция, у которой средняя линия равна Определить периметр трапеции и ее боковую сторону.

Решение:
Пусть K, L, N — точки касания окружности с описанной около нее равнобочной трапецией ABCD (рис. 15) и пусть , а — средняя линия трапеции.

Рис. 15

Тогда , а DN = DL . Поэтому DM = DC . Но поскольку отрезок $DM = frac{1}{2}(BC + AD) = EF = m$ , то DC = m . Отсюда периметр трапеции ABCD — это .

Ответ:

4 m; m

Пример 10

Доказать, что если центр вписанной в четырехугольник окружности совпадает с точкой пересечения диагоналей, то этот четырехугольник — ромб. Верно и обратное.

Решение:
Пусть точка — центр окружности, вписанной в четырехугольник ABCD (рис.16), — точки касания окружности с четырехугольником.

Рис. 16

Так как , то и, значит, Треугольники ABC и ADC — равнобедренные и — биссектриса, поэтому — равнобедренный и Тогда , т. е. четырехугольник ABCD — ромб. Наоборот, если — точка пересечения диагоналей ромба, которые по свойству ромба лежат на биссектрисах его углов, то расстояния от точки до каждой из сторон ромба равны. Отсюда и следует, что точка — центр вписанной в ромб окружности. Что и требовалось доказать.

Источник

В этой статье мы рассмотрим все основные свойства и признаки четырехугольника.

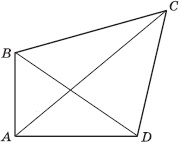
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Четырехугольники бывают выпуклые, если они расположены в одной полуплоскости относительно прямой, которая содержит одну из его сторон (ABCD) и невыпуклые (A₁B₁C₁D₁).

Если любые две противолежащие точки выпуклого четырёхугольника соединить между собой отрезком, то весь отрезок будет лежать внутри многоугольника. Для невыпуклого четырёхугольника это не выполняется (рисунок ниже).

Диагонали выпуклого четырёхугольника лежат внутри него и пересекаются. Одна из диагоналей невыпуклого четырёхугольника лежит снаружи, а другая внутри него, и эти диагонали не пересекаются.

Определения для четырехугольника

Данный четырёхугольник обозначается ABCD.
Точки A, B, C, D называются его вершинами, а отрезки AB, BC, CD, DA – его сторонами.
Смежные стороны – соседние стороны, имеющие общую вершину. Пары смежных сторон: AB и AD, AB и BC, BC и CD, CD и AD.
Противолежащие стороны – несмежные стороны, не имеющие общих вершин. Пары противолежащих сторон: AB и CD, BC и AD.
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. AC и BD – диагонали четырехугольника ABCD.

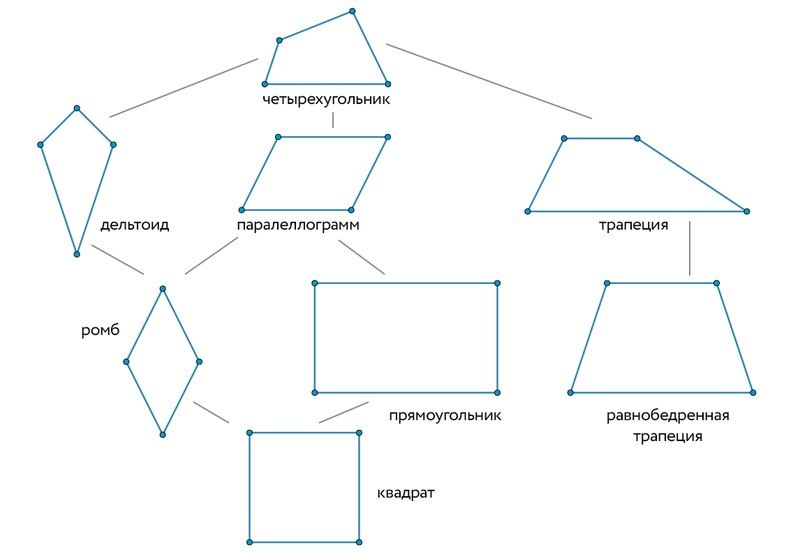
Виды четырехугольников:

Если рассмотреть схему, то каждый следующий четырехугольник обладает всеми свойствами предыдущего. Поэтому запоминать надо совсем немного.

Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны. Трапеции бывают: произвольная, равносторонняя, прямоугольная.

Параллелограмм — это четырехугольник у которого противолежащие стороны параллельны. В параллелограмме:
— противоположные стороны и противоположные углы равны.
— диагонали параллелограмма делятся точкой пересечения пополам.
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.

Прямоугольник — это параллелограмм, у которого все углы прямые. Прямоугольник является частным случаем параллелограмма, поэтому обладает всеми его свойствами.

Ромб — это параллелограмм, у которого все стороны равны. Ромб является частным случаем параллелограмма, поэтому обладает всеми его свойствами. В ромбе:
— противоположные углы равны,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали ромба являются биссектрисами углов.

Квадрат — это прямоугольник, у которого все стороны равны. Квадрат является частным случаем прямоугольника и частным случаем ромба, поэтому обладает всеми их свойствами. В квадрате:
— все углы равны 90 градусов,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали являются биссектрисами углов,
— диагонали равны.

Свойства углов четырехугольника

Сумма углов четырёхугольника равна 360°
Сумма внешних углов четырехугольника, взятых по одному при каждой вершине, равна 360°.
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.

Свойства сторон четырехугольника

Каждая сторона четырехугольника меньше суммы всех его других сторон.
Сумма диагоналей меньше его периметра.

Четырехугольник и окружность

Четырехугольник вокруг окружности.

Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны (AB+CD=AD+BC).
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырехугольник внутри окружности.

Вписанный четырёхугольник — это четырёхугольник, все вершины которого лежат на одной окружности. Эта окружность называется описанной.
Вокруг четырёхугольника можно описать окружность, если сумма двух его противоположных углов равна 180°.
Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон (AC*BD=AB*CD+AD*BC).

Частные случаи:

Параллелограмм, вписанный в окружность – это прямоугольник, центр окружности совпадает с точкой пересечения диагоналей.
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.

Диагонали четырехугольника

Диагонали выпуклого четырёхугольника пересекаются в одной точке.
Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.

Периметр и площадь четырехугольника

Периметр четырёхугольника равен сумме длин всех его сторон: где a, b, c, d – длины сторон четырёхугольника.

Площадь произвольного выпуклого четырёхугольника можно найти по формуле: где d1 и d2— диагонали четырёхугольника, a — угол между диагоналями.

Площадь вписанного четырёхугольника может быть вычислена по формуле: 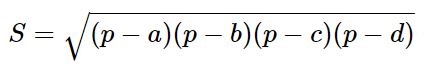где a, b, c, d – длины сторон четырёхугольника, p=(a+b+c+d)/2 – его полупериметр.

Площадь описанного четырёхугольника равна произведению его полупериметра на радиус вписанной окружности:

Источник

Кто сейчас на конференции

Содержание

Четырехугольник

Мнемоника

Окружность вписанная в четырехугольник

Почему нельзя вписать окружность?

Задача

Окружность, описанная около четырехугольника

Задача 1

Задача 2

Задача 3

Центр тяжести

Распределительное свойство центров тяжести

Центр тяжести четырехугольника

(1)

(2)

Метод отвеса

Метод балансировки

С помощью геометрического разложения

Центр тяжести объекта в форме буквы L

Барицентр

Барицентрическая система отсчета

Барицентрические координаты

Случай двух тел

Simple quadrilaterals[edit]

Convex quadrilateral[edit]

Concave quadrilaterals[edit]

Complex quadrilaterals[edit]

Special line segments[edit]

Area of a convex quadrilateral[edit]

Trigonometric formulas[edit]

Non-trigonometric formulas[edit]

Vector formulas[edit]

Diagonals[edit]

Properties of the diagonals in quadrilaterals[edit]

Lengths of the diagonals[edit]

Generalizations of the parallelogram law and Ptolemy’s theorem[edit]

Other metric relations[edit]

Angle bisectors[edit]

Bimedians[edit]

Trigonometric identities[edit]

Inequalities[edit]

Area[edit]

Diagonals and bimedians[edit]

Sides[edit]

Maximum and minimum properties[edit]

Remarkable points and lines in a convex quadrilateral[edit]

Other properties of convex quadrilaterals[edit]

Taxonomy[edit]

Skew quadrilaterals[edit]

See also[edit]

References[edit]

External links[edit]

Определения для четырехугольника

Виды четырехугольников:

Свойства углов четырехугольника

Свойства сторон четырехугольника

Четырехугольник и окружность

Диагонали четырехугольника

Периметр и площадь четырехугольника

Не пропустите также: