Окружность, вписанная в правильный треугольник
Окружность, вписанная в правильный треугольник, помимо свойств вписанной в произвольный треугольник окружности, обладает своими собственными свойствами.
1) Центр вписанной в треугольник окружности — точка пересечения его биссектрис.
Поскольку в равностороннем треугольнике биссектрисы, медианы и высоты совпадают, то центр вписанной в правильный треугольник окружности является точкой пересечения не только его биссектрис, но также медиан и высот.
Например, в правильном треугольнике ABC AB=BC=AC=a
точка O — центр вписанной окружности.
AK, BF и CD — биссектрисы, медианы и высоты треугольника ABC.
2) Расстояние от центра вписанной окружности до точки касания её со стороной треугольника равно радиусу. Так как центр вписанной в правильный треугольник окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус вписанной в равносторонний треугольник окружности равен одной третьей длины медианы:
Таким образом, формула для радиуса вписанной в правильный треугольник окружности
Обратно, сторона равностороннего треугольника через радиус вписанной окружности:
3) Так как формула для нахождения площади равностороннего треугольника через сторону
можем найти площадь через r:
Таким образом, формула площади правильного треугольника через радиус вписанной окружности —
3) Все отрезки, на которые стороны равностороннего треугольника делятся точками касания вписанной окружности, равны половине его стороны:
4) Центр вписанной в правильный треугольник окружности является также центром описанной около него окружности.
5) Радиус вписанной в равносторонний треугольник окружности в два раза меньше радиуса описанной окружности:
Свойства равностороннего треугольника: теория и пример задачи
В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
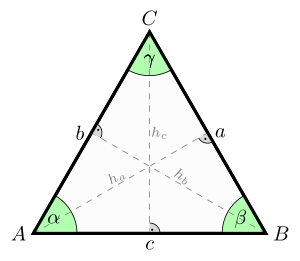
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Центр треугольника
Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.
Существует несколько понятий центра для треугольника.
Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.
Ортоцентр — точка пересечения его высот.
Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.
Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).
Как найти центр треугольника
Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.
Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.
Центр равностороннего треугольника является также центром вписанной и описанной окружности.
Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.
Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:
- ввести в поле калькулятора координаты вершин треугольника;
- нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.
Свойства равностороннего треугольника
Свойство 1. В равностороннем треугольнике все углы равны между собой и равны ({{60}^{o }})
Естественно, не правда ли? Три одинаковых угла, в сумме ({{180}^{o }}), значит, каждый по ({{60}^{o }})
Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).
Почему так? А посмотрим-ка на равносторонний треугольник.
Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!
В равностороннем треугольнике оказалось не (12) особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.
Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. (R=2cdot r)
Уже должно быть очевидно, отчего так.
Посмотри на рисунок: точка( O) – центр треугольника.
Значит, (OB) – радиус описанной окружности (обозначили его (R)), а (OK) – радиус вписанной окружности (обозначим (r)).
Но ведь точка (O) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Поэтому (OB=2cdot OK), то есть (R=2cdot r).
Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.
Давай удостоверимся в этом.
Центр треугольника
Точка, прямая, плоскость
Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.
Существует несколько понятий центра для треугольника.
Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.
Ортоцентр — точка пересечения его высот.
Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.
Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).
Как найти центр треугольника
Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.
Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.
Центр равностороннего треугольника является также центром вписанной и описанной окружности.
Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.
Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:
- ввести в поле калькулятора координаты вершин треугольника;
- нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.
From Wikipedia, the free encyclopedia
| Equilateral triangle | |
|---|---|
 |
|
| Type | Regular polygon |
| Edges and vertices | 3 |
| Schläfli symbol | {3} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | D3 |
| Area |  |
| Internal angle (degrees) | 60° |
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
Principal properties[edit]
An equilateral triangle. It has equal sides (


Denoting the common length of the sides of the equilateral triangle as 
Denoting the radius of the circumscribed circle as R, we can determine using trigonometry that:
- The area of the triangle is
Many of these quantities have simple relationships to the altitude («h») of each vertex from the opposite side:
In an equilateral triangle, the altitudes, the angle bisectors, the perpendicular bisectors, and the medians to each side coincide.
Characterizations[edit]
A triangle 













Sides[edit]
Semiperimeter[edit]
Angles[edit]
Area[edit]
Circumradius, inradius, and exradii[edit]
Equal cevians[edit]
Three kinds of cevians coincide, and are equal, for (and only for) equilateral triangles:[7]
- The three altitudes have equal lengths.
- The three medians have equal lengths.
- The three angle bisectors have equal lengths.
Coincident triangle centers[edit]
Every triangle center of an equilateral triangle coincides with its centroid, which implies that the equilateral triangle is the only triangle with no Euler line connecting some of the centers. For some pairs of triangle centers, the fact that they coincide is enough to ensure that the triangle is equilateral. In particular:
- A triangle is equilateral if any two of the circumcenter, incenter, centroid, or orthocenter coincide.[8]: p.37
- It is also equilateral if its circumcenter coincides with the Nagel point, or if its incenter coincides with its nine-point center.[6]
Six triangles formed by partitioning by the medians[edit]
For any triangle, the three medians partition the triangle into six smaller triangles.
- A triangle is equilateral if and only if any three of the smaller triangles have either the same perimeter or the same inradius.[9]: Theorem 1
- A triangle is equilateral if and only if the circumcenters of any three of the smaller triangles have the same distance from the centroid.[9]: Corollary 7
Points in the plane[edit]
Notable theorems[edit]
Visual proof of Viviani’s theorem
Morley’s trisector theorem states that, in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle.
Napoleon’s theorem states that, if equilateral triangles are constructed on the sides of any triangle, either all outward, or all inward, the centers of those equilateral triangles themselves form an equilateral triangle.
A version of the isoperimetric inequality for triangles states that the triangle of greatest area among all those with a given perimeter is equilateral.[11]
Viviani’s theorem states that, for any interior point 




independent of the location of 
Pompeiu’s theorem states that, if 








Geometric construction[edit]
Construction of equilateral triangle with compass and straightedge
An equilateral triangle is easily constructed using a straightedge and compass, because 3 is a Fermat prime. Draw a straight line, and place the point of the compass on one end of the line, and swing an arc from that point to the other point of the line segment. Repeat with the other side of the line. Finally, connect the point where the two arcs intersect with each end of the line segment
An alternative method is to draw a circle with radius 
In both methods a by-product is the formation of vesica piscis.
The proof that the resulting figure is an equilateral triangle is the first proposition in Book I of Euclid’s Elements.
Derivation of area formula[edit]
The area formula 

Using the Pythagorean theorem[edit]
The area of a triangle is half of one side 

An equilateral triangle with a side of 2 has a height of √3, as the sine of 60° is √3/2.
The legs of either right triangle formed by an altitude of the equilateral triangle are half of the base 

so that
Substituting 

Using trigonometry[edit]
Using trigonometry, the area of a triangle with any two sides 


Each angle of an equilateral triangle is 60°, so
The sine of 60° is 
since all sides of an equilateral triangle are equal.
Other properties[edit]
An equilateral triangle is the most symmetrical triangle, having 3 lines of reflection and rotational symmetry of order 3 about its center, whose symmetry group is the dihedral group of order 6, 
By Euler’s inequality, the equilateral triangle has the smallest ratio of the circumradius 

Given a point 








For any point 






For any point 



where 


For any point 



For any point 







Moreover, if point 








which also equals 

which is the optic equation.
For an equilateral triangle:
- The ratio of its area to the area of the incircle,
, is the largest of any triangle.[21]: Theorem 4.1
- The ratio of its area to the square of its perimeter,
is larger than that of any non-equilateral triangle.[11]
If a triangle is placed in the complex plane with complex vertices 



The equilateral triangle tiling fills the plane.
Notably, the equilateral triangle tiles two dimensional space with six triangles meeting at a vertex, whose dual tessellation is the hexagonal tiling. 3.122, 3.4.6.4, (3.6)2, 32.4.3.4, and 34.6 are all semi-regular tessellations constructed with equilateral triangles.[23]
A regular tetrahedron is made of four equilateral triangles.
In three dimensions, equilateral triangles form faces of regular and uniform polyhedra. Three of the five Platonic solids are composed of equilateral triangles: the tetrahedron, octahedron and icosahedron.[24]: p.238 In particular, the tetrahedron, which has four equilateral triangles for faces, can be considered the three-dimensional analogue of the triangle. All Platonic solids can inscribe tetrahedra, as well as be inscribed inside tetrahedra. Equilateral triangles also form uniform antiprisms as well as uniform star antiprisms in three-dimensional space. For antiprisms, two (non-mirrored) parallel copies of regular polygons are connected by alternating bands of 
As a generalization, the equilateral triangle belongs to the infinite family of 

In culture and society[edit]
Equilateral triangles have frequently appeared in man made constructions:
- The shape occurs in modern architecture such as the cross-section of the Gateway Arch.[29]
- Its applications in flags and heraldry includes the flag of Nicaragua[30] and the flag of the Philippines.[31]
- It is a shape of a variety of road signs, including the yield sign.[32]
See also[edit]
- Almost-equilateral Heronian triangle
- Isosceles triangle
- Ternary plot
- Trilinear coordinates
References[edit]
- ^ Bencze, Mihály; Wu, Hui-Hua; Wu, Shan-He (2008). «An equivalent form of fundamental triangle inequality and its applications» (PDF). Journal of Inequalities in Pure and Applied Mathematics. 10 (1): 1–6 (Article No. 16). ISSN 1443-5756. MR 2491926. S2CID 115305257. Zbl 1163.26316.
- ^ Dospinescu, G.; Lascu, M.; Pohoata, C.; Letiva, M. (2008). «An elementary proof of Blundon’s inequality» (PDF). Journal of Inequalities in Pure and Applied Mathematics. 9 (4): 1-3 (Paper No. 100). ISSN 1443-5756. S2CID 123965364. Zbl 1162.51305.
- ^ Blundon, W. J. (1963). «On Certain Polynomials Associated with the Triangle». Mathematics Magazine. Taylor & Francis. 36 (4): 247–248. doi:10.2307/2687913. JSTOR 2687913. S2CID 124726536. Zbl 0116.12902.
- ^ a b Alsina, Claudi; Nelsen, Roger B. (2009). When less is more. Visualizing basic inequalities. Dolciani Mathematical Expositions. Vol. 36. Washington, D.C.: Mathematical Association of America. pp. 71, 155. doi:10.5948/upo9781614442028. ISBN 978-0-88385-342-9. MR 2498836. OCLC 775429168. S2CID 117769827. Zbl 1163.00008.
- ^ a b Pohoata, Cosmin (2010). «A new proof of Euler’s inradius — circumradius inequality» (PDF). Gazeta Matematica Seria B (3): 121–123. S2CID 124244932.
- ^ a b c Andreescu, Titu; Andrica, Dorian (2006). Complex Numbers from A to…Z (1st ed.). Boston, MA: Birkhäuser. pp. 70, 113–115. doi:10.1007/0-8176-4449-0. ISBN 978-0-8176-4449-9. OCLC 871539199. S2CID 118951675.
- ^ Owen, Byer; Felix, Lazebnik; Deirdre, Smeltzer (2010). Methods for Euclidean Geometry. Classroom Resource Materials. Vol. 37. Washington, D.C.: Mathematical Association of America. pp. 36, 39. doi:10.5860/choice.48-3331. ISBN 9780883857632. OCLC 501976971. S2CID 118179744.
- ^ Yiu, Paul (1998). «Notes on Euclidean Geometry» (PDF). Florida Atlantic University, Department of Mathematical Sciences (Course Notes).
- ^ a b Cerin, Zvonko (2004). «The vertex-midpoint-centroid triangles» (PDF). Forum Geometricorum. 4: 97–109.
- ^ a b «Inequalities proposed in «Crux Mathematicorum»» (PDF).
- ^ a b Chakerian, G. D. «A Distorted View of Geometry.» Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
- ^ a b c Posamentier, Alfred S.; Salkind, Charles T. (1996). Challenging Problems in Geometry. Dover Publ.
- ^ Conway, J. H., and Guy, R. K., «The only rational triangle», in The Book of Numbers, 1996, Springer-Verlag, pp. 201 and 228–239.
- ^ Leon Bankoff and Jack Garfunkel, «The heptagonal triangle», Mathematics Magazine 46 (1), January 1973, 7–19,
- ^ Dörrie, Heinrich (1965). 100 Great Problems of Elementary Mathematics. Dover Publ. pp. 379–380.
- ^ Svrtan, Dragutin; Veljan, Darko (2012). «Non-Euclidean versions of some classical triangle inequalities» (PDF). Forum Geometricorum. 12: 197–209.
- ^ Lee, Hojoo (2001). «Another proof of the Erdős–Mordell Theorem» (PDF). Forum Geometricorum. 1: 7–8.
- ^ Gardner, Martin, «Elegant Triangles», in the book Mathematical Circus, 1979, p. 65.
- ^ Meskhishvili, Mamuka (2021). «Cyclic Averages of Regular Polygonal Distances» (PDF). International Journal of Geometry. 10: 58–65.
- ^ De, Prithwijit (2008). «Curious properties of the circumcircle and incircle of an equilateral triangle» (PDF). Mathematical Spectrum. 41 (1): 32–35.
- ^ Minda, D.; Phelps, S. (2008). «Triangles, ellipses, and cubic polynomials». American Mathematical Monthly. 115 (October): 679–689. doi:10.1080/00029890.2008.11920581. JSTOR 27642581. S2CID 15049234.
- ^ Dao, Thanh Oai (2015). «Equilateral triangles and Kiepert perspectors in complex numbers» (PDF). Forum Geometricorum. 15: 105–114.
- ^ Grünbaum, Branko; Shepard, Geoffrey (November 1977). «Tilings by Regular Polygons» (PDF). Mathematics Magazine. Taylor & Francis, Ltd. 50 (5): 231–234. doi:10.2307/2689529. JSTOR 2689529. MR 1567647. S2CID 123776612. Zbl 0385.51006.
- ^ a b Johnson, Norman W. (2018). Geometries and Transformations (1st ed.). Cambridge: Cambridge University Press. pp. xv, 1–438. doi:10.1017/9781316216477. ISBN 978-1107103405. S2CID 125948074. Zbl 1396.51001.
- ^ Cromwell, Peter T. (1997). «Chapter 2: The Archimedian solids». Polyhedra (1st ed.). New York: Cambridge University Press. p. 85. ISBN 978-0521664059. MR 1458063. OCLC 41212721. Zbl 0888.52012.
- ^ Klitzing, Richard. «n-antiprism with winding number d». Polytopes & their Incidence Matrices. bendwavy.org (Anton Sherwood). Retrieved 2023-03-09.
- ^ Webb, Robert. «Stella Polyhedral Glossary». Stella. Retrieved 2023-03-09.
- ^ H. S. M. Coxeter (1948). Regular Polytopes (1 ed.). London: Methuen & Co. LTD. pp. 120–121. OCLC 4766401. Zbl 0031.06502.
- ^ Pelkonen, Eeva-Liisa; Albrecht, Donald, eds. (2006). Eero Saarinen: Shaping the Future. Yale University Press. pp. 160, 224, 226. ISBN 978-0972488129.
- ^ White, Steven F.; Calderón, Esthela (2008). Culture and Customs of Nicaragua. Greenwood Press. p. 3. ISBN 978-0313339943.
- ^ Guillermo, Artemio R. (2012). Historical Dictionary of the Philippines. Scarecrow Press. p. 161. ISBN 978-0810872462.
- ^ Riley, Michael W.; Cochran, David J.; Ballard, John L. (December 1982). «An Investigation of Preferred Shapes for Warning Labels». Human Factors: The Journal of the Human Factors and Ergonomics Society. 24 (6): 737–742. doi:10.1177/001872088202400610. S2CID 109362577.
External links[edit]
- Weisstein, Eric W. «Equilateral Triangle». MathWorld.
Fundamental convex regular and uniform polytopes in dimensions 2–10 |
|||||
|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn |
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon |
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | |
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell |
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | ||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | |
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | |
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | |
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | ||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | ||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope |
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds |
Окружность, вписанная в правильный треугольник, помимо свойств вписанной в произвольный треугольник окружности, обладает своими собственными свойствами.
1) Центр вписанной в треугольник окружности — точка пересечения его биссектрис.
Поскольку в равностороннем треугольнике биссектрисы, медианы и высоты совпадают, то центр вписанной в правильный треугольник окружности является точкой пересечения не только его биссектрис, но также медиан и высот.

точка O — центр вписанной окружности.
AK, BF и CD — биссектрисы, медианы и высоты треугольника ABC.
2) Расстояние от центра вписанной окружности до точки касания её со стороной треугольника равно радиусу. Так как центр вписанной в правильный треугольник окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус вписанной в равносторонний треугольник окружности равен одной третьей длины медианы:
Таким образом, формула для радиуса вписанной в правильный треугольник окружности
Обратно, сторона равностороннего треугольника через радиус вписанной окружности:
3) Так как формула для нахождения площади равностороннего треугольника через сторону
можем найти площадь через r:
Таким образом, формула площади правильного треугольника через радиус вписанной окружности —
3) Все отрезки, на которые стороны равностороннего треугольника делятся точками касания вписанной окружности, равны половине его стороны:
4) Центр вписанной в правильный треугольник окружности является также центром описанной около него окружности.
5) Радиус вписанной в равносторонний треугольник окружности в два раза меньше радиуса описанной окружности:









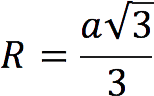


















![{displaystyle p^{4}+q^{4}+t^{4}=3left[left(R^{2}+L^{2}right)^{2}+2R^{2}L^{2}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b9926a561be54775a0fa6d3c7fc03ccf00c2378)











