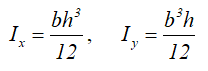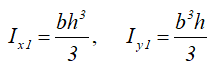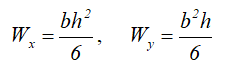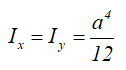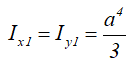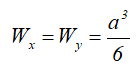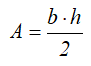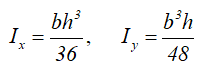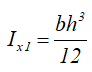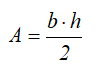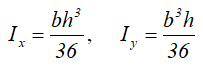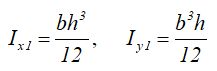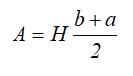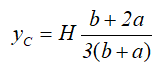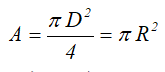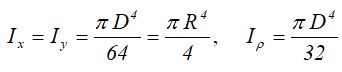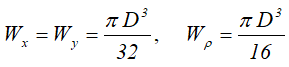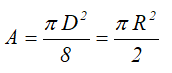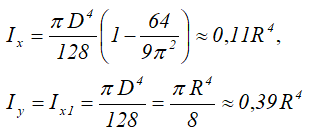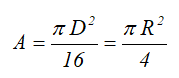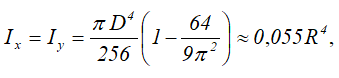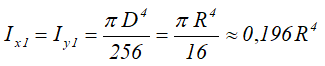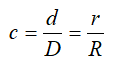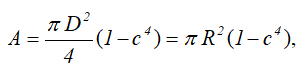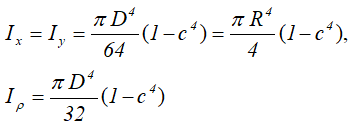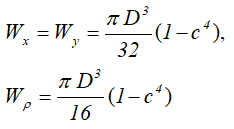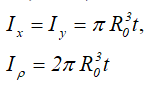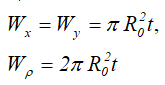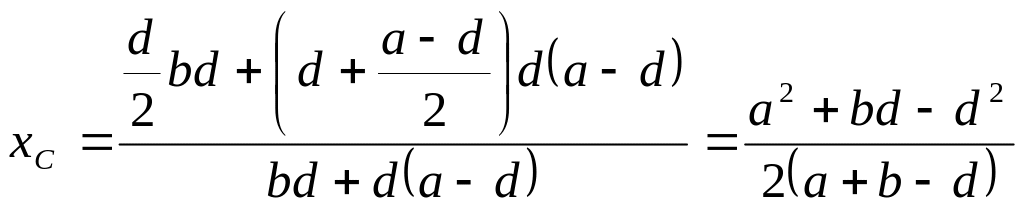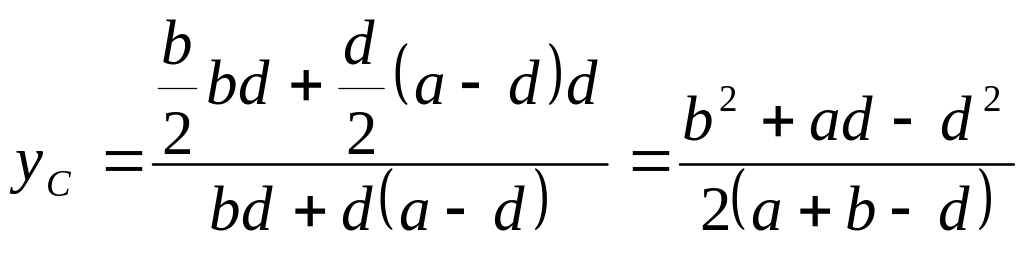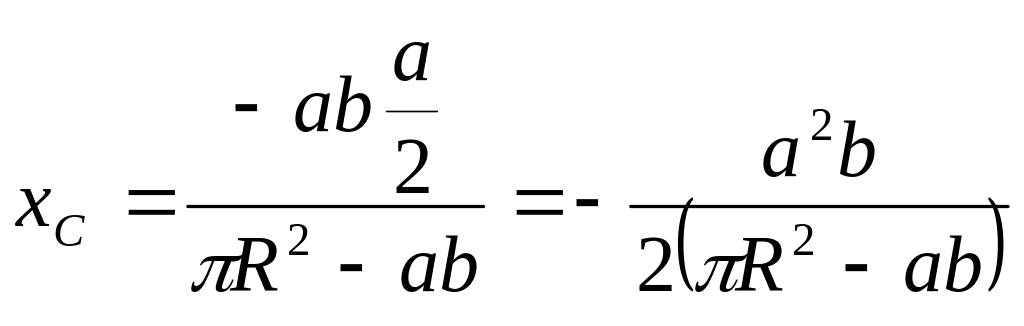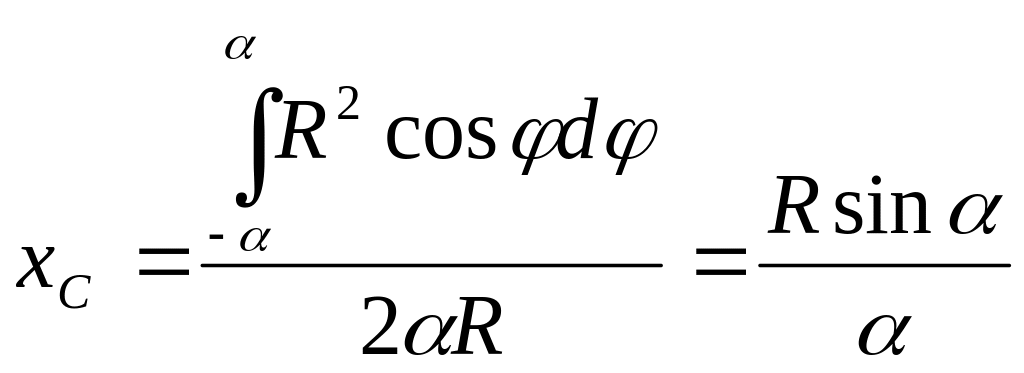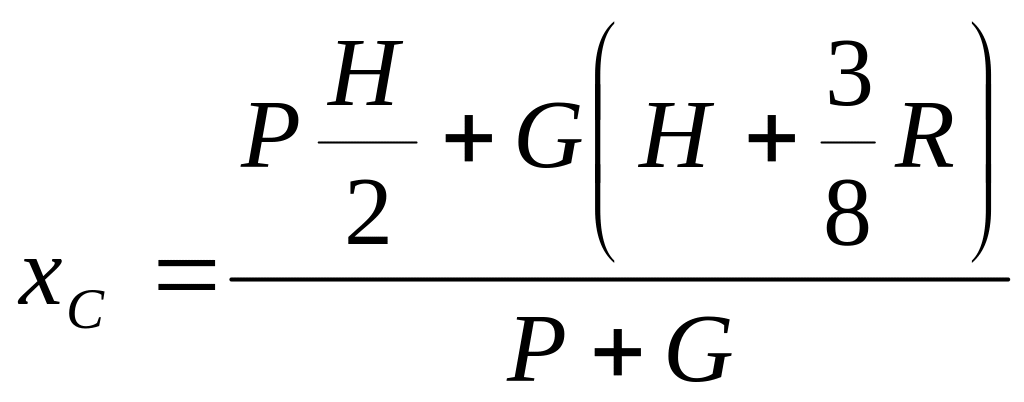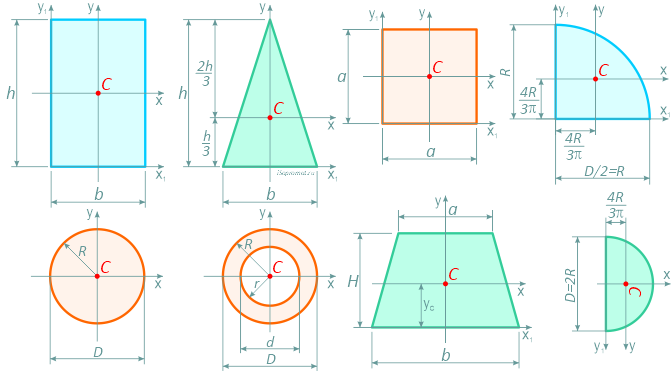
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.
Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
Ix , Iy — осевые моменты инерции сечения относительно главных осей;
Ix1 , Iy1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
Iρ — полярный момент инерции сечения;
Wx , Wy — осевые моменты сопротивления;
Wρ — полярный момент сопротивления
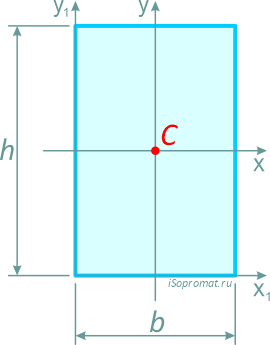
Прямоугольник
Прямоугольник высотой h и шириной b.
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.
Площадь
Центральные осевые моменты инерции прямоугольника
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевые моменты сопротивления прямоугольного сечения
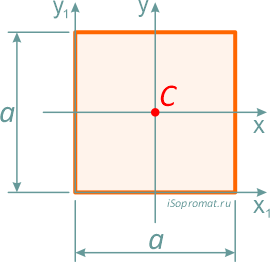
Квадрат
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.
Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.
Площадь
Центральные осевые моменты инерции квадрата
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевой момент сопротивления квадратного сечения
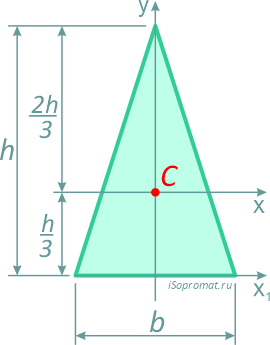
Треугольник равнобедренный
Равнобедренный треугольник высотой h и шириной основания b.
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.
Площадь
Центральные осевые моменты инерции треугольника
Момент инерции относительно смещенной оси x1, проходящей через его основание
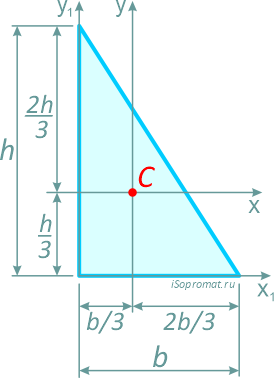
Прямоугольный треугольник
Прямоугольный треугольник высотой h и шириной основания b.
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.
Площадь
Центральные осевые моменты инерции прямоугольного треугольника
Моменты инерции относительно смещенных осей x1 и y1, проходящих через точку, соединяющую его катеты
Трапеция
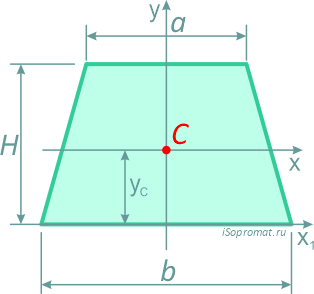
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.
Площадь трапеции
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:
Круг
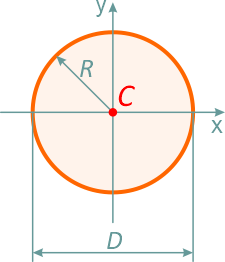
Круг диаметром D (d) или радиусом R (r)
Площадь круга через его диаметр и радиус
Центральные осевые и полярный моменты инерции круга
Осевые и полярный моменты сопротивления
Полукруг
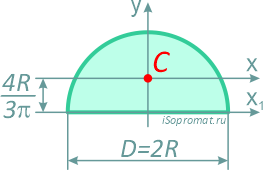
Половина круга диаметром D (d) или радиусом R (r)
Площадь
Осевые моменты инерции полукруга
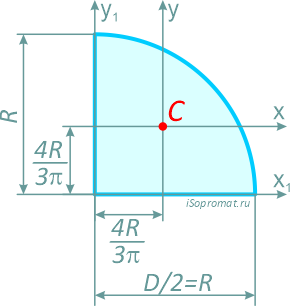
Четверть круга
Четверть круга диаметром D (d) или радиусом R (r)
Площадь
Центральные осевые моменты инерции четверти круга
Моменты инерции относительно смещенных осей x1 и y1
Кольцо
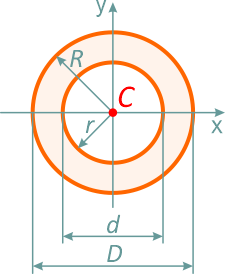
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.
Площадь
Центральные осевые и полярный моменты инерции кольца
Осевые и полярный моменты сопротивления
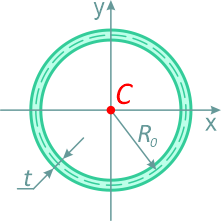
Тонкостенное сечение (труба)
Тонкостенный профиль (сечение трубы) средним радиусом R0 и толщиной стенки трубы t при R0>>t
Площадь
Центральные осевые и полярный моменты инерции трубного сечения
Осевые и полярный моменты сопротивления
Пример определения координат центра тяжести сложной фигуры:
Другие видео
Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
The formula for the distance from the base $b$ to the center of mass of a trapezoid
is
$$bar y = frac{b+2a}{3(a+b)} h.$$
You can find this in many on-line sources such as Wolfram Mathworld.
You can prove this by integrating $int_0^h y(b + (a-b)frac yh) dy$
and dividing by the area of the trapezoid. But here’s a derivation without calculus,
using the fact that the distance from a side of a triangle to the triangle’s
centroid is $frac13$ the height of the triangle.
Let $T$ be a trapezoid with bases $a$ and $b$.
For the case $a < b$, extend the non-parallel sides of the trapezoid
until they intersect. The base $b$ of the trapezoid and the two extended
sides form a triangle $B$; the base $a$ divides this triangle into two pieces,
one of which is $T$ and the other of which is a triangle which we’ll call $A$.
If the height of the trapezoid $T$ is $h$, the height of $B$ is $frac{b}{b-a}h.$
The centroid of $B$ is at a distance $frac{b}{3(b-a)}h$ from base $b$.
But another way to find the centroid of $B$ is to balance the two figures
$A$ and $T$ that compose $B$.
The triangle $A$ has height $frac{a}{b-a}h$, so its area is
$frac{a^2}{2(b-a)}h$ and its centroid is a distance $frac{a}{3(b-a)}h + h$
from the base $b$ of the trapezoid.
Trapezoid $T$ has area $frac{a+b}{2} h$ and a centroid at the unknown
distance $bar y$ from base $b$.
To «balance» the two regions, we take a weighted average
of the distance of their centroids from base $b$.
The «weights» in this average are just the areas of the two regions.
This weighted average is the same as the distance of the centroid of $B$
(the combined figure) from base $b$.
That is,
$$begin{eqnarray}
frac{b}{3(b-a)}h
&=&frac{mathop{Area}(A) cdot left(frac{a}{3(b-a)}h + hright)
+ mathop{Area}(T) cdot bar y}{mathop{Area}(A) + mathop{Area}(T)}\
&=&frac{frac{a^2}{2(b-a)}h cdot left(frac{a}{3(b-a)} + 1right)h
+ frac{a+b}{2} h cdot bar y}{frac{a^2}{2(b-a)}h + frac{a+b}{2} h}\
end{eqnarray}$$
Solve for $bar y$. This looks messy, but it can be simplified if you
realize that
$$frac{mathop{Area}(T)}{mathop{Area}(A)} = frac{b^2 — a^2}{a^2}.$$
If you divide both the numerator and denominator on the
right-hand side of the weighted average by $mathop{Area}(A)$, you get
$$
frac{b}{3(b-a)}h
= frac{ frac{3b — 2a}{3(b-a)} h
+ frac{b^2 — a^2}{a^2} cdot bar y}{1 + frac{b^2 — a^2}{a^2}}
$$
After you finish collecting all the terms in
$a$, $b$, and $h$ on the left side of this equation, and factor
$(b-a)^2$ out of $b^3 — 3ba + 2a^3$, it all simplifies to the formula
for $bar y$ shown above.
Очень часто при попытке найти центр тяжести трапеции ошибочно полагают, что он находится в точке пересечения диагоналей, в центре описанной окружности и т.д. Это совершенно неправильно.
Для произвольной трапеции (то есть она может быть прямоугольной, тупоугольной, равнобокой или любой другой) справедливо то, что центр ее тяжести лежит на прямой, которая соединяет середины оснований трапеции.
Найти, в какой именно точке этой прямой находится точка центра тяжести поможет следующая формула:
Данная формула показывает расстояние на прямой, которая соединяет середины оснований трапеции, от меньшего основания до центра тяжести трапеции.
Рассмотрим на примере возможность нахождения центра тяжести
Пример.
Высота трапеции равна 13 см, а основания 17 см и 29 см. Найдем расстояние, на котором расположен центр тяжести от большего основания трапеции.
Решение.
Воспользуемся формулой и найдем расстояние от меньшего основания до центра тяжести:
(см).
Найдем расстояние от большего основания до центра тяжести:
(см).
Ответ. (см).
Во многих случаях
центр тяжести тела можно определить с
помощью весьма простых методов. Рассмотрим
некоторые из них.
Симметрия. Если
тело однородно и имеет плоскость
симметрии, то задача определения центра
тяжести несколько упрощается.
Если однородное
тело имеет плоскость симметрии, то центр
тяжести лежит в этой плоскости.
Пусть однородное
тело имеет ось симметрии.
Если однородное
тело имеет ось симметрии, то его центр
тяжести лежит на этой оси.
Аналогично можно
показать, что если
однородное тело имеет ось симметрии,
то центр тяжести тела будет совпадать
с этой точкой.
Так, например, для
пластины, имеющей прямоугольную форму,
центр тяжести лежит в центре прямоугольника.
Разбиение. Иногда
представляется возможным разбить тело
на такие части, для которых вес и положение
центра тяжести заранее известны.
.
(8.19)
Для однородной
пластины, например, из формулы (8.19)
следует
,
,
(8.20) где
– площади частей плоской фигуры
,
– координаты центров тяжести этих
частей.
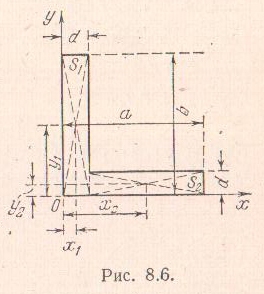
Задача 8.1. Способом разбиения найти
координаты центра тяжести площади
неравнобокого угольника, размеры
которого указаны на рис.
Решение. Разобьем угольник на два
прямоугольника, площади которых равны
,
.
На основании (8.20) формулы для координат
центра тяжести угольника имеют вид
,
,
где
,
– координаты центра тяжести первого
прямоугольника, а
,
– координаты центра тяжести второго
треугольника.
Очевидно, что
,
,
,
.
Таким образом, имеем
,
.
Отрицательные
веса. Этот
способ применяют при нахождении центра
тяжести тела, имеющего свободные (т.е.
пустые полости). Центр тяжести тела,
имеющего полости определяет вектор
.
(
8.21)
Таким образом, при нахождении центра
тяжести тела, имеющего свободные полости,
следует применять способ разбиения, но
считать, что полости имеют отрицательные
веса.
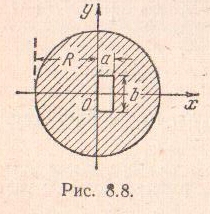
Задача 8.2. Найти центр тяжести
однородной круглой пластины радиуса
,
у которой вырезано отверстие в виде
прямоугольника со сторонами
и
,
использовав способ отрицательных весов.
П
ластина
симметрична относительно оси
;
следовательно,
.
Остается найти лишь одну координату
.
Согласно (8.21) будем иметь
.
где
,
,
,
.
Таким образом,
.
8.4. Центры тяжести простейших фигур
Ц
ентр
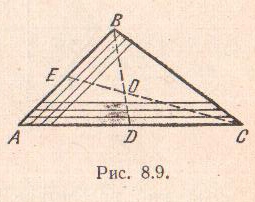
тяжести треугольника. Воспользуемся
способом разбиения и разделим треугольник
АВС
на элементарные полоски, проведя линии,
параллельные стороне АС
треугольника. Каждую такую полоску
можно принять за прямоугольник; центры
тяжести этих прямоугольников находятся
в их серединах, т.е. на медиане BD
треугольника. Следовательно, центр
тяжести треугольника должен лежать на
этой же медиане BD.
Разбивая теперь
треугольник на элементарные полоски
линиями, параллельными стороне АВ,
заключаем, что центр тяжести треугольника
должен быть расположен на медиане ЕС.
С
ледовательно,
центр
тяжести треугольника находится в точке
пересечения его медиан.
Эта точка, как известно, делит каждую
из медиан на отрезки в отношении
,
т.е
.
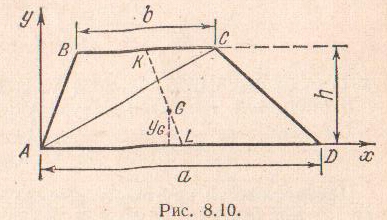
Центр тяжести
трапеции. Аналогично
предыдущему, разобьем трапецию ABCD
на элементарные полоски, параллельные
основаниям ВС
и АD.
Центры тяжести полосок расположатся
на прямой KL,
соединяющей середины оснований трапеции.
Следовательно, и центр тяжести трапеции
лежит на этой прямой. Для того, чтобы
найти его расстояние
от нижнего основания, разобьем трапецию
на треугольники АВС
и АСD.
Для этих треугольников соответственно
имеем
,
,
,
.
Используя формулу
(8.20), получаем
.
Центр тяжести
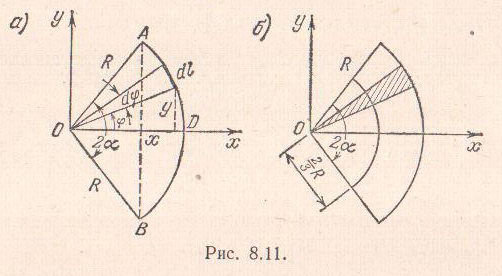
дуги окружности.
Рассмотрим дугу АDВ
окружности радиуса
с центральным углом
.
Поместим начало координат в центре
окружности и направим ось
перпендикулярно хорде АВ.
Т
ак
как вследствие симметрии фигуры
относительно оси
центр тяжести будет лежать на этой оси
,
т.е.
,
то остается только найти абсциссу центра
тяжести
;
для этого воспользуемся формулой (8.18).
Согласно рис.
имеем
,
,
и, следовательно,
,
(8.22) где
– половина центрального угла в радианах.
В частности, для
дуги полуокружности
будем иметь
.
Центр тяжести
кругового сектора. Для
определения положения центра тяжести
кругового сектора разобьем его на
элементарные секторы, как показано на
рис. Каждый элементарный сектор можно
принять за равнобедренный треугольник
с высотой, равной
.
Но высота в равнобедренном треугольнике
является также и его медианой;
следовательно, центр тяжести каждого
элементарного треугольника лежит на
расстоянии
от начала координат О.
Соответственно геометрическим местом
центров тяжести всех элементарных
треугольников является дуга окружности
радиусом
.
Это означает, что
центр тяжести площади кругового сектора
можно искать как центр тяжести материальной
линии, по которой непрерывно и равномерно
распределен вес этого сектора. Применив
формулу (8.22), получим координату центра
тяжести площади сектора
,
(8.23) где
– половина центрального угла в радианах.
В частности, для сектора в виде полукруга
получим
.
(8.24)
Задача 8.3. Пластина получена из
квадрата, сторона которого равна
,
после того,
как из него была вырезана часть,
составляющая четверть круга радиуса
с центром в вершине А квадрата.
Определить центр тяжести пластины.
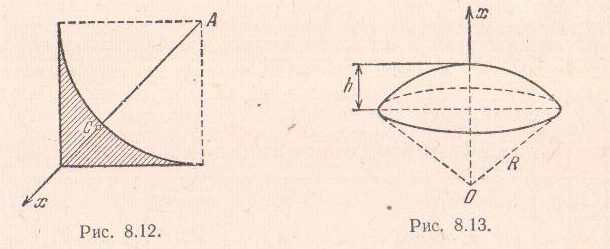
Решение. Ось
проведем по диагонали квадрата, взяв
начало оси в вершине А. Так как ось
является осью симметрии пластины, то
центр тяжести ее находится на этой оси.
Площадь квадрата без выреза
,
абсцисса его центра тяжести
;
площадь вырезанной части
,
абсцисса центра тяжести ее определяется
формулой (8.23), в которой
,
:
.
Центр тяжести пластины определим по
формуле
или, подставляя соответствующие
величины,
.
Приведем без вывода
формулы, определяющие положения центров
тяжести некоторых простейших однородных
тел.
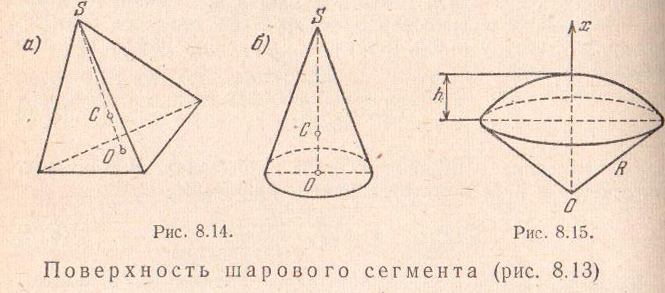
Поверхность
шарового сегмента
.
(8.25)
Пирамида и конус.
Центр тяжести
находится на прямой, соединяющей вершину
с центром тяжести О
площади основания, на
ее длины, считая от основания
.
(8.26)
Шаровой сектор.
,
(8.27) где
– радиус шара и
– высота сферической части сектора.
З
адача
8.4. Определить центр тяжести высоты
колонны, состоящей из однородного
цилиндра весом
,
высоты
и радиуса
,
на который установлена половина
однородного шара радиуса
.
Решение. Разделим колонну на
цилиндрическую и шаровую части. Центр
тяжести всей системы лежит на оси
симметрии. Абсцисса центра тяжести
цилиндра
.
Расстояние от центра полушария до его
центра тяжести найдем по формуле (8.27)
при
,
что дает
.
Следовательно,
.
Пользуясь равенством (8.19), найдем центр
тяжести колонны
.
*
Методы решения статически неопределимых
задач выходят за рамки теоретической
механики и относятся к курсу сопротивления
материалов и строительной механики.
1
Усилием в стержне называется алгебраическая
величина силы, действующей вдоль стержня
и растягивающей или сжимающей его; при
растяжении усилие считается положительным,
а при сжатии – отрицательным.
2
Здесь и в дальнейшем на протяжении
пятой главы предполагается, что все
силы расположены в одной плоскости ху
и что точки, относительно которых
вычисляются моменты, лежат в плоскости
действия сил. Ось z, перпендикулярная
плоскости действия сил, на рисунках не
показывается.
*
В тех случаях, когда стрела провеса f
не мала по сравнению с длиной пролета
l, уравнение кривой
равновесия тяжелой линии определяет
цепную линию.
3
Предполагается, что линии действия сил
параллельны оси z/
89
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
§1. Центр тяжести однородного тела.
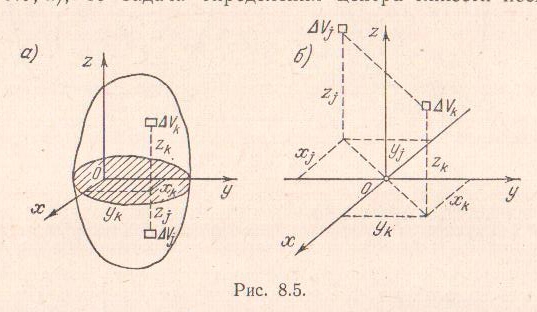
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
плоскости.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сплошной сложной геометрической фигуры по оси x;
— координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
имеющей отверстие
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сложной геометрической фигуры по оси x;
— координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
— Что называется центром параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных площадей?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести треугольника.