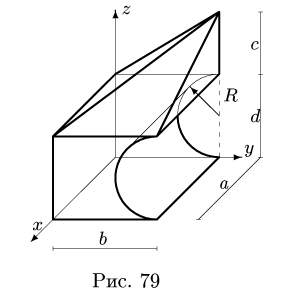
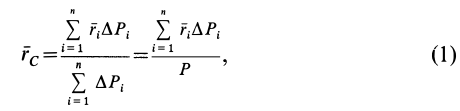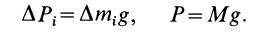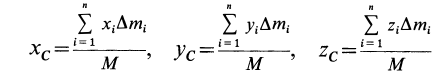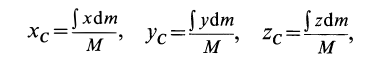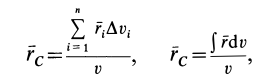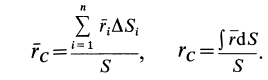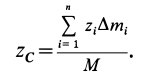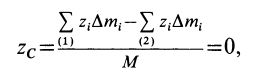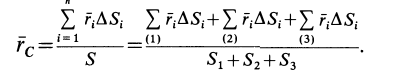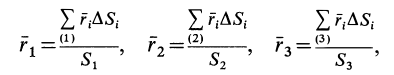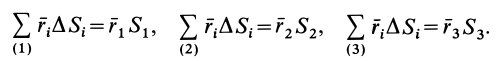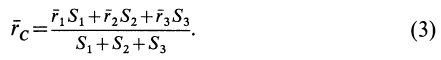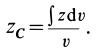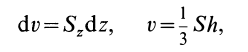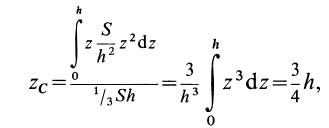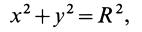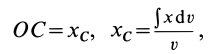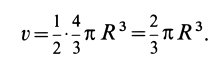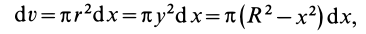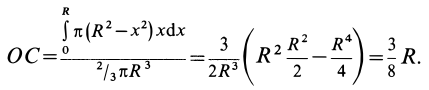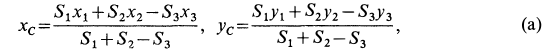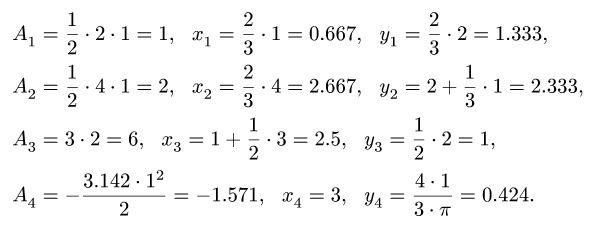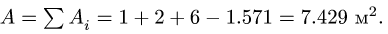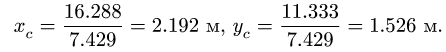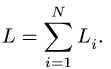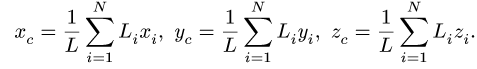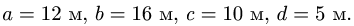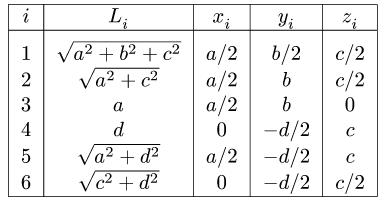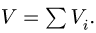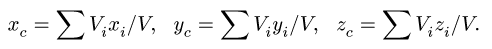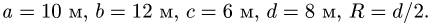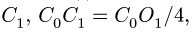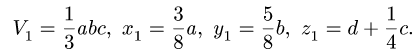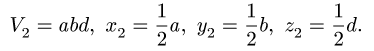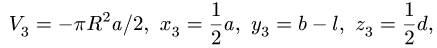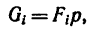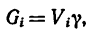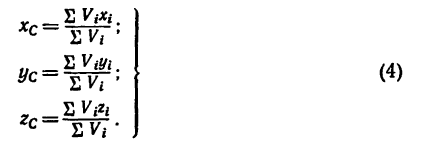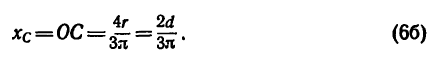Загрузить PDF
Загрузить PDF
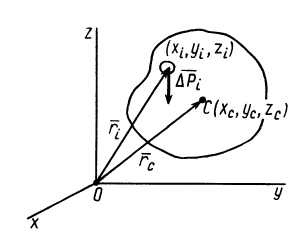
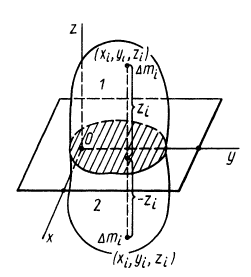
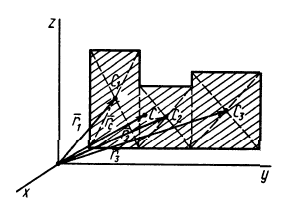
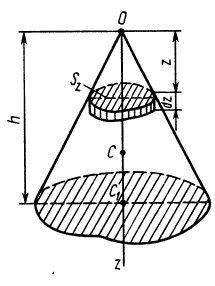
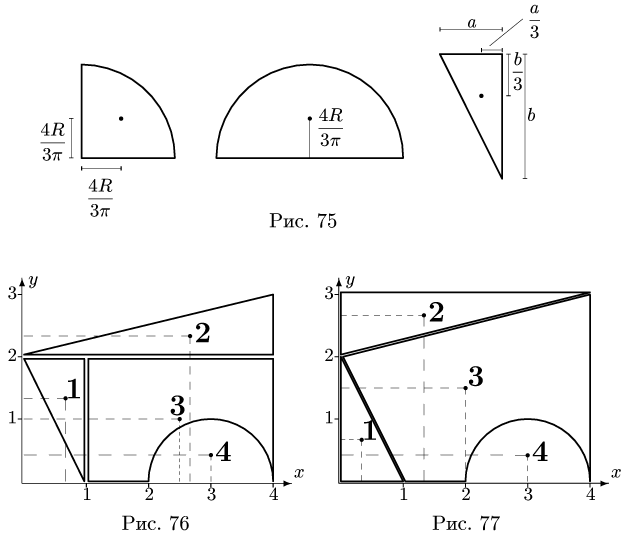
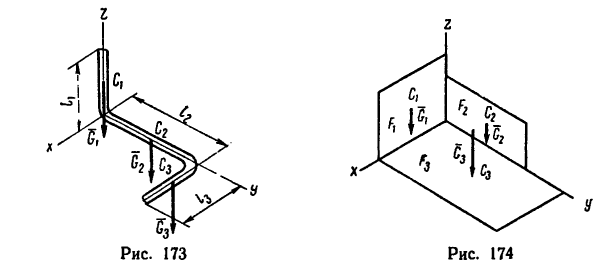
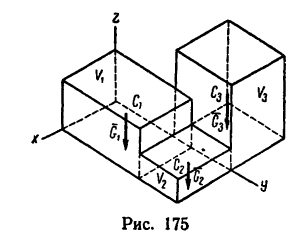
Центр тяжести – это точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. То есть это такая точка, в которой система находится в идеальном равновесии независимо от того, как система повернута или вращается вокруг этой точки. Чтобы найти центр тяжести системы, необходимо определить массу основного объекта и массу тел, входящих в систему, найти точку отсчета и подставить эти значения в формулу.
-
1
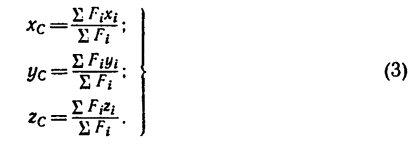
Определите вес основного объекта. Чтобы найти центр тяжести, сначала необходимо определить вес основного объекта. Например, рассмотрим качели-доску (качели-балансир) массой 12 кг. Таким образом, вес качелей равен 120 Н (Р=mg, где P – вес, m – масса, g – ускорение свободного падения, приблизительно равное 10 м/с2). Так как такие качели представляют собой симметричный объект, его центр тяжести находится точно по центру (когда на качелях никого нет). Но если на качелях сидят дети разной массы тела, задача усложняется.[1]
-
2
Определите дополнительные веса. Чтобы найти центр тяжести качелей с двумя детьми, необходимо определить вес каждого ребенка. Предположим, что масса тела первого ребенка равна 16 кг, а второго – 24 кг. Таким образом, вес первого ребенка равен 160 Н, а второго – 240 Н.
Реклама
-
1
Выберите точку отсчета. Точкой отсчета является любая точка, которая находится на одном (любом) конце доски. Предположим, что длина доски равна 5 м. Поместите точку отсчета на левой стороне доски возле первого ребенка.
-
2
Измерьте расстояние от точки отсчета до центра основного объекта и до дополнительных тел. Допустим, дети сидят на расстоянии 50 см от каждого конца доски. До центра доски 2,5 м (5/2=2,5). Вот расстояния от точки отсчета до центра основного объекта и двух дополнительных тел:
- Центр доски находится на расстоянии 2,5 м от точки отсчета.
- Первый ребенок находится на расстоянии 0,5 м от точки отсчета.
- Второй ребенок находится на расстоянии 4,5 м от точки отсчета.
Реклама
-
1
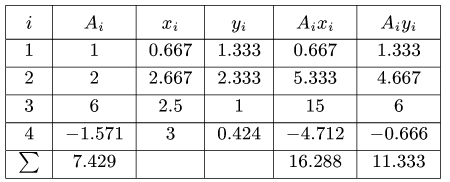
Перемножьте вес каждого тела и его расстояние до точки отсчета. Так вы найдете момент силы для каждого тела. Вот как умножить расстояние до каждого тела на его вес:
- Доска: 120 Н х 5 м = 600 Н х м.
- Первый ребенок: 160 Н x 0,5 м = 80 Н х м.
- Второй ребенок: 240 Н x 4,5 м = 1080 Н x м.
-
2
Сложите найденные значения. Сложение: 600 + 80 + 1080 = 1760 Н х м. Суммарный момент равен 1760 Н x м.
-
3
Сложите веса всех объектов. Найдите сумму веса качелей, веса первого ребенка и веса второго ребенка. Сумма: 120 Н + 160 Н + 240 Н = 520 Н.
-
4
Разделите суммарный момент на суммарный вес. Так вы найдете расстояние от точки отсчета до центра тяжести системы. В нашем примере разделите 1760 Н х м на 520 Н.
- 1760 Н х м / 520 Н = 3,4 м
- Центр тяжести находится на расстоянии 3,4 м от точки отсчета или на расстоянии 3,4 м от левого конца доски, где находится точка отсчета.
Реклама
-
1
Нарисуйте схему системы и отметьте на ней центр тяжести. Если найденный центр тяжести находится вне системы объектов, вы получили неверный ответ. Возможно, вы измерили расстояния от разных точек отсчета. Повторите измерения.
- Например, если на качелях сидят дети, центр тяжести будет где-то между детьми, а не справа или слева от качелей. Также центр тяжести никогда не совпадет с точкой, где сидит ребенок.
- Эти рассуждения верны в двумерном пространстве. Нарисуйте квадрат, в котором поместятся все объекты системы. Центр тяжести должен находиться внутри этого квадрата.
-
2
Проверьте математические вычисления, если вы получили маленький результат. Если точка отсчета находится на одном конце системы, маленький результат помещает центр тяжести возле конца системы. Возможно, это правильный ответ, но в подавляющем большинстве случаев такой результат указывает на ошибку. Когда вы вычисляли моменты, вы перемножали соответствующие веса и расстояния? Если вместо умножения вы сложили веса и расстояния, вы получите гораздо меньший результат.
-
3
Исправьте ошибку, если вы нашли несколько центров тяжести. Каждая система имеет только один центр тяжести. Если вы нашли несколько центров тяжести, скорее всего, вы не сложили все моменты. Центр тяжести равен отношению «суммарного» момента к «суммарному» весу. Не нужно делить «каждый» момент на «каждый» вес: так вы найдете положение каждого объекта.
-
4
Проверьте точку отсчета, если ответ отличается на некоторое целое значение. В нашем примере ответ равен 3,4 м. Допустим, вы получили ответ 0,4 м или 1,4 м, или другое число, оканчивающееся на «,4». Это потому, что в качестве точки отсчета вы выбрали не левый конец доски, а точку, которая расположена правее на целую величину. На самом деле, ваш ответ верен, независимо от того, какую точку отсчета вы выбрали! Просто запомните: точка отсчета всегда находится в положении x = 0. Вот пример:
- В нашем примере точка отсчета находилась на левом конце доски и мы нашли, что центр тяжести находится на расстоянии 3,4 м от этой точки отсчета.
- Если в качестве точки отсчета выбрать точку, которая расположена на расстоянии 1 м вправо от левого конца доски, вы получите ответ 2,4 м. То есть центр тяжести находится на расстоянии 2,4 м от новой точки отсчета, которая, в свою очередь, находится на расстоянии 1 м от левого конца доски. Таким образом, центр тяжести находится на расстоянии 2,4 + 1 = 3,4 м от левого конца доски. Получился старый ответ!
- Примечание: при измерении расстояния помните, что расстояния до «левой» точки отсчета отрицательные, а до «правой» – положительные.
-
5
Расстояния измеряйте по прямым линиям. Предположим, на качелях два ребенка, но один ребенок намного выше другого, или один ребенок висит под доской, а не сидит на ней. Проигнорируйте такую разницу и измерьте расстояния по прямой линии доски. Измерение расстояний под углами приведет к близким, но не совсем точным результатам.
- В случае задачи с качелями-доской помните, что центр тяжести находится между правым и левым концами доски. Позже вы научитесь вычислять центр тяжести более сложных двумерных систем.
Реклама
Советы
- Чтобы найти расстояние, на которое должен переместиться ребенок, чтобы сбалансировать качели-доску относительно точки опоры, используйте формулу: (перемещаемый вес)/(общий вес) = (расстояние движения центра тяжести)/(расстояние движения веса). Эту формулу можно переписать так: расстояние, на которое должен переместиться ребенок = (расстояние между центром тяжести и точкой опоры х вес ребенка)/(общий вес). Поэтому первому ребенку нужно переместиться на -0,9*160/520 = -0,28 м или -28 см (к концу доски), а второму ребенку нужно переместиться на -0,9*520/240 = -1,95 м или -195 см (к концу доски).
- Если нужно найти центр тяжести двумерного объекта, используйте формулу Xcg = ΣxW/W, чтобы найти центр тяжести вдоль оси X, и Ycg = ΣyW/ΣW, чтобы найти центр тяжести вдоль оси Y. Точка, в которой они пересекаются, является центром тяжести.
- Определение центра тяжести общего распределения масс: (∫ r dW/∫ dW), где dW – дифференциал веса, r – радиус-вектор, а интегралы должны интерпретироваться как интегралы Стилтьеса по всему телу. Но эти интегралы могут быть выражены как более общие интегралы (по плотности) Римана или Лебега для распределений, допускающих функцию плотности. Начиная с этого определения, все свойства центра тяжести (включая те, которые описаны в этой статье) могут быть получены из свойств интегралов Стилтьеса.
Реклама
Предупреждения
- Не пытайтесь применить описанные здесь методы, не поняв теорию. В противном случае вы получите неверный результат.
Реклама
Об этой статье
Эту страницу просматривали 52 750 раз.
Была ли эта статья полезной?
Download Article
Download Article
The center of gravity (CG) is the center to an object’s weight distribution, where the force of gravity can be considered to act. This is the point where the object is in perfect balance, no matter how turned or rotated around that point.[1]
If you want to know how to calculate the center of gravity of an object, then you have to find the weight of the object: and any objects on it, locate the datum, and plug the known quantities into the equation for calculating the center of gravity. If you want to know how to calculate the center of gravity, just follow these steps.
Calculator
-
1
Calculate the weight of the object. When you’re calculating the center of gravity, the first thing you should do is to find the weight of the object. Let’s say that you’re calculating the weight of a see-saw that has a weight of 30 lbs. Since it’s a symmetrical object, its center of gravity will be exactly in its center if it’s empty. But if the see-saw has people of different weights sitting on it, then the problem is a bit more complicated.[2]
-
2
Calculate the additional weights. To find the center of gravity of the see-saw with two children on it, you’ll need to individually find the weight of the children on it.[3]
The first child has a weight of 40 lbs. and the second child’s is 60 lbs.
Advertisement
-
1
Choose a datum. The datum is an arbitrary starting point placed on one end of the see-saw.[4]
You can place the datum on one end of the see-saw or the other. Let’s say the see-saw is 16 feet long. Let’s place the datum on the left side of the see-saw, close to the first child. -
2
Measure the datum’s distance from the center of the main object as well as from the two additional weights. Let’s say the children are each sitting 1 foot away from each end of the see-saw.[5]
The center of the see-saw is the midpoint of the see-saw, or at 8 feet, since 16 feet divided by 2 is 8. Here are the distances from the center of the main object and the two additional weights form the datum:- Center of see-saw = 8 feet away from datum.
- Child 1 = 1 foot away from datum
- Child 2 = 15 feet away from datum
Advertisement
-
1
Multiply each object’s distance from the datum by its weight to find its moment. This gives you the moment for each object. Here’s how to multiply each object’s distance from the datum by its weight:
- The see-saw: 30 lb. x 8 ft. = 240 ft. x lb.
- Child 1 = 40 lb. x 1 ft. = 40 ft. x lb.
- Child 2 = 60 lb. x 15 ft. = 900 ft. x lb.
-
2
Add up the three moments. Simply do the math: 240 ft. x lb. + 40 ft. x lb. + 900 ft. x lb = 1180 ft. x lb. The total moment is 1180 ft. x lb.
-
3
Add the weights of all the objects. Find the sum of the weights of the seesaw, the first child, and the second child. To do this, add up the weights: 30 lbs. + 40 lbs. + 60 lbs. = 130 lbs.
-
4
Divide the total moment by the total weight. This will give you the distance from the datum to the center of gravity of the object. To do this, simply divide 1180 ft. x lb. by 130 lbs.
- 1180 ft. x lb. ÷ 130 lbs = 9.08 ft.
- The center of gravity is 9.08 feet from the datum, or measured 9.08 feet from the end of the left side of the see-saw, which is where the datum was placed.
Advertisement
-
1
Find the center of gravity in the diagram. If the center of gravity you found is outside of the system of objects, you have the wrong answer.[6]
You may have measured the distances from more than one point. Try again with just one datum.- For example, for people sitting on a seesaw, the center of gravity has to be somewhere on the seesaw, not to the left or right of the seesaw. It does not have to be directly on a person.
- This is still true with problems in two dimensions. Draw a square just large enough to fit all of the objects in your problem. The center of gravity must be inside this square.
-
2
Check your math if you get a tiny answer. If you picked one end of the system as your datum, a tiny answer puts the center of gravity right next to one end. This can be the right answer, but it’s often the sign of a mistake. When you calculated the moment, did you multiply the weight and distance together? That’s the correct way to find the moment. If you accidentally added them together instead, you’ll usually get a much smaller answer.
-
3
Troubleshoot if you have more than one center of gravity. Every system only has a single center of gravity. If you find more than one, you might have skipped the step where you add all the moments together. The center of gravity is the total moment divided by total weight. You do not need to divide each moment by each weight, which only tells you the position of each object.
-
4
Check your datum if your answer is off by a whole number. The answer to our example is 9.08 ft. Let’s say you try it and get the answer 1.08 ft., 7.08 ft, or another number ending in «.08.» This most likely happened because we chose the left end of the seesaw as the datum, while you chose the right end or some other point an integer distance from our datum. Your answer is actually correct no matter which datum you choose! You just need to remember that the datum is always at x = 0. Here’s an example:
- The way we solved it, the datum is at the left end of the seesaw. Our answer was 9.08 ft, so our center of mass is 9.08 ft from the datum at the left end.
- If you pick a new datum 1 ft from the left end, you get the answer 8.08 ft for the center of mass. The center of mass is 8.08 ft from the new datum, which is 1 ft from the left end. The center of mass is 8.08 + 1 = 9.08 ft from the left end, the same answer we got before.
- (Note: When measuring distance, remember that distances to the left of the datum are negative, while distances to the right are positive.)
-
5
Make sure all your measurements are in straight lines. Let’s say you see another «kids on the seesaw» example, but one kid is much taller than the other, or one kid is hanging underneath the seesaw instead of sitting on top. Ignore the difference and take all your measurements along the straight line of the seesaw. Measuring distances at angles will lead to answers that are close but slightly off.
- For seesaw problems, all you care about is where the center of gravity is along the left-right line of the seesaw. Later, you might learn more advanced ways to calculate the center of gravity in two dimensions.
Advertisement
Add New Question
-
Question
Why do we calculate centers of gravity?
Danoyachtcapt
Top Answerer
Center of gravity (CG) is very important, especially in aircraft and other vehicles like cars and trains. The Vehicle has to be designed so the CG is within certain limits so the vehicle will be well-balanced while in motion.
-
Question
I have to find the center of gravity for a 1310 mm length MS Steel. How can I go about doing that?
Balance it on a knife edge and record the position by marking the edge. Then, turn the object approx. 30 degrees and re-balance it on the knife edge. Record the position by marking the edge — you should now have 2 intersecting lines, and the intersection point will give you the center of gravity.
-
Question
Why is the determination of the center of gravity necessary, and where might I apply it in real life?
It’s more useful in certain sports and careers. If you are an engineer, you don’t want whatever you’re building to be off center. In sports such as gymnastics, it’s easier to do harder moves if you know where your center of balance is.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
To find the distance a person needs to move to balance the see-saw over the fulcrum, use the formula: (
weight moved
) / (
total weight
) = (
distance CG moves
) / (
distance weight is moved
). This formula can be rewritten to show that the distance the weight (person) needs to move equals the distance between the CG and the fulcrum times the weight of the person divided by the total weight. So the first kid needs to move
-1.08ft * 40lb / 130lbs =
-.33ft or -4in. (toward the edge of the see-saw). Or, the second kid needs to move
-1.08ft * 130lb / 60lbs =
-2.33ft or -28in. (toward the center of the see-saw).[7]
-
The definition for center of gravity of a general mass distribution is (∫ r dW/∫ dW) where dW is the differential of weight, r the position vector and the integrals are to be interpreted as Stieltjes integrals over the entire body. They can however be expressed as more conventional Riemann or Lebesgue volume integrals for distributions that admit a density function. Starting with this definition all properties of CG including the ones used in this article may be derived from properties of Stieltjes integrals.
-
To find the CG of a two dimensional object, use the formula Xcg = ∑xW/∑W to find the CG along the x-axis and Ycg = ∑yW/∑W to find the CG along the y-axis. The point at which they intersect is the center of gravity.
Thanks for submitting a tip for review!
Advertisement
-
Trying to blindly apply this mechanical technique without understanding the theory may result in errors. Understand the laws/theories behind it first.
Advertisement
References
About This Article
Article SummaryX
To calculate the center of gravity of 2 objects on a see-saw, first identify the weight of each separate object. Choose a starting point, or datum, on one end of the see-saw and measure its distance from the center and each object. Find each object’s moment by multiplying the distance by the object’s weight, then add up the 3 moments. Add up the weights of the objects and divide the total moment by the total weight to get the datum’s distance from the center of gravity. For examples and ways to check your answer, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,423,926 times.
Did this article help you?
Определение массы и расположения центра тяжести груза
Стропальщик
должен уметь определять массу и центр
тяжести груза с целью обеспечения
безопасности погрузо-разгрузочных
работ.
Под
массой груза следует понимать (скалярную,
ненаправленную) физическую характеристику
тела, являющуюся
мерой его инерционных и гравитационных
свойств.
Значения массы тела не зависят от
ускорения свободного
падения в пункте определения. В состоянии
покоя
ее определяют взвешиванием на рычажных
весах. Результат
взвешивания показывает сравнительную
с массой гирь величину, выраженную в
единицах массы — граммах
(г), килограммах (кг), тоннах (т).
Под
силой
тяжести следует
понимать векторную (направленную)
величину, определяющую силу притяжения
тела к Земле или к другому небесному
телу. Значение
силы тяжести зависит от ускорения
свободного падения
в пункте измерения. Сила тяжести на
полюсе больше,
а на экваторе меньше. По мере удаления
тела от
поверхности Земли его сила тяжести
уменьшается. Эту
величину измеряют с помощью динамометра
в условиях
относительного покоя тела. Силу тяжести,
как и любую
другую силу, выражают в единицах силы
— ньютонах
(Н),
килоньютонах
(кН) и других дольных и кратных
значениях этой величины.
Вес
тела — сила, с которой тело действует
вследствие
силы тяжести к Земле на опору (или
подвес), удерживающую
его от падения. Вес тела равен его силе
тяжести,
если опора и тело неподвижны относительно
Земли.
Единица веса (и силы тяжести) в Международной
системе
единиц (СИ)—ньютон (Н).
Под
грузоподъемностью
крана,
автопогрузчика, электрокара
следует понимать максимальную массу
груза, которую
способно в один прием поднять, переместить
или
перевезти транспортное средство.
Грузоподъемность,
как и масса, — скалярная величина
и измеряется единицами массы — грамм
(г),
килограмм
(кг),
тонна
(т).
Грузоподъемная
(подъемная)
сила (по аналогии с силой
тяжести) — величина, характеризующая
способность
транспортного средства преодолевать
при подъеме
или перемещении массу груза. Единицами
грузоподъемной
силы служат ньютоны (Н),
килоньютоны
(кH)
и другие дольные и кратные значения
ньютона.
Перед
строповкой груза, предназначенного для
перемещения, стропальщик должен
определить его массу. Массу
изготовленной на заводе продукции
проставляют на
чертежах изделий. Массу оборудования,
приспособлений,
механизмов указывают в табличке,
прикрепленной
к раме или станине. Если груз упакован,
то массу его
указывают на обшивке. Однако массу
груза, подлежащего перемещению,
стропальщику часто приходится определять
визуально. Удельная масса часто
встречающихся
материалов приведена ниже, кг/м3
|
Алюмений |
2550—2700 |
Олово |
7300 |
|
|
Бетон |
2200 |
Парафин |
900 |
|
|
Вольфрам Древесина: береза, дуб сосна |
19300 700 800 500 |
Сталь: твердая расплавленная |
7300 6900—7300 |
|
|
Земля, Песок: сухой влажный |
1300—2500 1400—1600 1900—2000 |
Чугун: белый ковкий серый Уголь Кокс |
7650 7300 7550 900 450 |
|
|
Кирпичная |
1420—1700 |
Азот |
790 |
|
|
латунь |
8500 |
|||
|
Лед |
900 |
Воздух |
860 |
|
|
Медь |
8900 |
Керосин |
800 |
|
|
Мел |
2400 |
Кислород |
1140 |
|
|
Никель |
8900 |
Мазут |
900 |
Для
определения массы груза используют
следующие формулы:
для простых грузов
Q=mV;
для
сложных грузов Q=mVi,
где
Q — масса груза; т — удельная масса,
численно равная плотности материала;
V
— объем
груза; Vt
—
объем
отдельных частей груза;
— сумма всех частей груза.
Объем правильных
геометрических фигур приведен в табл.
1.
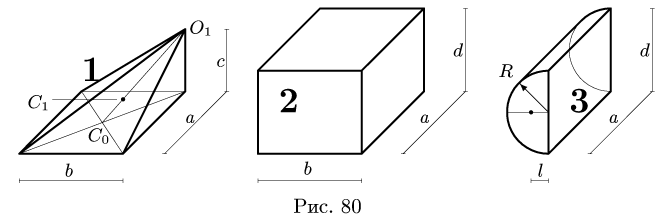
Пример.
Определим
массу слитка, размеры которого
приведены на рис. 6.
Разбиваем
условно слиток на три усеченных конуса
и
определяем объем каждого. Для этого в
табл. 1 находим
формулу объема усеченного конуса
V=
(3,14/3) h
(R2+
r2
+ Rr)
Находим объемы
каждого элемента слитка
V1.
~
(3,14/3) 1,700 [0,552
+ 0,452
+ 0,55-0,45]
1,34 м3;
V2
~
(3,14/3) 0,05 [0,552
+ 0,422
+ 0,55-0,42] ~ 0,04 м3;
Vз
~ (3,14/3) 0,4 [0,422
+ 0,42
+ 0,42-0,4]
0,21
м3.
Определяем суммарный
объем слитка
V=V1+V2+V3
=
1,34+0,04+0,21
= 1,59 м3.
Принимаем
удельную массу слитка равной 7,8 т/м3,
тогда
масса слитка
Q
= mV
= 7,8-1,59~
12,4 т.
При
выборе мест строповки груза возникает
_необходимость
определить расположение центра тяжести
поднимаемого
груза. Если при строповке это не учитывать,
то
возможны аварийные ситуации, связанные
с перегрузкой отдельных ветвей стропов,
грузоподъемных средств;
потерей устойчивости и опрокидыванием
поднимаемого
объекта.
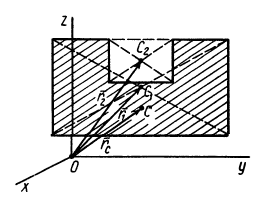
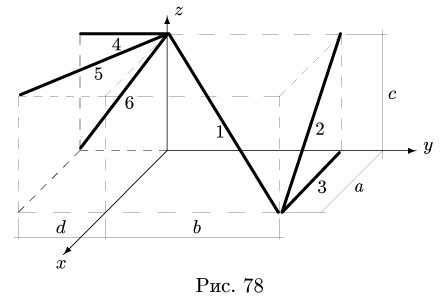
Положение
центра тяжести различных геометрических
тел находят по координатам хц.Т,
yц.т,
zц.т,
определяемым по формулам
хцТ,=Qixi
/Q
,
yц.т,
=Qiyi
/Q
zц.Т,=Qizi
/Q
где
хц.т,
yц.т,
zц.т,
—
расстояние от центра тяжести тела до
плоскости, проходящей перпендикулярно
измеряемой оси
через центр координат, м; xi,-,
yi,
zi—расстояние
от центра
тяжести отдельной рассматриваемой
части тела до
той же плоскости, м; Q
— общая
масса тела, т; Qi:—
— масса
отдельной рассматриваемой части тела,
т.
Координаты центра
тяжести правильных геометрических
фигур приведены в табл.1
Пример.
Определим
расположение центра тяжести
стального слитка, изображенного на рис.
1.
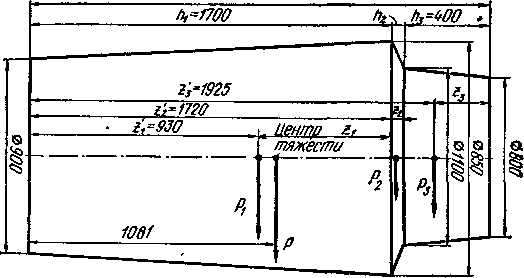
Условно
разбиваем слиток на три правильных
усеченных
конуса. По табл. 1 находим формулы,
определяющие
их координаты расположения центра
тяжести. Плоскость отсчета принимаем
проходящей через нижнее основание
слитка -перпендикулярно его оси. Из
предыдущего примера известно, что
отдельные части слитка
имеют массу q1
= 10,45;
Q2
=0,31; Q3=1,64
т, общая масса
12,4 т. Учитывая, что слиток симметричен
относительно
своей оси, определяем расположение
только координаты
zцт,
Координаты xцт,
уцт
будут
расположены
на оси. Формула для определения координаты
zцт
усеченного
конуса имеет вид
zцт
=h[(R2+2Rr+3r2)/(R2+Rr+r2)]/4
Рис. 1. Схема слитка
Зная,
что h1=l,7
м; R1=0,55
м; r1=0,45
м, имеем z1=0,77м
Величину
z1`
до
принятой плоскости отсчета определяют
как разность 1,7 — z1
= l,7
— 0,77=0,930 м. Зная
h2=0,05
м; R2=0,55
м; г2=0,425
м, имеем
Z2=0,021
До
принятой плоскости отсчета z2
определяют как сумму
1,7+z2==1,7+0,02=1,72
м.
Зная
hз=0,4
м; R3=0,425
м; г3=0,40
м, имеем
z3=0,176м
До
принятой плоскости отсчета zз определяют
как сумму
1,7+0,05+0,176= 1,926м.
Определяем
расположение центра тяжести по формуле
zцт
=(Q1Z1+Q2z2+Q3z3)/Q
подставляя
в формулу соответствующие значения,
находим
расстояние между центром тяжести и
началом координат
zцт
= (10,45-0,93+ 0,31-1,72+ 1,64.1,926)/12,4 = 1,081 м.
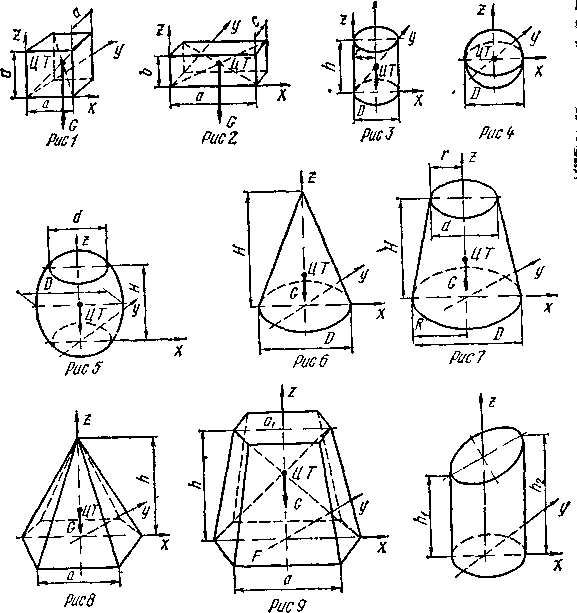
Таблица
1. Объем и расположение центра тяжести
простых геометрических тел
|
Наименование |
Изображение |
Объем |
Положение |
|
Куб |
Рис. |
V |
x
z х |
|
Прямоугольный |
Рис. |
V |
x
z х |
|
Цилиндр |
Рис. |
V |
х |
|
Шар |
Рис. |
V |
Если |
|
Боченок |
Рис. |
V=3,14/12Hx x(2D2 |
х |
|
Конус |
Рис. |
V= |
x |
|
Усеченный |
Рис. |
V=(3,14H/3)x(R2+r2+Rr) |
х z |
|
Пирамида |
Рис. |
V=(Fh)/3, |
х |
|
Усеченная пирамида |
Рис. |
V=h[F + |
x + |
|
Усеченный цилиндр |
Рис. |
V |
x=y=0, |
Определив
расстояние центра тяжести от принятого
начала координат, его переносят на
поднимаемый груз и делают пометку мелом
или другим способом.
Места
застроповки груза должны располагаться
симметрично центру тяжести таким
образом, чтобы отвесная прямая, проходящая
через центр тяжести, размещалась между
местами застроповки. Чем больше расстояние
между местами застроповки, тем устойчивее
положение груза при
прочих равных условиях.
На упакованных
грузах расположение центра тяжести
указывают на упаковке.
В тех
случаях, когда конфигурация груза
вызывает затруднения при расчете
положения центра тяжести, а его
необходимо определить, то можно
использовать практический
прием. После определения массы груза
подбирают соответствующий строп и им
приподнимают груз за один из краев. На
приподнятом грузе на двух плоскостях
проводят отвесные линии как продолжение
ветви стропа. Затем груз опускают и
приподнимают за другой конец. На тех же
плоскостях снова проводят отвесные
прямые.
Точки пересечения отвесов определяют
расположение
центра тяжести определяемого груза.
В тех
случаях, когда стропальщик затрудняется
определить массу перемещаемого груза
и расположения центра тяжести, он обязан
обратиться за уточнением к своему
бригадиру, мастеру или руководителю
работ.
При
монтаже несущих конструкций ОПЗ
из двух возможных схем перемещения
стрелового крана — вдоль пролетов или
поперек пролетов -обычно выбирают
первую, так как путь крана в этом случае
гораздо короче. При монтаже стеновых
панелей стреловой кран движется снаружи
по периметру здания. При строительстве
многоэтажных
жилых и гражданских зданий
башенный кран обычно передвигается
снаружи здания вдоль длинной его стороны.
Монтаж ведется в направлении «на
кран», то есть в первую очередь
устанавливаются наиболее удаленные от
крана конструкции. В многоэтажных
промышленных зданиях
башенный или стреловой кран может
перемещаться внутри здания, монтируя
его на всю высоту «на себя» с
постепенным выездом за пределы здания.
При совместной
работе нескольких монтажных кранов
схема движения разрабатывается с учетом
требований техники безопасности. Здание
разбивают на монтажные зоны по числу
работающих кранов, в пределах каждой
зоны разрешается работа только одного
из них. Другой в это время должен работать
в своей монтажной зоне или простаивать.
4)
Рабочая
привязка монтажных
кранов и подъемников — это установление
точного взаимного расположения
возводимого здания и грузоподъемных
машин. Правильная привязка обеспечивает
требуемый «охват» всего объекта
монтажными машинами и безопасные условия
производства работ.
Рабочая
привязка башенных
кранов состоит в поперечной и продольной
привязке крана, подкрановых путей и их
ограждений.
Поперечная
привязка при возведении надземной части
здания заключается в определении
расстояния от оси подкрановых путей до
ближайшей к крану грани строящегося
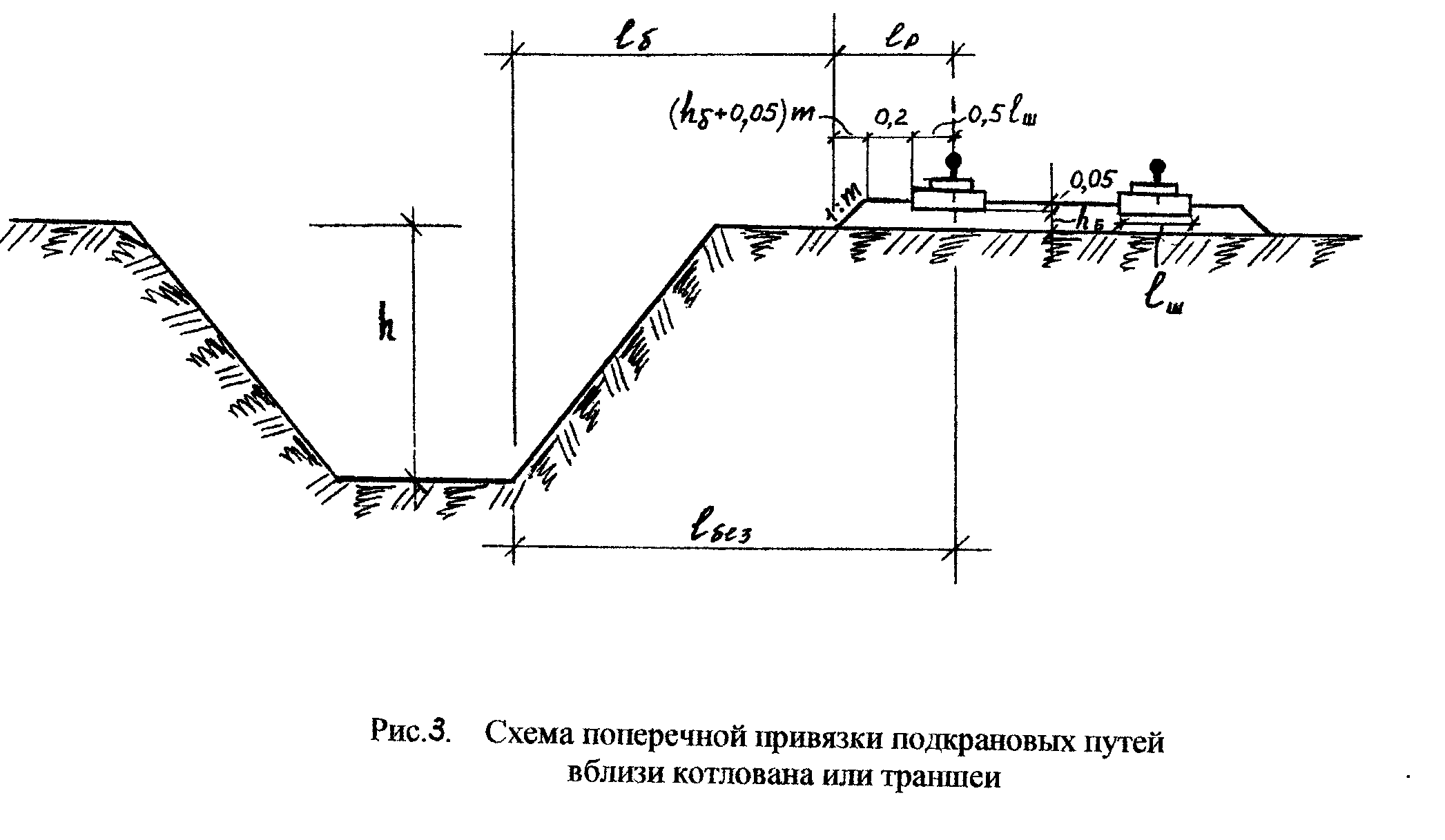
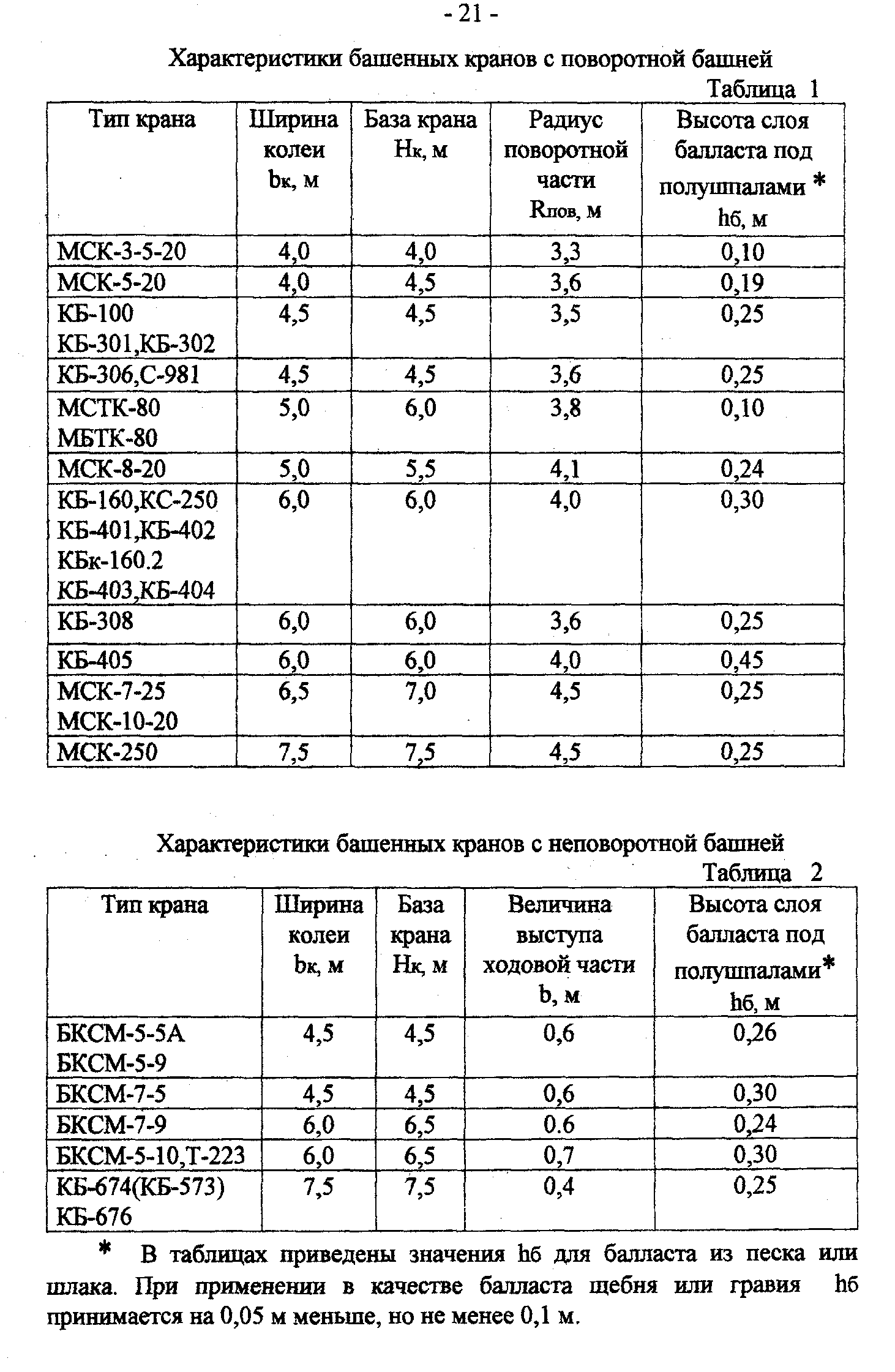
здания (рис.2: 1 — строящееся здание; 2 —
инвентарное ограждение путей; 3 — склад;
4 — водоотводная канава). Это расстояние
зависит от конструктивного исполнения
крана и ширины колеи. У кранов с
поворотной башней
наиболее приближены к зданию поворотная
платформа или нижний противовес. Привязка
таких кранов осуществляется по формуле:
B
= Rпов
+ 1без
,
где В —
минимальное расстояние от оси подкрановых
путей до наружной грани здания (м );
Rпов
— радиус поворотной части или противовеса,
принимают по справочникам или
таблице 1 (м );
1без
— минимально допустимое расстояние
по горизонтали между выступающей частью
крана и зданием, принимается на высоте
до 2 м от уровня земли не менее 0,7 м; на
высоте более 2 м — не менее 0,4 м.
Краны с неповоротной
башней могут располагаться ближе к
зданию, поскольку механизм поворота и
противовесная консоль располагаются
выше строящегося объекта. У этих кранов
наиболее приближенной к зданию является
ходовая часть, для них:
В =
0,5 Ьк + b
+ 1без ,
где Ьк — ширина
колеи крана ( м);
b
— величина выступающей за колею
ходовой части (м),
определяется по
паспорту крана или таблице 2 .
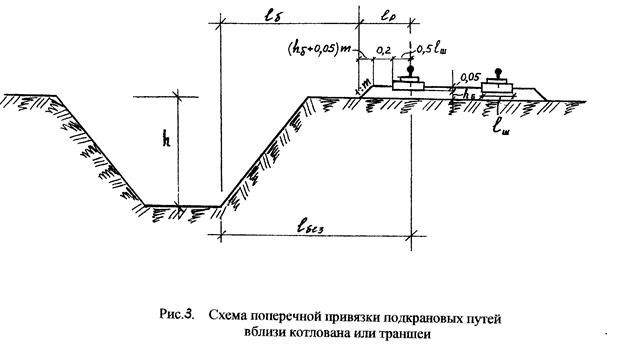
Привязку
башенных и рельсовых стреловых
кранов при возведении подземной части
здания у неукрепленных котлованов и
траншей производят исходя из глубины
выемки h
и вида грунта, что обеспечивает
расположение машин за пределами призмы
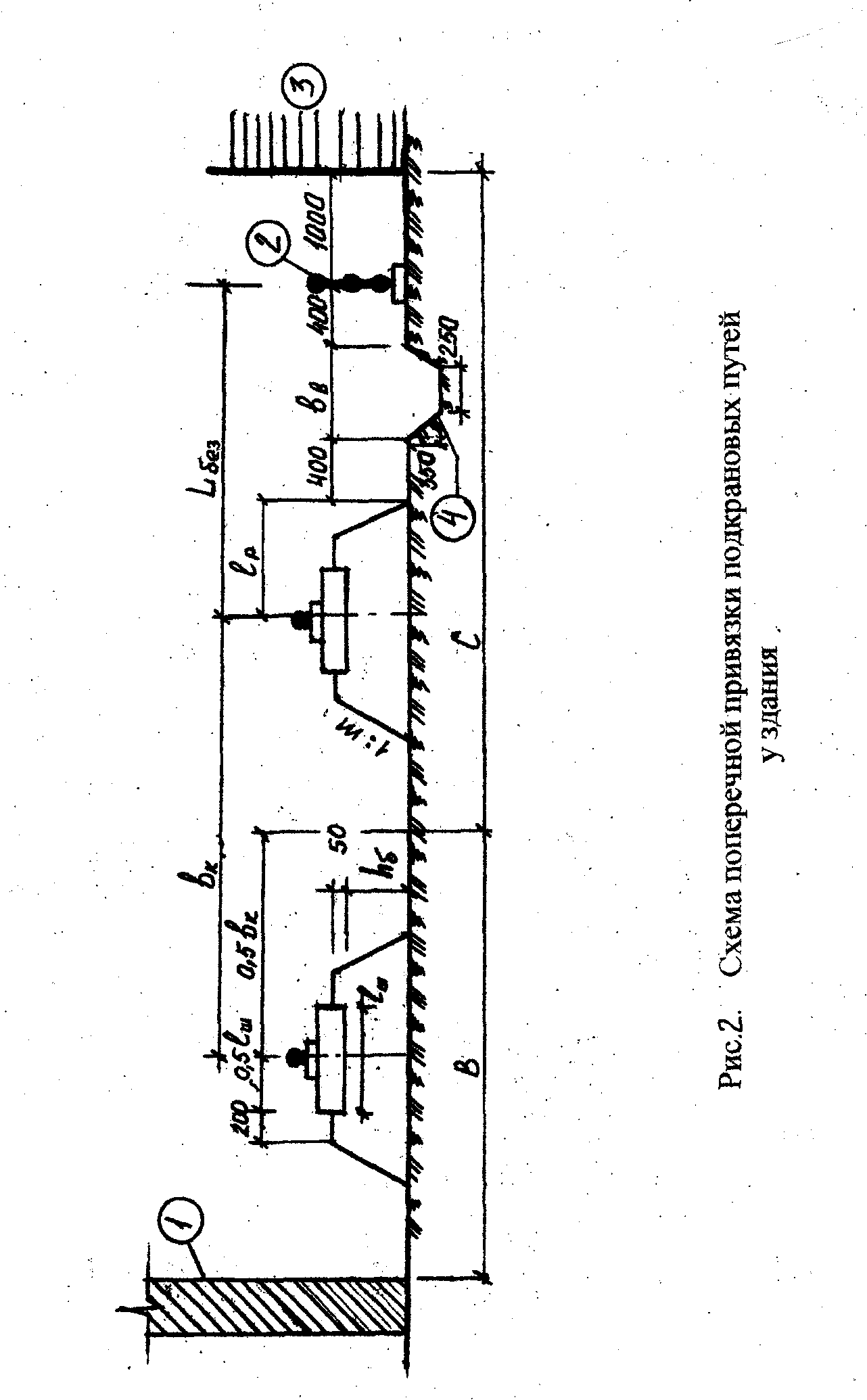
обрушения (рис.3). Безопасное расстояние
по горизонтали от основания откоса
выемки до оси ближайшего рельса
определяется по формуле:
lбез
= 1б
+ 1р
,
где
1б — минимальное расстояние от основания
откоса выемки до нижнего края балластной
призмы; для песчаных и супесчаных грунтов
1б > l,5h
+ 0,4; для глинистых и суглинистых грунтов
1б > h
+ 0,4(м); 1р — расстояние от нижнего края
балластной призмы до оси рельса (м),
определяется по формуле:
1р =
(hб
+ 0,05)m
+ 0,2 + 0,51ш
,
hб
— высота слоя балласта под полушпалами
(м), зависит от вида
балласта и типа
крана (таблицы 1,2);
0,05 — углубление
полушпалы в балласт (м);
m
— показатель крутизны откосов балластной
призмы, для щебня и гравия m
=1,5;
для
песка
и шлака т=2;
0,2 — минимально
допустимое расстояние от верхнего
края балластной призмы до конца
полушпалы (м);
1ш — длина деревянной
полушпалы, 1ш = 1,35 м.
Поперечную привязку
ограждений подкрановых путей к наружному
рельсу производят исходя из необходимости
соблюдения безопасного расстояния
между конструкциями крана и ограждением.
Для кранов с
поворотной башней расстояние от оси
ближнего к ограждению рельса до ограждения
определяют по формуле:
Lбез
= (Rпов
—
0,5bк)
+ 0,7
При
привязке ограждений башенных кранов с
неповоротной башней учитывается
выступающая за колею ходовая часть:
L без
= b
+ 0,7
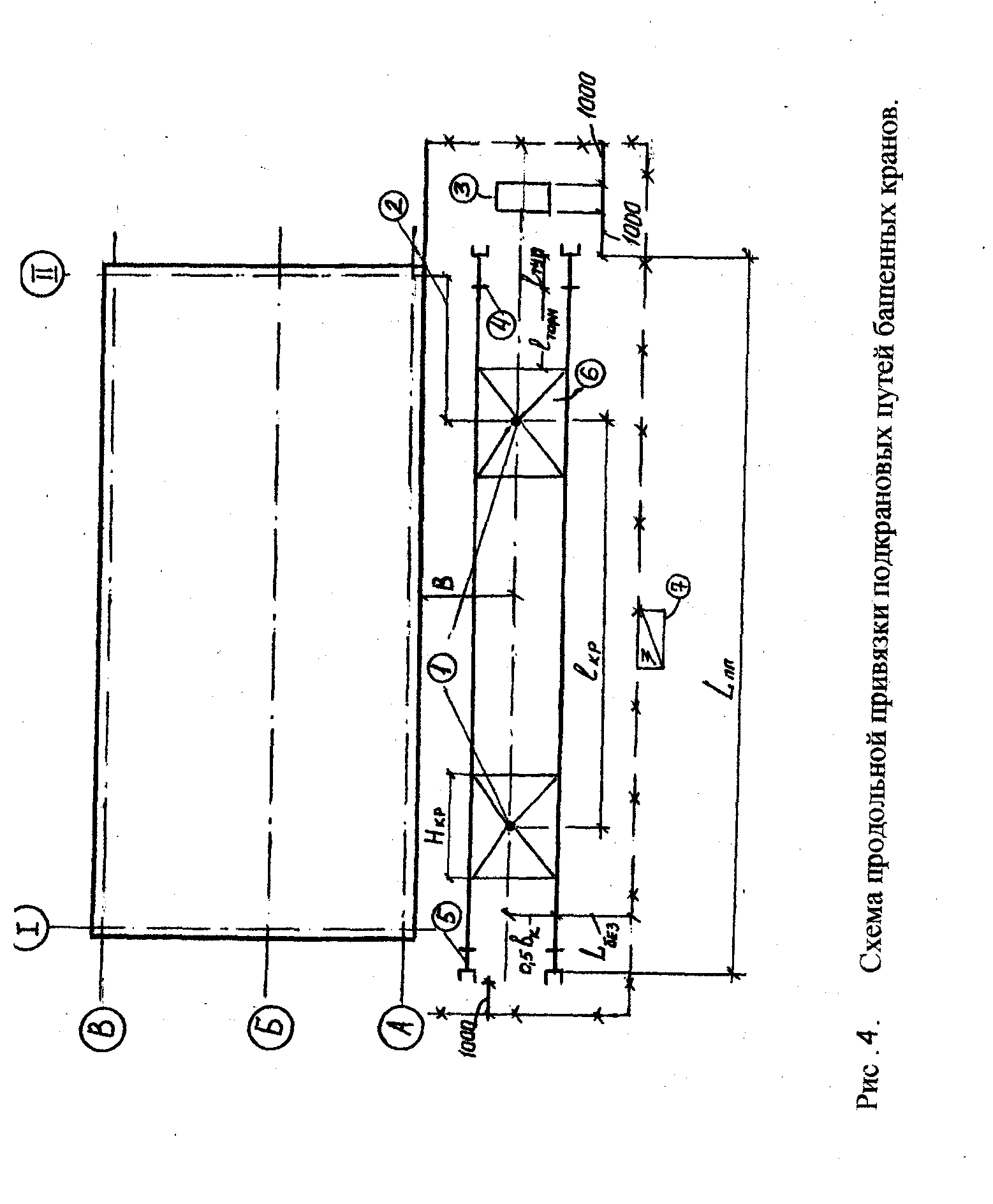
Крайние из этих засечек определяют
положение крайних стоянок, а измеренное
по чертежу в соответствии с принятым
масштабом расстояние и есть 1кр. На
стройгенплане крайние стоянки должны
быть обозначены и привязаны к осям
здания (рис.4: 1- крайние стоянки; 2 —
привязка крайних стоянок к оси; 3 —
контрольный груз; 4 — место установки
тупика; 5 — конец рельса; 6 — база крана; 7
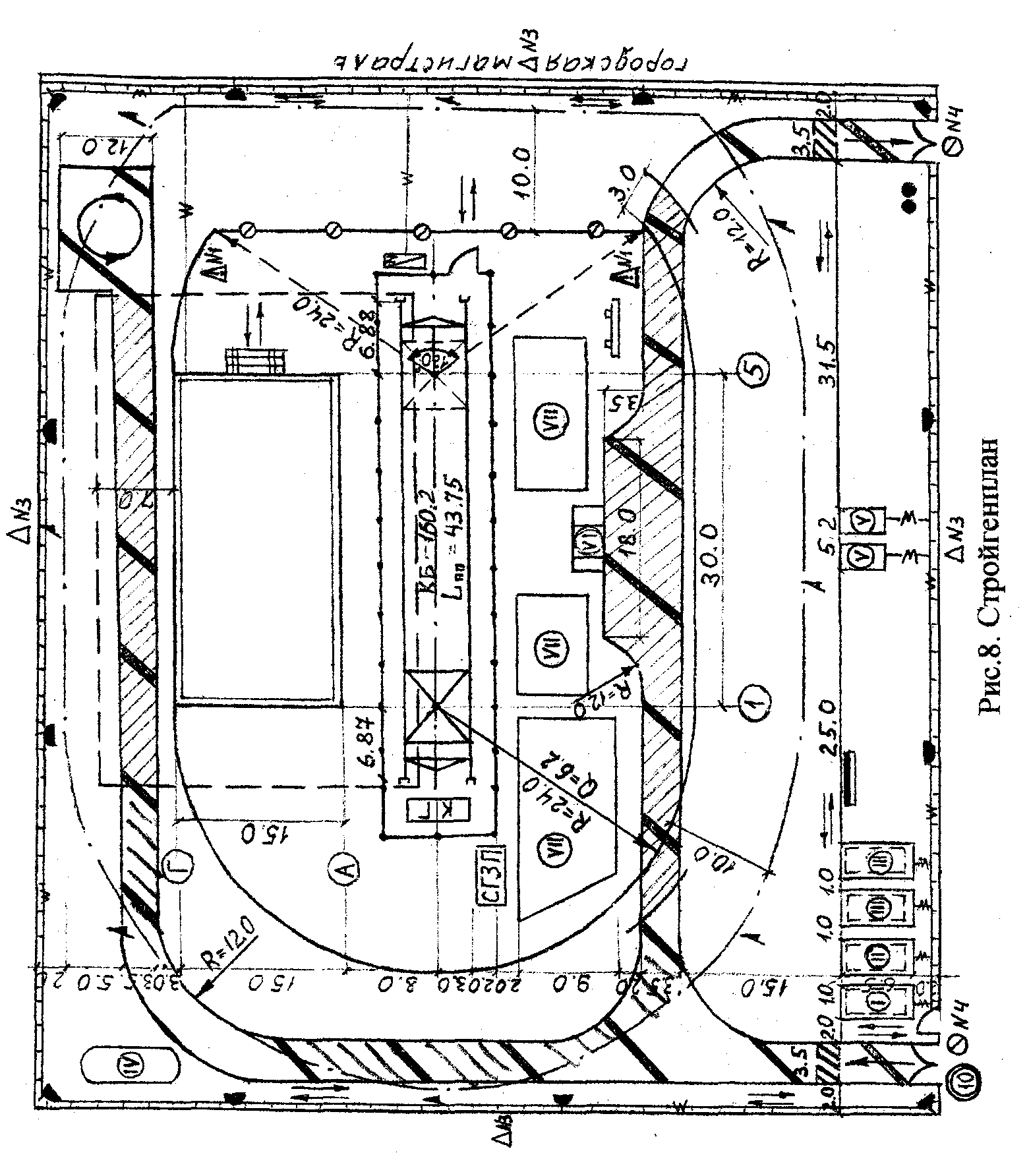
— шкаф электропитания ).
Длину подкрановых путей
корректируют в сторону увеличения с
учетом кратности длине полузвена (6,25
м). Минимально допустимая длина путей
согласно правилам Госгортехнадзора
составляет два звена (25 м). Таким образом,
принятая длина путей должна удовлетворять
условию: Ln.n
= 6,25пзв > 25 м, где nзв
— число полузвеньев. Например,
если по расчету длина путей составляет
40 м, следует принять Ln.n=43,75
м (7 полузвеньев).
При необходимости кран может быть
установлен и на одном звене, то есть на
приколе. В этом случае для исключения
просадки подкрановых путей звено должно
быть уложено на жестком основании,
например, на специальных сборных
железобетонных конструкциях.
При продольной привязке
ограждений подкрановых путей на
стройгенплане должно быть показано
место нахождения контрольного груза
для проверки ограничителей грузоподъемности.
При этом выдерживается минимальное
расстояние 1 м :
— от конца рельса до ограждения;
от конца рельса до контрольного груза;
от контрольного груза до ограждения.
На стройгенплане показывается шкаф
электропитания крана, который
устанавливается за ограждением с
наружной от здания стороны кранового
пути.
Рабочая привязка самоходных
стреловых кранов заключается в нанесении
на стройгенплан осей их движения и
стоянок. Установка и работа гусеничных,
пневмоколесных и автомобильных кранов
вблизи котлованов и траншей с
неукрепленными откосами разрешается
только за пределами призмы обрушения
грунта. Безопасное расстояние от
основания откоса выемки до оси перемещения
крана 1без
определяется по формуле:
1без
= 1оп
+ 0,5bк
,
где 1оп — минимальное расстояние по
горизонтали от основания откоса до оси
ближайшей к выемке гусеницы, колеса или
выносной опоры ( м), принимается по
таблице 3;
bк
— ширина колеи крана
(м), принимается по таблицам 4,5. При
монтаже подземной части объекта
самоходный стреловой кран обычно
передвигается вдоль бровки траншеи или
котлована. На выносных опорах пневмоколесные
и автомобильные краны устанавливаются
по направлению движения, при этом
продольная ось крана совпадает с осью
движения (рис.5).
Установка стрелового крана должна
производиться так, чтобы расстояние
между поворотной частью крана и
строениями, штабелями и другими предметами
было не менее 1 м [6]. Привязка крана при
монтаже надземной части здания
осуществляется по формуле:
В = Rпов
+ 1 ,
где В — минимальное расстояние от оси
движения крана до наружной
грани здания (м);
Rпов
— радиус поворотной части (м), принимается
по табл. 4,5.
Рабочая привязка строительных подъемников
производится так, чтобы основные
конструкции, материалы, изделия и
оборудование могли подаваться средствами
горизонтального транспорта в зоны их
действия без перегрузок. Стационарные
подъемники обычно располагаются на
границе или середине захваток, что
удобно с точки зрения обслуживания
грузоподъемных машин.
5) Зоны
влияния определяют
после привязки строительных машин с
целью обеспечения требований безопасности
труда. При организации строительной
площадки устанавливают опасные для
людей зоны, в пределах которых
постоянно действуют или потенциально
могут действовать опасные производственные
факторы.
К зонам постоянно
действующих опасных факторов относятся
зоны перемещения монтажных и грузоподъемных
машин, их частей и рабочих органов; зоны,
над которыми происходит перемещение
грузов кранами. Эти зоны во избежание
доступа посторонних лиц ограждаются
защитными ограждениями панельной или
панель-стоечной конструкции. К зонам
потенциально действующих
опасных факторов относятся
участки территории вблизи строящегося
здания. Эти зоны для предупреждения об
опасности ограждаются сигнальными
ограждениями из проволоки или каната
по стойкам. Защитные и сигнальные
ограждения должны соответствовать ГОСТ
Р 51 248 — 99. Следует устанавливать и
обозначать на стройгенплане следующие
опасные для людей зоны: -монтажную;
— зону обслуживания краном;
— опасную зону работы крана;
-опасную зону подкрановых путей или
опасную зону поворотной платформы;
— опасную зону работы подъемника.
Монтажной зоной
называют пространство, в котором возможно
падение элементов при их установке и
закреплении. Эта зона является потенциально
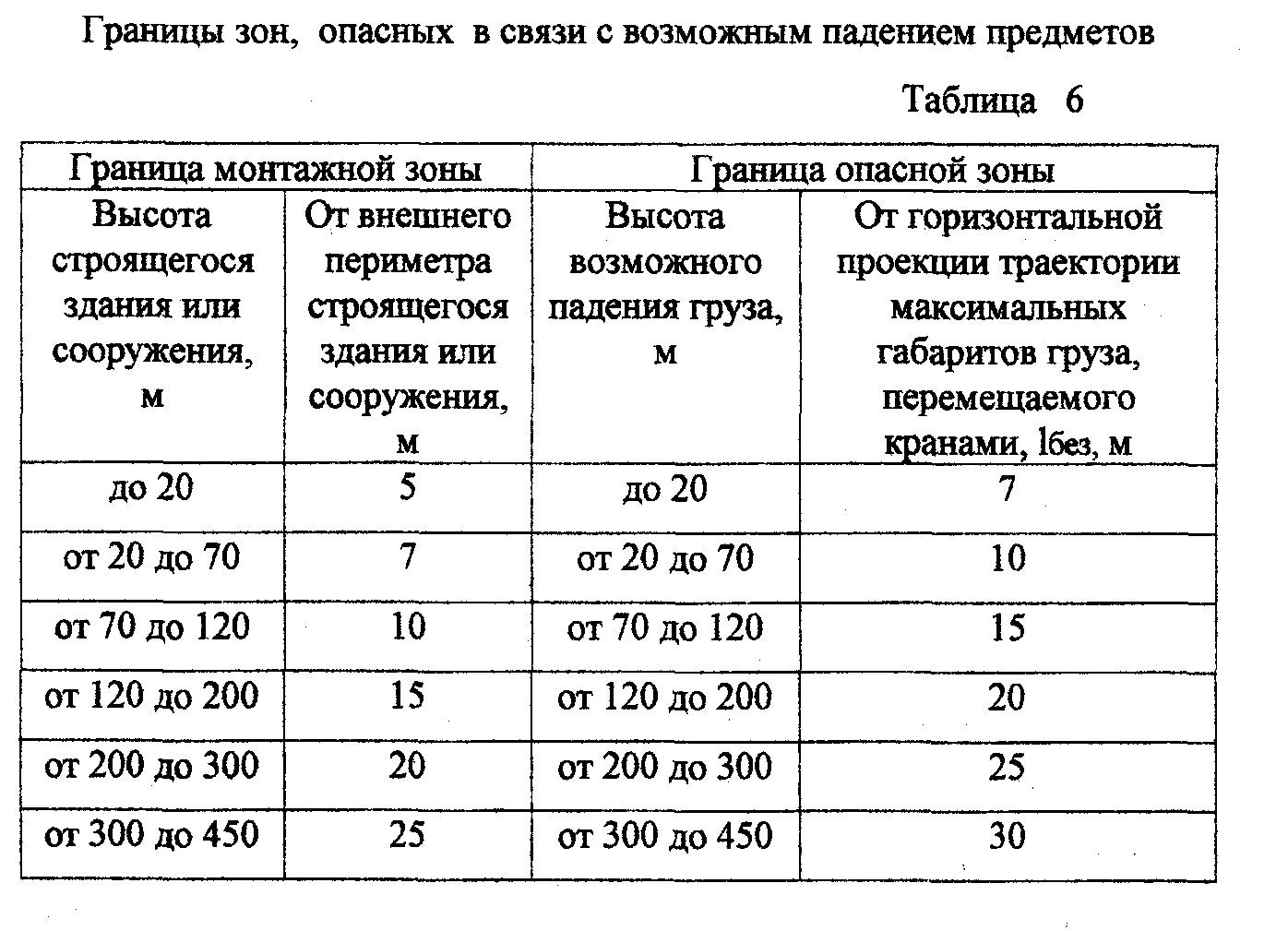
опасной. Согласно действующим нормативам,
границы этой зоны устанавливаются от
внешнего контура здания и зависят от
его высоты (табл.6; рис. 6а). В этой зоне
можно размещать только монтажный
механизм, складировать конструкции и
материалы здесь нельзя. Проход

людей через монтажную зону к строящемуся
зданию устанавливают со стороны, где
не работает кран; направление прохода
на стройгенплане показывают стрелками
в соответствии с принятыми условными
обозначениями. Места проходов через
эту зону защищают сплошными навесами
шириной не менее ширины входа с вылетом
не менее 2 м от стены здания. На стройгенплане
монтажную зону обозначают пунктирной
линией.
Все рассматриваемые ниже зоны влияния
относятся к зонам постоянно действующих
опасных производственных факторов.
Зона обслуживания краном
— это пространство, описываемое крюком
крана на максимальном необходимом для
работы вылете. Определяется для башенных
кранов путем нанесения на план из крайних
стоянок полуокружностей радиусом Rмакс
и соединения их прямыми линиями (рис. 6
). Для стреловых кранов зона обслуживания
тоже определяется максимальным рабочим
вылетом стрелы, но показывается по
отдельным стоянкам. На стройгенплане
обозначается утолщенной сплошной
линией.
Опасная зона работы крана
— это пространство, в
котором возможно падение груза при его
перемещении с учетом рассеивания при
падении. Рассеивание может быть вызвано
раскачиванием груза на крюке при движении
крана и под давлением ветра.
Для башенных кранов границу
опасной зоны Ron
определяют по формуле:
Rоп
= Rмакс
+ 0,51макс + 1без ,
где Rмакс
— максимальный рабочий вылет стрелы
крана ( м );
1макс — длина наибольшего перемещаемого
груза (м);
1без — дополнительное расстояние для
безопасной работы, зависит от высоты
подъема груза и устанавливается в
соответствии со СНИП [ 2 ] ( табл.6; рис.бв
).
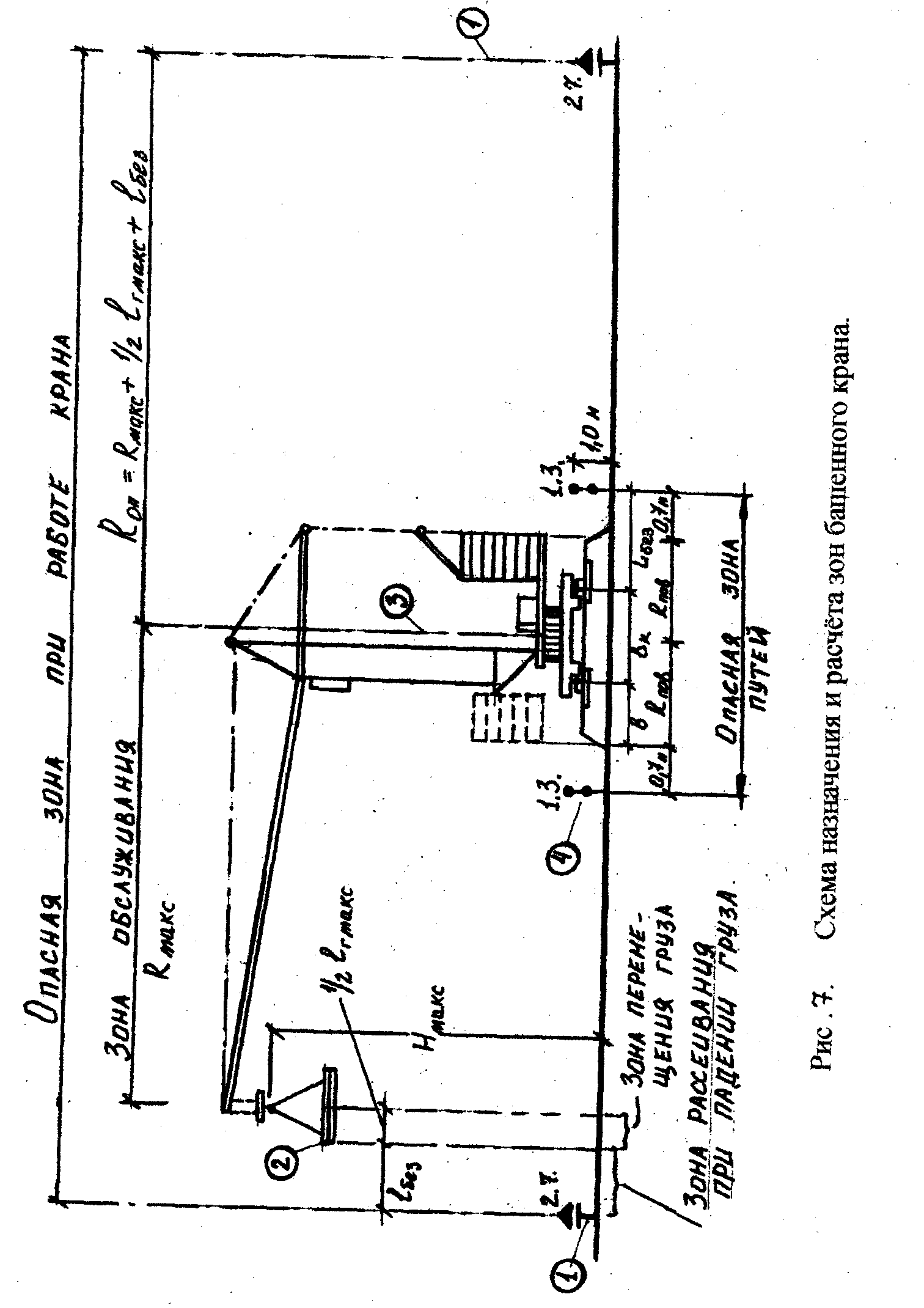
Опасная зона подкрановых
путей башенных кранов
определяется при поперечной привязке
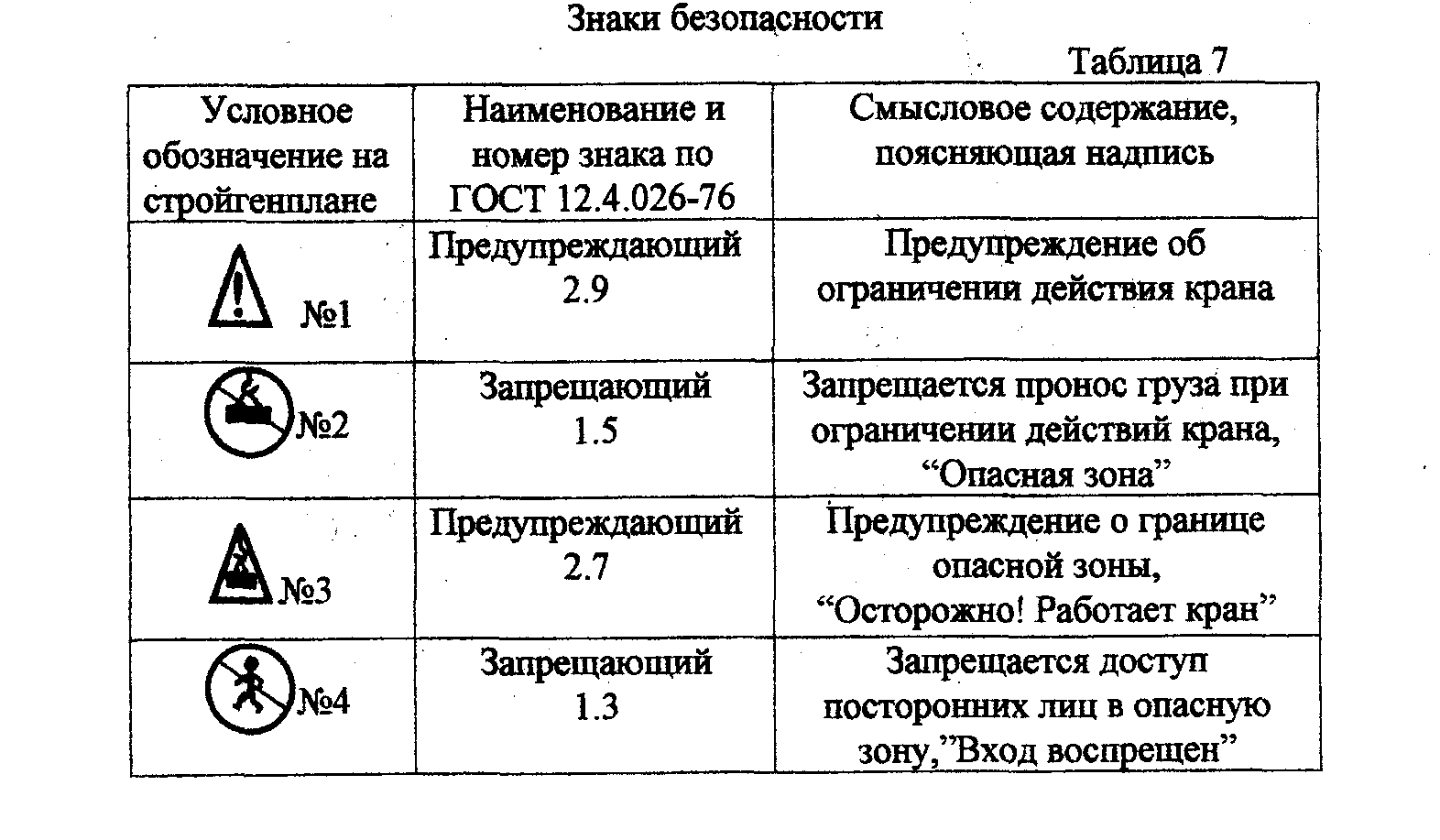
ограждений ( рис.7: 1 — знак безопасности
№3 на границе опасной зоны с обозначением
его номера 2.7 по ГОСТу; 2 — груз; 3 — ось
подкрановых путей; 4 — инвентарное
ограждение подкрановых путей и знак
безопасности №4 с обозначением его
номера 1.3 по ГОСТу ). На стройгенплане с
помощью условного обозначения показывают
инвентарное сетчатое ограждение
подкрановых путей с калиткой для прохода
машиниста.
Зону обозначают на
стройгенплане штрихпунктирной линией
( рис.бг, табл.8).
Технические характеристики строительных
подъемников
Таблица 8
|
Модель |
Назначение |
Грузоподъемность, кг |
Высота подъема, |
Габаритные размеры платформы (кабины), |
|
ТП-ЗА(С-598А) |
грузовой |
320 |
9 |
1,5×0,9 |
|
ТП-2(С-447) |
грузовой |
500 |
17 |
1,5 х 1,0 |
|
ТП-7(С-447М) |
грузовой |
500 |
27 |
1,5 х 1,0 |
|
ТП-9 |
грузовой |
500 |
17 |
1,5×0,9 |
|
ТП-12 |
грузовой |
500 |
27 |
1,5×0,9 |
|
ТП-14 |
грузовой |
500 |
50 |
1,45 хО,68 |
|
ПР-1-172 |
грузопассажирский |
580 |
70 |
2,4×1,2 |
|
ПГС-800-16 |
грузопассажирский |
800 |
80 |
3,1×1,5 |
|
МГП-1000 |
грузопассажирский |
1000 |
150 |
2,5 х 1,5 |
Опасная зона поворотной
части стреловых кранов
определяется по формуле:
Яоп.пов
= RnoB
+ 1 (м),
Расчет приводится в пояснительной
записке, зона на стройгенплане не
показывается. На местности эту опасную
зону обозначают инвентарной переставной
обноской из проволоки по стойкам.
Опасная зона работы
подъемника (А) — это
пространство, в котором возможно падение
поднимаемого груза. При высоте подъема
груза Н до 20 м зону следует принимать
не менее 5 м от габаритов подъемника в
плане, а при подъеме на большую высоту
величина зоны составляет:
А = 5 + 1/15(Н — 20)
Зону обозначают на стройгенплане
штрихпунктирной линией ( рис.бг, табл.8).
6) Ограничения
в работу вводят при
совместном использовании на объекте
нескольких кранов и при работе в
стесненных условиях.
Совместная работа нескольких механизмов
в одной монтажной зоне, как правило,
запрещена. В случае производственной
необходимости одновременная работа
допускается при условии осуществления
специальных мероприятий по технике
безопасности.
Если краны расположены с двух сторон
здания, совместная работа должна быть
организована так, чтобы траектории
движения их стрел не пересекались. Тогда
минимальное расстояние между осями
вращения кранов при их предельном
сближении определяется по формулам:
— для башенных кранов
С = Ll
+ L2
+ 0,5 (l1
+ 12)
+ Δ1
+ Δ2
+ 2Δб
— для стреловых кранов
С = Ll
+ L2
+ 0,5 (l1
+ 12)
+ Δ1
+ Δ2
,
где — L1,
L2
— вылеты стрел при совместной работе
(м);
ll,
12 —
максимальный горизонтальный размер
монтируемых конструкций (м);
Δ1,
Δ2
— отклонение конструкций от вертикали
при вращении стрелы:
Δ = 900L
/ (900 – ω2H)
— L
ω — максимальная частота
вращения поворотной части (мин
-1) [3]; ориентировочно
можно принять: для башенных кранов-
ω=0,7; для гусеничных- ω=0,3; для пневмоколесных-
ω=1,2; для кранов на спецшасси автомобильного
типа- ω=1,6; для автомобильных кранов- ω=
2,0;
Н — высота подъема конструкции (м);
Δб
— возможное отклонение от вертикали
башни крана в результате ее податливости
и уклона пути, Δб
=0,5 м.
Пример.
С двух сторон здания на монтаже плит
покрытия длиной 1 = 6 м работают два
башенных крана КБ-100. Вылет при совместной
работе L
= 20 м, высота подъема плит Н = 33 м.
Максимальная частота вращения башни
крана ω = 0,7 мин-1.
Расчет: Δ = 900* 20/ (900 — О,72х33)
— 20 = 0,37 м
С = 20 + 20 + 1/2(6 + 6) + 0,37 + 0,37 + 2*0,5
= 47,74 м.
Расстояние между крюками
должно быть не менее 47,74 – 20х2 = 7,74 м.
Если монтаж конструкций ведется двумя
кранами, расположенными с одной стороны,
то это та сторона здания, где нет входов
в него. При сближении башенных кранов,
установленных на общих рельсовых путях,
требованиями техники безопасности
предусматривается установка концевых
выключателей механизмов передвижения
для остановки кранов на расстоянии не
менее 5 м между перемещаемыми грузами
или выступающими конструкциями кранов.
При работе монтажного крана в стесненных
условиях приходится вводить ограничения
на определенные рабочие движения крана,
например, на поворот башни во избежание
проноса груза над действующей городской
магистралью. Ограничения могут быть
принудительными или условными, их
показывают на стройгенплане или
прилагаемых к нему схемах.
Принудительные ограничения
зоны обслуживания применяют при работе
кранов с электрическим приводом
(башенных, козловых). Эти ограничения
осуществляются установкой концевых
выключателей, при срабатывании которых
независимо от действий машиниста
происходит остановка определенного
механизма и исключается пронос груза
в зону ограничения. На башенных кранах
устанавливают концевые выключатели
механизмов передвижения крана и тележки,
поворота стрелы, изменения вылета. При
ограничении поворота стрелы после
срабатывания выключателей расстояние
до зоны ограничения должно быть не менее
тормозного пути стрелы крана с максимальным
грузом (указан в паспорте крана, можно
принять 2 м). В этом случае на стройгенплане
обозначают:
— угол
ограничения а, который
проставляется в запрещенном секторе;
— места
расположения предупреждающих знаков
Ml,
которые устанавливают
на расстоянии тормозного пути до места
срабатывания концевых выключателей;
— линию
запрещающих знаков №2, устанавливаемых
по контуру зоны ограничения (рис.8,9).
Условные (визуальные)
ограничения зоны обслуживания применяются
при работе башенных и стреловых самоходных
кранов; они рассчитаны на внимание
крановщика и стропальщиков. На местности
зону ограничения обозначают хорошо
видимыми с крана красными флажками, а
в темное время суток- гирляндами из
красных ламп. На стройгенплане показывают:
— места
расположения предупреждающих знаков
№1, которые
устанавливают на расстоянии тормозного
пути до линии ограничения;
— линия
запрещающих знаков М2, т.е.
линия ограничения, пронос груза за
которую запрещен;
— запись
об условиях работы крана, «крановщик
обязан остановить груз, не доходя 1 метра
до предупреждающего знака №1,далее до
места установки груза перемещать его
повторными короткими включениями «.
Определение массы и расположения центра тяжести груза
Стропальщик должен уметь определять массу и центр тяжести груза с целью обеспечения безопасности погрузо-разгрузочных работ.
Под массой груза следует понимать (скалярную, ненаправленную) физическую характеристику тела, являющуюся мерой его инерционных и гравитационных свойств. Значения массы тела не зависят от ускорения свободного падения в пункте определения. В состоянии покоя ее определяют взвешиванием на рычажных весах. Результат взвешивания показывает сравнительную с массой гирь величину, выраженную в единицах массы — граммах (г), килограммах (кг), тоннах (т).
Под силой тяжести следует понимать векторную (направленную) величину, определяющую силу притяжения тела к Земле или к другому небесному телу. Значение силы тяжести зависит от ускорения свободного падения в пункте измерения. Сила тяжести на полюсе больше, а на экваторе меньше. По мере удаления тела от поверхности Земли его сила тяжести уменьшается. Эту величину измеряют с помощью динамометра в условиях относительного покоя тела. Силу тяжести, как и любую другую силу, выражают в единицах силы — ньютонах (Н), килоньютонах (кН) и других дольных и кратных значениях этой величины.
Вес тела — сила, с которой тело действует вследствие силы тяжести к Земле на опору (или подвес), удерживающую его от падения. Вес тела равен его силе тяжести, если опора и тело неподвижны относительно Земли. Единица веса (и силы тяжести) в Международной системе единиц (СИ)—ньютон (Н).
Под грузоподъемностью крана, автопогрузчика, электрокара следует понимать максимальную массу груза, которую способно в один прием поднять, переместить или перевезти транспортное средство.
Грузоподъемность, как и масса, — скалярная величина и измеряется единицами массы — грамм (г), килограмм (кг), тонна (т).
Грузоподъемная (подъемная) сила (по аналогии с силой тяжести) — величина, характеризующая способность транспортного средства преодолевать при подъеме или перемещении массу груза. Единицами грузоподъемной силы служат ньютоны (Н), килоньютоны (кH) и другие дольные и кратные значения ньютона.
Перед строповкой груза, предназначенного для перемещения, стропальщик должен определить его массу. Массу изготовленной на заводе продукции проставляют на чертежах изделий. Массу оборудования, приспособлений, механизмов указывают в табличке, прикрепленной к раме или станине. Если груз упакован, то массу его указывают на обшивке. Однако массу груза, подлежащего перемещению, стропальщику часто приходится определять визуально. Удельная масса часто встречающихся материалов приведена ниже, кг/м 3
| Алюмений | 2550—2700 | Олово | |
| Бетон | 2200 1000 | Парафин | 900 11300 |
| Вольфрам Древесина: береза, дуб сосна | Сталь: твердая расплавленная | 7300 7500 6900—7300 | |
| Земля, глина Песчаник Песок: сухой влажный | 1300—2500 2200—2500 1400—1600 1900—2000 | Чугун: белый ковкий серый Уголь Кокс | |
| Кирпичная кладка | 1420—1700 | Азот жидкий | 790 700 |
| латунь | |||
| Лед | Воздух (жидкий) | ||
| Медь | Керосин | ||
| Мел | Кислород (жид) | ||
| Никель | Мазут |
Для определения массы груза используют следующие формулы:
для простых грузов Q=mV;
для сложных грузов Q=måVi,
где Q — масса груза; т — удельная масса, численно равная плотности материала; V — объем груза; Vt — объем отдельных частей груза; å — сумма всех частей груза.
Объем правильных геометрических фигур приведен в табл. 1.
Пример. Определим массу слитка, размеры которого приведены на рис. 6.
Разбиваем условно слиток на три усеченных конуса и определяем объем каждого. Для этого в табл. 1 находим формулу объема усеченного конуса
V= (3,14/3) h (R 2 + r 2 + Rr)
Находим объемы каждого элемента слитка
(3,14/3) 1,700 [0,55 2 + 0,45 2 + 0,55-0,45]» 1,34 м 3 ;
(3,14/3) 0,05 [0,55 2 + 0,42 2 + 0,55-0,42]
(3,14/3) 0,4 [0,42 2 + 0,4 2 + 0,42-0,4] »0,21 м 3 .
Определяем суммарный объем слитка
Принимаем удельную массу слитка равной 7,8 т/м 3 , тогда масса слитка
При выборе мест строповки груза возникает _необходимость определить расположение центра тяжести поднимаемого груза. Если при строповке это не учитывать, то возможны аварийные ситуации, связанные с перегрузкой отдельных ветвей стропов, грузоподъемных средств; потерей устойчивости и опрокидыванием поднимаемого объекта.
Положение центра тяжести различных геометрических тел находят по координатам хц.Т, yц.т, zц.т, определяемым по формулам
где хц.т, yц.т, zц.т, — расстояние от центра тяжести тела до плоскости, проходящей перпендикулярно измеряемой оси через центр координат, м; xi,-, yi, zi—расстояние от центра тяжести отдельной рассматриваемой части тела до той же плоскости, м; Q — общая масса тела, т; Qi:— — масса отдельной рассматриваемой части тела, т.
Координаты центра тяжести правильных геометрических фигур приведены в табл.1
Пример. Определим расположение центра тяжести стального слитка, изображенного на рис. 1.
Условно разбиваем слиток на три правильных усеченных конуса. По табл. 1 находим формулы, определяющие их координаты расположения центра тяжести. Плоскость отсчета принимаем проходящей через нижнее основание слитка -перпендикулярно его оси. Из предыдущего примера известно, что отдельные части слитка имеют массу q1 = 10,45; Q2 =0,31; Q3=1,64 т, общая масса 12,4 т. Учитывая, что слиток симметричен относительно своей оси, определяем расположение только координаты zцт, Координаты xцт, уцт будут расположены на оси. Формула для определения координаты zцт усеченного конуса имеет вид
zцт =h[(R 2 +2Rr+3r 2 )/(R 2 +Rr+r 2 )]/4
Рис. 1. Схема слитка
Величину z1 ` до принятой плоскости отсчета определяют как разность 1,7 — z1 = l,7 — 0,77=0,930 м. Зная h2=0,05 м; R2=0,55 м; г2=0,425 м, имеем
До принятой плоскости отсчета z2 определяют как сумму 1,7+z2==1,7+0,02=1,72 м.
До принятой плоскости отсчета zз определяют как сумму 1,7+0,05+0,176= 1,926м.
Определяем расположение центра тяжести по формуле
подставляя в формулу соответствующие значения, находим расстояние между центром тяжести и началом координат
zцт = (10,45-0,93+ 0,31-1,72+ 1,64.1,926)/12,4 = 1,081 м.
Таблица 1. Объем и расположение центра тяжести простых геометрических тел
| Наименование | Изображение | Объем | Положение центра тяжести |
| Куб | Рис. 1 | V = a 3 | x = а/2, у = а/2, z = а/2 х = у = z = а/2 |
| Прямоугольный параллелепипед | Рис. 2 | V = abc | x = а/2, у = c/2, z = b/2 х = r , y =0 , z = b/2 |
| Цилиндр | Рис. 3 | V = 3,14 xr 2 h | х = г, у= 0, г = h 2 /2 |
| Шар | Рис. 4 | V = 3,14/D 3 /6 | Если оси координат про» ходят через центр шара, то x=у=z=0 (центр тяжести совпадает с цент« ром шара) |
| Боченок | Рис. 5 | V=3,14/12Hx x(2D 2 + d 2 ) | х = у = 0, z=H/2 |
| Конус | Рис. 6 | V= 3,14/12D2H | x = у = 0, z=H/4 |
| Усеченный конус | Рис. 7 | V=(3,14H/3)x(R 2 +r 2 +Rr) | х = у= 0 z = H/4 [(R 2 + 3r 2 +2Rr)/(R 2 +r 2 +Rr) |
| Пирамида | Рис. 8 | V=(Fh)/3, где F — площадь основания многоугольника | х = у = 0, z=h/4 |
| Усеченная пирамида | Рис. 9 | V=h[F + f + + ÖFf]/3 | x = y = 0, z= h/4[F + + 2ÖFf + 3f/F] ÖFf+f |
| Усеченный цилиндр | Рис. 10 | V = 3,14R 2 (h1+h2)/2 | x=y=0, z=(h1+h2)/2 |
Определив расстояние центра тяжести от принятого начала координат, его переносят на поднимаемый груз и делают пометку мелом или другим способом.
Места застроповки груза должны располагаться симметрично центру тяжести таким образом, чтобы отвесная прямая, проходящая через центр тяжести, размещалась между местами застроповки. Чем больше расстояние между местами застроповки, тем устойчивее положение груза при прочих равных условиях.
На упакованных грузах расположение центра тяжести указывают на упаковке.
В тех случаях, когда конфигурация груза вызывает затруднения при расчете положения центра тяжести, а его необходимо определить, то можно использовать практический прием. После определения массы груза подбирают соответствующий строп и им приподнимают груз за один из краев. На приподнятом грузе на двух плоскостях проводят отвесные линии как продолжение ветви стропа. Затем груз опускают и приподнимают за другой конец. На тех же плоскостях снова проводят отвесные прямые. Точки пересечения отвесов определяют расположение центра тяжести определяемого груза.
В тех случаях, когда стропальщик затрудняется определить массу перемещаемого груза и расположения центра тяжести, он обязан обратиться за уточнением к своему бригадиру, мастеру или руководителю работ.
При монтаже несущих конструкций ОПЗ из двух возможных схем перемещения стрелового крана — вдоль пролетов или поперек пролетов -обычно выбирают первую, так как путь крана в этом случае гораздо короче. При монтаже стеновых панелей стреловой кран движется снаружи по периметру здания. При строительстве многоэтажных жилых и гражданских зданий башенный кран обычно передвигается снаружи здания вдоль длинной его стороны. Монтаж ведется в направлении «на кран», то есть в первую очередь устанавливаются наиболее удаленные от крана конструкции. В многоэтажных промышленных зданиях башенный или стреловой кран может перемещаться внутри здания, монтируя его на всю высоту «на себя» с постепенным выездом за пределы здания.
При совместной работе нескольких монтажных кранов схема движения разрабатывается с учетом требований техники безопасности. Здание разбивают на монтажные зоны по числу работающих кранов, в пределах каждой зоны разрешается работа только одного из них. Другой в это время должен работать в своей монтажной зоне или простаивать.
4) Рабочая привязка монтажных кранов и подъемников — это установление точного взаимного расположения возводимого здания и грузоподъемных машин. Правильная привязка обеспечивает требуемый «охват» всего объекта монтажными машинами и безопасные условия производства работ.
Рабочая привязка башенных кранов состоит в поперечной и продольной привязке крана, подкрановых путей и их ограждений.
Поперечная привязка при возведении надземной части здания заключается в определении расстояния от оси подкрановых путей до ближайшей к крану грани строящегося здания (рис.2: 1 — строящееся здание; 2 — инвентарное ограждение путей; 3 — склад; 4 — водоотводная канава). Это расстояние зависит от конструктивного исполнения крана и ширины колеи. У кранов с поворотной башней наиболее приближены к зданию поворотная платформа или нижний противовес. Привязка таких кранов осуществляется по формуле:
где В — минимальное расстояние от оси подкрановых путей до наружной грани здания (м );
Rпов — радиус поворотной части или противовеса, принимают по справочникам или таблице 1 (м );
1без — минимально допустимое расстояние по горизонтали между выступающей частью крана и зданием, принимается на высоте до 2 м от уровня земли не менее 0,7 м; на высоте более 2 м — не менее 0,4 м.
Краны с неповоротной башней могут располагаться ближе к зданию, поскольку механизм поворота и противовесная консоль располагаются выше строящегося объекта. У этих кранов наиболее приближенной к зданию является ходовая часть, для них:
В = 0,5 Ьк + b + 1без ,
где Ьк — ширина колеи крана ( м);
b — величина выступающей за колею ходовой части (м),
определяется по паспорту крана или таблице 2 .
Привязку башенных и рельсовых стреловых кранов при возведении подземной части здания у неукрепленных котлованов и траншей производят исходя из глубины выемки h и вида грунта, что обеспечивает расположение машин за пределами призмы обрушения (рис.3). Безопасное расстояние по горизонтали от основания откоса выемки до оси ближайшего рельса определяется по формуле:
где 1б — минимальное расстояние от основания откоса выемки до нижнего края балластной призмы; для песчаных и супесчаных грунтов 1б > l,5h + 0,4; для глинистых и суглинистых грунтов 1б > h + 0,4(м); 1р — расстояние от нижнего края балластной призмы до оси рельса (м), определяется по формуле:
hб — высота слоя балласта под полушпалами (м), зависит от вида
балласта и типа крана (таблицы 1,2);
0,05 — углубление полушпалы в балласт (м);
m — показатель крутизны откосов балластной призмы, для щебня и гравия m =1,5;
для песка и шлака т=2;
0,2 — минимально допустимое расстояние от верхнего края балластной призмы до конца полушпалы (м);
1ш — длина деревянной полушпалы, 1ш = 1,35 м.
Поперечную привязку ограждений подкрановых путей к наружному рельсу производят исходя из необходимости соблюдения безопасного расстояния между конструкциями крана и ограждением.
Для кранов с поворотной башней расстояние от оси ближнего к ограждению рельса до ограждения определяют по формуле:
При привязке ограждений башенных кранов с неповоротной башней учитывается выступающая за колею ходовая часть:
Крайние из этих засечек определяют положение крайних стоянок, а измеренное по чертежу в соответствии с принятым масштабом расстояние и есть 1кр. На стройгенплане крайние стоянки должны быть обозначены и привязаны к осям здания (рис.4: 1- крайние стоянки; 2 — привязка крайних стоянок к оси; 3 — контрольный груз; 4 — место установки тупика; 5 — конец рельса; 6 — база крана; 7 — шкаф электропитания ).
Длину подкрановых путей корректируют в сторону увеличения с учетом кратности длине полузвена (6,25 м). Минимально допустимая длина путей согласно правилам Госгортехнадзора составляет два звена (25 м). Таким образом, принятая длина путей должна удовлетворять условию: Ln.n = 6,25пзв > 25 м, где nзв — число полузвеньев. Например, если по расчету длина путей составляет 40 м, следует принять Ln.n=43,75 м (7 полузвеньев).
При необходимости кран может быть установлен и на одном звене, то есть на приколе. В этом случае для исключения просадки подкрановых путей звено должно быть уложено на жестком основании, например, на специальных сборных железобетонных конструкциях.
При продольной привязке ограждений подкрановых путей на стройгенплане должно быть показано место нахождения контрольного груза для проверки ограничителей грузоподъемности. При этом выдерживается минимальное расстояние 1 м :
— от конца рельса до ограждения;
от конца рельса до контрольного груза;
от контрольного груза до ограждения.
На стройгенплане показывается шкаф электропитания крана, который устанавливается за ограждением с наружной от здания стороны кранового пути.
Рабочая привязка самоходных стреловых кранов заключается в нанесении на стройгенплан осей их движения и стоянок. Установка и работа гусеничных, пневмоколесных и автомобильных кранов вблизи котлованов и траншей с неукрепленными откосами разрешается только за пределами призмы обрушения грунта. Безопасное расстояние от основания откоса выемки до оси перемещения крана 1без определяется по формуле:
где 1оп — минимальное расстояние по горизонтали от основания откоса до оси ближайшей к выемке гусеницы, колеса или выносной опоры ( м), принимается по таблице 3;
bк — ширина колеи крана (м), принимается по таблицам 4,5. При монтаже подземной части объекта самоходный стреловой кран обычно передвигается вдоль бровки траншеи или котлована. На выносных опорах пневмоколесные и автомобильные краны устанавливаются по направлению движения, при этом продольная ось крана совпадает с осью движения (рис.5).
Установка стрелового крана должна производиться так, чтобы расстояние между поворотной частью крана и строениями, штабелями и другими предметами было не менее 1 м [6]. Привязка крана при монтаже надземной части здания осуществляется по формуле:
где В — минимальное расстояние от оси движения крана до наружной
Rпов — радиус поворотной части (м), принимается по табл. 4,5.
Рабочая привязка строительных подъемников производится так, чтобы основные конструкции, материалы, изделия и оборудование могли подаваться средствами горизонтального транспорта в зоны их действия без перегрузок. Стационарные подъемники обычно располагаются на границе или середине захваток, что удобно с точки зрения обслуживания грузоподъемных машин.
5) Зоны влияния определяют после привязки строительных машин с целью обеспечения требований безопасности труда. При организации строительной площадки устанавливают опасные для людей зоны, в пределах которых постоянно действуют или потенциально могут действовать опасные производственные факторы.
К зонам постоянно действующих опасных факторов относятся зоны перемещения монтажных и грузоподъемных машин, их частей и рабочих органов; зоны, над которыми происходит перемещение грузов кранами. Эти зоны во избежание доступа посторонних лиц ограждаются защитными ограждениями панельной или панель-стоечной конструкции. К зонам потенциально действующих опасных факторов относятся участки территории вблизи строящегося здания. Эти зоны для предупреждения об опасности ограждаются сигнальными ограждениями из проволоки или каната по стойкам. Защитные и сигнальные ограждения должны соответствовать ГОСТ Р 51 248 — 99. Следует устанавливать и обозначать на стройгенплане следующие опасные для людей зоны: -монтажную;
— зону обслуживания краном;
— опасную зону работы крана;
-опасную зону подкрановых путей или опасную зону поворотной платформы;
— опасную зону работы подъемника.
Монтажной зоной называют пространство, в котором возможно падение элементов при их установке и закреплении. Эта зона является потенциально опасной. Согласно действующим нормативам, границы этой зоны устанавливаются от внешнего контура здания и зависят от его высоты (табл.6; рис. 6а). В этой зоне можно размещать только монтажный механизм, складировать конструкции и материалы здесь нельзя. Проход
людей через монтажную зону к строящемуся зданию устанавливают со стороны, где не работает кран; направление прохода на стройгенплане показывают стрелками в соответствии с принятыми условными обозначениями. Места проходов через эту зону защищают сплошными навесами шириной не менее ширины входа с вылетом не менее 2 м от стены здания. На стройгенплане монтажную зону обозначают пунктирной линией.
Все рассматриваемые ниже зоны влияния относятся к зонам постоянно действующих опасных производственных факторов.
Зона обслуживания краном — это пространство, описываемое крюком крана на максимальном необходимом для работы вылете. Определяется для башенных кранов путем нанесения на план из крайних стоянок полуокружностей радиусом Rмакс и соединения их прямыми линиями (рис. 6 ). Для стреловых кранов зона обслуживания тоже определяется максимальным рабочим вылетом стрелы, но показывается по отдельным стоянкам. На стройгенплане обозначается утолщенной сплошной линией.
Опасная зона работы крана — это пространство, в котором возможно падение груза при его перемещении с учетом рассеивания при падении. Рассеивание может быть вызвано раскачиванием груза на крюке при движении крана и под давлением ветра.
Для башенных кранов границу опасной зоны Ron определяют по формуле:
Rоп = Rмакс + 0,51макс + 1без ,
где Rмакс — максимальный рабочий вылет стрелы крана ( м );
1макс — длина наибольшего перемещаемого груза (м);
1без — дополнительное расстояние для безопасной работы, зависит от высоты подъема груза и устанавливается в соответствии со СНИП [ 2 ] ( табл.6; рис.бв ).
Опасная зона подкрановых путей башенных кранов определяется при поперечной привязке ограждений ( рис.7: 1 — знак безопасности №3 на границе опасной зоны с обозначением его номера 2.7 по ГОСТу; 2 — груз; 3 — ось подкрановых путей; 4 — инвентарное ограждение подкрановых путей и знак безопасности №4 с обозначением его номера 1.3 по ГОСТу ). На стройгенплане с помощью условного обозначения показывают инвентарное сетчатое ограждение подкрановых путей с калиткой для прохода машиниста.
Зону обозначают на стройгенплане штрихпунктирной линией ( рис.бг, табл.8).
Технические характеристики строительных подъемников
| Модель | Назначение | Грузоподъемность, кг | Высота подъема, м | Габаритные размеры платформы (кабины), м |
| ТП-ЗА(С-598А) | грузовой | 1,5×0,9 | ||
| ТП-2(С-447) | грузовой | 1,5 х 1,0 | ||
| ТП-7(С-447М) | грузовой | 1,5 х 1,0 | ||
| ТП-9 | грузовой | 1,5×0,9 | ||
| ТП-12 | грузовой | 1,5×0,9 | ||
| ТП-14 | грузовой | 1,45 хО,68 | ||
| ПР-1-172 | грузопассажирский | 2,4×1,2 | ||
| ПГС-800-16 | грузопассажирский | 3,1×1,5 | ||
| МГП-1000 | грузопассажирский | 2,5 х 1,5 |
Опасная зона поворотной части стреловых кранов определяется по формуле:
Яоп.пов = RnoB + 1 (м),
Расчет приводится в пояснительной записке, зона на стройгенплане не показывается. На местности эту опасную зону обозначают инвентарной переставной обноской из проволоки по стойкам.
Опасная зона работы подъемника (А) — это пространство, в котором возможно падение поднимаемого груза. При высоте подъема груза Н до 20 м зону следует принимать не менее 5 м от габаритов подъемника в плане, а при подъеме на большую высоту величина зоны составляет:
Зону обозначают на стройгенплане штрихпунктирной линией ( рис.бг, табл.8).
6) Ограничения в работу вводят при совместном использовании на объекте нескольких кранов и при работе в стесненных условиях.
Совместная работа нескольких механизмов в одной монтажной зоне, как правило, запрещена. В случае производственной необходимости одновременная работа допускается при условии осуществления специальных мероприятий по технике безопасности.
Если краны расположены с двух сторон здания, совместная работа должна быть организована так, чтобы траектории движения их стрел не пересекались. Тогда минимальное расстояние между осями вращения кранов при их предельном сближении определяется по формулам:
— для башенных кранов
— для стреловых кранов
где — L1, L2 — вылеты стрел при совместной работе (м);
ll, 12 — максимальный горизонтальный размер монтируемых конструкций (м);
Δ1, Δ2 — отклонение конструкций от вертикали при вращении стрелы:
Δ = 900L / (900 – ω 2 H) — L
ω — максимальная частота вращения поворотной части (мин -1 ) [3]; ориентировочно можно принять: для башенных кранов- ω=0,7; для гусеничных- ω=0,3; для пневмоколесных- ω=1,2; для кранов на спецшасси автомобильного типа- ω=1,6; для автомобильных кранов- ω= 2,0;
Н — высота подъема конструкции (м);
Δб — возможное отклонение от вертикали башни крана в результате ее податливости и уклона пути, Δб =0,5 м.
Пример. С двух сторон здания на монтаже плит покрытия длиной 1 = 6 м работают два башенных крана КБ-100. Вылет при совместной работе L = 20 м, высота подъема плит Н = 33 м. Максимальная частота вращения башни крана ω = 0,7 мин -1 .
Расчет: Δ = 900* 20/ (900 — О,7 2 х33) — 20 = 0,37 м
С = 20 + 20 + 1/2(6 + 6) + 0,37 + 0,37 + 2*0,5 = 47,74 м.
Расстояние между крюками должно быть не менее 47,74 – 20х2 = 7,74 м.
Если монтаж конструкций ведется двумя кранами, расположенными с одной стороны, то это та сторона здания, где нет входов в него. При сближении башенных кранов, установленных на общих рельсовых путях, требованиями техники безопасности предусматривается установка концевых выключателей механизмов передвижения для остановки кранов на расстоянии не менее 5 м между перемещаемыми грузами или выступающими конструкциями кранов.
При работе монтажного крана в стесненных условиях приходится вводить ограничения на определенные рабочие движения крана, например, на поворот башни во избежание проноса груза над действующей городской магистралью. Ограничения могут быть принудительными или условными, их показывают на стройгенплане или прилагаемых к нему схемах.
Принудительные ограничения зоны обслуживания применяют при работе кранов с электрическим приводом (башенных, козловых). Эти ограничения осуществляются установкой концевых выключателей, при срабатывании которых независимо от действий машиниста происходит остановка определенного механизма и исключается пронос груза в зону ограничения. На башенных кранах устанавливают концевые выключатели механизмов передвижения крана и тележки, поворота стрелы, изменения вылета. При ограничении поворота стрелы после срабатывания выключателей расстояние до зоны ограничения должно быть не менее тормозного пути стрелы крана с максимальным грузом (указан в паспорте крана, можно принять 2 м). В этом случае на стройгенплане обозначают:
— угол ограничения а, который проставляется в запрещенном секторе;
— места расположения предупреждающих знаков Ml, которые устанавливают на расстоянии тормозного пути до места срабатывания концевых выключателей;
— линию запрещающих знаков №2, устанавливаемых по контуру зоны ограничения (рис.8,9).
Условные (визуальные) ограничения зоны обслуживания применяются при работе башенных и стреловых самоходных кранов; они рассчитаны на внимание крановщика и стропальщиков. На местности зону ограничения обозначают хорошо видимыми с крана красными флажками, а в темное время суток- гирляндами из красных ламп. На стройгенплане показывают:
— места расположения предупреждающих знаков №1, которые устанавливают на расстоянии тормозного пути до линии ограничения;
— линия запрещающих знаков М2, т.е. линия ограничения, пронос груза за которую запрещен;
— запись об условиях работы крана, «крановщик обязан остановить груз, не доходя 1 метра до предупреждающего знака №1,далее до места установки груза перемещать его повторными короткими включениями «.
Масса и центр тяжести груза
Описание презентации по отдельным слайдам:
Описание слайда:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ЕНАКИЕВСКОЕ ПРОФЕССИОНАЛЬНО-ТЕХНИЧЕСКОЕ МЕТАЛЛУПРГИЧЕСКОЕ УЧИЛИЩЕ »
Автор:
Левченко Светлана Анатольевна
Преподаватель ГПОУ «ЕПТМУ»
МАССА И ЦЕНТР ТЯЖЕСТИ ГРУЗА
Описание слайда:
Преподаватель: Левченко Светлана Анатольевна
МДК 02.02 Слесарное дело и стропальное дело
ТЕМА: «МАССА И ЦЕНТР ТЯЖЕСТИ ГРУЗА»
Задание:
Изучить материал урока;
Ответить на контрольные вопросы;
Описание слайда:
Масса и центр тяжести груза
Описание слайда:
МАССА
Под массой груза следует понимать (скалярную, ненаправленную) физическую характеристику тела, являющуюся мерой его инерционных и гравитационных свойств. Значения массы тела не зависят от ускорения свободного падения в пункте определения. В состоянии покоя ее определяют взвешиванием на рычажных весах. Результат взвешивания показывает сравнительную с массой гирь величину, выраженную в единицах массы — граммах (г), килограммах (кг), тоннах (т).
Описание слайда:
Сила тяжести
Под силой тяжести следует понимать векторную (направленную) величину, определяющую силу притяжения тела к Земле или к другому небесному телу. Значение силы тяжести зависит от ускорения свободного падения в пункте измерения. Сила тяжести на полюсе больше, а на экваторе меньше. По мере удаления тела от поверхности Земли его сила тяжести уменьшается. Эту величину измеряют с помощью динамометра в условиях относительного покоя тела. Силу тяжести, как и любую другую силу, выражают в единицах силы — ньютонах (Н), килоньютонах (кН) и других дольных и кратных значениях этой величины.
Описание слайда:
Грузоподъемность крана
Под грузоподъемностью крана следует понимать максимальную массу груза, которую способно в один прием поднять, переместить или перевезти транспортное средство.
Грузоподъемность, как и масса, — скалярная величина и измеряется единицами массы — грамм (г), килограмм (кг), тонна (т).
Описание слайда:
Определение массы груза
Перед строповкой груза, предназначенного для перемещения, стропальщик должен определить его массу. Массу изготовленной на заводе продукции проставляют на чертежах изделий. Массу оборудования, приспособлений, механизмов указывают в табличке, прикрепленной к раме или станине. Если груз упакован, то массу его указывают на обшивке. Однако массу груза, подлежащего перемещению, стропальщику часто приходится определять визуально.
Описание слайда:
Определение массы груза
для простых грузов
Q = mV;
для сложных грузов
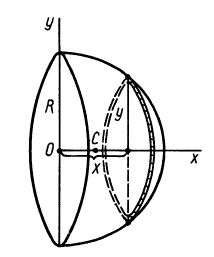
Q = m Σ Vi,
где Q — масса груза; т — удельная масса, численно равная плотности материала; V — объем груза; Vi — объем отдельных частей груза; Σ — сумма всех частей груза.
Описание слайда:
Удельная масса материалов
Алюминий-2550—2700 Олово- 7300
Бетон-2200 Парафин -900
Вода-1000 Свинец -11300
Вольфрам -19300 Цинк — 6900—7300
Сталь: Земля, глина- 1300—2500
Твердая — 7300 Песчаник – 2200-2500
Расплавленная-7500 Сухой песок – 1400-1600
Древесина: Влажный песок-1900-2000
Береза- 700 Уголь-900
Дуб-800 Кокс-450
Сосна-500 Мел-2400
Чугун: Медь-8900
Белый-7650 Никель-8900
Ковкий-7300 Мазут-900
Серый -7550 Латунь-8500
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Пример. Определим массу слитка, размеры которого приведены на рисунке.
Описание слайда:
Объем и центр тяжести простых фигур
Разбиваем условно слиток на три усеченных конуса и определяем объем каждого. Для этого в табл. 1 находим формулу объема усеченного конуса
V — (3,14/3) h (R2 + г2 + Rr).
Находим объемы каждого элемента слитка
Vx= (3,14/3) 1,700 (0,552 + 0,452 + 0,55-0,45] = 1,34 м3;
V2 = (3,14/3) 0,05 [0,552 + 0,422 + 0,55-0,42) = 0,04 м3;
У3 = (3,14/3) 0,4 [0,422 + 0,42 + 0,42-0,4] = 0,21 м3.
Определяем суммарный объем слитка V= V1+ V2+ V3 = 1,34+0,04+0,21 = 1,59 м3.
Принимаем удельную массу слитка равной 7,8 т/м3, тогда масса слитка
Q = mV = 7,8✖1,59
Описание слайда:
Объем и центр тяжести простых фигур
Пример. Определим расположение центра тяжести стального слитка, изображенного на рисунке.
Описание слайда:
Объем и центр тяжести простых фигур
Условно разбиваем слиток на три правильных усеченных конуса. Находим формулы, определяющие их координаты расположения центра тяжести. Плоскость отсчета принимаем проходящей через нижнее основание слитка перпендикулярно его оси. Из предыдущего примера известно, что отдельные части слитка имеют массу Q1 = 10,45; Q2 = 0,31; Q3 = 1,64 т, общая масса 12,4 т. Учитывая, что слиток симметричен относительно своей оси, определяем расположение только координаты Z ц.т. Координаты χ ц.т, У/ц.т будут расположены на оси.
Описание слайда:
Объем и центр тяжести простых фигур
Описание слайда:
Объем и центр тяжести простых фигур
Подставляя в формулу соответствующие значения, находим расстояние между центром тяжести и началом координат
χ ц.т = (10,45•0,93 + 0,31 • 1,72 + 1,64 • 1,926)/12,4 = 1,081 м.
Определив расстояние центра тяжести от принятого начала координат, его переносят на поднимаемый груз и делают пометку мелом или другим способом. Места застроповки груза должны располагаться симметрично центру тяжести таким образом, чтобы отвесная прямая, проходящая через центр тяжести, размещалась между местами застроповки. Чем больше расстояние между местами застроповки, тем устойчивее положение груза при прочих равных условиях.
Описание слайда:
Объем и центр тяжести простых фигур
На упакованных грузах расположение центра тяжести указывают на упаковке.
В тех случаях, когда конфигурация груза вызывает затруднения при расчете положения центра тяжести, а его необходимо определить, то можно использовать практический прием. После определения массы груза подбирают соответствующий строп и им приподнимают груз за один из краев.
Описание слайда:
Объем и центр тяжести простых фигур
На приподнятом грузе на двух плоскостях проводят отвесные линии как продолжение ветви стропа. Затем груз опускают и приподнимают за другой конец. На тех же плоскостях снова проводят отвесные прямые. Точки пересечения отвесов определяют расположение центра тяжести определяемого груза.
Описание слайда:
Объем и центр тяжести простых фигур
В тех случаях, когда стропальщик затрудняется определить массу перемещаемого груза и расположения центра тяжести, он обязан обратиться за уточнением к своему бригадиру, мастеру или механику.
Описание слайда:
Что такое масса груза?
Что понимают под силой тяжести?
Что называется грузоподъемностью крана?
Если стропальщик затрудняется самостоятельно определить массу перемещаемого груза, к кому ему нужно обратиться?
По какой формуле определяется масса простых грузов?
Домашнее задание
— Ответить на контрольные вопросы (ответы отправить преподавателю);
— Составить краткий конспект в своих рабочих тетрадях.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
Курс профессиональной переподготовки
Охрана труда
Курс повышения квалификации
Охрана труда
Онлайн-конференция для учителей, репетиторов и родителей
Формирование математических способностей у детей с разными образовательными потребностями с помощью ментальной арифметики и других современных методик
Международная дистанционная олимпиада Осень 2021
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Документ «Вопросы к рассказу Круглова «Месть»,
Методическая разработка практического занятия по ПМ 02 Изготовление несъемных протезов на тему «Методика изготовления разборных моделей»
Практическое задание для группы ТП 311
Задание по УП 02 ТП 311
«Наш любимый город Нарьян-Мар»
Внеурочное занятие Квест-игра по произведениям К.Воробьёва 4 класс
Доклад на ШМО на тему :» Портфолио, как современная эффективная форма оценивания».
Проект «Сказка своими руками»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5172115 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Екатерина Костылева из Тюменской области стала учителем года России – 2021
Время чтения: 1 минута
Меньше половины россиян довольны качеством обучения в школах
Время чтения: 2 минуты
В пяти регионах России протестируют новую систему оплаты труда педагогов
Время чтения: 2 минуты
На «Госуслугах» пройдет эксперимент по размещению документов об образовании
Время чтения: 2 минуты
Минпросвещения откроет центр образования на русском языке в Таджикистане
Время чтения: 1 минута
Российские студенты стали чемпионами мира по программированию
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Статья 70 КВВТ РФ. Определение массы грузов
1. При предъявлении грузов для перевозок грузоотправитель указывает в транспортной накладной их массу, определяемую им согласно трафарету, в соответствии со стандартом или путем взвешивания, а в отношении тарных и штучных грузов и количество грузовых мест. В случаях, установленных правилами перевозок грузов, допускается определение массы отдельных грузов расчетным путем (посредством обмера грузов, по осадке судна или условно). Определение массы грузов согласно трафарету, в соответствии со стандартом, расчетным путем (посредством обмера грузов или условно) проводится грузоотправителем. Масса грузов путем взвешивания определяется грузоотправителем за его счет совместно с перевозчиком на весовых приборах грузоотправителя, перевозчика или осуществляющей погрузку грузов в порту отправления организации.
2. Грузы в контейнерах принимаются для перевозок в соответствии с массой, указанной грузоотправителем.
3. Масса грузов, перевозимых наливом, определяется грузоотправителем в соответствии с замерами береговых резервуаров, для которых имеются утвержденные в установленном порядке калибровочные таблицы, а также на основании показаний счетчиков или замеров грузовых емкостей судов. В случаях, если такие грузы перевозятся с перегрузкой в пути с судна на судно или на одном судне в адрес нескольких грузополучателей, масса грузов определяется грузоотправителем с участием перевозчика.
Комментарии к ст. 70 КВВТ РФ
1. Комментируемая статья устанавливает порядок определения массы груза при перевозке.
Масса груза определяется грузоотправителем и указывается в транспортной накладной. Для тарных и штучных грузов также указывается количество грузовых мест.
Следует учитывать, что у перевозчика согласно комментируемой норме отсутствует право на оговорки в перевозочных документах относительно массы и количества груза. Тем не менее Будапештская конвенция о договоре перевозки грузов по внутренним водным путям (КПГВ) 2001 г. в п. 1 ст. 12 предусматривает право перевозчика вносить в транспортный документ оговорки относительно:
— размеров, количества мест или веса груза, если он имеет основания подозревать, что указанные грузоотправителем сведения неточны, или если отсутствуют достаточные средства для проверки этих сведений, в частности в том случае, когда этот груз не был пересчитан, обмерен или взвешен в его присутствии, либо когда без конкретной договоренности об этом размеры или вес были определены на основании данных судна;
— не являющейся четкой и нестираемой идентификационной маркировки, наносимой на сам груз, или, в случае тары, на емкости или упаковку;
— внешнего состояния груза.
2. Могут использовать следующие способы определения массы груза:
— в соответствии со стандартом;
— путем взвешивания — здесь есть особенности: масса грузов также определяется грузоотправителем и за его счет, но совместно с перевозчиком. Могут использоваться весовые приборы грузоотправителя, перевозчика или осуществляющей погрузку грузов в порту отправления организации. В проекте Правил перевозок грузов на внутреннем водном транспорте 2017 г. устанавливается, что взвешивание грузов должно производиться на исправных и тарированных весах. Если при проверке будет установлено, что взвешивание производилось на неисправных или нетарированных весах грузоотправителя, то масса таких грузов считается определенной грузоотправителем, в транспортные документы вносится оговорка «за массой отправителя», при этом грузоотправитель несет ответственность за количество погруженного, выгруженного груза;
— расчетным путем (посредством обмера грузов, по осадке судна или условно) — в случаях, установленных Правилами перевозок грузов. Поскольку Правила перевозок грузов (ч. 1), утв. Департаментом речного транспорта Минтранса 1 января 1994 г., были отменены Приказом Минтранса от 14 декабря 2004 г. N 44, в настоящее время в России отсутствуют правила перевозки грузов внутренним водным транспортом (подробнее см. комментарий к ст. 66). Есть только проекты, разработанные Минтрансом в разное время.
URL: https://regulation.gov.ru/p/67678 (дата обращения: 1 марта 2019 г.).
К примеру, в проекте Приказа об утверждении Правил перевозок грузов на внутреннем водном транспорте от 29 июля 2014 г. содержатся следующие правила определения массы груза по осадке судна . Масса груза по осадке судна определяется по разнице его водоизмещений с грузом и порожнем с учетом изменения за время грузовых операций количества балласта, судовых запасов (топливо, смазка, питьевая вода), хозяйственно-бытовых, сточных и нефтесодержащих вод. Водоизмещение судна в зависимости от средней осадки определяется по грузовой шкале. Водоизмещение порожнем определяется по судну с полными балластными цистернами, обычно используемыми для приема балласта на данном судне, при этом не используемые балластные цистерны должны быть пустыми.
URL: https://regulation.gov.ru/p/18034 (дата обращения: 1 марта 2019 г.).
Самоходные суда должны иметь грузовую шкалу, составленную с учетом натурных обмеров реек осадок; схемы расположения и калибровочные таблицы балластных и топливных цистерн.
Замеры осадок производятся в трех точках по каждому борту (визуально по рейкам осадок, переносным прибором для измерения высоты надводного борта или с использованием приборов дистанционного замера осадки судна): в носовой части судна по рейке форштевня, в средней части на миделе и в корме по рейке ахтерштевня. Средняя осадка определяется делением на 8 суммы всех замеров, причем значения осадок судна в средней части (у миделя) удваиваются.
Масса балласта, а при необходимости топлива, определяется по результатам замеров уровней заполнения цистерн градуированными метрштоками (футштоками) и соответствующим калибровочным таблицам.
Результаты замеров осадок, определения количества балласта и судовых запасов, а также расчет массы груза указываются в акте погрузки-выгрузки груза.
Если грузоотправитель или другое заинтересованное лицо привлекли на договорных основаниях в качестве независимого эксперта стороннюю организацию (сюрвейера) для определения массы груза в судне по его осадкам, то по результатам замеров осадок, определения количества балласта и судовых запасов, а также расчета массы груза, произведенные сюрвейером, составляется драфт — сюрвейерский акт, который подписывается представителем судна и сюрвейером.
В случае разногласий в расчетах между представителем судна и сюрвейером, представитель судна вправе отказаться от подписи акта и предъявить свой расчет груза.
Если грузоотправитель или другое заинтересованное лицо не согласен с судовым расчетом, то в этом случае количество груза указывается в соответствии с актом сюрвейера и в грузовые документы вносится оговорка «Вес груза по заявлению грузоотправителя или другого заинтересованного лица», при этом перевозчик освобождается от ответственности за погруженное и выгруженное количество груза;
— в соответствии с замерами береговых резервуаров, для которых имеются утвержденные в установленном порядке калибровочные таблицы, а также на основании показаний счетчиков или замеров грузовых емкостей судов, — для грузов, перевозимых наливом (п. 2). В случае расхождения массы груза, перевозимого наливом, определенной в соответствии с замерами береговых резервуаров, и массы, определенной на основании показаний счетчиков или замеров грузовых емкостей судов, грузоотправитель вносит в транспортные документы массу грузов, определенную в соответствии с замерами береговых резервуаров, с оговоркой «Масса по заявлению отправителя».
Если грузы, перевозимые наливом, следуют с перегрузкой в пути с судна на судно или на одном судне в адрес нескольких грузополучателей, масса грузов определяется грузоотправителем с участием перевозчика.
Для грузов в контейнерах установлено правило о том, что они принимаются для перевозок в соответствии с массой, указанной грузоотправителем (п. 3).
http://infourok.ru/massa-i-centr-tyazhesti-gruza-5336115.html
http://rulaws.ru/kvvt-rf/Glava-XI/Statya-70/
Содержание:
Центр тяжести:
При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.
Определения и формулы для вычисления центров тяжести
Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом
Радиус-вектор центра тяжести тела 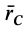
где 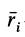

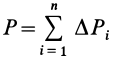

Рис. 88
Если в (1) перейти к пределу, увеличивая число элементарных частей 

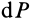
где 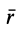
где 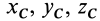
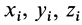
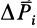
Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 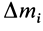
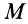

Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на 
и соответственно
По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:
и
где 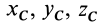
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
где 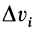


где 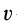


по которым определяют центр тяжести объема тела.
Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем
где 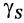
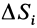
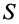
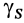
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
где 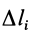
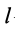
Методы определения центров тяжести (Центров масс)
Метод симметрии
При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 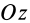
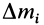
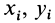
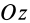
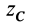
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что
так как симметричные части тела 1 и 2 одинаковы.
Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 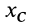
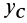
Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.
Рис. 89
Метод разбиения на части (метод группировки)
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 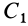
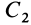
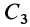
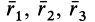
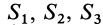
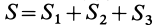
Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:
или
Используя эти формулы для радиуса-вектора всей фигуры, имеем
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.
Рис. 90
Метод отрицательных масс
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 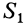
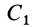
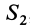
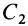
В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
Рис. 91
Центры тяжести простейших тел
Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.
Прямолинейный отрезок
Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.
Площадь треугольника
Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 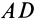

Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне 
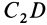

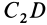
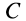

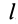
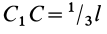
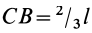
Рис. 92
Дуга окружности
Дуга окружности 
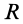
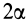
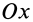

Рис. 93
В рассматриваемом случае
Подставляя эти значения в формулу для 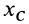
Таким образом,
Для полуокружности 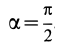
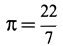
Площадь кругового сектора
Центр тяжести площади кругового сектора с радиусом 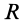
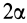
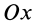
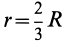
Рис. 94
Используя формулу для центра тяжести дуги окружности, получим
или
Для площади полукруга 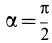
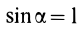
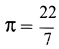
Объем пирамиды и конуса
Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 
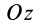
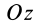
Разобьем конус плоскостями, перпендикулярными оси 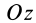
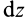
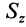
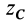
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 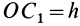
Учитывая, что
имеем
или
Таким образом, центр тяжести прямого конуса находится на расстоянии 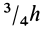
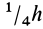
Рис. 95
Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 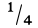
Объем полушара
Полушар имеет ось симметрии, которую примем за координатную ось 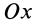
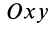
где 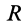
где 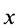
Объем элементарного диска
так как радиус диска 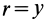
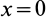
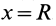
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии
Это расстояние меньше половины радиуса полушара.
Рис. 96
Задача №1
Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.
Рис.97
Рис. 98
Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем
где 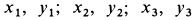
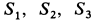
Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:
так как 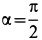
Подставляя полученные значения в (а), получим:
Центр тяжести плоской фигуры
постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.
План решения:
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2. Выбираем систему координат. Вычисляем площади и координаты 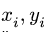
3. Находим общую площадь фигуры по формуле
4. Определяем координаты центра тяжести фигуры:
Задача №2
Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в 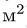
Площадь выреза берем со знаком минус.
3.Площадь фигуры
4. Находим координаты центра тяжести всей фигуры:
Вычисления удобно свести в таблицу:
Сначала заполняем столбцы 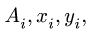
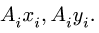
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 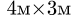
Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.
- Заказать решение задач по теоретической механике
Пространственная стержневая система
Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения:
1. Разбиваем фигуру на отдельные стержни.
2. Выбираем систему координат. Вычисляем длины и координаты 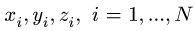
3. Находим суммарную длину стержней системы
4. Определяем координаты центра тяжести тела по формулам
Задача №3
Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры:
Решение
1. Разбиваем фигуру на шесть стержней.
2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 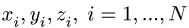
3. Находим суммарную длину стержней системы:
Промежуточные результаты удобно занести в таблицу:
4. Определяем координаты центра тяжести тела по формулам
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.
План решения:
1. Разбиваем тело на простые части, положение центров тяжести которых известно.
2. Выбираем систему координат. Вычисляем объемы 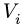
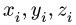
3. Находим общий объем тела по формуле
4. Определяем координаты центра тяжести тела:
Задача №4
Найти координаты центра тяжести однородного объемного тела (рис.79);
Решение
1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2. Выбираем систему координат. Вычисляем объемы 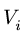
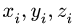
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
Объем половины цилиндра 3 берем со знаком минус:
где 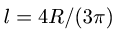
3. Находим общий объем тела:
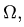
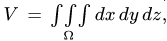
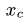
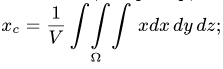
4. Определяем координаты центра тяжести тела:
Центр тяжести
Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 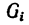
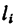
где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 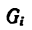
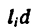
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),
то вес каждой плоскости (поверхности) можно представить так:
где 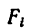
После подстановки этого значения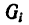
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
где 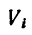
После подстановки значений 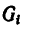
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой
Если же задана хорда 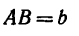
и тогда
В частном случае для полуокружности обе формулы примут вид (рис. 176, б)
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы
Если же задана хорда сектора, то
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
- выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
- разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
- определить или длины, или площади, или объемы составных частей;
- выбрать расположение осей координат;
- определить координаты центров тяжести составных частей;
- найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
- по найденным координатам указать на рисунке положение центра тяжести тела.
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Условия равновесия системы сил
- Плоская система сил
- Трение
- Пространственная система сил