Центр треугольника
Треугольник — наиболее распространенная форма деталей в сферах машиностроения и строительства. Точка пересечения 3-х медиан считается центром треугольника. На эту точку приходится также центр тяжести и центр симметрии предметов треугольной формы. При разработке дизайнерских, инженерных проектов очень важно точно рассчитать центр тяжести элементов металлической или бетонной конструкции.
Существует несколько понятий центра для треугольника.
Инцентр — точка пересечения его биссектрис. Это — центр описанной около треугольника окружности.
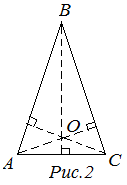
Ортоцентр — точка пересечения его высот.
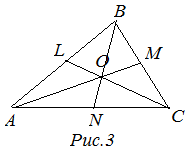
Центр тяжести,центр масс или центроид (обозн. М) — точка пересечения медиан треугольника.
Рассмотрим треугольник. Определим середины его сторон и соединим их с противолежащими углами. Точка пересечения медиан и будет центром тяжести тр-ка. Медиана делится этой точкой в пропорции 2:1 , (считая от вершины тр-ка).
Как найти центр треугольника
Если известны координаты его вершин, найдем сумму трех значений координат «х» и трех значений координат «у». Поделим каждую сумму на 3, получим среднее значение сумм координат «х» и «у», что и будет координатами центра тяжести.
Центром равностороннего треугольника является точка пересечения высот, биссектрис и медиан.
Центр равностороннего треугольника является также центром вписанной и описанной окружности.
Центроид расположен на отрезке, соединяющем ортоцентр и центр описанной окружности. Центроид делит отрезок 2:1.
Быстро найти центр треугольника G можно с помощью онлайн калькулятора. Для этого:
- ввести в поле калькулятора координаты вершин треугольника;
- нажать кнопку Вычислить. Калькулятор вычислит значение центра треугольника G.
Центр треугольника
Центр треугольника является центром симметрии одной из наиболее распространенных в машиностроении и строительстве формы деталей. Важным практическим применением вычисления данного параметра является потребность знать, в каком месте будет находиться центр тяжести того или иного элемента бетонной или металлической конструкции.
Центр треугольника, центр тяжести, центр симметрии находятся в одной точке. Именно на нее, точку пересечения трех медиан, приходится вес всей однородной детали треугольной формы. При выявлении значения центра треугольника G с помощью онлайнового калькулятора необходимо задать координаты его вершин:
o (x1, y1);
o (x2, y2);
o (x3, y3).
Важным направлением ряда инженерных расчетов является определение статических моментов в отношении тех или иных сложных по форме деталей. Следует иметь в виду, что любую фигуру можно представить совокупностью простых фигур, к которым относятся треугольник, прямоугольник и пр.
Статический момент сложной детали может быть определен как сумма статических моментов входящих в нее элементов. Отсюда вытекает важность умения быстро находить значения центра треугольника (центра тяжести), прямоугольника и пр.
Центры тяжести многоугольников и многогранников
Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где — массы точек, — их радиус-векторы (задающие их положение относительно начала координат), и — искомый радиус-вектор центра масс.
В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:
Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке , в которой сумма моментов всех сил равна нулю. В данном случае это превращается в условие того, чтобы сумма радиус-векторов всех точек относительно точки , домноженных на массы соответствующих точек, равнялась нулю:
и, выражая отсюда , мы и получаем требуемую формулу.
Центр масс каркаса
Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:
где — точка-середина -ой стороны многоугольника, — длина -ой стороны, — периметр, т.е. сумма длин сторон.
Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:
Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian «Finding Centroids the Easy Way».
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
Разобьём данный треугольник на четыре, соединив середины сторон, как показано на рисунке:
Четыре получившихся треугольника подобны треугольнику с коэффициентом .
Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого лежит в точке пересечения его диагоналей (поскольку это фигура, симметричная относительно обеих диагоналей, а, значит, её центр масс обязан лежать на каждой из двух диагоналей). Точка находится посередине общей стороны треугольников №1 и №2, а также лежит на медиане треугольника :
Пусть теперь вектор — вектор, проведённый из вершины к центру масс треугольника №1, и пусть вектор — вектор, проведённый из к точке (которая, напомним, является серединой стороны, на которой она лежит):
Наша цель — показать, что вектора и коллинеарны.
Обозначим через и точки, являющиеся центрами масс треугольников №3 и №4. Тогда, очевидно, центром масс совокупности этих двух треугольников будет точка , являющаяся серединой отрезка . Более того, вектор от точки к точке совпадает с вектором .
Искомый центр масс треугольника лежит посередине отрезка, соединяющего точки и (поскольку мы разбили треугольник на две части равных площадей: №1-№2 и №3-№4):
Таким образом, вектор от вершины к центроиду равен . С другой стороны, т.к. треугольник №1 подобен треугольнику с коэффициентом , то этот же вектор равен . Отсюда получаем уравнение:
Таким образом, мы доказали, что вектора и коллинеарны, что и означает, что искомый центроид лежит на медиане, исходящей из вершины .
Более того, попутно мы доказали, что центроид делит каждую медиану в отношении , считая от вершины.
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:
где — центроид -го треугольника в триангуляции заданного многоугольника, — площадь -го треугольника триангуляции, — площадь всего многоугольника.
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники , где .
Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка , а затем суммируются знаковые площади треугольников, образованных этой точкой и точками многоугольника: . Аналогичный приём можно применить и для поиска центра масс: только теперь мы будем суммировать центры масс треугольников , взятых с коэффициентами, пропорциональными их площадям, т.е. итоговая формула для центра масс такова:
где — произвольная точка, — точки многоугольника, — центроид треугольника , — знаковая площадь этого треугольника, — знаковая площадь всего многоугольника (т.е. ).
Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:
(это можно вывести из того факта, что центроид делит медианы в отношении )
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
http://allcalc.ru/node/846
http://e-maxx.ru/algo/gravity_center
Центр
описанной окружности.
56
В
§ 15 были указаны условия, при которых
перпендикулярные отрезки в
пространстве
имеют своими проекциями также
перпендикулярные отрезки. Если
плоскость
треугольника параллельна плоскости
проекций (например, треугольник
СОЕ
на рис. 133), то, опустив пер-. пендикуляры
из точек С», D» и Е» на
противоположные
им стороны, получаем проекции высот
треугольника. Но в
треугольнике
общего положения так поступить нельзя.
В
частном случае, когда одна сторона
треугольника параллельна пл. 1,
а
другая параллельна пл. 2 (рис. 143), проведя
С»Е» перпендикулярно к A»B»
и
В’Е’ перпендикулярно к A’C’, получаем в
пространстве CF» AB и ВЕ» АС;
точка
пересечения высот оказалась построенной
без каких-либо особых приемов.
В
сймом же общем случае для проведения
на проекционной! чертеже
перпендикулярных
линий приходится прибегать к особым
приемам, которые будут
изложены
дальше.
Построение
точки пересечения биссектрис треугольника
‘) также может
быть
произведено непосредственно лишь в
частных случаях расположения
треугольника
относительно плоскостей проекций.
Это объясняется Тем, что
деление
пополам проекции какого-либо утла
отвечает его делению пополам в
пространстве
только в том случае, если стороны
данного угла одинаково
наклонены
к той плоскости проекций, на которой
производится деление пополам
проекции
угла (см. § 15).
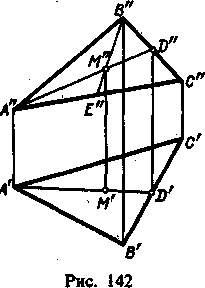
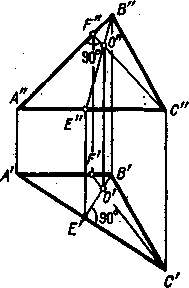
Рис.
143
При
построении проекций какого-либо
многоугольника необходимо обратить
внимание
на то, чтобы не нарушалось условие
нахождения всех точек данной
фигуры
в одной плоскости.
На
рис. 144 даны полностью горизонтальная
проекция некоторого
пятиугольника
ABCDE и фронтальные проекции только трех
его вершин: А», В» и
Е».
Справа
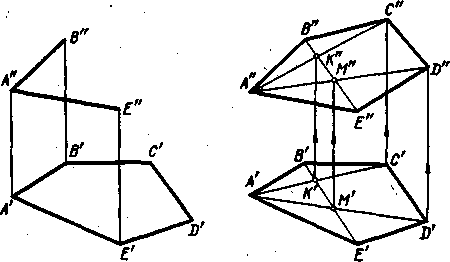
Рис.
144
на
рис. 144 показано построение проекций
остальных двух вершин, С» и
D»,
пятиугольника. Чтобы точки С и D лежали
в плоскости, определенной тремя
точками
А,
‘)
Центр вписанной окружности.
57
В
и Е, необходимо, чтобы они находились
на прямых, лежащих в этой
плоскости.
Этими прямыми являются диагонали AC,
AD и BE, горизонтальные
проекции
которых мы можем построить. На фронтальной
проекции пятиугольника
мы
можем провести лишь В»Е». Но в
плоскости пятиугольника лежат точки
пересечения
диагоналей К и М, горизонтальные
проекции которых (К’ и
М1)
имеются, а фронтальные проекции получаются
сразу, так как они
должны
лежать на В»Е». По двум точкам
строятся фронтальные проекции и
остальных
двух диагоналей А»К» и А»М»;
на них должны лежать точки С» и D»,
которые
определяются по их горизонтальным
проекциям. ·
Круг,
плоскость которого параллельна
какой-либо плоскости проекций,
проецируется
на эту плоскость без искажения (см.
рис. 140, где круг взят в
горизонтальной
плоскости). Если плоскость круга
расположена перпендикулярно
к
плоскости проекций, то на эту плоскость
круг проецируется в виде отрезка
прямой,
равного диаметру круга.
Но
если круг расположен плоскости,
составляющей с плоскостью проекций
какой-либо
острый угол , то проекцией круга является
фигура, называемая
эллипсом.
Эллипсом
называется также кривая, ограничивающая
эллипс-фигуру: если
эллипс-фигура
является проекцией круга, то эллипс-линия
является проекцией
окружности.
В дальнейшем изложении, говоря об
эллипсе, будем подразумевать
проекцию
окружности.
Эллипс
относится к числу кривых, называемых
кривыми второго порядка.
Уравнения
таких кривых в декартовых координатах
представляют собой уравнения
второго
порядка. Кривая второго порядка
пересекается с прямой линией в двух
точках.
Далее мы встретимся еще с параболой
и гиперболой, тоже кривыми
второго
порядка.
Эллипс
можно рассматривать как «сжатую»
окружность. Это показано на
рис.
145, слева. Положим, что на радиусе ОВ
отложен отрезок ОВ1 длиной b,
причем
b < а (т. е. меньше радиуса окружности).
Если теперь взять на
окружности
какую-либо точку К и, проведя из К
перпендикуляр на А 1 А2,
отметить
на КМ точку
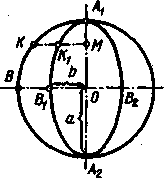
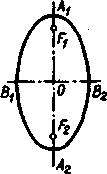
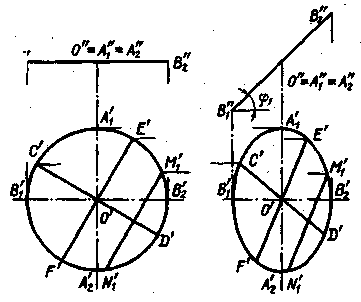
Рис.
145 Рис. 146
ку
k1 так, чтобы МК1 :МК = b:а, то эта точка
К, будет принадлежать
эллипсу.
Так можно преобразовать каждую точку
окружности в точку эллипса,
соблюдая
одно и то же отношение b:а. Окружность
как бы равномерно сжимается;
линия,
в которую при этом преобразуется
окружность, является эллипсом.
Отношение
b: a называется коэффициентом сжатия
эллипса. Если b приближается
к
а; то эллипс расширяется и при b = а
превращается в окружность.
Напомним
(из курса черчения средней школы), что
1)
отрезок А1А2=2а называется большой осью
эллипса;
2)
отрезок bib- = 2b называется малой осью
эллипса;
3)
большая и малая оси взаимно перпендикулярны;
точка
пересечения осей называется центром
эллипса;
58
5)
отрезок прямой между двумя точками
-эллипса, проходящий через -центр
эллипса,
называется его диаметром;
6)
точки A,, A2> В,, B2 называются вершинами
эллипса;
7)
эллипс симметричен относительно его
осей и относительно его центра;
эллипс
есть геометрическое место точек, сумма
расстояний которых до
двух
заданных точек Ft и F2 (рис. 145, справа)
имеет одно и то же значение
2а
(размер большой оси).
C’D’
делит хорду MN{, параллельную диаметру
E’F’, сопряженному с CD’,
пополам.
Но именно такие два диаметра эллипса,
из которых каждый делит
пополам
хорды, параллельные другому, являются
сопряженными.
Сопряженные
диаметры эллипса не перпендикулярны
один к другому;
исключение
составляют оси эллипса, Из рассмотрения
рис. 146 следует, что при
повороте
окружности вокруг диаметра AtA2 на
угол этот диаметр,
параллельный
пл. itlt сохраняет в горизонтальной
проекции свою величину и
становится
большой осью эллипса (см. рис. 146,
справа). Диаметр же В1В2,
повернутый
на угол 1 к пл. -, проецируется на нее с
сокращением:
Это
соответствует отношению осей эллипса,
т. е. его коэффициенту
сжатия.
Если
в окружности провести какие-либо два
взаимно перпендикулярных
диаметра,
то в проекции, представляющей собой
эллипс (рис. 146, справа),
проекции
таких диаметров окружности оказываются
диаметрами эллипса,
называемыми
сопряженными. Если в окружности (рис.
146, слева) провести,
например,
хорду [(, параллельную диаметру E’F’, то
диаметр C’D’ разделит
эту
хорду (и все хорды, ей параллельные)
пополам. Очевидно, что и в эллипсе
сохранится
это свойство (см. рис. 146, справа): диаметр
также являющиеся
парой
сопряженных диаметров.
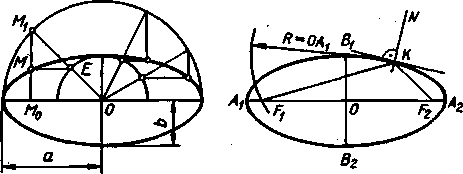
Рис.
147
Напомним,
как производится построение эллипса
по его осям (рис. 147,
слева).
Построение выполняется при помощи двух
концентрических окружностей,
проведенных
радиусами а (большая полуось) и b (малая
полуось). Если провести
какой-либо
радиус ОМ, и прямые 1Л/„ и ЕМ,
параллельные малой и
большой
осям эллипса, то при пересечении этих
прямых получится точка М,
принадлежащая
эллипсу. Действительно,
Проводя
ряд радиусов и повторяя указанное
построение, получаем ряд
точек
эллипса.
Построив
какую-нибудь точку эллипса, можно
построить еще три точки,
расположенные
симметрично найденной относительно
осей эллипса или его
центра.
На
рис. 147 справа показано построение
фокусов эллипса: засекая из
точки
B, большую ось дугой, радиуса, равного
большой полуоси oa 1, получаем
точки
f 1 и F2 — фокусы эллипса. Построив угол F
1КF2, где К — любая точка
эллипса,
проводим в нем биссектрису и
перпендикулярно к ней в точке К
касательную
к эллипсу. Прямая KN, перпендикулярная
каса-тельной, является
нормалью1)
к эллипсу в точке К.
‘)
От normal is (лат.) — прямолинейный.
59
Как
построить оси эллипса, если известны
его сопряженные диаметры?
Пусть
получены сопряженные полудиаметры
CA и СВ (рис. 148). Для
построения
осей эллипса:
1)
один из сопряженных полудиаметров,
например CB, поворачиваем на угол
90°
по направлению к другому (до положения
CB2);
2)
проводим отрезок AB2 и делим его пополам;
3)
из точки К проводим окружность радиусом
КС; ·
4)
прямую, определяемую отрезком АВ2,
продолжаем до пересечения с этой
окружностью
в точках D и E;
5)
проводим прямую DC, получаем направление
большой оси эллипса;
6)
проводим ЕС — направление малой оси
эллипса;
7)
откладываем С1 .= АЕ — большая полуось;

откладываем СЗ = AD — малая полуось;
9)
откладываем С2 = С;, С4 = СЗ, С5,= СА, Со = СВ.
Эллипс
может быть проведен через восемь точек
/, А, 3, В, 2,5,4 и 6 или
построен
по большой и малой осям, как показано
на рис. 147.
Итак,
проведя прямые CD и СЕ, мы получили
направления большой и малой
осей
эллипса; точка A, принадлежащая эллипсу,
делит диаметр ED на два
отрезка,
из которых один (АЕ) равен большой полуоси
этого эллипса, а другой
(AD)
— малой полуоси. Если (рис. 149)
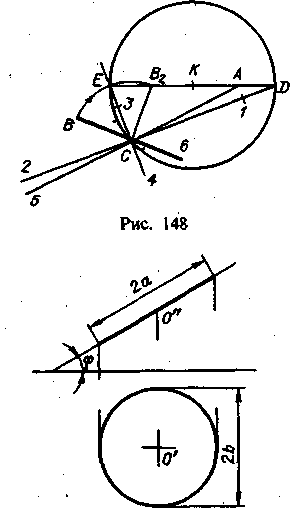
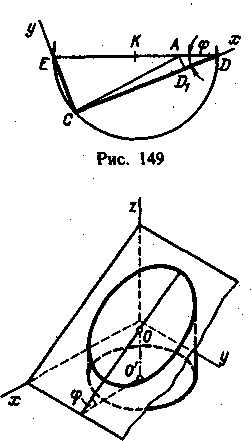
Рис.
150 Рис. 151
взять
оси координат и у соответственно по
прямым CD и СЕ и из точки А
провести
перпендикуляр AD к прямой CD, то
координаты,,точки А могут быть
выражены
следующим образом:
Отсюда
Это
уравнение эллипса, у которого АЕ —
большая полуось, а АО — малая
полуось.
На
рис. 146 было показано построение
горизонтальной проекции
окружности,
расположенной в фронтально-проецирующей
плоскости, наклоненной к
пл.
1. Пусть теперь в такой
60
плоскости
лежит эллипс с полуосями а и b. Его
проекцией иногда может
оказаться
окружность с диаметром, равным малой
оси эллипса: это будет тогда,
когда
для угла между плоскостью, в которой
лежит эллипс, и пл. 1 имеет
место
соотношение
(рис.
150). Полученная окружность будет
служить проекцией ряда
эллипсов,
если изменять угол и размер а, оставляя
b неизменным. Представим
себе
прямой круговой цилиндр с вертикальной
осью (рис. 151); наклонные
сечения
этого цилиндра будут эллипсами, малая
ось которых равна диаметру
цилиндра.
ВОПРОСЫ
К §§ 20-21
1.
Как изображается на чертеже
фронтально-проецирующая плоскость,
проведенная
через прямую общего положения?
2.
Как построить проекции центра
тяжести в заданном чертеже
треугольника?
3.
Что могут представлять собой проекции
круга в зависимости от
положения
его плоскости относительно плоскости
проекций?
4.
Можно ли рассматривать эллипс как
«сжатую» окружность?
5.
Что такое коэффициент сжатия эллипса?
6.
Имеет ли эллипс: а) оси симметрии, б)
центр симметрии?
7.
Какие диаметры эллипса называются:
а) осями, б) сопряженными
диаметрами?
8.
Как по заданным сопряженным диаметрам
эллипса построить его оси?
В этой статье и разберу как нарисовать центр тяжести треугольника и найти его координаты.
1) Рисуем треугольник ABC
2) Ставим точку M — середина BC
3) Ставим точку H — середина AC
4) Пересечение BH и AM — и есть центр тяжести треугольника ABC
5) Найдем его координаты (координаты точки O
(x_(o), y_(o), z_(o))
)
[x_{0}=frac{x_{1}+x_{2}+x_{3}}{3}, y_{0}=frac{y_{1}+y_{2}+y_{3}}{3}, z_{0}=frac{z_{1}+z_{2}+z_{3}}{3}]
Пример: Найти координаты центра тяжести треугольника с вершинами A(2;3;4), B(3;1;2) и C(4;-1;3). Решение.
Просмотры: 42909 |
Статью добавил: slava191 |
Категория: аналитическая_геометрия
Содержание:
Методы преобразования эпюра Монжа:
Как видно из предыдущего материала, все геометрические задачи решаются проще, если объекты (или хотя бы один объект) заданы в частном положении.
Для перевода объектов из общего положения в частное с целью упрощения решения задач разработаны методы преобразования эпюра Монжа. Они делятся на два вида:
- Геометрический объект при преобразовании остается неподвижным, а плоскости проекций меняют свое положение так, чтобы объект находился относительно них в частном положении (метод перемены или замены плоскостей проекций);
- Плоскости проекций при преобразовании остаются неподвижными , а объект меняет свое положение так, чтобы относительно плоскостей проекций он занял частное положение (метод вращения вокруг проецирующей оси, метод совмещения, метод вращения вокруг линий уровня, метод плоско-параллельного перемещения).
Метод замены (перемены) плоскостей проекций
Смысл метода заключается в том, что в систему плоскостей проекций вводятся дополнительные плоскости проекций, по отношению к которым объект занимает частное положение (другими словами, плоскости проекций заменяются другими плоскостями). Ортогональность новых систем плоскостей проекций при этом сохраняется.
Замена плоскостей проекций осуществляется в последовательности:
Обычно производят одну или две замены плоскостей проекций.
На рисунке 6.1 в наглядной форме показана методика проведения замены плоскостей проекций. На рисунке 6.1а представлена замена одной фронтальной плоскости проекций (V —> Vi), а на рисунке 6.16 — замена двух плоскостей проекций
Из представленных наглядных изображений и эпюров вытекают следующие правила построения новых фронтальных и горизонтальных проекций точки на дополнительные плоскости проекций:
необходимо от новой оси по новой линии связи отложить аппликату точки из предыдущей системы плоскостей проекций.
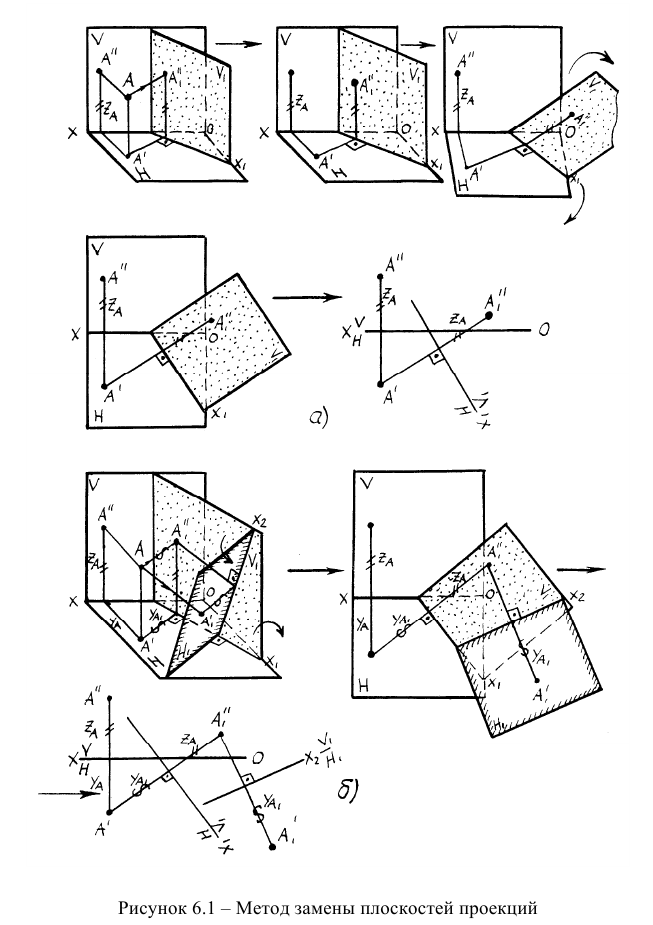
В методе замены плоскостей проекций выделяют две основные задачи:
- Перевод прямой общего положения в проецирующую;
- Перевод плоскости общего положения в проецирующую.
На рисунке 6.2а показано преобразование прямой общего положения в проецирующую прямую, которое выполнено двумя заменами плоскостей проекций 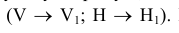
прямой AВ, а вторая — перпендикулярно прямой АВ. Следует заметить, что при решении задачи определяется натуральная величина прямой (новая фронтальная проекция 
На рисунке 6.26 показано преобразование плоскости общего положения, заданной треугольником АВС, в проецирующую плоскость, которое выполнено одной заменой плоскостей проекций 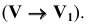
Рассмотренные задачи положены в основу решения многих геометрических задач.
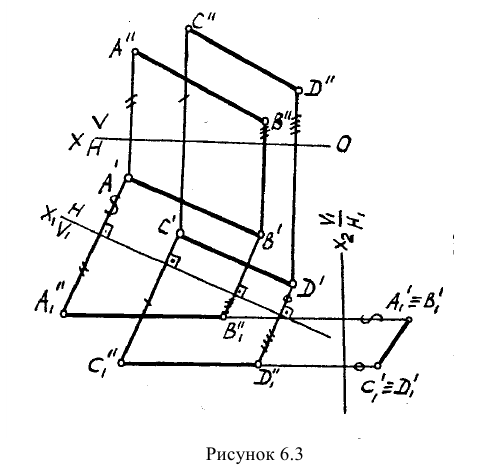
Пример: Определить расстояние между двумя параллельными прямыми АВ и CD (Рис.6.3).
Решение: Расстояние между параллельными прямыми определится, если обе прямые преобразовать в проецирующие. Тогда расстояние между двумя полученными точками будет являться искомым расстоянием. Преобразование произведем двумя заменами
Пример: Определить угол между двумя плоскостями (двугранный угол).
Решение: Двугранный угол определится, если общее ребро угла перевести в проецирующее положение (см. рисунок 6.2а). Тогда ребро «вырождается» в точку, а плоскости — в линии. Угол между линиями является искомым углом (рисунок 6.4).
Пример: Определить натуральную величину треугольника АВС.
Решение: Натуральную величину треугольника определим двумя заменами
Сначала треугольник переведем в проецирующее положение, а затем — в параллельное. В последнем положении плоскость треугольника будет параллельна новой плоскости проекций 
Метод вращения вокруг проецирующих осей
Метод заключается в том, что геометрический объект (прямую или плоскость) вращают вокруг проецирующей оси до положения параллельности какой-либо плоскости проекций. В результате вращения геометрический объект проецируется на плоскость проекций в натуральную величину. На рисунке 6.6 в наглядной форме представлено вращение вокруг горизонтально-проецирующей оси (а) и вокруг фронтально-проецирующей оси (б) точки А.
Из приведенных схем видно, что если точка вращается вокруг горизонтально-проецирующей оси, то её горизонтальная проекция перемещается по дуге окружности, а фронтальная — по прямой линии, параллельной оси ОХ. При вращении вокруг фронтально-проецирующей оси наблюдается обратная картина.
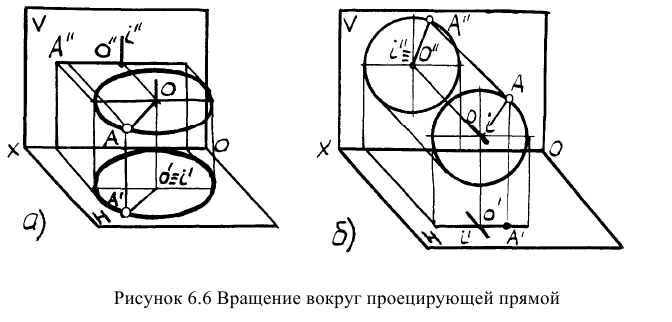
Пример: Определить угол наклона прямой к плоскости проекций Н и натуральную величину прямой.
Решение: НВ прямой и угол 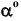
Вращение вокруг линий уровня (горизонтали или фронтали)
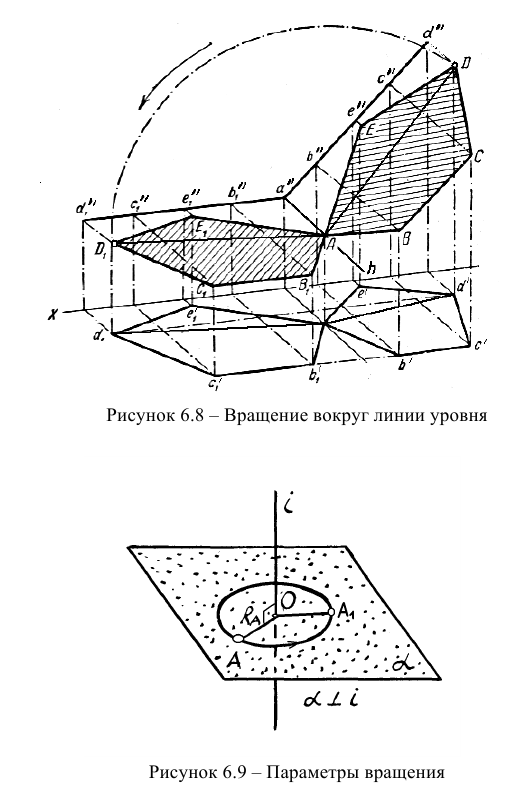
Метод вращения вокруг горизонтали или фронтали заключается в том, что объект, например, плоскую фигуру вращают вокруг горизонтали или фронтали, проведенной в плоскости, до положения параллельности какой-либо плоскости проекций. После окончания вращения объект проецируется на плоскость проекций в натуральную величину (рисунок 6.8).
Главным вопросом метода вращения вокруг линий уровня является вопрос о параметрах вращения. Параметры вращения — это аппарат для решения задач с использованием этого метода.
Параметрами вращения являются (рисунок 6.9):
- Объект вращения. Под объектом вращения следует понимать точку на геометрическом теле. Поэтому в каждой задаче важно определить точки, которые будут вращаться и конечное положение которых надо определить, чтобы получить решение;
- Ось вращения (выбирается произвольно, если не задана);
- Плоскость вращения объекта. Она проводится перпендикулярно оси вращения;
- Центр вращения объекта. Это точка пересечения оси с плоскостью вращения;
- Радиус вращения объекта. Это расстояние между точкой и центром вращения.
- Новое положение объекта вращения (выбирается такое, чтобы геометрический объект занял частное положение).
Конечное положение объекта вращения (на рисунке 6.8, например, точка D) определится, когда радиус вращения (отрезок AD) станет проецироваться на плоскость проекции в натуральную величину.
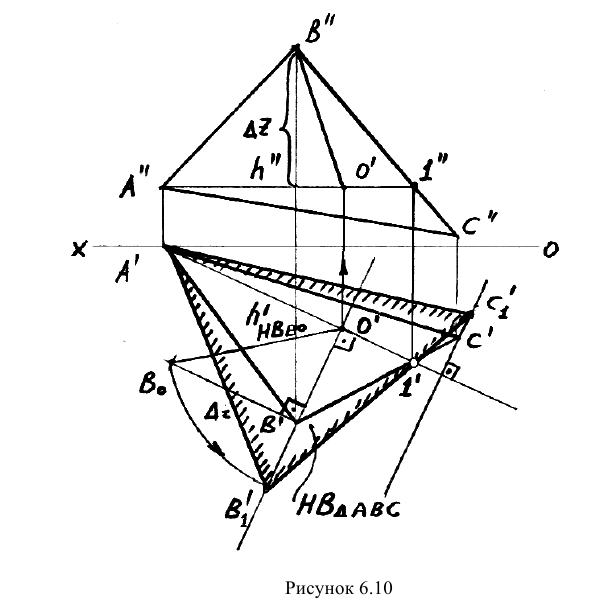
Пример: Определить натуральную величину треугольника АВС методом вращения вокруг горизонтали (рисунок 6.10).
Решение: План решения задачи и его реализация:
1) В плоскости треугольника проводим горизонталь h;
2) Определяем объекты вращения — точки В и С. Точка А не может являться объектом вращения, так как она находится на оси и не будет перемещается в плоскости вращения;
3) Проводим плоскости вращения точек В и С перпендикулярно
4) Начинаем вращать точку, например. В;
5) В месте пересечения плоскости вращения точки В с осью вращения находим центр вращения О
6) Строим проекции радиуса вращения точки В (отрезок ОВ);
7) Находим НВ радиуса вращения ОВ и откладываем его на плоскости вращения точки В отточки

9) Положение точки С можно найти таким же способом или другим способом, соединив точки 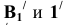
10) Полученные точки соединяем. Треугольник 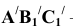
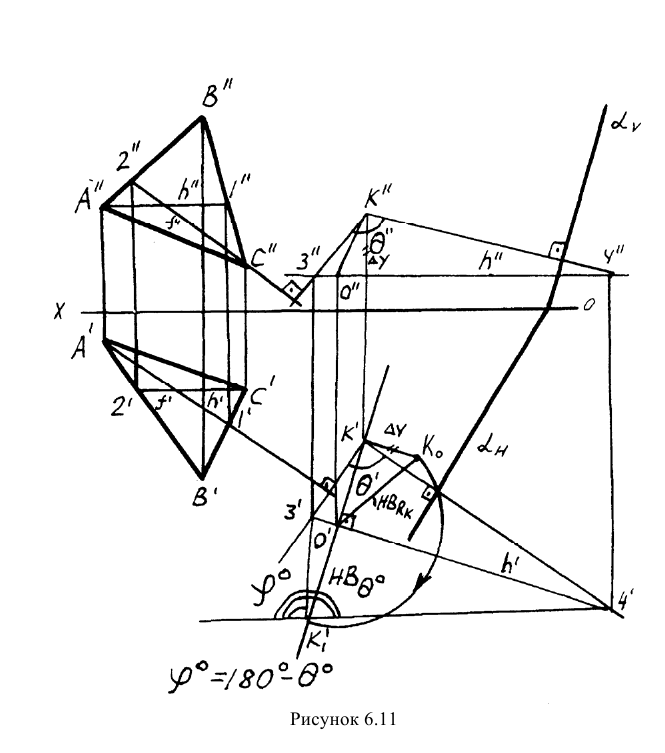
Ранее рассматривался вопрос об определении углов между прямой и плоскостью и между двумя плоскостями (см. раздел «Метрические задачи») с помощью дополнительных углов. Было показано, что натуральную величину дополнительных углов наиболее целесообразно определять методами преобразования, например, методом вращения вокруг горизонтали или фронтали. Рассмотрим пример задачи на определение угла между двумя плоскостями.
Пример: Определить угол между плоскостью треугольника АВС и плоскостью а, заданной следами.
Решение: План решения и его реализация:
- В растворе двугранного угла возьмем любую точку К;
- Из точки К опустим перпендикуляры на обе плоскости (см. тему «Перпендикуляр к плоскости»);
- Между двумя перпендикулярами получаем дополнительный угол
- Определяем натуральную величину дополнительного угла методом вращения вокруг горизонтали h (см. тему «Вращение вокруг линий уровня»);
- Достраиваем полученную натуральную величину дополнительного угла до 180 градусов и получаем искомый угол
(рисунок 6.11).
- Заказать чертежи
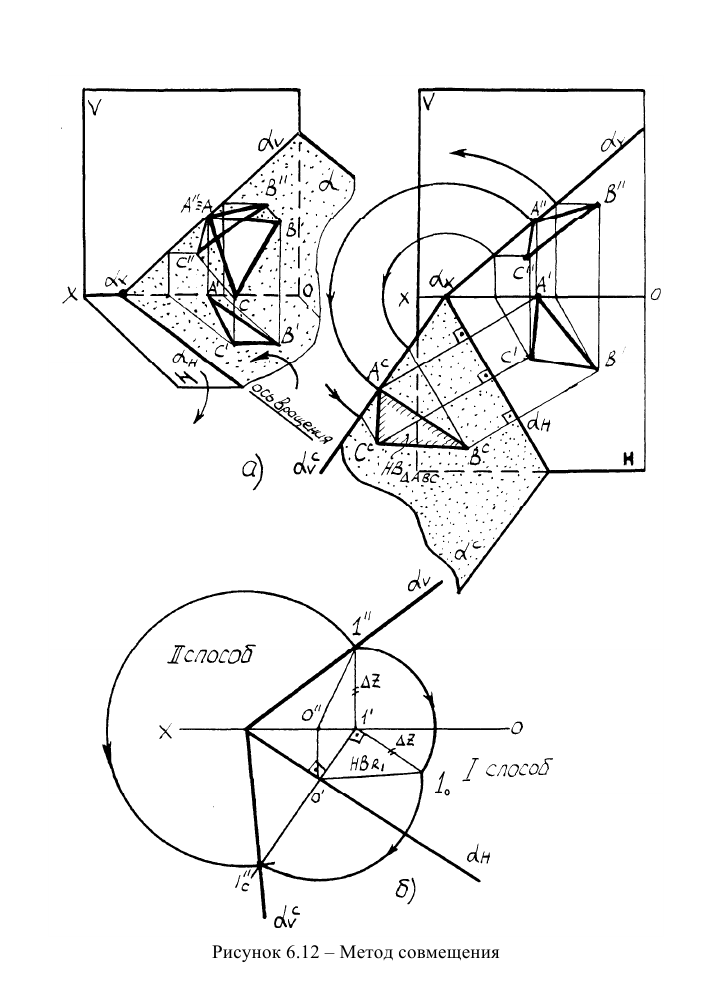
Метод совмещения
Метод совмещения представляет из себя частный случай вращения вокруг линии уровня. За ось вращения в этом случае принимают один из следов плоскости. Сущность метода заключается в том, что плоскость вместе с объектом, находящимся в ней, вращают до совмещения с плоскостью проекций.
Наглядное изображение способа совмещения вокруг
горизонтального следа представлено на рисунке 6.12. Исходное положение плоскостей проекций и плоскости дано на рисунке 6.12а. После поворота плоскости проекций Н и плоскости а образуется единая плоская система, в которой заданная плоскость вместе с треугольником, принадлежащим этой плоскости, совмещена с плоскостью Н (рисунок 6.12а). Для метода совмещения характерны все параметры вращения, которые рассматривались выше.
Главным вопросом метода совмещения является построение совмещенного следа 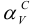
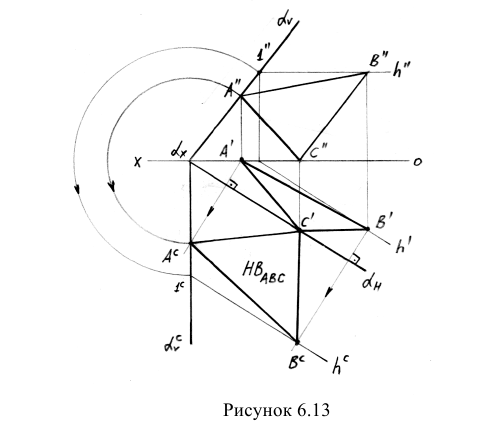
Пример: Найти натуральную величину треугольника AВС, принадлежащего плоскости а.
Решение: С помощью точки А, принадлежащей фронтальному следу, найдем совмещенный фронтальный след 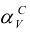
Точка С треугольника находится на горизонтальном следе плоскости и поэтому не будет вращаться (горизонтальный след плоскости — ось вращения). Через точку В треугольника проведем горизонталь h и точку 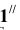
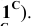
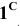
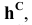
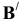
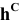
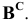
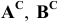
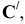
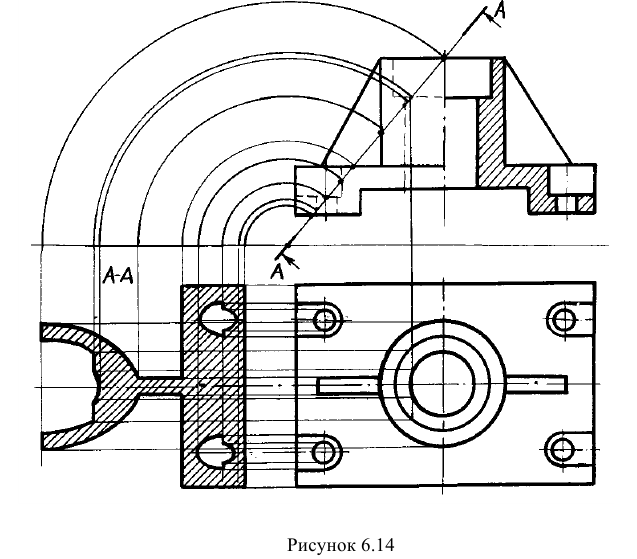
Пример: Методом совмещения построить наклонное сечение детали.
Решение: Секущая плоскость А-А в данном случае является фронтально проецирующей. Совмещение осуществлялось вращением вокруг горизонтального следа, который перпендикулярен горизонтальной оси проекций (рисунок 6.14).
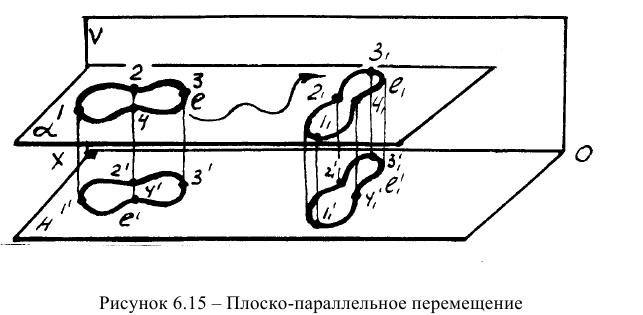
Метод плоско-параллельного перемещения
Плоско-параллельное перемещение — это вид механического движения объекта, когда каждая его точка перемещается в плоскости, параллельной какой-либо плоскости проекций, в результате чего объект перемещается на новое место и ему придаётся новое положение (рисунок 6.15).
Различают плоско-параллельное перемещение относительно плоскости Н — ППП(Н) и относительно плоскости V — ППП(У).
При плоско-параллельном перемещении объекта относительно плоскости Н горизонтальная проекция объекта изменяет свое положение, не изменяя своей формы и размеров. Фронтальная проекция объекта при этом изменяется по форме и размерам, а каждая точка объекта перемещается по прямым линиям, параллельным оси ОХ. ППП(Н) показано на рисунке 6.16а. Обратная картина наблюдается при ППП(V) -рисунок 6.166.
Оба вида плоско-параллельного перемещения, представленные на рисунке, применяются при решении типовых задач на определение натуральной величины плоских фигур.
Для решения задачи по определению натуральной величины отрезка прямой общего положения необходимо сделать одно перемещение и разместить одну из проекций так, чтобы она стала параллельна оси ОХ.
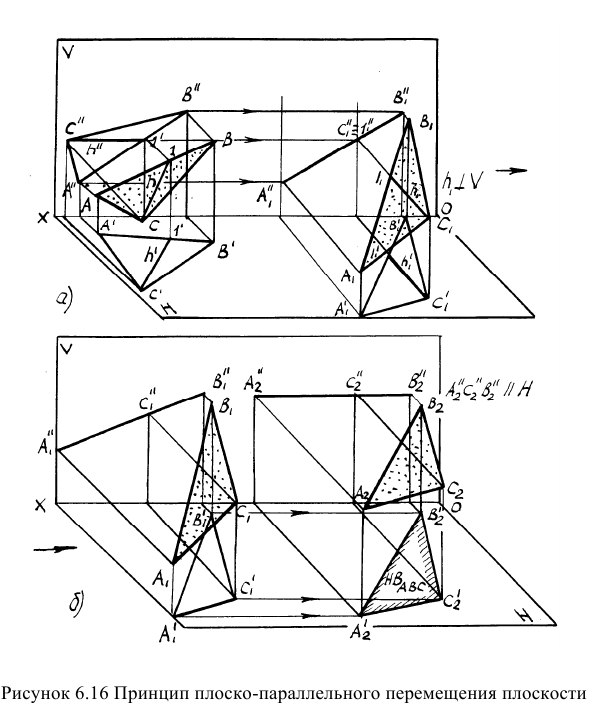
Для решения задачи на определение натуральной величины плоскости совершают два плоско-параллельных перемещения: сначала относительно одной плоскости проекций, а затем относительно другой.
Целью первого перемещения является перевод плоскости из общего положения в проецирующее. Плоскость станет проецирующей, если будет содержать прямую, перпендикулярную плоскости проекций. В качестве такой прямой используют горизонталь или фронталь. При первом перемещении проекция натуральной величины горизонтали или фронтали плоскости должна принять положение, перпендикулярное оси ОХ. Целью второго перемещения является перевод плоскости из проецирующего положения в положение, параллельное плоскости проекции. После этого плоскость проецируется в натуральную величину.
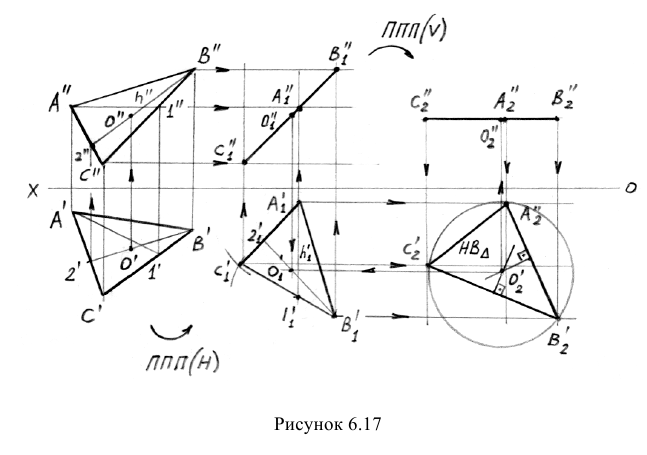
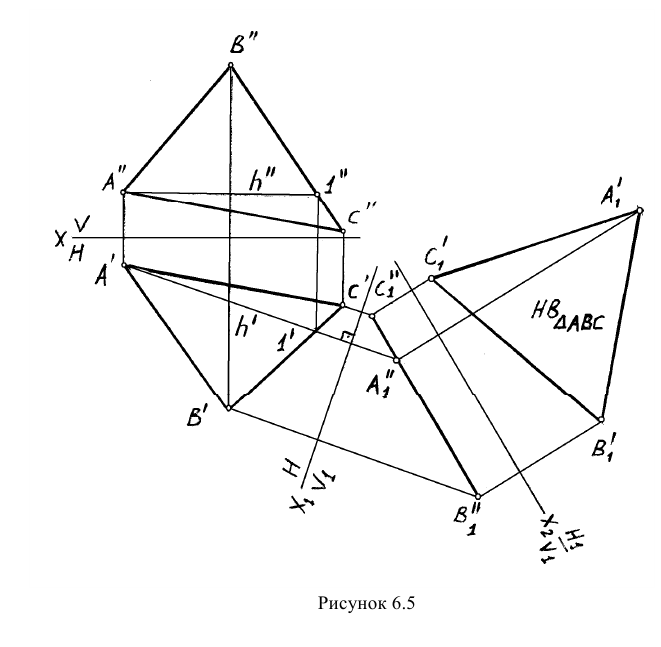
Пример: Методом плоско-параллельного перемещения определить центр окружности, описанной вокруг треугольника AВС.
Решение: Для того, чтобы найти центр описанной окружности треугольника, необходимо определить его натуральную величину. На основании вышерассмотренного материала совершим два плоскопараллельного перемещения: ППП(Н) и ППП(V) (рисунок 6.17).
Для преобразования плоскости треугольника во фронтально-проецирующую плоскость проведем в треугольнике горизонталь h и расположим её при первом ППП перпендикулярно оси ОХ. На ней построим треугольник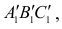
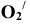
- Касательные плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Проецирование прямой линии
- Проецирование плоскости
- Плоскость на эпюре Монжа
- Позиционные задачи
Центр треугольника
В треугольнике можно определить несколько понятий «центра». Это ортоцентр, инцентр и центр тяжести (или центроид).
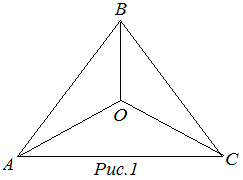
Инцентр треугольника – это точка пересечения биссектрис треугольника. Эта точка является центром окружности, описанной около треугольника (рис. 1).
Ортоцентр треугольника – это точка пересечения трех высот треугольника или их продолжений (рис. 2). Ортоцентр может находиться внутри треугольника (для остроугольных треугольников), вне треугольника (для тупоугольных треугольников) или находиться в вершине прямого угла (для прямоугольных треугольников).
Центр тяжести (центроид) треугольника – точка пересечения медиан треугольника (рис. 3). Центр тяжести делит медиану в отношении , считая от вершины
Примеры решения задач
откуда . Из прямоугольного треугольника
Из подобия треугольников и
следует, что
или
откуда см.
Тогда площадь треугольника равна
Найдем уравнения медиан и
:
Найдем точку пересечения этих прямых как решение системы уравнений
Таким образом, имеем точку .
Центр тяжести треугольника
Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.
Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.
Как найти центр тяжести треугольника
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Количество просмотров этой статьи: 129 665.
Центр тяжести треугольника (центроид) – это точка центра масс. Представьте себе треугольную линейку, положенную на кончик карандаша. Линейка будет балансировать, если кончик карандаша будет находиться в ее центре тяжести. Расположение центроида, которое легко находится с помощью геометрии, необходимо знать при работе над дизайнерским или инженерным проектом.

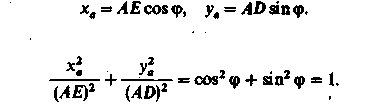
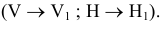
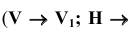
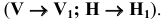
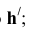
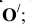
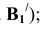
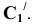
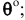
 (рисунок 6.11).
(рисунок 6.11).