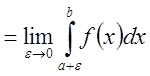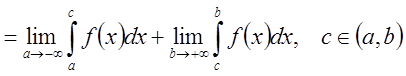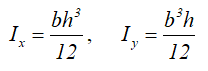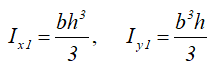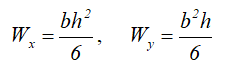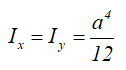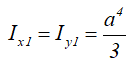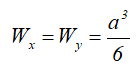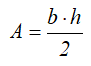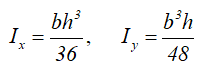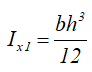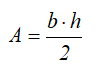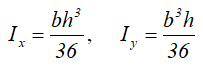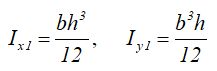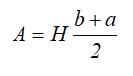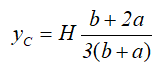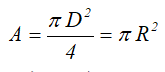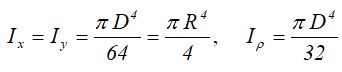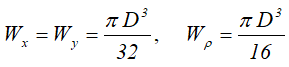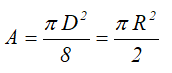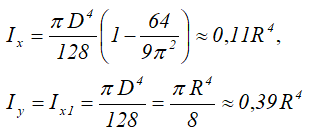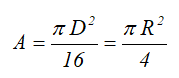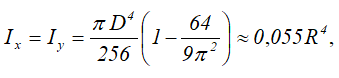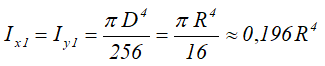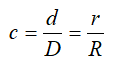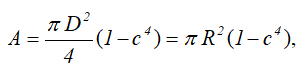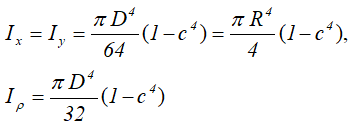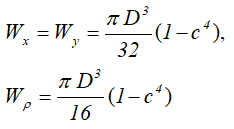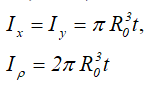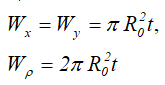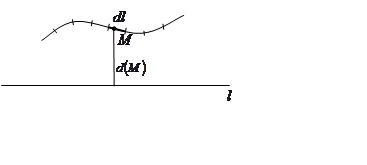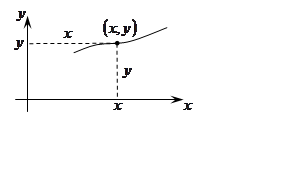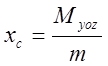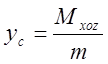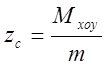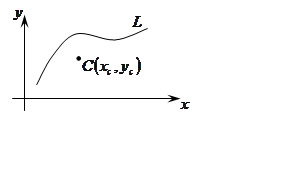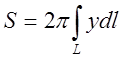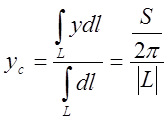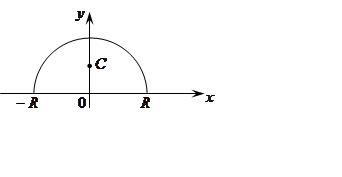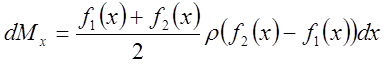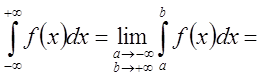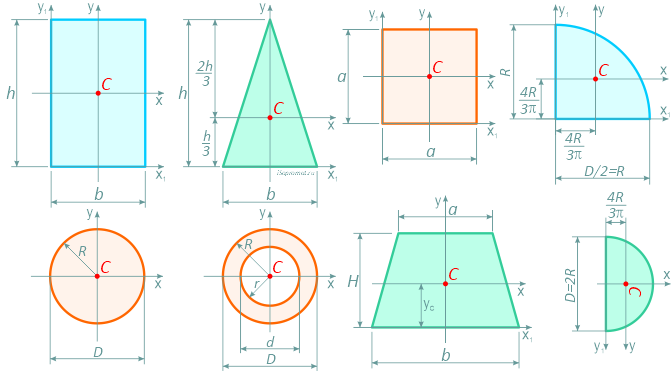
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.
Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
Ix , Iy — осевые моменты инерции сечения относительно главных осей;
Ix1 , Iy1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
Iρ — полярный момент инерции сечения;
Wx , Wy — осевые моменты сопротивления;
Wρ — полярный момент сопротивления
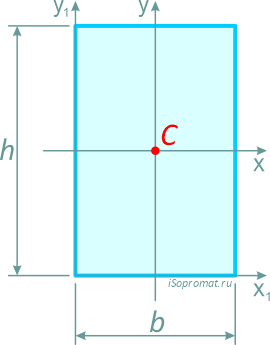
Прямоугольник
Прямоугольник высотой h и шириной b.
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.
Площадь
Центральные осевые моменты инерции прямоугольника
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевые моменты сопротивления прямоугольного сечения
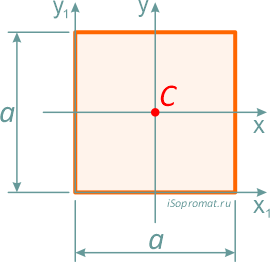
Квадрат
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.
Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.
Площадь
Центральные осевые моменты инерции квадрата
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевой момент сопротивления квадратного сечения
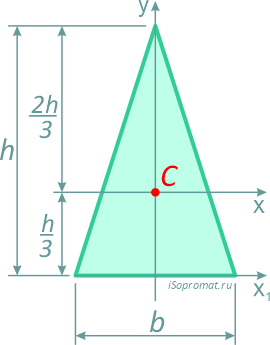
Треугольник равнобедренный
Равнобедренный треугольник высотой h и шириной основания b.
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.
Площадь
Центральные осевые моменты инерции треугольника
Момент инерции относительно смещенной оси x1, проходящей через его основание
Прямоугольный треугольник
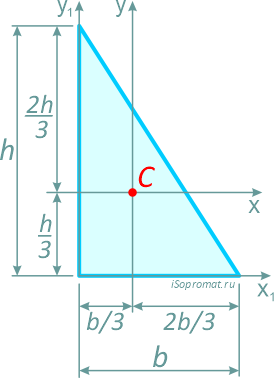
Прямоугольный треугольник высотой h и шириной основания b.
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.
Площадь
Центральные осевые моменты инерции прямоугольного треугольника
Моменты инерции относительно смещенных осей x1 и y1, проходящих через точку, соединяющую его катеты
Трапеция
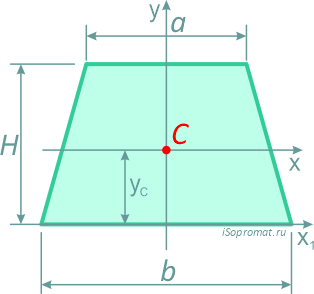
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.
Площадь трапеции
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:
Круг
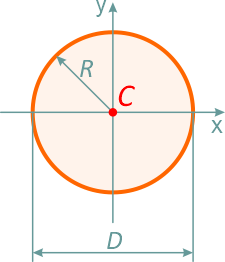
Круг диаметром D (d) или радиусом R (r)
Площадь круга через его диаметр и радиус
Центральные осевые и полярный моменты инерции круга
Осевые и полярный моменты сопротивления
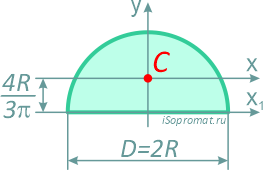
Полукруг
Половина круга диаметром D (d) или радиусом R (r)
Площадь
Осевые моменты инерции полукруга
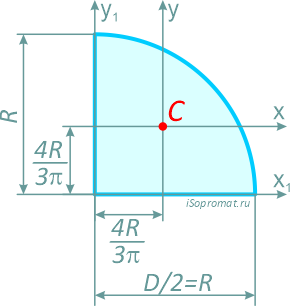
Четверть круга
Четверть круга диаметром D (d) или радиусом R (r)
Площадь
Центральные осевые моменты инерции четверти круга
Моменты инерции относительно смещенных осей x1 и y1
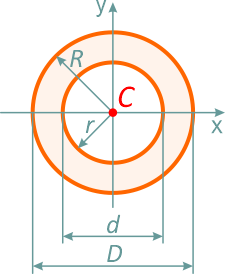
Кольцо
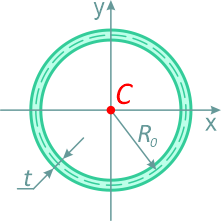
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.
Площадь
Центральные осевые и полярный моменты инерции кольца
Осевые и полярный моменты сопротивления
Тонкостенное сечение (труба)
Тонкостенный профиль (сечение трубы) средним радиусом R0 и толщиной стенки трубы t при R0>>t
Площадь
Центральные осевые и полярный моменты инерции трубного сечения
Осевые и полярный моменты сопротивления
Пример определения координат центра тяжести сложной фигуры:
Другие видео
Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Математическая
техника вычисления центра масс относится
к области курсов математики; там подобные
задачи служат хорошими примерами по
интегральному исчислению. Но, даже умея
интегрировать, полезно знать некоторые
трюки для вычисления положения центра
масс. Один из таких трюков основан на
использовании так называемой теоремы
Паппа, которая работает следующим
образом. Если мы возьмем какую-то
замкнутую фигуру и образуем твердое
тело, вращая эту фигуру в пространстве
так, чтобы каждая точка двигалась
перпендикулярно к плоскости фигуры,
то объем образующегося при этом тела
равен произведению площади фигуры на
расстояние, пройденное ее центром
тяжести! Разумеется, эта теорема верна
и в том случае, когда плоская фигура
движется по прямой линии, перпендикулярной
к ее площади, однако если мы движем ее
по окружности или какой-то другой кривой,
то при этом получается гораздо более
интересное тело. При движении по кривому
пути внутренняя часть фигуры продвигается
меньше, чем внешняя, и эти эффекты
компенсируют друг друга. Так что если
мы хотим определить центр масс плоской
фигуры с однородной плотностью, то нужно
помнить, что объем, образуемый вращением
его относительно оси, равен расстоянию,
которое проходит
Например,
если нам нужно найти центр масс
прямоугольного треугольника с
основанием D
и
высотой H
(фиг.
19.2), то это делается следующим образом.
Ф
19.2. Прямоугольный треугольник и
прямой круговой конус, образованный
вращением этого треугольника.
Вообразите
себе ось, проходящую вдоль H,
и
поверните треугольник на 360° вокруг
этой оси. Это дает нам конус. Расстояние,
которое проходит x-координата
центра масс, равно 2х,
а площадь
области, которая двигалась, т. е.
площадь треугольника, равна 1/2HD.
Произведение
расстояния, пройденного центром масс,
на площадь треугольника равно объему
конуса, т. е. 1/3D2H.
Таким
образом, (2х)(1/2HD)=1/3D2H,
или
x=D/3.
Совершенно аналогично вращением вокруг
второго катета или просто по соображениям
симметрии находим, что у=Н/3.
Вообще
центр масс любого однородного треугольника
находится в точке пересечения трех
его медиан (линий, соединяющих вершину
треугольника с серединой противоположной
стороны), которая отстоит от основания
на расстоянии, равном 1/3
длины
каждой медианы.
Как это увидеть?
Рассеките треугольник линиями,
параллельными основанию, на множество
полосок. Заметьте теперь, что медиана
делит каждую полоску пополам, следовательно,
центр масс должен лежать на медиане.
Возьмем
теперь более сложную фигуру. Предположим,
что требуется найти положение центра
масс однородного полукруга, т. е. круга,
разрезанного пополам. Где будет находиться
центр масс в этом случае? Для полного
круга центр масс расположен в геометрическом
центре, но для полукруга найти его
положение труднее. Пусть r
— радиус
круга, а x
— расстояние центра масс от прямолинейной
границы полукруга. Вращая его вокруг
этого края как вокруг оси, мы получаем
шар. При этом центр масс проходит
расстояние 2х,
а
площадь полукруга равна 1/2r2
(половине
площади круга). Так как объем шара равен,
конечно, 4r3/3,
то отсюда находим
или
Существует
еще другая теорема Паппа, которая
фактически является частным случаем
сформулированной выше теоремы,
а
потому тоже справедлива. Предположим,
что вместо твердого полукруга мы взяли
полуокружность, например кусок проволоки
в виде полуокружности с однородной
плотностью, и хотим найти ее центр масс.
Оказывается, что площадь,
которая
«заметается» плоской кривой при ее
движении, аналогичном вышеописанному,
равна расстоянию, пройденному центром
масс, умноженному на длину
этой
кривой. (Кривую можно рассматривать
как очень узкую полоску и применять к
ней предыдущую теорему.)
Соседние файлы в папке Фейнман Р., Леймон Р., Сендс М. — Фейнмановские лекции по физике, том 2 — 1965
- #
26.04.2017168.45 Кб4015.doc
- #
26.04.2017131.07 Кб3916.doc
- #
26.04.2017135.17 Кб4417.doc
- #
26.04.2017122.88 Кб4018.doc
- #
26.04.2017163.33 Кб4019.doc
- #
26.04.2017169.98 Кб4020.doc
- #
- #
26.04.2017174.59 Кб4322.doc
- #
26.04.2017274.43 Кб4023.doc
- #
26.04.2017159.23 Кб4124.doc
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
плоскости.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сплошной сложной геометрической фигуры по оси x;
— координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
имеющей отверстие
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сложной геометрической фигуры по оси x;
— координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
— Что называется центром параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных площадей?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести треугольника.
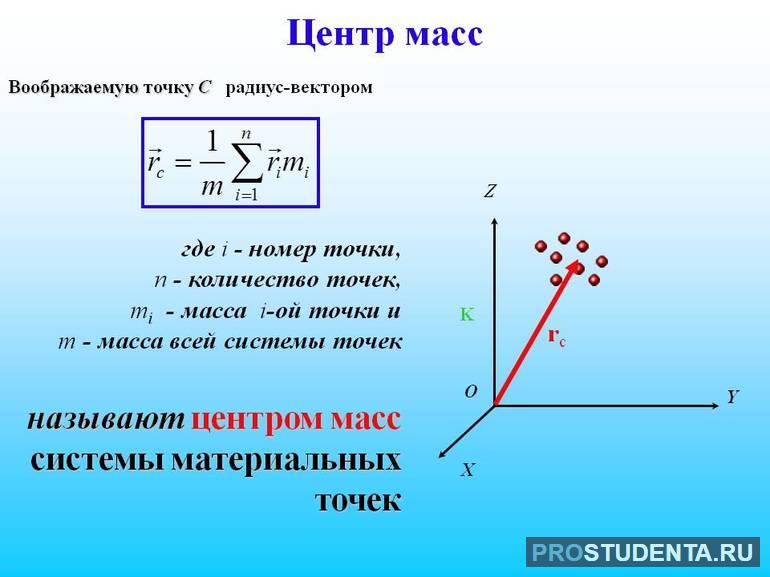
Точку, в которой происходит равное распределение величины, определяющей инерционные и гравитационные свойства, называют центром масс. Формула для определения параметра зависит от радиус-вектора частиц системы и их полной энергии. Эту характеристику тела отличают от тяжести, при этом в трудах советских учёных Ландау, Лифшица для неё используется термин «центр инерции».
Оглавление:
- Общие сведения
- Связь с центром тяжести
- Вычисление положения
- Геометрический способ определения
Общие сведения
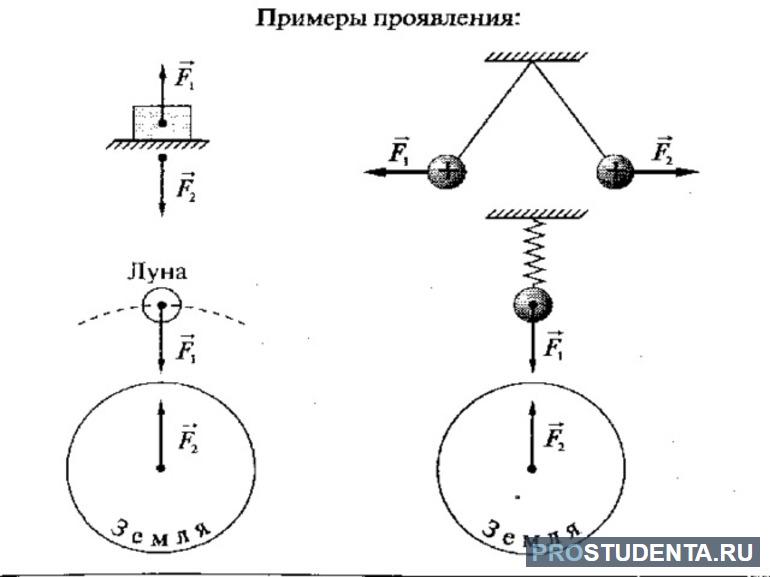
Допустим, имеется тело, на которое действуют скомпенсированные силы. В этом случае оно будет в состоянии покоя или прямолинейного равномерного движения. Пусть тело будет неподвижным. Например, лодка на воде. К ней можно приложить воздействие F1 в районе её кормы. Под действием силы она начнёт разворачиваться. Аналогично если воздействовать на её нос F2, то она тоже будет поворачиваться, но при этом разворот будет происходить в другую сторону.
Получается, что можно подобрать такую линию, на которой действие сил приведёт её к ускоренно поступательному движению. Пусть это будет F3. На самом деле таких сил может быть несколько. При этом их можно перемещать вдоль линии их воздействия. Если все такие силы изобразить в виде линий, то они пересекутся в одной точке. Такое место и называют центром масс тела (ЦМ). То есть точку, в которой пересекаются линии действия сил, вызывающие только ускоренное поступательное механическое движение.
Эта важная точка в теле и движется она довольно просто. Перемещение любого тела можно представить, как комбинацию двух видов движения:
- центра масс;
- вращения.
Существует теорема: ЦМ тела движется так, как перемещалась бы материальная точка, в которой сосредоточена вся масса и к которой приложены все воздействия, действующие на объект. Таким образом, различные виды изменения положения точек в пространстве можно описать с помощью законов Ньютона. Согласно же теореме их можно применять и к телу, если считать, что все силы приложены к центру масс.
Рассматривая объект, можно не учитывать его размер, форму, а брать во внимание только инерцию, ускорение и принцип парного взаимодействия. Фактически в механике перемещение сколь угодно сложного вида рассматривается по принципу суперпозиции и закона сохранении энергии. При этом довольно удобно изучать изменение положения в системе отсчёта связанной с этим центром. В ней полный импульс всегда будет равным нулю, что позволяет упростить уравнение движения.
Связь с центром тяжести
Пусть имеется объект, находящийся на Земле. Говорят, что на него действует сила тяжести. Но на самом деле она воздействует не на вещество, а на каждый его атом, частичку. Если предположить, что ускорение свободного падения буде одинаковым, то на объект действует очень множество сил тяжести. Рассматривать такую систему неудобно. Поэтому все воздействия заменяют равнодействующей. И считают, что действует одна сила, которая приложена к центру тяжести твёрдого тела.
Для того чтобы найти взаимосвязь между тяжестью и массой нужно представить, что объект вдруг распался на отдельные равные кусочки. Они держатся вместе, но не прикреплены друг к другу. Если тело отпустить, то они будут падать вместе, так как ускорение свободного падения не зависит от массы. При этом движение будет поступательным. Значит, сила, приложенная к телу в целом, будет приложена к центру масс.
Получается, что центральная точка является общей как для тяжести, так и для масс. Это две точки положение которых совпадает несмотря на разный их принцип определения в физике. Но существуют условия, когда это правило не выполняется. Например, если система материальных точек неоднородна по объёму плотности в гравитационном поле, то центры не совпадут.
Для примера можно привести список однородных фигур с указанием их центральной точки:
- отрезок — середина;
- параллелограмм — место пересечения диагоналей;
- треугольник — точка пересечения медиан (центроид);
- любой правильный многоугольник — центр поворотной симметрии;
- полукруг — точка, в которой перпендикулярный радиус делится в отношении 4:3p считая от центра круга.
Чтобы найти координату центра масс объекта, который можно представить, как совокупность связанных материальных точек используют два метода: аналитический и геометрический. Но второй способ не всегда можно применить. В однородном гравитационном поле центры тяжести и масс всегда совпадают. И это часто подтверждается на практике, из-за того, что внешнее гравитационное поле в задачах, связанных с действиями на Земле, считают постоянным в пределах объёма тела.
Поэтому эти термины объединяют в геометрии, статике и так далее. То есть в тех областях, где применение определения можно назвать метафорическим и предполагается ситуация их эквивалентности.
При таком понимании оба термина синонимичны, но при этом чаще предпочитают использовать термин, связанный с тяжестью. Это происходит в силу того, что исторически он появился раньше.
Вычисление положения
Пусть тело представляет собой совокупность материальных точек, лежащих на одной прямой при этом их массы разные. Задача состоит в нахождении его центра. Для этого следует вести систему координат с осью икс, которая будет совпадать с линией расположения точек. При этом тело пусть подвешено на невесомой опоре и находится под действием Земного тяготения. Это условие даёт возможность воспользоваться тем фактом, что положения центров масс и тяжести совпадают.
На каждую из материальных точек действует своя сила: m1g, m2g… mng. Если предоставить это тело самому себе, то оно будет в состоянии свободного падения. Остановить тело — подпереть, но при этом так, чтобы оно находилось в равновесии. Это значит, что сила реакции опоры должна проходить через центр тяжести, так как равнодействующая тоже её пересекает.
Получится, что сила реакции опоры будет лежать на одной прямой с силой тяжести действующей на тело в совокупности и их моменты тоже будут проходить через неё. С помощью координатной оси точкам можно присвоить положение, x1, x2… xn, а ЦМ xц. Чтобы тело находилось в равновесии необходимо выполнение двух условий:
- векторная сумма всех сил должна быть равной нулю: m1g + m2g +…+mng + F = 0;
- сумма моментов равняться нулю: Mm 1 g + Mm 2 g +…+ Mmng + MF = 0.
Из первого условия можно найти силу реакции опоры: F = (m1 + m2 +…+mn) * g. Если вращение выбрать против часовой стрелки, тогда относительно оси все моменты силы тяжести будут отрицательными, а опоры — положительные. Тогда справедливо записать: F * хц = (m1 x 1 + m2 x 2 +…+mn xn) * g.
Из последнего равенства можно выразить координату ЦМ: xц = ((m1 x 1 + m2 x 2 +…+mn xn) * g) / F. В эту формулу можно подставить выражение для F. В результате ускорение свободного падения сократится и получится: xц = (m1 x 1 + m2 x 2 +…+mn xn) / (m1 + m2 +…+mn). Это формула выглядит громоздко, но запомнить её легко. В числителе стоят произведения масс материальных точек на их координаты, а в знаменателе — вес всего тела.
Если точки не будут лежать на одной прямой, то координата ЦМ тоже не изменится. То есть приведённая формула справедлива для любого положения тела относительно координаты y.
При этом её можно применять и для рассмотрения предметов в пространстве, так как все направления в существующем мире равноправные.
Геометрический способ определения
Для простейших симметричных фигур ЦМ можно определить геометрическим методом. Для этого используются свойства диагоналей и медиан. Пусть имеется произвольной формы четырёхугольник. Изготовлен он из однородного материала.
Идея вычисления состоит в том, что эту фигуру необходимо разбить на два треугольника. Для этого нужно провести диагональ, которая разделит фигуру на два тела. Затем провести в каждом треугольном теле три медианы. Точка их пересечения и будет ЦМ. В результате вместо четырёхугольника можно рассматривать две материальные точки.
Несмотря на то что масса у них разная ЦМ будет находиться на соединяющем их отрезке. Теперь четырёхугольник можно разбить на два других треугольника и выполнить аналогичные действия уже для них. Получится два отрезка, на которых одновременно расположен ЦМ. Значит, его положение будет определяться точкой их пересечения.
Для более сложной фигуры, например, шести или восьмиугольника можно использовать такой же подход. Сначала нужно разделить тело на прямоугольники, а затем треугольники. Найти ЦМ для полученных фигур и определить точку пересечения. Следует понимать, что ЦМ может находиться и за пределами объекта.
Но в реальных ситуациях бывают фигуры, которые имеют неправильную форму. Для них нельзя применить расчёт или геометрический метод. Поэтому выясняют, где расположен ЦМ экспериментальным путём.
Например, пусть имеется тело сложной неправильной формы. Чтобы найти ЦМ необходимо фигуру подвесить в пространстве. На неё действует две силы: тяжести и реакции оси. Первая заставляет фигуру поворачиваться с определённой скоростью до тех пор, пока момент силы тяжести относительно оси крепления не станет равным нулю. То есть точка опоры, ось и центр тяжести окажутся на одной вертикале.
Чтобы узнать, где же находится ЦМ, тело нужно подвесить, используя другую точку. При этом на самой фигуре следует отметить, как проходит вертикаль.
Повторяя такой опыт минимум три раза, можно увидеть точку пересечения осей, которая и будет искомым ЦМ. Причём чем будет больше экспериментов, тем точнее он будет определён.
Пусть задана кривая и
непересекающая ее прямая . Будем считать, что на
кривой распределена масса с плотностью (задана
линейная плотность кривой)
Под линейной плотностью кривой понимаем предел
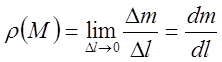
где – длина дуги, которой принадлежит т.
;
– масса дуги
. (при
дуга стягивается в точку
).
Найдём статический момент кривой относительно прямой.
Пусть – произвольная точка
кривой. Рассмотрим элементарную дугу длины ,
содержащую точку . Пусть масса этой дуги
и расстояние от точки
до прямой
равно
.
Тогда
и
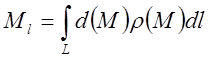
Зададим кривую радиус
— вектором .
Тогда
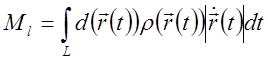
Частные случаи:
1.
Предположим, что кривая лежит на плоскости и задана в параметрической форме
,
,
.
Тогда,
очевидно,
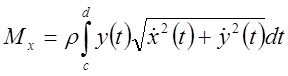
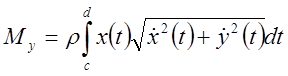
2. Если кривая
задана на плоскости в явном виде
,
,
, то
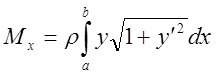
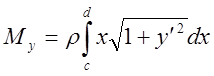
Определение: Центром масс системы материальных точек называется точка с
координатами , такая, что если в ней
сосредоточить всю массу системы, то статические моменты данной материальной
точки относительно любой координатной плоскости равны соответствующим моментам
системы.
В
развернутом виде
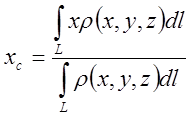
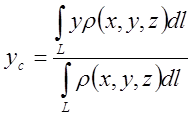
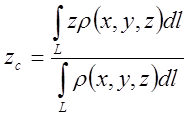
2.15.11. Первая теорема
Гульдина
Теорема: Площадь
поверхности, полученной в результате вращения кривой вокруг непересекающей ее
оси, равна произведению длины кривой на длину окружности, описанной центром
тяжести кривой.
Следовательно,
.
Пример.
Найти координаты центра тяжести полуокружности радиуса .
Решение:
Очевидно
.
Чтобы
найти , воспользуемся теоремой Гульдина:
.
,
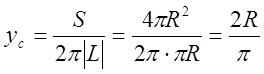
Координаты центра тяжести
полуокружности 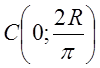
2.15.12. Статические
моменты и центр масс
плоской фигуры
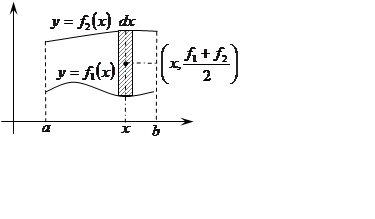
Пусть дана фигура, ограниченная линиями ,
,
,
. В этой фигуре распределена
масса с поверхностной плотностью
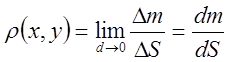
.
где
– часть (малая) фигуры, содержащая точку
;
– максимальный диаметр площадки
;
– масса
(при
площадка
стягивается
в точку ).
Найдём статические моменты плоской фигуры относительно
осей и
. Пусть
. Разобьем фигуру на элементарные полоски
и выделим элементарную полоску шириной на расстоянии
(см. рис.). Очевидно, центр масс этой
полоски находится в точке 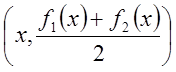
Тогда
и
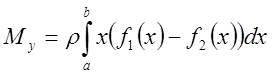
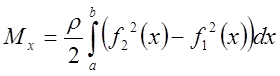
Масса рассматриваемой фигуры, очевидно, равна
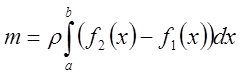
Если
— центр масс фигуры, то
,
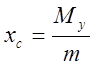
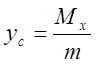
Замечание: Объём
тела, полученного в результате вращения фигуры вокруг оси , равен
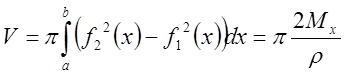
Тогда
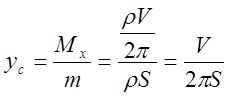
.
2.15.13.
Вторая теорема Гульдина
Теорема: Объём
тела вращения фигуры вокруг непересекающей ее оси равен площади этой фигуры,
умноженной на длину окружности, описываемой центром масс фигуры.
Пример
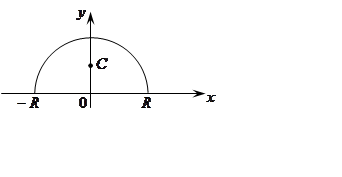
Найти координаты центра тяжести полукруга радиуса .
Очевидно,
.
По
второй теореме Гульдина
.
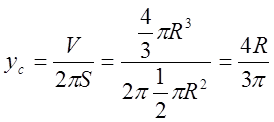
Координаты
центра тяжести круга 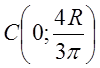
Работа
Пример.
Какую работу необходимо затратить, чтобы выкачать жидкость из резервуара,
имеющего форму параллелепипеда со сторонами .
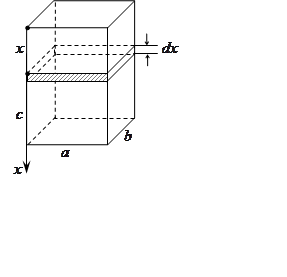
. На глубине
рассмотрим
элементарный слой жидкости толщиной .
Масса
этого слоя ,
а
вес
.
Элементарная работа по выкачиванию этого слоя будет
равна
.
Вся
работа 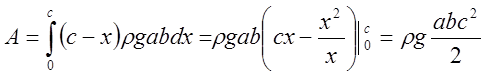
3. Несобственные
интегралы
Определение:Пусть функция определена
на ,
и
интегрируема по Риману на отрезке
. Если существует предел
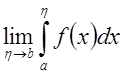
интегрируема в несобственном смысле на
, а указанный предел называется ее
несобственным интегралом и обозначается 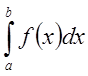
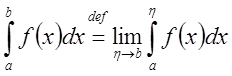
Если предел существует и конечен, то интеграл 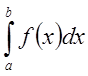
противном случае — расходящимся.
При говорят о
несобственном интеграле 1 рода, при конечном – о
несобственном интеграле 2 рода.
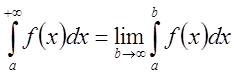
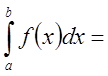
— неограниченна}
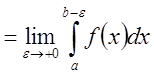
Аналогично
определяются и записываются интегралы с бесконечным нижним пределом и с
конечным нижним пределом, но неограниченной в нем функции:
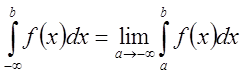
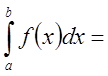
в точке
— неограниченна}