Как найти центр колебаний

§
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные
формулы

• Уравнение
гармонических колебаний

где х
— смещение
колеблющейся точки от положения
равновесия;
t
— время; А,
ω,
φ—
соответственно амплитуда, угловая
частота,
начальная фаза колебаний;
—
фаза колебаний в момент t.

• Угловая частота
колебаний

, или
,

где ν
и
Т — частота и период колебаний.

• Скорость точки,
совершающей гармонические колебания,

• Ускорение при
гармоническом колебании

• Амплитуда
А
результирующего
колебания, полученного при сложении
двух колебаний с одинаковыми частотами,
происходящих по одной прямой, определяется
по формуле

где
a₁
и
А₂—
амплитуды
составляющих колебаний; φ₁
и
φ₂—
их
начальные фазы.

•
Начальная фаза φ
результирующего колебания может быть
найдена
из формулы

•
Частота биений,
возникающих при сложении двух колебаний,
происходящих
по одной прямой с различными, но близкими
по зна­чению
частотами ν₁
и
ν₂,

•
Уравнение траектории
точки, участвующей в двух взаимно
перпендикулярных
колебаниях с амплитудами A₁
и A₂
и начальны­ми
фазами φ₁
и φ₂,

Если
начальные фазы φ₁
и
φ₂
составляющих колебаний одинако­вы,
то уравнение траектории принимает вид

т. е. точка движется
по прямой.

В том
случае, если разность фаз
,
уравнение
принимает вид

т. е. точка движется
по эллипсу.

• Дифференциальное
уравнение гармонических колебаний
ма­териальной точки

, или
,
где
m
—
масса точки; k
—
коэффициент
квазиупругой силы (k=тω²).

•
Полная энергия
материальной точки, совершающей
гармони­ческие
колебания,

• Период
колебаний тела, подвешенного на пружине
(пружин­ный
маятник),

где
m
—
масса тела; k
—
жесткость
пружины.
Формула справедлива для упругих
колебаний в пределах, в ко­торых
выполняется закон Гука (при малой массе
пружины в срав­нении
с массой тела).

Период колебаний
математического маятника

где
l
— длина маятника; g
—
ускорение
свободного падения. Период
колебаний физического маятника

где J
— момент инерции колеблющегося тела
относительно оси

колебаний;
а
— расстояние центра масс маятника от
оси колебаний;

— приведенная
длина физического маятника.

Приведенные
формулы являются точными для случая
бесконеч­но малых амплитуд. При
конечных амплитудах эти формулы дают
лишь приближенные результаты. При
амплитудах не более
ошибка в значении периода не превышает
1 %.

Период
крутильных колебаний тела, подвешенного
на упругой нити,

где J
—
момент
инерции тела относительно оси, совпадающей
с упругой нитью; k
—
жесткость
упругой нити, равная отношению упругого
момента, возникающего при закручивании
нити, к углу, на который нить закручивается.

• Дифференциальное
уравнение затухающих колебаний

, или
,

где r
— коэффициент сопротивления; δ
— коэффициент
затухания:

; ω₀—
собственная угловая частота колебаний
*

• Уравнение
затухающих колебаний

где A
(t) —
амплитуда
затухающих колебаний в момент t;
ω
— их угловая частота.

• Угловая частота
затухающих колебаний

О Зависимость
амплитуды затухающих колебаний от
времени

I

где
А₀
— амплитуда
колебаний в момент t=0.

• Логарифмический
декремент колебаний

где
A
(t) и
A
(t+T) —
амплитуды
двух последовательных колеба­ний,
отстоящих по времени друг от друга на
период.

• Дифференциальное
уравнение вынужденных колебаний

, или

,

где

—
внешняя периодическая сила, действующая
на
колеблющуюся
материальную точку и вызывающая
вынужденные
колебания;
F₀
—
ее
амплитудное значение;

•
Амплитуда вынужденных
колебаний

•
Резонансная частота
и резонансная амплитуда

и

Примеры решения
задач

Пример
1. Точка
совершает колебания по закону
x(t)= ,
где
А=2
см.
Определить начальную фазу φ,
если

x(0)= см
и х^,(0)<0.
Построить векторную диаграмму для
мо-­
мента t=0.

Решение.
Воспользуемся уравнением движения и
выразим смещение в момент t=0
через начальную фазу:

Отсюда
найдем начальную фазу:

*
В приведенных ранее формулах
гармонических колебаний та же
величина
обозначалась просто ω
(без индекса 0).

Подставим
в это выражение заданные значения x(0)
и А:
φ=
= .
Значению аргумента

удовлетворяют
два
значения угла:

Для
того чтобы решить, какое из этих значений
угла φ
удовлет-­
воряет
еще и условию
,
найдем сначала
:

Подставив
в это выражение значение t=0
и поочередно значения
начальных
фаз
и
,
найдем

Так
как всегда A>0
и ω>0,
то условию удовлетворяет
толь­
ко
первое значение начальной фазы.
Таким
образом, искомая начальная
фаза

По
найденному значению φ
постро-­
им
векторную диаграмму (рис. 6.1).
Пример
2. Материальная
точка
массой т=5
г совершает гармоничес-­
кие колебания
с частотой ν
=0,5 Гц.
Амплитуда
колебаний A=3
см. Оп-­
ределить: 1) скорость υ
точки
в мо-­
мент времени, когда смещение
х=
=
1,5 см; 2) максимальную силу
F_max,
действующую
на точку; 3)
Рис.
6.1 полную
энергию Е
колеблющейся
точ­
ки.

Решение.
1. Уравнение гармонического колебания
имеет вид

(1)

а
формулу скорости получим, взяв первую
производную по времени от смещения:

(2)

Чтобы
выразить скорость через смещение, надо
исключить из формул (1) и (2) время. Для
этого возведем оба уравнения в квад­рат,
разделим первое на А²,
второе
на A²
ω
²
и сложим:

, или

Решив
последнее уравнение относительно υ,
найдем

Выполнив вычисления
по этой формуле, получим

см/с.

Знак
плюс соответствует случаю, когда
направление скорости совпадает
с положительным направлением оси х,
знак
минус — ког­да
направление скорости совпадает с
отрицательным направлением оси
х.

Смещение при
гармоническом колебании кроме уравнения
(1) может быть определено также уравнением

Повторив
с этим уравнением такое же решение,
получим тот же ответ.

2.
Силу действующую на точку, найдем по
второму закону Нью­тона:

(3)

где а
— ускорение
точки, которое получим, взяв производную
по времени
от скорости:

, или

Подставив выражение
ускорения в формулу (3), получим

Отсюда максимальное
значение силы

Подставив
в это уравнение значения величин π,
ν,
т
и
A,
найдем

3.
Полная энергия колеблющейся точки есть
сумма кинетической и
потенциальной энергий, вычисленных для
любого момента вре­мени.

Проще
всего вычислить полную энергию в момент,
когда кинети­ческая
энергия достигает максимального
значения. В этот момент потенциальная
энергия равна нулю. Поэтому полная
энергия E
колеблющейся точки равна максимальной
кинетической энергии

T_max:

(4)

Максимальную
скорость определим из формулы (2),
положив

:
.
Подставив выражение скорости в фор­-
мулу
(4), найдем

Подставив
значения величин в эту формулу и произведя
вычис­ления, получим

или

мкДж.

Пример
3.
На концах тонкого стержня длиной l
=
1 м и массой m₃=400
г
укреплены шарики малых размеров массами
m₁=200
г
и
m₂=300г.
Стержень
колеблется около горизонтальной оси,
перпен-

дикулярной
стержню и проходящей через его середину
(точка О на рис. 6.2). Определить период Т
колебаний,
совершаемых стержнем.

Решение.
Период колебаний физического маятника,
каким является стержень с шариками,
определяется соотношением

(1)

где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; l_С
— расстояние
от центра масс ма­ятника
до оси.

Момент
инерции данного маятника равен сумме
моментов
инерции шариков J₁
и
J₂
и
стержня J₃:

(2)

Принимая
шарики за материальные точки, вы­разим
моменты их инерции:

Так
как ось проходит через середину стержня,
то
его
момент инерции относительно этой оси
J₃=
= .
Подставив
полученные выражения
J₁
,
J₂
и

J₃
в формулу (2), найдем общий момент инерции
фи-­
зического маятника:

Произведя
вычисления по этой формуле, найдем

Рис.
6.2 Масса маятника состоит из масс шариков
и массы
стержня:

Расстояние
l_С
центра
масс маятника от оси колебаний найдем,
исходя
из следующих соображений. Если ось х
направить
вдоль стержня
и начало координат совместить с точкой
О,
то
искомое рас­стояние
l
равно координате центра масс маятника,
т. е.

, или

Подставив
значения величин m₁,
m₂,
m,
l
и произведя вычисле­ния,
найдем

см.

Произведя
расчеты по формуле (1), получим период
колебаний физического
маятника:

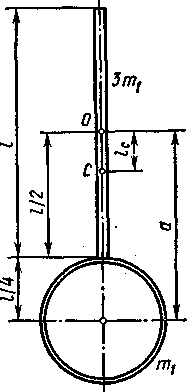
Пример
4. Физический
маятник представляет собой стержень
длиной
l=
1 м и массой 3т₁
с прикрепленным
к одному из его концов
обручем
диаметром
и
массой т₁.
Горизонтальная
ось Oz

маятника
проходит через середину стержня
перпендикулярно ему (рис. 6.3). Определить
период Т
колебаний
такого маятника.

Решение.
Период
колебаний физического маятника
опреде­ляется
по формуле

(1)

где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; l_C
— расстояние
от центра масс
маятника до оси колебаний.

Момент
инерции маятника равен сумме мо­ментов
инерции стержня J₁
и
обруча J₂:

(2).

Момент
инерции стержня относительно
оси,
перпендикулярной
стержню и проходящей
через
его центр масс, определяется по форму-­
ле
.
В данном случае т=3т₁
и

Момент
инерции обруча найдем, восполь-­
зовавшись
теоремой Штейнера
,
где
J
—
момент
инерции относительно про-­
извольной
оси;
J₀
—
момент
инерции отно-­
сительно
оси, проходящей через центр масс
параллельно
заданной оси; а
— расстояние
между
указанными осями. Применив эту фор-­
мулу
к обручу, получим

Рис. 6.3

Подставив
выражения J₁
и
J₂
в форму­лу
(2), найдем момент инерции маятника
относительно оси вра­щения:

Расстояние
l_С
от
оси маятника до его центра масс равно

Подставив
в формулу (1) выражения J,
l_с
и массы маятника

, найдем период его колебаний:

После
вычисления по этой формуле получим
T=2,17
с.

Пример
5. Складываются
два колебания одинакового направле-­
ния,
выражаемых уравнениями
;
х₂=
=,
где А₁=1
см,
A₂=2
см,

с,

с, ω
=
=.
1. Определить начальные фазы φ₁
и φ
₂
составляющих коле-

баний.
2. Найти амплитуду А
и
начальную фазу φ
результирующего колебания.
Написать уравнение результирующего
колебания.

Решение.
1. Уравнение гармонического колебания
имеет вид

(1)

Преобразуем
уравнения, заданные в условии задачи,
к такому же
виду:

(2)

Из
сравнения выражений (2) с равенством (1)
находим начальные фазы
первого и второго колебаний:

рад и

рад.

2.
Для определения амплитуды А
результирую­щего
колебания удобно воспользоваться
векторной диаграммой,
представленной на рис.
6.4.
Согласно теореме косинусов, получим

(3)

где

— разность фаз составляющих колебаний.
Так
как
,
то, подставляя найденные
значения
φ₂
и φ₁
получим

рад.

Рис. 6.4

Подставим
значения А₁
,
А₂
и

в формулу (3)
и
произведем вычисления:

A=2,65
см.

Тангенс
начальной фазы φ
результирующего колебания опреде-­
лим
непосредственно из рис. 6.4:

, отку-­
да
начальная фаза

Подставим
значения А₁,
А₂,
φ
₁,
φ
₂
и произведем вычисления:

= рад.

Так
как угловые частоты складываемых
колебаний одинаковы,
то
результирующее колебание будет иметь
ту же частоту ω.
Это
позволяет
написать уравнение результирующего
колебания в виде

, где A=2,65
см,
,

рад.

Пример
6. Материальная
точка участвует одновременно в двух
взаимно перпендикулярных гармонических
колебаниях, уравне­ния
которых

(1).

(2)

где
a₁=1
см,
A₂=2
см,
.
Найти уравнение траектории точ-­
ки.
Построить траекторию с соблюдением
масштаба и указать
направление
движения точки.

Решение.
Чтобы
найти уравнение траектории точки,
ис­ключим
время t
из
заданных уравнений (1) и (2). Для этого
восполь-

зуемся
формулой
.
В данном случае

, поэтому

Так
как согласно формуле (1)
,
то уравнение траекто-­
рии

(3)

Полученное
выражение представляет собой уравнение
параболы, ось которой совпадает с осью
Ох.
Из
уравнений (1) и (2) следует, что смещение
точки по осям координат ограничено и
заключено в пределах от —1 до +1 см по
оси Ох
и
от —2 до +2 см по оси Оу.

Для
построения траектории найдем по уравнению
(3) значения у,
соответствующие
ряду значений х,
удовлетворяющих
условию

см, и составим таблицу:

Начертив
координатные оси и выбрав масштаб,
нанесем на пло­скость
хОу
найденные
точки. Соединив их плавной кривой,
получим траекторию точки, совершающей
колеба­ния
в соответствии с уравнениями движе­ния
(1) и (2) (рис. 6.5).

Рис. 6.5

Для
того чтобы указать направление движения
точки, проследим за тем, как из­меняется
ее положение с течением времени. В
начальный момент t=0
координаты точ­ки
равны x(0)=1
см и y(0)=2
см. В по­следующий
момент времени, например при t₁=l
с,
координаты точек изменятся и ста­нут
равными х
(1)=
—1
см, y(t)=0.
Зная
положения
точек в начальный и последую­щий
(близкий) моменты времени, можно указать
направление движения точки по траектории.
На рис. 6.5 это направление движения
указано стрелкой (от точки А
к
началу
координат). После того как в мо­мент
t₂
= 2 с колеблющаяся точка достиг­нет
точки D,
она
будет двигаться в обратном направлении.

Задачи

Кинематика
гармонических колебаний

6.1.
Уравнение колебаний точки имеет вид
,
где
ω=π
с^-1,
τ=0,2
с. Определить период Т
и
начальную фазу φ
колебаний.

6.2.
Определить
период Т,
частоту
v
и
начальную фазу φ
коле­баний,
заданных уравнением
,
где ω=2,5π
с^-1,
τ=0,4
с.

6.3.
Точка
совершает колебания по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

;
2)
х(0)
=см
и
;
3) х(0)=2см
и
;
4)
х(0)=
и
.
Построить векторную диаграмму
для
момента
t=0.

6.4.
Точка
совершает колебания .по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

; 2) x(0)=
см и
;
3) х(0)=
см и
;
4)
x(0)=см
и
.
Построить векторную диаграмму для
момента
t=0.

Механические колебания.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

к оглавлению ▴

Гармонические колебания.

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

(1)

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

(2)

(3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):

.

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

.

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

.

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

к оглавлению ▴

Уравнение гармонических колебаний.

Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:

. (4)

Теперь дифференцируем полученное равенство (4):

. (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

. (6)

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

. (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

к оглавлению ▴

Пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

. (8)

Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

Тогда соотношение (8) принимает вид:

или

.

Мы получили уравнение гармонических колебаний вида (6), в котором

.

Циклическая частота колебаний пружинного маятника, таким образом, равна:

. (9)

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

. (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

к оглавлению ▴

Математический маятник.

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

,

и спроектируем его на ось :

.

Если маятник занимает положение как на рисунке (т. е. ), то:

.

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

.

Итак, при любом положении маятника имеем:

. (11)

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

,

или

.

Это — уравнение гармонических колебаний вида (6), в котором

.

Следовательно, циклическая частота колебаний математического маятника равна:

. (12)

Отсюда период колебаний математического маятника:

. (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

к оглавлению ▴

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:

.

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Рис. 7. Резонанс

Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

Теорема о центре колебаний физического маятника  [c.86]

Теорема о связи между моментами инерции относительно параллельных осей дает возможность доказать важную теорему о центре колебаний физического маятника, найденную X. Гюйгенсом ).  [c.86]

Сравнивая найденное выражение СК с формулой (1. 102), видим, что точка К является центром колебаний физического маятника, у которого ось  [c.410]

Следовательно, ось Ог не подвергается удару, если она является главной осью инерции, ударный импульс перпендикулярен к ней и точка его приложения лежит в -одной плоскости с осью вращения и центром инерции тела. Расстояние точки приложения импульса S от оси вращения Ог определяется формулой (III. 101). Сравнивая ее с формулой (1.85), приходим к выводу, что при отсутствии импульсов динамических реакций точкой М приложения ударного импульса S является центр колебаний физического маятника с моментом инерции относительно оси вращения, равным 1 , и расстоянием центра инерции от оси вращения, равным ус- Точка М называется центром удара.  [c.474]

Длина li такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника, называется приведенной длиной физического маятника. Точка К, отстоящая от оси подвеса на расстоянии OK=h, называется центром качаний физического маятника (см. рис. 324).  [c.327]

Следствие 6.4.1. Уравнение колебаний физического маятника совпадает с уравнением колебаний математического маятника (определение 3.9.1), вся масса которого сосредоточена в центре качания. Теория движения математического маятника может быть полностью применена к анализу движения физического маятника.  [c.458]

Если от точки Oi отложить отрезок /i = I, то получим точку О, т. е. центр качаний и точка привеса взаимны. Периоды малых колебаний физических маятников вокруг горизонтальных осей, проходящих через точку привеса и цеЕ тр качаний, одинаковы.  [c.453]

Важное прикладное значение теории малых колебаний физического маятника состоит в том, что ее можно положить в основу экспериментального определения моментов инерции тел. Для опытного определения момента инерции тела силой тяжести Р относительно какой-либо оси достаточно сделать эту ось горизонтальной осью привеса, определить период малых колебаний тела вокруг этой оси и расстояние от точки привеса до центра масс. Тогда согласно (53) момент инерции относительно горизонтальной оси привеса определится по формуле  [c.453]

По экспериментально определенному периоду малых колебаний физического маятника можно вычислить его момент инерции относительно оси подвеса этим пользуются при экспериментальном определении моментов инерции тел. Зная расстояние от оси подвеса до центра тяжести тела, найдем момент инерции тела относительно оси, параллельной оси подвеса и проходящей через центр тяжести С. Вычисление проводится по формуле (57), из которой по известным 7 и s находим р , а потом 4с  [c.180]

Работы Галилея по динамике были продолжены и развиты знаменитым голландским ученым Гюйгенсом (1629—1695), который создал теорию колебаний физического маятника, введя при этом понятия о центре качаний, о приведенной длине физического маятника и о моменте инерции тела относительно оси. Кроме того, Гюйгенс обобщил введенное Галилеем понятие ускорения на случай криволинейного движения точки и установил понятие о центростремительной и центробежной силах. Ряд его работ относится к теории удара упругих твердых тел.  [c.14]

Длина L такого математического маятника, период малых колебаний которого равен периоду малых колебаний данного физического маятника, называется приведенной длиной физического маятника. Точка О1, отстоящая от точки подвеса О на расстоянии 001= Д, называется центром качаний физического маятника (рис. 379).  [c.684]

Физический маятник, так же как математический, обладает свойством изохронности, пока отклонения малы. Период колебаний физического маятника существенно зависит не только от расстояния от оси вращения до центра тяжести, но и от момента инерции маятника относительно оси, т. е. от расположения отдельных элементов массы маятника.  [c.409]

Так как период маятника зависит от g, то маятником можно пользоваться для определения величины g. При точных измерениях, конечно, уже ни один реальный маятник нельзя рассматривать как математический. Поэтому при точных измерениях силы тяжести для периода физического маятника пришлось бы пользоваться формулой (13.21). Но расчет момента инерции маятника также не может быть произведен с большой точностью. Для устранения этих трудностей используют свойство центра качаний, которое заключается в следующем. Если мы перенесем точку подвеса физического маятника в центр качаний, то прежняя точка подвеса окажется новым центром качаний. Точка подвеса и центр качаний обратимы. Поэтому период колебаний физического маятника остается прежним (так как прежней осталась приведенная длина).  [c.409]

Замечание Лагранжа относится и к проблеме маятника. Маятник Галилея, т. е. математический маятник, реально воплощался телом, которое могло вращаться вокруг неподвижной оси,— физическим маятником. Изохронность колебаний маятника, пусть не совсем точную, естественно было использовать для измерения времени. Достаточно точное измерение времени с помощью прибора, который можно было бы перевозить с собой на корабле, решало проблему определения долгот на море — в то время основную проблему кораблевождения в открытом море. Создать достаточно точные и пригодные в морских путешествиях маятниковые часы пытался еще Галилей, он даже вступил с нидерландскими властями в переговоры об использовании маятниковых часов. Галилей не добился достаточно хороших результатов и, таким образом, оставил открытыми две проблемы теоретическую — о центре качаний физического маятника, т. е. о приведенной длине физического маятника, и техническую — проблему маятниковых часов.  [c.254]

Собственные колебания физического маятника, т. е. тяжелого тела, свободно вращающегося вокруг некоторой оси, будут происходить так же, как и колебания рассмотренного выше математического маятника. Пусть тело А (рис. 347) свободно вращается вокруг горизонтальной оси О, перпендикулярной к чертежу. Расстояние от центра масс до оси равно а тогда при повороте тела от положения равновесия на угол а возникнет возвращающий момент силы тяжести, равный  [c.425]

Всегда можно подо-рать такой математический маятник, период колебаний которого будет равен периоду колебаний данного физического маятника. Через центр тяжести физического маятника проведем прямую, перпендикулярную к оси подвеса, и на этой прямой отложим от оси отрезок, равный длине / пО добранного математического маятника. Мы получим точку, которая и называется центром качания физического маятника. Расстояние от центра качания до оси подвеса, равное длине I  [c.236]

Другим примером являются колебания физического маятника — тела произвольной формы массы от, закрепленного на горизонтальной оси О так, что его центр масс находится в точке О, удаленной от оси на расстояние а. При отклонении маятника от вертикали на небольшой угол а он будет совершать свободные гармонические колебания под действием силы тяжести, приложенной к центру масс (рис. 1.2).  [c.8]

Период колебаний физического маятника (а, следовательно, и его приведенная длина I) немонотонно зависит от расстояния а. Это легко заметить, если в соответствии с теоремой Гюйгенса-Штейнера момент инерции J выразить через момент инерции относительно параллельной горизонтальной оси, проходящей через центр масс J = J + та . Тогда период колебаний (1.14) будет равен  [c.9]

Рассмотрим колебания физического маятника, представляющего собой тело с моментом инерции I, вращающееся вокруг оси, проходящей через точку О. Центр тяжести тела находится в точке С, расстояние которой от оси вращения O =d (рис.5). При малых отклонениях от положения равновесия энергии физического маятника может быть записана в виде  [c.121]

Начальная фаза колебания в формуле (36.14) обозначена буквой а. ) Таким образом малые колебания физического маятника в хорощем приближении являются гармоническими, а их круговая частота зависит от массы т маятника, его момента инерции / относительно оси вращения и от расстояния г между осью вращения и центром тяжести маятника. Амплитуда А и начальная фаза а определяются через начальные данные, т.е. значения угла и угловой скорости в начальный момент времени >(0) = Ро и ПД0) = П(, по формулам, аналогичным (36.6) (угловая скорость здесь обозначена буквой П, чтобы не спутать с круговой частотой колебаний а>).  [c.117]

В сейсмографах — приборах для регистрации землетрясений— применяется физический маятник, ось подвеса которого образует угол а с вертикалью. Расстояние от оси подвеса до центра масс маятника равно а, момент инерции маятника относительно оси, проходящей через его центр масс параллельно оси подвеса, равен /с, масса маятника равна М. Определить период колебаний маятника.  [c.287]

Два одинаковых физических маятника подвешены па параллельных горизонтальных осях, расположенных в одной горизонтальной плоскости, и связаны упругой пружиной, длина которой в ненапряженном состоянии равна расстоянию между осями маятников. Пренебрегая сопротивлением движению и массой пружины, определить частоты и отношения амплитуд главных колебаний системы при малых углах отклонения от равновесного положения. Вес каждого маятника Р радиус инерции его относительно оси, проходящей через центр масс параллельно осп подвеса, р жесткость пружины с, расстояния от центра масс маятника и от точки прикрепления пружины к маятникам до оси подвеса равны соответственно I и Н. ( м. рисунок к задаче 56.4,)  [c.418]

Теорема 6.4.1. (Гюйгенс). Точка подвеса физического маятника и центр качания суть точки взаимные. Если центр качания принять за точку подвеса, то прежняя точка подвеса будет центром качания. Период колебаний маятника при этом не изменится.  [c.459]

Центральный радиус инерции физического маятника составляет 0,05м. Каким должно быть расстояние между точкой подвеса и центром масс маятника, чтобы период его малых колебаний составил 1 с Сколько решений имеет задача Как практически можно реализовать эти решения  [c.520]

Если перенести ось вращения физического маятника параллельно своему первоначальному положению в центр колебаний, то приведенная длина физического маятника не изменится.  [c.86]

Теперь докажем теорему о центре колебаний. Допустим, что ось вращения перенесена параллельно ее первоначальному положению из точки О в точку О1. Вычислим новую приведенную длину физического маятника й[ и докажем, что она равна а, используя при этом соотнощение (I. 102).  [c.87]

Величины S и s входят в эти соотношения симметрично. Поэтому данную длину / эквивалентного математического маятника, или, что то же, данный период колебаний Т можно получить, поместив ось подвеса на расстоянии s пли на расстоянии s от центра тяжести тела в первом случае ось качаний будет находиться на расстоянии s = I — s, а во втором — на расстоянии. S == -s от центра тяжести. Иными словами, ось качаний станет во втором случае осью подвеса, а ось подвеса—осью качаний. Это свойство физического маятника используется в оборотном маятнике, служащем для определения ускорения силы тяжести g. Построение отрезка s по известным s и п показано на рис. 301.  [c.180]

Геометрическим местом точек подвеса физического маятника, для которых период колебаний маятника один и тот яге, являются, как отсюда следует, две окружности с центрами в точке G II с радиусами 0G и O G (рис. 130). Если Z > р, то имеем маятник если <р — коромысло.  [c.180]

Для случая нескольких масс решение будет аналогичным. Кроме идеи сведения изучения движения тела к изучению его равновесия с учетом сил инерции, Я. Бернулли высказал мысль о возможном определении реакции связи. Истинное движение 161 ( 2 2) он разложил на свободное а 0 а2Я) и движение O l Qb2) вдоль стержня. Каждому движению он ставит в соответствие силу. Вертикальному движению alO a2Q), естественно, соответствует сила тяжести, а сила, соответствующая движению вдоль стержня, уравновешивается опорой А. По современным представлениям — реакцией связи. Ученик Я. Бернулли — Якоб Германн дал иную интерпретацию идеи использования сил инерции. В наиболее известном сочинении Форономия или две книги о силах и движениях твердых и жидких тел [200], решая задачу о нахождении центра колебаний физического маятника, он разлагает силу тяжести каждой материальной точки на две составляющие одна направлена по линии подвеса, другая — перпендикулярно  [c.137]

Гюйгенс рассмотрел и более трудную задачу о колебаниях физического маятника. Он определил центр колебаний физического маятника и ег период. При этом знаменателен принцип, которым пользуется Гюйген и который отражает уровень знаний того времени о законе сохранения энергии Если любое число весомых тел приходит в движение благодар их тяжести, то общий центр тяжести этих тел не может подняться выше, чем он был в начале движения . И далее Если бы изобретатели новы  [c.23]

Следовательно, не изменится период колебаний физического маятника. Новый центр колебаний перейдет в точку пересечения О первоначальной осп вращения с иерпендикулярной плоскостью, проведенной через центр инерции С маятника (рис. 16).  [c.86]

Голландский ученый механик, физик и математик Христиан Гюйгенс (1629-1695) впервые решил задачу об определении центра качаний физического маятника. Согласно этой задаче, между центром качаний и точкой подвеса существует зависимость если физический маятник перевернуть и сделать центр качаний точкой подвеса, то прежняя точка подвеса сделается центром качаний и маятник будет качаться так же, как и ранее, Задача 9.65. На каком расстоянии от центра масс должен быть подвешен физический маятник, чтобы период его малых колебаний был наименьшим (Foppl).  [c.279]

Для современников основным произведением Гюйгенса была книга Маятниковые часы (1673 г.) Это классическое произведение по богатству и ценности содержания имеет мало себе равных. Прежде всего, оно, в соответствии со своим названием, содержит (в первой части) описание великого изобретения Гюйгенса — маятниковых часов. Разрабатывая теорию математического маятника, Гюйгенс показал неизохронность колебаний кругового маятнйка и для него разработал метод расчета периода колебаний, равносильный приближенному вычислению соответствующего эллиптического интеграла. Гюйгенс строго доказал точную изохронность колебаний (любой амплитуды) циклоидального маятника, дал формулу для вычисления периода этих колебаний, а также и для периода малых колебаний кругового маятника, разработал и осуществил конструкцию циклоидального маятника. В связи с этим Гюйгенс создал новый раздел дифференциальной геометрии — учение об эволютах и эвольвентах. Он изобрел часы с коническим маятником. Попутно Гюйгенс открыл явление параметрического резонанса (наблюдая установление консонанса двух маятников, прикрепленных на одной балке) и правильно объяснил его. Кроме того, в Маятниковых часах изложены многочисленные математические результаты, как, например, спрямление многих кривых, определение площадей некоторых кривых поверхностей, метод построения касательных к рулеттам и т. д. Не располагая алгоритмом анализа бесконечно малых, Гюйгенс, проявляя исключительную изобретательность, систематически применяет инфинитезимадьные методы в геометрическом оформлении — этим аппаратом он овладел в совершенстве, и в этом среди его современников никто, кроме Ньютона, не мог с ним соперничать. Но мы еще не сказали о том, что в четвертой части Маятниковых часов , под названием О центре качания , решена поставленная Мерсенном проблема определения периода колебаний физического маятника. Это — первая глава динамики твердого тела. В этой созданной Гюйгенсом главе одинаково значительны результат и метод. В ней налицо то сочетание эксперимента и теории, технической направленности и обобщающего физического мышления, которое характерно для рассматриваемого периода. Проявить это сочетание в своем творчестве дано было только деятелям экстра-класса — Галилею, Гюйгенсу, Ньютону.  [c.110]

Проблема центра качаний была поставлена, можно сказать, в конкурсном порядке, тем же Мерсенном, который так интересовался открытиями Галилея в акустике. Отсылая за подробностями к гл. V (см. стр. 97), укажем здесь, что Гюйгенсу принадлежит не только решение задачи о центре качания, т. е. приведенной длине физического маятника, но и точная трактовка вопроса о периоде малых колебаний математического маятника. Таким образом, была решена задача и о периоде малых колебаний физического маятника. Гюйгенс определил также центры тяжести и центры качания для многих фигур, открыл циклоидальный маятник и доказал (строгую) изохронность его колебаний. Все это шло об руку с техническими изобретениями часов с коническим маятником, часов с циклоидальным маятником, с существенным усовершенствованием обычных маятниковых часов, идея которых возникла у Гюйгенса, видимо, вполне самостоятельно. Гюйгенсу не удалось создать хронометра, удовлетворяющего требованиям моряков, но его технические изобретения во всяком случае позволили значительно уточнить измерение времени, столь существенное и для исследования колебаний. Его вклад в теорию колебаний тоже велик помимо указанного выше явления, он открыл явление, названное позже принудительным консонансом . С этими (конструк-  [c.254]

Физически III класс соответствует неустойчивым периодическим и асимптотическим к ним решениям. При с = О периодическое движение для части ветви III а) является колебаниями физического маятника в меридиональной плоскости, проходящей через центр масс, а для части IIIЬ) — вращениями в этой же плоскости. Эти решения сходятся в точке h = 1, которая является верхним неустойчивым положением равновесия. Его неустойчивость может быть строго доказана различными способами [152]. Далее это доказательство будет получено путем явного построения асимптотического решения.  [c.119]

Физический маятник представляет собой тело массы т, вращающееся вокруг горизонтальной оси его момент инерции I и смещение / центра масс относительно оси считаются заданными. Силы сопротивления, пропорциональные скорости, таковы, что при свободных колебаниях маятника отношение предыдущего разма.ха к последующему равно q. Точка подвеса маятника совершает горизонтальные случайные колебания. Ускорение т точки подвеса можно считать белым шумом постоянной интенсивности Определить установившееся среднее квадратическое значение угла отклонения маятника при вынужденных колебаниях, а также среднее число выбросов п угла за уровень, в 2 раза превышающий среднее 1свадратнческое значение в течение времени Т.  [c.447]

Из полученного выражения для чувствительности весов легко усмотреть, каковы пути П0ВЫН1СНИЯ чувствительности весов. Прежде всего для повышения чувствительности следует увеличивать длину коромысла и длину стрелки. Предел, однако, ставится тем, что очень длинное коромысло и очень длинная стрелка будут сами изгибаться, если не делать их достаточно массивными. Увеличение же их массивности, т. е. их веса Р , уменьшает чувствительность весов. Последняя возможность увеличения чувствительности весов — это уменьшение d, расстояния между центром тяжести и точкой подвеса. Для регулировки чувствительности весов в некоторых пределах обычно этим пользуются. На коромысле весов над или под точкой О помещается грузик, положение которого можно изменять при помощи винта. Поднимая грузик, мы приближаем центр тяжести весов к точке О и тем самым увеличиваем чувствительность весов. Однако и в этом направлении нельзя идти слишком далеко, поскольку весы представляют собой физический маятник и уменьшение d увеличивает период колебаний этого маятника, а вместе с тем и то время, которое необходимо, чтобы весы остановились в положении равновесия. Чтобы сократить это время, в чувствительных весах с большим периодом колебаний, не дожидаясь, пока весы установятся в положении равновесия, наблюдают наибольшие отклоне-иил весов при колебаниях. Из этих наблюдений определяют положение равновесия, около которого вссы колеблются.  [c.417]

Физическим маятником называют абсолютно твердое тело, способное соверщать колебания вокруг неподвижной точки, не совпадающей с его центром тяжести (рис. 135). При отклонении маятника из положения равновесия на угол ф возникает вращающий момент М, стремящийся возвратить маятник в положение равновесия. Если центр тяжести маятника находится в точке С на расстоянии I от точки О подвеса (рис. 135), то М = пщ1 s n(( , где т — масса маятника.  [c.171]

Что такое центр колебания?

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см.

Что такое физический и математический маятник?

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести. Момент силы относительно точки О: , и момент инерции: … 7.

Для чего нужен маятник?

Различные виды маятников включают бифилярный маятник, маятник Фуко и торсионный маятник. Бифилярный маятник использовался для регистрации нерегулярного вращения Земли, а также для обнаружения землетрясений. Маятник Фуко, который изобрел французский физик Леон Фуко, используется для демонстрации вращения Земли.

Что называется оборотным маятником?

Оборотный маятник — прибор для экспериментального определения ускорения свободного падения g. Представляет собой физический маятник. Физическим маятником называется любое твердое тело, которое под действием силы тяжести может совершать свободные колебания вокруг неподвижной точки.

Как устроен оборотный маятник?

Представляет собой тело, например массивную пластину (рис.), с двумя трёхгранными ножами, из которых один неподвижен, а другой может перемещаться вдоль прорези на пластине. Острые ребра ножей O1 и О2, помещаемые попеременно на неподвижную опору, служат осями качаний О.

Как найти приведенную длину физического маятника?

здесь l – длина математического маятника. Кроме того, приведенную длину физического маятника можно определить, как расстояние между точкой подвеса и центром качания (расстояние ОК на рисунке 1а). Точка К (рисунок 1), отстоящая от точки подвеса на расстоянии приведенной длины lпр, называется центром качания.

Как найти ускорение свободного падения через период колебаний?

За основу решения задачи примем формулу периода математического маятника: T=2π√lg(1.

Как найти ускорение математического маятника?

T=2π√lg(2.

Как изменяется ускорение свободного падения в зависимости от высоты?

Ускорение свободного падения обратно пропорционально квадрату расстояния. Поэтому если высота будет равна радиусу Земли, то расстояние будет в 2 раза больше от центра Земли, чем для тела на поверхности. В этом случае ускорение свободного падения уменьшится в 4 раза.

Можно ли измерить ускорение свободного падения Если вместо математического маятника?

Нет. В невесомости при «отклонении» его не возникнет сила, возвращающая в положение равновесия, т к нить не натянута и он колебаться не будет. cliffffy4h и 490 других пользователей посчитали ответ полезным!

Можно ли измерить ускорение свободного падения с помощью математического?

С помощью математического маятника можно измерять ускорение свободного падения (в том числе и в невесомости, но с некоторой точностью). Пермод колебаний математического маятника T=2*пи*sqrt(L/g).

Можно ли измерить ускорение свободного падения в условиях невесомости?

Нет, помощью математического маятника в условиях невесомости невозможно измерить ускорение свободного падения. Маятник совершает колебания под действием силы тяжести, которой нет в условиях невесомости. 1jaiz4 и 112 других пользователей посчитали ответ полезным!

Как измерить ускорение свободного падения?

Измерение Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно.

Что такое среднее ускорение?

Определение ускорения Средним ускорением (⟨a⟩) за промежуток времени Δt=t2−t1 называют физическую величину, равную отношению изменения скорости (Δv=v2−v1) в единицу времени: ⟨a⟩=ΔvΔt(2). Единицей измерения ускорения в Международной системе единиц (СИ) является метр на секунду в квадрате: [a]=мс2.

Что называется ускорением в каких единицах измеряется ускорение?

Ускорение – это физическая величина ( a , от лат. acceleratio ), характеризующая быстроту изменения скорости тела. Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2).

Как найти угол между скоростью и ускорением?

1,б). Поэтому угол между скоростью и ускорением может быть равен 0° . – А ведь свободное падение это не только движение вниз, – вмешалась Маша. – Свободным падением можно называть любое движение тела под действием только силы тяжести, например в отсутствие сопротивления воздуха.

Что такое ускорение и для чего нужно знать?

Что такое ускорение и для чего его нужно знать? … Ускорением называют величину, характеризующую изменение скорости в единицу времени. Зная ускорение тела и его начальную скорость, можно найти скорость тела в любой момент времени.

Что такое отрицательное ускорение?

Отрицательное ускорение указывает, что скорость объекта изменяется в отрицательном направлении, что может означать, что он движется медленнее или быстрее. … «Скорость» аналогична скорости, но указывает не только фактическую скорость, но и направление, в котором движется объект, что делает его векторной величиной.