Октаэдр и площадь полной его поверхности: описание, формулы, примеры
Содержание:
Существует несколько способов определить площадь поверхности октаэдра. Он представляет собой один из пяти правильных многоугольников или так называемых Платоновых тел. Имеет восемь одинаковых граней (поверхностей) в виде равносторонних треугольников, к каждой из его вершин прилагается по четыре грани. Рассмотрим, что собой представляет тело, где встречается в природе, как вычисляется его площадь и объём.
Что такое октаэдр
Свойства октаэдра
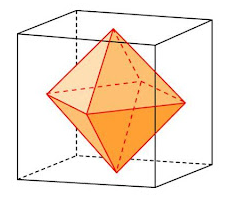
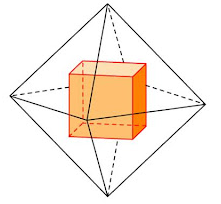
- В тело вписывается куб, вершины которого находятся в центрах граней куба.
- Симметрия куба и вписанного (описанного) октаэдра совпадают.
- Двойственен кубу.
- Является полным усечением тетраэдра.
- Имеет равные ребра и диагонали.
- Состоит из равносторонних треугольников.
- Диагонали тела взаимоперпендикулярны, в точке пересечения делятся на равные отрезки.
- Октаэдр симметричен, причём 3 оси пролегают через противоположные вершины, 6 – через центры ребер.
- Центр симметрии тела расположен в точке пересечения диагоналей.
- Ребра равны по длине, поверхности – по площади.
Математические характеристики тела
Как вычислить площадь поверхности октаэдра
Площадь октаэдра равна сумме площадей составляющих его треугольников:
Здесь Sтреуг – площадь треугольника.
После подстановки значения получится требуемый результат.
Если известна длина ребра, придётся вычислить площадь треугольников.
Подставляем значение в первое выражение:
Упрощаем: после сокращения дроби на четыре получается формула площади поверхности октаэдра:
2. S = 8 * Sтреуг = 2 sqrt <3>a^2.
Существует ещё один способ проведения вычислений. Он менее точный чем предыдущие, однако позволяет обойтись без калькулятора. При приблизительном подсчёте 2 sqrt <3>равняется 3,464 или 3,46.
Здесь a – длина стороны треугольника (равны).
Для примера, имеется фигура октаэдр с длиной стороны 5 см.
S=2sqrt <3>a^2=2*sqrt <3>*5^2=2*sqrt <3>*25=50sqrt <3>approx 86,6 см.
Как вычислить объём правильного октаэдра
Объём показывает размер внутреннего пространства геометрического тела. Объем правильного октаэдра вычисляется, если знаете длину ребра геометрического тела, по формуле:
После проведения приблизительных расчётов frac<sqrt 2> <3>approx 0,47 формула принимает следующий вид :
Рассчитаем двумя методами на примере правильного многоугольника с гранью, равной 5 см:
V= 0,47 * a^3 = 0,47*125 approx 58,93
Значения совпали, во втором случае нужно выполнять гораздо меньше операций. Подходит он только, если не требуется исключительная точность – при округлении до 4-5 знаков после запятой точность снизится.
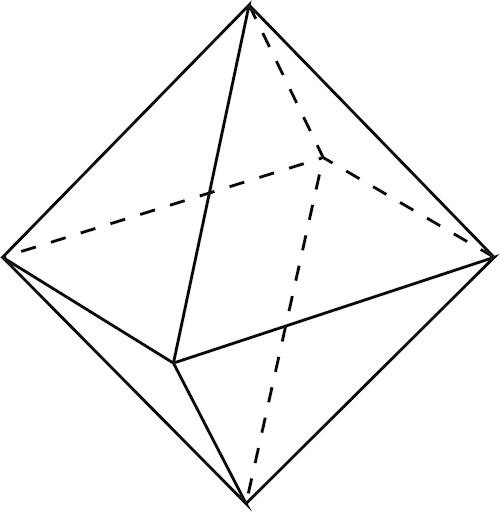
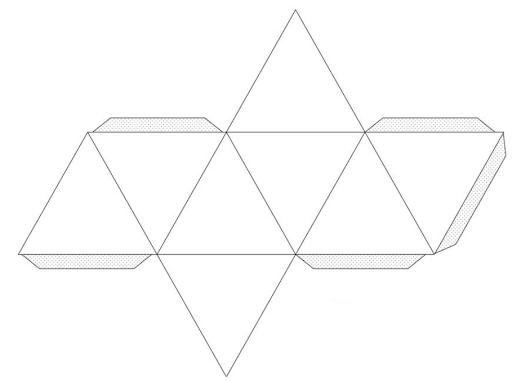
Развёртка
Октаэдр, как большинство гомерических тел, имеет развёртку поверхности – это плоская фигура, полученная путём совмещения поверхности модели с одной плоскостью без пересечения либо наложения граней друг на друга.
Рисунок развёртки октаэдра.
В природе насчитывается 11 разновидностей развёртки октаэдра, позволяющих создать его модель из бумаги или картона. Наиболее распространённая выглядит как восемь одинаковых треугольников. Шесть из них размещено в ряд, к третьему и четвёртому основаниям прилегает ещё по одному, их вершины направлены в противоположные стороны.
Октаэдр.
Октаэдр — один из 5-ти выпуклых правильных многогранников — Платоновых тел.
У октаэдра 8 треугольных граней, 12 рёбер, 6 вершин, к каждой его вершине сходятся 4 ребра.
На примере октаэдра легко проверить формулу Эйлера 6в+8г-12р=2. В каждой из вершин октаэдра сходятся 4 треугольника, т.о., сумма плоских углов у вершины октаэдра равна 240°. Из понятия правильного многогранника делаем вывод, что каждое ребра октаэдра имеет одинаковую длину, а грань — одинаковую площадь.
Обозначим длину ребра октаэдра как а, значит площадь полной поверхности октаэдра (S) и объём октаэдра (V) найдем из таких формул:
Радиус описанной сферы около октаэдра:
Радиус вписанной сферы около октаэдра:
Сумма длин всех ребер равна 24а.
Двугранный угол: α=2ϕ≈109,47°, где 
Свойства октаэдра.
Октаэдр легко вписывается в тетраэдр, при этом 4 из 8-ми граней октаэдра совместятся с 4-мя гранями тетраэдра, каждая из 6-ти вершин октаэдра совместится с центрами 6-ти ребер тетраэдра.
Октаэдр легко вписывается в куб (гексаэдр), при этом каждая из 6-ти вершин октаэдра совместится с центрами 6-ти граней куба.
В октаэдр легко вписать куб, при этом каждая из 8-ми вершин куба будут располагаться в центрах 8-ми граней октаэдра.
У правильного октаэдра есть симметрия Oh, которая совпадает с симметрией куба.
Развёртка октаэдра.
Симметрия октаэдра.
3 из девяти осей симметрии октаэдра проходят сквозь противолежащие
вершины, 6 — квозь середины ребер.
Центр симметрии октаэдра — точка пересечения осей симметрии октаэдра.
3 из девяти плоскостей симметрии тетраэдра проходят сквозь все 4 вершины октаэдра, которые лежат в одной плоскости.
6 плоскостей симметрии проходят через 2 вершины, которые не принадлежат одной грани, и середины противолежащих ребер.
Октаэдр
Древние греки дали многограннику имя по числу граней. «Окто» означает восемь, «хедра» — означает грань (октаэдр – восьмигранник).
Поэтому на вопрос — «что такое октаэдр?», можно дать следующее определение: » Октаэдр это геометрическое тело из восьми граней, каждая их которых — правильный треугольник «.
Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .
Октаэдр имеет следующие характеристики:
- Тип грани – правильный треугольник;
- Число сторон у грани – 3;
- Общее число граней – 8;
- Число рёбер, примыкающих к вершине – 4;
- Общее число вершин – 6;
- Общее число рёбер – 12;
Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.
Октаэдр имеет центр симметрии — центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
Математические характеристики октаэдра
Октаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы октаэдра определяется по формуле:
, где a — длина стороны.
Сфера может быть вписана внутрь октаэдра.
Радиус вписанной сферы октаэдра определяется по формуле:
Площадь поверхности октаэдра
Для наглядности, площадь поверхности октаэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон октаэдра (это площадь правильного треугольника) умноженной на 8. Либо воспользоваться формулой:
Объем октаэдра определяется по следующей формуле:
Октаэдр можно представить в виде двух правильных пирамид с четырехугольным основанием, соединенных друг с другом через это основание.
Вариант развертки
Октаэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка — единая деталь с линиями сгибов.
Древнегреческий философ Платон ассоциировал октаэдр с «земным» элементом воздух, поэтому для построения модели этого правильного многогранника мы выбрали серый цвет.
Заметим, что это не единственный вариант развертки.
Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
— если Вы предполагаете распечатать на цветном принтере — цветная развертка
— если Вы предполагаете использовать для сборки цветной картон — развертка
Классический вариант раскраски предполагает окраску октаэдра четырьмя различными цветами, причем таким образом, что каждая грань имеет свой цвет отличный от соседней и только противоположные не соприкасающиеся друг с другом грани окрашиваются в одинаковые цвета.
Вариант окраски представлен на рисунке. Вы можете скачать развертку с соответствующей раскраской граней.
Видео. Октаэдр из набора «Волшебные грани»
Вы можете изготовить модель октаэдра воспользовавшись деталями для сборки из набора «Волшебные грани».
Сборка многогранника из набора:
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
Подробная сборка от Алексея Жигулева (youtube-канал PRO)
вращение готового многогранника:
Видео. Вращение правильных многогранников
http://www.calc.ru/Oktaedr.html
http://mnogogranniki.ru/oktaedr.html
вот так
Правильный октаэдр состоит из 8 равносторонних треугольников.
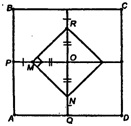
ABCD — одна из плоскостей симметрии. Выполним построение для верхней половины октаэдра, тогда построение для нижней части есть зеркальное отображение построения в верхней части. Совместим половины октаэдра и получим полное построение.
ABCD — квадрат, все боковые грани равные между собой равносторонние треугольники. Возьмем грани: ΔАВЕ и ΔADE. Центром равностороннего треугольника является точка пересечения медиан, высот и биссектрис.
Пусть L и К — такие точки для граней ΔАВЕ и ΔADE (соответственно). Построим проекции L и К на ABCD. Пусть это будут точки М и N (соответственно). Аналогично простроим проекции двух других центров боковых граней на ABCD.
Итак, мы построили многогранник, докажем, что он — прямо угольный параллелепипед.
Центры противоположных боковых граней лежат в плоскостях, проходящих через середины противоположных сторон квадрата ABCD и вершину Е. Эти плоскости взаимно перпендикулярны. Т.о. четырехугольники, являющиеся основаниями полученного многогранника, имеют взаимно перпендикулярные диагонали, т.е. они или ромбы, или квадраты.
Т.к. грани АВЕ и AQE одинаково наклонены к плоскости основания, то
ΔPLN=ΔQKN (прямоугольные, равны по 2-му признаку).
Из равенства треугольников имеем: PM=NQ.
ОМ = ON. Все четыре прямоугольных треугольника равны, следовательно, прямой. Отсюда имеем, что основания — квадраты.
Боковые грани многогранника также прямоугольники LK || MN).
Докажем теперь, что полученный многогранник — половина куба, т.е.
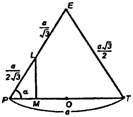
Пусть сторона основания пирамиды — а.
Построим сечение верхней половины октаэдра плоскостью, проходящей через вершину Е и середины противоположных сторон квадрата.
Из ΔВРЕ:
По т. косинусов из ΔРЕТ имеем:
Совместим зеркальное построение для нижней половины и получим куб с ребром
Вывод: центры граней правильного октаэдра есть вершины куба.
-
Вы здесь:
- Главная
- Октаэдр
Октаэдр
Древние греки дали многограннику имя по числу граней. «Окто» означает восемь, «хедра» — означает грань (октаэдр – восьмигранник).
Поэтому на вопрос — «что такое октаэдр?», можно дать следующее определение: «Октаэдр это геометрическое тело из восьми граней, каждая их которых — правильный треугольник«.
Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел.
Октаэдр имеет следующие характеристики:
- Тип грани – правильный треугольник;
- Число сторон у грани – 3;
- Общее число граней – 8;
- Число рёбер, примыкающих к вершине – 4;
- Общее число вершин – 6;
- Общее число рёбер – 12;
Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.
Октаэдр имеет центр симметрии — центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
Математические характеристики октаэдра
Октаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы октаэдра определяется по формуле:
, где a — длина стороны.
Сфера может быть вписана внутрь октаэдра.
Радиус вписанной сферы октаэдра определяется по формуле:
Площадь поверхности октаэдра
Для наглядности, площадь поверхности октаэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон октаэдра (это площадь правильного треугольника) умноженной на 8. Либо воспользоваться формулой:
Объем октаэдра определяется по следующей формуле:
Октаэдр можно представить в виде двух правильных пирамид с четырехугольным основанием, соединенных друг с другом через это основание.
Популярное
Многогранный очаг
Для первобытного человека когда-то костер стал новой формой общественной жизни. Ночь перестала быть неотвратимым черным провалом и ценность огня заставила…
Домик для птиц
Студией Артемия Лебедева (https://www.artlebedev.ru/) была предложена форма скворечника в виде многогранника.
В качестве геометрической…
Звезда надежды
Звезда — это образ божественной идеи, божественной воли, согласно которой возник и начал вращаться в Пространстве и жить наш Свет, Мир.
Естественные многогранники
В естественной среде правильные многогранники можно встретить в виде кристаллов (минералов).
Форму тетраэдра передает сурьмянистый сернокислый натрий.
Новоталицкая школа
Под руководством учителя математики Тимофеевой Татьяны Юрьевны ребята работали над проектом «Удивительный мир многогранников». Делали свои развертки и использовали развертки из…
Тема
занятия « Октаэдр»
Цель: отработка
навыков решения задач по теме «Октаэдр»
Задачи: 1.
Вспомнить
определение октаэдра и его свойства.
2.
Решение
задач с использованием формул.
План урока
I.
Организационный момент
II. Проверка
домашнего задания
III. Повторение
знаний по теме «Октаэдр»
IV. Решение
задач.
V. Подведение
итогов
VI. Рефлексия
Ход урока.
I.
Приветствие.
Проверка присутствующих.
II. Вопросы по домашнему заданию, если есть.
III. Продолжаем изучать виды правильных
многогранников. На очереди у нас октаэдр. Какую фигуру мы называем октаэдром?
(Октаэдр — правильный многогранник, поверхность которого состоит из восьми
правильных треугольников). Октаэдр визуально
можно представить в виде двух склеенных основаниями четырёхугольных правильных
пирамид.
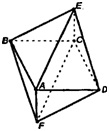
Рис. 1 — Правильный октаэдр
Свойства:
1. Состоит из 8 равносторонних треугольников, в каждой из вершин
которого сходится равное количество граней, а именно 4.
1.
Так как все его грани равны, равны и его межгранные углы, каждый из которых
равняется 60, а сумма плоских углов любой из вершин составляет, таким образом,
240.
Октаэдр тесно связан с кубом, по свойству взаимности: центры граней куба являются вершинами
правильного октаэдра и наоборот. Если
соединять отрезками центры соседних граней куба, то эти отрезки станут рёбрами октаэдра; если проделать ту же
операцию с октаэдром, получится куб. Исходя из этого, понятно, что число вершин
октаэдра равно числу граней куба, и наоборот; более того, количества ребер у
них совпадают.
Изобразим октаэдр
в кубе. Учитель у доски, ребята в тетради.
Формулы которые
нужно знать:
Объем октаэдра — V=,
Площадь
поверхности октаэдра — S=2a2,
Радиус описанной
сферы — r=,
Радиус вписанной
сферы — R=.
IV.
Что мы можем сказать про радиус R описанной
сферы правильного октаэдра?
Ответ: он будет равен
радиуса описанной сферы гексаэдра, так как октаэдр и гексаэдр двойственные
фигуры.
№2 Найдите
радиус r, вписанной сферы правильного октаэдра, если его ребро
равно а.
Решение:
Точка О является центром
этой сферы. Радиус этой сферы равен длине отрезка OK, проведённого из
точки О к центру K грани ADE.
TO=a.
Найдем OK.
Рассмотрим треугольник OET:
Рассмотрим треугольник TKO:
Ответ: .
№3 Найдите площадь
поверхности правильного октаэдра, если радиус описанной сферы равен R .
Решение:
OA = OB = R
Рассмотрим треугольник AEL:
AB = R
В треугольнике AEL:
EL = 
R
Площадь одной грани октаэдра равна:
Sграни =AB*EL=
R
*
R
=
R2
Sповерх. = 8Sграни =8*R2
=
4 R2
Ответ: Sповерх. =
4 R2.
Задача. По ребру a октаэдра
найти его объем.
Решение. Разобьём октаэдр
на 2 правильные четырёхугольные пирамиды. Площадь основания пирамиды S=a2.Высота
пирамиды О1О проходит через центр окружности, описанной около
квадрата, лежащего в основании. Значит, АО=
По теореме Пифагора: О1О=
Объём октаэдра равен
удвоенному объёму пирамиды
Ответ:
№5. Найдите угол
между двумя рёбрами правильного октаэдра, которые имеют общую вершину, но не
принадлежат одной грани.
Решение.
ABCD —
квадрат, значит BAD
=90º
Рассмотрим
пирамиду ЕABCD,
она правильная, отсюда следует, что О — проекция точки Е на АВС
совпадает с центром ABCD,
значит .
Треугольник АОЕ
— прямоугольный.
По теореме
Пифагора найдём ОЕ, ОЕ=АО, получаем
ЕАО= АЕО=45º.
АЕС= 2* АЕО=90º
Ответ: 90º
Домашняя работа.
Задача 1. Найдите двугранные углы
октаэдра.
Решение. Проведём ось , которая
перпендикулярна плоскости АВСD.
Так как верхняя часть октаэдра —
правильная пирамида, то О — центр окружности, вписанной в квадрат АВСD.
Обозначим ребро октаэдра х. Тогда, если ОК
┴DС,
то ОК=r=
Проведём SK и
S1K , тогда по теореме о трех перпендикулярах
имеем SK┴ DS и
S1K
┴DS
Так что —
линейный угол искомого двугранного угла.
Далее из прямоугольного треугольника SOK
по теореме Пифагора получаем: .
Так
что SS1=2OS=
Из треугольника SOK ,
SK=; из треугольника S1OK ,
S1K=
По теореме косинусов в треугольнике:
То есть,
Так что, .
Тогда
Остальные двугранные углы равны
найденному.
Ответ:
Задача 2. (Задача для рассуждения).
Можно ли вписать октаэдр в куб так, чтобы вершины октаэдра
находились на рёбрах куба?
Решение
Можно. На рисунке изображён восьмигранник, вписанный куб с ребром длины 4; вершины
восьмигранника делят рёбра куба в отношении 1:3. Квадрат длины каждого из
рёбер восьмигранника равен 18
(либо 3²+3², либо 4²+1²+1²), то есть все его рёбра равны.
Посмотрите на следующие пять многогранников.
Они являются правильными, так как у каждого из них все
грани – одинаковые правильные многоугольники, в каждой вершине одного
многоугольника сходится одно и то же число рёбер, а соседние грани сходятся под
равными углами.
Правильный тетраэдр –
многогранник, составленный из 4 правильных треугольников.
Куб – многогранник, составленный
из 6 квадратов.
Правильный октаэдр –
многогранник, составленный из 8 правильных треугольников.
Правильный додекаэдр –
многогранник, составленный из 12 правильных пятиугольников.
Правильный икосаэдр –
многогранник, составленный из 20 правильных треугольников.
Давайте составим таблицу, в которую запишем число вершин, рёбер и
граней у каждого многогранника. Затем для каждого многогранника найдём число,
равное числу вершин плюс число граней минус число рёбер.
Тетраэдр. У него 4 вершины, 4 грани и 6
рёбер.
Куб. У него 8 вершин, 6 граней и 12
рёбер.
Октаэдр. У этого многогранника 6
вершин, 8 граней и 12 рёбер.
Додекаэдр. У него 20 вершин, 12
граней и 30 рёбер.
Икосаэдр. У этого многогранника 12
вершин, 20 граней и 30 рёбер.
Заполним последний столбец таблицы. Найдём число, равное числу
вершин плюс число граней минус число рёбер.
Обратите внимание, что в последнем столбце таблицы для всех
многогранников получился один и тот же результат – два.
Число вершин, граней и рёбер связано таким соотношением не только у
правильных, но и у всех других многогранников. Вы можете проверить это для
любых взятых наугад многогранников.
Это соотношение называется формулой Эйлера.
Его доказал математик Леонард Эйлер. Этот величайший учёный
родился в Швейцарии, но почти полжизни провёл в России. Он внёс огромный вклад
в становление русской науки. В 1750 году Леонард Эйлер установил связь между
числом вершин, рёбер и граней для многогранников. Это заложило фундамент нового
раздела математики – топологии.
Рассмотрим ещё одну особенность правильных многогранников.
Тетраэдр. Если центры его граней
считать вершинами нового многогранника, то мы снова получим тетраэдр.
Теперь давайте сразу возьмём куб и октаэдр. Заметим,
что если центры граней куба считать вершинами нового многогранника, то получим
октаэдр, а если центры граней октаэдра считать вершинами нового многогранника,
то получим куб.
Аналогично для додекаэдра и икосаэдра. Если центры
граней додекаэдра считать вершинами нового многогранника, то получим икосаэдр,
а если центры граней икосаэдра считать вершинами нового многогранника, то
получим додекаэдр.
История правильных многогранников уходит в глубокую древность.
Совершенные формы и математические закономерности, присущие правильным
многогранникам, являлись причиной того, что им приписывались различные
магические свойства. Все 5 геометрических фигур (тетраэдр, куб, октаэдр,
додекаэдр и икосаэдр) издавна были спутниками волшебников и звездочётов.
Сейчас вы видите развёртки эти многогранников.
Если вы потрудитесь над их изучением, то сможете изготовить модели
многогранников из бумаги.
Если сделать такие модели из цветной бумаги, то у вас получатся
геометрические игрушки, которые вы можете использовать как украшение для новогодней
ёлки.