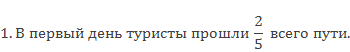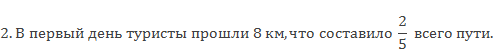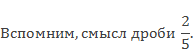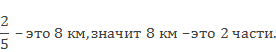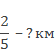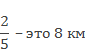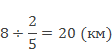Как найти целую часть числа видео

Правильная и неправильная дробь

Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.

Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.

Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.

Дроби

Дроби вида $frac{n}{m}$  называют «обыкновенные дроби». В дроби $frac{n}{m}$ число над чертой называют числителем дроби, а число под чертой – знаменателем дроби.

Знаменатель показывает, на сколько долей делят, а числитель — сколько таких долей взято.

Таким образом, если нам нужно обозначить не один «кусочек» числа, а больше, мы просто пишем в верхней части дроби не единицу, а другое число, например, так:

Дроби нужно уметь читать правильно: числитель читается как количественное числительное женского рода (одна, две и т.д.), а знаменатель как порядковое числительное (вторая, пятая) и согласуется с первым числительным.Например: $frac{1}{2}$  — одна вторая, $frac{2}{5}$ — две пятых,  $frac{6}{11}$  — шесть одиннадцатых.

На рисунке 6 изображён отрезок АВ, его длина 10 см, то есть 1 дм. Длина отрезка АС будет 1 см.

А какую долю составит сантиметр от метра?

Показать ответ

Скрыть

$frac{1}{100}$ 

А грамм от килограмма?

Показать ответ

Скрыть

$frac{1}{1000}$ 

Видео

Нахождение части от целого (дроби от числа)

Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.

Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.

Вычитание дробей

Алгоритм действий при вычитании двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Нахождение целого числа по дроби

Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.

А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.

Например, если  длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.

Требуется найти длину всей линейки по дроби . Известно, что  длины всей линейки составляют 6 см.

Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби  это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби  это число 2.

Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:

Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2

6 см : 2 = 3 см

Итак, мы нашли длину одной части. Одна часть из пяти или  длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5

3 см × 5 = 15

Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.

Видно, что пять частей из пяти или  составляют пятнадцать сантиметров.

Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:

Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.

Пример 2. Число 20 это  от всего числа. Найдите это число.

Знаменатель дроби  показывает, что число, которое мы должны найти, разделено на пять частей. Если  этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти  (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби

20 : 4 = 5

Мы нашли  от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби

5 × 5 = 25

Мы нашли  от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.

Пример 3. Десять минут это  времени приготовления каши. Найдите общее время приготовления каши.

Знаменатель дроби  показывает, что общее время приготовления каши разделено на три части. Если  времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти  времени приготовления. Для этого 10 нужно разделить на числитель дроби

10 мин : 2 = 5 мин

Мы нашли  времени приготовления каши.  времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби

5 мин × 3 = 15 мин

Мы нашли  времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.

Пример 4.     массы мешка цемента составляет 30 кг. Найти общую массу мешка.

Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти массы мешка. Для этого 30 надо разделить на числитель дроби .

30кг : 2 = 15кг

Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби

15кг × 4 = 60кг

Мы нашли массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.

Как перевести десятичную дробь в обыкновенную или смешанную

Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:

1. Записать дробь в виде десятичная дробь1
2. Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
3. Найти наибольший общий делитель и сократить дробь.

Например, переведем 0.36 в обыкновенную дробь:

1. Записываем дробь в виде: 0.361
2. Умножаем на 10 два раза, получим 36100
3. Сокращаем дробь 36100 = 925

Применение нахождения дроби от числа для решения задач

В начале урока мы уже разобрали пример с тортом, сейчас посмотрим на другие примеры.

Задача 1

Остап зарабатывает 40 000 рублей в месяц.

Из них (mathbf{frac{1}{4}}) это подработка.

Сколько рублей Остапу приносит подработка?

Решение:

В данной случае числом будет являться сумма заработка за месяц — 40 000

Ну а дробью, очевидно, будет (mathbf{frac{1}{4}}).

Тогда, чтобы найти прибыль от подработки, надо просто умножить дробь на число.

(mathbf{40000cdotfrac{1}{4}=frac{40000}{4}=10000})

Ответ: 10 000 рублей.

Теперь рассмотрим что-нибудь посложнее.

Задача 2

Порфирий живет в комнате площадью 18 квадратных метров.

3 кровати занимают (mathbf{frac{1}{3}}) площади комнаты.

Какую площадь занимает одна кровать?

Решение:

Сначала найдем, какую площадь занимают 3 кровати, затем разделим это число на 3, чтобы получить площадь одной кровати.

1) (mathbf{18cdotfrac{1}{3}=frac{18}{3}=6}) (квадратных метров) занимают 3 кровати

2) (mathbf{6div3=2}) (квадратных метра) занимает одна кровать

Ответ: 2 квадратных метра.

Теперь посмотрим, как в задачах применяются проценты.

Задача 3

Пересвет работает на заводе и производит 100 деталей в день.

Начальник Елисей пообещал Пересвету выдать премию, если он будет делать на 20% деталей больше.

Сколько деталей в день должен делать Пересвет, чтобы получить премию?

Решение:

Для начала надо понять, на сколько в количественном измерении больше деталей нужно выпустить Пересвету, чтобы получить премию.

Для этого домножим текущее количество деталей на процент или долю, учитывая, что 20% — это 20 частей из 100, или иначе 0,20, и получим искомую прибавку.

1) (mathbf{20%=20div100=0.2})

2) (mathbf{100cdot0.2=20}) (деталей)- то, насколько больше деталей нужно производить

Теперь, чтобы найти общее количество деталей, надо прибавить эту прибавку к тому, что Пересвет производит уже сейчас.

3) (mathbf{100+20=120}) (деталей) в день нужно производить для получения премии

Ответ: 120 деталей.

В некоторых задачах нужно несколько раз применять нахождение процентов от числа.

Задача 4

Глубина реки в начале мая была равна 10 метрам, к началу июня она обмелела на 10%, а к началу июля еще на 15% относительно показателей начала июня. Вычислите, какая глубина реки была в начале июля.

Решение:

Исходное число- 10 метров, дробь задана в виде процентов.

Первым действием нужно будет найти глубину реки в начале июня.

Здесь можно пойти двумя разными путями:

I. Посчитаем, на сколько метров опустился уровень воды, а затем вычтем это из исходных показателей.

0) (mathbf{10%=10div100=0.1})

1) (mathbf{10-10cdot0.1=10-1=9}) (метров)- глубина реки в начале июня

II. Можно вместо того, чтобы считать разницу и вычитать ее, посчитать сколько процентов останется и найти сразу именно эту часть от исходного числа.

Учитывая, что всего у нас 100%, да если глубина уменьшилась на 10%, то осталось 90%.

0) (mathbf{100-10=90}) (процентов) останется

1) (mathbf{90%=90div100=0.9})

2) (mathbf{10cdot0.9=9}) (метров)- глубина реки в начале июня

Как мы видим, эти два подхода дают одинаковый результат.

Поэтому вы можете выбирать любой из них в зависимости от задачи и ваших предпочтений.

Таким образом, мы посчитали глубину в начале июня. Теперь нужно понять, какая будет глубина в начале июля, когда глубина уменьшится еще на 15 процентов.

Используем в этом случае второй способ.

3) (mathbf{100-15=85}) (процентов) останется в июле от уровня июня

4) (mathbf{85%=85div100=0.85})

5) (mathbf{0.85cdot9=7.65}) (метров) составит глубина реки в начале июля

Ответ: 7.65 метра.

Пройти тест Закрыть тест

Пройти тест и получить оценку можно после входа или регистрации Вход Регистрация

Нахождение числа по значению дроби

Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:

m = m : a / b

 Пример:

Один ряд кинозала вмещает 20 кресел, что составляет2 / 5

от всей вместимости зала. Определите, сколько всего посадочных мест в зале.

 Решение

Общее количество кресел равняется:

20 :2 / 5

= 20 ⋅5 / 2

=20 ⋅ 5 / 2

= 50

Теги

Обращение числа с целой и дробной частями в неправильную дробь

Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Например, .

.

Вообще, чтобы записать число в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к произведению прибавить числитель дробной части. Полученная сумма будет числителем дроби, а знаменателем будет знаменатель дробной части.

Видео

Неправильные дроби. Выделение целой части

Если числитель меньше знаменателя, такая дробь называется правильной. В противном случае (т.е. когда числитель больше или хотя бы равен знаменателю) дробь называется неправильной, и в ней можно выделить целую часть.

Целая часть записывается крупным числом спереди перед дробью и выглядит так (отмечена красным):

Чтобы выделить целую часть в неправильной дроби, надо выполнить три простых шага:

1. Найдите, сколько раз знаменатель помещается в числителе. Другими словами, найдите максимальное целое число, которое при умножении на знаменатель все равно будет меньше числителя (в крайнем случае — равно). Это число и будет целой частью, поэтому записываем его спереди;
2. Умножьте знаменатель на целую часть, найденную в предыдущем шаге, а результат вычтите из числителя. Полученный «огрызок» называется остатком от деления, он всегда будет положительным (в крайнем случае — ноль). Записываем его в числитель новой дроби;
3. Знаменатель переписываем без изменений.

Ну как, сложно? На первый взгляд, может быть и сложно. Но стоит немного потренироваться — и вы будете делать это почти устно. А пока взгляните на примеры:

Задача. Выделите целую часть в указанных дробях:

Во всех примерах целая часть выделена красным цветом, а остаток от деления — зеленым.

Обратите внимание на последнюю дробь, где остаток от деления оказался равным нулю. Получается, что числитель полностью разделился на знаменатель. Это вполне логично, ведь 24 : 6 = 4 — суровый факт из таблицы умножения.

Если все делать правильно, числитель новой дроби обязательно будет меньше знаменателя, т.е. дробь станет правильной. Отмечу также, что лучше выделять целую часть в самом конце задачи, перед записью ответа. Иначе можно значительно усложнить вычисления.

Дробь означает деление

Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.

Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:

Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:

Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Основное свойство дроби

Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.

Например, рассмотрим дробь .  Умножим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь .  Если верить основному свойству дроби, то дроби   и  равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.

Поэтому между дробями и  можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.

Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь . Если верить основному свойству дроби, то дроби  и равны между собой. Так ли это? Давайте проверим,  нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь  (четыре куска из восьми), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.

Поэтому между дробями  и  можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.

Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Как выделить целую часть из неправильной дроби

Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления будет целой частью числа, остаток — числителем, а делитель — знаменателем. Например, .

Теги