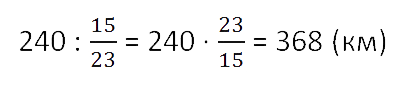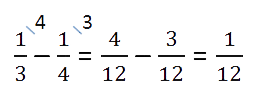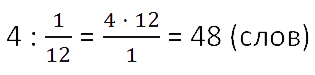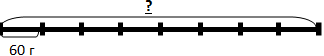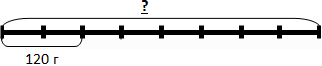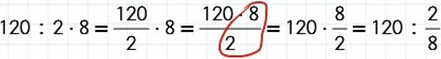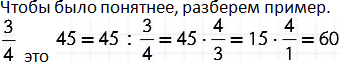Как найти целое число между дробями

Если известно сколько составляет часть от целого, то по известной части можно «восстановить»
целое.

Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).

Запомните!

Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.

Пример. Рассмотрим задачу.

Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?

Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет

часть пути.

240 : 15 = 16 (км)

Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью

Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:

16 · 23 = 368 (км)

Кратко запись решения такой задачи можно сделать следующим образом.

Ответ: поезд должен пройти 368 км.

Сложные задачи на нахождение числа по его части

Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.

Рассмотрим задачу.

При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?

Решение. Как обычно подчеркнём в условии задачи все важные данные.

Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.

Такую часть всех слов составляют 4 слова.

Итак, 4 слова — это

от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь

Ответ: всего 48 слов надо было выучить к диктанту.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Как найти целое, если известна его часть?

Например, 3/8 торта весит 300 грамм. Как узнать, сколько весит весь торт?

Нахождение целого по его части

Если у нас известна какая-либо часть (доля) от целого, то можно всегда «восстановить» целое.

При этом нужно помнить, что часть от целого числа может быть выражена либо в виде дроби (обычно обыкновенной), либо в виде процента.

Рассмотрим оба случая.

1) Часть числа — это обыкновенная дробь.

В этом случае для нахождения целого нужно число, соответствующее данной части, разделить на дробь.

Для того, чтобы число разделить на обыкновенную дробь, нужно умножить его на знаменатель дроби и разделить на числитель.

Пример 1:

Специалист отдела кадров получил премию 2000 рублей, что составляет 1/15 часть от его месячной зарплаты. Требуется узнать, сколько составляет зарплата у данного сотрудника.

Решение:

Зарплата = 2000 / (1/15) = 2000 * 15 = 30000 рублей.

Значит, сотрудник получает зарплату 30000 рублей в месяц.

Пример 2:

Было засеяно пшеницей 12 гектаров поля, что составляет 3/5 от его общей площади. Нужно посчитать, чему равна площадь поля.

Решение:

Площадь поля = 12 / (3/5) = 12 * (5/3) = 20 гектаров.

2) Часть числа представлена в процентах.

Если доля от целого является процентом, а не обыкновенной дробью, то подобные задачи можно решать с помощью составления пропорции.

Пример:

Цена апельсинов со скидкой равна 120 рублей, величина скидки равна 20%. Нужно узнать, сколько стоили апельсины изначально.

Решение:

Так как скидка = 20%, то от исходной цены апельсинов осталось 100% — 20% = 80%.

80% — 120 рублей.

100% — x рублей.

0,8x = 120 рублей.

x = 120 / 0,8 = 150 рублей.

Таким образом, до скидки апельсины стоили 150 рублей.

модератор выбрал этот ответ лучшим

Алиса в Стране
[364K]

3 года назад

Часть числа может быть выражена в виде десятичной или простой дроби, в виде процентов, что по сути то же самое, что десятичная дробь, всем понятно, что 0,1 это 10%, например.

Если известна часть числа в абсолютном выражении и то, какую часть она составляет от целого, то нет ничего проще, чем определить это целое.

Допустим, 20 яблок это 25 % от всех яблок, надо 20 поделить на 0,25, чтобы определить общее количество яблок, 20/0,25 = 80, вот так мы нашли целое по его части.

Еще один пример разберем, 12 мест в автобусе это 1/3 от всех мест в автобусе, как найти общее число всех мест в автобусе, делим 12 на 1/3, то есть по правилам деления на дробь умножаем 12 на 3, получается 36.

Ну и в итоге решим задачку автора из его вопроса:

300 граммов делим на 3/8 получаем 800 граммов.

smile6008
[28.5K]

3 года назад

В математике и жизни бывают случаи, когда необходимо найти число, зная только его часть. Для этого можно использовать различные способы расчётов, использовать дроби , но удобнее всего рассчитать в процентном соотношении.

Итак мы знаем, что 300 грамм составляют 3/8 торта. Нужно узнать сколько же весит торт целиком. Переводим в процентное соотношение, поделим 8 на 3, получим 0,26666 в процентах — это 26,6%. Теперь найдём 100 %, для этого посчитаем пропорцию. 26,6% = 300 ;100 % = x. X = 26,6*300/100.Получаем 799,8 округляем по закону округление в большую сторону, получаем 800 гр весит весь торт.

[пользователь заблокирован]
[3.3K]

5 лет назад

Для лучшего понимания процесса можно делать так (хотя математически это нерационально).

Узнайте чему равна ОДНА часть. Для этого заданное число разделите на количество заданных частей в дроби, их 3.

300 делим на 3, получаем 300/3=100

Это одна восьмая часть.

Целое — это восемь восьмых, потому предыдущий результат умножаем на 8, получаем 100*8=800

Если же дробь задана, как десятичная, т.е. 0.375, то представляем её, как натуральную (это 375/1000) и поступаем точно так же.

Узнаём, чему равна одна тысячная часть 300/375=0.8

Ну, а далее узнаём чему равно само целое 0.8*1000=800

Эл Лепсоид
[139K]

5 лет назад

В общем случае, конечно, следует прибегнуть к составлению пропорции, поставив в соответствие к имеющейся части ее вес, а к целому (т.е. единице) — неизвестную «х». Но, поскольку, у нас во второй части пропорции стоит «1», то решить задачу можно значительно проще: просто разделить на величину известной части. В нашем случае получается: 300/(3/8) = 300*8/3 = 800.

Таким образом, весь торт будет весить 800 грамм.

СТА 1106
[295K]

3 года назад

3/8- означает, что на три части из восьми приходится 300 грамм. Требуется узнать вес целого, в данном случае, торта. Для этого нужно узнать, что приходится на одну часть. Можно решить методом пропорции, мой любимый метод. Итак:

3 части — 300 грамм.

8 частей — Х грамм.

Решаем пропорцию.

8 × 300 ÷ 3 = 800 грамм.

Общий алгоритм решения следующий. Зная, сколько приходится на долю от целого, нужно определить, сколько приходится на единицу измерения ( грамм, килограмм, метр, час и т.д). Затем зная это, просто умножает на все количество долей, на которое поделён данный предмет. В данном случае- это восемь частей.

Второй вариант решения задачи.

300 : 3 × 8 = 800 грамм.

Ответ. 800 грамм , в обоих вариантах таз решения задачи.

Проще не бывает. Надо число означающее часть разделить на количество этих частей и полученный результат умножить на целое. Получим число выражающее целую часть.

Пример:

Дано 4/15 равняется 40. Делим сорок на четыре и умножаем на 15. Получаем сумму в 150 — это и будет целое.

Или 2/10 равняется 40. Делим сорок на два, получаем двадцать. Умножаем двадцать на десять, получаем двести. Целое число двести.

Master-Margarita
[135K]

5 лет назад

Чтобы узнать, сколько весит торт в данном случае, надо провести следующие арифметический действия: (300*8)/3=800 грамм.

То есть, чтобы найти целое нужно часть умножить на знаменатель дроби и разделить на числитель дроби. В данном случае числитель — 3, а знаменатель — 8.

Рина19
[31.2K]

5 лет назад

Сначала найдём чем у равна 1 часть из всех имеющихся. А затем умножим её на общее число всех частей.

На данном примере.

Известно, что 3/8 торта весит 300 г, т.е. 3 части из 8 на которые был нарезан торт или, по другому, 3 куска торта из 8 нарезанных кусочков весят 300 г.

Тогда 1 кусочек будет весить: 300/3=100 г. Теперь находим чему будет весить все 8 кусков, т.е. весь торт.

100*8=800 г

Бекки Шарп
[71.2K]

3 года назад

Если 3/8 торта весит 300 грамм, то сначала узнаем сколько весит одна часть. 300/3=100 грамм.

Теперь умножаем на 8 и получаем, что весь торт весит 800 грамм.

Приведем еще пример как найти целое число, если известна часть.

В классе присутствует 27 человек и это 3/4 общего количества. Сколько человек в классе?

Решить задачу можно так:

27 : 3/4 = 36 человек.

Знаете ответ?

Источник

Какая десятичная дробь между 1 и 2? – Обзоры Вики
- Какая дробь стоит перед 1 2?
- Какое из следующих рациональных чисел находится между 1 и 2?
- Какой тип числа 1 2?
- Как найти середину между двумя дробями?
  - Что находится между половиной и четвертью?
Между какими целыми числами заключено число?
Творческий проект для классов К-8
Дробь между двумя дробями: определения и примеры
- Определение дроби
  - Примеры дробей
- Дробь между двумя дробями
- Решаемые примеры – дробь между двумя заданными дробями
- Резюме
- Часто задаваемые вопросы (FAQ)

Какая десятичная дробь между 1 и 2? – Обзоры Вики

1.5 находится точно между 1 и 2, но есть много других чисел, таких как 1.157, 1.781, 1.3312.

Итак, какая дробь находится между 1 и 2? Между любыми двумя целыми числами стоит дробь. Между 0 и 1 12, между 1 и 2 112=3/2, и так далее. На самом деле между любыми двумя целыми числами бесконечно много дробей.

Сколько действительных чисел находится между 1 и 2? Первоначальный ответ: Сколько действительных чисел находится между 1 и 2? Есть бесконечные действительные числа между 1 и 2. Между 1 и 1.1 лежат бесконечные действительные числа.

Дополнительно Что такое 1 как число? 1 (число)

← 0 1 2 →
Кардинальный	one
порядковый	1-й (первый)
Система счисления	унарный
факторизация	1

Как найти середину между двумя числами? Середина между двумя числами — это число, находящееся ровно посередине двух чисел. Вычисление средней точки — это то же самое, что вычисление среднего значения двух чисел. Следовательно, вы можете вычислить среднюю точку между любыми двумя числами. сложив их вместе и разделив на два.

Какая дробь стоит перед 1 2?

Таблица преобразования десятичных и дробных чисел

Доля	Эквивалентные дроби
1/2	2/4	4/8
1/3	2/6	4/12
2/3	4/6	8/12
1/4	2/8	4/16

Что находится между 1 2 и 3/4 на числовой прямой? Итак, средняя дробь между 1/2 и 3/4 равна 5/8.

Что находится между половиной и 3 4? Числитель и знаменатель требуемого числа должны быть между заданным числом, т. е. числитель может быть равен 3, а знаменатель может быть равен 5. Следовательно, рациональное число между 1/2 и 3/4 равно 3/5.

Какое из следующих рациональных чисел находится между 1 и 2?

Следовательно, четыре рациональных числа между 1 и 2 — это 9/8, 5 / 4, 3 / 2 и 7 / 4.

Также Какие два рациональных числа между 1 и 2? Следовательно, 4 / 3 и 5 / 3 два рациональных числа между 1 и 2.

Сколько иррациональных чисел находится между 1 и 2?

Это может быть любое число между двумя с любым количеством цифр. Следовательно, у нас есть бесконечное количество иррациональных чисел между двумя числами.

Что такое два как число? 2 (два) — число, цифра и цифра. Это натуральное число после 1 и до 3 . Это наименьшее и единственное четное простое число.
…

← 1 2 3 →
-1 0 1 2 3 4 5 6 7 8 9 → Список чисел — Целые числа ← 0 10 20 30 40 50 60 70 80 90 →
Кардинальный	два
порядковый	2-й (второй/второй)
Система счисления	двоичный

Какой тип числа 1 2?

Рациональное число (В). Это все дроби, в которых верхние и нижние числа являются целыми числами; например, 1/2, 3/4, 7/2, ⁻4/3, 4/1 [Примечание: знаменатель не может быть равен 0, но числитель может быть]. Вещественные числа (R) (также называемые измерительными числами или числами измерений).

Кто изобрел ноль в мире?

Первый современный эквивалент цифры ноль происходит от индуистский астроном и математик Брахмагупта в 628 году. Его символом для изображения числа была точка под числом.

Как найти половину расстояния между двумя точками? Определите половину расстояния

Разделите полное расстояние на два.
Измерьте это расстояние от одной из двух исходных точек и отметьте на карте.
Проверьте свою работу, проделав то же самое с другой отправной точки.

Как найти режим? Мода набора данных — это число, которое чаще всего встречается в наборе. Чтобы легко найти режим, расположите числа по порядку от наименьшего к наибольшему и посчитайте, сколько раз встречается каждое число. Число, которое встречается чаще всего, — это режим!

Как найти середину между двумя дробями?

Что такое 1/2 в целом числе? Следовательно, 1/2 как целое число будет 0 или 1.

1 2 — натуральное число?

Множеством натуральных чисел в математике называется множество {1, 2, 3, …}. Итак, -1 — отрицательное число, поэтому это не натуральное число. 0 тоже не натуральное число. 1/2, будучи дробное число, тоже не натуральное число.

Что находится между третью и половиной? Если умножить числитель и знаменатель обеих дробей на 2, то получим 6/12 и 4/12, здесь мы можем вставить одну дробь т.е. 5/12. Между ними можно вставить три дроби 11/24, 10/24 или 5/12, 9/24 или 3/8. …

Что находится между половиной и четвертью?

Нарежьте пиццу, и мы получим дроби:

¹ / ₂	¹ / ₄	³ / ₈
(Одна половина)	(Одна четверть)	(три восьмых)

Что такое 0. 75, переведенное в дробь? Значение 0.75 как дробь равно 3/4.

Между какими целыми числами заключено число?

Задача #1 (номер задачи на fipi.ru — 8F6802). Между какими целыми числами заключено число 130/11?

10 и 11
11 и 12
12 и 13
13 и 14

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 11 и 12.

Ответ: 2 — 11 и 12.

Задача #2 (номер задачи на fipi.ru — 344704). Между какими целыми числами заключено число 140/17?

5 и 6
6 и 7
7 и 8
8 и 9

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 8 и 9.

Ответ: 4 — 8 и 9.

Задача #3 (номер задачи на fipi.ru — B64AD1). Между какими целыми числами заключено число 172/15?

9 и 10
10 и 11
11 и 12
12 и 13

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 11 и 12.

Ответ: 3 — 11 и 12.

Задача #4 (номер задачи на fipi.ru — F2CF43). Между какими целыми числами заключено число 110/13?

8 и 9
9 и 10
10 и 11
11 и 12

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 8 и 9.

Ответ: 1 — 8 и 9.

Задача #5 (номер задачи на fipi.ru — F4AE19). Между какими целыми числами заключено число 230/19?

11 и 12
12 и 13
13 и 14
14 и 15

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 12 и 13.

Ответ: 2 — 12 и 13.

Задача #6 (номер задачи на fipi.ru — 4DD651). Между какими целыми числами заключено число 160/11?

12 и 13
13 и 14
14 и 15
15 и 16

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 14 и 15.

Ответ: 3 — 14 и 15.

Задача #7 (номер задачи на fipi.ru — 9179F3). Между какими целыми числами заключено число 131/12?

10 и 11
11 и 12
12 и 13
13 и 14

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 10 и 11.

Ответ: 1 — 10 и 11.

Задача #8 (номер задачи на fipi.ru — 648BA1). Между какими целыми числами заключено число 124/15?

8 и 9
9 и 10
10 и 11
11 и 12

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 8 и 9.

Ответ: 1 — 8 и 9.

Задача #9 (номер задачи на fipi.ru — 2FC0DC). Между какими целыми числами заключено число 190/17?

10 и 11
11 и 12
12 и 13
13 и 14

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 11 и 12.

Ответ: 2 — 11 и 12.

Задача #10 (номер задачи на fipi.ru — 37B64D). Между какими целыми числами заключено число 170/19?

8 и 9
9 и 10
10 и 11
11 и 12

Решение:

Выделим целую часть в дроби:

Очевидно, что из предложенных вариантов число заключено между 8 и 9.

Ответ: 1 — 8 и 9.

Творческий проект для классов К-8

Планы уроков

Задача «3N+1»
Задача с Всероссийской олимпиады по математике
Доказательство теоремы Пифагора с использованием подобных треугольников
Головоломка с 1089
Дополнительная плата
Прибавление в детском саду и первом классе
Арифметический вундеркинд из 1899 года
Старый купец и четверо его детей
Древний узел
Анимации на TI
Районы и границы
Площадь и периметр
Средний балл за тест
Мяч в коробке
Банан
Бочки, бочонки и другие изогнутые емкости
Большие числа АКА Зерна риса на шахматной доске
Блочные дома
Сборка собачьей будки в масштабе
Создание каркасной коробки в соответствии со спецификациями
Свечи
Корзины для конфет
Емкость
Наутилус с камерой
Проверка, является ли число простым
Коробка с китайским календарем
Аккорды по кругу
Круг, квадрат и треугольник
Часы и время
Монеты
Раскрашивание линий в шестиугольнике
Разноцветные треугольники
Конгруэнтные треугольники
Счет
Счетная доска для юных учащихся
Счет до 100
Биговка бумаги по изгибам
Кубики
Куб со срезанным краем
Кулинарные полоски
Вырезание прямоугольника
Вырезание треугольника
Разрезание треугольника на две части равной площади и равного периметра
Вырезание равностороннего треугольника
Резка многогранников
Вывод формулы площади треугольника
Диагональ квадрата
Разделение квадрата
Дивизион с остатком на ТИ-108: Два экземпляра
Собаки, кошки и мыши
Точка за точкой
Удвоение и деление пополам
Рисование прямоугольника
Рисование простой фигуры по словесным инструкциям
Рисование треугольников
Легкие квадраты
Яичная дилемма (Часть 1)
Возведение в степень
Факторинг
Необычные конверты
Нахождение дроби между двумя дробями
Пятиконечная трехмерная звезда
Подбрасывание монет
Сложенный бумажный цветок с шестью лепестками
Четыре жука
Четыре карты
Четыре кубика
От одного миллиарда до нуля
От одного до одного триллиона
Игра кругов и звезд
Игра десятков
Гигантская энчилада
Шапка для Хэллоуина
Орел или решка?
Шестиугольная головоломка
Как калькулятор вычисляет квадратный корень числа?
Сколько пентамино?
Как измерить угол без транспортира
Как преобразовать прямоугольник в другой прямоугольник
Гиперболы и эллипсы
Вписанный треугольник
Интерес
Юлекурв АКА Валентинка Корзина
Воздушные змеи
Дырявая крыша
Ушастые твари
Волшебные бобы
Волшебный складной кубик
Волшебный квадрат
Создание животных путем вырезания многоугольников
Изготовление блоков из четырех кубиков
Изготовление коробок
Изготовление эвольвенты
Лабиринт
Мини-слот-машина
Луны
Больше задач с точностью до точки
Больше старых словесных задач
Умножения «Сделано по Адаму Райсу»
Натан подбрасывает монету 20 раз
Числовая игра с кубиками
Одна треть
Парадокс средних
Разделение квадрата
Пазлы Пентагона
Алгебра телефонных номеров
Копилка
Игра с формами
Powerball 55
Красивая подарочная коробка
Тыквы
Пазл с камешками
Пирамида на четверти
Пирамида кубов
Пирамида из мрамора
Четырехугольники
Правильные многоугольники с равными площадями
Связанные проблемы
Прямоугольный треугольник
Последовательности составных чисел: конкурс
Формы чисел
Формы чисел с использованием треугольников
Шесть пирамид
Шестнадцать квадратных дюймов
Печать Соломона
Сортировочная игра
Спираль (марки К-4)
Спираль (5-8 классы)
Спираль Феодора на калькуляторе ТИ-83/84
Квадратные и кубические единицы
Квадрат в треугольнике
Соломенные многогранники
Алгоритм вычитания
Вычитание со счетчиками
Сумма двух квадратов
Выживший на шестиугольном острове
Татами
Чайные коробки
Преобразование температуры
Мозаика круга
Задача о лестнице и ящике
Контейнеры для сыра «Смеющаяся корова»
Практическая ценность доказательств
Три четверти
Круглая головоломка из трех частей
Бросание одного кубика
От треугольника к квадрату: Шарнирное рассечение
Превращение прямоугольника в квадрат путем рассечения
Двенадцать простых фигур
Двадцать четыре кубика
Две старые проблемы
Два брата пастуха
Понимание длинного деления
Необычные контейнеры
Что дальше?
Что это за прямоугольник?
Инь Ян

Дробь между двумя дробями: определения и примеры

Автор
Рачана
Последнее изменение 19-10-2022

Фракция между двумя фракциями: Фракция — это небольшая часть большего целого или набора. Когда объект или целое делится на равные части, каждая часть представляет собой часть данного объекта или целого. В числовом выражении дробь состоит из двух частей: числителя и знаменателя.

Числитель показывает, сколько у нас есть выделенных или заштрихованных частей, тогда как знаменатель показывает, сколько всего частей объекта или целого у нас есть. Мы можем найти дроби между любыми двумя дробями. В этой статье обсуждается, как найти дробь между двумя заданными дробями. Прочитайте полную статью, чтобы получить полную информацию.

Определение дроби

Дроби представлены в виде числовых значений в математике и могут быть определены как части целого. Дробь — это часть или часть целого, которая может быть любым числом, заданным значением или элементом.

Таким образом,

({text{Дробь}} = frac{{{text{Число}},{text{из}},{text{выбрано}},{text {или}} , { text {заштриховано}} , { text {части}} , { text {из}} , { text {an}} , { text {объект}} , { text {или}} , { text {a}} , { text {целое}}}} {{{ text {Всего}} , { text {число}} , { текст {из}} , { текст {равно}} , { текст {частей}} , { текст {из}} , { текст {an}} , { текст {объект}} ,{text{или}},{text{a}},{text{целое}}}} = frac{{{text{Числитель}}}}{{{text{Знаменатель }}}})

Учитывать дробь (frac{5}{{12}}) Эта дробь читается как «пять двенадцатых», что означает, что (5) частей из (12) равны разделить на целое.

В дроби (frac{7}{{12}},7) известен как числитель, а (12) известен как знаменатель.

Ниже приведены еще несколько примеров:

Дробь	Значение дроби	Числитель	0355 Знаменатель
(frac{5}{{11}}) или Пять одиннадцатых	Пять равных частей из (11) равных частей, на которые делится целое.	(5)	(11)
(frac{3}{{8}}) или Три восьмых	Три равные части из (8) равных частей в котором целое разделено.	(3)	(8)
(frac{1}{{3}}) или Одна треть	Одна часть из (3) равных частей в что целое разделено.	(1)	(3)

Примеры дробей

Дробь — это число, представляющее часть целого. Один объект или группа объектов могут составлять целое. Возьмите прямоугольный лист и сложите его пополам. Сложите его по горизонтали и вертикали, чтобы разделить на четыре равные части. Как показано на рисунке ниже, один из четырех компонентов должен быть затенен. Заштрихованная область составляет четверть всей композиции. Число одна четвертая записывается как (frac{1}{{4}},), что не что иное, как дробь.

Если три части затемнены, как на рисунке ниже, заштрихованная часть представляет собой три четверти от общего числа. Три четверти записываются как (frac{3}{{4}}) и читаются как «три на четыре» или «три на четыре». Таким образом, три части из (4) равных частей равны (frac{3}{{4}}.)

Аналогично, (frac{3}{{7}}) получается, когда делим целое на (7) равных частей и берем три части (см. рис. ниже).

Для (frac{1}{{8}},) делим целое на восемь равных частей и берем одну его часть (см. рис. ниже).

Дробь между двумя дробями

Дробь состоит из двух элементов. Число в верхней части строки или дроби называется числителем. Он определяет, сколько берется равных частей всей коллекции или целого. Знаменатель – это число под чертой. Он отображает общее количество равных частей, на которые делится целое, или общее количество равных частей в коллекции.

Калькулятор нахождения дроби между двумя дробями не сложный процесс. Просто сделайте сумму числителей в качестве нового числителя и сумму знаменателей в качестве нового знаменателя, чтобы получить дробь между двумя заданными дробями.

Ниже приведены примеры того, как вставить дробь между двумя дробями:

Если (frac{p}{q}) и (frac{r}{s}) две заданные дроби и ( гидроразрыв {р} {q}

Где (p,q,r) и (s) — натуральные числа.

Пример. Вставьте дробь между двумя дробями (frac{5}{7}) и (frac{3}{5},), учитывая (frac{5}{7})

Решение. Требуемая дробь между (frac{5}{7}) и (frac{2}{5}) равна (frac{{(5 + 2)}}{{(7 + 5)}} = frac{7}{{12}})

Следовательно, (frac{5}{7}

Решаемые примеры – дробь между двумя заданными дробями

Q.1. Вставьте дробь между двумя дробями (frac{1}{3}) и (frac{2}{5},) учитывая (frac{1 }{3} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Здесь сумма числителей(=1+ 2=3) и
сумма знаменателей(=3+5=8)
Итак, новая дробь образовалась между двумя дробями (frac{1}{3}) и (frac{2}{5} ) равно (frac{3}{8}.)

Q.2. Найдите дробь между двумя дробями (frac{2}{7}) и (frac{4}{5},) при заданном (frac{2 }{7} < frac{4}{5}.)
Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Требуемая дробь между двумя дробями (frac{2}{7}) и (frac{4}{5}) равна (frac{{(2 + 4)}}{{( 7 + 5)}} = frac{6}{{12}} = frac{1}{2}.)

Q.3. Найдите дробь между двумя дробями (frac{4}{7}) и (frac{1}{3},) при заданном (frac{4 {7} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Требуемая дробь между двумя дробями (frac{4}{7}) и (frac{1}{3}) равна (frac{{(4 + 1)}}{{( 7 + 3)}} = frac{5}{{10}} = frac{1}{2}.)

Q.4. Вставьте дробь между двумя дробями (frac{5}{6}) и (frac{7}{11},) учитывая (frac{5 {6} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Требуемая дробь между двумя дробями (frac{5}{6}) и (frac{7}{11}) равна (frac{{(5 + 7)}}{{( 6 + 11)}} = frac{{12}}{{17}}.)

Q.5. Вставьте дробь между двумя дробями (frac{5}{7}) и (frac{8}{11},) учитывая (frac{5 {7} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Здесь сумма числителей(=5+8=13) и
сумма знаменателей(=7+11=18)
Итак, между двумя дробями образовалась новая дробь (frac {5}{7}) и (frac{8}{11}) равно (frac{13}{18}.)

Резюме

В этой статье мы узнали об определении дроби, примеры дробей, калькулятор нахождения дроби между двумя дробями, решенные примеры дроби между двумя заданными дробями и часто задаваемые вопросы о дроби между двумя заданными дробями. Вы также можете найти «Как найти дробь между двумя дробями» в приложении и на веб-сайте Embibe.

В результате изучения этой статьи мы поняли, как вставить дробь между двумя заданными дробями. Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.

Узнайте о различных типах фракций

Часто задаваемые вопросы (FAQ)

Q.1. Как найти дробь между двумя дробями?
Ответ. Нахождение дроби между двумя дробями — несложный процесс. Просто сделайте сумму числителей новым числителем и знаменателей новым знаменателем, чтобы получить дробь между двумя дробями.
Ниже приведены примеры того, как вставить дробь между двумя предоставленными дробями:
Если (frac{p}{q}) и (frac{r}{s}) две заданные дроби и (frac{p} {q} < frac{r}{s}), затем (frac{p}{q} < frac{{p + r}}{{q + s}} < frac{r}{s}. )

Q.2. Всегда ли между любыми двумя дробями есть дробь?
Ответ: Между любыми двумя целыми числами есть дробь. Существует (frac{1}{2}) между (0) и (1,frac{3}{2}) между (1) и (2,) и т.д. на. Между любыми двумя целыми числами может быть бесконечное количество дробей.
Существуют также (frac{1}{3},frac{1}{4},frac{1}{5},) и любые другие числа, которые могут быть выражены как (frac{1 {n},), где (n) — целое число, от (0) до бесконечности, а значение дроби лежит между (0) и (1.). дроби, такие как (frac{2}{3},frac{3}{4},frac{4}{5},) и так далее. (frac{m}{n}) — дробь между (0) и (1), если m и n оба являются положительными целыми числами и (m) меньше, чем (n. ) Точно так же существует бесконечное число дробей между любыми двумя целыми числами.

Q.3. Какая дробь находится между 1/3 и 2/3?
Ответ: Чтобы найти дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Даны две дроби: (frac{1}{3}) и (frac{2}{3},frac{1}{3} < frac{2}{3})
Здесь сумма числителей(=1+2=3) и
сумма знаменателей(=3+3=6)
Итак, между двумя дробями образовалась новая дробь (frac{ 1}{3}) и (frac{2}{3}) равно (frac{3}{6} = frac{1}{2}. )

Q.4. Какая дробь находится между 1 и 2?
Ответ: Чтобы найти дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Даны две дроби: (frac{1}{1}) и (frac{2}{1},1 Здесь сумма числителей(=1+2=3) и

сумма знаменателей(=1+1=2)
Итак, новая дробь, образованная между двумя дробями (1) и (2), равна (frac{3}{2}. )

Q.5. Что такое дробь?
Ответ: В математике дроби представлены числовыми значениями и могут быть определены как части целого. Дробь — это часть или часть целого, которая может быть любым числом, заданным значением или элементом.
Рассмотрим дробь (frac{3}{5}.) Эта дробь читается как «три пятых», что означает, что (3) частей из (5) равных частей, в которых целое поделен. В дроби (frac{3}{5},3) называется числителем, а (5) называется знаменателем.

Q.6. Чему равно в дробях?
Ответ: Равные дроби — это дроби с одинаковым значением, но разными числителями и знаменателями. (frac{6}{9}) и (frac{10}{15},), например, являются эквивалентными дробями, поскольку они обе равны (frac{2}{3}. )

Q.7. Как определить, равны ли дроби?
Ответ: Когда различные дроби упрощаются и сводятся к одной дроби, они являются эквивалентными дробями. Кроме того, существует несколько альтернативных подходов к определению сопоставимости поставляемых фракций. Вот несколько примеров:
1. Сделать числители и знаменатели одинаковыми.
2. Нахождение десятичной версии обеих дробей является первым шагом.
3. Метод перекрестного умножения.
4. Наглядным способом.

Теперь у вас есть вся необходимая информация о дроби между двумя дробями, и мы надеемся, что эта подробная статья будет вам полезна.

Источник

Мы уже научились находить часть от числа (см. здесь).

А сегодня мы поговорим о том, как найти число по его части (число по его дроби). Эти умения необходимы при решении задач.

Обратимся опять же к пицце.

1. Пиццу разрезали на 8 кусков. Один кусок весит 60 г. Надо узнать вес пиццы. Мы знаем, что пиццу разрезали на 8 частей, т.е. 1 кусок – это 1/8 от целого.

Изобразим это на схеме:

Если 1 кусок весит – 60 г, значит, вся пицца весит в 8 раз больше и надо 60 г умножить на 8.

В дроби 1/8 – знаменатель 8. Итак, чтобы найти целое – надо вес 1 части умножить на знаменатель.

2. Рассмотрим другой пример:

2 куска пиццы весят 120 г. Надо узнать вес целой пиццы.

Как поступим в этом случае?

Вес целой пиццы мы узнавали в предыдущем случае: вес одного куска умножали на число кусков. Значит, надо узнать вес одного куска. Для этого 120 : 2 = 60 (г)

А потом 60 умножим на 8 (как в примере 1).

Итак: 2/8 = 120

данное число 120 разделили на 2 (это числитель дроби), а потом умножили на 8 (это знаменатель дроби):

120 : 2 х 8

Заменим деление на дробь: