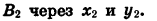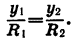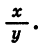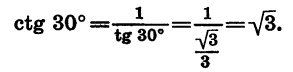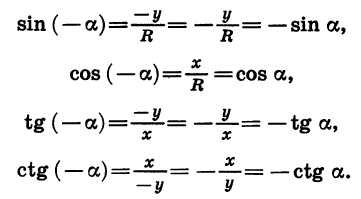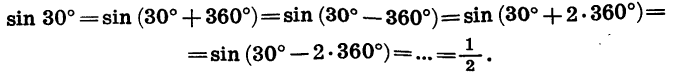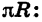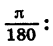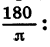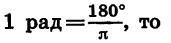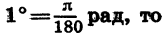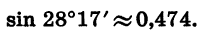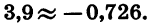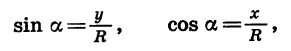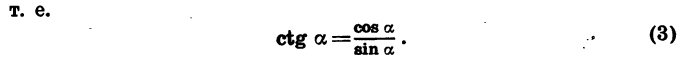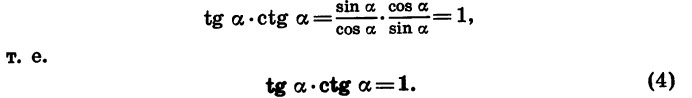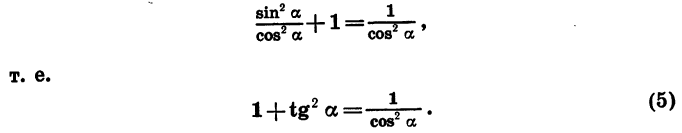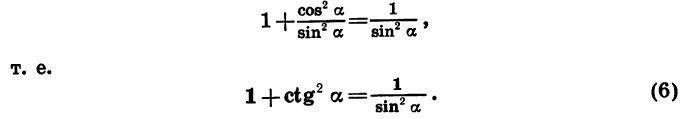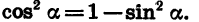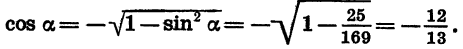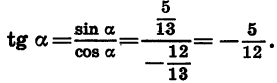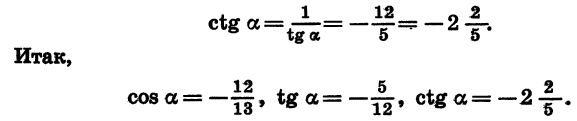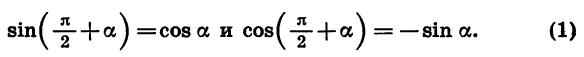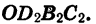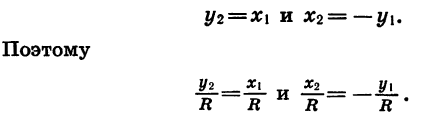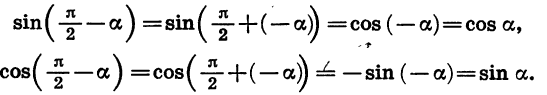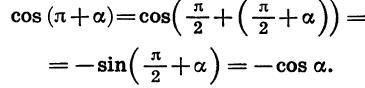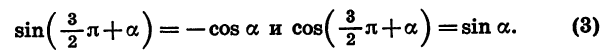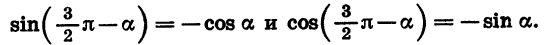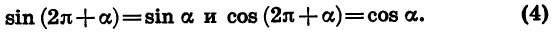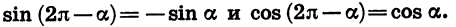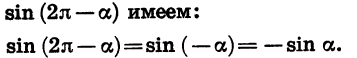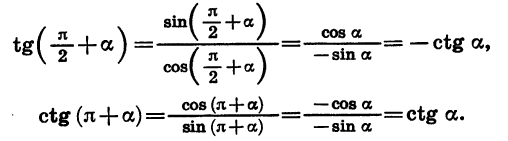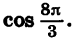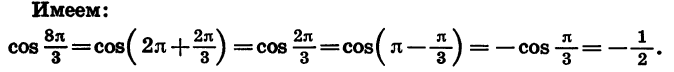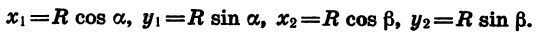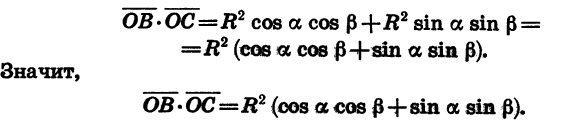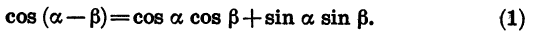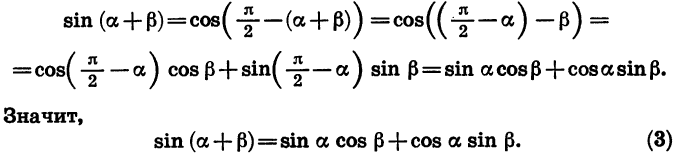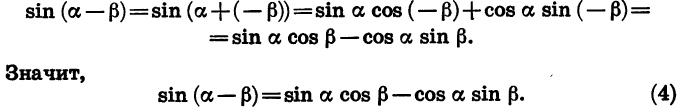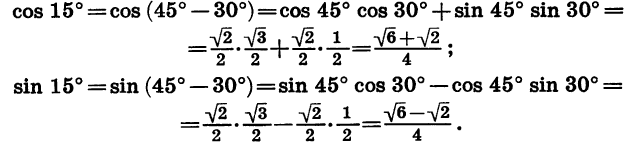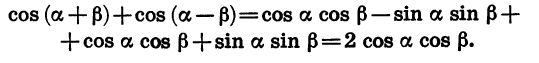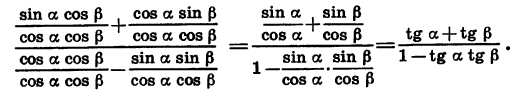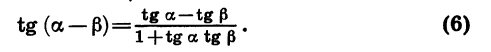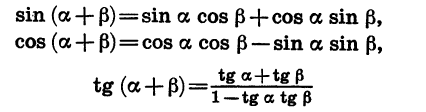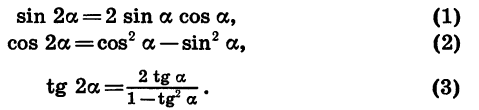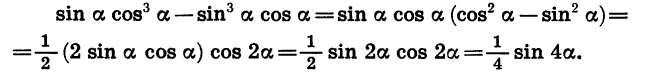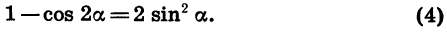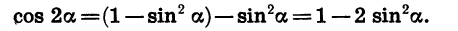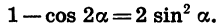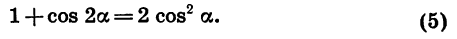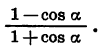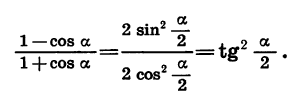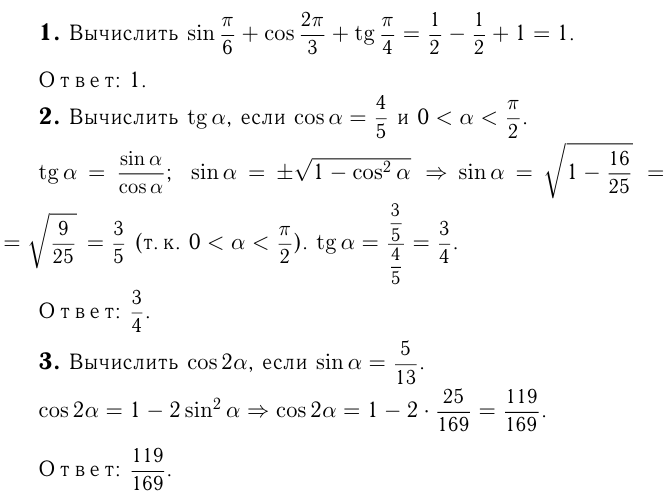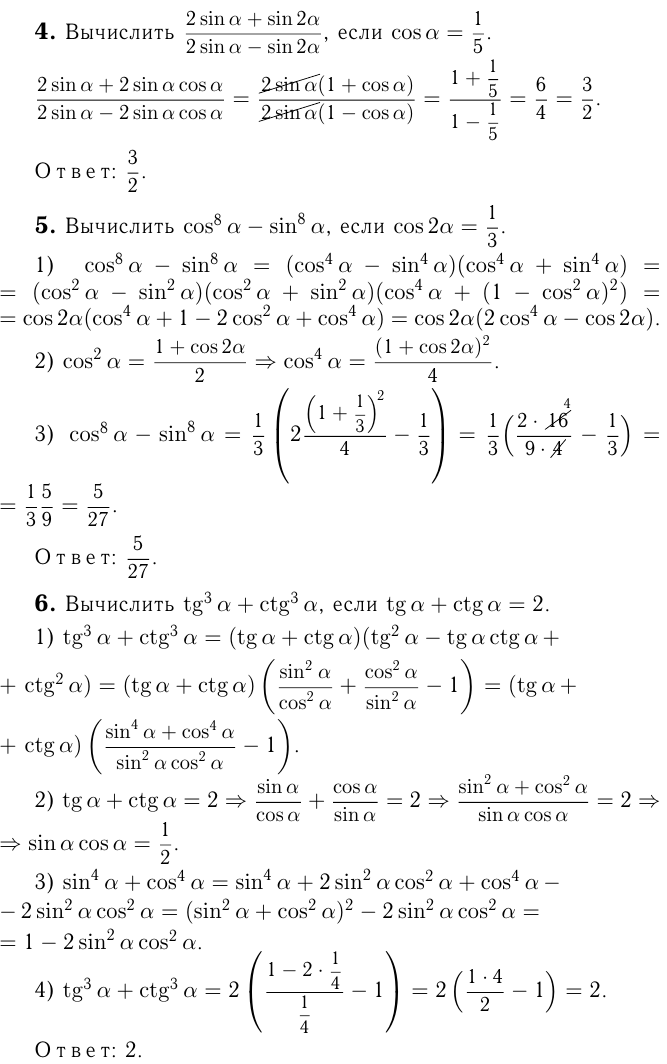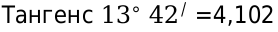9. Преобразование числовых и буквенных выражений
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Числовые тригонометрические выражения
(blacktriangleright) Алгоритм применения формул приведения:
Шаг 1: определить, меняется ли функция на кофункцию: [sin
longleftrightarrow cos] [mathrm{tg} longleftrightarrow mathrm{ctg}]
Шаг 2: определить знак, который имеет изначальная функция, поняв, в какой четверти тригонометрической окружности находится изначальный угол (предполагая, что (alpha) – острый)
(blacktriangleright) Если угол можно представить в виде ((pi npm
alpha)), где (n) – натуральное, то функция на кофункцию не меняется.
Пример: (sin (pi npm alpha)=bigodot sin alpha), где на месте (bigodot) должен стоять знак синуса для угла ((pi npm alpha))
(blacktriangleright) Если угол можно представить в виде (left(dfrac{pi}2npm alpharight)), где (n) – нечетное число, то функция на кофункцию меняется
Пример: (sin left(dfrac{pi}2npm alpharight)=bigodot cos
alpha), где на месте (bigodot) должен стоять знак синуса для угла (left(dfrac{pi}2npm alpharight))
(blacktriangleright) Основные формулы:
[begin{array}{|ccc|}
hline sin^2 alpha+cos^2 alpha =1&& mathrm{tg} alpha cdot
mathrm{ctg}alpha
=1\ &&\
mathrm{tg} alpha=dfrac{sin alpha}{cos alpha}&&mathrm{ctg}
alpha
=dfrac{cos alpha}{sin alpha}\&&\
cos {2alpha}=cos^2 alpha — sin^2 alpha&&cos
{2alpha}=1-2sin^2
alpha\&&\
cos {2alpha}=2cos^2alpha -1&&sin {2alpha}=2sin alpha cos
alpha\
hline
end{array}]
Задание
1
#573
Уровень задания: Легче ЕГЭ
Найдите значение выражения (2sin^2 30^circ + cos^2 30^circ).
Используя основное тригонометрическое тождество, исходное выражение можно преобразовать следующим образом: [2sin^2 30^circ + cos^2 30^circ = sin^2 30^circ + (sin^2 30^circ + cos^2 30^circ) = sin^2 30^circ + 1.] Так как (sin 30^circ = 0,5), то значение исходного выражения равно (0,5^2 + 1 = 1,25).
Ответ: 1,25
Задание
2
#2958
Уровень задания: Равен ЕГЭ
Найдите значение выражения [dfrac{24}{sin^2127^circ+1+sin^2217^circ}]
Заметим, что (217^circ=90^circ+127^circ). Так как по формуле приведения (sin(90^circ+alpha)=cos alpha), то [sin
217^circ=sin (90^circ+127^circ)=cos 127^circ] Следовательно, выражение можно переписать в виде: [dfrac{24}{sin^2127^circ+cos^2127^circ+1}=dfrac{24}{1+1}=12,] так как по основному тригонометрическому тождеству (sin^2alpha+cos^2alpha=1) для любого угла (alpha).
Ответ: 12
Задание
3
#2626
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[sqrt{48}-sqrt{192}sin^2dfrac{19pi}{12}]
(Задача от подписчиков.)
Заметим, что (192=48cdot 4), следовательно, (sqrt{192}=2sqrt{48}). Таким образом, выражение примет вид (по формуле косинуса двойного угла (cos2x=1-2sin^2x)):
[sqrt{48}left(1-2sin^2dfrac{19pi}{12}right)=
sqrt{48}cdot cosdfrac{19pi}6]
Т.к. (dfrac{19pi}6=dfrac{18pi+pi}6=3pi+dfrac{pi}6), то по формуле приведения:
[sqrt{48}cosleft(3pi+dfrac{pi}6right)=
sqrt{48}cdot left(-cosdfrac{pi}6right)=-sqrt{48}cdot
dfrac{sqrt3}2=-4sqrt3cdot dfrac{sqrt3}2=-6.]
Ответ: -6
Задание
4
#2434
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[8left(sindfrac{pi}{12}cosdfrac{pi}{12}-1right)]
По формуле синуса двойного угла (sin2alpha=2sinalphacosalpha) имеем: (sinalphacosalpha=frac12sin2alpha). Следовательно,
[8left(dfrac12sin2cdotdfrac{pi}{12}-1right)=8left(dfrac12sindfrac{pi}6-1right)=
8left(dfrac12cdot dfrac12-1right)=-6.]
Ответ: -6
Задание
5
#2625
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[dfrac{32}{sinleft(-dfrac{35pi}4right)cdot cos dfrac{25pi}4}]
(Задача от подписчиков.)
Т.к. синус — нечетная функция, то есть (sin (-alpha)=-sin
alpha), то (sinleft(-frac{35pi}4right)=-sin frac{35pi}4).
Заметим, что :
(dfrac{35pi}4=dfrac{36pi
-pi}4=9pi-dfrac{pi}4);
(dfrac{25pi}4=dfrac{24pi+pi}4=6pi+dfrac{pi}4).
Таким образом, по формулам приведения:
(sin
dfrac{35pi}4=sinleft(9pi-dfrac{pi}4right)=sindfrac{pi}4);
(cos
dfrac{25pi}4=cosleft(6pi+dfrac{pi}4right)=cosdfrac{pi}4).
Следовательно, выражение принимает вид:
[dfrac{32}{-sindfrac{pi}4cosdfrac{pi}4}=
-dfrac{32}{dfrac{sqrt2}2cdot dfrac{sqrt2}2}=-64.]
Ответ: -64
Задание
6
#581
Уровень задания: Равен ЕГЭ
Найдите значение выражения (dfrac{7sin{11^circ}}{cos{79^circ}}).
Используя формулу приведения (sin(90^circ pm alpha) = cos alpha), исходное выражение можно преобразовать следующим образом: [dfrac{7sin{11^circ}}{cos{79^circ}} = dfrac{7sin{(90^circ — 79^circ)}}{cos{79^circ}} = dfrac{7cos{79^circ}}{cos{79^circ}} = 7.]
Ответ: 7
Задание
7
#1841
Уровень задания: Равен ЕГЭ
Найдите значение выражения (dfrac{15}{sin{(-frac{20pi}{3})}
cdot cos{(-frac{43pi}{6})}}).
Используя формулы приведения, а также четность косинуса и нечетность синуса, исходное выражение можно преобразовать следующим образом: [dfrac{15}{-sin{left(6pi + frac{2pi}{3}right)} cdot
cos{left(7pi + frac{pi}{6}right)}} =
dfrac{15}{-sin{left(frac{2pi}{3}right)} cdot
(-cos{left(frac{pi}{6}right)})} =
dfrac{15}{-frac{sqrt{3}}{2} cdot ({-frac{sqrt{3}}{2})}} = 20.]
Ответ: 20

УСТАЛ? Просто отдохни
В статье мы рассмотрим, как найти значения:
(cosfrac{π}{6}), (sin(-frac{7π}{3})), (cosfrac{3π}{4}), (sin(-frac{27π}{2}))
и других тригонометрических выражений без тригонометрической таблицы.
Для начала внимательно прочтите статью о числовой окружности. Вы должны научиться находить точки на окружности в числах с Пи.
Уже умеете? Тогда два ключевых утверждения:
Например, пусть нам нужно найти синус и косинус числа (frac{π}{6}). Обозначим на числовой окружности точку со значением (frac{π}{6}).
Если построить все точно и крупно, то можно убедиться, что абсцисса этой точки будет равна (0,866…) , что соответствует числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Значит, что (cos(frac{π}{6}) = frac{sqrt{3}}{2}), а (sin(frac{π}{6}) =frac{1}{2}).
Аналогично и для любой другой точки: значение абсциссы совпадает со значением косинуса, а ординаты – синуса. Поэтому:
В тригонометрии ось абсцисс часто называют «ось косинусов», а ординат – «ось синусов».
И обычно на них не наносят значения в десятичных ((0,1); (0,2); (0,3) и т.д.), а сразу отмечают стандартные значения для синуса и косинуса: (frac{1}{2} =0,5); (frac{sqrt{2}}{2} ≈0,707); (frac{sqrt{3}}{2}≈0,866), причем, как со знаком плюс, так и минус. Почему стандартные значения синуса и косинуса именно (frac{1}{2}),(frac{sqrt{2}}{2}) и (frac{sqrt{3}}{2}) вы можете узнать из этого видео.
Как находить значения синуса и косинуса без таблицы, а только с помощью круга?
Алгоритм прост:
- Начертите круг и оси косинусов и синусов.
- Отметьте на круге число, синус и косинус которого надо найти. Если с этим возникают проблемы, прочитайте здесь о том, как расставлять числа на числовой окружности.
- Найдите координаты точки, используя картинку ниже.

Пример. Найдите синус и косинус для числа (-frac{7π}{6}).
Решение:(-frac{7π}{6}=-frac{6π}{6}-frac{π}{6}=-π-frac{π}{6}) , то есть, чтобы отметить на окружности точку (-frac{7π}{6}) сначала находим число (-π) и от него в отрицательную сторону откладываем дугу длиной (frac{π}{6}).

Отмечаем число, синус и косинус которого надо найти:

Получается, что (sin(-frac{7π}{6})=frac{1}{2}), (cos(-frac{7π}{6})=-frac{sqrt{3}}{2}).
Пример. Вычислите (sinfrac{5π}{2}) и (cosfrac{5π}{2}).
Решение: (frac{5π}{2}=frac{4π+π}{2}=frac{4π}{2}+frac{π}{2}=2π+frac{π}{2}).

Точка (frac{5π}{2}) совпадает с (1) на оси синусов, значит (sinfrac{5π}{2}=1). А если провести перпендикуляр из точки (frac{5π}{2}) до оси косинусов, то можно убедиться, что он попадет в (0). Поэтому (cosfrac{5π}{2}=0).

И тут некоторые из вас подумали: «с кругом, на котором подписаны числа, каждый дурак сможет посчитать, а что делать, когда его под рукой нет? Что делать на ЕГЭ?» Ответ прост – нарисуйте круг сами! Для этого вам будет нужно понять логику расположения чисел на осях (подробнее об этом читайте в статье «Как запомнить тригонометрический круг»).
Пример. Найдите а) (sinfrac{3π}{2}), б) (cosfrac{3π}{4}), в) (sin(-frac{π}{3})) .
Решение: а) Чертим круг, оси и отмечаем число (frac{3π}{2}). Обращаем внимание на ось синусов и понимаем, что точка совпала с (-1), получается (sinfrac{3π}{2}=-1).
б) (frac{3π}{4}=frac{4π}{4}-frac{π}{4}=π-frac{π}{4}) — отмечаем число на круге. Проводим перпендикуляр до оси косинусов и вспоминаем, что точки со знаменателем (4) находятся посередине. Мы еще попали и в отрицательную часть оси косинусов, получается (cosfrac{3π}{4}=-frac{sqrt{2}}{2}).
в) (-frac{π}{3}) – отмечаем число на круге. Видим, что перпендикуляр к оси синусов попал в точку близкую к (-1), значит (sin(-frac{π}{3})=-frac{sqrt{3}}{2}).

Как видите не обязательно рисовать, очень красивую или очень большую окружность — вы можете определить нужное вам значение, быстро набросав круг. И ничего не надо учить!
Если вы хотите еще примеров с вычислением синусов и косинусов без тригонометрической таблицы, то прочтите эту статью.
Пример (ЕГЭ). Найдите значение выражения (frac{8}{sin(-frac{27π}{4}) cos(frac{31π}{4})}) .
Решение. (-frac{27π}{4}=-frac{28π}{4}+frac{π}{4}=-7π+frac{π}{4}).
(frac{31π}{4}=frac{32π}{4}-frac{π}{4}=8π-frac{π}{4}).

(sin(-frac{27π}{4})=-frac{sqrt{2}}{2}), (cos(frac{31π}{4})=frac{sqrt{2}}{2}).
(frac{8}{sin(-frac{27π}{4}) cos(frac{31π}{4})})(=) (frac{ 8}{-frac{sqrt{2}}{2}cdotfrac{sqrt{2}}{2}})(=-8:frac{2}{4}=-8cdotfrac{2}{1}=-16).
Ответ: (-16).
Смотрите также:
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
Тригонометрические функции любого угла и определение синуса, косинуса, тангенса и котангенса:
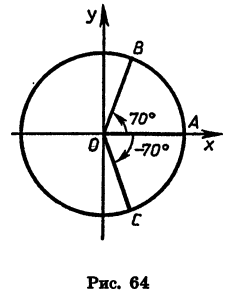
Отметим на оси х справа от начала координат точку А и проведем через нее окружность с центром в точке О (рис. 64). Радиус OA будем называть начальным радиусом.
Повернем начальный радиус около точки О на 70° против часовой стрелки. При этом он перейдет в радиус ОВ. Говорят, что угол поворота равен 70°. Если повернуть начальный радиус около точки О на 70° по часовой стрелке, то он перейдет в радиус ОС. В этом случае говорят, что угол поворота равен —70°. Углы поворота в 70° и —70° показаны стрелками на рисунке 64.
Вообще при повороте против часовой стрелки угол поворота считают положительным, а при повороте по часовой стрелке — отрицательным.
Из курса геометрии известно, что мера угла в градусах выражается числом от 0 до 180. Что касается угла поворота, то он может выражаться в градусах каким угодно действительным числом от 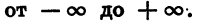
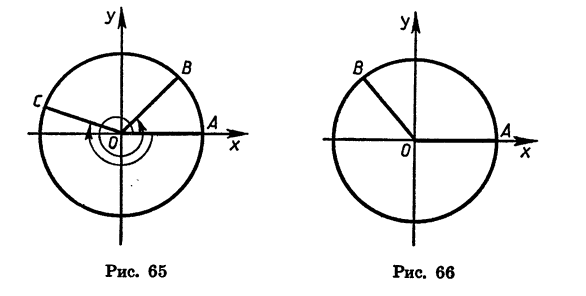
радиус повернуть против часовой стрелки на 180°, а потом еще на 30°, то угол поворота будет равен 210°. Если начальный радиус сделает полный оборот против часовой стрелки, то угол поворота будет равен 360°; если он сделает полтора оборота в том же направлении, то угол поворота будет равен 540° и т. д. На рисунке 65 стрелками показаны углы поворота в 405° и -200°.
Рассмотрим радиусы OA и ОВ (рис. 66). Существует бесконечно много углов поворота, при которых начальный радиус OA переходит в радиус ОВ. Так, если 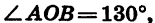
Пусть при повороте на угол а начальный радиус OA переходит в радиус ОВ. В зависимости от того, в какой координатной четверти окажется радиус ОВ, угол а называют углом этой четверти. Так, если 0° < а < 90°, то а — угол I четверти; если 90° < а <180°, то а — угол II четверти; если 180° < а < 270°, то а — угол III четверти; если 270° < а < 360°, то а — угол IV четверти. Очевидно, что при прибавлении к углу целого числа оборотов получается угол той же четверти. Например, угол в 430° является углом I четверти, так как 430° = 360°+ 70° и 0°<70°<90°; угол в 920° является углом III четверти, так как 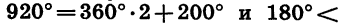
Углы 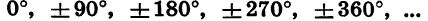
В курсе геометрии были определены синус, косинус и тангенс угла а при 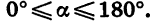
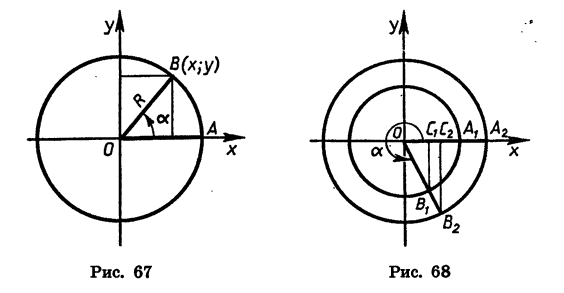
Пусть при повороте около точки О на угол а начальный радиус OA переходит в радиус ОВ (рис. 67).
Синусом угла а называется отношение ординаты точки В к длине радиуса.
Косинусом утла а называется отношение абсциссы точки В к длине радиуса.
Тангенсом угла а называется отношение ординаты точки В к ее абсциссе.
Котангенсом угла а называется отношение абсциссы точки В к ее ординате.
Если координаты точки В равны х и у, а длина начального радиуса равна R, то
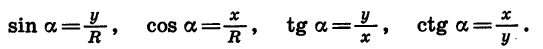
В курсе геометрии было показано, что значения синуса, косинуса и тангенса угла а, где 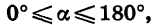
Покажем, например, что sin а не зависит от R.
Пусть при повороте луча 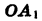
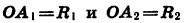
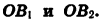
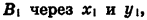
Опустим перпендикуляры из точек 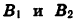
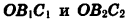
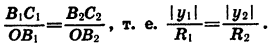
Так как точки 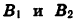
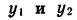
Заметим, что это равенство верно и в том случае, когда точки 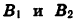
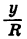
Выражения sin а и cos а определены при любом а, так как для любого угла поворота можно найти соответствующие значения дробей 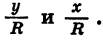
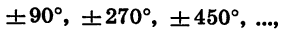
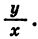
Каждому допустимому значению а соответствует единственное значение sin a, cos а, tg а и ctg а. Поэтому синус, косинус, тангенс и котангенс являются функциями угла а. Их называют тригонометрическими функциями.
Можно доказать, что областью значений синуса и косинуса является промежуток [—1; 1], а областью значений тангенса и котангенса — множество всех действительных чисел.
Приведем примеры вычисления значений тригонометрических функций.
Пример:
Найдем с помощью чертежа приближенные значения sin 110°, cos 110°, tg 110° и ctg 110°.
Начертим окружность с центром в начале координат и радиусом OA = R = 3 (рис. 69). Повернем радиус OA на 110°. Получим радиус ОВ. Найдем по рисунку координаты х и у точки В: 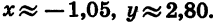
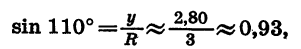
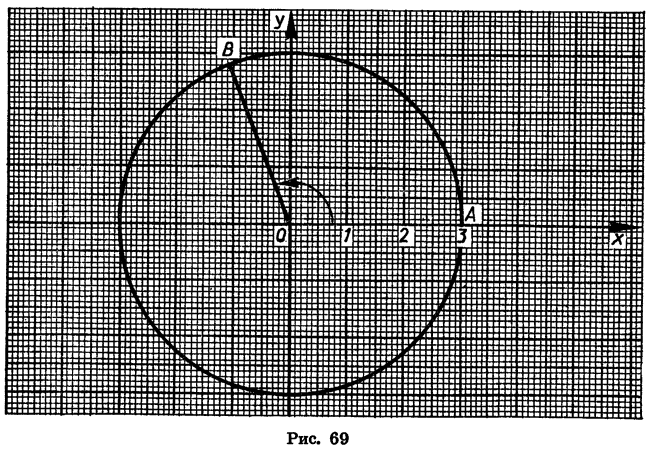
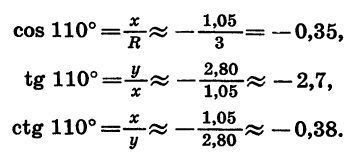
В таблице приведены известные из курса геометрии значения синуса, косинуса и тангенса углов 0°, 30°, 45°, 60° и 90°. Прочерк сделан в том случае, когда выражение не имеет смысла.
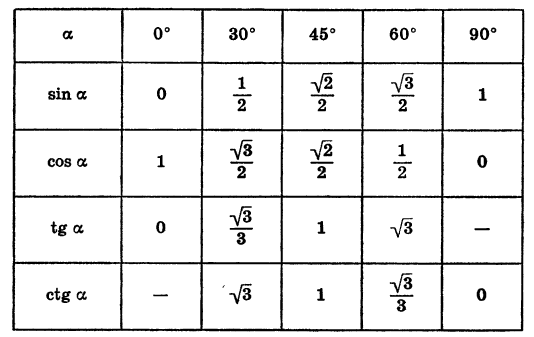
Значения котангенса могут быть получены из значений тангенса, так как котангенс угла является числом, обратным тангенсу этого же угла. Поэтому, например,
Пример:
Найдем синус, косинус, тангенс и котангенс углов 180° и 270°.
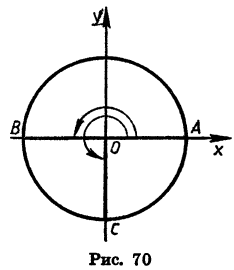
При повороте на 180° около точки О радиус OA, равный 1, (рис. 70) переходит в радиус ОВ, а при повороте на 270° — в радиус ОС.
Так как точка В имеет координаты х = — 1 и у = 0, то
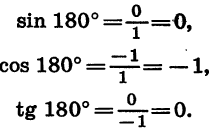
Так как точка С имеет координаты х = 0 и у = —1, то

Напомним, что выражения ctg 180° и tg 270° не имеют смысла.
Свойства синуса, косинуса, тангенса и котангенса
Рассмотрим некоторые свойства тригонометрических функций.
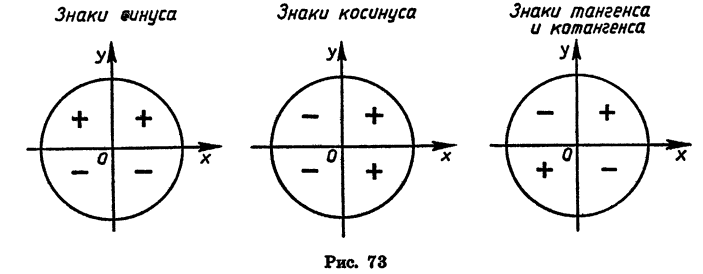
Выясним сначала, какие знаки имеют синус, косинус, тангенс и котангенс в каждой из координатных четвертей.
Пусть при повороте радиуса OA, равного R, на угол а точка А перешла в точку В с координатами х и у (см. рис. 67).
Так как 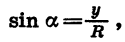
В I и II четвертях у > 0, а в III и IV четвертях у < 0. Значит, sin a > 0, если а является углом I или II четверти, и sin a < 0, если а является углом III или IV четверти.
Знак cos а зависит от знака х, так как 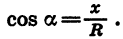
Так как 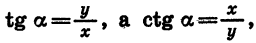
Знаки синуса, косинуса, тангенса и котангенса в каждой из четвертей показаны на рисунке 73.
Выясним теперь вопрос о четности и нечетности тригонометрических функций.
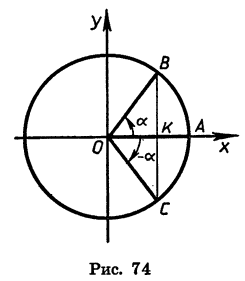
Пусть при повороте на угол а радиус OA переходит в радиус ОВ, а при повороте на угол — а в радиус ОС х (рис. 74). Соединив отрезком точки В и С, получим равнобедренный треугольник ВОС. Луч OA является биссектрисой угла ВОС. Значит, отрезок ОК является медианой и высотой треугольника ВОС. Отсюда следует, что точки В и С симметричны относительно оси абсцисс.
Пусть координаты точки В равны х и у, тогда координаты точки С равны х и -у. Пользуясь этим, найдем, что
Мы получили формулы, выражающие зависимость между синусами, косинусами, тангенсами и котангенсами противоположных углов:
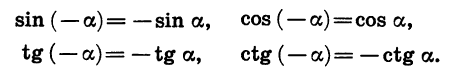
Например:
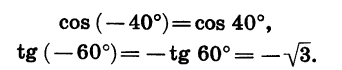
Итак, синус, тангенс и котангенс являются нечетными функциями, а косинус является четной функцией.
Рассмотрим еще одно свойство тригонометрических функций.
Если при повороте радиуса OA на угол а получен радиус ОВ (см. рис. 67), то тот же радиус получится и при повороте OA на угол, отличающийся от а на целое число оборотов. Отсюда следует, что при изменении угла на целое число оборотов значения синуса, косинуса, тангенса и котангенса не изменяются.
Например:
Рассмотренные свойства позволяют свести нахождение значений синуса, косинуса, тангенса и котангенса любого угла к нахождению их значений для неотрицательного угла, меньшего 360°.
Пример:
Найдем sin 765° и cos ( — 1170°). Имеем:
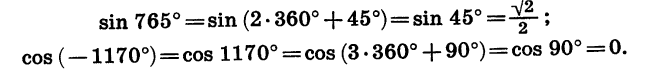
Радианная мера угла. Вычисление значении тригонометрических функции с помощью микрокалькулятора
Как известно, углы измеряются в градусах, минутах, секундах. Эти единицы измерения связаны между собой соотношениями
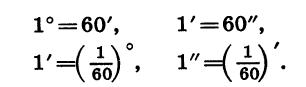
Кроме указанных, используется также единица измерения углов, называемая радианом.
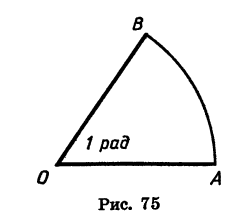
Углом в один радиан называют центральный угол, которому соответствует длина дуги, равная длине радиуса окружности.
Угол, равный 1 рад, изображен на рисунке 75.
Радианная мера угла, т. е. величина угла, выраженная в радианах, не зависит О А от длины радиуса. Это следует из того, что фигуры, ограниченные углом и дугой окружности с центром в вершине этого угла, подобны между собой (рис. 76).
Установим связь между радиан-ным и градусным измерениями углов.
Углу, равному 180°, соответствует полуокружность, т. е. дуга, длина l которой равна
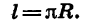
Чтобы найти радианную меру этого угла, надо длину дуги l разделить на длину радиуса R. Получим:
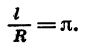
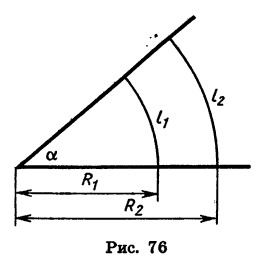
Следовательно, радианная мера угла в 180° равна
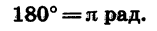
Отсюда получаем, что радианная мера угла в 1° равна
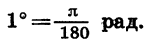
Приближенно 1° равен 0,017 рад.
Из равенства 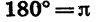
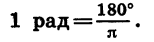
Приближенно 1 рад равен 57°.
Рассмотрим примеры перехода от радианной меры к градусной и от градусной меры к радианной.
Пример:
Выразим в градусах 4,5 рад.
Так как
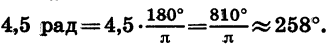
Пример:
Найдем радианную меру угла в 72°.
Так как
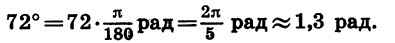
При записи радианной меры угла обозначение «рад» часто опускают. Например, вместо равенства 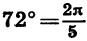
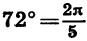
Выразим в радианной мере углы 30°, 45°, 60°, 90°, 270° и 360°. Получим:
Радианная мера угла часто используется в тригонометрических выражениях. Так, запись sirfl означает синус угла в 1 радиан, запись sin ( — 2,5) означает синус угла в —2,5 радиана, запись 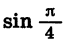
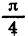
Значения тригонометрических функций для углов, выраженных как в градусах, так и в радианах, можно находить, используя микрокалькулятор. Так, с помощью микрокалькулятора «Электроника БЗ-З6» значения синуса, косинуса и тангенса вычисляют следующим образом. Переводят переключатель «ГРАД — РАД», находящийся в нижней части корпуса, в положение «ГРАД», если угол задан в градусах, или в положение «РАД», если угол задан в радианах. Вводят угол, нажимают клавишу 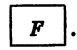
Пример:
Найдем с помощью микрокалькулятора значение выражения с точностью до 0,001:
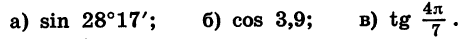
а) Установим переключатель в положение «ГРАД», затем выразим 28°17′ в градусах и нажмем «последовательно клавиши 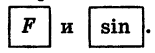
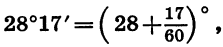

Получаем, что
б) Устанавливаем переключатель в положение «РАД» и находим значение cos 3,9 по программе:
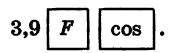
Получаем, что cos
в) Переключатель устанавливаем в положение «РАД». При нахождении значения выражения 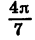
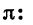
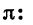
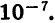

Получаем, что
Отметим, что для вычисления котангенса угла надо сначала найти значение тангенса этого угла, а потом обратное число, нажав клавиши
Основные тригонометрические формулы
Соотношения между тригонометрическими функциями одного и того же угла:
Рассмотрим, как связаны между собой синус и косинус одного и того же угла.
Пусть при повороте радиуса OA вокруг точки О на угол а получен радиус ОВ (рис. 77). По определению
где х — абсцисса точки В, у — ее ордината, a R — длина радиуса OA. Отсюда

Так как точка В принадлежит окружности с центром в начале координат, радиус которой равен R, то ее координаты удовлетворяют уравнению
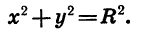
Подставив в это уравнение вместо х и у выражения R cos а и R sin а, получим:
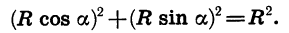
Разделив обе части последнего равенства на 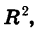

Равенство (1) верно при любых значениях а. Выясним теперь, как связаны между собой тангенс, синус и косинус одного и того же угла.
По определению 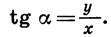
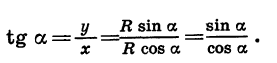
Таким образом,
Аналогично
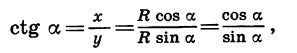
Равенство (2) верно при всех значениях а, при которых cos 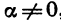
С помощью формул (1) — (3) можно получить другие формулы, выражающие соотношения между тригонометрическими функциями одного и того же угла.
Из равенств (2) и (3) получим:
Равенство (4) показывает, как связаны между собой тангенс и котангенс угла а. Оно верно при всех значениях а, при которых tg а и ctg а имеют смысл.
Заметим, что формулу (4) можно получить и непосредственно из определения тангенса и котангенса.
Выведем теперь формулы, выражающие соотношения между тангенсом и косинусом, а также между котангенсом и синусом одного и того же угла.
Разделив обе части равенства (1) на 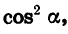
Если обе части равенства (1) разделить на 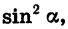
т. е.
Равенство (5) верно, когда cos 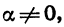
Равенства (1) — (6) являются тождествами. Их называют основными тригонометрическими тождествами. Рассмотрим примеры использования этих тождеств для нахождения значений тригонометрических функций по известному значению одной из них.
Пример:
Найдем cos a, tg а и ctg а, если известно, что sin
Найдем сначала cos а. Из формулы 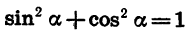
Так как а является углом II четверти, то его косинус отрицателен. Значит,
Зная синус и косинус угла а, можно найти его тангенс:
Для отыскания котангенса угла а удобно воспользоваться формулой tg a • ctg a = 1. Имеем:
Пример:
Известно, что 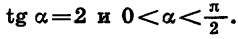
Воспользовавшись формулой 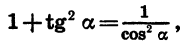
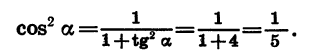
По условию угол a является углом I четверти, поэтому его косинус положителен. Значит,
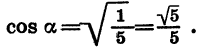
Зная cos а и tg а, можно найти sin а. Из формулы 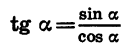
По известному tg а легко найти ctga:
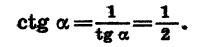
Итак,
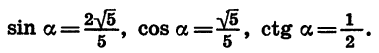
Применение основных тригонометрических формул к преобразованию выражении
Мы уже встречались с некоторыми простейшими преобразованиями тригонометрических выражений. Рассмотрим более сложные примеры.
Пример:
Упростим выражение
Воспользовавшись формулами 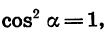
Пример:
Упростим выражение
Пример:
Докажем тождество
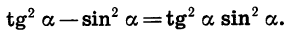
Преобразуем левую часть данного равенства:
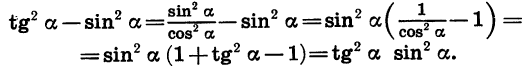
Мы получили выражение, стоящее в правой части равенства. Таким образом, тождество доказано.
Формулы приведения
Тригонометрические функции углов вида 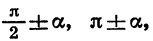
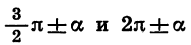
Выведем сначала формулы приведения для синуса и косинуса.
Докажем, что для любого а
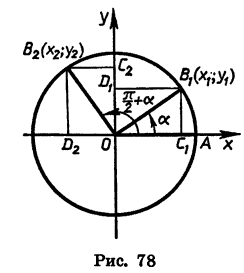
Повернем радиус OA, длина которого равна R, на угол а и на угол 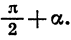
Опустим из точки В1 перпендикуляры 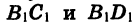
Повернем прямоугольник 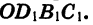
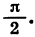
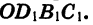
Отсюда следует, что ордината точки В2 равна абсциссе точки В1, а абсцисса точки В2 равна числу, противоположному ординате точки В1. Обозначим координаты точки B1 через 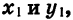
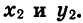
Значит,
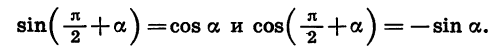
Из формул (1) следует, что
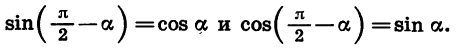
Действительно, представим разность 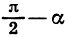
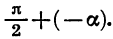
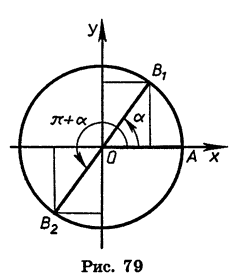
Формулы приведения для синуса и косинуса угла 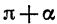
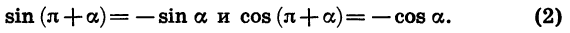
Для доказательства достаточно представить 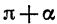
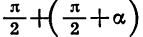
Заметим, что к формулам (2) легко прийти и из геометрических соображений (рис. 79). При повороте радиуса OA на угол а и на угол 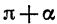
начала координат точек равны по модулю и противоположны по знаку. Отсюда следует, что 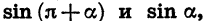
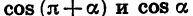
Из формул (2) следует, что
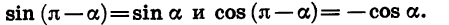
Для доказательства достаточно представить 
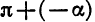
Формулы приведения для синуса и косинуса угла 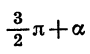
Чтобы доказать формулы (3), достаточно представить 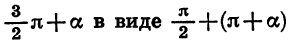
Из формул (3) нетрудно получить, что
Наконец, формулы приведения для синуса и косинуса угла 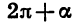
Справедливы также формулы
Например, для
Формулы приведения для тангенса и котангенса можно получить с помощью формул приведения для синуса и косинуса. Например:
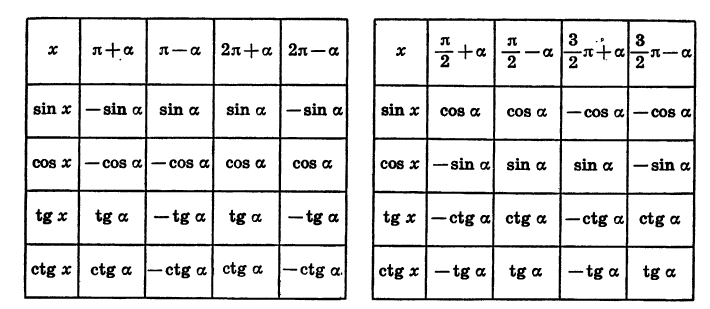
Все формулы приведения сведем в две таблицы, поместив в первой из них формулы для углов 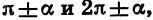
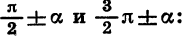
Цо таблицам легко проследить закономерности, имеющие место для формул приведения. Эти закономерности позволяют сформулировать правило, с помощью которого можно записать любую формулу приведения, не прибегая к таблице:
Функция в правой части равенства берется с тем же знаком, какой имеет исходная функция, если считать, что угол а является углом 1 четверти;
для углов 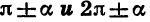
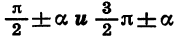
Пример:
Выразим 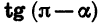
Если считать, что a — угол I четверти, то 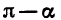
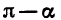
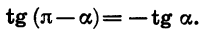
С помощью формул приведения нахождение значений тригонометрических функций любого угла можно свести к нахождению значений тригонометрических функций угла от 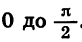
Пример:
Найдем значение
Пример:
Найдем значение sin (— 585°).
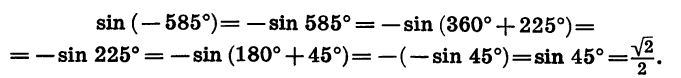
Формулы сложения и их следствия
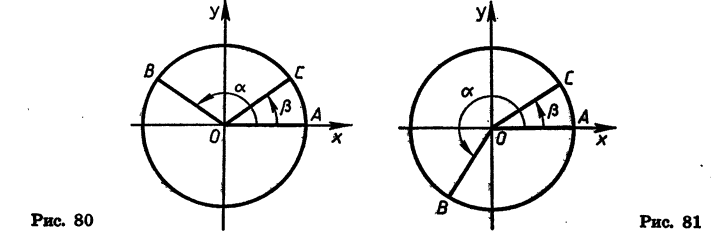
Выведем формулы, выражающие тригонометрические функции суммы и разности двух углов через тригонометрические функции этих углов.
Повернем радиус OA, равный R, около точки О на угол а и на угол 
Найдем скалярное произведение векторов 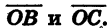
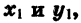
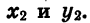
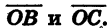
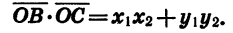
Выразим скалярное произведение 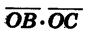

Подставив значения 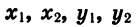
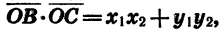
С другой стороны, по теореме о скалярном произведении векторов имеем:

Угол ВОС между векторами 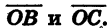

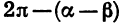
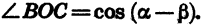
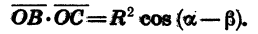
Так как 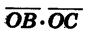
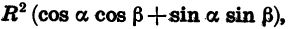
Формулу (1) называют формулой косинуса разности.
Косинус разности двух углов равен произведению косинусов этих углов плюс произведение синусов этих углов.
С помощью формулы (1) легко получить формулу косинуса суммы:
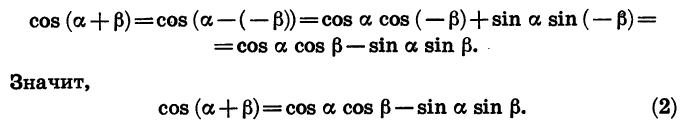
Косинус суммы двух углов равен произведению косинусов этих углов минус произведение синусов этих углов.
Выведем теперь формулы синуса суммы и синуса разности. Используя формулы приведения и формулу (1), получим:
Синус суммы двух углов равен произведению синуса первого угла на косинус второго плюс произведение косинуса первого угла на синус второго.
Для синуса разности имеем:
Синус разности двух углов равен произведению синуса первого угла на косинус второго минус произведение косинуса первого угла на синус второго.
Формулы (1) — (4) называют формулами сложения для синуса и косинуса.
Приведем примеры использования формул сложения.
Пример:
Вычислим cos 15° и sin 15°. Представим 15° в виде разности 45° — 30°. Тогда
Пример:
Упростим выражение 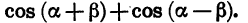
Используя формулы (1) — (4), можно вывести формулы сложения для тангенса и котангенса. Выведем, например, формулу тангенса суммы:
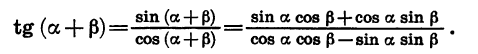
Разделим числитель и знаменатель полученной дроби на произведение cos a cos 
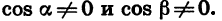
Значит,
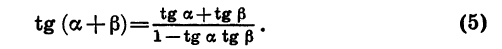
Аналогично можно доказать, что
Формулы двойного угла
Формулы сложения позволяют выразить sin 2a, cos 2a и tg 2a через тригонометрические функции угла a. Положим в формулах

Эти тождества называют формулами двойного угла.
Приведем примеры применения формул двойного угла для нахождения значений тригонометрических функций и преобразования тригонометрических выражений.
Пример:
Найдем значение sin 2а, зная, что cosa = — 0,8 и a — угол III четверти.
Сначала вычислим sin а. Так как a — угол III четверти, то sin а < 0. Поэтому
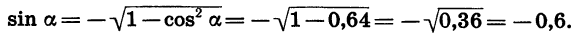
По формуле синуса двойного угла
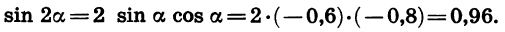
Пример:
Упростим выражение
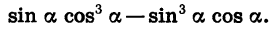
Вынесем за скобки sin a cos a и воспользуемся формулами двойного угла:
Из формулы (2) следует, что
Действительно, выразив cos 2a через sin a, получим:
Отсюда
Аналогично, выразив cos 2a через cos a, получим:
Формулы (4) и (5) используются в вычислениях и преобразованиях.
Пример:
Упростим выражение
Применим формулы (4) и (5) к выражениям 1 — cos а и 1 + cos а, представив а в виде произведения 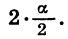
Формулы суммы и разности тригонометрических функции
Сумму и разность синусов или косинусов можно представить в виде произведения тригонометрических функций. Формулы, на которых основано такое преобразование, могут быть получены из формул сложения.
Чтобы представить в виде произведения сумму sin a + sin 
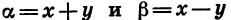
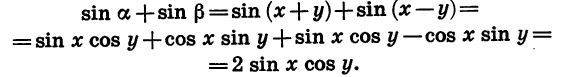
Из равенств a = x + y и 
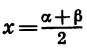
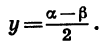
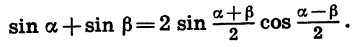
Мы получили формулу суммы синусов двух углов.
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
Аналогично можно вывести формулы разности синусов, суммы и разности косинусов.
Формула разности синусов:
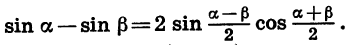
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.
Формула суммы косинусов:
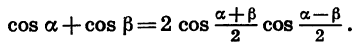
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы, этих углов на косинус их полуразности.
Формула разности косинусов:
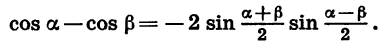
Разность косинусов двух углов равна взятому со знаком *минус» удвоенному произведению синуса полусуммы этих углов на синус их полуразности.
Учитывая, что 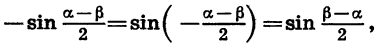
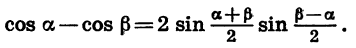
Приведем примеры применения полученных формул.
Пример:
Упростим сумму sin 10° + sin 50°.
Воспользовавшись формулой суммы синусов, получим:
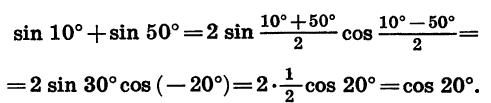
Пример:
Представим в виде произведения разность
Воспользовавшись формулой приведения, представим данное выражение в виде разности косинусов и преобразуем ее в произведение. Тогда
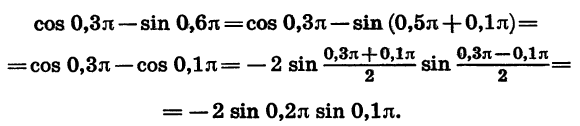
Пример:
Представим в виде произведения выражение 1 — sin а.
Так как 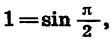
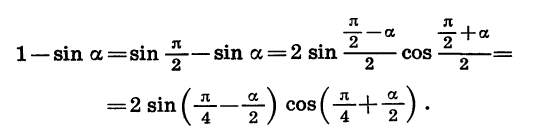
Эту задачу можно решить иначе:
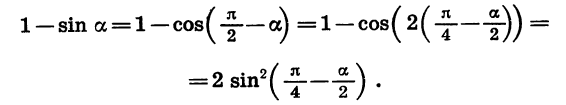
С помощью формул приведения первое из полученных выражений можно преобразовать во второе и наоборот.
Вычисление значений тригонометрических выражений
Возможно вам будут полезны эти страницы:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Определение значения синуса, косинуса, тангенса и котангенса
Определение
Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.
Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.
Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.
Процесс работы и расчета функций данного вида, очень непростой. Решение задач и уравнение, очень часто вызывают сложности. Поэтому, со временем, были созданы и разработаны несколько видов решений, чтобы облегчить жизнь математика и всем представителям технических наук. Преобразовывая тригонометрические формулы, необходимо руководствоваться следующими правилами:
- Нельзя продумывать весь процесс решения от начала до самого конца сразу. Нужно определиться с основными задачами и данными.
- Весь пример, подвергать упрощению или преобразования постепенно;
- Разрешается применять все преобразования и действия, связанные с алгеброй, а именно: вынести значение за пределы скобок. сократить значение и многое другое:
[ sin x=frac{a}{c} ; cos x=frac{b}{c} ; operatorname{tg} x=frac{sin x}{cos x} ; operatorname{ctg}=frac{1}{operatorname{tg} x}=frac{sin x}{cos x} ]
Зная основные определения тригонометрических функций, можно определить их угловые значения. Для углов от нуля до трехсот шестидесяти градусов, вычислим данные и запишем их в виде таблицы.
Значения вышеупомянутых математических функций, в частности в разделе геометрия, вычисляются как соотношения длин прямоугольного треугольника.
Углы геометрической фигуры имеют соответствующие значения в градусах. Используя основные определения математики, а именно тригонометрии можно определить нужные нам данные.
Определим основные значения
1.синуса (sin):
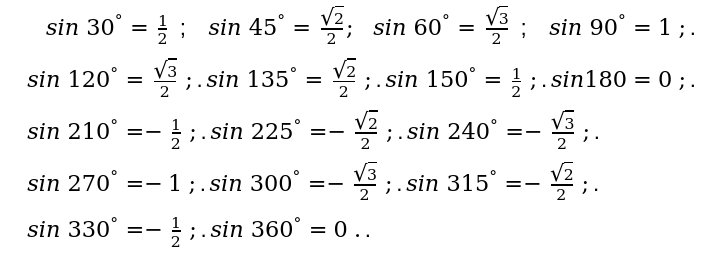
2. косинуса (cos):
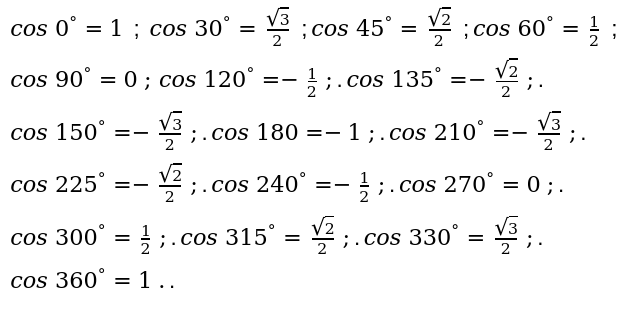
3. тангенса(tg):
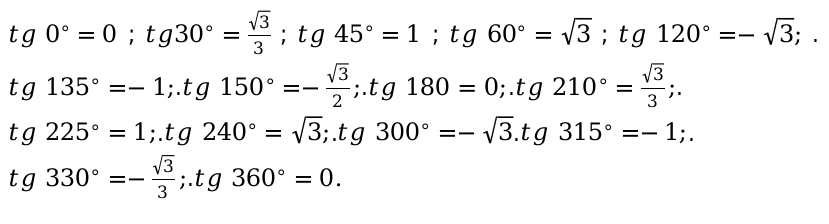
[ operatorname{tg} 90^{circ}, 270^{circ} ]
Данные выше угловые значения, не определяются, согласно основным законам геометрии и математики.
4. котангенса (ctg)
[ operatorname{ctg} 0^{circ}, 180^{circ}, 360^{circ} ]
Для перечисленных выше угловых значений по законам математики и всех технических наук в целом, значения не определяются
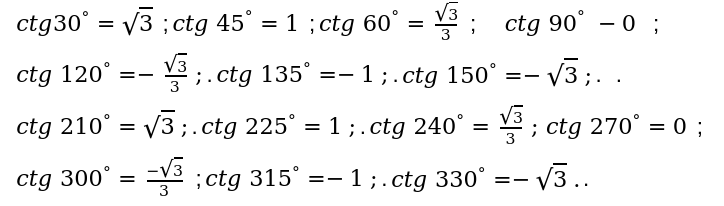
Мы произвели основные расчеты. Определили результаты угловых значений.
Мы определились с основными угловыми значениями функций. Следующим шагом будет их сведение в таблицу.
Таблица1. Основные значения функций косинус, синус, тангенс и котангенс, для угловых значений и радиан
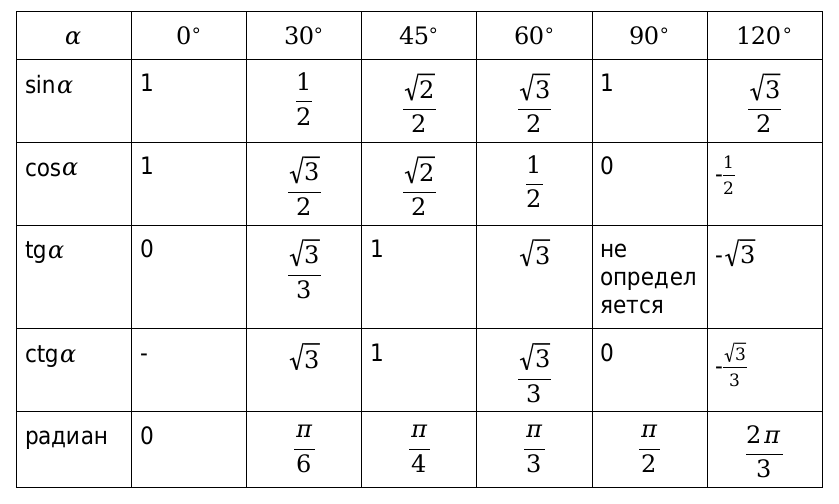
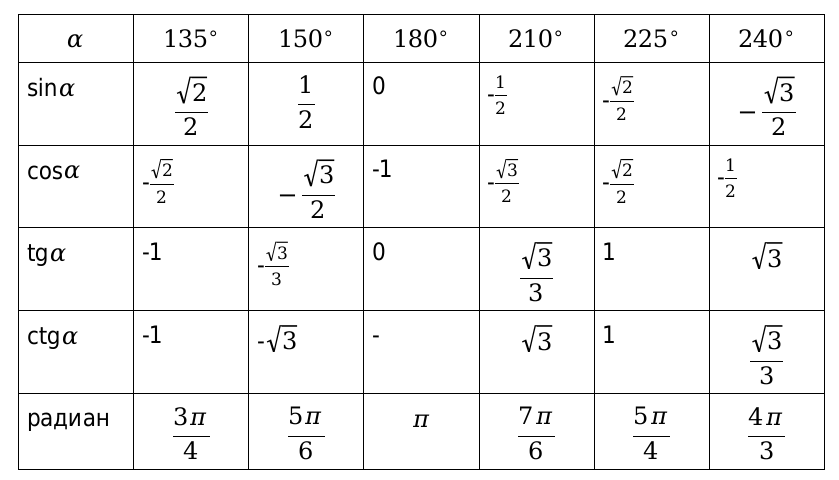
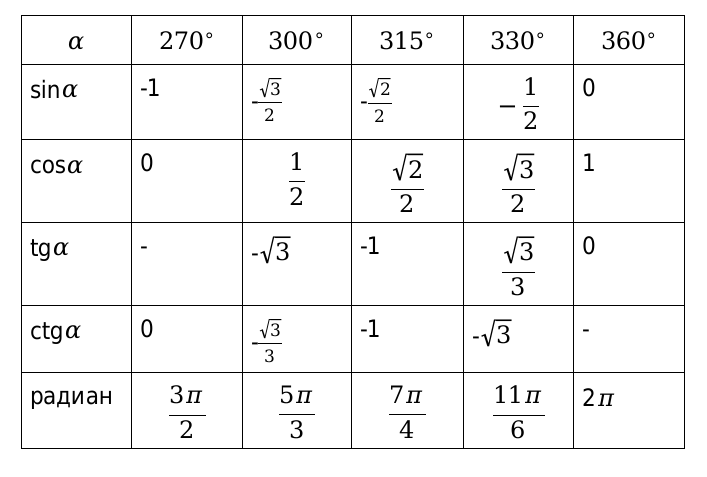
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более лучшего восприятия. Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.
Таблица 2. Нестандартные углы функций косинус, синус, тангенс и котангенс в тригонометрии

В данной таблице приведены значения углов, которые считаются нестандартными, также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Например:
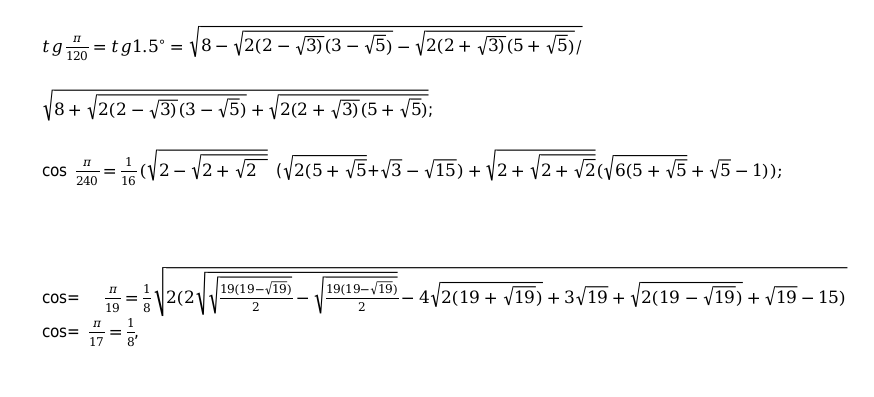
Значение заданной функции берется из таблицы. Оно равняется данному, которое попадает на пересечение столбца и строки.
Пример №1. Необходимо определить чему равен [operatorname{tg} 300]
Берем левый столбец с наименованием функции, находим в верхней строке нужный градус, и на пересечении определяем нужный ответ.
Следовательно:[operatorname{tg} 300^{circ}=-sqrt{3}].
Пример №2. Необходимо определить чему равен [cos frac{5 pi}{3}].
Берем левый столбец с наименованием функции, находим в нижней строке значение радиан, поднимается на верх таблицы и определяем градусы.
[text { Следовательно: } operatorname{tg} 300^{circ}=frac{1}{2} .]
Пример №3. Необходимо определить чему равен [cos frac{11 pi}{6}].
Проводим аналогичные действия, как в предыдущих двух примерах и определяем угловое значение.
[text { Следовательно } cos =frac{sqrt{3}}{2}=330^{circ}.]
Таблица Брадиса для решения основных задач по тригонометрии
Первое упоминание о таблице, датируется 20-ми годами прошлого века. Основоположником, является советский ученый математик, и талантливый педагог Владимир Брадис. Созданная Брадисом таблица, позволяет определить значения тригонометрических функций, с большой точностью, а именно до четырех знаков. На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения. Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме. В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.
Можно определить точность углового значения до минуты. Существуют также таблицы, где есть семизначные значения.
Для того чтобы составить таблицы следует пользовался методом разложения функций (либо метод разложения на степень в ряд)
Примеры решения задач
Пример 1:
Необходимо определить синус угла 18 ° 44 ‘.
По таблице значений определяем данные синуса 18 ° 42 ‘. Далее используем поправку, равную две минуты. Плюсуем ее и заданные минуты: 18 ° 44 ‘ − 18 ° 42 ‘ = 2 ‘
Нужное значение равняется — 0,0006.
Узнав все необходимые значения, находим окончательное решение:
sin 18 ° 44 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 2:
Условие задачи, заключается в необходимости вычислить угол функции синус 76 ° 12. В таблице находим столбец с название угол и ищем 76 градусов и строку со значением 12. Далее, исходя из найденных ячеек, находим значение угла — 0,2284.
Ответ: синус 76 ° 12 =0,2284.
Пример 3:
Нужно найти значение синус 16 градусов 32 минут. Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть
sin 16 ° 32 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 4:
Нужно найти значение синус 22 градусов 10 минут. Чтобы посчитать значение 22 ° 12, в таблице найдем значение необходимого угла, наиболее подходящее заданному. Это sin16 30 =0.3778. Так как 22 ° 10= 22 ° 12+2, то тогда выбираем поправку равную двум и видим, что нужный нам градус равный 22 ° имеет значение 0,0005. Далее записываем:
sin 22 ° 10 ‘ = (22 12-2) =0. 3778 + 0. 0005 = 0. 3773
Пример 5:
Нужно найти значение косинус 50 градусов 33 минут. Для того, чтобы посчитать значение 53 31 в таблице найдем значение нужного угла, наиболее близкого к искомому со знаком минус. Это косинус 50 33 =0.6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение:
косинус 50 ° 33 ‘ = (50 30-3) =0. 6361 +(- 0. 0007) = 0. 6454
Пример 6:
Нужно найти tg 35 градусов 6 минут. В таблице значений функции, в столбце найдем значение 35 градусов, а в строке 6 минут. Определяем нужное значение по таблице равное 0,7028.
Пример 7:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102.
Пример 8:
Нужно найти значение косинус для 49° 33 минут.
Для того чтобы вычислить значение 49° 31. В таблице найдем значение угла, наиболее близкого по значению к заданному, но только с отрицательным знаком минус. Это косинус 49° 31/ =0.6361 Так как 49° 31/=50 30+3, из этого следует, что поправка равняется трем. Значение 49 градусов равно 0,0007, поэтому: косинус 49° 33 ‘ = ( 49° 31-3) =0 . 6361 +(- 0 . 0007) = 0,6454
Нет времени решать самому?
Наши эксперты помогут!
Основные способы, которые помогут заполнить таблицу функций
1 Действие: Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс (sec).
2. Действие: Заполняем пустые ячейки со значение синус. Берем выражение [frac{sqrt{x}}{2}] и подставляем числовые значения, то есть величины углов. они записаны в первом столбике. Далее применяя [frac{sqrt{x}}{2}] можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу.
Для наглядности все прописанные действия, можно разобрать на конкретном примере.
Например, мы заполняем ячейку sin 0 градусов. На месте неизвестного значения в выражении [frac{sqrt{x}}{2}] записываем значение угла.
Получаем следующую запись: [frac{sqrt{x}}{2}=frac{0}{2}=0]. Затем, проводим те же операции для заполнения оставшихся пустых строк.
[ frac{sqrt{1}}{2}=frac{1}{2} ; frac{sqrt{2}}{2}=frac{(sqrt{2 cdot 2})}{(2 cdot sqrt{2})}=frac{2}{2 cdot sqrt{2}}=frac{1}{sqrt{2}} ; frac{sqrt{3}}{2} frac{sqrt{4}}{2}=frac{2}{2}=1 ]
Необходимо первым делом заполнять неизвестные ячейки, для функции синус. Это значительно в будущем облегчит заполнение всей таблицы. Так как именно за данной функции и ее данных и завязана вся работы таблицы.
3. Действие: Продолжаем считать таблицу. для этого значения синуса, которые подсчитаны были ранее, переписываем для функции косинус. Только делаем это в порядке обратном значению синусу. Данная теория действительна, потому что sin x° = cos (90-x). Если в самой крайней ячейке синус, имеется 1(sin90°=1). То в первую строку значения косинус, перепишется это числовое значение, cos 0° = 1. Таким образом заканчиваем заполнение до конца.
4. Действие: Для определения тангенса. Необходимо произвести деление данных синуса на косинус. Так как тангенс равен данной функции. [operatorname{tg}=frac{sin }{cos }]. Выходим что искомое значение равно данному выражению. Если [operatorname{tg} 45^{circ}=frac{sin }{cos }=frac{sqrt{1}}{2} / frac{sqrt{3}}{2}=frac{1}{sqrt{3}} .]
Аналогично поступаем и далее.
5. Действие: Для заполнения граф косеканс и секанс нужно 1/sin и 1/cos.
[text { Так как, } operatorname{cosec}=frac{1}{sin } . text { Например, } sin 40^{circ}=frac{1}{2}, text { поэтому } operatorname{cosec} 40^{circ}=frac{1}{frac{1}{2}}=2]
Действие 6: Оставшиеся функции тангенс и котангенс. также записываются обратно значениям. Если tg90 равняется ctg0, значение tg60 будет соответственно равен значению ctg 30 градусов.
[text { Таким же методом заполняются оставшиеся строки таблицы. Так } text { как } operatorname{ctg}=frac{1}{t g}, text { в свою очередь } operatorname{ctg}=frac{cos }{sin }]
Вычисление данных при помощи фигуры — прямоугольный треугольник
Для этого строится нужный треугольник заданным углом, который необходимо определить. Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.
Вычисление при помощи длин сторон треугольника происходит следующим образом:
- обозначается катет;
- сторона возле угла;
- сторона напротив угла с прямым значением.
Функции могут выражаться по-разному в отношении сторон. Например, нам нужно определим значение sin 45°. Поделим имеющуюся длину значения противолежащего катета на значение длины гипотенузы. Если заданные значения длины равны 4 и 6 соответственно. Тогда, составим следующее выражение и получим sin[45^{circ}=frac{4}{6}=0,67]
Для определения значений основных функций в математике, необходимо заучить наизусть определение основных понятий, связанный с данной темой.
В процессе решения задачи, это придется применять постоянно.
Значения косеканса и секанса определяются в обратном порядке. Для этого необходимо знать какие стороны нужно делить для определения вышеперечисленных функций.
Косеканс находится [operatorname{cosec}=frac{1}{sin }] следовательно, нужно разделить гипотенузу на противолежащий катет. Секанс, наоборот к прилежащему катету [mathrm{sec}=frac{1}{cos }].
Например, для определения cosec 40°, если катет равен 5, а гипотенуза соответственно равна 8. Нужно разделить 5/8 и получим ответ cosec 40° = 0,63.
При вычислениях всегда рекомендуется исключать значение под корнем в знаменателе, это наиболее облегчает процесс расчета.
Рассмотренная тема преобразования и расчета функций, является довольно громоздкой, на первый взгляд. Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
Вычисление значений углов по окружности
Самый простой и понятный способ для вычисления углов и радиан.
Для этого вычерчиваем окружность с радиусом R. Он в свою очередь, равен единичному значению. Центр окружности равен центру системы координат. От положительной оси считаем углы, по часовой стрелке, выполняющей движении против хода. Точка, имеющая координаты 1;0 равняется угловому значению ноль. если координаты -1;0, тогда угол равен 90 градусов. Точка, находящаяся на окружности, соответствует углу от нуля до 360 градусов. Так как окружность является единичной, значения углов для синуса и косинуса находятся в пределах от -1 до 1:
Определяются знаки функций, также по окружности. если угловое значение более 360 градусов, делается два оборота по часовой стрелке и плюсуется еще дополнительно 12 минут.
[ cos (alpha+360 cdot n)=sin alpha ;] [ sin (alpha+360 cdot n)=sin alpha / ]
Значения тангенсов и котангенсов, можно вычислить аналогично, по окружности. Однако легче посчитать по формулам, уже известных данных.
[ operatorname{tg} alpha=frac{sin alpha}{cos alpha} ; operatorname{ctg} alpha=frac{cos alpha}{sin alpha} ]
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
| sin |
sin |
|
| cos |
1+tg |
cos |
| tg |
1+ctg |
sin |
| ctg |
tg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим. Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
получаем
то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
| 0 | |||||
| sin |
0 | ||||
| cos |
0 | ||||
| tg |
0 | − | |||
| ctg |
− | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и
и равными острыми углами А и
Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos
и
т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол
равен
,
,
.
Найдите .
Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:
Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:
AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен
tg A =
Найдите AB.
Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A =
Найдите AH.
Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно
откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.
Решение:
Так как sin A = тогда
c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
=
получим
тогда BH = = 0,5,
AH = AB — BH = 18 — 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.
Решение:
Так как для АВС:
A =
sin В =
а для ВНС: sin В =
=
, откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.
Решение:
По определению sin A= =
=
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A =
= 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.
Решение:
По определению sin A = =
=
cos A =
=
=
тогда tg A = который найдем из
BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A =
Найдите АН.
Решение:
По определению tg A=
Для BHC:
, значит
СН =
Для АHC: tg A=
то
AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A =
Найдите АВ.
Решение:
Так как cos В = = sin A =
Из СВН имеем cos В =
=
тогда ВС =
В АВС имеем sinA =
=
тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:
Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A =
получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит
или
k = тогда
АС =
;
АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда
АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:
Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А =
= cos C =
Для АНВ: sin А =
=
то
=
АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:
В прямоугольном АСЕ sin А =
значит
= 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:
A-общий,
),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:
Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A =
то есть
АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A =
AC = 10
Найдите АВ.
Решение:
1-й способ.
Поскольку sin A =
то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то
откуда АВ =
= 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:
Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30
АВ = 2
Найдите высоту CH.
Решение:
Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС =
АВ =
В BHC:
то
следовательно, ВН =
BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2,
Найдите АH.
Решение:
Из АВС найдем ВС =
АВ = 1 (по свойству катета, лежащего против угла 30
),
то
Из ВСН:
то
следовательно,
ВН = ВС =
АН = АВ — НВ = 2 — = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.
Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023