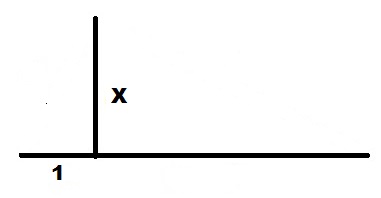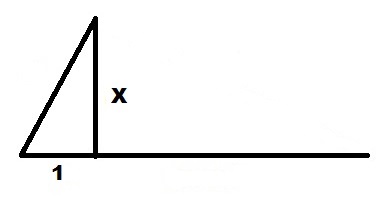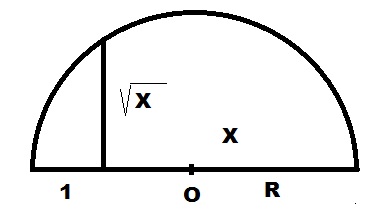Действия, обратные возведению в степень
7. В виду последней особенности действий возведения в степень для него можно составить 2 обратных задачи. Напр.:
1) Я задумал число, возвел его в третью степень (или: в куб), получилось 64; какое число я задумал?
Эту задачу можно записать в виде
(?)3 = 64
2) Я взял число 3, возвел его в некоторую степень, – получилось 81. В какую степень было возведено число 3.
Эту задачу можно записать в виде:
3? = 81
Теперь уже, так как возведение в степень не обладает переместительным законом, эти две задачи следует считать совершенно различными.
Сначала решать их можно подбором: попробуем число 1, 13 = 1, а не 64, след., 1 не годится; 23 = 8, а не 64, след., 2 не годится, 33 = 27, а не 64, след., 3 не годится; 43 = 64, след., в 1 задаче было задумано число 4. Также выясним, что во второй задаче число 3 было возведено в 4-ую степень.
Так как таких задач можно составить очень много, то для их решения необходимо изобрести новые действия. Эти действия обратны возведению в степень. Итак, для возведения в степень существуют два обратных действия: первое из них называется извлечением корня и служит для решения вопросов, подобных первой из наших задач; второе называется нахождением логарифма и служит для решения вопросов, подобных второй задаче.
Если мы обратим внимание на то, что в первой задаче нам даны степень 64 и показатель степени 3, то мы установим определение:
Извлечением корня называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному показателю находят основание степени.
Также точно: во второй задаче даны степень (81) и основание степени (3), а надо найти показателя степени. Поэтому
нахождением логарифма называется действие, обратное возведению в степень, при помощи которого по данной степени и по данному основанию находится показатель степени.
|
Если известен квадрат числа, как быстро найти квадрат следующего …?Wale 9 лет назад
и предыдущего числа? Как быстро найти квадраты чисел которые отличаются от известно на 2 и в «+» и в «-«. например есть число 10 квадрат соответственно 100, найти квадрат чисел 9 и 11, а также 8 и 12 tranquillity 9 лет назад Это можно легко сделать по формуле квадрата суммы. (x^2 читать как «x квадрат») (a+b)^2=a^2+2ab+b^2, в нашем частном случае — (a+1)^2=a^2+2a+1 (a-1)^2=a^2-2a+1 (a+2)^2=a^2+4a+4 (a-2)^2=a^2-4a+4 Например, 11^2=10^2+2*10+1=121. система выбрала этот ответ лучшим комментировать
в избранное
ссылка
отблагодарить Да ответ tranquillity правильный, но по-моему мнению есть возможность упростить следующим образом: для отыскания квадрата следующего числа надо прибавить само число и следующее, а для отыскания предыдущего или отнять само и следующее для 11 это будет 11=100+10+11=121 для 9=100-10-9=81 а для 8 и 12 надо отнять, или, соответственно прибавить учетверенное предыдущее число т.е. для 8 это будет 8=100-4*9=64 для 12=100+4*11=144 Мне так кажется мои способом в уме несколько проще будет посчитать комментировать
в избранное
ссылка
отблагодарить Ушакова Полина 6 месяцев назад Если нужно найти квадрат следующего/предыдущего, то формула такова: x±2?x+1. Следовательно нужно два раза провернуть её, подставив на место х сначала данный квадрат, затем получившийся. Можно ли упростить? Ну… x±2(2?x+1)? Пусть х=1, тогда: 1+2(2?1+1)=1+2(2+1)=3?3=9 ?9=3, 1 от трёх отличается на 2 => да, если нужно найти квадрат числа, отличающегося на ±n от данного, то формула х±n(2?х+1). комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Download Article
Download Article
Need to find the square of a number? Finding a number’s square is as simple as multiplying it by itself. To square fractions, find the squares of both the numerator and denominator. Then reduce or simplify the result. Keep reading for helpful tips and examples!
-
1
Learn how to do basic multiplication. When you square a number, you simply multiply the number by itself so it’s important to know how to multiply. To make it easier to square commonly used single digits, try to memorize basic times tables.[1]
- For example, learn how to multiply single digit times tables.
-
2
Multiply the single digit number by itself. Write down the number you want to square. Remember that when you’re squaring a number, you multiply it by the same number, not 2.[2]
- For example,
is not 5 x 2 = 10. Instead, it’s 5 x 5 = 25.
Advertisement
- For example,
-
3
Recognize other terms for squaring a number. If you read word problems asking you to square a number, keep in mind that they may also ask you to raise the number to the 2 power or factor. This is just another way of asking you to square the number.[3]
- You may also see a problem written as 6^2. This is another way of asking you to square 6.
-
4
Distinguish between squaring and finding the square root. It’s easy to get these terms mixed up, but remember that finding the square root of a number is the opposite of squaring a number. Finding the square root means that you’re looking for the number that can be multiplied by itself to get the number in the square.[4]
Advertisement
-
1
Write the problem out. To find the square of a number with more than 1 digit, it will help if you rewrite the problem as a double digit multiplication problem. Start by writing the same number on top of itself.[5]
- For example, to do
, write 24 x 24.
- For example, to do
-
2
Multiply the number on the bottom ones place by the 1 directly above it. Write a line below the numbers and place the result below the ones space.[6]
- For example, with 24 x 24, multiply the 4 by 4 to get 16. Write a 6 below the ones space and carry the 1 above the top tens number.
-
3
Multiply the bottom ones place by the top tens number. Take the same number on the bottom and multiply it by the top tens number. Remember to add the number you carried and write the result below the line.[7]
- For example, with 24 x 24, multiply 4 by 2 and add the 1 you carried. The result below the line should be 96.
-
4
Put a 0 under the result and multiply the bottom tens number by the top ones. The 0 will act as a placeholder. Write the result of multiplying the bottom tens number by the top ones number next to the 0.[8]
- For the 24 x 24 example, multiply 2 by 4. You should now see 80 below the 96.
-
5
Multiply the bottom tens number by the top tens number. If you carried any numbers, remember to add them to your result. Write the result below the line.[9]
- To finish multiplying 24 by 24, multiply the 2 by 2 to get 4. The result on this line should be 480.
-
6
Add the 2 results to get your answer. If you multiplied a number with 3 or more digits, you’ll have more lines to add together. Write the answer from your results to show the square of the number.
- Add 96 + 480 to get the answer for 24 x 24.
= 576.
- Add 96 + 480 to get the answer for 24 x 24.
Advertisement
-
1
Square the numerator. Multiply the top number of the fraction by itself to find its square. Write the result and place the fraction line below it.[10]
- For example, with (8/2)2, you’d multiply 8 by 8 to get a numerator of 64.
-
2
Square the denominator. Multiply the bottom number of the fraction by itself. Write the result of this square below the fraction line.[11]
- So for (8/2)2, multiply 2 by 2 to get a denominator of 4.
-
3
Simplify the result. While you could leave the fraction large or improper, most directions will tell you to simplify or reduce the result. If you have an improper fraction, turn it into a mixed number.[12]
- For example, (8/2)2 = (64/4) can be simplified to 16 because 4 goes into 64 16 times.
Advertisement
Add New Question
-
Question
How do I calculate the square root?
-
Question
√5 is the square of what number?
√5 is the square of plus-or-minus the fourth root of 5.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Remember that if you square a negative number, the answer will be positive because the 2 negatives cancel each other out.
-
To square a number using a calculator, enter the number x the number. For example, for
, enter 4 x 4 to get 16.
Advertisement
About This Article
Article SummaryX
To find the square of a number, multiply the number by itself. For example, if you’re trying to find the square of 5, you would multiply 5 by 5 and get 25, which is the square. To learn how to square fractions, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 120,537 times.
Did this article help you?
☰
Что обратно возведению в степень?
Возведению в степень обратны два действия:
- извлечение корня,
- нахождение логарифма.
Во-первых, сначала надо разобраться, что значит обратное действие. Так деление есть обратное действие умножению, а вычитание — сложению. Это вытекает из рассуждений, что произведение, получившееся от перемножения двух множителей, позволяет найти один из множителей, если известен другой. Например, 5 * 3 = 15. Если нам неизвестен второй множитель (5 * ? = 15), то его можно найти, выполнив деление: 15 : 5 = 3. Операция не меняется, если неизвестен первый множитель: ? * 3 = 15, 15 : 3 = 5. Это связано с тем, что умножение подчиняется переместительному закону (от перемены мест множителей произведение не меняется).
Аналогично и для вычитания: ? + 10 = 33, 33 — 10 = 23 или ? + 23 = 33, 33 — 23 = 10. Неважно, какое слагаемое неизвесто, его всегда находят вычитанием.
Но не все так просто с возведением в степень. Здесь от перестановки основания степени и показателя степени результат изменяется, т.е. возведение в степень не подчиняется переместительному закону: 43 = 64, но 34 = 81. (Хотя есть исключения: 24 = 16 и 42 = 16.)
Поэтому, если нам известен результат операции возведения в степень и показатель степени, то, чтобы найти основание степени, надо извлечь корень известной по показателю степени из результа возведения в степень:
?3 = 125, следовательно 3√125 = 5.
Если же известны основание степени и результат возведения в степень, а надо найти показатель степени, то используется такая операция как нахождение логарифма:
2? = 64, отсюда log264 = 6
Как с помощью циркуля и линейки находить корни, квадраты и обратные величины чисел
Время на прочтение
3 мин
Количество просмотров 16K
Представьте, что у вас нет под рукой калькулятора (но есть циркуль и линейка или угольник) и вам нужно посчитать результат в виде отрезка. Задача решается за менее чем 5 простых шагов.
Базовая формула вычисления
Для начала докажем одну формулу, которая нам будет помогать с дальнейшим решением.
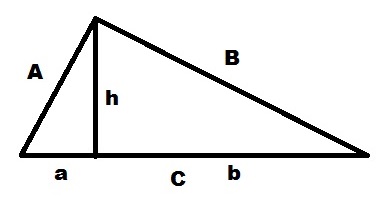
В прямоугольном треугольнике ABC проведем высоту h на сторону C. По теореме Пифагора выводим:
Подставляем всё в первую формулу:
И если раскрыть скобки:
После сокращения получаем:
Вот с помощью этой формулы и будем выводить наши решения.
Единичная мера длины
Так как мы вычисления проводим на плоскости с отрезками, нам необходимо определиться с мерой единичной длины равной 1. Если мы отложим отрезок 1 дециметр, то он так же будет равен 10 сантиметрам, 100 миллиметрам или 4 дюймам. Один отрезок и 4 разных чисел разной меры длины его определяют. Что бы выбрать одну систему счисления длин отрезков, примем за единицу длины какой-то отрезок. Какой — определим по ходу расчетов, и он зафиксирует нужную меру длины.
Циркуль как универсальный инструмент
Циркуль удобно использовать как средство:
-
отмерить отрезок определенной длины, при этом знать величину этой длины совершенно нет надобности.
-
прочертить дугу на одинаковом расстоянии от определённой точки.
-
отложить перпендикуляр к линии через определённую точку. Для этой цели удобнее использовать угольник с прямым углом, чем циркулем чертить 4 дуги.
Вычисление квадрата длины
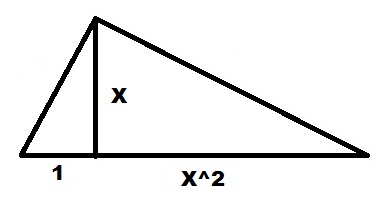
Для вычисления квадрата величины X используем нашу формулу в виде:
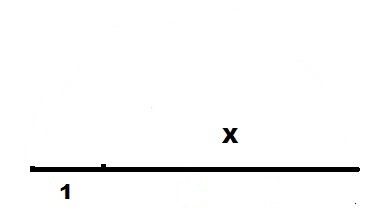
Чертим прямую линию достаточной длины.
Откладываем на ней отрезок единичной длины.
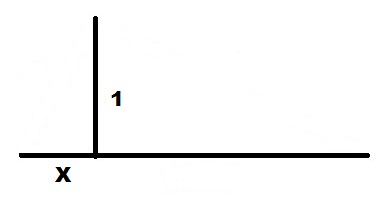
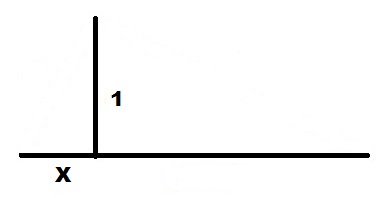
От правого конца единичного отрезка 1 откладываем вверх перпендикуляр длиной X.
Проводим линию от левого конца единичного отрезка 1 до верхнего конца отрезка X.
От этого отрезка откладываем перпендикуляр на линию продолжения единичного отрезка 1. Их пересечение и есть правый край квадрата длины. Левый край начинается от точки, где отложена высота.
Пример. У вас есть какой-то квадрат, со стороной X, начерченный на плоскости или на земле. Нужно узнать его площадь в попугаях. Одна сторона квадрата длиной X у нас уже есть. На соседней стороне откладываем длину одного попугая (там где 1 находится). Соединяем концы линией, откладываем перпендикуляр, продлеваем отрезок с попугаями до перпендикуляра и получаем решение в квадратных попугаях.
Вычисление квадратного корня длины
Для вычисления квадратного корня величины используем нашу формулу в виде:
Чертим прямую линию достаточной длины.
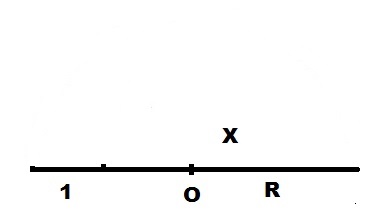
Откладываем на ней единичный отрезок длины 1.
На продолжении единичного отрезка откладываем отрезок длины X.
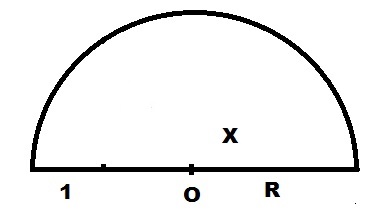
Полученный отрезок 1+X делим пополам с помощью циркуля и получаем точку O. Как это сделать, приводить здесь не буду, это задачка из школьного курса. Обозначим длину найденной половины как R.
Вокруг центра O, циркулем нарисуем дугу радиусом R.
От правого конца отрезка 1 отложим вверх перпендикуляр до пересечения с дугой окружности. Длина этого перпендикуляра и будет равна корню квадратному из длины X.
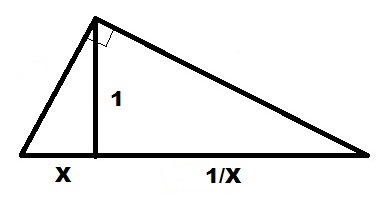
Вычисление обратной величины длины
Для вычисления обратной величины длины используем нашу формулу в виде:
Решение очень похоже на нахождение квадрата величины, только a и h меняются местами.
Чертим прямую линию достаточной длины.
Откладываем на ней отрезок длины X.
От правого края отрезка X откладываем вверх перпендикуляр единичной длины 1.
Соединяем концы отрезков линией.
От верхнего конца отрезка X откладываем перпендикуляр к линии продолжения отрезка 1. Полученный отрезок и есть решение.
Выводы
Приведенные выкладки удобны, когда не хочется возиться с цифрами и их арифметическими вычислениями, которые всё равно будут обратно приложены к длинам отрезков.
Если величина X сильно отличается от единичного отрезка 1, ошибка вычисления может быть значительной. Но если применить масштабирование, то ошибку можно значительно уменьшить. Например, при захождении корня длины 20, его можно поделить на 16 (4 раза поделить пополам), а потом ответ умножить на 4 (4 раза отложить полученный отрезок).