Найти число по остатку от деления
| Модуль (пробел) остаток (запятая) Модуль (пробел) остаток и т.д. |
Одна древняя китайская задача гласила:
«Найти число, которое при делении на 3 дает остаток 2, при делении на 5 дает остаток 3, а при делении на 7 дает остаток 2»
Что бы решать подобные задачи, сделаем следущее
Исходное число по исходным данным можно выразить вот так
Где k — целые числа
Выпишем ряды меняя k от 0 по возрастающей
Несложно заметить что 23, встречается во всех трех рядах.
Это и есть наш ответ, следущее число (128) встретится только через 105=3*5*7 отсчетов. Так как эти числа взаимно простые, то и берем просто их произведение.
И таким образом общий ответ нашей задачи имеет вид
Легкий алгоритм для понимания, не правда ли?
Но он не совсем неудобен, когда встречаются большие числа, и опять же, при составлении элементов ряда можно банально ошибиться.
Есть другой способ
Пусть нам дана система сравнений
где 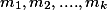
Пусть 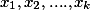
Такие уравнения мы уже можем решать Сравнения 1 степени. Теория чисел.
Узнав эти корни, мы можем вычислить наше исходное число по формуле
Для нашего примера исходные данные выглядят так
Тогда система сравнений будет иметь вид
Решая их получим
И наше решение имеет вид
Или то же самое что и
Как видите, ответ совпадает.
Наш бот решает подобные задачи используя библиотеку PHP GMP. Поэтому к точности расчетов и ограничений на длину значений, это к ним 
Хотя есть и свои материалы в частности: Расчет значения функции Эйлера, Остаток числа в степени по модулю и Диофантовое уравнение с тремя неизвестными
Важно: Логично и это надо учитывать при ввводе чисел, в паре чисел (модуль- остаток), модуль (всегда!) больше чем остаток.
Второе важное замечание. Модуль всегда(!) положительное число, остаток, может быть отрицательным, но лучше все таки привести его к положительному числу.
Как это сделать? Все ссылки на сопутствующие материалы уже приведены.
Пример
Узнать какое загадано число, если остаток при делении его на 37 равно 11, при делении на 9 равно 4, при делении на 7 равно 1, а при делении на 100 остаток равен 25.
Заметим, что модули, то есть числа (37, 9, 7, 100) на которые мы делим неизвестное число, попарно взаимно простые. То есть у нас нет ни одной пары из этих чисел, так что бы они имели общий делитель.
Раз так, то мы можем решать подобную задачу тем, методом который описан выше.Вводим в поле ввода
37 11, 9 4, 7 1, 100 25
За мгновение получим ответ
| Полученное число |
mod(233100)) |
Удачных расчетов!
|
Число возводится в степень 5 и делится на 1089671048441. После этого становится известен остаток от деления. Вопрос, как найти число? Т.е. Найти x при известном y. Пример:
|
6 ответов
|
Если не известно разложение числа на простые множители, но эта задача не решается. Как раз на этом эффекте основан криптографический алгоритм RSA. Однако, если разложение получено, как в данном случае, то далее проще всего поступить так. У нас есть число $%n=pq$%, где $%p,q$% — различные простые. Тогда можно найти значение функции Эйлера $%varphi(n)=(p-1)(q-1)$%. Считая, что $%y$% не делится ни на $%p$%, ни на $%q$%, что легко проверить, имеем то же самое для числа $%x$%, которое нам пока не известно. Далее применяем теорему Эйлера: $%x^{varphi(n)}equiv1pmod{n}$%. Поэтому для нахождения $%x$% достаточно возвести $%y$% в подходящую степень $%k$%, чтобы выполнялось условие $%xequiv y^kequiv x^{5k}pmod n$%. Оно будет выполняться, если $%5kequiv1pmod{varphi(n)}$%, а это есть линейное сравнение по известному нам модулю, которое легко решается. |
|
Для нахождения остатков при делении больших чисел на большие нужно использовать среду программирования. Там нужно реализовывать алгоритмы работы с большими натуральными числами. Один из способов реализации-использование массивов. |
|
Поскольку ряд пятых степеней натуральных чисел не ограничен, а количество различных остатков ограничено, то коллизии неизбежны, т.е. однозначно восстановить первоначальное число невозможно. Как вариант, можно попробовать найти алгоритм для нахождения минимального исходного числа для заданного остатка, но кроме полного перебора пока ничего не придумывается) |
|
Если я правильно понял, Алгоритм такой:
|
|
Подобные функции используются для алгоритма Диффи-Хеллмана ,и как известное для чисел больше 10^50 она не решаема и на супер компьютерах .Поэтому в общем виде нормального решение рассказать не могу. Если числа именно такого порядка ,то можно попробовать частичный перебор : он может не принести результата в некоторых случаях , но если числа лежат хорошо — то мы быстро найдем решение. $$x^5 mod b = y$$ |
|
Разложим число 1089671048441 на простые множители: оно равно 1011077х1077733. Решим отдельно уравнения $%x_1^5$% mod 1011077=y mod 1011077 и $%x_2^5$% mod 1077733=y mod 1077733, для этого годится и полный перебор (если надо решать данную задачу для большого набора различных y, то стоит сделать таблицы или другое кэширование). Получим до пяти групп решений вида $%1011077n_1+x_1$% для первого уравнения и $%1077733n_2+x_2$% для второго. Уверен, что можно найти формулу, по которой сразу находится x из этих двух уравнений (как-то при помощи обратного по модулю, наверно), но даже банальный перебор $%n_1$% даст результат за приемлемое время. |
Как уловки древних полководцев воскресают в современной математике
Время на прочтение
5 мин
Количество просмотров 20K
Легенда гласит, что китайские военные использовали математическую хитрость, чтобы скрыть численность своих войск. Этот же метод используется во многих областях современных математических исследований.
Представьте, что вы — полководец в Древнем Китае и хотите скрыть численность своей армии от противника. Но вам также необходимо знать точное количество бойцов. Чтобы узнать численность армии и не дать противнику возможность получить эти сведения, можно прибегнуть к интересной математической хитрости.
Во время утреннего построения ваши солдаты выстраиваются в ряд по пять человек. Вы заметили, что в последнем ряду у вас осталось трое солдат. Затем вы перестраиваете их в ряд по восемь человек, в результате чего в последнем ряду останется семь, а затем в ряд по девять, в результате чего в одном ряду находится два солдата. Ни разу не подсчитав всех своих солдат, вы имеете достаточно информации, чтобы определить общую численность армии. И при этом можете не называть точную цифру, которую может узнать враг.
Согласно одной легенде, древнекитайские полководцы неоднократно прибегали к такой хитрости. Неизвестно, зачем они так поступали и поступали ли вообще. Зато известно, что эта математическая техника, также известная как «Китайская теорема об остатках», была изобретена где-то между третьим и пятым веками нашей эры китайским математиком Сунь Цзы (не тот Сунь Цзы, который написал «Искусство войны» за 1000 лет до него).
Эта теорема позволяет восстановить целое число по множеству его остатков от деления на числа из некоторого набора попарно взаимно простых чисел. Сунь Цзы не смог доказать теорему, но это сделал индийский математик и астроном Ариабхата, который придумал процесс решения любого конкретного случая теоремы.
Китайская теорема об остатках дает вам отличный способ определения числа.
Чтобы лучше понять эту теорему, вернёмся к нашему примеру. Наша цель: найти целое число X, которое имеет остаток 3 при делении на 5 и остаток 7 при делении на 8 (позже мы добавим третье условие, что при делении на девять остаток будет 2). Математики называют это системой конгруэнции (системой соответствий) и пишут так:
X ≡ 3(mod 5)
X ≡ 7(mod 
Решение первой конгруэнции равно 3, так как 3 по модулю 5 равно 3. Если мы увеличим 3 на 5, их суммы также будут удовлетворять первой конгруэнции X может быть любым числом в последовательности 3, 8, 13, 18, 23 и так далее.
Наличие второй конгруэнции позволяет уточнить решение. Числа, которые удовлетворяют этой конгруэнции — оставляя остаток 7 при делении на 8, — это 7, 15, 23, 31 и так далее. Теперь нам нужно найти число, которое появляется в обоих списках:
3, 8, 13, 18, 23, 28, 33
7, 15, 23, 31, 39, 47, 55
Видите его? Наше загадочное число — 23. Но это не единственное решение.
Мы всегда можем найти другое число, взяв произведение наших делителей и добавив кратные ему числа к 23. Наши делители равны 5 и 8. Их произведение равно 40. Прибавьте 40 к 23, и мы получим 63, что также удовлетворяет обеим конгруэнциям. Как и 103, 143, 183, 223 и так далее. Таким образом, вы можете найти решение каждые 40 чисел, подключив разные целые числа для K в следующей формуле:
X=23+40×K
Однако наименьшее целое число, удовлетворяющее этим конгруэнциям, равно 23.
Если вы генерал и знаете, что у вас не более 300 солдат, то числа 23, 63 или 103 могут быть недостаточно точными. Тогда вы добавляете третье равенство к первым двум (опять же, убедитесь, что ваше новое число попарно взаимно просто с 5 и 8):
X ≡ 3(mod 5)
X ≡ 7(mod 
X ≡ 2(mod 9)
Какое число удовлетворяет всем трём конгруэнциям? Мы возвращаемся к нашему списку чисел: 23, 63, 103, 143, 183, 223. Ни одно из них не оставляет остатка от 2 при делении на 9. Однако следующее число в последовательности: 263. И если бы мы хотели большей точности, мы могли бы добавить четвертую конгруэнциям — или столько, сколько захочется.
До сих пор мы использовали делители, которые являются взаимно простыми. Но что, если мы не сможем выбрать делители? Например, предположим, что мы астрономы, следящие за двумя кометами с орбитальными периодами в четыре года и 10 лет. В последний раз они достигли своего перигелия — точки, где комета находится ближе всего к Солнцу, — в 1991 и 1997 годах соответственно. Как нам определить, когда в следующий раз они оба достигнут своих перигелиев в один и тот же год?
Китайская теорема об остатках по-прежнему может нам помочь. Когда делители не являются взаимно простыми, вместо того, чтобы использовать кратные их произведения для определения возможных решений, мы используем кратные их наименьшему общему кратному. Поэтому в данном случае вместо умножения 4 и 10 мы используем их наименьшее общее кратное: 20.
Теперь мы ищем загадочный год X, который удовлетворяет следующей системе соответствий:
X ≡ 1991(mod 4)
X ≡ 1997(mod 10)
Если мы продолжим следовать процессу, который использовали в предыдущих примерах, в этом случае добавляя кратные 20 к наименьшему целому числу, которое удовлетворяет обеим конгруэнциям (которое оказывается равным 7), то мы найдём общий год, в котором обе кометы достигают своих перигелиев: 2007 г.
Этот пример демонстрирует широкую применимость теоремы, что делает её полезной в практических целях. Например, в астрономии для расчёта древних календарей или выборе кирпичей правильного размера для здания (теорема, вероятно, использовалась для строительства Великой китайской стены). Спустя более 1500 лет теорема остается полезным способом решения современных проблем, включая шифрование RSA, современный протокол безопасности.
Но китайская теорема об остатках — это не просто инструмент. Она лежит в основе операции в фундаментальной ветви теории чисел, называемой модульной арифметикой, которая представляет собой способ выполнения математических вычислений в системах с меньшими числами, как мы это делали в примерах, которые мы проработали выше, с участием войск и комет.
Математики часто используют модульную арифметику для исследования самых глубоких вопросов в своей области. На протяжении веков центральным направлением исследований в теории чисел было определение того, когда различные типы полиномиальных уравнений, таких как x²+y²=z², имеют целочисленные решения. Для любого полиномиального уравнения существует бесконечно много комбинаций, которые вы могли бы вычислить, что делает поиск методом перебора неосуществимым.
Но для начала вы можете сначала попытаться ответить на вопрос в модульной системе счисления, где действительно можно проверить все возможные значения. Есть много примеров такого подхода в действии. Например, в 17 веке Пьер Ферма бросил вызов британским математикам, доказывая, что уравнение y2=x3−2 имеет только две пары целочисленных решений: (3, 5) и (3, -5). Математики обнаружили, что первым шагом к решению этой проблемы было изучение проблемы в mod 4, что помогло им найти «точку опоры» и установить, что, по крайней мере, x должно быть нечётным.
В других случаях модульная арифметика может исключить возможность того, что полиномиальное уравнение имеет целочисленные решения. Во-первых, ищите решения в модульных системах счисления. Если вы их не найдёте, то можете взять то, что узнали, и перевести это в утверждения об отсутствии решений одного и того же уравнения среди всех целых чисел.
Если нет решений по простому модулю, то это означает ваше знание о том, что решений нет.
Вот такой любопытный пример того, как спустя более 1000 лет китайская теорема об остатках по-прежнему даёт ключи к более важным истинам, что делает её мощным математическим инструментом, даже если полководцам больше не нужно скрывать численность своих армий.
Что ещё интересного есть в блоге Cloud4Y
→ Изучаем своё железо: сброс паролей BIOS на ноутбуках
→ Реклама в Windows 11 сломала «Пуск» и панель задач некоторых пользователей
→ Клавиатуры, которые постигла неудача
→ Мониторинг СУБД VMware Cloud Director и vCenter Server Appliance с помощью Zabbix
→ Космический вызов: защита суперкомпьютеров от внеземной угрозы
Подписывайтесь на наш Telegram-канал, чтобы не пропустить очередную статью. Пишем не чаще двух раз в неделю и только по делу.
П
Пример [1]. Найти натуральное число, которое при делении на $ 3_{} $ дает в остатке $ 2_{} $,
при делении на $ 7_{} $ дает в остатке $ 3_{} $, а при делении на $ 10_{} $ — в остатке $ 9_{} $.
Решение. Пусть $ u,v,w $ — частные от деления неизвестного числа на $ 3, 7 $ и $ 10_{} $ соответственно. Имеем:
$$ 3,u+2=7,v+3, 3,u+2=10, w+9, 7,v+3=10, w+9 . $$
Решаем последнее уравнение в целых числах, применяя рассуждения, приведенные
☞
ЗДЕСЬ:
$$ w=7,t_1-2, v=10,t_1-2 quad npu quad forall t_1 in mathbb Z . $$
Подставим найденное выражение для $ v_{} $ в первое уравнение $ 3,u+2=7,v+3 $:
$$ 3,u-70, t_1=-13 , $$
которое также можно решить: $ u=19+70, t_2 $ при $ forall t_2 in mathbb Z $. Следовательно,
общий вид искомых чисел:
$$ 3,u+2=3 (19+70, t_2)+2=59+210, t_2 quad npu quad forall t_2 in mathbb Z . $$
Наименьшее положительное число получается при $ t_2=0 $.
Ответ. $ 59 $.
Т
Теорема [Китайская теорема об остатках (КТО)].
Пусть числа $ M_1 , M_2, dots, M_k $ — попарно взаимно простые, и
$$ M= M_1 M_2 times dots times M_k .$$
Тогда система
$$
x equiv B_1 pmod{M_1}, x equiv B_2 pmod{M_2}, dots,
x equiv B_k pmod{M_k}
$$
имеет единственное решение среди чисел $ {0,1,dots,M-1 } $, и это решение
может быть представлено в одном из следующих видов:
1.
либо $ x = x_1 pmod{M} $ при
$$
x_1= frac{M}{M_1} B_1 y_1 +frac{M}{M_2} B_2 y_2+ dots + frac{M}{M_k} B_k y_k
$$
и $ y_j $ обозначающем число, обратное числу $ Mbig/ M_j $
относительно умножения по модулю $ M_j $:
$$frac{M}{M_j} y_j equiv 1 pmod{M_j} ;$$
2.
либо $ x = x_2 pmod{M} $ при
$$
x_2= B_1 +z_1M_1+z_2M_1M_2 +dots + z_{k-1}M_1M_2times dots times M_{k-1}
,
$$
и числах $ z_1,dots,z_{k-1} $ последовательно определяемых из сравнений
$$
begin{array}{lcl}
B_1+z_1M_1 &equiv B_2 pmod{M_2} , , & \
B_1 +z_1M_1+z_2M_1M_2 &equiv B_3 pmod{M_3} , ,& \
dots & dots & \
B_1 +z_1M_1+z_2M_1M_2 +dots + z_{k-1}M_1M_2times dots times M_{k-1} & equiv B_k pmod{M_k} , . &
end{array}
$$
Доказательство.
1.
При любых целых числах $ y_2,dots,y_k $ число $ x_{1} $, определяемое формулой
1
, удовлетворяет сравнению
$$x_1equiv frac{M}{M_1} B_1 y_1 pmod{M_1}$$
(поскольку числа $ M/M_2,dots,M/M_k $ делятся на $ M_{1} $).
Пусть число $ y_1in { 1, dots ,M_1-1 } $ удовлетворяет сравнению
$$frac{M}{M_1} y_1 equiv 1 pmod{M_1}$$
(на основании теоремы существования и предположений доказываемой теоремы
такое число существует и оно единственно).
Тогда $ x_1equiv B_1 pmod{M_1} $, т.е. удовлетворяет первому из сравнений системы. Аналогично показывается справедливость остальных сравнений.
2.
Фактически, этот алгоритм заключается в последовательном решении сравнений
системы. Решение первого имеет вид $ B_1+M_1t_1 $
при $ t_1in mathbb Z $;
оно подставляется во второе, из которого находим представление для $ t_1 $
в виде $ t_1=z_1+M_2t_2 $ при $ t_2in mathbb Z $, и т.д. Формально:
число $ x_2 $, определяемое формулой
2
, очевидно
удовлетворяет первому из сравнений системы: $ x_2 equiv B_1 pmod{M_1} $.
Далее, $ x_2equiv B_1+ z_1M_1 pmod{M_2} $ и сравнение
$ x_2 equiv B_2 pmod{M_2} $ будет выполнено, если $ z_1 $ удовлетворяет
сравнению $ B_1+ z_1M_1 equiv B_2 pmod{M_2} $. Поскольку $ operatorname{HOD} (M_1,M_2)=1 $, то
на основании теоремы существования,
такое число существует и оно единственно при условии
$ z_1in { 1, dots ,M_2-1 } $.
Установив его, продолжаем далее по индукции.
В заключение покажем, что любые два решения
$ tilde{x} $ и $ tilde{tilde{x}} $
системы сравнимы между собой по модулю $ M_{} $. В самом деле:
$$ tilde{x} equiv B_j pmod{M_j},
tilde{tilde{x}} equiv B_j pmod{M_j} Rightarrow
tilde{x} — tilde{tilde{x}} equiv 0 pmod{M_j}
$$
для $ forall j in {1,dots, k } $.
Поскольку числа $ M_1,dots,M_{k} $ попарно взаимно просты, то
на основании теоремы 4, приведенной
☞
ЗДЕСЬ, имеем:
$ tilde{x} — tilde{tilde{x}} equiv 0 pmod{M_1times dots
times M_k} $.
♦
Первое упоминание утверждения КТО встречается в
книге
Математическое руководство Сунь Цзы
китайского математика Сунь Цзы1)(孫子, ок. 400 — ок. 460), о котором не известно ничего, кроме того, что он является автором этой книги; годы его жизни устанавливались историками науки на основе анализа текста.
Задача 26 главы 3. Предположим, что имеется неизвестное количество
объектов. Разбив их на тройки, получаем в остатке 2, разбив на пятерки
— 3, разбив на семерки — 2. Сколько имеется объектов?
После решения этой конкретной задачи, в книге приводится алгоритм
решения и общей — при произвольных остатках:
«Умножь число остатков при делении на тройки на $ 70 $, добавь к
полученному произведение числа остатков при делении на пятерки на $ 21 $,
и затем добавь произведение числа остатков при делении на семерки на $ 15 $.
Если результат равен $ 106 $ или более — вычти кратное $ 105 $.»
Эти рассуждения фактически соответствуют представлению решения системы
формулой
2
.
Некоторые специалисты полагают, что алгоритм решения системы сравнений позволял китайским генералам пересчитывать армию без особых усилий последовательностью однотипных распоряжений:

«В колонну по $ 7_{} $ становись!»
По выполнении команды, подсчитывалось количество солдат, стоящих в последнем ряду.
Затем производились аналогичные подсчеты по результатам выполнения команд:
«В колонну по $ 11 $ становись!»
«В колонну по $ 13 $ становись!»
«В колонну по $ 17 $ становись!»
В соответствии с утверждением теоремы, по четырем остаткам однозначно восстанавливается число солдат, если оно не превосходит $ 17017=7times 11times 13 times 17 $.
Однако некоторые соображения, основанные на знании реалий армейской жизни, позволяют усомниться в практической пользе подобных — математически абсолютно безупречных —
рассчетов… — см. упражнение ниже.
П
Пример 1. Решить систему сравнений
$$x equiv 7 pmod{8}, x equiv -1 pmod{11}, x equiv 3 pmod{15}
.$$
Решение. Проиллюстрируем оба способа из теоремы. Для представления
1
сначала решаем сравнения
$$165 cdot y_1 equiv 1 pmod{8} ,quad
120 cdot y_2 equiv 1 pmod{11} ,quad
88 cdot y_3 equiv 1 pmod{15} , $$
которые, очевидно, эквивалентны следующим:
$$ 5 cdot y_1 equiv 1 pmod{8} ,quad
10 cdot y_2 equiv 1 pmod{11} ,quad
13 cdot y_3 equiv 1 pmod{15} . $$
Алгоритм решения линейного сравнения даст решения в виде
$$y_1=5, quad y_2=10 , quad y_3=7 . $$
По формуле
1
получаем
$$x_1= underbrace{7cdot 5 cdot 165 + (-1)cdot 10 cdot 120 +
3 cdot 7 cdot 88}_{6423} = 1143+1320times 4 equiv 1143
pmod{1320} .$$
Для
2
решением сравнения $ 7+ 8, z_1 equiv -1 pmod{11} $
очевидно является $ z_1 equiv_{_{11}} -1 equiv_{_{11}} 10 $. Сравнение
$ 7+8 cdot 10 + 8cdot 11 , z_2 equiv 3 pmod{15} $ эквивалентно
$ 13, z_2 equiv 6 pmod{15} $ и имеет решение $ z_2=12 $.
Окончательно
$$x_2= 87 + 8cdot 11 cdot 12 =1143 .$$
Ответ. $ x equiv 1143 pmod{1320} $.
При вычислениях по формуле
1
один из коэффициентов $ y_jM/{M_j} $ можно легко установить, если все остальные уже вычислены:
?
Доказать, что при условиях (и в обозначениях) теоремы имеет место сравнение
$$ frac{M}{M_1} y_1 +frac{M}{M_2} y_2+ dots + frac{M}{M_k} y_k equiv 1 pmod{M} . $$
Какой из алгоритмов теоремы —
1
или
2
— предпочтителен при расчетах
?
Для фиксированной системе сравнений эти
алгоритмы равноэффективны. Однако если идет речь о решении
серии однотипных систем с изменением входящих в них параметров,
то проявляются преимущества каждого из алгоритмов. Рассмотрим сначала
серию систем сравнений
$$
x equiv B_1 pmod{M_1}, x equiv B_2 pmod{M_2}, dots,
x equiv B_k pmod{M_k}
$$
при фиксированном их числе $ k_{} $
и фиксированных же модулях $ M_1,dots,M_{k} $, но варьируемых $ B_1,dots,B_{k} $.
В этом случае имеет смысл использовать представление решения в форме
1
, поскольку для получения решения каждой новой системы серии
нужно будет произвести лишь пересчет суммы при уже вычисленных ранее
величинах $ y_1,dots,y_k $. С другой стороны, если решается серия систем
сравнений, в которой каждая следующая система получается из предыдущей
добавлением одного нового сравнения — т.е., например, система
дополняется сравнением $ xequiv B_{k+1} pmod{M_{k+1}} $ —
то более удобным для вычисления решения становится вариант
2
, так как
при его использовании приходится дополнительно решать лишь одно новое сравнение относительно
$ z_{k} $ и
добавить соответствующее слагаемое в сумму —
т.е. просто прибавить его к решению стартовой системы.
П
Пример 2. Решить системы сравнений
а) $ x equiv 3 pmod{8}, x equiv 1 pmod{11}, x equiv 12 pmod{15} $;
б) $ x equiv 7 pmod{8}, x equiv -1 pmod{11}, x equiv 3 pmod{15},
x equiv 4 pmod{7} $.
Решение. Обе системы могут рассматриваться как
вариации одной и той же системы примера 1, и решение каждой
из этих систем может быть получено модифицированием соответствующего
варианта решения того примера. Так, для системы а) получить решение
не представляет труда, если были заранее вычислены величины $ y_1,y_2 $ и $ y_3 $:
$$x_1= underbrace{3cdot 5 cdot 165 + 1cdot 10 cdot 120 +
12 cdot 7 cdot 88}_{11,067} equiv 507 pmod{1320} .$$
А для системы б) удобнее использовать алгоритм
2
теоремы, тем
более, что решение системы из первых трех сравнений у нас уже имеется.
$$ 1320, z_4 equiv 4 pmod{7} quad Rightarrow quad z_4 =4
quad Rightarrow quad x_2 =1143+1320, z_4 =6423
. $$
Ответ. а) $ x equiv 507 pmod{1320} $; б) $ x equiv 6423 pmod{9240} $.
?
Определить число $ x_{} $ солдат китайской армии, если
а) $ x equiv 3 pmod{7}, x equiv 1 pmod{11}, x equiv 12 pmod{13}, x equiv 10 pmod{17}
$;
б) $ x equiv 3 pmod{7}, x equiv 1 pmod{11}, x equiv 12 pmod{13}, x equiv 11 pmod{17} $.
?
Доказать, что если
$ p_1,p_2,p_3 $ — различные простые числа, то а) решение системы
$$
x equiv B_1 pmod{p_1}, x equiv B_2 pmod{p_2},
$$
можно представить в виде
$$
x equiv p_2^{p_1-1}B_1 + p_1^{p_2-1}B_2 pmod{p_1p_2} ,
$$
а б) решение системы
$$
x equiv B_1 pmod{p_1}, x equiv B_2 pmod{p_2},
x equiv B_3 pmod{p_3}
$$
— в виде
$$
x equiv p_2^{p_1-1}p_3^{p_1-1} B_1 + p_1^{p_2-1} p_3^{p_2-1} B_2 +
p_1^{p_3-1}p_2^{p_3-1} B_3 pmod{p_1p_2p_3} .
$$
Решить эти системы при $ B_1=1,B_2=2,B_3=3 $ и $ p_1=7,p_2=11,p_3=17 $.
Cистема сравнений может иметь решения и при нарушении условий КТО.
?
[Фибоначчи]. Крестьянка несла на базар корзину яиц. Неосторожный
всадник, обгоняя женщину, задел корзину, и все яйца разбились. Желая
возместить ущерб, всадник спросил у крестьянки, сколько яиц было в корзине.
Женщина ответила, что числа яиц не знает, но когда она раскладывала их по
два, по три, по четыре, по пять и по шесть, то каждый раз одно яйцо оставалось
лишним, а когда она разложила по семь, лишних яиц не осталось. Сколько яиц
несла крестьянка на базар?
Т
Теорема. Система
$$
x equiv B_1 pmod{M_1}, x equiv B_2 pmod{M_2}, dots,
x equiv B_k pmod{M_k}
$$
разрешима тогда и только тогда, когда числа
$$
B_j-B_{ell} qquad mbox{ делятся на } qquad operatorname{HOD}(M_j,M_{ell}) quad mbox{ при } quad {j,{ell}} subset {1,dots,k} quad .
$$
Если это условие выполнено, то решение единственно по модулю
$ operatorname{HOK}(M_1,M_2,dots,M_k) $.
§
По поводу КТО см. оригинальный результат
☞
ЗДЕСЬ.
?
Решить систему сравнений
$$
x equiv M_1-1 pmod{M_1}, x equiv M_2-1 pmod{M_2}, dots,
x equiv M_k-1 pmod{M_k} .
$$
Читатель, знакомый с проблемой интерполяции, безусловно
заметит аналогию вариантов
1
и
2
китайской теоремы об остатках с формами соответственно
Лагранжа и Ньютона представления интерполяционного полинома $ y_{}=f(x) $, составляемого по таблице значений
$$
begin{array}{c|ccc}
x & M_1 & dots & M_k \ hline
f(x) & B_1 & dots & B_k
end{array}
$$
Действительно, задачу интерполяции можно «перевести на язык остатков»: найти полином $ f(x)_{} $,
дающий при делении на $ x-M_1 $ в остатке число $ B_{1} $, при делении на $ x-M_2 $ в остатке $ B_{2} $
и т.д.
П
Пример. Верно ли равенство
$$
left| begin{array}{rrrr}
51239 & 79922 & 55538 & 29177 \
46152 & 16596 & 37189 & 82561 \
71489 & 23165 & 26563 & 61372 \
44350 & 42391 & 91185 & 64809
end{array}
right|=0
?
$$
Решение. Фактическое вычисление подобного определителя —
каким бы методом мы не воспользовались —
задача довольно трудоемкая. Однако
вопрос ставится не о фактическом значении, а о равенстве его нулю.
Это обстоятельство может упростить вычисления. Обозначим неизвестное
значение определителя через $ x_{} $; очевидно это число целое. Если $ x=0_{} $,
то и его остаток при делении на любое число $ Min mathbb Z $ тоже должен
быть равным нулю. Если же хоть для
одного $ Min mathbb Z $ выполнится условие $ xnotequiv 0 pmod M $, то и $ xne 0 $.
Вычисление определителя фактически сводится к
умножению элементов определителя. Если же мы ставим задачу определения остатка
от деления этого выражения на $ M_{} $, то имеет смысл
сразу же «сократить» каждый элемент определителя до его остатка от деления
на $ M_{} $.
Возьмем сначала $ M=10 $, т.е. от каждого элемента определителя оставляем
только последнюю цифру:
$$
left| begin{array}{rrrr}
9 & 2 & 8 & 7 \
2 & 6 & 9 & 1 \
9 & 5 & 3 & 2 \
0 & 1 & 5 & 9
end{array}
right| equiv_{_{10}}
left| begin{array}{rrrr}
-1 & 2 & -2 & -3 \
2 & -4 & -1 & 1 \
-1 & 5 & 3 & 2 \
0 & 1 & 5 & -1
end{array}
right| =
left| begin{array}{rrrr}
-1 & 2 & -2 & -3 \
0 & 0 & -5 & -5 \
0 & 3 & 5 & -5 \
0 & 1 & 5 & -1
end{array}
right|=
$$
$$
=-
left| begin{array}{rrr}
0 & -5 & -5 \
3 & 5 & -5 \
1 & 5 & -1
end{array}
right| equiv_{_{10}} 0 .
$$
Итак, полученный ответ является необходимым, но не достаточным условием
равенства определителя нулю. Сделаем еще одну проверку: возьмем $ M=7 $.
$$
left| begin{array}{rrrr}
6 & 3 & 0 & 1 \
1 & 6 & 5 & 3 \
5 & 2 & 5 & 3 \
5 & 6 & 3 & 3
end{array}
right|equiv_{_{7}} 3 ne 0
.
$$
Ответ. Равенство неверно.
Понятно, что если бы определитель был равен нулю, то каждое вычисление
по модулю только «увеличивало бы достоверность» этого события.
Можно ли на основе серии модулярных вычислений установить истинное значение
определителя?
Попробуем это сделать для определителя из примера. Прежде всего,
оценим сверху абсолютную величину определителя. Каждое слагаемое в разложении
определителя по формуле из его определения представляет собой произведение
четырех пятизначных чисел; очевидно, это произведение не превосходит $ 10^{24} $.
Всего таких слагаемых $ 24_{} $, из них половина — с отрицательным знаком.
Поэтому $ |x|<1.2cdot 10^{25} $. Берем теперь все последовательные простые
числа2) $ p_j $, так чтобы их произведение превысило эту оценку:
$$L = underbrace{2cdot 3 cdot 5 times dots times 67 cdot 71}_{20} > 1.2cdot 10^{25}
$$
и вычисляем остатки $ B_{p_j }= x pmod{p_j} $:
$$B_2=0, B_3=0, B_5=0, B_7=3, B_{11}=7,dots, B_{67}=64, B_{71}=39 .$$
Китайская теорема об остатках позволяет однозначно определить
величину $ x_{} $ если она находится в пределах $ 0<x< L $:
$$x=+557940821520864633874788300 . $$
Однако, поскольку мы не знаем знака определителя, то должны предложить
еще один вариант ответа
— из полученного положительного значения следует вычесть величину $ L_{} $:
$$x=-8605834327092627090 . $$
Из двух получившихся вариантов только один — именно последний —
удовлетворяет оценке $ |x|<1.2cdot 10^{25} $. Это и есть величина нашего
определителя.
На самом деле, в только что решенном примере эффективность применения КТО в сравнении с методом вычисления определителя $ 4_{} $-го порядка, основанном на формуле из его определения, не очень очевидна: первый способ из КТО содержит сумму в $ 20 $ слагаемых — по сравнению с $ 24 $ из определения определителя, но каждое из этих слагаемых более громоздко! Можно, однако, слегка уменьшить количество этих слагаемых — скажем, до $ 17 $, если воспользоваться оценкой величины определителя по неравенству Адамара: $ |x|<1.6times 10^{21} $.
Вычислительные эксперименты с определителями порядка $ 16 $ с ОЧЕНЬ БОЛЬШИМИ элементами
☞
ЗДЕСЬ.
?
Остатки от деления числа $ x_{} $ на последовательность целых чисел
$$ x equiv 1 pmod{7}, x equiv 4 pmod{8}, x equiv 4 pmod{9},
$$
$$
x equiv 2 pmod{10}, x equiv 2 pmod{11}, x equiv 5 pmod{13}
$$
вычислены с ошибками; известно, однако, что не более двух остатков ложные. Установите число $ x_{} $.
[1]. Малининъ А., Буренинъ К. Руководство алгебры и собранiе алгебраическихъ задачъ для гимназiй, реальныхъ училищъ и учительскихъ институтовъ. Изданiе седьмое. М. Издание книжнаго магазина наследников бр. Салаевыхъ. 1884.
[2]. Бухштаб А.А. Теория чисел. М. Просвещение. 1966
[3]. LeVeque W.J. Topics in Number Theory. V.1. Addison-Wesley. Mass. 1956.
[4]. Утешев А.Ю., Калинина Е.А. Лекции по высшей алгебре. Часть I.
Учеб. пособие. СПб. «СОЛО». 2007. 246 c.
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
Число возводится в степень 5 и делится на 1089671048441. После этого становится известен остаток от деления. Вопрос, как найти число? Т.е. x^5 mod 1089671048441 = y; Найти x при известном y. Пример: Остаток от деления = 252260378, число 956044873207; ДОПОЛНЕНИЕ однозначно восстановить первоначальное число — не требуется, любое которое подходит под условие. задача решается в целых числах
|
||
| Вернуться к началу |
|
||
|
DarkMaster13 |
Заголовок сообщения: Re: Как найти число по остатку от деления?
|
|
Спасибо за ответ. скажем a = 1089671048441, b = 252260378 тогда x = 1089671048441 mod 252260378 * 5 = 1089671048441 mod 1261301890 = 1167517371; подставляем число в равенство т.е. не получили остаток от деления b = 252260378
|
|
| Вернуться к началу |
|
|
dr Watson |
Заголовок сообщения: Re: Как найти число по остатку от деления?
|
|
vorvalm писал(а): [math]x^5equiv apmod{b}[/math] Это Вы о чём? Возьмем [math]x=5, a=1, b=2[/math]
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Узнать остаток от деления степени на число
в форуме Алгебра |
Djwiccdeqd |
10 |
688 |
30 дек 2018, 20:42 |
|
Является ли число остатком от деления при тесте Люка—Лемера
в форуме Теория чисел |
xsx |
3 |
480 |
24 ноя 2016, 08:37 |
|
Можно ли по известному остатку подобрать показатель степени?
в форуме Теория чисел |
testuser7 |
20 |
551 |
29 дек 2019, 20:24 |
|
Найти остаток от деления
в форуме Алгебра |
afraumar |
4 |
3323 |
12 авг 2013, 15:20 |
|
Найти остаток от деления
в форуме Задачи со школьных и студенческих олимпиад |
Nadzor_26 |
2 |
1613 |
04 июн 2014, 21:24 |
|
Найти остаток от деления
в форуме Теория чисел |
kicultanya |
6 |
791 |
04 апр 2018, 18:27 |
|
Найти остаток от деления
в форуме Теория чисел |
Sec |
4 |
875 |
20 янв 2015, 22:15 |
|
Найти остаток от деления
в форуме Алгебра |
afraumar |
3 |
895 |
15 авг 2013, 13:05 |
|
Найти остаток от деления
в форуме Теория чисел |
Math137 |
17 |
344 |
29 сен 2022, 13:50 |
|
Найти остаток от деления
в форуме Теория чисел |
Trek |
2 |
777 |
16 янв 2015, 20:46 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 3 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |



mod(105))
mod(m_1),%20&%20x=(c_2)mod(m_2),....,x=(c_k)mod(m_k))
mod(m_1)\\m_1m_3...m_kx_2=(1)mod(m_2)\\.........\\m_1m_2...m_{k-1}x_k=(1)mod(m_k))
mod%20(m_1m_2...m_k))
mod(3),%20&%20x=(3)mod(5),x=(2)mod(7))
mod(3)=1\\%20&%20(21x_2)mod(5)=1\\(15x_3)mod(7)=1)
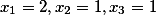
mod(3*5*7)=(233)mod(105))
mod(105)=(233-105-105)mod(105)=23mod(105))





