- Категория: Математика

Разберем на примере задачи нахождение дроби от числа.
От дома до школы 560 м. Саша прошел 2/5 этого пути. Сколько метров прошел Саша?
Весь путь — это 5 частей или одно целое (5/5). Найдем одну часть:
1) 560 : 5 = 112 (м) — составляет одна часть Сашиного пути. А он прошел 2 таких части
2) 112 * 2 = 224 (м) — составляет 2/5 пути.
Ответ: 224 м.
А теперь ту же задачу превратим в нахождение числа по его дроби.
Саша прошел 224 м, что составляет 2/5 всего пути от дома до школы. Найди расстояние от дома до школы?
224 м — это часть пути, значит весь путь будет больше. Эта информация нужна для самопроверки. Найдем сначала 1/5 пути
1) 224 : 2 = 112 (м) — составляет 1/5 пути
2) 112 * 5 = 560 (м) — составляет весь путь
Ответ: 560 м.
Проверим себя. При нахождении дроби от числа результат будет меньше этого числа, если у нас правильная дробь, и больше, если неправильная (то есть целое + еще какая-то часть).
При нахождении числа от дроби — все наоборот, результат будет больше этого числа, если у нас правильная дробь, и меньше, если неправильная.
Калькулятор на нахождения дроби от числа и числа по его дроби
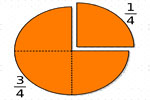
На нашем сайте мы уже рассматривали смежную статью, где все надо было делать с точностью наоборот. То есть где дробь также являлась частью известного числа, и надо было найти значение этой части в численном значении. Например, найти часть от числа 20, при этом часть представлено в виде дроби 2/5. Надеюсь, вы еще не потеряли мысль…
Что же вернемся к нашему первоначальному варианту и продолжим размышлять именно над ним!
Что является целым
В нашем конкретном случае целым будет неизвестное. Ведь нам известна лишь часть от него, которая является также дробью. То есть можно утверждать, что раз известное число это часть, то целое число, которое мы находим, должно быть больше по значению. Исходя из этих истин, теперь разберемся с частями от целого.
Что является частью
Ну и из абзаца выше понятно, что часть нам известна, она выражается дробью и известным числом. При этом дробь указывает на часть от целого, а вот само число является количественным показателем части. По факту это опять похожие понятия, но совсем не одно и то же.
Здесь уже можно проанализировать, как же найти целое число…
Как найти значение целого, зная о части в виде дроби и значении этой части
Собственно ответ на эту задачу весьма банален. Это все равно, что найти число, когда известно, что оно во сколько то раз меньше чем его часть и эта часть составляет известную величину. Опять же лучше будет разобрать этот случай на конкретном примере.
Смотрите, у нас есть 8 яблок и это 2/5 от всего, что имеется в корзине. Сколько должно быть яблок в корзине?
Здесь вначале надо бы найти 1 часть из 5, а потом взять эту часть 5 раз, так как их всего 5. То есть делаем так. 8/2*5=20 яблок в корзине.
Мне кажется это весьма логично и вполне понятно. Поэтому самое время закрепить эти знания путем решения еще одной задачи.
Задачи на нахождение значения дроби от числа
Давайте приведу такую задаче на нахождение числа. Если известна часть в виде дроби 1/3, и эта часть в количественном значении равна 30…
Задача.
В магазин привезли 1/3 часть планируемого объема сахара, что составило 30 кг. Сколько килограммов сахара должны привезти в магазин всего.
30/1*3=90 кг сахара должны привезти в магазин.
Ответ: 90 кг.
Онлайн калькулятор нахождения значения дроби от числа
Ну, и теперь приведу активный онлайн калькулятор, с помощью которого легко можно будет вычислить часть от числа, представленную в виде дроби, так и обратное число, если известна его часть в виде дроби и числовое значение этой части.
Введите значения дроби для вычисления ее в виде части от исходного:
Дробь
Находим то число, где дробь часть от «исходного числа»
Находим то число, где известно, что его часть равна дроби, а дробь по количественному значению -«исходному числу»
Калькулятор дробей
- Главная
- /
- Математика
- /
- Арифметика
- /
- Калькулятор дробей
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа — это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅66 + 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅66 + 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅26⋅2=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
12:23=12⋅32=1⋅32⋅2=34
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅1616 + 1116=11116
См. также
Используя этот онлайн калькулятор с дробями, вы сможете сложить, вычесть, умножить, разделить или возвести в степень обыкновенные дроби, смешанные числа (дроби с целой частью), десятичные дроби и целые числа, соответственно найти их сумму, разность, произведение или частное.
Воспользовавшись онлайн калькулятором дробей, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения задач с дробями и закрепить пройденный на уроках материал.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Выполнить сложение дробей путем сложения их числителей.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

