Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
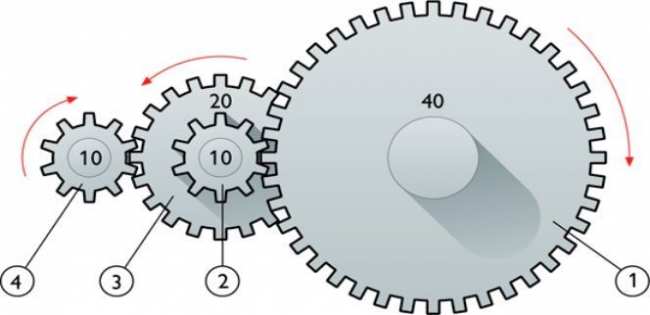
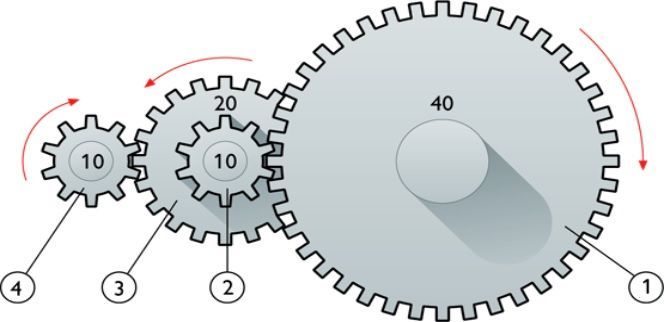
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
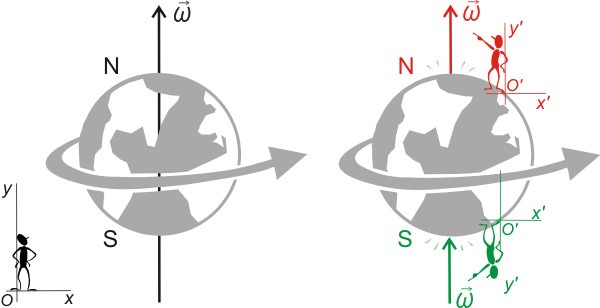
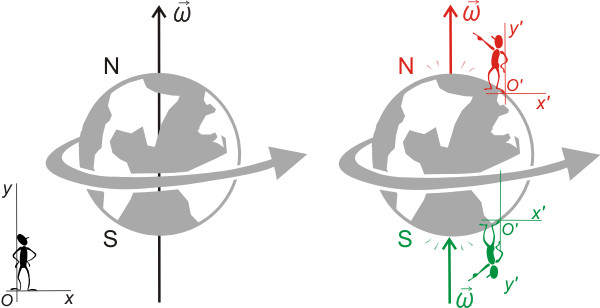
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Или:
Отсюда:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22.1k
Вращательное движение (Движение тела по окружности)
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
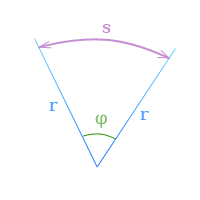
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
[
φ = frac{s}{r}
]
Соотношение между единицами угла
[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]
|
$ 1 enspace рад = 57.3° $ |
$ 1° = 17.45 enspace мрад $ |
$ 1´ = 291 enspace мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
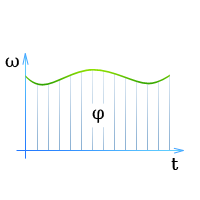
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
[
T = frac{1}{f} = frac{1}{n}
]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
[
φ = 2 π N
]
Угловая скорость
Из формулы для одного оборота следует:
[
ω = 2 π f = frac{2π}{T}
]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Вращательное движение (движение тела по окружности) |
стр. 422 |
|---|
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения
— это время, за которое совершается один оборот.
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле:
Итак,
чтобы найти период обращения, надо время, за которое совершено п оборотов, разделить на число оборотов
.
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения
— это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой
V
(читается: ню) и определяется по формуле:
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с -1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
Формулы (6.1) и (6.3) позволяют найти период обращения Т, если известны число n и время оборотов t или частота обращения
V
. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела
V
и радиус окружности r, по которой оно движется.
Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (l
окр = 2
П
r, где
П
≈3,14- число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,
Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
. 1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
Отослано читателями из интернет-сайтов
Сборник конспектов уроков по физике, рефераты на тему из школьной программы. Календарно тематическое планирование. физика 8 класс онлайн, книги и учебники по физике. Школьнику подготовиться к уроку.
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Номинальная скорость вращения
Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:
К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.
Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Угловая скорость
Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.
Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.
Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:
где:
- ω – угловая скорость (рад./с);
- ∆ϕ – изменение угла отклонения при повороте (рад.);
- ∆t – время, затраченное на отклонение ©.
Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.
Угловая скорость в конкретных случаях
На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.
Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.
Главное отличие между сидерическим и синодическим периодами
Как уже было сказано, сидерический — это реальный период обращения, а синодический — это кажущийся, однако в чем же главная разница между этими понятиями?
Вся разница заключается в количестве объектов, относительно которых измеряется временная характеристика. Понятие «сидерический период» принимает во внимание всего один относительный объект, например, Марс вращается вокруг Солнца, то есть движение рассматривается только относительно одной звезды. Синодический же временной период — это характеристика, которая учитывает относительное положение двух и более объектов, например, два одинаковых положения Юпитера относительно земного наблюдателя. То есть здесь необходимо учитывать положение Юпитера не только относительно Солнца, но и относительно Земли, которая также вращается вокруг Солнца.
Угол поворота и период обращения
Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.
Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать ½, ¼ оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.
Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.
Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.
В этом случае находят применения такие характеристики, как:
- период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
- частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.
Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.
Понятие о синодическом и сидерическом временных периодах
Вам будет интересно:Двусторонняя симметрия — это что такое? Кто имеет двустороннюю симметрию тела?
Практически каждый из нас знает, что планеты движутся по эллиптическим орбитам вокруг своих звезд. Звезды, в свою очередь, совершают орбитальные движения вокруг друг друга или вокруг центра Галактики. Иными словами, все массивные объекты космоса имеют определенные траектории движения, включая кометы и астероиды.
Важной характеристикой для всякого космического объекта является время, которое он затрачивает, чтобы совершить один полный оборот по своей траектории. Это время принято называть периодом. Чаще всего в астрономии при изучении Солнечной системы пользуются двумя периодами: синодическим и сидерическим.
Сидерический временной период — это время, которое требуется объекту, чтобы он совершил полный оборот по своей орбите вокруг своей звезды, при этом за точку отчета берется другая удаленная звезда. Этот период также называют реальным, поскольку именно такое значение времени обращения по орбите получит неподвижный наблюдатель, который будет следить за процессом вращения объекта вокруг его звезды.
Синодический период — это время, через которое объект появится в одной и той же точке на небосводе, если смотреть на него с какой-либо планеты. Например, если взять Луну, Землю и Солнце и задаться вопросом о том, через какое время Луна будет находиться в точке на небе, в которой она находится в данный момент, ответом на него будет значение синодического периода Луны. Этот период также называют кажущимся, поскольку от реального орбитального периода он отличается.
Переход от угловой к линейной скорости
Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:
ν = 2*π*R / Т = 2*π*R* ν.
Так как ω = 2*π*ν, то получается:
Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.
К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.
Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:
а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.
Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.
Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.
Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости 2) изменяется только направление его скорости 3) изменяются и модуль, и направление его скорости 4) не изменяется ни модуль, ни направление его скорости
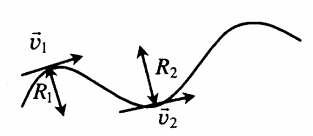
2. Линейная скорость точки 1, находящейся на расстоянии ( R_1 ) от центра вращающегося колеса, равна ( v_1 ). Чему равна скорость ( v_2 ) точки 2, находящейся от центра на расстоянии ( R_2=4R_1 )?
1) ( v_2=v_1 ) 2) ( v_2=2v_1 ) 3) ( v_2=0,25v_1 ) 4) ( v_2=4v_1 )
3. Период обращения точки по окружности можно вычислить по формуле:
1) ( T=2pi!Rv ) 2) ( T=2pi!R/v ) 3) ( T=2pi v ) 4) ( T=2pi/v )
4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:
1) ( omega=a^2R ) 2) ( omega=vR^2 ) 3) ( omega=vR ) 4) ( omega=v/R )
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза 2) уменьшилась в 2 раза 3) увеличилась в 4 раза 4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось 2) уменьшилось в 16 раз 3) уменьшилось в 4 раза 4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз 2) уменьшилось в 9 раз 3) уменьшилось в 3 раза 4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с 2) 3300 с 3) 3·10-4 с 4) 5·10-6 с
9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?
1) 0,05 Гц 2) 2 Гц 3) 20 Гц 4) 200 Гц
10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?
1) 14 с 2) 7 с 3) 0,07 с 4) 0,44 с
11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА А) линейная скорость Б) угловая скорость В) частота обращения
ФОРМУЛА 1) ( 1/T ) 2) ( v^2/R ) 3) ( v/R ) 4) ( omega R ) 5) ( 1/n )
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце. В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА A) угловая скорость Б) линейная скорость B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ 1) увеличилась 2) уменьшилась 3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
Видео
- Как найти период обращения
- Как найти скорость частицы
- Как определить частоту
- — секундомер;
- — калькулятор;
- — справочные данные по орбитам планет.
- как найти обращения в тексте
Что такое линейная скорость?
Речь идет о физической величине, которая показывает, какое расстояние в пространстве проходит тело за единицу времени. Как правило, скорость обозначают буквой v¯, где символ черты говорит о том, что она является векторной величиной. Измеряется скорость в метрах в секунду (м/с), километрах в час (км/ч), милях в час (мил/ч) и других единицах, предполагающих отношение расстояния ко времени.
Вам будет интересно:«Почаще»: слитно или раздельно? Как написание зависит от части речи?
Вектор скорости v¯ показывает направление реального перемещения тела. Этим он отличается от вектора ускорения, который направлен в сторону действующей силы, но не в сторону движения тела, хотя они могут совпадать.
Вращение тел
Под вращением понимают тип движения, при котором траектория перемещающегося тела представляет собой окружность. Вращение может происходить вокруг оси или вокруг фиксированной точки. Вращение колеса, планет по своим орбитам, спортсменов во время соревнований по фигурному катанию — все это примеры указанного типа движения.
По аналогии с линейным перемещением, главной формулой динамики вращения является следующая:
M = I*α.
Здесь M и I — моменты силы и инерции, соответственно, α — ускорение угловое.
Для описания вращения удобно пользоваться не линейной, а угловой скоростью. Она определяется так:
ω = θ/t.
Где θ — угол, на который тело повернулось за время t. С записанным ускорением α скорость ω связана следующим равенством:
ω = α*t.
Для измерения всех угловых величин используются радианы.
Содержание
- Линейная скорость вращения, частота и частота угловая
- Число оборотов
- Угловая скорость
- Описывающие вращение физические величины
- Мощность вращающихся объектов
- Задача на определение циклической частоты вращения вала
- Линейная скорость вращения, частота и частота угловая
- Коэффициент полезного действия электромотора
- Угловая частота, период и угловая скорость
- Переменный синусоидальный ток
- Угловая частота, период и угловая скорость
- Вращательное движение тела, формулы
- Экономическое обоснование эффекта от инвертора
- Основные формулы расчета мощности двигателей
- Угловая скорость в спорте
- Описывающие вращение физические величины
- Описывающие вращение физические величины
- Как подключить частотный преобразователь
- Циклическая частота вращения (обращения)
- Задача на определение циклической частоты вращения вала
- Период пульсаций и частота
- Интенсивность циклов
- Опасность разночастотных зарядов
- Генерирование переменного тока
- Инвертор
- Фазорасщепитель
Линейная скорость вращения, частота и частота угловая
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.
Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:
Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:
Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.
Линейная скорость v связана со скоростью угловой ω следующим равенством:
Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:
Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если n — число оборотов, f — частота, T — продолжительность одного оборота, период, ? — угловое перемещение, N — полное число оборотов, t — время, продолжительность вращения, ? — угловая частота,
то
Угловое перемещение равно произведению полного числа оборотов на 2?:
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:• формулы справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.• вопреки своему названию число оборотов n — это не число, а физическая величина.• следует различать число оборотов n и полное число оборотов N
Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
n = θ/(2*pi);
L = θ*r.
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
ω = θ/t
Мощность вращающихся объектов
Для расчета подобной системы применяют формулу:
N = M * w = (2π * M* n)/60,
где:
- M – момент силы;
- w – угловая скорость, характеризующая вращение;
- n – количество оборотов, которое совершает двигатель или другое устройство за 60 секунд.
Приведенные сведения используют с учетом целевого назначения и реальных условий. Так, в термодинамике необходимо помнить о зависимости эффективности системы от температуры окружающей среды. Тепловые потери нагревателя оценивают по соответствующей мощности на единицу площади поверхности. Аналогичным образом поступают при решении механических задач для расчета тяги, КПД, иных рабочих параметров. Как правило, приходится специальным коэффициентом компенсировать трение.
В электрических цепях ток ограничивает сопротивление проводника. Для небольших расстояний при малой мощности тщательные расчеты не нужны. Однако проект магистральной трассы обязательно содержит соответствующие вычисления. На основе полученных результатов делают выводы о среднегодовых экономических показателях. Следует помнить о необходимости учета искажений, которые добавляют при работе с переменным напряжением реактивные нагрузки.
Задача на определение циклической частоты вращения вала
Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?
Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:
f = 2*pi*μ
Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.
Линейная скорость вращения, частота и частота угловая
В технике для некоторых вращающих конструкций, например, шестерен и валов, известны их рабочие частоты μ и линейные скорости v. Тем не менее каждую из этих характеристик можно использовать для определения угловой или циклической частоты.
Выше отмечалось, что частота μ измеряется в герцах. Она показывает количество оборотов вращающегося тела за одну секунду. Формула для нее принимает вид:
μ = 1/T
Если сравнить это выражение с соответствующим равенством для f, то формула, как найти частоту вращения f через μ описывающая, будет иметь вид:
f = 2*pi*μ
Эта формула интуитивно понятна, поскольку μ показывает количество оборотов за единицу времени, а f отражает ту же самую величину, только представленную в радианах.
Линейная скорость v связана со скоростью угловой ω следующим равенством:
v = ω*r
Поскольку модули величин f и ω равны, то из последнего выражения легко получить соответствующую формулу частоты вращения циклической. Запишем ее:
f = v/r
Где r — радиус вращения. Заметим, что скорость v линейно растет при увеличении радиуса r, при этом отношение этих величин является константой. Последнее умозаключение означает, что если измерять циклическую частоту вращения в любой точке сечения вращающегося массивного объекта, то она будет везде одинаковой.
Коэффициент полезного действия электромотора
КПД — это характеристика, которая отражает эффективность работы системы при преобразовании энергии в механическую. Выражается отношением полезной энергии к потраченной. По единой системе единиц измерений он обозначается как «eta» и является безразмерным значением, исчисляемым в процентах. Формула КПД электродвигателя через мощность:
eta = P2 ÷ P1, где:
P1 — электрическая (подаваемая) мощность, Вт;
P2 — полезная (механическая) мощность, Вт;
Также он может быть выражен как:
eta = A ÷ Q × 100 %, где:
A — полезная работа, Дж;
Q — затраченная энергия, Дж.
Чаще коэффициент вычисляют по формуле потребляемой мощности электродвигателя, так как эти показатели всегда легче измерить.
Снижение эффективности работы электродвигателя происходит по причине:
Электрических потерь. Это происходит в результате нагрева проводников от прохождения по ним тока. Магнитных потерь
Вследствие излишнего намагничивания сердечника появляется гистерезис и вихревые токи, что важно учитывать в формуле мощности электродвигателя. Механических потерь
Они связаны с трением и вентиляцией. Дополнительных потерь. Они появляются из-за гармоник магнитного поля, так как статор и ротор имеют зубчатую форму. Также в обмотке присутствуют высшие гармоники магнитодвижущей силы.
Следует отметить, что КПД является одним из самых важных компонентов формулы расчета мощности электродвигателя, так как позволяет получить цифры, наиболее приближенные к действительности. В среднем этот показатель варьирует от 10% до 99%. Она зависит от конструктивного устройства механизма.
Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
T = 2*pi/ω
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
f = 2*pi/T
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
f = ω
Это равенство означает следующее:
- формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
- так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
Переменный синусоидальный ток
Это тот ток, который периодически меняется во времени, и его изменения подчиняются закону синусоиды. Это элементарное движение электрических зарядов, потому дальнейшему разложению на простые токи оно не подлежит.
Вид формулы такого переменного тока:
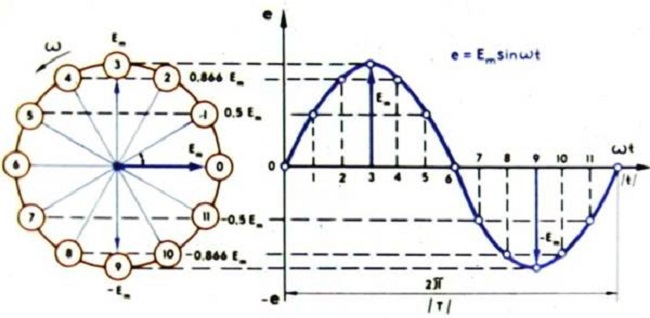
i = Im*sinωt,
где:
- Im – амплитуда;
- sinωt – фаза синусоидального тока, рад.
Здесь ω = const, называется угловой частотой переменного электричества, причём угол ωt находится в прямой временной зависимости.
Зная частоту f исходного тока, можно вычислить его угловую частоту, применив выражение:
ω = 2πf = 2π/Т.
Тут 2π – это выраженное в радианах значение центрального угла окружности:
- Т = 2 π радиан = 3600;
- Т/2 = π = 1800;
- Т/4 = π/2 = 900.
Если выразить 1 рад в градусах, то он будет равен 57°17′.
Угловая частота, период и угловая скорость
Выше уже отмечалось, что важным свойством любого вращательного движения является время, за которое совершается один оборот. Это время называется периодом вращения. Его обозначают буквой T и измеряют в секундах. Формулу для периода T можно записать через угловую скорость ω. Соответствующее выражение имеет вид:
Величина, обратная периоду, называется частотой. Ее измеряют в герцах (Гц). Для кругового движения удобно использовать не саму частоту, а ее угловой аналог. Обозначим ее f. Формула частоты вращения угловой f имеет вид:
Чтобы рассчитать угловую частоту, необходимо знать период вращательного движения.
Сравнивая две последние формулы, приходим к следующему равенству:
Это равенство означает следующее:
- формулы угловой частоты и угловой скорости совпадают, поэтому эти величины равны численно между собой;
- так же как и скорость, частота показывает, на какой угол в радианах поворачивается тело за одну секунду.
Различие между этими величинами единственное: угловая частота является величиной скалярной, скорость же — это вектор.
Вращательное движение тела, формулы
Кроме того, эти величины связаны определенным образом с угловым перемещением ?, угловой скоростью ? и угловым ускорением ?.
| Sл | перемещение тела по траектории, | метр |
|---|---|---|
| Uл | скорость тела при движении по траектории, | метр / секунда |
| aл | ускорение данного тела при движении по траектории, | метр / секунда2 |
| r | радиус траектории, | метр |
| d | диаметр траектории, | метр |
| ? | угловое перемещение тела, | радиан |
| ? | угловая скорость тела, | радиан / секунда |
| ? | угловое ускорение тела, | радиан / секунда2 |
| f | частота, | Герц |
Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.
Экономическое обоснование эффекта от инвертора
Время окупаемости инвертора рассчитывается отношением затрат на покупку к экономии энергии. Экономия обычно равна от 20 до 40% от номинальной мощности мотора.
Затраты снижают факторы, повышающие производительность частотных преобразователей:
- Уменьшение затрат на обслуживание.
- Повышение ресурса двигателя.
Экономия рассчитывается:
где Э – экономия денег в рублях;
Рпч – мощность инвертора;
Ч – часов эксплуатации в день;
Д – число дней;
К – коэффициент ожидаемого процента экономии;
Т – тариф энергии в рублях.
Время окупаемости равно отношению затрат на покупку инвертора к экономии денег. Расчеты показывают, что период окупаемости получается от 3 месяцев до 3 лет. Это зависит от мощности мотора.
Модуль №4. Частотное регулирование скорости асинхронного двигателя

Основные формулы расчета мощности двигателей
Для вычисления реальных характеристик механизмов всегда нужно учитывать много параметров. в первую очередь нужно знать, какой ток подается на обмотки электродвигателя: постоянный или переменный. Принцип их работы отличается, следовательно, отличаются метод вычислений. Если упрощенный вид расчета мощности привода выглядит как:
Pэл = U × I, где
I — сила тока, А;
U — напряжение, В;
Pэл — подведенная электрическая мощность. Вт.
В формуле мощности электродвигателя переменного тока необходимо также учитывать сдвиг фаз (alpha). Соответственно, расчеты для асинхронного привода выглядят как:
Pэл = U × I × cos(alpha).
Кроме активной (подведенной) мощности существует также:
- S — реактивная, ВА. S = P ÷ cos(alpha).
- Q — полная, ВА. Q = I × U × sin(alpha).
В расчетах также необходимо учитывать тепловые и индукционные потери, а также трение. Поэтому упрощенная модель формулы для электродвигателя постоянного тока выглядит как:
Pэл = Pмех + Ртеп +Ринд + Ртр, где
Рмех — полезная вырабатываемая мощность, Вт;
Ртеп — потери на образование тепла, ВТ;
Ринд — затраты на заряд в индукционной катушке, Вт;
Рт — потери в результате трения, Вт.
Угловая скорость в спорте
Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.
При первобытнообщинном строе главными охотниками были мужчины

У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.
В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.
Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.
Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
Описывающие вращение физические величины
Для численного описания вращения в физике был введен ряд характеристик. Перечислим их и охарактеризуем.
В первую очередь это угол поворота, обозначается θ. Поскольку полная окружность характеризуется центральным углом в 2*pi радиан, то, зная величину θ, на которую повернулось вращающееся тело за определенный промежуток времени, можно определить число оборотов за это время. Кроме того, угол θ позволяет рассчитать линейный путь, пройденный телом вдоль кривой окружности. Соответствующие формулы для числа оборотов n и пройденного пути L имеют вид:
n = θ/(2*pi);
L = θ*r.
Где r — радиус окружности или радиус вращения.
Следующей характеристикой рассматриваемого типа движения является угловая скорость. Ее обычно обозначают буквой ω. Она измеряется в радианах в секунду, то есть показывает величину угла в радианах, на которые поворачивается вращающееся тело за одну секунду. Для угловой скорости в случае равномерного вращения справедлива формула:
ω = θ/t
Как подключить частотный преобразователь
Если кабель для подключения на 220 В с 1-й фазой, применяется схема «треугольника». Нельзя подключать частотник, если выходной ток выше 50% от номинального значения.
Если кабель питания на три фазы 380 В, то делается схема «звезды». Чтобы проще было подключать питание, предусмотрены контакты и клеммы с буквенными обозначениями.
- Контакты R, S, T предназначены для подключения сети питания по фазам.
- Клеммы U , V , W служат соединением электродвигателя. Для реверса достаточно изменить подключение двух проводов между собой.
В приборе должна быть колодка с клеммой подключения к земле. Подробней, как подключить, здесь.
Циклическая частота вращения (обращения)
Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.
Циклическая частота вращения – это количество оборотов тела за 2*π секунды.
У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.
Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.
При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:
- частоты питающей сети;
- количества пар полюсов.
Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.
Задача на определение циклической частоты вращения вала
Угловые частоты вращения содержат полезную информацию, поскольку позволяют рассчитать такие важные физические характеристики, как момент импульса или угловую скорость. Решим такую задачу: известно, что рабочая частота вращения вала составляет 1500 оборотов в минуту. Чему равна циклическая частота для этого вала?
Из единиц измерения, приведенный в условии, понятно, что дана обычная частота μ. Поэтому формула частоты вращения вала циклической имеет вид:
Прежде чем ею пользоваться, следует перевести указанную в условии цифру к стандартным единицам измерения, то есть к обратным секундам. Поскольку вал за минуту делает 1500 оборотов, то за секунду он сделает в 60 раз меньше оборотов, то есть 25. То есть частота его вращения равна 25 Гц. Подставляя это число в записанную выше формулу, получаем значение циклической частоты: f = 157 рад/с.
Период пульсаций и частота
Частота переменного тока может иметь другое название – пульсация. Периодом пульсации называют время единичной пульсации.
Интенсивность циклов
Для электросети с частотой 50 Гц период пульсации составит:
Т = 1/50 = 0,02 с.
При необходимости, зная эту зависимость, можно по времени цикла вычислить частоту.
Опасность разночастотных зарядов
Как постоянный, так и переменный ток при определённых значениях представляет опасность для человека. До 500 В разница в безопасности находится в соотношении 1:3 (42 В постоянного к 120 В переменного).
При значениях выше 500 В это соотношение выравнивается, причём константное электричество вызывает ожоги и электролизацию кожных покровов, изменяющееся – судороги, фибрилляцию и смерть. Тут уже частота пульсации имеет большое значение. Самый опасный интервал частот – от 40 до 60 Гц. Далее с повышением частоты риск поражения уменьшается.

Частота переменного электричества – важный параметр. Она влияет не только на работу электроустановок потребителей, но и на человеческий организм. Изменяя частоту электрических колебаний, можно менять технологические процессы на производстве и качество вырабатываемой энергии.
Генерирование переменного тока
Кроме стандартных генераторов, для производства переменного тока применяются инверторы и фазорасщепители.
Инвертор
Это устройство, с помощью которого из постоянного тока получают его переменный вид. В процессе этого величина выходного напряжения тоже меняется. Схема устройства представляет собой электронный генератор синусоидального импульсного напряжения периодического характера. Есть варианты инверторов, работающих с дискретным сигналом. Инверторы применяют для автономного питания оборудования от аккумуляторов постоянного напряжения.

Фазорасщепитель
Ещё один способ получить несколько фаз из какого-либо сигнала – это выполнить его расщепление на несколько фаз. Это делается с помощью фазорасщепителя. Принудительная обработка сигналов цифрового или аналогового формата используется, как в радиоэлектронике, так и в силовой электротехнике.
Для электроснабжения трёхфазных асинхронных двигателей применяют выполненный на их же базе фазорасщепитель. Для этого обмотки трёхфазного двигателя соединяют не «звездой», а иначе. Две катушки присоединяют между собой последовательно, третью – подключают к средней точке второй обмотки. Двигатель запускают, как однофазный, после разгона в его третьей обмотке наводится ЭДС.
Интересно. В случае расщепления фаз подобным методом сдвиг фаз между 2 и 3 обмоткой составляет не 1200, как должно быть в идеале, а 900.
Под скоростью вращения асинхронного электродвигателя обычно понимают угловую частоту вращения его ротора, которая приведена на шильдике (на паспортной табличке двигателя) в виде количества оборотов в минуту. Трехфазный двигатель можно питать и от однофазной сети, для этого достаточно добавить конденсатор параллельно одной или двум его обмоткам, в зависимости от напряжения сети, но конструкция двигателя от этого не изменится.
Так, если ротор под нагрузкой совершает 2760 оборотов в минуту, то угловая частота данного двигателя будет равна 2760*2пи/60 радиан в секунду, то есть 289 рад/с, что не удобно для восприятия, поэтому на табличке пишут просто «2760 об/мин». Применительно к асинхронному электродвигателю, это обороты с учетом скольжения s.
Синхронная же скорость данного двигателя (без учета скольжения) будет равна 3000 оборотов в минуту, поскольку при питании обмоток статора сетевым током с частотой 50 Гц, каждую секунду магнитный поток будет совершать по 50 полных циклических изменений, а 50*60 = 3000, вот и получается 3000 оборотов в минуту — синхронная скорость асинхронного электродвигателя.
3000 оборотов в минуту
Таким образом становится ясно, что для определения синхронных оборотов асинхронного электродвигателя достаточно определить количество пар его полюсов, что легко сделать, сняв крышку и взглянув на статор.
Общее число пазов статора разделите на число пазов, приходящихся на одну секцию обмотки одной из фаз. Если получится 2, то перед вами двигатель с двумя полюсами — с одной парой полюсов. Следовательно синхронная частота составляет 3000 оборотов в минуту или примерно 2910 с учетом скольжения. В простейшем случае 12 пазов, по 6 пазов на катушку, и таких катушек 6 — по две на каждую из трех фаз.
Обратите внимание, количество катушек в одной группе для одной пары полюсов может быть не обязательно 1, но и 2 и 3, однако для примера мы рассмотрели вариант с одиночными группами на пару катушек (не будем в рамках данной статьи заострять внимание на способах намотки).
1500 оборотов в минуту
Для получения синхронной скорости в 1500 оборотов в минуту, количество полюсов статора увеличивают вдвое, чтобы за 1 колебание из 50 магнитный поток совершил бы только пол оборота — 180 градусов.
Для этого на каждую фазу делают по 4 секции обмотки. Таким образом, если одна катушка занимает четверть всех пазов, то перед вами двигатель с двумя парами полюсов, образованными четырьмя катушками на фазу.
Например, 6 пазов из 24 занимает одна катушка или 12 из 48, значит перед вами двигатель с синхронной частотой 1500 оборотов в минуту, или с учетом скольжения примерно 1350 оборотов в минуту. На приведенном фото каждая секция обмотки выполнена в виде двойной катушечной группы.
1000 оборотов в минуту
Как вы уже поняли, для получения синхронной частоты в 1000 оборотов в минуту, каждая фаза образует уже три пары полюсов, чтобы за одно колебание из 50 (герц) магнитный поток обернулся бы всего на 120 градусов, и соответствующим образом повернул бы за собой ротор.
Таким образом, минимум 18 катушек установлены на статор, причем каждая катушка занимает шестую часть всех пазов (по шесть катушек на фазу — по три пары). Например, если пазов 24, то одна катушка займет 4 из них. Получится частота с учетом скольжения около 935 оборотов в минуту.
750 оборотов в минуту
Для получения синхронной скорости в 750 оборотов в минуту, необходимо, чтобы три фазы формировали на статоре четыре пары движущихся полюсов, это по 8 катушек на фазу — одна напротив другой — 8 полюсов. Если например на 48 пазов приходится по катушке на каждые 6 пазов — перед вами асинхронный двигатель с синхронными оборотами 750 (или около 730 с учетом скольжения).
500 оборотов в минуту
Наконец, для получения асинхронного двигателя с синхронной скоростью в 500 оборотов в минуту необходимо 6 пар полюсов — по 12 катушек (полюсов) на фазу, чтобы на каждое колебание сети магнитный поток поворачивался бы на 60 градусов. То есть, если например статор имеет 36 пазов, при этом на катушку приходится по 4 паза — перед вами трехфазный двигатель на 500 оборотов в минуту (480 с учетом скольжения).
Как определить мощность?
Существует несколько способов определения мощности электродвигателя: диаметру вала, по габариту и длине, по току и сопротивлению, замеру счетчиком электроэнергии.
По габаритным размерам
Все электродвигатели отличаются по габаритным размерам. Определить мощность двигателя можно сравнив габаритные размеры с таблицей определения мощности электродвигателя, перейдя по ссылке габаритно-присоединительные размеры электродвигателей АИР.
Какие размеры необходимо замерить:
По диаметру вала
Определение мощности электродвигателя по диаметру вала — частый запрос для поисковых систем. Но для точного определения этого параметра недостаточно – два двигателя в одном габарите, с одинаковыми валами и частотой вращения могут иметь различную мощность.
Таблица с привязкой диаметров валов к мощности и оборотам для двигателей АИР и 4АМ.
| Мощность электродвигателя Р, кВт | Диаметр вала, мм | Переход к модели | |||
| 3000 об/мин | 1500 об/мин | 1000 об/мин | 750 об/мин | ||
| 0,18 | 11 | 11 | 14 | — | АИР56А2, АИР56В4, АИР63А6 |
| 0,25 | 14 | 19 | АИР56В2, АИР63А4, АИР63В6, АИР71В8 | ||
| 0,37 | 14 | 19 | 22 | АИР63А2, АИР63В4, АИР71А6, АИР80А8 | |
| 0,55 | 19 | АИР63В2, АИР71А4, АИР71В6, АИР80В8 | |||
| 0,75 | 19 | 22 | 24 | АИР71А2, АИР71В4, АИР80А6, АИР90LA8 | |
| 1,1 | 22 | АИР71В2, АИР80А4, АИР80В6, АИР90LB8 | |||
| 1,5 | 22 | 24 | 28 | АИР80А2, АИР80В4, АИР90L6, АИР100L8 | |
| 2,2 | 24 | 28 | 32 | АИР80В2, АИР90L4, АИР100L6, АИР112МА8 | |
| 3 | 24 | 32 | АИР90L2, АИР100S4, АИР112МА6, АИР112МВ8 | ||
| 4 | 28 | 28 | 38 | АИР100S2, АИР100L4, АИР112МВ6, АИР132S8 | |
| 5,5 | 32 | 38 | АИР100L2, АИР112М4, АИР132S6, АИР132М8 | ||
| 7,5 | 32 | 38 | 48 | АИР112M2, АИР132S4, АИР132М6, АИР160S8 | |
| 11 | 38 | 48 | АИР132M2, АИР132М4, АИР160S6, АИР160М8 | ||
| 15 | 42 | 48 | 55 | АИР160S2, АИР160S4, АИР160М6, АИР180М8 | |
| 18,5 | 55 | 60 | АИР160M2, АИР160M4, АИР180М6, АИР200М8 | ||
| 22 | 48 | 55 | 60 | АИР180S2, АИР180S4, АИР200М6, АИР200L8 | |
| 30 | 65 | АИР180M2, АИР180M4, АИР200L6, АИР225М8 | |||
| 37 | 55 | 60 | 65 | 75 | АИР200M2, АИР200M4, АИР225М6, АИР250S8 |
| 45 | 75 | 75 | АИР200L2, АИР200L4, АИР250S6, АИР250M8 | ||
| 55 | 65 | 80 | АИР225M2, АИР225M4, АИР250M6, АИР280S8 | ||
| 75 | 65 | 75 | 80 | АИР250S2, АИР250S4, АИР280S6, АИР280M8 | |
| 90 | 90 | АИР250М2, АИР250M4, АИР280M6, АИР315S8 | |||
| 110 | 70 | 80 | 90 | АИР280S2, АИР280S4, АИР315S6, АИР315M8 | |
| 132 | 100 | АИР280M2, АИР280M4, АИР315M6, АИР355S8 | |||
| 160 | 75 | 90 | 100 | АИР315S2, АИР315S4, АИР355S6 | |
| 200 | АИР315M2, АИР315M4, АИР355M6 | ||||
| 250 | 85 | 100 | АИР355S2, АИР355S4 | ||
| 315 | — | АИР355M2, АИР355M4 |
По показанию счетчика
Как правило измерение счетчика отображаются в киловаттах (далее кВт). Для точности измерения стоит отключить все электроприборы или воспользоваться портативным счетчиком. Мощность электродвигателя 2,2 кВт, подразумевает что он потребляет 2,2 кВт электроэнергии в час.
Для измерения мощности по показанию счетчика нужно:
Расчет мощности по току
Для начала нужно подключить двигатель к сети и замерить показатели напряжения. Замеряем потребляемый ток на каждой из обмоток фаз с помощью амперметра или мультиметра. Далее, находим сумму токов трех фаз и умножаем на ранее замеренные показатели напряжения, наглядно в формуле расчета мощности электродвигателя по току.
Как посчитать число оборотов двигателя
Опытный электрик может легко отличить 1.5 от 2.2 кВт всего лишь взглянув на его габариты. Помимо этого он сможет определить количество оборотов двигателя по размеру статора, количеству пар полюсов и диаметра вала.
Основные способы определения мощности двигателя
Самый быстрый способ — посчитать количество катушек (катушечных групп)
Определяем мощность по расчетным таблицам
. С помощью штангенциркуля замеряем диаметр вала, длину мотора (без выступающего вала) и расстояние до оси.Замеряем вылет вала и его выступающую часть, диаметр фланца если он есть, а также расстояние крепежных отверстий.
По этим данным с помощью сводной таблицы можно легко определить мощность двигателя и другие характеристики
Источник
Определение оборотов вала
Асинхронные трехфазные двигатели по частоте вращения ротора делятся 4 типа: 3000, 1500, 1000 и 750 об. мин. Приводим пример маркировки на основании АИР 180:
Самый простой способ определить количество оборотов трехфазного асинхронного электродвигателя – снять задний кожух и посмотреть обмотку статора.
У двигателя на 3000 об/мин катушка обмотки статора занимает половину окружности — 180 °, то есть начало и конец секции параллельны друг другу и перпендикулярны центру. У электромоторов 1500 оборотов угол равен 120 °, у 1000 – 90 °. Схематический вид катушек изображен на чертеже. Все обмоточные данные двигателей смотрите в таблице.
Узнать частоту вращения с помощью амперметра
Узнать обороты вала двигателя, можно посчитав количество полюсов. Для этого нам понадобится миллиамперметр — подключаем измерительный прибор к обмотке статора. При вращении вала двигателя стрелка амперметра будет отклонятся. Число отклонений стрелки за один оборот – равно количеству полюсов.
Фото оборотов электродвигателя
-
-
Характеристики электродвигателей: основные параметры и расшифровка маркировки современных электродвигателей
-
Конденсатор для электродвигателя: советы по подбору и правила подключения пускового конденсатора
Читайте здесь! Мощность электродвигателя — методика определения и правила подбора двигателя по мощности (инструкция + фото)
Как определить мощность, частоту вращения, начало и конец обмоток двигателя без бирки.
При этом паспорта или какой-то другой технической документации у вас под рукой нет. Можно ли в этом случае узнать параметры двигателя самостоятельно?
Конечно же да, причем несколькими способами. Давайте рассмотрим самые популярные из них.
Первоначально для точного определения мощности потребуется выяснить синхронную частоту вращения вала, а перед этим узнать, где у нас начало каждой обмотки, а где ее конец.
По ГОСТ 26772-85 обмотки трехфазных асинхронных двигателей должны маркироваться буквами:
По старому госту обозначение было несколько иным:
Еще раньше можно было встретить надписи Н1-К1 (начало-конец обмотки №1), Н2-К2, Н3-К3.
На некоторых движках для облегчения распознавания концов обмоток их выводят из разных отверстий на одну или другую сторону. Как например на фото снизу.
Но не всегда можно доверять таким выводам. Поэтому проверить все вручную никогда не помешает.
Если никаких обозначений и букв на барно нет, и вы не знаете, где у вас начало, а где конец обмотки, читайте инструкцию под спойлером.
В помощники берете мультиметр и устанавливаете его в режим замера сопротивления.
Одним щупом дотрагиваетесь до любого из шести выводов, а другим поочередно прикасаетесь к остальным пяти проводам, тем самым, ища соответствующую пару.
При ее нахождении на табло мультиметра должна высветиться цифра, показывающее некое сопротивление в Омах.
В остальных случаях с другими проводами сопротивление будет равняться бесконечности (обрыв).
Отмечаете данную обмотку бирками и переходите к оставшимся проводам. Таким нехитрым способом буквально за одну минуту можно «вызвонить» концы всех обмоток.
Однако это еще не все. Главная проблема заключается в том, что вы пока не знаете, какой из двух выводов является началом обмотки, а какой ее концом.
Для того, чтобы это выяснить, соединяете между собой по два вывода от разных обмоток. То есть, условное начало V1 первой обмотки, соединяем с условным концом второй обмотки — U2.
При этом у вас пока нет точной информации начало это или конец. Вы их сами так промаркировали для себя, чтобы сделать последующие замеры.
На другие концы этих двух обмоток (U1 и V2) подаете переменное напряжение 220В или меньше. Зависит это от того, на какое напряжение рассчитан ваш движок.
Смысл всего этого действия – замерить какое напряжение появится на концах третьей обмотки W1-W2. Это так называемый метод трансформации.
Если между W1-W2 будет какое-то значение (10-15В или больше), значит первые две обмотки у вас включены согласовано, то есть правильно. Все подписанные концы V1-V2, U1-U2 вы угадали верно.
Бирки на них менять не нужно.
Если же напряжение между W1-W2 будет очень маленьким или его вообще не будет, то получается, что первые две обмотки вы включили по встречной схеме (неправильно). Бирки на одной из обмоток придется поменять местами.
Разобравшись с двумя фазами переходим к третьей. Здесь процедура та же самая. Соединяете между собой условные начало и конец W1 и U2, а на U1 и W2 подаете 220V.
Замеры делаете между выводами V1 и V2. Если угадали, то двигатель может даже запуститься на двух фазах, ну или по крайней мере между V1 и V2 будет несколько вольт.
Если нет, то просто поменяйте местами бирки W1 и W2.
Второй метод определения начала и конца обмоток еще более простой.
Сперва находите три разные обмотки, как было указано выше. Соединяете их последовательно (условный конец первой с началом второй U2-V1, а конец второй с началом третье V2-W1).
На два оставшихся вывода U1-W2 подаете напряжение 220В. После этого поочередно подносите лампочку к концам каждой из обмоток (U1-U2, V1-V2, W1-W2).
Если она горит везде с одинаковой яркостью, то вы угадали со всеми выводами.
Если яркость будет отличаться, это говорит о том, что данная обмотка перевернута по отношению к двум другим.
На ней бирки нужно поменять местами. Вообще-то по ТБ с лампочкой в качестве контрольки уже давно запрещено работать, поэтому вместо нее лучше используйте мультиметр с функцией замера напряжения.
Для определения частоты по первому способу вам потребуется обычный китайский стрелочный мультиметр (аналоговый, не электронный!).
Определять частоту нужно при положении переключателя мультиметра в режиме измерения тока (100мА). Далее подключаете измерительные щупы в соответствующие разъемы:
Источник
Как определить частоту вращения электродвигателя?
Очевидно, что правильная эксплуатация любой электрической машины предполагает соответствие такого важного ее технического параметра как частота вращения условиям эксплуатации.
Все основные параметры асинхронного электродвигателя изготовителем указываются на металлической бирке — шильдике, прикрепленной к его корпусу. И конечно, в приведенных технических данных обязательно присутствует информация о частоте вращения при номинальной нагрузке.
Однако, на практике, совсем нередки случаи, когда необходимо определить частоту вращения двигателя с отсутствующим шильдиком или с нечитаемыми — стершимися надписями на нем.
Конечно, в таких случаях опытный мастер-электроприводчик, наверняка сможет определить частоту вращения, но у начинающих специалистов-электриков, занимающихся обслуживанием электрического оборудования при решении этого вопроса могут возникнуть некоторые затруднения.
Проще всего определить скорость вращения вала работающего “асинхронника” тахометром. Но, учитывая, что ввиду узкой специфики использования, наличие этого измерительного прибора — большая редкость, данный метод здесь не рассматривается.
Надеемся, предложенный ниже способ окажется полезным. Он применим для асинхронных электродвигателей небольшой и средней мощности, имеющих однослойные статорные обмотки.
Итак, в нашем случае определение частоты вращения электродвигателя предполагает осмотр его статорной обмотки. Поэтому, с двигателя потребуется снять крышку (пошипниковый щит). Если на его валу закреплены шкив или полумуфта для передачи движения, то рекомендуем снять задний щит.
Расчет параметров частотного преобразователя для асинхронных двигателей
Зачастую приходится понижать скорость вращения двигателя, выполняющего определенные задачи в механизме. Уменьшение числа оборотов элеткродвигателя можно добиться с помощью самодельных приборов, управляющих схем стандартного изготовления.
Электродвигатели переменного тока часто используются в деятельности человека, на металлообрабатывающих станках, транспорта, крановых механизмов и другого оборудования. Двигатели превращают энергию переменного тока питания во вращение вала и агрегатов. Используются в основном асинхронные двигатели переменного тока.
Ротор, а также и статор двигателя состоят из катушек провода, уложенного в сердечник, изготовленный из специальной стали. Классификация электродвигателей следует от способа закладки обмотки.
Обмотка из латунных и медных стержней вставляется в сердечник, по краям устанавливаются кольца. Такая катушка провода называется короткозамкнутым (КР) ротором. Электродвигатели небольшой мощности имеют стержни, а также диски, которые были отлиты вместе. Для электродвигателей с мощным моментом детали отливаются отдельно, затем свариваются. Обмотка статора может быть подключена двумя методами: треугольником, звездой.
Фазный ротор состоит из 3-фазной роторной обмотки, подключенной контактными кольцами и щетками к питанию. Обмотка соединена «звездой».
Расчет количества оборотов асинхронного двигателя
Распространенным двигателем на станках и подъемных устройствах является двигатель с короткозамкнутым ротором, поэтому пример для расчета следует брать для него. Сетевое напряжение поступает на статорную обмотку. Обмотки смещены друг от друга на 120 градусов. Возникшее поле электромагнитной индукции возбуждает электрический ток в обмотке. Ротор начинает работать под действием ЭМС.
Основной характеристикой работы двигателя является число оборотов в минуту. Рассчитываем это значение:
n = 60 f / p, обор / мин;
где f – частота сети, герц, р – количество полюсов статора (в парах).
На корпусе электродвигателя имеется табличка с техническими данными. Если ее нет, то можно самому рассчитать число оборотов вала оборудования по другим имеющимся данным. Расчет производится тремя способами.
2 p = Z1 / y, где 2р – количество полюсов, Z1 – число пазов в статоре, у – шаг обмотки.
Выбираем из таблицы подходящие обороты двигателя:
2p = 0,35 Z1 b / h или 2 p = 0,5 Di / h,
где 2р – количество полюсов, Z1 – число пазов, b – размер зуба, см, h – высота спинки, см, Di – диаметр по зубцам, см.
По результатам расчета и индукции следует число витков обмотки, сравнивается со значениями мотора по паспорту.
Способы определения характеристик электромотора.
Чтобы определить, к какой из этих групп относится двигатель, не нужно разбирать его, как это советуют некоторые специалисты, чтобы обеспечить себе заказ на работу. Дело в том, что разбор электродвигателя может осуществить только мастер достаточной квалификации. На самом же деле достаточно открыть защитную крышку (другое название подшипниковый щит) и найти катушку обмотки. Таких катушек может быть несколько, но достаточно одной. В случае если к валу прикреплены полумуфта или шкив, потребуется снять еще и нижний щит.
Если катушки соединены при помощи деталей, которые мешают рассмотреть информацию, эти детали ни в коем случае нельзя отсоединять. Нужно попробовать определить на глаз соотношение размера катушки и статора.
Статором называется неподвижная часть электромотора, подвижная же имеет название ротор. В зависимости от конструктивных особенностей, в качестве ротора может выступать как сама катушка, так и магниты.
Если катушка закрывает собой половину кольца статора, такой двигатель относится к третьей группе, то есть способен выдавать до 3000 оборотов. Если размер катушки составляет треть от размеров кольца, это мотор второго типа, соответственно, он способен развить 1500 оборотов в минуту. Наконец, если катушка только на четверть закрывает собой кольцо, это первый тип. Электромотор развивает мощность в 1000 оборотов.
Существует еще один способ определения частоты вращения вала роторной части. Для этого также нужно снять крышку и найти верхнюю часть обмотки. По расположению секций обмотки и определяется скорость. Обычно внешняя секция занимает 12 пазов. Если сосчитать общее количество пазов и разделить на 12, можно получить число полюсов. Если число полюсов равно 2, двигатель имеет скорость вращения около 3000 об/мин. Если полюсов получилось 4, это соответствует 1500 оборотам в минуту. Если 6, то 1000 об/мин. Если 8, то 700 оборотов.
Третий способ определения количества оборотов внимательно осмотреть бирку на самом двигателе. Цифра на маркировке в конце и соответствует числу полюсов. Например, для маркировки АИР160S6 последняя цифра 6 указывает, сколько полюсов использует катушка.
Как изменить скорость работы двигателя?
Изменять скорость вращающего момента механизма оборудования можно различными способами, например, механическими редукторами с переключением передач, муфтами и другими устройствами. Но это не всегда возможно. Практически используется 7 способов коррекции частоты вращения регулируемых приводов. Все способы разделены на два основных направления.
Регулировка частоты и напряжения с помощью частотного преобразователя, путем создания дополнительной катушки с переключением полюсов пар, являются самыми востребованными способами.
Распространенные схемы регуляторов
Существует множество частотных преобразователей для асинхронных двигателей, а также различных регуляторов для них. Самостоятельно возможно изготовить прибор для регулировки частоты, применяя транзисторы или тиристоры. Прибор работает как в быту, так и для станочного оборудования, крановых механизмов, различных регулируемых приводов агрегатов.
Мощный регулятор частоты и напряжения показан на схеме. Прибор плавно изменяет параметры привода, экономит энергию, снижает расходы на обслуживание.
Для применения этой схемы в быту, она сложная. Если использовать симистор рабочим элементом, то схема упрощается, и выглядит иначе.
Регулировка будет происходить работой потенциометра, определяюцим фазу импульса входа, и открывающего симистор.
Эффект эксплуатации станков, обрабатывающих металл, подъемных устройств также следует из вращения двигателя, как и сами его эксплуатационные параметры. В продаже имеется множество приборов для регулировки частоты, однако можно вполне собрать такой прибор собственными силами.
Окупаемость преобразователя частоты
Электроэнергия постоянно дорожает, руководители организаций вынуждены экономить разными путями. В условиях промышленного производства большая часть энергии расходуется механизмами, имеющими электродвигатели.
Изготовители устройств для электротехнических машин и агрегатов предлагают специальные устройства и приборы для управления электромоторами. Такие устройства экономят энергию электрического тока. Они называются инверторами или частотными преобразователями.
Финансовые затраты на покупку частотника не всегда оправдывают экономию средств, так как стоимость их сопоставима со стоимостью сэкономленной энергии. Не всегда привод механизма можно быстро оснастить инвертором. Какие сложности при этом возникают? Разберем способы запуска асинхронных двигателей для пониманию достоинств инверторов.