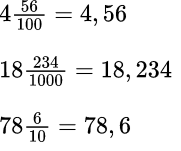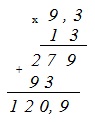Дробь — это значение в двух частях; каждая часть, числитель или знаменатель, является целым числом. Числитель — это верхнее число дроби, а знаменатель — ее нижнее число. Дробная математика младшего порядка, такая как сложение и вычитание, требует, чтобы знаменатели участвующих дробей имели одинаковое значение. Находя дробь, которая находится между двумя другими, вы игнорируете нормальную дробную математику в пользу более простого метода.
-
Запишите начальные дроби
-
Добавьте Числители Вместе
-
Добавьте знаменатели вместе
-
Написать новую фракцию
-
Упростить дробь
-
Чтобы проверить свой ответ, напишите дроби с общими знаменателями и сравните числители. Дробные примеры 1/2, 2/3 и 3/4 с общими знаменателями становятся 6/12, 8/12 и 9/12. Числитель 8 находится между 6 и 9, поэтому созданная вами дробь — 8/12 или 2/3 в упрощенном виде — находится между двумя дробями, с которых вы начали.
Получить две фракции для примера. Для этого примера пусть дроби будут 1/2 и 3/4.
Суммируйте числители дробей. В этом примере 1 + 3 = 4.
Суммируйте знаменатели дроби. В этом примере 2 + 4 = 6.
Запишите новую дробь с суммой числителей в качестве нового числителя и суммой знаменателей в качестве нового знаменателя. В этом примере новая фракция 4/6.
Упростите дробь, исключив наибольший общий множитель, разделяемый числителем и знаменателем. Для этого перечислите факторы каждого числа и выведите наибольшее общее число.
В этом случае коэффициенты 4 равны 1, 2 и 4, а коэффициенты 6 равны 1, 2, 3 и 6. Оба числа имеют коэффициенты 1 и 2, причем 2 является наибольшим фактором.
Исключение 2 из числителя и знаменателя приводит к (4 ÷ 2) / (6 ÷ 2), который становится 2/3.
подсказки
Десятичные дроби — для чайников
Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.
Все это здесь.
Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.
Так что читай эту статью и отрабатывай скиллы.
Десятичные дроби — коротко о главном
1. Определение
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени.
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right)))
3. Свойства десятичных дробей
- Десятичная дробь не меняется, если справа добавить нули ( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.;
- Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: ( 0,014330000=0,01433);
- Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо: ( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз);
- Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево: ( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз).
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Деление десятичных дробей друг на друга
- Считаем количество знаков справа от запятой в десятичной дроби.
- Умножаем и делимое, и делитель на 10, 100 или 1000 и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.
Десятичные дроби — подробнее
Конечно, ты знаешь, что такое обыкновенная дробь. Например, ( displaystyle frac{1}{3}, frac{1}{4},frac{5}{112}).
Наравне с приведенными выше дробями существуют дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) и т.д.
Такие дроби можно записать намного удобнее и более кратко, то есть:
( displaystyle frac{8}{10}=0,8)
( displaystyle frac{13}{100}=0,13)
( displaystyle frac{49}{1000}=0,049)
Данного вида дроби называются десятичными. Иными словами:
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).
Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:
Это огромное число читается по следующему алгоритму:
- Сначала читается число, стоящее до запятой и добавляется слово «целых»: ««( 46) целых»;
- Затем читается как обыкновенное число слева после запятой и добавляется слово, обозначающее название самой последней цифры. В нашем случае – «одна тысяча двести тридцать четыре десятитысячные».
А теперь прочитаем все вместе – «( 46) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!
Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат ( 10) на ( 10) и закрась какую-нибудь его часть равную:
- ( 0,05;)
- ( 0,4;)
- ( 0,27;)
- ( 0,245)
Справился? Проверяем, что у тебя получилось.
Во-первых, квадрат ( 10) на ( 10) состоит из ( 100) клеточек. Соответственно, ( 0.05) – ( 5) клеточек из ( 100); ( 0,4) – ( 40) клеточек из ( 100) и так далее.
Наверняка, наибольшее затруднение составило последнее число – ( -0,245). На картинке это необходимо отразить как 24,5 клетки.
В общем, смотри:
С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.
Перевод из десятичной дроби в обыкновенную и обратно
Попробуй перевести:
- ( 0,136)
- ( 0,2436)
- ( 0,0456)
- ( 0,21)
Сравним ответы:
- ( displaystyle 0,136=frac{136}{1000})
- ( displaystyle 0,2436=frac{2436}{10000})
- ( displaystyle 0,0456=frac{456}{10000})
- ( displaystyle 0,21=frac{21}{100})
Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?
Попробуй свои силы на вот этих дробях:
- ( displaystyle frac{2}{10})
- ( displaystyle frac{3}{100})
- ( displaystyle frac{4}{1000})
- ( displaystyle frac{4562}{100})
А вот и ответы:
- ( displaystyle frac{2}{10}=0,2)
- ( displaystyle frac{3}{100}=0,03)
- ( displaystyle frac{4}{1000}=0,004)
- ( displaystyle frac{4562}{100}=45frac{62}{100}=45,62)
Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.
- Смотрим на дробь и определяем, есть ли у нее целая часть? Если есть, выделяем целую часть, записываем ее, и ставим запятую.
- После запятой должно быть столько знаков, сколько нулей стоит в знаменателе. Например, дробь ( displaystyle frac{4}{1000}) — ( 3) нуля в знаменателе, соответственно, мы как бы мысленно выделяем ( 3) ячейки.
- Затем записываем числитель – ( 4), но выравниваем его по правому краю, а в пустые ячейки вставляем нули.
Разобрался? Посмотри еще раз эту маленькую «инструкцию»:
Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:
- ( displaystyle frac{26}{10})
- ( displaystyle frac{43}{100})
- ( displaystyle frac{99}{1000})
- ( displaystyle frac{3562}{100})
А теперь ответы:
- ( displaystyle frac{26}{10}=2,6)
- ( displaystyle frac{43}{100}=0,43)
- ( displaystyle frac{99}{1000}=0,099)
- ( displaystyle frac{3562}{100}=35,62)
Виды десятичных дробей
Десятичная дробь может быть:
- конечной, если она содержит конечное число цифр после запятой (( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}));
- бесконечной, в том числе периодичной, если конечное число цифр определить не определено (( 0,05882352941…));
- периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр (( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))).
Поговорим сначала о конечных дробях.
Конечная десятичная дробь
Само собой понятно, что дроби ( displaystyle frac{8}{10}, frac{13}{100},frac{49}{1000}) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: ( displaystyle frac{1}{4})? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:
( displaystyle frac{1}{4}=frac{1cdot 25}{4cdot 25}=frac{25}{100}=0,25)
То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен ( 10), ( 100), ( 1000) и так далее.
Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:
- ( displaystyle frac{1}{5})
- ( displaystyle frac{1}{8})
- ( displaystyle frac{3}{5})
- ( displaystyle frac{1}{16})
Сравним наши ответы:
- ( displaystyle frac{1cdot 2}{5cdot 2}=frac{2}{10}=0,2)
- ( displaystyle frac{125}{1000}=0,125)
- ( displaystyle frac{3}{5}=frac{6}{10}=0,6)
- ( displaystyle frac{1}{16}=frac{625}{10000}=0,0625)
Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.
Бесконечная десятичная дробь
Итак, бери калькулятор и дели ( 1) на ( 17). Поделил? Ты получил ( 0,05882352941) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?
Десятичной дробью называется обыкновенная дробь, знаменателем которой является ( 10) в какой-либо степени (первый пример – ( 10) в первой степени, второй – ( 10) во второй степени и т.д.).
Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к ( {{10}^{n}}), с учетом, что ( n) это какое-либо бесконечное число, которое мы не можем «обозреть» взглядом», или иными словами – ( nto +infty )
Таким образом:
Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.
Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как ( displaystyle frac{1}{17}).
Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число ( pi ) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что ( pi =3,14), но это далеко не так. Число ( pi ) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа ( pi ). Мировой рекорд по запоминанию знаков числа ( pi ) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:
( pi =3,1415926535text{ }8979323846text{ }2643383279text{ }5028841971)
Думаю, этого хватит, чтобы оценить «масштабы» данного числа.
Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь ( displaystyle frac{1}{3}). Что у тебя получилось?
( displaystyle frac{1}{3}=0,333333333….)
Чтобы не повторять число ( 3) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:
Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.
Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:
( displaystyle frac{1}{3}=0,underbrace{3}_{период}33333333….=0,left( 3 right))
( displaystyle frac{1}{7}=0,underbrace{142857}_{{период}}underbrace{142857}_{период}142…=0,left( 142857 right))
Важно, что период не может начинаться слева от запятой:
( displaystyle frac{100}{7}=underbrace{14,2857}_{не период}1428571428571…=14,left( 285714 right)).
Свойства десятичных дробей
Существует четыре свойства десятичных дробей. Они очень простые, и ты 100% знаешь о всех них, но давай их перечислим и вспомним:
1. Десятичная дробь не меняется, если справа добавить нули
( displaystyle frac{3}{100}=0,03=0,030=0,030000)и т.д.
2. Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби:
( 0,014330000=0,01433)
ВНИМАНИЕ!!! Нельзя удалять нули, расположенные не в конце десятичной дроби!!!!
( 0,014330000ne 0,1433)
3. Десятичная дробь возрастает в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо:
( 0,0125cdot 100=1,25) (перенесли запятую на ( 2) знака вправо – умножили на ( 100) и дробь возросла в ( 100) раз)
4. Десятичная дробь уменьшается в ( 10), ( 100), ( 1000) и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево:
( 124,56:100=1,2456) (перенесли запятую на ( 2) знака влево – разделили на ( 100) и дробь уменьшилась в ( 100) раз)
Последние два свойства позволяют быстро умножать и делить десятичные дроби на ( 10), ( 100), ( 1000) и т.д. о чем подробнее мы поговорим чуть ниже.
Действия с десятичными дробями
Десятичные дроби – это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить.
Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит твоя оценка на экзамене.
Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению.
Как складывать десятичные дроби
При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. Соответственно, запятые стоят четко друг под другом.
Разберемся на примере:
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставится четко на том же месте, как и в складываемых числах.
Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Если при сложении в сумме мы получаем больше ( 10), то одна единица прибавляется к сумме при сложении цифр следующего разряда.
Решим наш пример, учтя все правила:
Разобрался? Посчитай в столбик самостоятельно:
- ( 0,0125+0,141)
- ( 2,4225+0,34)
- ( 122,4355+1,34)
- ( 2,435+12,3)
Сравним ответы:
- ( 0,0125+0,141=0,1535)
- ( 2,4225+0,34=2,7625)
- ( 122,4355+1,34=123,7755)
- ( 2,435+12,3=14,735)
Как вычитать десятичные дроби
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения.
Соответственно, запятые стоят четко друг под другом.
Вычитание происходит, как и вычитание натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в числах, с которыми мы работаем.
Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.
Если при вычитании получается, что мы из меньшего числа вычитаем большее, то мы как бы занимаем десяток у более высокого разряда (при вычитании сотых частей, берем десяток у десятых, при вычитании десятых – у единиц и так далее), не забывая уменьшить вычитаемое число у заимствованного разряда.
Посмотрим подробно на примере:
Думаю, с рисунком тебе стало все понятно. Попробуй посчитать в столбик следующие выражения:
- ( 0,0125-0,141)
- ( 2,4225-0,34)
- ( 122,4355-1,34)
- ( 12,435-12,3)
Сравним полученные ответы:
- ( 0,0125-0,141=-0,1285)
- ( 2,4225-0,34=2,0825)
- ( 122,4355-1,34=121,0955)
- ( 12,435-12,3=0,135)
Как умножать десятичные дроби
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
Мы начинаем запись числа, получающего при перемножении, под тем разрядом второго числа, на который умножаем. Далее мы суммируем полученные числа и только затем ставим запятую.
Чтобы определить, между какими числами должна стоять запятая, мы должны посмотреть, сколько чисел стоит после знака запятой у первого множителя, сколько у второго, сложить их и отсчитать справа данное количество чисел.
Непонятно? Смотри:
Как ты видишь, при перемножении мы будем складывать столько слагаемых, сколько разрядов содержится во втором множителе, поэтому удобней записывать числа так, чтобы первый множитель был по количеству чисел больше, чем второй.
Таким способом мы значительно снизим вероятность ошибок.
Не веришь? Смотри:
Если при умножении мы получаем число, которое больше ( 9), например ( 12), то единицу мы прибавляем к значению, полученному при умножении последующих чисел следующего десятка.
Соответственно, если получаем, например, ( 24), то прибавляем ( 2).
Проиллюстрируем данное правило:
Разобрался? Дорешай данный пример самостоятельно.
Сколько у тебя получилось? У меня ( 10,33911).
А теперь пора приступить к некоторым очень важным моментам, которые помогут сохранить время на экзамене.
Как делить десятичные дроби
Теперь ты знаешь о десятичных дробях почти все. Осталось только разобраться с тем, как их делить друг на друга.
Если ты отлично это представляешь, смело пропускай данный подраздел. Если нет – смотри инструкцию к применению.
Итак. Мы рассмотрим два вида деления:
- деление десятичной дроби на натуральное число;
- деление десятичной дроби на десятичную дробь.
Начнем с деления десятичной дроби на натуральное число.
Чтобы делить десятичную дробь на натуральное число, необходимо пользоваться следующими правилами:
- Делим десятичную дробь на натуральное число по правилам деления в столбик, не обращая внимания на запятую в делимом (то число, которое мы делим на какое-либо другое число)
- Ставим в частном запятую, когда заканчивается деление целой части делимого.
Важно!!!
Если целая часть делимого меньше делителя, то в частном ставим ( 0) целых. Логично, правда?
Рассмотрим на конкретном примере:
Усвоил? Раздели столбиком следующие числа:
- ( 135,2:5)
- ( 16,4:2)
- ( 158,14:4)
- ( 2,456:2)
- ( 0,626:2)
Сравним наши ответы:
- ( 135,2:5=27,04)
- ( 16,4:2=8,2)
- ( 158,14:4=39,535)
- ( 2,456:2=1,228)
- ( 0,626:2=0,313)
Вспомни теперь свойства десятичных дробей, описанные ранее: если нам необходимо разделить дробь на ( 10), ( 100), ( 1000) и так далее, нет необходимости делать это в столбик – мы можем просто перенести запятую на столько цифр влево, сколько нулей у нас в делителе.
Например: ( 135,2:10=13,52).
А теперь попробуй самостоятельно:
- ( 135,2:100)
- ( 16,4:10)
- ( 158,14:1000)
- ( 2,456:10)
Перенес? Смотри, что у меня получилось:
- ( 135,2:100=1,352)
- ( 16,4:10=1,64)
- ( 158,14:1000=0,15814)
- ( 2,456:10=0,2456)
Молодец! Переходим к делению десятичных дробей друг на друга.
Деление десятичных дробей друг на друга
Итак, для того чтобы это делать существует три правила:
- Считаем количество знаков справа от запятой в десятичной дроби.
- Умножаем и делимое, и делитель на ( 10), ( 100) или ( 1000) и т.д., в зависимости от того, сколько мы насчитали знаков в первом пункте. Умножать необходимо, чтобы превратить десятичную дробь в целое число.
- Делим числа как натуральные.
ВАЖНО!!! При умножении мы смотрим, в каком из чисел, участвующих в делении, присутствует наибольшее количество знаков после запятой? Ориентируясь именно на это число мы умножаем на ( 10), ( 100), ( 1000) и так далее.
Рассмотрим на примере ( 16,4:0,02)
В каком числе у нас стоит наибольшее количество знаков после запятой? Правильно, во втором, то есть в делителе: после нуля стоит два знака. Что из этого следует? Что мы умножаем и делимое и делитель на ( 100)!
Что дальше? Мы получаем следующий пример: ( 1640:2) Посчитай, сколько это будет самостоятельно. У меня получилось ( 820).
Рассмотрим примерчик посложнее: ( 5,31:0,3)
Самое большое количество знаков после запятой содержится в первом числе – их два, соответственно, умножаем оба числа, участвующего в делении на ( 100). Получаем: ( 531:30).
А теперь делим в столбик:
Ты видишь, что нацело разделить не получилось, мы «снесли» еще один ноль, и только тогда пришли к ответу, поэтому сразу после окончания деления нашего делимого, мы ставим запятую.
Теперь ты полностью готов совершать любые действия с десятичными дробями. Молодец! Рассмотрим только, как их сравнивать, хотя я думаю, ты уже и сам с этим справишься!
Как сравнивать десятичные дроби
Мы можем сравнивать десятичные дроби двумя способами.
Способ первый – поразрядно.
Допустим, нам необходимо сравнить ( 5,365 V 5,36)
1. Смотрим, одинаковое ли количество знаков после запятой стоит у каждой дроби? Нет? Значит дописываем справа необходимое количество нулей (ты же помнишь, что от дописывания нулей дробь неизменна, правда?)
Что у нас получилось? Верно: ( 5,365 V 5,360)
2. Начинаем сравнивать слева направо: целую часть с целой, десятые части с десятыми и так далее. Когда одна из частей дроби оказывается больше аналогичной части другой, эта дробь и больше.
Перейдем к нашему примеру: целые части у нас одинаковы – их значение ( 5). Десятые тоже – ( 3). Сотые – ( 6), а вот тысячные у первой дроби ( 5), а у второй ( 0). Что больше: ( 5) или ( 0)? Верно, ( 5), соответственно:
( 5,365 > 5,360)
Способ второй – с помощью умножения.
Внимательно смотрим на дроби. На сколько нам нужно умножить два числа, чтобы сравнивать целые числа? Смотрим на ту дробь, у которой знаков после запятой больше, то есть на первую. У нее после запятой ( 3) знака, соответственно, чтобы сделать из нее целое число, необходимо умножить на ( 1000) Умножаем обе дроби на это значение:
( 5,365cdot 1000 V 5,36cdot 1000)
( 5365 V 5360)
Эти числа ты сравнишь без проблем:
( 5365 > 5360)
Заметь, результат получился одинаковый. Теперь попробуй сравнить дроби самостоятельно любым наиболее удобным для тебя способом:
- ( 21,34 V 20,34)
- ( 0,34 V 0,341)
- ( 120,15 V 1210,16)
- ( 10,565 V 10,465)
Справился? Смотри что вышло:
- ( 21,34 > 20,34)
- ( 0,34 < 0,341)
- ( 120,15 < 1210,16)
- ( 10,565 > 10,465)
Вот теперь ты усвоил дроби полностью!
Подготовка к ЕГЭ на 90+ в мини-группах
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Какая десятичная дробь между 1 и 2? – Обзоры Вики
1.5 находится точно между 1 и 2, но есть много других чисел, таких как 1.157, 1.781, 1.3312.
Итак, какая дробь находится между 1 и 2? Между любыми двумя целыми числами стоит дробь. Между 0 и 1 12, между 1 и 2 112=3/2, и так далее. На самом деле между любыми двумя целыми числами бесконечно много дробей.
Сколько действительных чисел находится между 1 и 2? Первоначальный ответ: Сколько действительных чисел находится между 1 и 2? Есть бесконечные действительные числа между 1 и 2. Между 1 и 1.1 лежат бесконечные действительные числа.
Дополнительно Что такое 1 как число? 1 (число)
| ← 0 1 2 → | |
|---|---|
| Кардинальный | one |
| порядковый | 1-й (первый) |
| Система счисления | унарный |
| факторизация | 1 |
Как найти середину между двумя числами? Середина между двумя числами — это число, находящееся ровно посередине двух чисел. Вычисление средней точки — это то же самое, что вычисление среднего значения двух чисел. Следовательно, вы можете вычислить среднюю точку между любыми двумя числами. сложив их вместе и разделив на два.
Какая дробь стоит перед 1 2?
Таблица преобразования десятичных и дробных чисел
| Доля | Эквивалентные дроби | |
|---|---|---|
| 1/2 | 2/4 | 4/8 |
| 1/3 | 2/6 | 4/12 |
| 2/3 | 4/6 | 8/12 |
| 1/4 | 2/8 | 4/16 |
Что находится между 1 2 и 3/4 на числовой прямой? Итак, средняя дробь между 1/2 и 3/4 равна 5/8.
Что находится между половиной и 3 4? Числитель и знаменатель требуемого числа должны быть между заданным числом, т. е. числитель может быть равен 3, а знаменатель может быть равен 5. Следовательно, рациональное число между 1/2 и 3/4 равно 3/5.
Какое из следующих рациональных чисел находится между 1 и 2?
Следовательно, четыре рациональных числа между 1 и 2 — это 9/8, 5 / 4, 3 / 2 и 7 / 4.
Также Какие два рациональных числа между 1 и 2? Следовательно, 4 / 3 и 5 / 3 два рациональных числа между 1 и 2.
Сколько иррациональных чисел находится между 1 и 2?
Это может быть любое число между двумя с любым количеством цифр. Следовательно, у нас есть бесконечное количество иррациональных чисел между двумя числами.
Что такое два как число? 2 (два) — число, цифра и цифра. Это натуральное число после 1 и до 3 . Это наименьшее и единственное четное простое число.
…
| ← 1 2 3 → | |
|---|---|
| -1 0 1 2 3 4 5 6 7 8 9 → Список чисел — Целые числа ← 0 10 20 30 40 50 60 70 80 90 → | |
| Кардинальный | два |
| порядковый | 2-й (второй/второй) |
| Система счисления | двоичный |
Какой тип числа 1 2?
Рациональное число (В).
Кто изобрел ноль в мире?
Первый современный эквивалент цифры ноль происходит от индуистский астроном и математик Брахмагупта в 628 году. Его символом для изображения числа была точка под числом.
Как найти половину расстояния между двумя точками? Определите половину расстояния
- Разделите полное расстояние на два.
- Измерьте это расстояние от одной из двух исходных точек и отметьте на карте.
- Проверьте свою работу, проделав то же самое с другой отправной точки.
Как найти режим? Мода набора данных — это число, которое чаще всего встречается в наборе. Чтобы легко найти режим, расположите числа по порядку от наименьшего к наибольшему и посчитайте, сколько раз встречается каждое число.
Как найти середину между двумя дробями?
Что такое 1/2 в целом числе? Следовательно, 1/2 как целое число будет 0 или 1.
1 2 — натуральное число?
Множеством натуральных чисел в математике называется множество {1, 2, 3, …}. Итак, -1 — отрицательное число, поэтому это не натуральное число. 0 тоже не натуральное число. 1/2, будучи дробное число, тоже не натуральное число.
Что находится между третью и половиной? Если умножить числитель и знаменатель обеих дробей на 2, то получим 6/12 и 4/12, здесь мы можем вставить одну дробь т.е. 5/12. Между ними можно вставить три дроби 11/24, 10/24 или 5/12, 9/24 или 3/8. …
Что находится между половиной и четвертью?
Нарежьте пиццу, и мы получим дроби:
| 1 / 2 | 1 / 4 | 3 / 8 |
| (Одна половина) | (Одна четверть) | (три восьмых) |
Что такое 0.
Между какими целыми числами заключено число?
Задача #1 (номер задачи на fipi.ru — 8F6802). Между какими целыми числами заключено число 130/11?
- 10 и 11
- 11 и 12
- 12 и 13
- 13 и 14
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 11 и 12.
Ответ: 2 — 11 и 12.
Задача #2 (номер задачи на fipi.ru — 344704). Между какими целыми числами заключено число 140/17?
- 5 и 6
- 6 и 7
- 7 и 8
- 8 и 9
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 8 и 9.
Ответ: 4 — 8 и 9.
Задача #3 (номер задачи на fipi.ru — B64AD1). Между какими целыми числами заключено число 172/15?
- 9 и 10
- 10 и 11
- 11 и 12
- 12 и 13
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 11 и 12.
Ответ: 3 — 11 и 12.
Задача #4 (номер задачи на fipi.ru — F2CF43). Между какими целыми числами заключено число 110/13?
- 8 и 9
- 9 и 10
- 10 и 11
- 11 и 12
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 8 и 9.
Ответ: 1 — 8 и 9.
Задача #5 (номер задачи на fipi.ru — F4AE19). Между какими целыми числами заключено число 230/19?
- 11 и 12
- 12 и 13
- 13 и 14
- 14 и 15
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 12 и 13.
Ответ: 2 — 12 и 13.
Задача #6 (номер задачи на fipi.ru — 4DD651). Между какими целыми числами заключено число 160/11?
- 12 и 13
- 13 и 14
- 14 и 15
- 15 и 16
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 14 и 15.
Ответ: 3 — 14 и 15.
Задача #7 (номер задачи на fipi.ru — 9179F3). Между какими целыми числами заключено число 131/12?
- 10 и 11
- 11 и 12
- 12 и 13
- 13 и 14
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 10 и 11.
Ответ: 1 — 10 и 11.
Задача #8 (номер задачи на fipi.ru — 648BA1). Между какими целыми числами заключено число 124/15?
- 8 и 9
- 9 и 10
- 10 и 11
- 11 и 12
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 8 и 9.
Ответ: 1 — 8 и 9.
Задача #9 (номер задачи на fipi.ru — 2FC0DC). Между какими целыми числами заключено число 190/17?
- 10 и 11
- 11 и 12
- 12 и 13
- 13 и 14
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 11 и 12.
Ответ: 2 — 11 и 12.
Задача #10 (номер задачи на fipi.ru — 37B64D). Между какими целыми числами заключено число 170/19?
- 8 и 9
- 9 и 10
- 10 и 11
- 11 и 12
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 8 и 9.
Ответ: 1 — 8 и 9.
Творческий проект для классов К-8
Планы уроков
- Задача «3N+1»
- Задача с Всероссийской олимпиады по математике
- Доказательство теоремы Пифагора с использованием подобных треугольников
- Головоломка с 1089
- Дополнительная плата
- Прибавление в детском саду и первом классе
- Арифметический вундеркинд из 1899 года
- Старый купец и четверо его детей
- Древний узел
- Анимации на TI
- Районы и границы
- Площадь и периметр
- Средний балл за тест
- Мяч в коробке
- Банан
- Бочки, бочонки и другие изогнутые емкости
- Большие числа АКА Зерна риса на шахматной доске
- Блочные дома
- Сборка собачьей будки в масштабе
- Создание каркасной коробки в соответствии со спецификациями
- Свечи
- Корзины для конфет
- Емкость
- Наутилус с камерой
- Проверка, является ли число простым
- Коробка с китайским календарем
- Аккорды по кругу
- Круг, квадрат и треугольник
- Часы и время
- Монеты
- Раскрашивание линий в шестиугольнике
- Разноцветные треугольники
- Конгруэнтные треугольники
- Счет
- Счетная доска для юных учащихся
- Счет до 100
- Биговка бумаги по изгибам
- Кубики
- Куб со срезанным краем
- Кулинарные полоски
- Вырезание прямоугольника
- Вырезание треугольника
- Разрезание треугольника на две части равной площади и равного периметра
- Вырезание равностороннего треугольника
- Резка многогранников
- Вывод формулы площади треугольника
- Диагональ квадрата
- Разделение квадрата
- Дивизион с остатком на ТИ-108: Два экземпляра
- Собаки, кошки и мыши
- Точка за точкой
- Удвоение и деление пополам
- Рисование прямоугольника
- Рисование простой фигуры по словесным инструкциям
- Рисование треугольников
- Легкие квадраты
- Яичная дилемма (Часть 1)
- Возведение в степень
- Факторинг
- Необычные конверты
- Нахождение дроби между двумя дробями
- Пятиконечная трехмерная звезда
- Подбрасывание монет
- Сложенный бумажный цветок с шестью лепестками
- Четыре жука
- Четыре карты
- Четыре кубика
- От одного миллиарда до нуля
- От одного до одного триллиона
- Игра кругов и звезд
- Игра десятков
- Гигантская энчилада
- Шапка для Хэллоуина
- Орел или решка?
- Шестиугольная головоломка
- Как калькулятор вычисляет квадратный корень числа?
- Сколько пентамино?
- Как измерить угол без транспортира
- Как преобразовать прямоугольник в другой прямоугольник
- Гиперболы и эллипсы
- Вписанный треугольник
- Интерес
- Юлекурв АКА Валентинка Корзина
- Воздушные змеи
- Дырявая крыша
- Ушастые твари
- Волшебные бобы
- Волшебный складной кубик
- Волшебный квадрат
- Создание животных путем вырезания многоугольников
- Изготовление блоков из четырех кубиков
- Изготовление коробок
- Изготовление эвольвенты
- Лабиринт
- Мини-слот-машина
- Луны
- Больше задач с точностью до точки
- Больше старых словесных задач
- Умножения «Сделано по Адаму Райсу»
- Натан подбрасывает монету 20 раз
- Числовая игра с кубиками
- Одна треть
- Парадокс средних
- Разделение квадрата
- Пазлы Пентагона
- Алгебра телефонных номеров
- Копилка
- Игра с формами
- Powerball 55
- Красивая подарочная коробка
- Тыквы
- Пазл с камешками
- Пирамида на четверти
- Пирамида кубов
- Пирамида из мрамора
- Четырехугольники
- Правильные многоугольники с равными площадями
- Связанные проблемы
- Прямоугольный треугольник
- Последовательности составных чисел: конкурс
- Формы чисел
- Формы чисел с использованием треугольников
- Шесть пирамид
- Шестнадцать квадратных дюймов
- Печать Соломона
- Сортировочная игра
- Спираль (марки К-4)
- Спираль (5-8 классы)
- Спираль Феодора на калькуляторе ТИ-83/84
- Квадратные и кубические единицы
- Квадрат в треугольнике
- Соломенные многогранники
- Алгоритм вычитания
- Вычитание со счетчиками
- Сумма двух квадратов
- Выживший на шестиугольном острове
- Татами
- Чайные коробки
- Преобразование температуры
- Мозаика круга
- Задача о лестнице и ящике
- Контейнеры для сыра «Смеющаяся корова»
- Практическая ценность доказательств
- Три четверти
- Круглая головоломка из трех частей
- Бросание одного кубика
- От треугольника к квадрату: Шарнирное рассечение
- Превращение прямоугольника в квадрат путем рассечения
- Двенадцать простых фигур
- Двадцать четыре кубика
- Две старые проблемы
- Два брата пастуха
- Понимание длинного деления
- Необычные контейнеры
- Что дальше?
- Что это за прямоугольник?
- Инь Ян
Дробь между двумя дробями: определения и примеры
- Автор
Рачана - Последнее изменение 19-10-2022
Фракция между двумя фракциями: Фракция — это небольшая часть большего целого или набора.
Числитель показывает, сколько у нас есть выделенных или заштрихованных частей, тогда как знаменатель показывает, сколько всего частей объекта или целого у нас есть. Мы можем найти дроби между любыми двумя дробями. В этой статье обсуждается, как найти дробь между двумя заданными дробями. Прочитайте полную статью, чтобы получить полную информацию.
Определение дроби
Дроби представлены в виде числовых значений в математике и могут быть определены как части целого. Дробь — это часть или часть целого, которая может быть любым числом, заданным значением или элементом.
Таким образом,
({text{Дробь}} = frac{{{text{Число}},{text{из}},{text{выбрано}},{text {или}} , { text {заштриховано}} , { text {части}} , { text {из}} , { text {an}} , { text {объект}} , { text {или}} , { text {a}} , { text {целое}}}} {{{ text {Всего}} , { text {число}} , { текст {из}} , { текст {равно}} , { текст {частей}} , { текст {из}} , { текст {an}} , { текст {объект}} ,{text{или}},{text{a}},{text{целое}}}} = frac{{{text{Числитель}}}}{{{text{Знаменатель }}}})
Учитывать дробь (frac{5}{{12}}) Эта дробь читается как «пять двенадцатых», что означает, что (5) частей из (12) равны разделить на целое.
В дроби (frac{7}{{12}},7) известен как числитель, а (12) известен как знаменатель.
Ниже приведены еще несколько примеров:
| Дробь | Значение дроби | Числитель | 0355 Знаменатель |
| (frac{5}{{11}}) или Пять одиннадцатых | Пять равных частей из (11) равных частей, на которые делится целое. | (5) | (11) |
| (frac{3}{{8}}) или Три восьмых | Три равные части из (8) равных частей в котором целое разделено. | (3) | (8) |
| (frac{1}{{3}}) или Одна треть | Одна часть из (3) равных частей в что целое разделено. |
(1) | (3) |
Примеры дробей
Дробь — это число, представляющее часть целого. Один объект или группа объектов могут составлять целое. Возьмите прямоугольный лист и сложите его пополам. Сложите его по горизонтали и вертикали, чтобы разделить на четыре равные части. Как показано на рисунке ниже, один из четырех компонентов должен быть затенен. Заштрихованная область составляет четверть всей композиции. Число одна четвертая записывается как (frac{1}{{4}},), что не что иное, как дробь.
Если три части затемнены, как на рисунке ниже, заштрихованная часть представляет собой три четверти от общего числа. Три четверти записываются как (frac{3}{{4}}) и читаются как «три на четыре» или «три на четыре». Таким образом, три части из (4) равных частей равны (frac{3}{{4}}.)
Аналогично, (frac{3}{{7}}) получается, когда делим целое на (7) равных частей и берем три части (см.
Для (frac{1}{{8}},) делим целое на восемь равных частей и берем одну его часть (см. рис. ниже).
Дробь между двумя дробями
Дробь состоит из двух элементов. Число в верхней части строки или дроби называется числителем. Он определяет, сколько берется равных частей всей коллекции или целого. Знаменатель – это число под чертой. Он отображает общее количество равных частей, на которые делится целое, или общее количество равных частей в коллекции.
Калькулятор нахождения дроби между двумя дробями не сложный процесс. Просто сделайте сумму числителей в качестве нового числителя и сумму знаменателей в качестве нового знаменателя, чтобы получить дробь между двумя заданными дробями.
Ниже приведены примеры того, как вставить дробь между двумя дробями:
Если (frac{p}{q}) и (frac{r}{s}) две заданные дроби и ( гидроразрыв {р} {q}
Где (p,q,r) и (s) — натуральные числа.
Пример. Вставьте дробь между двумя дробями (frac{5}{7}) и (frac{3}{5},), учитывая (frac{5}{7})
Решение.
Следовательно, (frac{5}{7}
Решаемые примеры – дробь между двумя заданными дробями
Q.1. Вставьте дробь между двумя дробями (frac{1}{3}) и (frac{2}{5},) учитывая (frac{1 }{3} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Здесь сумма числителей(=1+ 2=3) и
сумма знаменателей(=3+5=8)
Итак, новая дробь образовалась между двумя дробями (frac{1}{3}) и (frac{2}{5} ) равно (frac{3}{8}.)
Q.2. Найдите дробь между двумя дробями (frac{2}{7}) и (frac{4}{5},) при заданном (frac{2 }{7} < frac{4}{5}.)
Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Требуемая дробь между двумя дробями (frac{2}{7}) и (frac{4}{5}) равна (frac{{(2 + 4)}}{{( 7 + 5)}} = frac{6}{{12}} = frac{1}{2}.)
Q.3. Найдите дробь между двумя дробями (frac{4}{7}) и (frac{1}{3},) при заданном (frac{4 {7} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Требуемая дробь между двумя дробями (frac{4}{7}) и (frac{1}{3}) равна (frac{{(4 + 1)}}{{( 7 + 3)}} = frac{5}{{10}} = frac{1}{2}.)
Q.4. Вставьте дробь между двумя дробями (frac{5}{6}) и (frac{7}{11},) учитывая (frac{5 {6} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Требуемая дробь между двумя дробями (frac{5}{6}) и (frac{7}{11}) равна (frac{{(5 + 7)}}{{( 6 + 11)}} = frac{{12}}{{17}}.)
Q.5. Вставьте дробь между двумя дробями (frac{5}{7}) и (frac{8}{11},) учитывая (frac{5 {7} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Здесь сумма числителей(=5+8=13) и
сумма знаменателей(=7+11=18)
Итак, между двумя дробями образовалась новая дробь (frac {5}{7}) и (frac{8}{11}) равно (frac{13}{18}.)
Резюме
В этой статье мы узнали об определении дроби, примеры дробей, калькулятор нахождения дроби между двумя дробями, решенные примеры дроби между двумя заданными дробями и часто задаваемые вопросы о дроби между двумя заданными дробями. Вы также можете найти «Как найти дробь между двумя дробями» в приложении и на веб-сайте Embibe.
В результате изучения этой статьи мы поняли, как вставить дробь между двумя заданными дробями. Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Узнайте о различных типах фракций
Часто задаваемые вопросы (FAQ)
Q.1. Как найти дробь между двумя дробями?
Ответ. Нахождение дроби между двумя дробями — несложный процесс. Просто сделайте сумму числителей новым числителем и знаменателей новым знаменателем, чтобы получить дробь между двумя дробями.
Ниже приведены примеры того, как вставить дробь между двумя предоставленными дробями:
Если (frac{p}{q}) и (frac{r}{s}) две заданные дроби и (frac{p} {q} < frac{r}{s}), затем (frac{p}{q} < frac{{p + r}}{{q + s}} < frac{r}{s}. )
Q.2. Всегда ли между любыми двумя дробями есть дробь?
Ответ: Между любыми двумя целыми числами есть дробь.
Существуют также (frac{1}{3},frac{1}{4},frac{1}{5},) и любые другие числа, которые могут быть выражены как (frac{1 {n},), где (n) — целое число, от (0) до бесконечности, а значение дроби лежит между (0) и (1.). дроби, такие как (frac{2}{3},frac{3}{4},frac{4}{5},) и так далее. (frac{m}{n}) — дробь между (0) и (1), если m и n оба являются положительными целыми числами и (m) меньше, чем (n. ) Точно так же существует бесконечное число дробей между любыми двумя целыми числами.
Q.3. Какая дробь находится между 1/3 и 2/3?
Ответ: Чтобы найти дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Даны две дроби: (frac{1}{3}) и (frac{2}{3},frac{1}{3} < frac{2}{3})
Здесь сумма числителей(=1+2=3) и
сумма знаменателей(=3+3=6)
Итак, между двумя дробями образовалась новая дробь (frac{ 1}{3}) и (frac{2}{3}) равно (frac{3}{6} = frac{1}{2}.
Q.4. Какая дробь находится между 1 и 2?
Ответ: Чтобы найти дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Даны две дроби: (frac{1}{1}) и (frac{2}{1},1 Здесь сумма числителей(=1+2=3) и
сумма знаменателей(=1+1=2)
Итак, новая дробь, образованная между двумя дробями (1) и (2), равна (frac{3}{2}. )
Q.5. Что такое дробь?
Ответ: В математике дроби представлены числовыми значениями и могут быть определены как части целого. Дробь — это часть или часть целого, которая может быть любым числом, заданным значением или элементом.
Рассмотрим дробь (frac{3}{5}.) Эта дробь читается как «три пятых», что означает, что (3) частей из (5) равных частей, в которых целое поделен. В дроби (frac{3}{5},3) называется числителем, а (5) называется знаменателем.
Q.6. Чему равно в дробях?
Ответ: Равные дроби — это дроби с одинаковым значением, но разными числителями и знаменателями. (frac{6}{9}) и (frac{10}{15},), например, являются эквивалентными дробями, поскольку они обе равны (frac{2}{3}. )
Q.7. Как определить, равны ли дроби?
Ответ: Когда различные дроби упрощаются и сводятся к одной дроби, они являются эквивалентными дробями. Кроме того, существует несколько альтернативных подходов к определению сопоставимости поставляемых фракций. Вот несколько примеров:
1. Сделать числители и знаменатели одинаковыми.
2. Нахождение десятичной версии обеих дробей является первым шагом.
3. Метод перекрестного умножения.
4. Наглядным способом.
Теперь у вас есть вся необходимая информация о дроби между двумя дробями, и мы надеемся, что эта подробная статья будет вам полезна.
Сравнение десятичных дробей
- Калькулятор сравнения десятичных дробей
Десятичные дроби сравнивают по тем же правилам, что и натуральные числа:
- Из двух десятичных дробей больше та, у которой больше разрядов в целой части. Например:
647,78 > 43,952,
потому что число 647 имеет больше разрядов в целой части, чем число 43.
- Из двух десятичных дробей с одинаковым числом разрядов больше та, у которой больше первая (слева направо) из неодинаковых цифр. Например:
432,35 > 432,21,
потому что у первого числа, цифра в разряде десятых больше, чем цифра в этом же разряде у второго числа.
- Две десятичные дроби равны, если у них одинаковое число разрядов и цифры одинаковых разрядов равны. Например, числа 7832,0954 и 7832,0954 равны. В этом легко убедиться, записав их одно под другим:
7832,0954
7832,0954
Калькулятор сравнения десятичных дробей
Данный калькулятор поможет вам сравнить десятичные дроби. Просто введите две десятичные дроби и нажмите кнопку Сравнить
. Вместо запятой, в записи десятичной дроби, используйте точку:
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых
18,234 – восемнадцать целых двести тридцать четыре тысячных
78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять – один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
- Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
- Уравнять количество знаков после запятой, добавляя недостающие нулями.
- Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
- Поставить запятую под запятыми.
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
34,145
5,678
39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
9,235 – 2,34 = 6,895
9,235
2,340
6,895
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
56 + 12,74 = 68,74
56,00
12,74
68,74
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
- Написать числа одно под другим, не обращая внимания на запятую
- Выполнить умножение в столбик
- В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3
0,125
× 2,3
00375
0250
0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
34,2 × 8
34,3
× 8
274,4
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
- При делении десятичной дроби на целое число выполняют сначала деление целой части, а затем десятичной.
- При делении десятичной дроби на другую десятичную дробь необходимо в делителе убрать запятую, а в делимом передвинуть ее вправо на столько цифр, сколько их в делителе после запятой. Затем выполнить деление на целое число.
- Есть случаи, когда цифр после запятой при переносе запятой у дроби не хватает. Тогда необходимо дополнить число нулями.
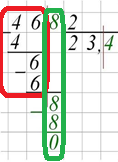
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
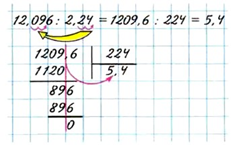
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №15. 45,982 : 10 = 4,5982 Перенесли запятую влево на 1 цифру, так как у 10 один нуль.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №18. 6,5746 : 0,1 = 65,746 Перенос запятой на 1 цифру вправо, так как в числе 0,1 одна цифра после запятой.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Задание OM0706o
На координатной прямой точки А, В, С и D соответствуют числам -0,201; -0,012; -0,304; 0,021.
Какой точке соответствует число -0,304?
1) А
2) В
3) С
4) D
Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304<–0,201<–0,012.
В итоге имеем возрастающий ряд: –0,304; –0,201; –0,012; 0,021.
Поскольку стрелка положительного направления на координатной прямой направлена вправо, то А<B<C<D. Следовательно, А=–0,304; В=–0,201; С=–0,012; D=0,021. Значит, числу –0,304 соответствует точка А.
Ответ: A
pазбирался: Даниил Романович | обсудить разбор
Задание OM0606o
Найдите значение выражения:
–0,3·(–10)4+4·(–10)2–59
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
–0,3·(–10)4+4·(–10)2–59 =
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
= –0,3·10000+4·100–59 =
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
= –3000+400–59 =
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
= –2600–59 =
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
= –(2600+59) = –2659
Ответ: -2659
pазбирался: Даниил Романович | обсудить разбор
Задание OM0605o
Найдите значение выражения:
–13•(–9,3)–7,8
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
–13·(–9,3)–7,8 =
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
= 120,9–7,8 =
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
= 113,1
Ответ: 113,1
pазбирался: Даниил Романович | обсудить разбор
Задание OM0601o
Найдите значение выражения:
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
4,5 • 2,5
Можно произвести вычисления в столбик, тогда получим:
4,5 • 2,5 = 11,25
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
Ответ: 0,8
pазбирался: Даниил Романович | обсудить разбор
Алла Василевская | Просмотров: 10.1k