Подсчёт листьев бинарного дерева
20.04.2021, 21:28. Показов 4381. Ответов 10

Здравствуйте, такое задание:
Создать сбалансированное дерево поиска с числами от -50 до 50 и распечатать информацию прямым, обратным обходом и по возрастанию. Сделать функции добавления нового значения, удаления значения и поиска. Всю память надо освободить.
а) Посчитать число листьев в дереве.
б) удалить элементы кратные X.
В общем-то практически всё сделала, но функция подсчёта листьев печатает пустой результат, всё остальное, вроде, работает. (Хотя не уверена в том, что моё дерево сбалансированное, хотя код из методички)
Вот код:
| C++ | ||
|
Добавлено через 2 минуты
Ещё не уверена в правильности удаления, в принципе, в задании не уточняется, как его правильно делать. Но, когда я ввожу числа: 4, 3, 5, 1, 7, 8, 6, 2, 9, 12, то удаляется только 6 и 12, оно и понятно, в принципе, 3 и 9 не удаляется, потому что есть листья дальше, а у 6 и 12 указатели на left и right = NULL. В принципе, я думаю, что меня устраивает, но, можно ли как-то сделать удаление прям всех кратных элементов и вывод оставшихся, чтоб ветви соединялись как-то
0
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
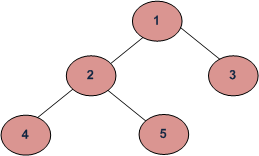
A node is a leaf node if both left and right child nodes of it are NULL.
Here is an algorithm to get the leaf node count.
getLeafCount(node)
1) If node is NULL then return 0.
2) Else If left and right child nodes are NULL return 1.
3) Else recursively calculate leaf count of the tree using below formula.
Leaf count of a tree = Leaf count of left subtree +
Leaf count of right subtree
Leaf count for the above tree is 3.
Algorithm:
Step 1: Start
Step 2: Create a function named “getLeafCount”of int return type that take node as input parameter.
Step 3: Set the conditions:
a. If the node is NULL, return 0.
b. If the node has no left or right child, return 1.
c. Recursively call “getLeafCount” on the left and right child nodes if the node has left or right children, and then return the total of the results.
Step 4: End
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
struct node
{
int data;
struct node* left;
struct node* right;
};
unsigned int getLeafCount(struct node* node)
{
if(node == NULL)
return 0;
if(node->left == NULL && node->right == NULL)
return 1;
else
return getLeafCount(node->left)+
getLeafCount(node->right);
}
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Leaf count of the tree is : "<<
getLeafCount(root) << endl;
return 0;
}
C
#include <stdio.h>
#include <stdlib.h>
struct node
{
int data;
struct node* left;
struct node* right;
};
unsigned int getLeafCount(struct node* node)
{
if(node == NULL)
return 0;
if(node->left == NULL && node->right==NULL)
return 1;
else
return getLeafCount(node->left)+
getLeafCount(node->right);
}
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Leaf count of the tree is %d", getLeafCount(root));
getchar();
return 0;
}
Java
class Node
{
int data;
Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
Node root;
int getLeafCount()
{
return getLeafCount(root);
}
int getLeafCount(Node node)
{
if (node == null)
return 0;
if (node.left == null && node.right == null)
return 1;
else
return getLeafCount(node.left) + getLeafCount(node.right);
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
System.out.println("The leaf count of binary tree is : "
+ tree.getLeafCount());
}
}
Python3
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def getLeafCount(node):
if node is None:
return 0
if(node.left is None and node.right is None):
return 1
else:
return getLeafCount(node.left) + getLeafCount(node.right)
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print ("Leaf count of the tree is %d" %(getLeafCount(root)))
C#
using System;
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
public Node root;
public virtual int LeafCount
{
get
{
return getLeafCount(root);
}
}
public virtual int getLeafCount(Node node)
{
if (node == null)
{
return 0;
}
if (node.left == null && node.right == null)
{
return 1;
}
else
{
return getLeafCount(node.left) + getLeafCount(node.right);
}
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine("The leaf count of binary tree is : " + tree.LeafCount);
}
}
Javascript
<script>
class node
{
constructor(data) {
this.left = null;
this.right = null;
this.data = data;
}
}
function getLeafCount(node)
{
if(node == null)
return 0;
if(node.left == null && node.right == null)
return 1;
else
return getLeafCount(node.left)+
getLeafCount(node.right);
}
function newNode(data)
{
let Node = new node(data);
return(Node);
}
let root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
document.write("The leaf count of binary tree is : " + getLeafCount(root));
</script>
Output
Leaf count of the tree is : 3
Time & Space Complexities: Since this program is similar to traversal of tree, time and space complexities will be same as Tree traversal (Please see our Tree Traversal post for details)
Another Approach(Iterative):
The given problem can be solved by using the Level Order Traversal(https://www.geeksforgeeks.org/level-order-tree-traversal/). Follow the steps below to solve the problem:
1) Create a queue(q) and initialize count variable with 0, and store the nodes in q along wise level order and iterate for next level.
2) Perform level order traversal and check if current node is a leaf node(don’t have right and left child) then increment the count variable.
3) After completing the above steps, return count variable.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node{
int data;
struct Node* left;
struct Node* right;
};
Node* newNode(int data){
Node *new_node = new Node();
new_node->data = data;
new_node->left = NULL;
new_node->right = NULL;
return new_node;
}
int getLeafCount(Node* root){
queue<Node*> q;
q.push(root);
int count = 0;
while(!q.empty()){
Node* temp = q.front();
q.pop();
if(temp->left == NULL && temp->right == NULL)
count++;
if(temp->left) q.push(temp->left);
if(temp->right) q.push(temp->right);
}
return count;
}
int main(){
struct Node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Leaf count of the tree is : "<< getLeafCount(root) << endl;
return 0;
}
Java
import java.util.LinkedList;
import java.util.Queue;
class Node{
int data;
Node left, right;
public Node(int item){
data = item;
left = null;
right = null;
}
}
class BinaryTree{
static Node newNode(int data){
return new Node(data);
}
static int getLeafCount(Node root){
Queue<Node> q = new LinkedList<Node>();
q.add(root);
int count = 0;
while(!q.isEmpty()){
Node temp = q.poll();
if(temp.left == null && temp.right == null) count++;
if(temp.left != null) q.add(temp.left);
if(temp.right != null) q.add(temp.right);
}
return count;
}
public static void main(String args[]){
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
System.out.println("Leaf count of the tree is : " + getLeafCount(root));
}
}
Python
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def newNode(data):
return Node(data)
def getLeafCount(root):
q = []
q.append(root)
count = 0
while(len(q) > 0):
temp = q.pop(0)
if(temp.left is None and temp.right is None):
count += 1
if(temp.left is not None):
q.append(temp.left)
if(temp.right is not None):
q.append(temp.right)
return count
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(4)
root.left.right = newNode(5)
print("Leaf count of the tree is : ")
print(getLeafCount(root))
C#
using System;
using System.Collections.Generic;
public class Node{
public int data;
public Node left, right;
public Node(int data){
this.data = data;
this.left = null;
this.right = null;
}
}
public class BinaryTree{
static Node newNode(int data){
return new Node(data);
}
static int getLeafCount(Node root){
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
int count = 0;
while(q.Count > 0){
Node temp = q.Dequeue();
if(temp.left == null && temp.right == null) count++;
if(temp.left != null) q.Enqueue(temp.left);
if(temp.right != null) q.Enqueue(temp.right);
}
return count;
}
public static void Main(){
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
Console.WriteLine("Leaf Count of the tree is : " + getLeafCount(root));
}
}
Javascript
class Node{
constructor(data){
this.data = data;
this.left = null;
this.right = null;
}
}
function newNode(data){
return new Node(data);
}
function getLeafCount(root){
let q = [];
q.push(root);
let count = 0;
while(q.length > 0){
let temp = q.shift();
if(temp.left == null && temp.right == null) count++;
if(temp.left) q.push(temp.left);
if(temp.right) q.push(temp.right);
}
return count;
}
let root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
console.log("Leaf count of the tree is : " + getLeafCount(root));
Output
Leaf count of the tree is : 3
Time Complexity: O(N) where N is the number of nodes in binary tree.
Auxiliary Space: O(N) due to queue data structure.
Please write comments if you find any bug in the above programs/algorithms or other ways to solve the same problem.
Last Updated :
03 Apr, 2023
Like Article
Save Article
В
приведенных ниже алгоритмах предполагается,
что узел (элемент) дерева декларирован
сл
Type
PNode
= ^TNode;
TNode
= record
Data
: integer; {информационное
поле}
left,right
: PNode;
end;
едующей записью:
А1. Вычисление суммы значений информационных полей элементов
Алгоритм
реализован в виде функции, возвращающей
значение суммы информационных полей
всех элементов. Тривиальным считается
случай, когда очередной узел – пустой,
и, следовательно, не имеет информационного
поля.
function
Sum(Root : PNode) : integer;
begin
if
Root=Nil then
{узел
— пустой}
Sum
:= 0
else
Sum
:= Root^.Data + Sum(Root^.left)
+
Sum(Root^.right);
{end
if}
end;
Для
нетривиального случая результат
вычисляется как значение информационного
элемента в корне (Root^.Data)
плюс суммы информационных полей левого
и правого поддеревьев.
А
выражение Sum(Root^.left)представляет
собой рекурсивный вызов левого поддерева
для данного корня Root.
А2. Подсчет количества узлов в бинарном дереве
function
NumElem(Tree:PNode):integer;
begin
if
Tree = Nil then
NumElem
:= 0
else
NumElem
:= NumElem(Tree^.left)
+
NumElem(Tree^.right) + 1;
{end
if}
end;
А3. Подсчет количества листьев бинарного дерева
function
Number(Tree:PNode):integer;
begin
if
Tree = Nil then
Number := 0 {дерево
пустое – листов нет}
else
if (Tree^.left=Nil)
and (Tree^.right=Nil) then
Number
:= 1 {дерево
состоит из одного узла — листа}
else
Number
:= Number(Tree^.left) + Number(Tree^.right);
{end
if}
end;
Анализ
приведенных алгоритмов показывает, что
для получения ответа в них производится
просмотр всех узлов дерева. Ниже будут
приведены алгоритмы, в которых порядок
обхода узлов дерева отличается. И в
зависимости от порядка обхода узлов
бинарного упорядоченного дерева, можно
получить различные результаты, не меняя
их размещения.
Примечание:
Просмотр
используется не сам по себе, а для
обработки элементов дерева, а просмотр
сам по себе обеспечивает только некоторый
порядок выбора элементов дерева для
обработки. В приводимых ниже примерах
обработка не определяется; показывается
только место, в котором предлагается
выполнить обработку текущего
А4. Алгоритмы просмотра дерева
Самой
интересной особенностью обработки
бинарных деревьев является та, что при
изменении порядка просмотра дерева, не
изменяя его структуры, можно обеспечить
разные последовательности содержащейся
в нем информации. В принципе возможны
всего четыре варианта просмотра:
слева-направо, справа-налева, сверху-вниз
и снизу-вверх. Прежде чем увидеть, к
каким результатам это может привести,
приведем их.
а.
Просмотр дерева слева – направо
procedure
ViewLR(Root:PNode); {LR -> Left – Right }
begin
if
Root<>Nil then
begin
ViewLR(Root^.
left); {просмотр
левого поддерева}
{Операция
обработки корневого элемента –
вывод
на печать, в файл и др.}
ViewLR(Root^.right);
{
просмотр правого поддерева
}
end;
end;
б.
Просмотр справа налево
procedure
ViewRL(Root:PNode); {LR -> Right – Left}
begin
if
Root<>Nil then
begin
ViewRL(Root^.right);
{просмотр
правого поддерева}
{Операция
обработки корневого элемента –
вывод
на печать, в файл и др.}
ViewRL(Root^.left);
{
просмотр левого поддерева
}
end;
end;
в.
Просмотр сверху – вниз
procedure
ViewTD(Root:PNode); {TD –> Top-Down}
begin
if
Root<>Nil then
begin
{Операция
обработки корневого элемента –
вывод
на печать, в файл и др.}
ViewTD(Root^.left);
{просмотр
левого поддерева}
ViewTD(Root^.right);
{
просмотр правого поддерева
}
end;
end;
г.
Просмотр снизу-вверх
procedure
ViewDT(Root:PNode); {DT –> Down — Top}
begin
if
Root<>Nil then
begin
ViewDT(Root^.left);
{просмотр
левого поддерева}
ViewDT(Root^.right);
{
просмотр правого поддерева
}
{Операция
обработки корневого элемента –
вывод
на печать, в файл и др.}
end;
end;
П
1. Рассмотрим
результаты просмотра для приведенных
алгоритмов, при условии, что обработка
корневого элемента сводится к выводу
значения его информационного поля, а
дерево в этот момент имеет следующие
узлы:
Результаты
просмотра:
|
Алгоритм |
1, |
|
Алгоритм |
98, |
|
Алгоритм |
10, |
Из
приведенной таблицы видно, что, просто
изменяя порядок просмотра дерева
(слева-направо и справа-налево), можно
получить отсортированные по возрастанию
или по убыванию числа.
Пример
2. Пусть в
узлах дерева расположены элементы
арифметического выражения:
Р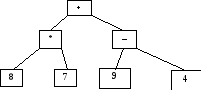
просмотра:
|
«Слева |
8 * 7 + 9 – |
инфиксная |
|
«Сверху |
+ |
префиксная |
|
«Снизу |
8 |
постфиксная |
A
{
Определить
существование значения SearchValue
и
вернуть указатель на элемент, содержащий
его,
или
вернуть Nil,
если
элемент не найден}
function
Search(SearchValue:integer;Root:PNode):PNode;
begin
if
(Root=Nil) or
(Root^.Data=SearchValue) then
Search
:= Root
else
if
(Root^.Data > SearchValue) then
Search
:= Search(SearchValue,Root^.left)
else
Search
:= Search(SearchValue,Root^.right);
{end
if}
end;
5. Поиск элемента
в двоичном упорядоченном дереве
Вывод.
Тексты приведенных алгоритмов очень
компактны и просты в понимании.
В
заключение отметим, что рекурсивные
алгоритмы широко используются в базах
данных и при построении компиляторов,
в частности для проверки правильности
записи арифметических выражений,
синтаксис которых задается с помощью
синтаксических диаграмм.
Для
закрепления материала предлагается
решить следующую задачу:
Данные
о студентах содержат фамилию и три
оценки, полученные на экзаменах. Занести
их с клавиатуры или из текстового файла
в бинарное дерево поиска, упорядоченное
по значению средней оценки. Затем вывести
на экран список студентов, упорядоченный
по убыванию средней оценки. Кроме фамилий
вывести все три оценки и их среднее
значение с точностью до одного знака
после запятой.
Соседние файлы в папке лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
Здравствуйте, у меня вроде все получилось сделать, только, почему всегда ответ получается 0, как это можно исправить
#include "stdafx.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
//структура, описывающая узел бинарного дерева
typedef struct node
{
char str[200];
int kol;
node *left;
node *right;
} tree;
void create(tree **root);
void add(tree **root, char word[], int i);
void print(tree *root);//Обход в прямом порядке
void print2(tree *root);//Симметричное отображение
void print3(tree *root);//реверсивный вывод
int list_count(tree *root);
int main()
{
int result = 0;
tree *root = NULL;
create(&root);//создание
print(root);//вывод прямой
// print2(root); //симметричный
// print3(root); //реверсивный
list_count(root);
printf("n%dn", result);
return 0;
}
void create(tree **root)
{
FILE *in;
int i = 0;
char word[20];
char a;
if((in = fopen("C:\text.txt", "r")) == NULL)
{
printf("nError opening filen");
}
else
{
while(!feof(in))
{
fread(&a, sizeof(char), 1, in);
if(a != ' ')
{
if(a != 'n')
{
word[i] = a;
word[i + 1] = '';
i++;
}
}
if(( a == ' ') || (a == 'n'))
{
add(root, word, i);
i = 0;
}
}
}
fclose(in);
}
void add(tree **root, char word[], int i)
{
if((*root) == NULL)
{
(*root) = (tree *)malloc(sizeof(node));
strncpy((*root)->str, word, sizeof(char) * (i + 1));
(*root)->kol = 1;
(*root)->right = NULL;
(*root)->left = NULL;
return;
}
if(strcmp(word, (*root)->str) > 0)
{
add(&(*root)->right, word, i);
}
else if(strcmp(word, (*root)->str) < 0)
{
add(&(*root)->left, word, i);
}
else
(*root)->kol++;
}
void print(tree *root) //в прямом порядке
{
if (root!=NULL)
{
printf("Word: %st tNumber tree: %dtn",root->str, root->kol);
print(root->left);
print(root->right);
}
}
void print2(tree *root)//симметричный порядок
{
if (root!=NULL)
{
print2(root->left);
printf("Word: %st tNumber tree: %dtn",root->str, root->kol);
print2(root->right);
}
}
void print3(tree *root)//реверсивный вывод
{
if (root!=NULL)
{
print3(root->left);
print3(root->right);
printf("Word: %st tNumber tree: %dtn",root->str, root->kol);
}
}
int list_count(tree *root)
{
int result;
if ((root->left==NULL)&&(root->right==NULL))
{
result = 1;
}
else
{
result = 0;
}
if (root->left)
{
result += list_count(root->left);
}
if (root->right)
{
result += list_count(root->right);
}
return result;
}
Найдите ошибку или как посоветуете исправить
Люди, это же должно быть просто
Код к задаче: «Найти количество листьев в дереве»
1. Основные понятия
Каждый узел имеет не более двух поддеревьев, левое и правое поддеревья, порядок нельзя изменить.
Природа:
1. На n-м уровне непустого двоичного дерева имеется не более 2 ^ (n-1) элементов.
2. Бинарное дерево с глубиной h имеет не более 2 ^ h-1 узлов.
3. Если для любого двоичного дерева T число конечных узлов (т. е. число конечных узлов) равно n0, а число узлов со степенью 2 равно n2, то n0 = n2 + 1.
Полное двоичное дерево: все терминалы находятся на одном уровне, а степень нетерминальных узлов равна 2.
Если глубина полного двоичного дерева равна h, количество содержащихся в нем узлов должно быть 2 ^ h-1.
Полное двоичное дерево: все узлы, кроме самого большого уровня, становятся полным двоичным деревом, а слой с наивысшим уровнем выравнивается по левому краю, то есть концентрируется в левой позиции, не может быть пустой позиции ,
Для полного двоичного дерева, если узлом является i, его родительским узлом является i / 2, 2i — это левый дочерний узел, а 2i + 1 — правый дочерний узел.
Во-вторых, обход двоичного дерева
Обходите все узлы двоичного дерева и заходите только один раз. Согласно различным позициям корневых узлов, он делится на обход до заказа, обход среднего порядка и обход после заказа.
Обход предварительного заказа: корневой узел-> левое поддерево-> правое поддерево (корневой узел впереди)
Порядок обхода: левое поддерево-> корневой узел-> правое поддерево (корневой узел посередине)
Обход после заказа: левое поддерево-> правое поддерево-> корневой узел (корневой узел находится позади)
Например: найдите три обхода следующего дерева

Обход предварительного заказа: abdefgc
Обратный путь в порядке: debgfac
Обход после заказа: edgfbca
Три, двоичное деревоТри обходаПуть и спросГлубина дерева Количество листьев Метод реализации
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<queue>
#include<stack>
using namespace std;
// Цепная структура хранения двоичного дерева
typedef struct Bitnode{
char data;
struct Bitnode *lchild;
struct Bitnode *rchild;
}Bitnode,*Bitree;
// Создать двоичное дерево в последовательности
void creatBitree(Bitree &T)
{
char ch;
scanf("%c",&ch);
getchar();
if(ch ==' ')
T = NULL;
else
{
T=(Bitree)malloc(sizeof(Bitnode));
T->data=ch;
printf("Введите левое поддерево% c:",ch);
creatBitree(T->lchild);
printf("Введите правильное поддерево% c:",ch);
creatBitree(T->rchild);
}
}
// Первый ход
void preOrder(Bitree T)
{
if(T==NULL) return ;
else
{
printf("%c",T->data);
preOrder(T->lchild);
preOrder(T->rchild);
}
}
// Обход последовательности
void InOrder(Bitree T)
{
if(T==NULL) return;
else{
InOrder(T->lchild);
printf("%c",T->data);
InOrder(T->rchild);
}
}
// Последующий обход
void PostOrder(Bitree T){
if(T==NULL) return ;
else{
PostOrder(T->lchild);
PostOrder(T->rchild);
printf("%c",T->data);
}
}
// Обход слоя
void levelOrder(Bitree T)
{
Bitree p=T;
queue<Bitree> Q;
Q.push(p);
while(!Q.empty())
{
p=Q.front();
Q.pop();
printf("%c",p->data);
if(p->lchild!=NULL)
Q.push(p->lchild);
if(p->rchild!=NULL)
Q.push(p->rchild);
}
}
// Находим глубину дерева
int TreeDeep(Bitree T)
{
int deep=0;
if(T)
{
int leftdeep=TreeDeep(T->lchild);
int rightdeep=TreeDeep(T->rchild);
deep=leftdeep>=rightdeep?leftdeep+1:rightdeep+1;
}
return deep;
}
// Находим количество листьев
int Leafcount(Bitree T,int &num)
{
if(T)
{
if(T->lchild==NULL && T->rchild==NULL)
num++;
Leafcount(T->lchild,num);
Leafcount(T->rchild,num);
}
return num;
}
int main()
{
Bitree T;
int num=0;
printf(«Введите корень дерева:»);
creatBitree(T);
printf("Обход предварительного заказа: n");
preOrder(T);
printf("n");
printf("Обход среднего порядка: n");
InOrder(T);
printf("n");
printf("Обход после заказа: n");
PostOrder(T);
printf("n");
printf("Обход слоя: n");
levelOrder(T);
printf("n");
printf(«Найдите глубину дерева: n»);
printf("%dn",TreeDeep(T));
printf("Найдите количество листьев: n");
printf("%dn",Leafcount(T, num));
return 0;
}