Как найти число кинематических пар

Кинематической
парой (КП) называется
подвижное непосредственное соединение
двух звеньев. При соединении n
звеньев
образуется n-1
кинематических пар (сложный шарнир),
например, в механизме, изображенном на
рис. 1.2. (грохот конвейера, качающегося
конвейера, уплотняющей машины)
кинематических пар 7 (перечислим их:
6-1, 1-2, 2-3, 3-4, 3-6,4-5, 5-6), в шарнире С
лишней является пара звеньев 2-4.

Рассмотрим
цилиндрическую зубчатую передачу,
условное изображение которой приведено
на рисунке 1.3. Звенья 1 и 2 подвижны, звено
3- неподвижно (станина). Определим число
кинематических пар, образуемых звеньями
1,2,3. Звено 1 со звеном 3 — первая кинематическая
пара, звено 1 со звеном 2- вторая КП, звено
2 со звеном 3- третья КП. Зубчатое колесо
1 жестко закреплено на своем валу —
колесо 1 и вал вместе с крепёжными
деталями образуют одно звено. Аналогично
колесо 2 с валом также образуют одно
звено. Звено 1 со звеном 3 и звено 2 со
звеном 3 соприкасаются по цилиндрическим
поверхностям, а звено 1 со звеном 2- по
линии.

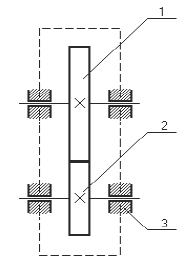
Рисунок 1.3 — Схема
редуктора

Те поверхности,
линии или точки, которыми звенья
непосредственно соприкасаются друг с
другом, называются элементами
кинематических пар. Если
звенья, образующие КП, в силу характера
их соприкосновения, могут совершать
только простейшие движения относительно
друг друга (вращательное, прямолинейное
поступательное или, в общем случае,
винтовое), то пара является низшей.
Более сложные
относительные движения можно реализовать
в парах, характер соприкосновения
звеньев в которых допускает не только
относительное скольжение, но и
перекатывание. Такие пары называются
высшими.
Таким образом,
по характеру касания звеньев кинематические
пары делятся на высшие и низшие.
Низшими КП
называются
такие пары, звенья которых соприкасаются
по поверхностям. Высшими
КП
называются
такие пары, звенья которых соприкасаются
по линии или в точке. Механические
передачи в структуре которых присутствуют
высшие кинематические пары являются
следующие механизмы
с гибкими звеньями (цепные, ременные);
фрикционные; зубчатые; кулачковые,
поводковые механизмы (мальтийские) и
др.

Примеры низших
кинематических пар приведены на рисунках
1.4. и 1.5. На рисунке 3 показана вращательная
кинематическая пара. Звено 1 может
совершать вращательное дви­жение по
отношению к звену 2. Касание звеньев
здесь происходит по цилиндрической
поверхности. Ползун 1 движется в
направляющей 2 (рис. 1.4.). Касание звеньев
1 и 2 происходит по плоскостям. Это
поступательная кинематическая пара.

Примером высших
кинематических пар могут быть цилиндр
на плоскости — касание звеньев происходит
по линии — образующей цилиндра (рис.
1.6.); и шар на плоскости — касание звеньев
происходит в точке (рис. 1.7.).

По характеру
относительного движения звеньев КП
делятся на плоские и пространственные.
Плоскими
называются
такие кинематические пары, относительное
движение звеньев которых плоское.

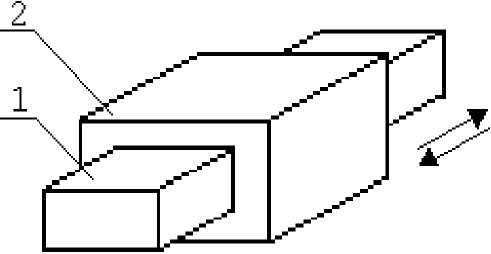
Рисунок 1.4 —
Вращательная КП Рисунок 1.5 — Поступательная
КП

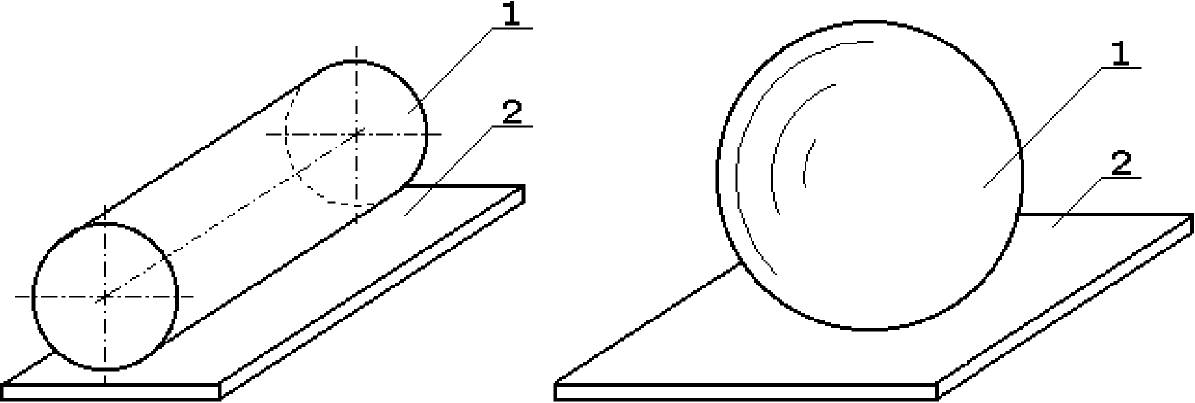
Рисунок 1.6 — Цилиндр
на плоскости Рисунок 1.7 — Шар на плоскости

Напомним сведения,
известные из механики материального
тела: перемещающееся в плоскости
(движущееся плоско) твердое тело, имеет
3 степени свободы (для определения
положения тела необходимо определить
три обобщённые координаты — перемещения
вдоль осей x,
y
и угловая координата φ).

Относительное
движение — движение одного звена при
мысленно неподвижном втором. Плоским
движением тела называется такое движение,
при котором все точки тела движутся
параллельно некоторой неподвижной
плоскости — плоскости параллелизма.
Плоские КП совершают, следующие виды
относительного движения звеньев: плоско
— параллельное — параллельно некоторой
неподвижной плоскости; поступательное
— любая прямая тела движется параллельно
некоторой прямой на неподвижной
плоскости; вращательное — вращение тела
вокруг неподвижной оси.
При изучении
характера движения звеньев и вида
кинематических пар особое внимание
следует обратить на плоско — параллельное
(сложное) движение: сочетание относительного
с переносным, или поступательного с
вращательным.

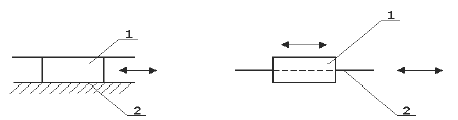
Рисунок 1.8 —
Поступательная плоская КП

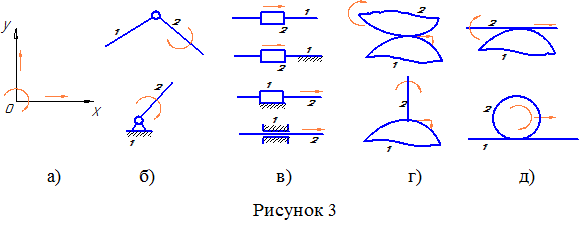
На рисунках 1.8-1.9
приведены примеры плоских кинематических
пар. На рисунке 6 изображена плоская
кинематическая пара при одном неподвижном
звене 2, а на рисунке 7 — поступательная
плоская пара с двумя подвижными звеньями.
На рисунке 1.9.
а) показана
вращательная плоская кинематическая
пара — шарнирное соединение двух звеньев
(рычагов). Вращательной кинематической
парой является также и колесо со станиной
(рис. 1.9.б).
На рисунке 1.9 в)
показана плоско-параллельная КП
(колесо-рельс). Качение окружности по
прямой — плоско-параллельное движение.

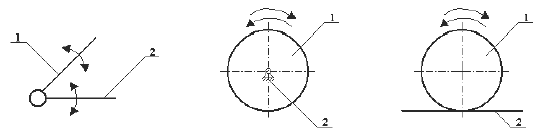
а)
б) в)

Рисунок 1.9 — Плоская
вращательная пара (а
и
б) и
плоско-параллельная пара (в)

Кинематическая
пара называется пространственной, если
относительное движение её звеньев не
плоское. Пространственный механизм
образован подвижными звеньями, которые
описывают траектории, лежащие в
пересекающихся плоскостях. На рисунке
1.10. приведен пример пространственной
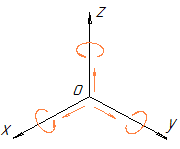
кинематической пары — шаровой шарнир.
Шар в шаровом гнезде может совершать
вращение вокруг любой из трех осей x,
y,
z.
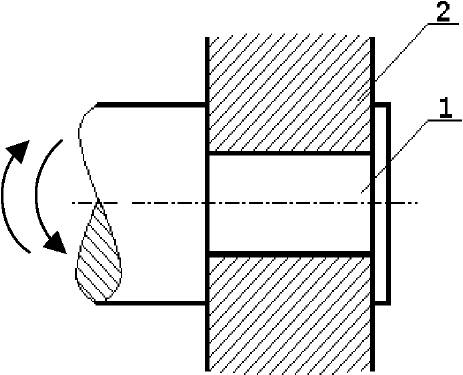
На рисунке 1.11. показана также
пространственная кинематическая пара
— винтовая пара. Любая точка гайки при
мысленно закреплённом винте совершает
пространственное движение. Траектория
любой точки гайки — винтовая линия.

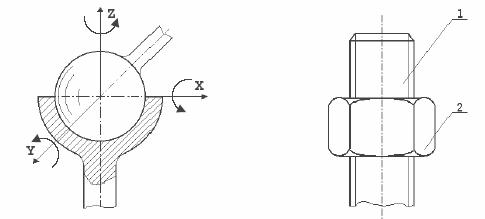
Рисунок 1.10 — Шаровой
шарнир Рисунок. 1.11 — Винтовая пара

По характеру
замыкания звеньев кинематические пары
делятся на замкнутые геометрически
и замкнутые
не геометрически:
силой или кинематической цепью. Соединение
звеньев в кинематические пары может
быть осуществлено по-разному. При
геометрическом замыкании звенья
конструктивно соединены в кинематические
пары. В качестве примера можно рассмотреть
колесо со станиной (рис. 1.9. б)
или шарнирное соединение двух рычагов
(рис. 1.9. а).
При силовом замыкании кинематическая
пара существует за счёт сил веса или
сил пружин. Например, шар на плоскости
(рис. 1.7.) или колесо рельс (рис. 1.9. в).
При замыкании кинематической цепью
пара существует за счёт других
кинематических пар в кинематической
цепи, которые не позволяют нарушить
контакт звеньев, образующих кинематическую
пару. Например, кинематическая пара,
образованная зацеплением двух зубчатых
колёс 1,2 (рис. 1.3.).

По числу потерянных
степеней свободы Н
в относительном движении или по числу
условий связей S
кинематические пары делятся на 5 классов
(или по степеням подвижности — 1-но,
2-х, 3х, 4-х и 5-ти,
т.е. Н-подвижные
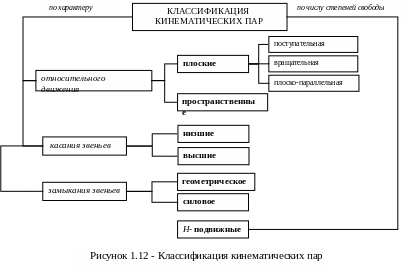
кинематические пары). Все перечисленные
виды кинематических пар приведены на
схеме (рис. 1.12.)

Класс пары —
это число условий связей S,
накладываемых парой на относительное
движение звеньев, или число потерянных
степеней свободы в относительном
движении звеньев. Тело, свободно
перемещающееся в пространстве, имеет
6 степеней свободы: движение вдоль осей
x,
y,
z
и вращение вокруг этих осей. Степень
свободы — обобщённая координата — это
число независимых параметров, которыми
определяется положение тела в пространстве
или его движение. Соединяя звенья в
кинематические пары, мы тем самым лишаем
их одной или нескольких степеней свободы.
При соединении звеньев в кинематические
пары теряются 1 или 2 степени свободы.
Поэтому плоские кинематические пары
могут быть только 2-х
классов:
1-го и 2—го.

Пример поступательной
плоской кинематической пары показан
на рисунке 1.8. Пары низшие 2 класса
(одноподвижные) — кинематической пары,
в которых потеряно 2 степени подвижности.
Пример вращательной плоской пары 2
класса
показан на рисунке 1.9. а.
Примером высшей плоской кинематической
пары 1 класса (2-хподвижной) является
зацепление профилей зубьев эвольвентных
колёс. В этой паре потеряна одна степень
подвижности — перемещение вдоль оси
x.
Возможно перекатывание профилей вокруг
точки контакта и смещение вдоль оси y.

В зависимости от
числа потерянных степеней свободы в
относительном движении звеньев, связанных
в кинематические пары, пространственные
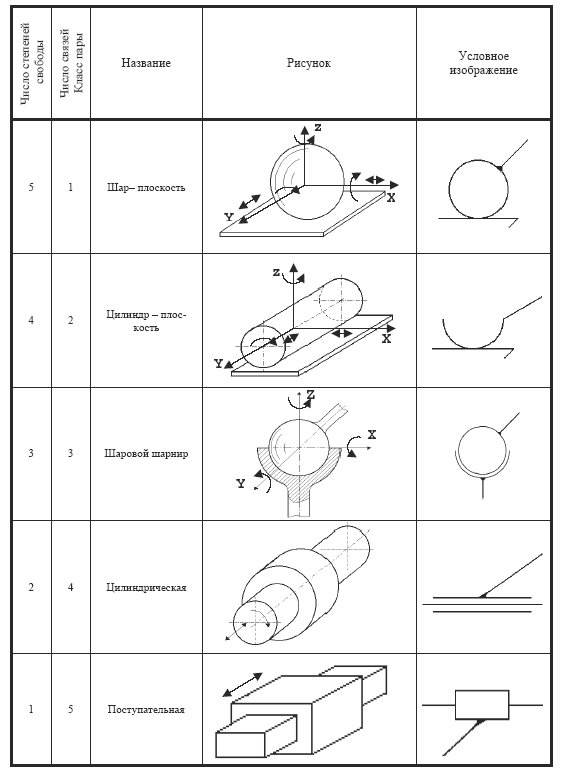
пары делятся на 5 классов. Для иллюстрации
классификации кинематических пар
составим таблицу, включающую примеры
всех 5 классов пространственных пар
(табл. 1.1.).

Для определения
класса кинематической пары необходимо
подсчитать число простейших движений,
которыми обладает звено кинематической
пары в относительном движении; вычесть
полученное число из шести, получив при
этом число связей, налагаемых данной
кинематической парой на относительное
движение её звеньев, и этим определим
класс пары. Таким образом, степень
свободы с условием связи связана
следующим образом

.

По характеру
повторяемости траекторий точек элементов
кинематических пар пары делятся на
обратимые и
необратимые.

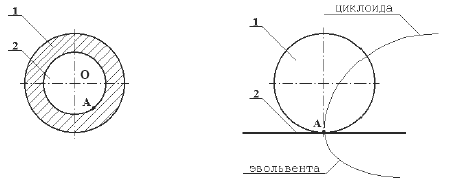
Рисунок. 1.13.
Обратимая пара Рисунок. 1.14. Необратимая
пара

Обратимыми
называются
такие кинематические пары, траектории
точек элементов кинематических пар
которых повторяются. Например, во
вращательной паре (рисунок. 1.13) при
движении звена 1 по отношению к звену 2
траектория точки А, лежащей на поверхности
соприкосновения звеньев и принадлежащей
звену 1, — окружность. При мысленно
закрепленном звене 1 траектория точки
А, принадлежащей звену 2, в относительном
движении, также окружность радиуса ОА.

Необратимыми
называются
такие кинематические пары, траектории
точек элементов которых в относительном
движении не повторяются. Примером
является плоская кинематическая пара
колесо — рельс. При перекатывании колеса
по направляющей точка А (рис. 1.14) описывает
циклоиду, а при перекатывании прямой
по окружности — эвольвенту.

Таблица 1.1 — Примеры
кинематических пар

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Механизм — это искусственно созданная система тел, предназначенная для преобразования движения одного или нескольких тел в требуемые движения других тел.

Звено механизма — каждое из тел, входящих в состав механизма, состоящее часто из комплекса неподвижно сочлененных между собой деталей.

Звенья механизма бывают:

• жесткие;
• упругие (пружины, рессоры, металлорезиновые соединения и др. Воздух или газ, заключенный в пространстве с переменным объемом, также рассматривается как упругое звено);
• гибкие (канаты, ремни, цепи. Свойствами гибких звеньев (переносить движение от одного жесткого звена к другому) обладают также жидкость и система твердых тел в гидростатической и в шариковой передачах).

Среди звеньев механизма всегда выделяют входные и выходные звенья (при этом остальные звенья называются соединительными).

Входные звенья — звенья механизма, которым сообщается движение, преобразуемое в требуемое движение других звеньев механизма.

Выходные звенья — звенья механизма, совершающие требуемое движение, для которого предназначен механизм.

Ведущее звено — звено, для которого сумма элементарных работ всех внешних сил, приложенных к нему, является положительной.

Ведомое звено — звено, для которого сумма элементарных работ всех внешних сил, приложенных к нему, является отрицательной.

Положение и перемещение ведомого звена однозначно зависит от положения и перемещения ведущего звена (звеньев).

В большинстве случаев входное звено является и ведущим.

Кинематическая пара — это соединение двух соприкасающихся звеньев, допускающее их относительное движение.

Элемент кинематической пары — точка, линия или поверхность одного звена, входящая в соприкосновение с другим звеном.

Кинематические пары механизмов классифицируют:

1) По количеству условий связи в относительном движении звеньев (по Малышеву А.П.).

Пространственные кинематические пары можно разделить на 5 классов:

• 1 класс — уничтожается одно возможное относительное движение звеньев;
• 2 класс — уничтожается два возможных относительных движения звеньев;
• 3 класс — уничтожается три возможных относительных движения звеньев;
• 4 класс — уничтожается четыре возможных относительных движения звеньев;
• 5 класс — уничтожается пять возможных относительных движений звеньев.

2) По числу оставшихся степеней свободы (по Добровольскому В.В.):

• пара I рода — осталась неуничтоженной одна степень свободы в относительном движении;
• пара II рода — остались неуничтоженными две степени свободы в относительном движении;
• пара III рода — остались неуничтоженными три степени свободы в относительном движении;
• пара IV рода — остались неуничтоженными четыре степени свободы в относительном движении;
• пара V рода — остались неуничтоженными пять степеней свободы в относительном движении.

При определении рода кинематической пары необходимо установить число независимых относительных движений, и тогда найденное число и будет номером рода кинематической пары.

В плоском механизме возможно существование только кинематических пар I и II рода (т.е. 5 и 4 класса).

3) По характеру соприкосновения элементов кинематические пары (КП) подразделяются на:

— низшие (элементы кинематических пар представляют собой взаимно облегающие поверхности или отдельные их части).

Особенность: обратимость движения (т.е. характер относительной траектории, независимо от того, на каком из звеньев выбирается точка, один и тот же, а если две точки разных звеньев взяты на одинаковом расстоянии от центра, то их траектории совпадают).

Преимущество: способность элементов кинематической пары воспринимать и передавать значительные силы при меньшем износе.

— высшие (элементы кинематических пар касаются в точке или по линии).

Относительным движением звеньев, соединенных высшей КП, может быть:

• чистое качение;
• качение со скольжением;
• чистое скольжение.

Особенность: высшие КП не обладают обратимостью движения (если катить окружность по прямой, то любая из точек окружности опишет при этом циклоиду, а если катить по окружности прямую, то каждая из точек прямой перемещается по эвольвенте круга).

Преимущество: возможность воспроизводить достаточно сложные относительные движения.

4) Различают также кинематические пары с односторонней или с двусторонней связью.

Для того, чтобы элементы КП находились в постоянном соприкосновении, КП должны быть замкнуты. Замыкание кинематической пары может быть:

• геометрическое (осуществляется соответствующими геометрическими формами элементов звеньев КП);
• силовое (осуществляется силой веса, силой упругости пружин и т.п.).

Кинематическая цепь — это совокупность некоторого количества звеньев, соединенных при помощи кинематических пар последовательно или разветвлено.

Кинематическая цепь (КЦ) может быть:

1) Простой или сложной. В простой КЦ каждое из звеньев образует подвижное соединение с двумя звеньями. В сложную КЦ включены сложные звенья, соединяющиеся более чем с двумя другими звеньями.

2) Открытой или замкнутой. В открытой (т.е. незамкнутой) КЦ есть звенья, входящие только в одну кинематическую пару.

3) Плоской или пространственной. В плоской кинематической цепи точки всех звеньев могут перемещаться в параллельных плоскостях.

В пространственной кинематической цепи точки описывают либо пространственные кривые, расположенные в различных плоскостях, либо плоские кривые, расположенные в различных непараллельных плоскостях.

Относительная подвижность соединяемых звеньев может быть обеспечена введением не кинематической пары, а кинематического соединения, в котором между подвижно сочленяемыми звеньями вводятся промежуточные тела. Примеры кинематического соединения: шариковые и роликовые подшипники, шарико-винтовая передача, роликовые направляющие. Относительная подвижность звеньев, связываемых кинематическим соединением, в зависимости от его вида, совпадает с подвижностью какой-либо из простых кинематических пар. Кинематические соединения относят к соответствующему классу на тех же основаниях, что и кинематические пары.

Число степеней свободы кинематической цепи относительно звена, принятого за неподвижное, определяется по формуле Сомова–Малышева. Её можно записать в одном из двух видов: «через род кинематической пары» или «через класс кинематической пары»:

W = 6n – 5P_I – 4P_II – 3P_III – 2P_IV– P_V

или, что то же,

W = 6n – 5p₅ – 4p₄ – 3p₃ – 2p₂ – p₁

где:

n – число подвижных звеньев кинематической цепи;

P_i – количество кинематических пар i-го рода (т.е. P_I – количество одноподвижных пар, P_II – количество двухподвижных пар, P_III – количество трехподвижных пар, P_IV – количество четырехподвижных пар, P_V – количество пятиподвижных пар);

p_i — количество кинематических пар i-го класса (т.е. р₅ – количество КП 5 класса, где 5 степеней свободы уничтожены, а одна остается (пара — одноподвижная); р₄ – количество КП 4 класса, где четыре степени свободы уничтожены, а две остаются (пара — двухподвижная) и т.д.).

Для плоского механизма эта формула принимает вид

W = 3n – 2P_I – P_II

где:

Р_I — количество одноподвижных пар,

Р_II — количество двухподвижных пар;

или, что то же,

W = 3n – 2p₅ – p₄

p₅ — количество кинематических пар 5 класса (т.е. одноподвижных),

р₄ — количество кинематических пар 4 класса (т.е. двухподвижных).

Кинематическая цепь i-го семейства (i = 0; 1; 2; 3; 4) — кинематическая цепь, на движение всех звеньев которой накладывается i ограничений.

Основные виды механизмов с низшими парами:

• двухзвенный (с вращательной кинематической парой или с поступательной);
• трехзвенный (клиновой механизм, винтовой механизм);
• четырехзвенный (четырехзвенный шарнирный механизм, четырехзвенный рычажный механизм).

Четырехзвенный шарнирный механизм (шарнирный четырехзвенник) служит для преобразования одного вида вращательного движения в другое. Подвижные звенья этого механизма имеют следующие названия: кривошип, коромысло, ползун и шатун.

Кривошип — звено, которое может совершать полный оборот вокруг неподвижной оси. Если длина кривошипа мала, то его часто выполняют в виде эксцентрика – диска, насаженного на вал с эксцентриситетом, равным длине кривошипа.

Коромысло — звено, которое совершает неполный оборот вокруг неподвижной оси.

Ползун — звено, образующее поступательную пару со стойкой.

Шатун — звено, которое не образует кинематических пар со стойкой; совершает сложное движение.

Примером четырехзвенного рычажного механизма может служить кулисный механизм (двухкривошипный кулисный механизм или кривошипно-коромысловый). Разновидности кулисных механизмов следующие:

• двухползунный рычажный механизм (механизм Кардана);
• кулисный кривошипно-ползунный механизм (или иначе – кулисный синусный механизм);
• кулисный коромыслово-ползунный механизм (или иначе – кулисный тангенсный механизм);
• двухкулисный двухкривошипный механизм.

Среди звеньев кулисного механизма выделяют «кулису» и «кулисный камень».

Кулиса — подвижное звено рычажного механизма, образующее поступательную пару с другим подвижным звеном — камнем.

Кулисный камень выполняют:

• в виде ползушки, которая перемещается внутри прямолинейного паза кулисы;
• в виде втулки, скользящей по прямолинейному стержню кулисы.

Основные виды механизмов с высшими парами:

• кулачковые механизмы;
• зубчатые механизмы;
• фрикционные механизмы.

Обобщенные координаты механизма — это независимые между собой координаты (линейные или угловые), определяющие положение всех звеньев механизма относительно стойки.

За обобщенные координаты механизма можно взять любые координаты звеньев.

Начальное звено — звено, которому приписывается одна или неколько обобщенных координат механизма.

Определение положений всех звеньев механизма начинается с определения положений начальных звеньев.

Начальное звено не обязательно совпадает с входным звеном (если при этом упрощается анализ механизма).

Если все связи в кинематических парах геометрические (т.е. налагают ограничения только на положения точек звеньев), число степеней свободы механизма (число возможных перемещений) равно числу обобщенных координат механизма.

Избыточные связи — повторяющиеся связи, которые можно удалить, сохранив при этом заданное число степеней свободы.

Избыточные связи могут возникать:

• в кинематических парах (например, коленчатый вал четырехцилиндрового двигателя образует с подшипником одноподвижную вращательную пару, что вполне достаточно с точки зрения кинематики данного механизма с одной степенью свободы. Однако, учитывая большую длину вала и значительные силы, нагружающие коленчатый вал, приходится добавлять ещё два подшипника, иначе система будет неработоспособной из-за недостаточной прочности и жесткости);
• в кинематических цепях (для обеспечения нужной прочности и жесткости системы, особенно при передаче больших сил). Избыточные связи в кинематических цепях следует устранять или оставлять минимальное количество.

Избыточные связи бывают:

• локальные (появляются, если помимо необходимых элементов кинематическая пары, обусловленных требуемыми геометрическими связями, при конструировании используются дополнительные элементы. При наличии избыточных локальных связей относительное движение звеньев либо становится невозможным (зацикливание, защемление элементов), либо осуществляется за счет деформации звеньев между реальными поверхностями элементов или их износа). Увеличение числа избыточных локальных связей в кинематических парах способствует уменьшению податливости конструкции, а потому может оказаться вредным:

• в случае изменения температурного режима работы;
• при деформации стойки;
• при отклонениях размеров, формы и расположения поверхностей элементов кинематической пары.

• контурные (если есть контурные избыточные связи, то сборка механизма и движение его звеньев становится возможным только при деформировании звеньев).

Источники:

• Фролов К.В., Попов С.А., Мусатов А.К. Теория механизмов и машин. Под ред. Фролова К.В. — М.: Высш. шк., 1987. — 496 с.
• Кожевников С.Н. Теория механизмов и машин. — М.: Машиностроение, 1969. — 584 с.
• Левитский Н.И. Теория механизмов и машин. — 2-е изд., перераб. и доп. — М.: Наука, 1990. — 592 с.
• Артоболевский И.И. Теория механизмов и машин. — 4-е изд., перераб. и доп. — М.: Наука, 1988. — 640 с.

Кинематической парой называется подвижное соединение двух звеньев.

Рассмотрим классификацию и примеры кинематических пар:

Классификация кинематических пар

Кинематические пары классифицируются по различным признакам:

1) по числу связей, накладываемых на относительное движение звеньев, соединенных в кинематическую пару. По этому признаку кинематические пары подразделяются на классы. Приняты следующие обозначения:

W – число степеней свободы;
S – число связей, накладываемых на относительное движение звеньев.

Свободное звено в пространстве имеет шесть степеней свободы. При соединении звеньев некоторые из этих степеней свободы отнимаются («накладываются связи»). Зависимость между числом накладываемых связей и оставшимся числом степеней свободы в относительном движении звеньев очевидна:

W=6–S

или

S=6–W,

таким образом, существует пять классов кинематических пар (если отнять все шесть степеней свободы, то получится неподвижное соединение).

Примеры кинематических пар

На рисунке 2 приведены примеры некоторых кинематических пар.

а)

W = 5
S = 1 => I кл.

б)

W = 4
S = 2 => II кл.

в)

W = 3
S = 3 => III кл.

г)

Рисунок 2

Шар относительно плоскости (рисунок 2б), не отрываясь от нее, может совершать вращательные движения вокруг всех трех осей координат, а также двигаться вдоль осей «X» и «Y». При движении вдоль оси «Z» шар оторвется от плоскости, т.е. будет два свободных звена – кинематическая пара перестанет существовать. Таким образом, на относительное движение звеньев накладывается одна связь – это кинематическая пара I класса.

Аналогично без нарушения характера контакта нельзя цилиндр переместить вдоль оси «Z» и повернуть вокруг оси «Y» (рисунок 2в), т.е. число связей равно двум – пара II класса.

Плоскость относительно другой плоскости без нарушения характера контакта может двигаться поступательно вдоль осей «X» и «Y», а также вращаться вокруг оси «Z». Невозможно поступательное движение вдоль оси «Z» и вращательные движения вокруг осей «X» и «Y» (рисунок 2г). Таким образом, число связей равно трем – кинематическая пара III класса.

Примечание: если в кинематической паре имеются два функционально связанных движения (одно без другого существовать не может), то они дают одну степень свободы.

Например, болт с гайкой составляют кинематическую пару пятого класса. В данном случае имеется два движения гайки при неподвижном болте – вращательное движение вокруг оси болта и поступательное движение вдоль этой оси, но нельзя переместить гайку вдоль оси, не повернув ее, или повернуть гайку так, чтобы она не переместилась вдоль оси. Более того, зная параметры резьбы, легко определить зависимость между углом поворота и поступательным перемещением гайки.

Эти два движения образуют одно сложное (в данном случае – винтовое) движение. Оно определяет одну степень свободы в относительном движении этих звеньев, т.е. число связей равно пяти;

2) по характеру контакта звеньев, соединенных в кинематическую пару. По этому признаку кинематические пары подразделяются на высшие и низшие. Высшие пары имеют точечный или линейный контакт звеньев, составляющих данную кинематическую пару.

В низшей паре звенья контактируют друг с другом по какой-либо поверхности (в частном случае по плоскости).

Низшие кинематические пары обладают большей несущей способностью, т.к. имеют большую площадь контакта (в высшей паре площадь контакта теоретически равна нулю, а реально получается за счет деформации элементов кинематической пары – «пятно контакта»). Но в низших парах при работе происходит скольжение одной поверхности относительно другой, в то время как в высших парах может происходить и скольжение и качение.

Как правило, сопротивление скольжению больше, чем сопротивление перекатыванию одной поверхности относительно другой, т.е. потери на трение в высшей паре (если использовать только качение) меньше по сравнению с низшей парой (поэтому для увеличения коэффициента полезного действия вместо подшипников скольжения обычно ставят подшипники качения).

Кинематические пары, изображенные на рисунке 2б и 2в, являются высшими, а пара на рисунке 2г – низшая кинематическая пара;

3) по траектории движения точек, принадлежащих звеньям, составляющим кинематическую пару. По этому признаку выделяют пространственные и плоские кинематические пары.

В плоской кинематической паре все точки движутся в одной или в параллельных плоскостях, а траектории их движения представляют собой плоские кривые. В пространственных парах точки движутся в различных плоскостях и имеют траектории в виде пространственных кривых.

Значительное число механизмов, применяемых на практике, являются плоскими механизмами (по классификации И.И. Артоболевского – механизмами третьего семейства), поэтому необходимо более подробно рассмотреть плоские кинематические пары.

Свободное звено, помещенное в плоскость, имеет три степени свободы (поступательные движения вдоль осей координат и вращательное вокруг оси, перпендикулярной данной плоскости). Таким образом, размещение звена в плоскости отнимает у него три степени свободы (накладывает три связи). Но соединение данного звена с другим в кинематическую пару накладывает на относительное движение еще связи (минимальное число – 1). В результате на плоскости могут существовать только кинематические пары, имеющие две или одну степень свободы в относительном движении.

По общей классификации это пары четвертого и пятого классов. Простейшие пары пятого класса обеспечивают только одно движение – вращательное или поступательное (вращательная кинематическая пара в технике называется шарниром, поступательную пару по аналогии с поступательно движущимся звеном иногда также называют ползуном).

Две степени свободы в относительном движении на плоскости обычно обеспечивают два соприкасающихся профиля (на кинематической схеме контакт в точке, в реальном механизме это возможно линия, которая проецируется в точку). Таким образом, плоские кинематические пары пятого класса (шарниры и ползуны) одновременно являются низшими парами, а кинематические пары четвертого класса – высшими парами.

На рисунке 3 показано схематическое изображение плоских кинематических пар.

4) по характеру замыкания звеньев, соединенных в кинематическую пару. Существует два вида кинематических пар, отличающихся друг от друга по этому признаку. Кинематические пары с геометрическим замыканием и кинематические пары с силовым замыканием.

В парах с геометрическим замыканием конфигурация звеньев препятствует их разъединению в процессе работы. Например, присоединение шатуна к коленчатому валу при помощи шатунной крышки, или любые другие шарниры (дверь с косяком, окно с оконной рамой и т.д.).

В парах с силовым замыканием контакт звеньев в процессе работы обеспечивается постоянно действующей силой. На рисунке 2 все кинематические пары являются парами с силовым замыканием, причем в качестве замыкающей силы выступает вес. Если веса недостаточно, то обычно для создания прижимающего усилия применяют различные  упругие элементы (чаще всего пружины).

Кинематическая цепь и механизм >
Курсовой проект по ТММ >

Число — кинематические пары

Cтраница 1

Число кинематических пар, связывающих в узле несколько стержней ( а также стойку), определяют как число стержней и вычитают 1 ( см. схемы узлов на рнс.
 [1]

Число кинематических пар, связывающих в узле несколько стержней ( а также стойку), определяется как число стержней за вычетом / ( см. схемы узлов на фиг.
 [2]

Число кинематических пар в этом соединении не изменится, если, в частности, оси вращательных пар ( К, L) совпадут ( рис. 2.66, а) и образуют сложный шарнир.
 [3]

Рг — число кинематических пар соответственно III, II и I классов.
 [4]

Так как число кинематических пар V класса р & т и число звеньев яг должны быть целыми числами, то, следовательно, число звеньев в группе Ассура ( г) — всегда четное число, а число кинематических пар V класса ( р6г) кратно трем.
 [6]

Так как число кинематических пар V класса ръг и число звеньев иг должны быть целыми числами, то, следовательно, число звеньев в группе Ассура ( пг) — всегда четное число, а число кинематических пар V класса ( р6г) кратно трем.
 [8]

Так как число кинематических пар V класса Рьт и число звеньев пг должны быть иелыми числами, то, следовательно, число звеньев в группе Ассура ( лг) — всегда четное число, а число кинематических пар V класса ( р6г) кратно трем.
 [10]

При определении числа кинематических пар следует иметь в виду, что в случае сложного шарнира ( рис. 1.5) число кинематических пар будет на единицу меньше числа сходящихся звеньев.
 [11]

При определении числа кинематических пар следует иметь в виду, что в случае сложного шарнира число кинематических пар будет k — 1, если k — число звеньев, сходящихся в шарнире ( фиг.
 [12]

Полученные сочетания определяют числа кинематических пар различной подвижности.
 [13]

При таких сочетаниях чисел кинематических пар из последних уравнений системы (3.71) следует, что в синтезируемых группах должно быть пять ( р 5) кинематических пар и три ( и1 3) подвижных звена.
 [15]

Страницы:  

   1

   2

   3

   4