Как найти число граней в одной вершине

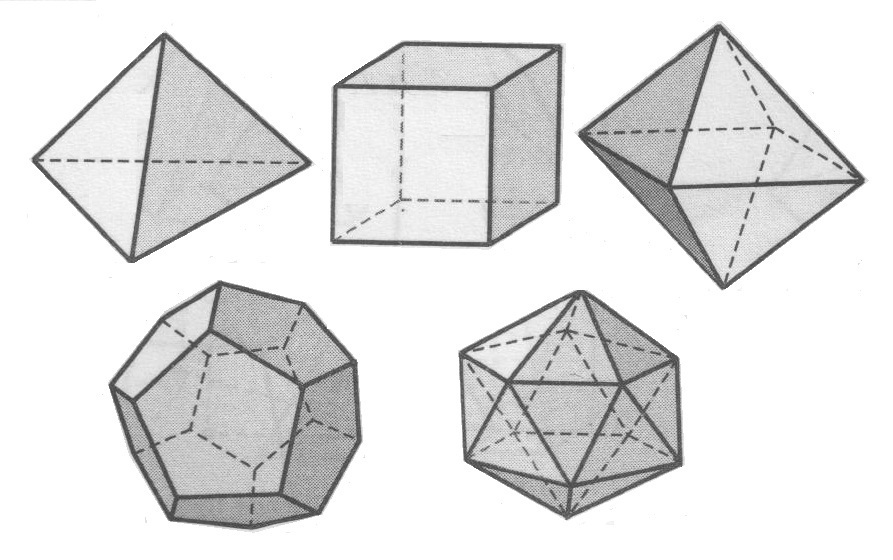
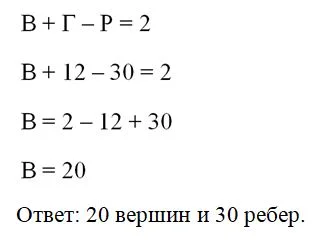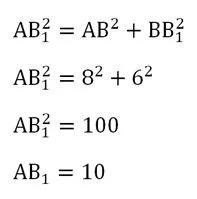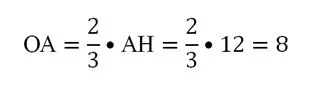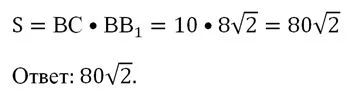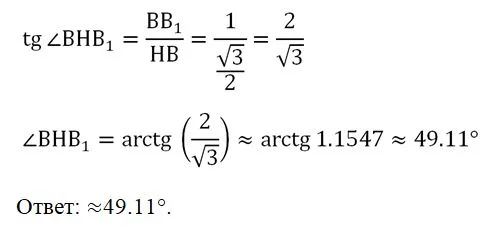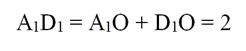Тетраэдр — треугольная пирамида. В каждой вершине сходятся 3 грани.
У куба 6 равных граней — квадратов. В каждой вершине сходятся 3 грани.
У октаэдра 8 граней: равные равносторонние треугольники. В каждой вершине сходятся 4 грани.
У додекаэдра 12 граней: равные правильные пятиугольники. В каждой вершине сходятся 3 грани.
У икосаэдра 20 граней: равные равносторонние треугольники. В каждой вершине сходятся 5 граней.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Эпиграф

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»

Л. Кэрролл

Задачи урока:

• Обучающие:

• Ввести понятие правильного многогранника ;
• Рассмотреть свойств о правильных многогранников ;

2. Развивающие:

• Формирование пространственных представлений ;
• Формирование умения обобщать, систематизировать, видеть закономерности;

3. Воспитательные:

• Воспитание эстетического чувства ;
• Формирование интереса к предмету.

Мозговая атака

многогранник

правильный

рёбра

грани

выпуклый

вершины

многоугольник

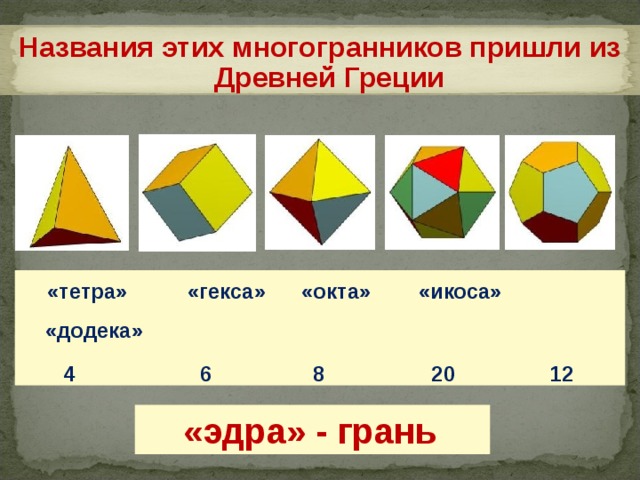
Названия этих многогранников пришли из Древней Греции

«тетра» «гекса» «окта» «икоса» «додека»

4 6 8 20 12

«эдра» — грань

4

• Какое тело носит имя Хеопса?
• Что представляет собой боковая грань пирамиды?
• Как называется правильный четырехугольник?
• Наука об измерении земли?
• У пятиугольника их пять
• У любой призмы их два

4

4

Согласно философии Платона

огонь

тетраэдр

вода

икосаэдр

воздух

октаэдр

земля

гексаэдр

вселенная

додекаэдр

Иоганн Кеплер

(1571-1630 )

«Космический кубок»

немецкий астроном и

математик

Выпуклый многогранник называется правильным , если все его грани – равные правильные многоугольники, в каждой его вершине сходится одно и то же число ребер и все его двугранные углы равны.

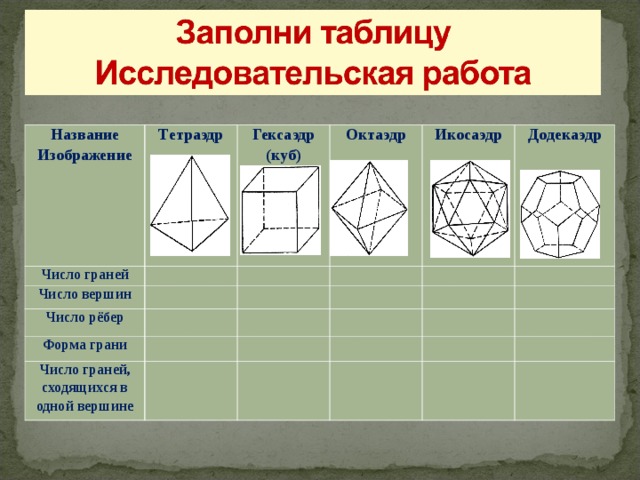
Название

Изображение

Число граней

Тетраэдр

Число вершин

Гексаэдр (куб)

Октаэдр

Число рёбер

Икосаэдр

Форма грани

Додекаэдр

Число граней, сходящихся в одной вершине

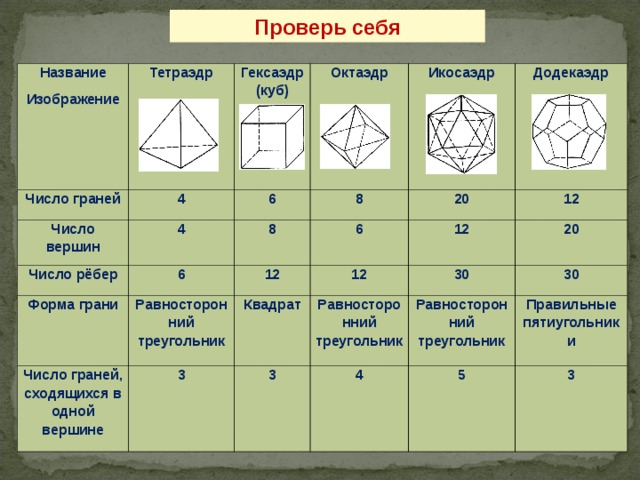
Проверь себя

Название

Изображение

Тетраэдр

Число граней

4

Гексаэдр (куб)

Число вершин

Октаэдр

6

4

Число рёбер

Икосаэдр

8

8

6

Форма грани

Додекаэдр

20

6

12

Число граней, сходящихся в одной вершине

Равносторонний треугольник

12

12

12

Квадрат

3

30

20

3

Равносторонний треугольник

30

Равносторонний треугольник

4

Правильные пятиугольники

5

3

Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и, вообще, n – угольники при n больше 5.

Теорема Эйлера

Теорема о числе граней, вершин и рёбер

выпуклого многогранника – 1755 год

Число вершин плюс число граней минус число рёбер равно двум.            

Леонард Эйлер (1707 – 1783 гг.) немецкий математик и физик

В + Г – Р = 2

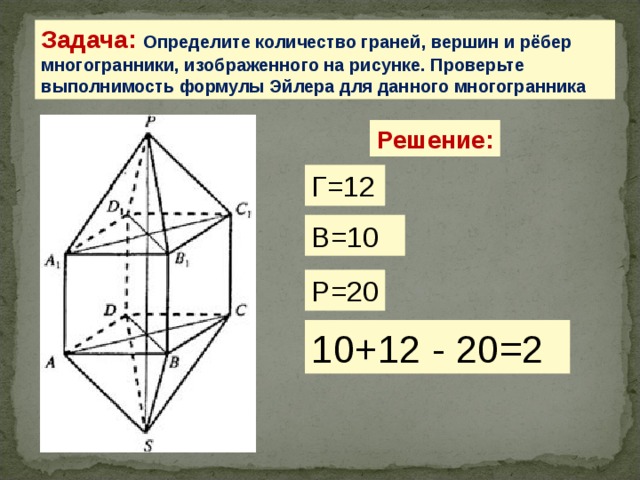
Задача: Определите количество граней, вершин и рёбер многогранники, изображенного на рисунке. Проверьте выполнимость формулы Эйлера для данного многогранника

Решение:

Г=12

В=10

Р=20

10+12 — 20=2

Правильные многогранники в других науках

Тетраэдр

Строение молекулы метана, к ристаллы белого фосфора , кристалл сернокислого натрия имеет форму тетраэдра.

Уголковый отражатель — устройство в виде тетраэдра. Излучение, попавшее в уголковый отражатель, отражается в строго обратном направлении. Используется:

• для точного измерения расстояний (топографическая съемка, строительстве);
• для возврата излучения точно назад (катафот).

Мало того, молекулы воды тоже имеют форму тетраэдра.

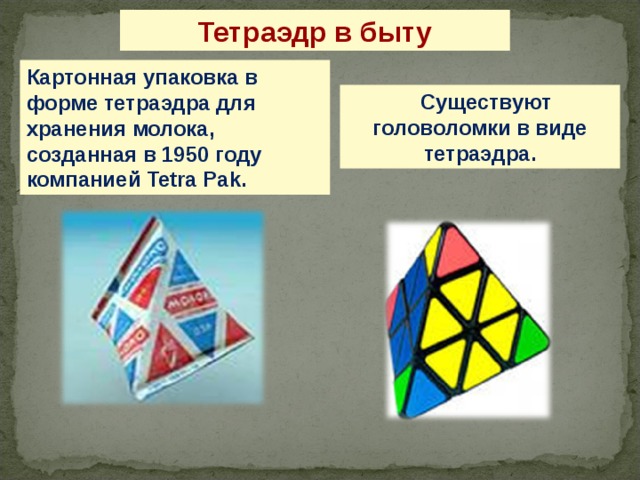
Тетраэдр в быту

Картонная упаковка в форме тетраэдра для хранения молока, созданная в 1950 году компанией Tetra Pak.

Существуют головоломки в виде тетраэдра.

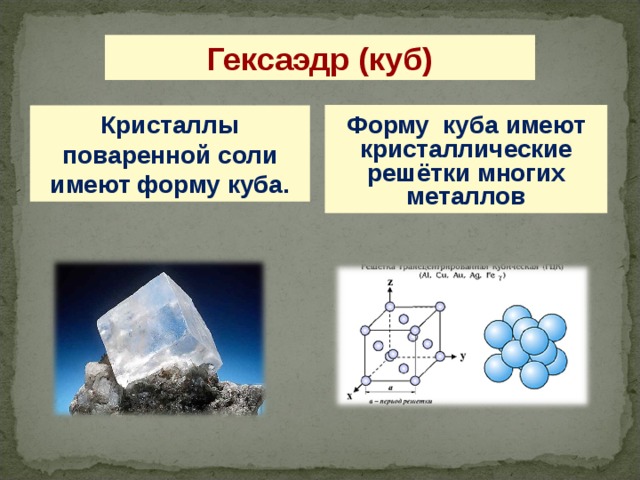
Гексаэдр (куб)

Форму  куба имеют кристаллические решётки многих металлов

Кристаллы поваренной соли имеют форму куба.

Октаэдр

При производстве алюминия пользуются алюминиево-калиевыми кварцами, монокристалл которых имеет форму октаэдра. Правильная форма алмаза —

Октаэдр.

Икосаэдр

Икосаэдр отличился тем, что его форму сочли для себя удобной живые существа.

Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр. Из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи .

16

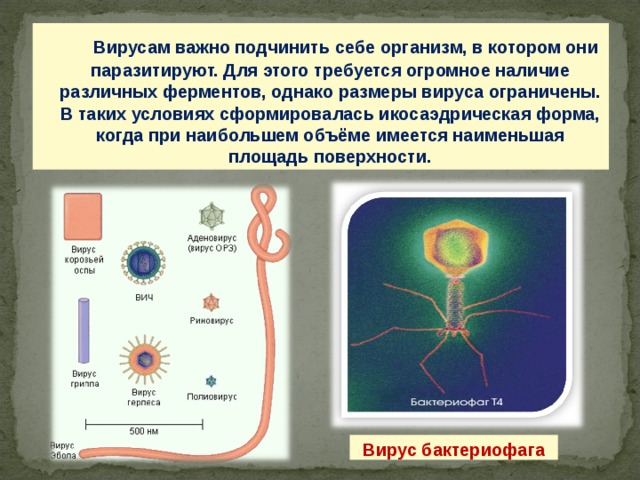
Вирусам важно подчинить себе организм, в котором они паразитируют. Для этого требуется огромное наличие различных ферментов, однако размеры вируса ограничены. В таких условиях сформировалась икосаэдрическая форма, когда при наибольшем объёме имеется наименьшая площадь поверхности.

Вирус бактериофага

Додекаэдр

Вирус полиомиелита имеет

форму додекаэдра.

кристалл пирита (сернистый колчедан), используется для получения особых сортов цемента— природная модель додекаэдра

Додекаэдр в искусстве

Художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) , в гравюре «Меланхолия»

На переднем плане изобразил додекаэдр.  

Сальвадор Дали на картине «Тайная вечеря» изобразил Иисуса Христа со своими учениками на фоне огромного прозрачного додекаэдра

Полагают, что четырем геологическим эрам Земли соответствуют четыре силовых каркаса правильных Платоновских тел:

Протозою — тетраэдр (четыре плиты), Палеозою — гексаэдр (шесть плит) ,Мезозою — октаэдр (восемь плит) ,

Кайнозою — додекаэдр (двенадцать плит).

Икосаэдро — додекаэдровая

структура Земли

Существует гипотеза, которую в начале 80-х гг. высказали московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, имеют икосаэдро-додекаэдровую структуру Земли.

24

Тест по теме «Правильные многогранники»

1.Сколько существует видов правильных многогранников?

а) 4; б) бесконечное множество; в) 5; г) 10

2.Как называются правильные многогранники?

а) тела Евклида; в) тела Пифагора;

б) тела Эйлера; г) тела Платона

3.Из скольких правильных треугольников составлен октаэдр?

а) 8; б) 12; в) 6; г) 20

4. Каждая вершина додекаэдра является вершиной…

а) трёх правильных шестиугольников ;

б) трёх квадратов ;

в) трёх правильных пятиугольников ;

г) пяти правильных треугольников

5.Чему равен периметр октаэдра, если его ребро равно а ?

а) 8а; б) 20а; в) 12а; г) 6а

24

ОТВЕТЫ теста по теме «Правильные многогранники»

1. Сколько существует видов правильных многогранников?

в) 5

2. Как называются правильные многогранники?

г) тела Платона

3. Из скольких правильных треугольников составлен октаэдр?

а)8

4. Каждая вершина додекаэдра является вершиной…

в) трёх правильных пятиугольников

5. Чему равен периметр октаэдра, если его ребро равно а?

в) 12а

24

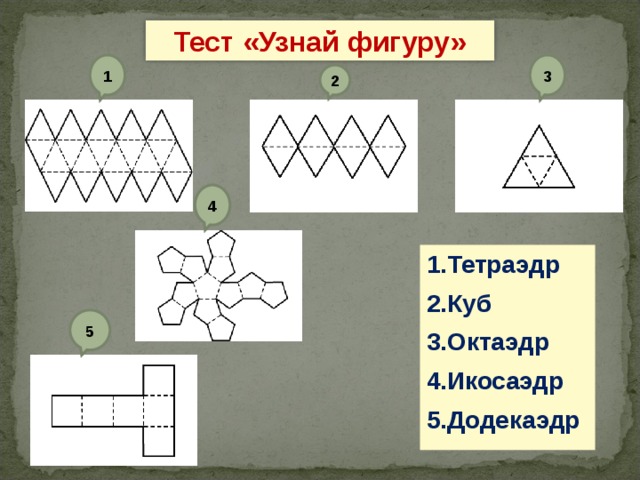
Тест «Узнай фигуру»

1

3

2

4

1.Тетраэдр

2.Куб

3.Октаэдр

4.Икосаэдр

5.Додекаэдр

5

Составление синквейна

1. первая строка – тема, выраженная ОДНИМ словом, обычно именем существительным;

2.вторая строка – описание темы в ДВУХ словах, как правило, именами прилагательными;

3.третья строка – описание действия в рамках этой темы ТРЕМЯ словами, обычно глаголами;

4.четвертая строка – фраза из ЧЕТЫРЕХ слов, выражающая отношение автора к данной теме;

5.пятая строка – ОДНО слово – синоним к первому, на эмоционально-образном или философско-обобщенном уровне повторяющее суть темы.

28

Синквейн

Многогранник

Выпуклый, правильный

Строит, измеряет, восхищает

Поверхность, составленная из многоугольников

Совершенство

Считать несчастным тот день или тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию.

Ян Амос Коменский

• С какими новыми геометрическими телами мы сегодня познакомились?

• Почему Л. Кэрролл так высоко оценил значение этих многогранников?

28

Спасибо за внимание!

 ***

Статья

***

Правильные многогранники

Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.

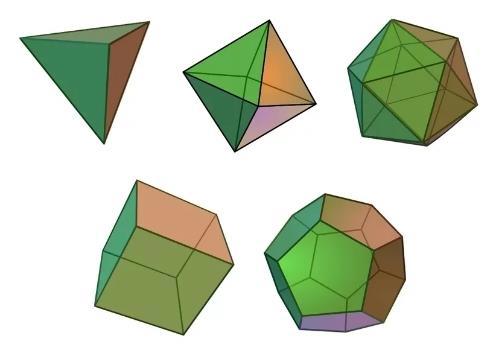
В трёхмерном евклидовом пространстве  существует всего пять правильных многогранников (упорядочены по числу граней):

упорядочены по числу граней):

Изображение	Правильный многогранник	Число вершин	Число рёбер	Число граней	Число сторон у грани	Число рёбер, примыкающих к вершине	Тип пространственной симметрии
	тетраэдр	4	6	4	3	3	Td
	гексаэдр	8	12	6	4	3	Oh
	октаэдр	6	12	8	3	4	Oh
	додэкаэдр	20	30	12	5	3	Ih
	икосаэдр	12	30	20	3	5	Ih

Правильный многогранник может быть комбинаторно описан символом Шлефли {p, q}, где:
p — число рёбер в каждой грани; q — число рёбер, сходящихся в каждой вершине.

Символы Шлефли для правильных многогранников приведены в следующей таблице:

Много-гранник	Вер- шины	Рёб-ра	Гра-ни	символ Шлефли
тетраэдр		4	6	4	{3, 3}
гексаэдр (куб)		8	12	6	{4, 3}
октаэдр		6	12	8	{3, 4}
додэкаэдр		20	30	12	{5, 3}
икосаэдр		12	30	20	{3, 5}

Огню соответствовал тетраэдр, 

земле — гексаэдр, 

воздуху — октаэдр, 

воде — икосаэдр. 

Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.

Малый звездчатый додекаэдр

Малый звездчатый октаэдр

***

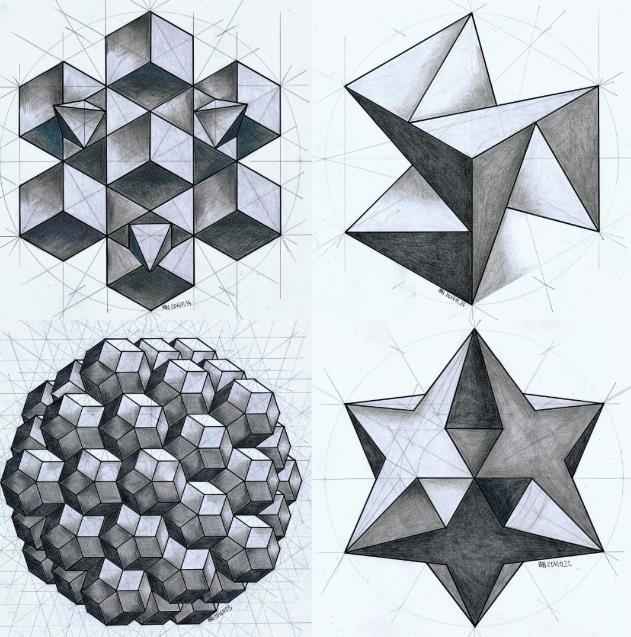
Некоторые примеры более сложных форм

***

P.S.  В статье использованы материалы с сайтов Wiki

* * *

P.P.S. Ссылка на первую книгу на сайте «Author Today»:

https://author.today/work/158738

* * *

Ссылка на вторую книгу на сайте «Author Today»:

https://author.today/work/160692

* * *

Ссылка на третью книгу на сайте «Author Today»:

https://author.today/work/160794

* * *

Ссылка на четвертую книгу на сайте «Author Today»:

https://author.today/work/160793

* * *

План урока:

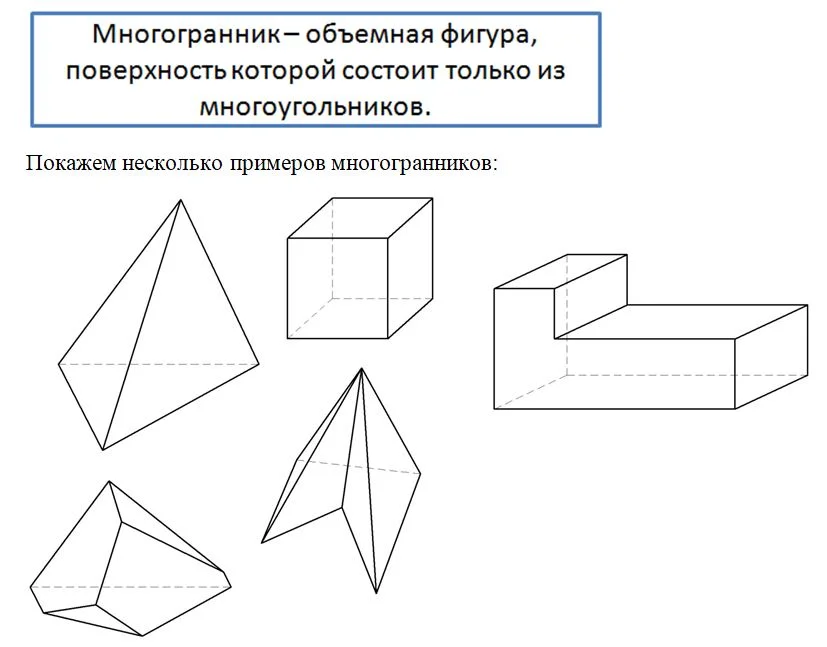
Понятие многогранника

Теорема Эйлера

Призма

Типичные задачи на призмы

Понятие многогранника

Ранее мы уже познакомились с тетраэдром и параллелепипедом. Поверхность тетраэдра состоит из 4 треугольников, а параллелепипеда – из 6 параллелограммов. Они являются частными случаями такой фигуры, как многогранник.

Надо понимать, что под многогранником понимают одновременно как поверхность, составленную из многоуг-ков, так и тот объем, который эта поверхность ограничивает. Иногда, чтобы отличать два этих понятия, используют термин «поверхность многогранника».

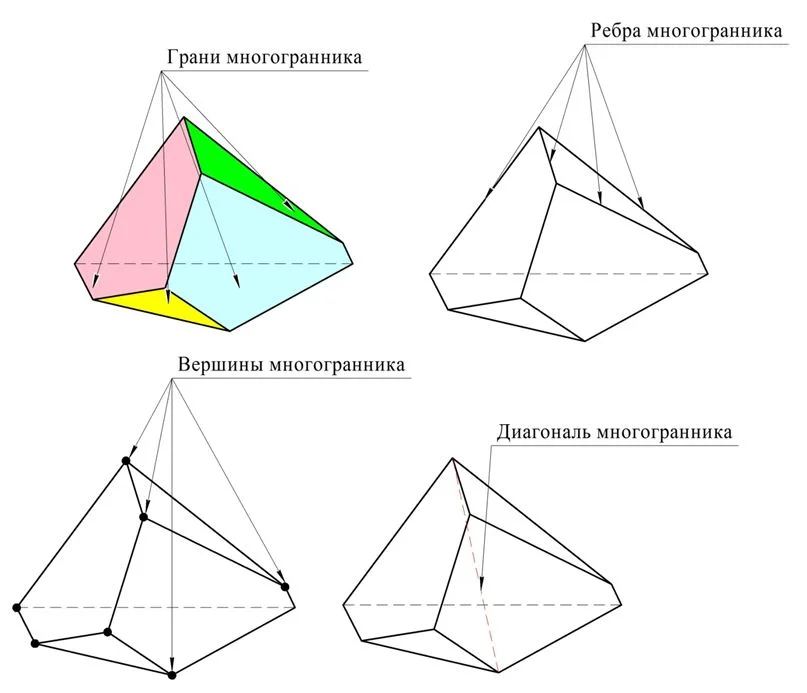
Каждый многоугольник, образующий поверхность многогранника, именуется гранью многогранника. При этом предполагается, что любые две соседние грани находятся в разных плос-тях.

Многоугольники, образующие поверхность многогранника, имеют свои стороны,которые именуют ребрами многогранника. Вершины же этих многоуг-ков именуют вершинами многогранников. Можно утверждать, что ребра – это отрезки, по которым пересекаются соседние грани. В свою очередь вершины – это точки, где пересекаются соседние ребра. Отрезок, соединяющий две вершины, которые не принадлежат одной грани, именуется диагональю многогранника. Важно отметить, что каждое ребро принадлежит ровно 2 граням. Вершина принадлежит как минимум трем граням, однако может принадлежать и большему их числу.

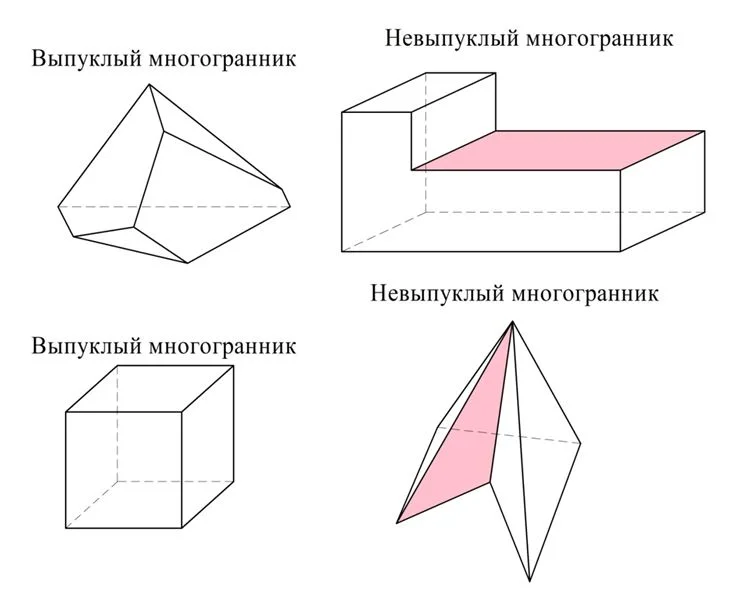
Если все точки многогранника находятся по одну сторону от любой плос-ти, проходящей через какую-либо грань многогранника, то он называется выпуклым. В противном случае, если через одну из граней проходит плос-ть, «разрезающая» многогранник на две других фигуры, многогранник именуют невыпуклым. На бытовом уровне это означает, что выпуклый многогранник можно поставить на ровную поверхность (например, стол) на любую грань. А вот у невыпуклого многогранника найдется такая грань, на которую его поставить нельзя. Покажем несколько примеров:

На рисунке у невыпуклых многогранников красным цветом показаны плос-ти, которые рассекают многогранник. На эти грани не получится «поставить» многогранник – будет мешать выступающая часть. Заметим, что в выпуклом многограннике всякая диагональ лежит внутри фигуры. А вот у невыпуклого многогранника можно соединить вершины отрезком, лежащим вне объема фигуры. Добавим, что у выпуклого многогранника каждая грань обязательно является выпуклым многоугольником.

Теорема Эйлера

У каждого многогранника можно подсчитать количество граней, вершин и ребер. Например, у тетраэдра 4 грани, 4 вершины и 6 ребер. В свою очередь у параллелепипеда уже 6 граней, 8 вершин и 12 граней. Есть ли какая-то взаимосвязь между этими числами?

Можно заметить, что если у тетраэдра сложить число вершин и граней, а далее вычесть из суммы количество ребер, то получится число 2:

4 + 4 — 6 = 2

Если выполнить такие же действия для параллелепипеда, то снова получится двойка:

6 + 8 — 12 = 2

Оказывается, это не просто совпадение. Для любого выпуклого многогранника справедлива теорема Эйлера:

Мы не будем доказывать эту теорему, так как ее доказательство достаточно сложное. Отдельно отметим, что для невыпуклых многогранников эта теорема может и не выполняться.

Задание. Известно, что некоторый выпуклый многогранник состоит из 20 граней и имеет 30 ребер. Сколько у него вершин?

Решение. Запишем теорему Эйлера:

Задание. Поверхность выпуклого многогранника составлена из 12 пятиугольников. Сколько у такого многогранника ребер и вершин?

Решение. У многогранника будет ровно 12 граней. Попробуем подсчитать количество ребер. Так как каждая представляет собой пятиугольник, то все вместе они имеют 12•5 = 60 ребер. Однако при этом мы каждое ребро подсчитали дважды, ведь любое ребро принадлежит строго 2 граням. То есть на самом деле есть только 60:2 = 30 ребер. По теореме Эйлера легко подсчитаем и количество вершин:

Задание. Выпуклый многогранник имеет 8 граней, из них 4 – это четырехугольники, а ещё 4 – пятиугольники. Сколько у него ребер и вершин?

Решение. Как и в предыдущей задаче, снова сложим количество сторон всех граней:

Задание. Существует ли выпуклый многогранник, каждая грань которого является шестиугольником?

Предположим, что такой многогранник существует, и у него Г граней. Тогда его грани имеют в сумме 6Г сторон. Но каждая из этих сторон будет ребром ровно для 2 граней, поэтому всего будет 3Г ребер:

Теперь вспомним, что в каждой вершине сходятся не менее трех ребер. Значит, если мы посчитаем все ребра, выходящие из каждого ребра, то получим величину, не меньшую 3В. Но, так как каждое ребро проходит строго через 2 вершины, мы снова подсчитали ребра дважды. То есть количество ребер будет не меньше 3/2В, или 1,5В:

Это неравенство противоречит полученному ранее равенству Р = 3Г. Противоречие показывает, что на самом деле не может существовать выпуклый многогранник, каждая грань которого – шестиугольник, ч. т. д.

Примечание. Аналогично можно продемонстрировать, что не может существовать и выпуклый многогранник, поверхность которого состоит из многоуг-ков, каждый из которых имеет не менее 6 сторон. Другими словами, любой выпуклый многогранник имеет хотя бы одну грань, которая является треугольником, четырехугольником или пятиугольником.

Призма

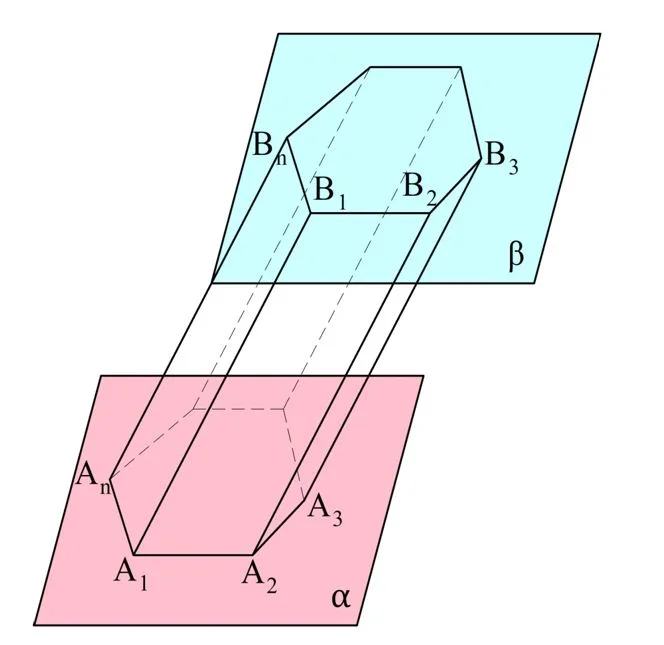
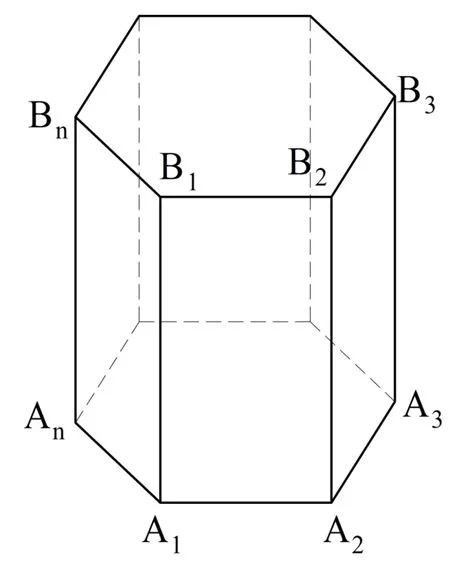
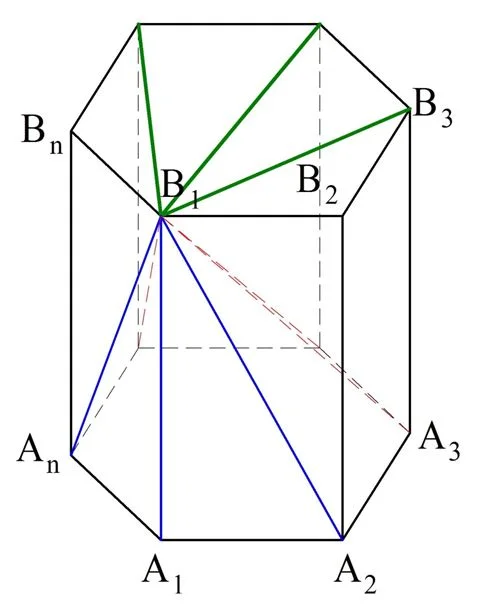
Пусть в некоторой плос-ти α есть n-угольник с вершинами А₁, А₂, А₃,…, А_n. Пусть в другой плос-ти β, которая параллельна α, есть равный ему многоуг-к В₁В₂В₃…В_n, причем отрезки А₁В₁, А₂В₂, А₃В₃…, А_nВ_n параллельны друг другу:

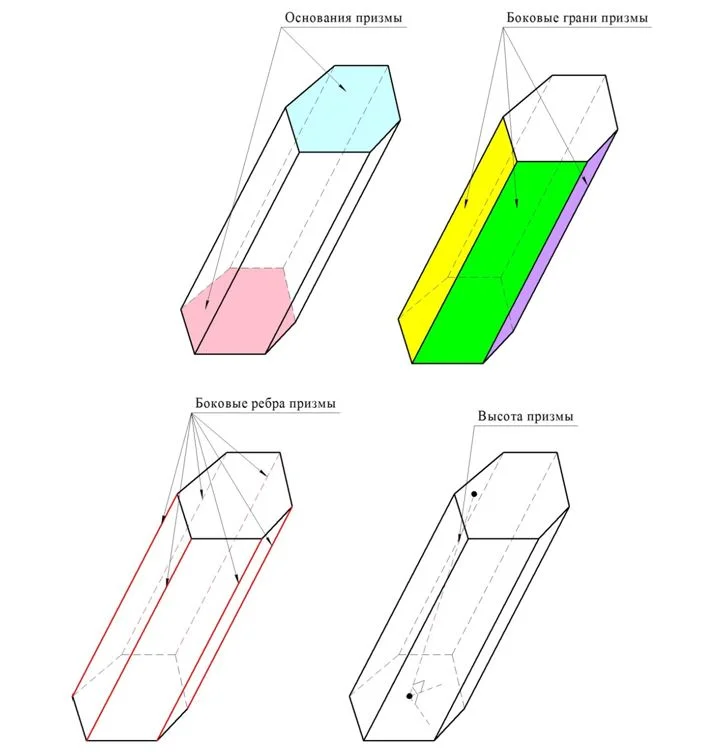
В результате мы получили геометрическую фигуру, которую именуют призмой. Многоуг-ки А₁А₂А₃…А_n и В₁В₂В₃…В_n именуются основаниями призмы, а все остальные грани – это боковые грани призмы. Можно доказать, что боковые грани – это параллелограммы. Действительно, в четырехуг-ке А₁А₂В₂В₁ стороны А₁В₁ и А₂В₂ параллельны по условию. Также они равны по теореме 12 из этого урока. Это и значит, что А₁А₂В₂В₁ – это параллелограмм (по одному из его признаков). Тоже самое можно доказать и для остальных боковых граней. Теперь мы можем сформулировать определение призмы:

Ребра призмы, не принадлежащие основанию, именуются боковыми ребрами призмы. Ясно, что любые два соседних ребра параллельны, ведь они являются сторонами параллелограммами. Но тогда по свойству транзитивности параллельности получается, что вообще любые два боковых ребра параллельны. Если из какой-нибудь точки основания построен перпендикуляр к противоположному основанию, то он именуется высотой призмы:

Естественно, что высота перпендикулярна обоим основаниям. Возможна ситуация, когда высота падает не на основание, а на какую-нибудь точку плос-ти основания, не находящуюся внутри него. Ясно, что все высоты призмы имеют одинаковую длину независимо от того, через какие точки они проведены, ведь высота по своей сути – это расстояние между плос-тями оснований.

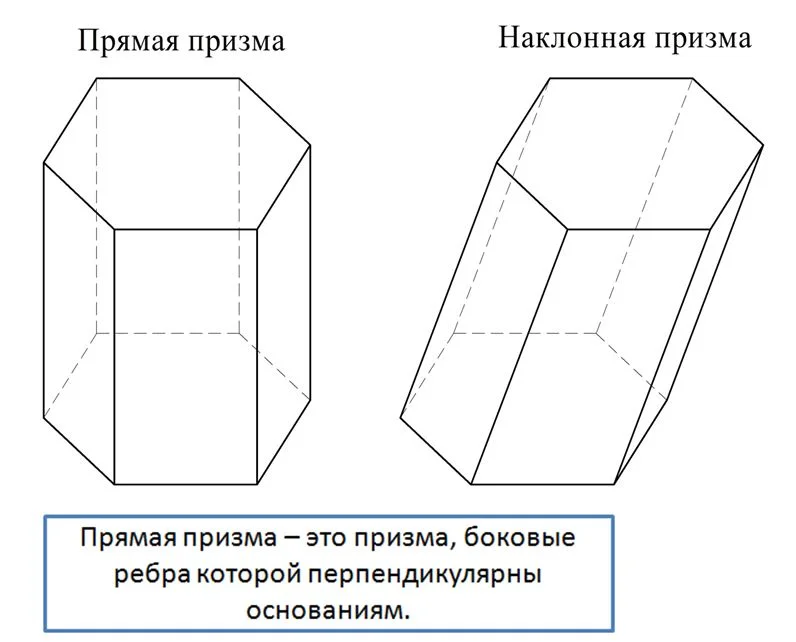
Особый интерес вызывают призмы, где боковые ребра и основания перпендикулярны друг другу. Такие призмы именуются прямыми. Ясно, что у них боковые грани оказываются уже не просто параллелограммами, а уже прямоуг-ками. При этом любое боковое ребро одновременно является и высотой. Все остальные призмы именуют наклонными.

Если в основании призмы находится n-угольник, то призму называют n-угольной. В частности, в основании треугольной призмы лежит треуг-к, в основании десятиугольной призмы находится десятиугольник и т. д. Наконец, в особую группу выделяют прямые призмы, основаниями которых представляют собой правильные многоуг-ки. Их так и именуют – правильные призмы.

Если сложить площадь всех граней призмы, то получится сумма, которую именуют площадью полной поверхности призмы. Обычно ее обозначают как S_полн. Если же складываются только площади боковых граней, то в сумме получается площадь боковой поверхности призмы, обозначаемая как S_бок. Если площадь основания призмы обозначить как S_осн., то справедлива будет очевидная формула:

Действительно, пусть есть прямая призма с основаниями А₁А₂…А_n и B₁B₂…B_n:

Так как ее боковые ребра перпендикулярны основаниям, то они должны быть перпендикулярны и тем ребрам, которые образуют основания. Это значит, каждая боковая грань – это прямоуг-к. При этом боковые ребра – это одновременно и высоты призмы. Тогда площадь боковых граней вычисляется так:

Отметим наконец, что параллелепипед можно считать частным случаем призмы, а прямоугольный параллелепипед – частным случаем прямой призмы.

Типичные задачи на призмы

Призмы нередко встречаются в заданиях ЕГЭ, поэтому важно уметь решать задачи, в которых используются эти фигуры.

Задание. Сколько диагоналей имеет n-угольная призма?

Решение. В любом многограннике диагональ соединяет точки, не лежащие на одной грани. Каждая вершина призмы принадлежит одному из оснований, причем в n-угольной призме каждому основанию принадлежат n вершин.

Возьмем произвольную вершину на одном из оснований и посчитаем, сколько диагоналей из нее можно провести. Если соединять ее отрезками с другими вершинами, принадлежащему тому же основанию, то получатся диагонали грани, но не диагонали призмы (зеленые линии на рисунке):

Значит, остается только провести прямые к тем вершинами, которые лежат в другом основании. Так как в другом основании находятся n вершин, то и отрезков будет ровно n. Однако три из них не будут диагоналями (показаны на рисунке синим цветом), так как будут либо являться одним из ребер призмы либо одной из диагоналей. Получается, что из вершины можно провести (n – 3) диагоналей. Так как в основании находятся n вершин, то всего можно построить n•(n– 3) диагоналей.

Ответ: n•(n – 3) диагоналей.

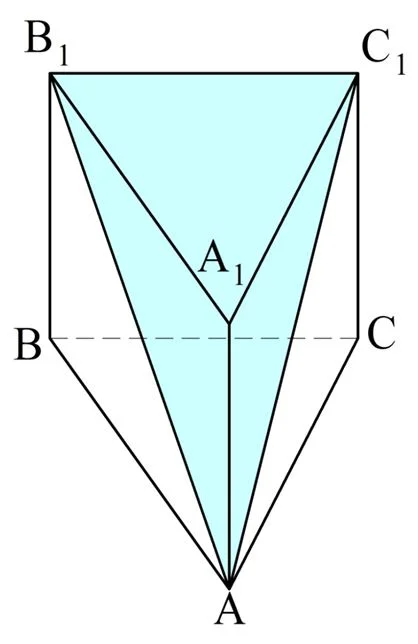
Задание. Длина стороны правильной треугольной призмы составляет 8 см, а ее боковое ребро имеет длину 6 см. Через сторону основания проведено сечение, которое пересекает другое основание в противолежащей вершине. Какова площадь этого сечения?

Решение. Выполним построение по условию задачи:

Здесь сечение проведено через ребро В₁С₁ и противолежащую ей вершину А. Призма правильная, поэтому ее основания ∆АВС и ∆А₁В₁С₁ – это равносторонние треуг-ки, и все их стороны равны 8 см. По определению правильная призма обязательно ещё и прямая. Тогда боковые грани – прямоуг-ки.

∆АВВ₁ – прямоугольный, с помощью теоремы Пифагора мы можем вычислить его гипотенузу АВ₁:

Аналогично можно вычислить, что и диагональ АС₁ также равна 10 см. Вообще в правильных призмах все грани – это равные друг другу прямоуг-ки, поэтому и диагонали у них одинаковы.

Длина ребра В₁С₁ составляет 8 см. Получается, нам надо вычислить площадь равнобедренного ∆АВ₁С₁ с основанием 8 см и боковыми сторонами 10 см. Это можно сделать множеством способов. Самый простой из них заключается в использовании формулы Герона. Для ее применения сначала вычислим полупериметр ∆АВ₁С₁:

Задание. В основании призмы находится равносторонний ∆АВС. Ребро АА₁ образует одинаковые углы с ребрами АС и АВ. Докажите, что ребра АА₁ и ВС перпендикулярны и что СС₁В₁В – прямоуг-к.

Решение. Выполняем построение:

По условию ∠А₁АВ и ∠А₁АС одинаковы. Проведем диагонали А₁В и А₁С. В итоге мы получим ∆А₁АВ и А₁АС. У них есть АА₁ – общая сторона, стороны АВ и АС одинаковы (ведь ∆АВС – равносторонний), а углы между ними одинаковы. Значит, ∆А₁АВ и А₁АС равны, и тогда диагонали А₁В и А₁С одинаковы.

Получается, что точка А₁ равноудалена вершин В и С. Аналогично и точка А равноудалена от В и С, ведь АВ и АС одинаковы. Это значит, что и А₁, и А лежат на серединных перпендикулярах, проведенных к отрезку ВС:

Обозначим середину ВС как Н, тогда НА₁ и НА – серединные перпендикулярны. То есть ВС⊥АН и ВС⊥А₁Н. Но это значит (по признаку перпендикулярности прямой и плос-ти), что ВС перпендикулярен всей плос-ти АНА₁. Из этого вытекает, что ВС⊥АА₁, ч. т. д.

Осталось показать, что грань СС₁В₁В – это прямоуг-к. Так как ВВ₁||АА₁, и ВС⊥АА₁, то и ВС⊥ВВ₁. Значит в параллелограмме СС₁В₁В (напомним, что в призме все боковые грани – параллелограммы) есть прямой угол. Это значит, что он является прямоуг-ком, ч. т. д.

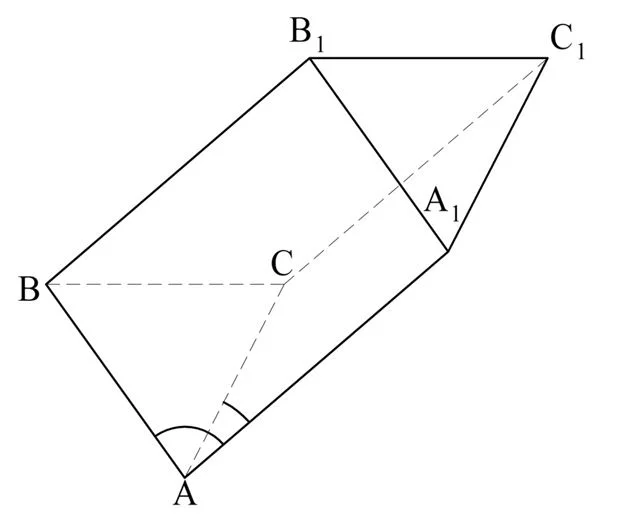
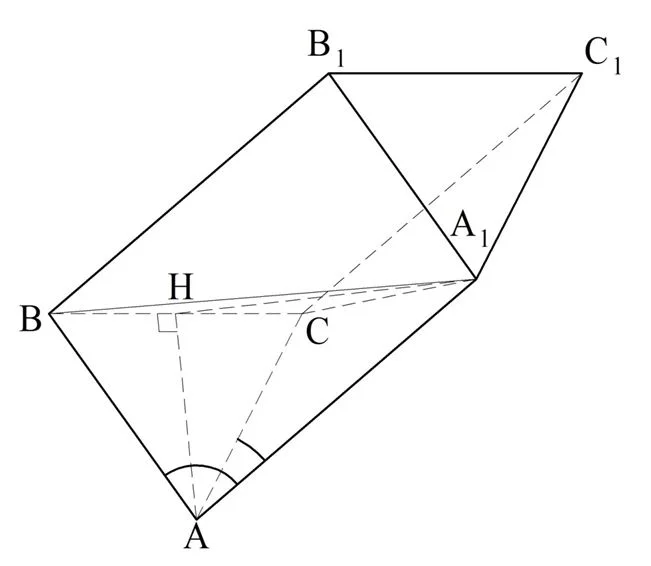
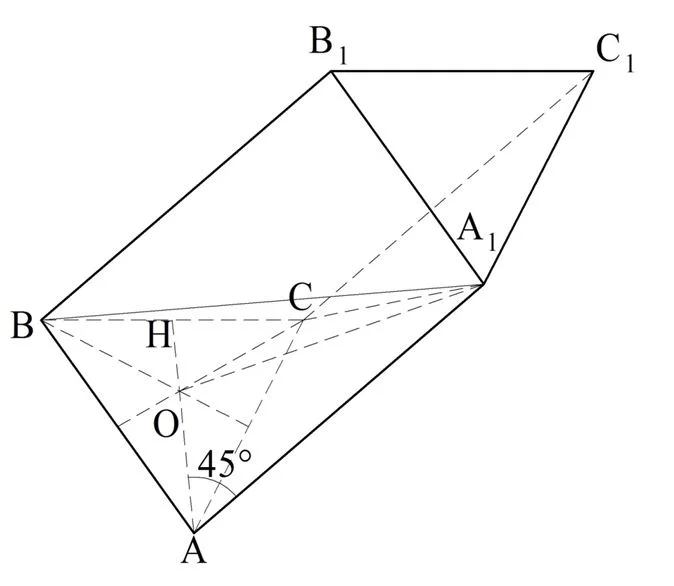
Задание. Призма АВСА₁В₁С₁ – наклонная. Известно, что АС = АВ = 13 и ВС = 10. Боковые ребра призмы образуют с основанием АВС угол 45°. Проекция точки А₁ на плос-ть АВС совпадает с точкой пересечения медиан в ∆АВС. Какова площадь грани СС₁В₁В?

Решение. Снова выполняем построение:

Здесь О – это проекция точки А₁ и одновременно точка пересечения медиан. H– середина отрезка ВС, то есть АН – как раз одна из медиан. Заметим, что так как ∆АВС равнобедренный, и ВС – это его основание, то АН одновременно является и высотой, то есть ∠ВНА = 90°. Раз Н – середина ВС, то ВН будет вдвое короче ВС:

Напомним, точка пересечения медиан делит их в отношении 2:1, поэтому мы можем найти ОА:

Понятно, что ОА – это проекция прямой ОА на плос-ть АВС. Тогда угол между ребром АА₁ и плос-тью АВС, по условию равный 45° – это ∠ОАА₁.

Из прямоугольного ∆АОА₁ с помощью тригонометрии мы найдем длину ребра АА₁:

Теперь покажем, что грань СС₁В₁В – прямоуг-к. Ясно, что ОА₁⊥ВН, ведь ОА₁ – перпендикуляр ко всей плос-ти АВС. Но также ВН⊥АН. Значит, ВН перпендикулярен плос-ти АОА₁, и, в частности, перпендикулярен ребру АА₁. Но тогда и ВВ₁⊥ВН, ведь ВВ₁||АА₁. Значит, грань СС₁В₁В – прямоуг-к, ведь в ней есть прямой угол. Для нахождения площади прямоуг-ка надо перемножить две его смежные стороны:

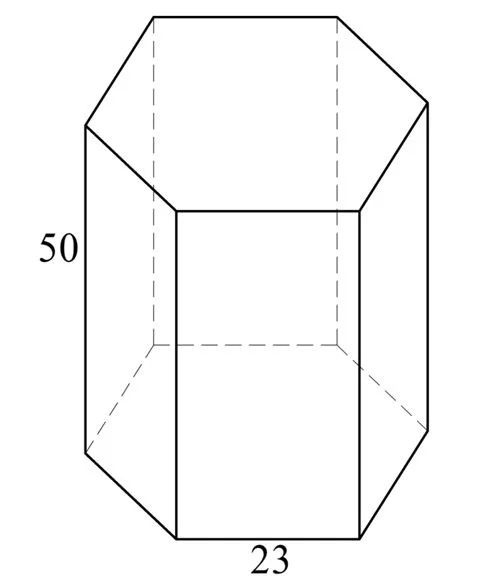
Задание. Ребро при основании правильной 6-угольной призмы имеет длину 23, а боковое ребро равно 50. Вычислите площадь поверхности призмы (и полную, и боковую).

Решение.

Сначала найдем площадь и периметр основания. Формулы для правильных многоуг-ков мы уже изучали:

Здесь а – сторона шестиугольника, R и r – радиусы описанной и вписанной окружности, n– число сторон шестиугольника. Во второй формуле мы использовали известный факт, что длина стороны правильного 6-угольника совпадает с радиусом описанной около него окружности.

Далее вычисляем площадь боковой поверхности:

Добавив к этому значению удвоенную площадь поверхности основания, найдем и полную площадь призмы:

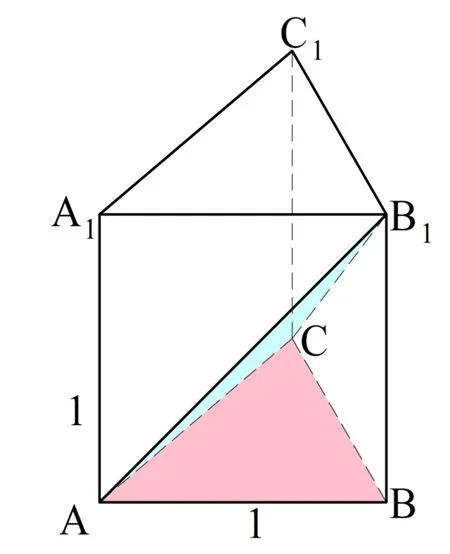
Задание. В правильной треугольной призме АВСА₁В₁С₁, у которой все ребра одинаковы и равны единице, вычислите угол между гранью АВС и сечением АСВ₁:

Решение. Вспомним, что для нахождения угла между плос-тями необходимо построить в этих плос-тях перпендикуляры к линии их пересечения, причем эти перпендикуляры должны падать на одну и ту же точку.

Пересекаются плос-ти АВС и АСВ₁ по грани АС. Заметим, что и ∆АВС, и ∆АСВ₁ – равнобедренные, причем у них общее основание АС. Действительно, АВ = ВС, так как в основании правильной призмы лежит равносторонний треуг-к, а АВ₁ = СВ₁, так как это диагонали равных граней АВВ₁А₁ и ВСС₁В₁.

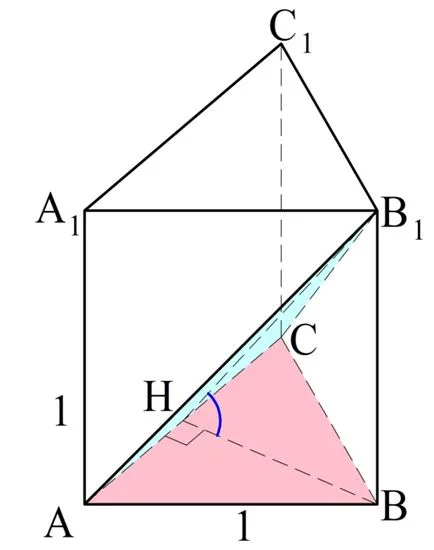
Если мы отметим середину отрезка АС (например, точкой Н) и соединим ее с В и В₁, то мы получим две медианы НВ и НВ₁, которые одновременно будут и высотой. Это значит, что именно ∠ВНВ₁ и будет искомым углом между плос-тями:

Осталось найти ∠ВНВ₁. Длину ВВ₁ мы уже знаем, она составляет 1.

АН вдвое короче АС:

Теперь заметим, что ∆НВВ₁ – прямоугольный, поэтому для него можно использовать тригонометрию:

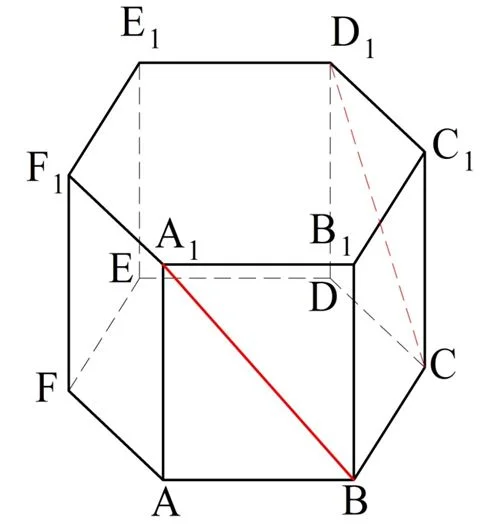
Задание. Найдите угол между прямыми А₁D и СD₁ в правильной призме, показанной на рисунке:

Все ребра этой призмы равны единице.

Решение. Сначала внимательно рассмотрим верхнее основание призмы. Так как оно представляет собой правильный многоуг-к, то вокруг него можно описать окружность. Обозначим центр этой окружности как О и проведем радиусы к вершинам:

Так как в правильном шестиуг-ке радиус описанной окружности равен стороне шестиугольника, то получается, что ∆А₁ОВ₁, ∆В₁ОС₁ и ∆С₁ОD₁ – равносторонние. Тогда ∠А₁ОВ₁, ∠B₁OC₁ и ∠С₁ОD₁ составляют по 60°. Тогда ∠А₁ОD₁ равен 180°, то есть точки А₁, О и D₁ находятся на одной прямой А₁D₁. Также заметим, что эта прямая параллельна ребру В₁С₁, ведь ∠D₁OC₁и ∠ОС₁B₁ являются накрест лежащими для этих прямых (при секущей ОС₁) и при том они одинаковы. Так как отрезки А₁О и D₁O как стороны равносторонних треуг-ков равны 1, то

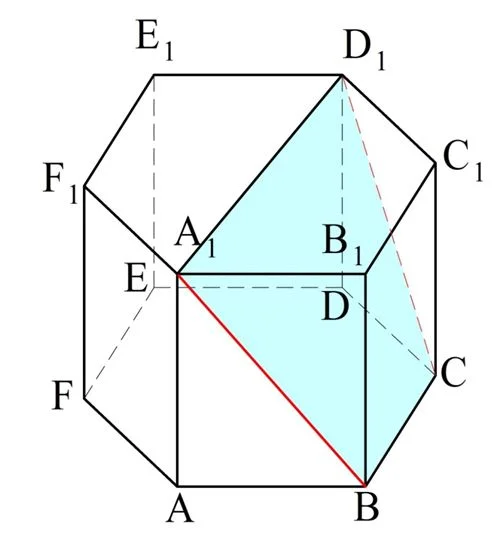
Теперь вернемся к призме:

Так как А₁D₁||В₁С₁ и В₁С₁||ВС, то и А₁D₁||ВС. Это значит, что через А₁D₁ и ВС можно провести плос-ть, в которой будут лежать и интересующие нас прямые А₁В и СD₁. Для нахождения угла между ними надо рассмотреть четырехуг-к А₁D₁CB. Раз А₁D₁||ВС, то этот четырехуг-к является трапецией.

Далее найдем длину А₁В. Для этого используем ∆АВА₁:

Аналогично из ∆СDD₁ можно определить, что СD₁ имеет такую же длину. Это значит, что А₁D₁CB – равнобедренная трапеция.

Теперь рассмотрим отдельно эту трапецию, чтобы найти искомый угол:

Опустим из вершин трапеции В и С перпендикуляры на А₁D₁. В итоге получим прямоуг-к ВСРН, где

Сегодня мы более детально изучили понятие многогранника и познакомились с новой геометрической фигурой – призмой. Призма довольно часто встречается в задаче С2 на ЕГЭ. Также мы узнали о теореме Эйлера, из которой вытекают некоторые важные факты. Один из них заключается в том, что не бывает выпуклых многогранников, у которых ни одна грань не является треуг-ком, четырехуг-ком или пятиуг-ком.