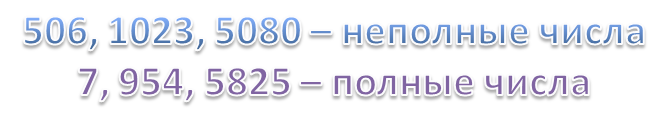|
0 / 0 / 0 Регистрация: 02.09.2014 Сообщений: 32 |
|
|
1 |
|
Найти число десятков и единиц в двузначном числе08.09.2014, 17:31. Показов 40649. Ответов 8
Дано двузначное число. Найти:
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
08.09.2014, 17:31 |
|
Ответы с готовыми решениями:
Найти число десятков 8 |
|
Котовчанин 942 / 482 / 200 Регистрация: 16.02.2010 Сообщений: 3,338 Записей в блоге: 37 |
|
|
08.09.2014, 17:57 |
2 |
|
И снова вопрос встречный — где код?
0 |
|
0 / 0 / 0 Регистрация: 02.09.2014 Сообщений: 32 |
|
|
08.09.2014, 18:03 [ТС] |
3 |
|
а нету кода, есть пример по какому написать, но нечего не понятно, кто бы написал
0 |
|
3 / 3 / 2 Регистрация: 06.09.2014 Сообщений: 82 |
|
|
08.09.2014, 18:03 |
4 |
|
Тамика, Не по теме: ну учитывая тему *Напишите*, я полагаю что кода не будет =)
0 |
|
Котовчанин 942 / 482 / 200 Регистрация: 16.02.2010 Сообщений: 3,338 Записей в блоге: 37 |
|
|
08.09.2014, 18:06 |
5 |
|
а нету кода, есть пример по какому написать, но нечего не понятно, кто бы написал ) Так спрашивайте чего не понятно-то. Мы люди не гордые, поможем, ответим на вопросы. Добавлено через 20 секунд Не по теме:
Тамика, ну учитывая тему *Напишите*, я полагаю что кода не будет =) Это точно.:)))
0 |
|
MousePro 50 / 31 / 4 Регистрация: 25.04.2013 Сообщений: 366 |
||||
|
08.09.2014, 18:11 |
6 |
|||
0 |
|
Тамика Котовчанин 942 / 482 / 200 Регистрация: 16.02.2010 Сообщений: 3,338 Записей в блоге: 37 |
||||
|
08.09.2014, 18:14 |
7 |
|||
0 |
|
zss Модератор 13111 / 10381 / 6209 Регистрация: 18.12.2011 Сообщений: 27,767 |
||||
|
08.09.2014, 18:17 |
8 |
|||
|
а нету кода Ну как же нету! Можете же написать
Тем самым покажете, что работали над задачей
0 |
|
_Ivana 4816 / 2276 / 287 Регистрация: 01.03.2013 Сообщений: 5,944 Записей в блоге: 27 |
||||||||
|
08.09.2014, 22:16 |
9 |
|||||||
|
Добавлено через 39 минут
Добавлено через 32 минуты
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
08.09.2014, 22:16 |
|
9 |
На чтение 4 мин Просмотров 5.4к.
Содержание
- Числа от 1 до 100
- Однозначные и двузначные числа
- Состав двузначного числа
- Сравнение двузначных чисел
- Счёт десятками
- Действия с десятками и единицами
- Ответ или решение 2
- Составим алгоритм и будем его придерживаться в решении задачи
- Найдем двухзначное число в котором число единиц на 8 больше чем число десятков
- Задание №1
- Правило
- Задание № 2
- Задание № 3
- Задача № 1
- Задача № 2
- Задание № 4
Числа от 1 до 100
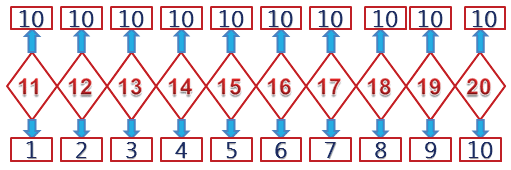
Предыдущее и последующее число
Предыдущее число – то число, которое при счете следует перед данным числом.
56 , 57
Последующее число – то число, которое при счете называют сразу после данного числа.
56, 57
Однозначные и двузначные числа
Вспомни, что каждая цифра в записи занимает определенное место.
Единицы стоят на первом месте справа.
Десятки стоят на втором месте справа.
Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.
Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.
Самое маленькое однозначное число – .
Самое большое однозначное число – 9.
Самое маленькое двузначное число – 10.
Самое большое двузначное число – 99.
Состав двузначного числа
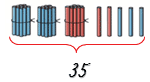
Всего на рисунке 35 палочкек.
35 = 30 + 5
Состав числа 35 – 3 дес. 5 ед.
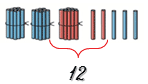
Красных палочек 12.
12 = 10 + 2
Состав числа 12 – 1 дес. 2 ед.
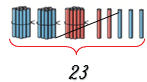
Синих палочек всего 23.
23 = 2 дес. 3 ед.
23 = 20 + 3
Состав числа 23 – 2 дес. 3 ед.
Теперь научимся представлять числа в виде суммы разрядных слагаемых.
Какие разряды выделяют в двузначных числах?
В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:
В числе 35 три десятка и 9 единиц:
Сравнение двузначных чисел
Числа 42 и 24 похожи тем, что в их записи использованы одинаковые цифры: цифра 4 и цифра 2. Но цифра 4 для числа 42 означает десятки, а для 24 – единицы, цифра 2 для числа 42 означает единицы, а для 24 – десятки.
| Число | 42 | 24 |
| Количество десятков | 4 | 2 |
| Количество единиц | 2 | 4 |
1. Сравнение двузначных чисел всегда начинается с десятков.
2. Если количество десятков одинаково, тогда переходят к сравнению единиц.
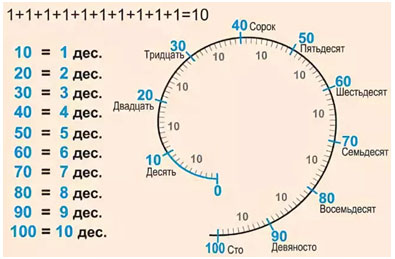
Круглые числа
Числа, которые оканчиваются на 0, называются круглыми. – 60, 30, 20.
В разряде единиц у круглого числа – число 0. – 70, 90, 40.
10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
1 дес. + 4 дес. = 5 дес.
5 дес. = 50, значит,
10 + 40 = 50
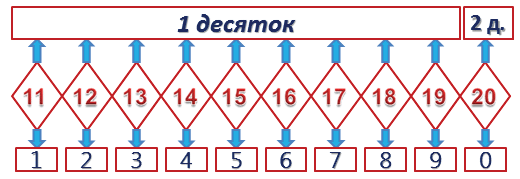
Счёт десятками
Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.
Десятками можно считать:

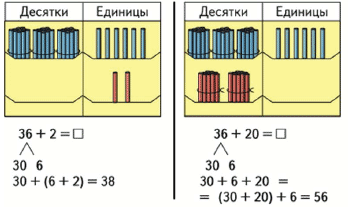
Действия с десятками и единицами
Как решить пример 34 + 25?
34 – это 3 дес. и 4 ед.
25 – это 2 дес. и 5 ед.
3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.
Можно записать короче:
Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:
Сначала складываю единицы:
Теперь складываю десятки:
Запись решения выглядит так:
34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59
Десятки складываются с десятками.
Единицы складываются с единицами.
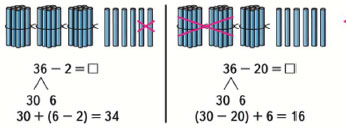
Как решить пример 38 – 16?
Число 38 – можно представить как 3 дес. и 8 ед.
Число 16 – это 1 дес. 6 ед.
3 дес. 8 ед. – 1 дес. 6 ед. = 2 дес. 2 ед.
38 – 16 = (30 – 10) + (8 – 6) = 20 + 2 = 22
Можно рассуждать так:
Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.
38 – 16 = 22
Десятки вычитаются из десятков.
Единицы вычитаются из единиц.
Мы рассмотрели случаи устных вычислений с двузначными числами.
Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.
Поделись с друзьями в социальных сетях:
Ответ или решение 2
Из условия известно, что нам задано двухзначное число на которое наложено условие, что число единиц на 8 больше чем число десятков.
Составим алгоритм и будем его придерживаться в решении задачи
- первым действием мы вспомним понятие двухзначного числа в математике и из каких разрядов оно состоит;
- введем переменные a и b, обозначив ими соответственно единицы и десятки двухзначного числа;
- с помощью уравнения с двумя переменными запишем условие, что число единиц на 8 больше числа десятков;
- методом подбора решим полученное уравнение с двумя переменными;
- запишем ответ.
Найдем двухзначное число в котором число единиц на 8 больше чем число десятков
Давайте следовать составленному алгоритму и вспомним понятие двухзначного числа в математике.
Двухзначными числами в математике называются числа, которые состоят из двух цифр.
Это цифры от 10 до 99.
Двухзначное число состоит из разряда единиц, которые принимают значение от 0 до 9 и десятков — они принимают значение от 10, 20, 30 до 90.
Введем переменные обозначив за a число десятков, а за b число единиц.
То есть наше число должно иметь вид ab.
В условии сказано, что число единиц должно быть больше на 8 числа десятков.
С помощью введенных переменных это можно записать так:
то есть: b – a = 8.
В результате мы получили уравнение с двумя переменными.
Решать уравнение будем методом подбора.
Числа a и b могут принимать значения от 0 до 9.
Под это условие подходит только число такая комбинация единиц и десятков как:
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Рис. 1. Связь разрядов чисел (Источник)
Задание №1
1. Что будет за число, если в нём 1 сотня и 2 десятка?
2. Сколько всего десятков в этом числе?
3. Выразите число 120 в единицах.
Решение: 1. Число, в котором одна сотня и два десятка, – это 120.
2. Одна сотня – это десять десятков. Ещё в этом числе два десятка. Всего двенадцать десятков.
3. 120 – это 100 единиц и 20 единиц. Получается 120 единиц.
Правило
Чтобы определить общее число единиц (десятков, сотен), необходимо все разрядные единицы перевести в нужные единицы разряда и полученные результаты сложить.
Задание № 2
1. Сколько всего десятков в числе 150?
2. Сколько десятков в числе 270?
3. Сколько всего десятков в числе 400?
4. Сколько всего сотен в числе 300?
5. Сколько всего сотен в числе 900?
Решение: 1. В числе 150 одна сотня. 1 сот. = 10 дес. Также в числе 5 дес. Общее число десятков – 15.
2. В числе 270 две сотни. 2 сот. = 20 дес. Также в числе 7 дес. Общее число десятков – 27.
3. В числе 400 четыре сотни. 4 сот. = 40 дес. Всего 40 десятков.
4. В числе 300 три сотни. Всего 3 сотни.
5. В числе 900 девять сотен.
Задание № 3
1. Сколько единиц составляет 25 десятков?
2. Сколько всего единиц составляет 5 сотен?
Решение: 1. В 1 десятке 10 единиц. В 25 десятках 250 единиц.
2. 1 сотня = 100 единиц. Тогда в пяти сотнях всего 500 единиц.
Задача № 1
Рост мальчика (рис. 2) – 1 м 27 см. Сколько это сантиметров?
Рис. 2. Рост мальчика (Источник)
Решение: 1. Для того чтобы ответить на вопрос, надо вспомнить, что в 1 м = 100 см. Тогда к 100 см добавим 27 и получим 127 см.
Задача № 2
Ширина окна – 150 см. Помоги Микки (рис. 3) определить, сколько это дециметров?
Рис. 3. Микки и окно (Источник)
Решение: 1. 1 дм = 10 см
2. В числе 150 десять и пять десятков, получаем 15 дм.
Задание № 4
Запиши пять чисел (рис. 4), каждое из которых содержит 37 десятков. Сколько таких чисел можно записать?
Решение: 1 37 десятков – это число 370. Если менять количество единиц, то количество десятков не изменится, поэтому запишем 370, 371, 372, 373, 374.
2. Всего таких чисел можно записать десять: 370, 371, 372, 373, 374, 375, 376, 378, 379.
Список литературы
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012. – 112 с.: ил. – (Школа России).
- Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. – М.: ВЕНТАНА-ГРАФ.
- Петерсон Л.Г. Математика, 3 класс. – М.: Ювента.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012., ст. 51 № 1–5.
- Назови правило, по которому можно определить общее число единиц или десятков, или сотен в числе.
- Сколько можно написать трёхзначных чисел, у которых 52 десятка?
- * Сколько единиц составляет семь сотен? А сколько единиц в 70 десятках? Сравни полученные числа.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
“>
пятница, 20 марта 2020 г.
Задача №3462. Число десятков двузначного числа
Дано двузначное число. Найдите число десятков в нем.
Входные данные
Вводится единственное число (гарантируется, что оно соответствует условию задачи).
Выходные данные
Выведите ответ на задачу.
Ответ:
a = int(input())
print(a//10)Комментариев нет:
Отправить комментарий
Задача №3477. Улитка
Улитка ползет по вертикальному шесту высотой h метров, поднимаясь за день на a метров, а за ночь спускаясь на b метров. На какой де…

-
Дано целое число n. Выведите следующее за ним четное число. Задачу необходимо решить целочисленными операциями без использования условн…
-
Расставьте скобки в выражении a and b or not a and not b в соответствии с порядком вычисления выражения (приоритетом операций…
-
Из передачи “Здоровье” Аня узнала, что рекомендуется спать хотя бы A часов в сутки, но пересыпать тоже вредно и не стоит спать более…
Двузначное число можно записать в виде 10*а + к, где а — число десятков, к — число единиц. По условию а=2/3 к или к = 1,5*а. Если запишем это число в обратном порядке, то получим число 10*к + а. По условию 10*к + а = 10*а + к + 18. Подставляем вместо к, 1,5*а получим уравнение: 10*1,5*а + а = 10*а + 1,5*а + 18 или 4,5*а = 18. Решаем его и получим значение а = 4. Тогда к = 1,5*4 = 6. Значит первоначальное двузначное число равно 46. Проверяем: 46 + 18 = 64.
Это решение более универсальное. Например, если в условии было бы сказано, что число записанное в обратном порядке на 9 больше, то мы быстро получили бы ответ — 23 (23 + 9 = 32).
Что такое число десятков и число единиц
Предыдущее число – то число, которое при счете следует перед данным числом.
56 , 57
Последующее число – то число, которое при счете называют сразу после данного числа.
56, 57
Однозначные и двузначные числа
Вспомни, что каждая цифра в записи занимает определенное место.
Единицы стоят на первом месте справа.
Десятки стоят на втором месте справа.
Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.
Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.
Самое маленькое однозначное число – .
Самое большое однозначное число – 9.
Самое маленькое двузначное число – 10.
Самое большое двузначное число – 99.
Состав двузначного числа
Всего на рисунке 35 палочкек.
35 = 30 + 5
Состав числа 35 – 3 дес. 5 ед.
Красных палочек 12.
12 = 10 + 2
Состав числа 12 – 1 дес. 2 ед.
Синих палочек всего 23.
23 = 2 дес. 3 ед.
23 = 20 + 3
Состав числа 23 – 2 дес. 3 ед.
Теперь научимся представлять числа в виде суммы разрядных слагаемых.
Какие разряды выделяют в двузначных числах?
В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:
В числе 35 три десятка и 9 единиц:
Сравнение двузначных чисел
Числа 42 и 24 похожи тем, что в их записи использованы одинаковые цифры: цифра 4 и цифра 2. Но цифра 4 для числа 42 означает десятки, а для 24 – единицы, цифра 2 для числа 42 означает единицы, а для 24 – десятки.
| Число | 42 | 24 |
| Количество десятков | 4 | 2 |
| Количество единиц | 2 | 4 |
1. Сравнение двузначных чисел всегда начинается с десятков.
2. Если количество десятков одинаково, тогда переходят к сравнению единиц.
Круглые числа
Числа, которые оканчиваются на 0, называются круглыми. – 60, 30, 20.
В разряде единиц у круглого числа – число 0. – 70, 90, 40.
10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
1 дес. + 4 дес. = 5 дес.
5 дес. = 50, значит,
10 + 40 = 50
Счёт десятками
Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.
Десятками можно считать:

Действия с десятками и единицами

Как решить пример 34 + 25?
34 – это 3 дес. и 4 ед.
25 – это 2 дес. и 5 ед.
3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.
Можно записать короче:
Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:
Сначала складываю единицы:
Теперь складываю десятки:
Запись решения выглядит так:
34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59
Десятки складываются с десятками.
Единицы складываются с единицами.
Число 38 – можно представить как 3 дес. и 8 ед.
Число 16 – это 1 дес. 6 ед.
3 дес. 8 ед. – 1 дес. 6 ед. = 2 дес. 2 ед.
38 – 16 = (30 – 10) + (8 – 6) = 20 + 2 = 22
Можно рассуждать так:
Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.
38 – 16 = 22
Десятки вычитаются из десятков.
Единицы вычитаются из единиц.
Мы рассмотрели случаи устных вычислений с двузначными числами.
Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.
Поделись с друзьями в социальных сетях:
Ответ или решение 2
Из условия известно, что нам задано двухзначное число на которое наложено условие, что число единиц на 8 больше чем число десятков.
Составим алгоритм и будем его придерживаться в решении задачи
- первым действием мы вспомним понятие двухзначного числа в математике и из каких разрядов оно состоит;
- введем переменные a и b, обозначив ими соответственно единицы и десятки двухзначного числа;
- с помощью уравнения с двумя переменными запишем условие, что число единиц на 8 больше числа десятков;
- методом подбора решим полученное уравнение с двумя переменными;
- запишем ответ.
Найдем двухзначное число в котором число единиц на 8 больше чем число десятков
Давайте следовать составленному алгоритму и вспомним понятие двухзначного числа в математике.
Двухзначными числами в математике называются числа, которые состоят из двух цифр.
Это цифры от 10 до 99.
Двухзначное число состоит из разряда единиц, которые принимают значение от 0 до 9 и десятков — они принимают значение от 10, 20, 30 до 90.
Введем переменные обозначив за a число десятков, а за b число единиц.
То есть наше число должно иметь вид ab.
В условии сказано, что число единиц должно быть больше на 8 числа десятков.
С помощью введенных переменных это можно записать так:
то есть: b – a = 8.
В результате мы получили уравнение с двумя переменными.
Решать уравнение будем методом подбора.
Числа a и b могут принимать значения от 0 до 9.
Под это условие подходит только число такая комбинация единиц и десятков как:
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Рис. 1. Связь разрядов чисел (Источник)
Задание №1
1. Что будет за число, если в нём 1 сотня и 2 десятка?
2. Сколько всего десятков в этом числе?
3. Выразите число 120 в единицах.
Решение: 1. Число, в котором одна сотня и два десятка, – это 120.
2. Одна сотня – это десять десятков. Ещё в этом числе два десятка. Всего двенадцать десятков.
3. 120 – это 100 единиц и 20 единиц. Получается 120 единиц.
Правило
Чтобы определить общее число единиц (десятков, сотен), необходимо все разрядные единицы перевести в нужные единицы разряда и полученные результаты сложить.
Задание № 2
1. Сколько всего десятков в числе 150?
2. Сколько десятков в числе 270?
3. Сколько всего десятков в числе 400?
4. Сколько всего сотен в числе 300?
5. Сколько всего сотен в числе 900?
Решение: 1. В числе 150 одна сотня. 1 сот. = 10 дес. Также в числе 5 дес. Общее число десятков – 15.
2. В числе 270 две сотни. 2 сот. = 20 дес. Также в числе 7 дес. Общее число десятков – 27.
3. В числе 400 четыре сотни. 4 сот. = 40 дес. Всего 40 десятков.
4. В числе 300 три сотни. Всего 3 сотни.
5. В числе 900 девять сотен.
Задание № 3
1. Сколько единиц составляет 25 десятков?
2. Сколько всего единиц составляет 5 сотен?
Решение: 1. В 1 десятке 10 единиц. В 25 десятках 250 единиц.
2. 1 сотня = 100 единиц. Тогда в пяти сотнях всего 500 единиц.
Задача № 1
Рост мальчика (рис. 2) – 1 м 27 см. Сколько это сантиметров?
Рис. 2. Рост мальчика (Источник)
Решение: 1. Для того чтобы ответить на вопрос, надо вспомнить, что в 1 м = 100 см. Тогда к 100 см добавим 27 и получим 127 см.
Задача № 2
Ширина окна – 150 см. Помоги Микки (рис. 3) определить, сколько это дециметров?
Рис. 3. Микки и окно (Источник)
Решение: 1. 1 дм = 10 см
2. В числе 150 десять и пять десятков, получаем 15 дм.
Задание № 4
Запиши пять чисел (рис. 4), каждое из которых содержит 37 десятков. Сколько таких чисел можно записать?
Решение: 1 37 десятков – это число 370. Если менять количество единиц, то количество десятков не изменится, поэтому запишем 370, 371, 372, 373, 374.
2. Всего таких чисел можно записать десять: 370, 371, 372, 373, 374, 375, 376, 378, 379.
Список литературы
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012. – 112 с.: ил. – (Школа России).
- Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. – М.: ВЕНТАНА-ГРАФ.
- Петерсон Л.Г. Математика, 3 класс. – М.: Ювента.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012., ст. 51 № 1–5.
- Назови правило, по которому можно определить общее число единиц или десятков, или сотен в числе.
- Сколько можно написать трёхзначных чисел, у которых 52 десятка?
- * Сколько единиц составляет семь сотен? А сколько единиц в 70 десятках? Сравни полученные числа.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
интернет проект BeginnerSchool.ru
С самого детства нас учат считать игрушки, конфетки, яблоки. Люди издревле находили способ подсчитывать урожай, поголовье скота или звезды. Способ образования, названия и записи чисел назвали системой счисления или нумерацией.
Чтобы запомнить, сколько собрали урожая или сколько звезд на небе люди придумали символы. В разных местностях эти символы были разными.
Но с развитием торговли, чтобы понимать обозначения другого народа, люди стали пользоваться наиболее удобными символами. Мы, например, пользуемся арабскими символами. А арабскими они называются потому, что европейцы их узнали от арабов. А вот арабы эти символы узнали от индийцев.
Символы, которые используются для записи чисел, называются цифрами .
Слово цифра пошло от арабского названия числа 0 (сифр). Это очень интересная цифра. Она называется незначащей и обозначает отсутствие чего либо.
На рисунке мы видим тарелку, на которой лежит 3 яблока, и пустую тарелку, на которой нет яблок. В случае с пустой тарелкой мы можем сказать, что на ней 0 яблок.
Остальные цифры: 1, 2, 3, 4, 5, 6, 7, 8, 9 называются значащими .
Разрядные единицы
Система счисления , которой мы пользуемся, называется десятичной . Потому что именно десять единиц одного разряда составляет одну единицу следующего разряда.
Мы считаем единицами, десятками, сотнями, тысячами и так далее. Это и есть разрядные единицы нашей системы счисления.
10 единиц – 1 десяток (10)
10 десятков – 1 сотня (100)
10 сотен – 1 тысяча (1000)
10 раз по 1 тысяче – 1 десяток тысяч (10 000)
10 десятков тысяч – 100 тысяч (100 000) и так далее…
Разряд это место цифры в записи числа.
Например, в числе 12 два разряда: разряд единиц состоит из 2 единиц , разряд десятков состоит из одного десятка .
Мы говорили о том, что 0 – незначащая цифра, которая обозначает отсутствие чего либо. В числах цифра 0 обозначает отсутствие единиц в разряде.
В числе 190 цифра 0 указывает на отсутствие разряда единиц. В числе 208 цифра 0 указывает на отсутствие разряда десятков. Такие числа называются неполными .
А числа, в разрядах которых нет нулей, называются полными .
Разряды считают справа налево:
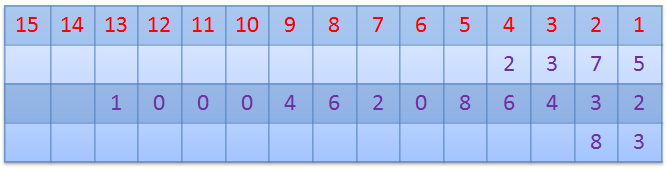
Понятнее будет, если изобразить разрядную сетку следующим образом:
- В числе 2375 :
5 единиц первого разряда, или 5 единиц
7 единиц второго разряда, или 7 десятков
3 единицы третьего разряда, или 3 сотни
2 единицы четвертого разряда, или 2 тысячи
Произносится это число так: две тысячи триста семьдесят пять
- В числе 1000462086432
8 десятков тысяч
2 единицы миллионов
6 десятков миллионов
4 сотни миллионов
0 единиц миллиардов
0 десятков миллиардов
0 сотен миллиардов
1 единица триллионов
Произносится это число так: один триллион четыреста шестьдесят два миллиона восемьдесят шесть тысяч четыреста тридцать два .
- В числе 83 :
Произносится так: восемьдесят три .
Разрядными , называют числа, состоящие из единиц только одного разряда:
Например, числа 1, 3, 40, 600, 8000 – разрядные, в таких числах нулей (незначащей цифры) может быть сколько угодно или не быть совсем, а значащая цифра только одна.
Остальные числа, например: 34, 108, 756 и так далее, неразрядные , их называют алгоритмическими .
Что такое классы и разряды в математике?
В многозначных числах при записи цифры как бы разбивают на группы справа налево по три цифры в одну группу. Вот как раз таки эти самые группы и называются классами.
При записи многозначного числа на письме каждой цифре отводится определённое место — позиция. И вот это самое место, занимаемое конкретной цифрой носит название разряд.
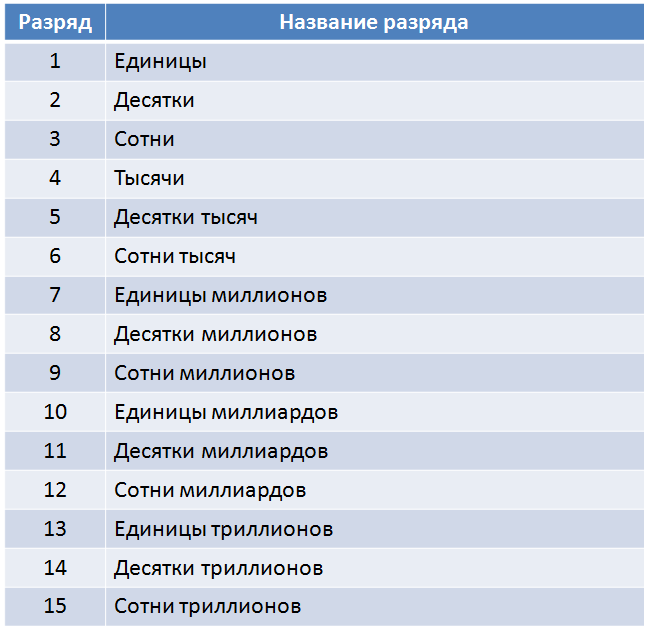
Всем нам, наверное, известно (даже гуманитарию), что в математике есть классы и разряды. К разрядам относятся:
1 разряд — единицы;
2 разряд — десятки;
3 разряд — сотни.
А вот к классам относятся единицы, тысячи, миллионы, миллиарды и так далее.
Вот таблица классов и разрядов для наглядности, чтобы было понятнее:
Чтобы было проще понять, нужно взять для примера некое число. Пусть это будет 38 593 501.
Цифры в записи любого натурального числа справа налево можно разделить в том порядке, в котором они стоят, на группы по 3 цифры в каждой группе. В последней группе может оказаться меньше трёх цифр, можно считать, что в недостающих позициях стоят нули, то есть ничего.
Каждая такая группа — это класс. Названия у классов определяются по порядку: единицы, тысячи, миллионы и т.д.
501 — класс единиц;
593 — класс тысяч;
38 — класс миллионов.
Разряд — позиция каждой цифры. Условно их можно пронумеровать (справа налево).
1 — первый разряд;
0 — второй разряд;
Также разряды можно назвать. В каждом отдельном классе первая цифра (справа налево) будет единицей, вторая — десятком, третья — сотней. Начиная, с класса тысяч перед «единица», «десяток», «сотня» добавляют название класса ( иногда вместо «единица» пишут название класса).
3 — единицы тысяч (тысячи);
9 — десятки тысяч;
8 — единицы миллионов (миллионы);
3 — десятки миллионов.
Вроде звучит сложно, но на самом деле просто все. Ребенок, изучая математику, а вместе с ней самые разные числа — и малые, и большие, понимает идею систематизации на основе классов и разрядов даже на интуитивном уровне.
Классы — понятие более крупное, оно стоит над разрядами, то есть включает их в себя. Классы бывают такого толка:
- класс единиц: это все числа до 999;
- класс тысяч: это все числа до 999 999;
- класс миллионов: числа от 1 000 000 и далее.
Вы могли обратить внимание, что в каждом последующем классе происходит добавление на три позиции для чисел, а точнее, на новую тройку разрядов: если мы говорим о классе единиц, то там есть самый малый разряд — единицы, за ними следует разряд десятков, и, наконец, разряд сотен. В классе тысяч там уже такие разряды: тысячи, десятки тысяч, сотни тысяч. В классе миллионов тройка такая: миллионы, десятки миллионов, сотни миллионов. Помню, в школе нас поначалу специально заставляли ставить пробелы между этими тройками, чтобы было нагляднее и понятнее.
Обратите внимание: если значение какого-то разряда отсутствует, мы его не пропускаем при записи числа, но пишем ноль. Например, дан класс единиц, где разряд единиц — это 8, разряд десятков — это 0, разряд сотен — 2. Это будет число 208 (запись производится справа налево).


 В числе 5672 найти число тысяч, сотен, десятков и единиц
В числе 5672 найти число тысяч, сотен, десятков и единиц )
)





.</p><p><strong>1 сотня = 10 десятков = 100 единиц</strong> </p><p><strong>10 сотен = 100 десятков = 1000 единиц</strong> </p><p style=)