Найти число по остатку от деления
| Модуль (пробел) остаток (запятая) Модуль (пробел) остаток и т.д. |
Одна древняя китайская задача гласила:
«Найти число, которое при делении на 3 дает остаток 2, при делении на 5 дает остаток 3, а при делении на 7 дает остаток 2»
Что бы решать подобные задачи, сделаем следущее
Исходное число по исходным данным можно выразить вот так
Где k — целые числа
Выпишем ряды меняя k от 0 по возрастающей
Несложно заметить что 23, встречается во всех трех рядах.
Это и есть наш ответ, следущее число (128) встретится только через 105=3*5*7 отсчетов. Так как эти числа взаимно простые, то и берем просто их произведение.
И таким образом общий ответ нашей задачи имеет вид
Легкий алгоритм для понимания, не правда ли?
Но он не совсем неудобен, когда встречаются большие числа, и опять же, при составлении элементов ряда можно банально ошибиться.
Есть другой способ
Пусть нам дана система сравнений
где 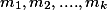
Пусть 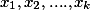
Такие уравнения мы уже можем решать Сравнения 1 степени. Теория чисел.
Узнав эти корни, мы можем вычислить наше исходное число по формуле
Для нашего примера исходные данные выглядят так
Тогда система сравнений будет иметь вид
Решая их получим
И наше решение имеет вид
Или то же самое что и
Как видите, ответ совпадает.
Наш бот решает подобные задачи используя библиотеку PHP GMP. Поэтому к точности расчетов и ограничений на длину значений, это к ним 
Хотя есть и свои материалы в частности: Расчет значения функции Эйлера, Остаток числа в степени по модулю и Диофантовое уравнение с тремя неизвестными
Важно: Логично и это надо учитывать при ввводе чисел, в паре чисел (модуль- остаток), модуль (всегда!) больше чем остаток.
Второе важное замечание. Модуль всегда(!) положительное число, остаток, может быть отрицательным, но лучше все таки привести его к положительному числу.
Как это сделать? Все ссылки на сопутствующие материалы уже приведены.
Пример
Узнать какое загадано число, если остаток при делении его на 37 равно 11, при делении на 9 равно 4, при делении на 7 равно 1, а при делении на 100 остаток равен 25.
Заметим, что модули, то есть числа (37, 9, 7, 100) на которые мы делим неизвестное число, попарно взаимно простые. То есть у нас нет ни одной пары из этих чисел, так что бы они имели общий делитель.
Раз так, то мы можем решать подобную задачу тем, методом который описан выше.Вводим в поле ввода
37 11, 9 4, 7 1, 100 25
За мгновение получим ответ
| Полученное число |
mod(233100)) |
Удачных расчетов!
П
Пример [1]. Найти натуральное число, которое при делении на $ 3_{} $ дает в остатке $ 2_{} $,
при делении на $ 7_{} $ дает в остатке $ 3_{} $, а при делении на $ 10_{} $ — в остатке $ 9_{} $.
Решение. Пусть $ u,v,w $ — частные от деления неизвестного числа на $ 3, 7 $ и $ 10_{} $ соответственно. Имеем:
$$ 3,u+2=7,v+3, 3,u+2=10, w+9, 7,v+3=10, w+9 . $$
Решаем последнее уравнение в целых числах, применяя рассуждения, приведенные
☞
ЗДЕСЬ:
$$ w=7,t_1-2, v=10,t_1-2 quad npu quad forall t_1 in mathbb Z . $$
Подставим найденное выражение для $ v_{} $ в первое уравнение $ 3,u+2=7,v+3 $:
$$ 3,u-70, t_1=-13 , $$
которое также можно решить: $ u=19+70, t_2 $ при $ forall t_2 in mathbb Z $. Следовательно,
общий вид искомых чисел:
$$ 3,u+2=3 (19+70, t_2)+2=59+210, t_2 quad npu quad forall t_2 in mathbb Z . $$
Наименьшее положительное число получается при $ t_2=0 $.
Ответ. $ 59 $.
Т
Теорема [Китайская теорема об остатках (КТО)].
Пусть числа $ M_1 , M_2, dots, M_k $ — попарно взаимно простые, и
$$ M= M_1 M_2 times dots times M_k .$$
Тогда система
$$
x equiv B_1 pmod{M_1}, x equiv B_2 pmod{M_2}, dots,
x equiv B_k pmod{M_k}
$$
имеет единственное решение среди чисел $ {0,1,dots,M-1 } $, и это решение
может быть представлено в одном из следующих видов:
1.
либо $ x = x_1 pmod{M} $ при
$$
x_1= frac{M}{M_1} B_1 y_1 +frac{M}{M_2} B_2 y_2+ dots + frac{M}{M_k} B_k y_k
$$
и $ y_j $ обозначающем число, обратное числу $ Mbig/ M_j $
относительно умножения по модулю $ M_j $:
$$frac{M}{M_j} y_j equiv 1 pmod{M_j} ;$$
2.
либо $ x = x_2 pmod{M} $ при
$$
x_2= B_1 +z_1M_1+z_2M_1M_2 +dots + z_{k-1}M_1M_2times dots times M_{k-1}
,
$$
и числах $ z_1,dots,z_{k-1} $ последовательно определяемых из сравнений
$$
begin{array}{lcl}
B_1+z_1M_1 &equiv B_2 pmod{M_2} , , & \
B_1 +z_1M_1+z_2M_1M_2 &equiv B_3 pmod{M_3} , ,& \
dots & dots & \
B_1 +z_1M_1+z_2M_1M_2 +dots + z_{k-1}M_1M_2times dots times M_{k-1} & equiv B_k pmod{M_k} , . &
end{array}
$$
Доказательство.
1.
При любых целых числах $ y_2,dots,y_k $ число $ x_{1} $, определяемое формулой
1
, удовлетворяет сравнению
$$x_1equiv frac{M}{M_1} B_1 y_1 pmod{M_1}$$
(поскольку числа $ M/M_2,dots,M/M_k $ делятся на $ M_{1} $).
Пусть число $ y_1in { 1, dots ,M_1-1 } $ удовлетворяет сравнению
$$frac{M}{M_1} y_1 equiv 1 pmod{M_1}$$
(на основании теоремы существования и предположений доказываемой теоремы
такое число существует и оно единственно).
Тогда $ x_1equiv B_1 pmod{M_1} $, т.е. удовлетворяет первому из сравнений системы. Аналогично показывается справедливость остальных сравнений.
2.
Фактически, этот алгоритм заключается в последовательном решении сравнений
системы. Решение первого имеет вид $ B_1+M_1t_1 $
при $ t_1in mathbb Z $;
оно подставляется во второе, из которого находим представление для $ t_1 $
в виде $ t_1=z_1+M_2t_2 $ при $ t_2in mathbb Z $, и т.д. Формально:
число $ x_2 $, определяемое формулой
2
, очевидно
удовлетворяет первому из сравнений системы: $ x_2 equiv B_1 pmod{M_1} $.
Далее, $ x_2equiv B_1+ z_1M_1 pmod{M_2} $ и сравнение
$ x_2 equiv B_2 pmod{M_2} $ будет выполнено, если $ z_1 $ удовлетворяет
сравнению $ B_1+ z_1M_1 equiv B_2 pmod{M_2} $. Поскольку $ operatorname{HOD} (M_1,M_2)=1 $, то
на основании теоремы существования,
такое число существует и оно единственно при условии
$ z_1in { 1, dots ,M_2-1 } $.
Установив его, продолжаем далее по индукции.
В заключение покажем, что любые два решения
$ tilde{x} $ и $ tilde{tilde{x}} $
системы сравнимы между собой по модулю $ M_{} $. В самом деле:
$$ tilde{x} equiv B_j pmod{M_j},
tilde{tilde{x}} equiv B_j pmod{M_j} Rightarrow
tilde{x} — tilde{tilde{x}} equiv 0 pmod{M_j}
$$
для $ forall j in {1,dots, k } $.
Поскольку числа $ M_1,dots,M_{k} $ попарно взаимно просты, то
на основании теоремы 4, приведенной
☞
ЗДЕСЬ, имеем:
$ tilde{x} — tilde{tilde{x}} equiv 0 pmod{M_1times dots
times M_k} $.
♦
Первое упоминание утверждения КТО встречается в
книге
Математическое руководство Сунь Цзы
китайского математика Сунь Цзы1)(孫子, ок. 400 — ок. 460), о котором не известно ничего, кроме того, что он является автором этой книги; годы его жизни устанавливались историками науки на основе анализа текста.
Задача 26 главы 3. Предположим, что имеется неизвестное количество
объектов. Разбив их на тройки, получаем в остатке 2, разбив на пятерки
— 3, разбив на семерки — 2. Сколько имеется объектов?
После решения этой конкретной задачи, в книге приводится алгоритм
решения и общей — при произвольных остатках:
«Умножь число остатков при делении на тройки на $ 70 $, добавь к
полученному произведение числа остатков при делении на пятерки на $ 21 $,
и затем добавь произведение числа остатков при делении на семерки на $ 15 $.
Если результат равен $ 106 $ или более — вычти кратное $ 105 $.»
Эти рассуждения фактически соответствуют представлению решения системы
формулой
2
.
Некоторые специалисты полагают, что алгоритм решения системы сравнений позволял китайским генералам пересчитывать армию без особых усилий последовательностью однотипных распоряжений:

«В колонну по $ 7_{} $ становись!»
По выполнении команды, подсчитывалось количество солдат, стоящих в последнем ряду.
Затем производились аналогичные подсчеты по результатам выполнения команд:
«В колонну по $ 11 $ становись!»
«В колонну по $ 13 $ становись!»
«В колонну по $ 17 $ становись!»
В соответствии с утверждением теоремы, по четырем остаткам однозначно восстанавливается число солдат, если оно не превосходит $ 17017=7times 11times 13 times 17 $.
Однако некоторые соображения, основанные на знании реалий армейской жизни, позволяют усомниться в практической пользе подобных — математически абсолютно безупречных —
рассчетов… — см. упражнение ниже.
П
Пример 1. Решить систему сравнений
$$x equiv 7 pmod{8}, x equiv -1 pmod{11}, x equiv 3 pmod{15}
.$$
Решение. Проиллюстрируем оба способа из теоремы. Для представления
1
сначала решаем сравнения
$$165 cdot y_1 equiv 1 pmod{8} ,quad
120 cdot y_2 equiv 1 pmod{11} ,quad
88 cdot y_3 equiv 1 pmod{15} , $$
которые, очевидно, эквивалентны следующим:
$$ 5 cdot y_1 equiv 1 pmod{8} ,quad
10 cdot y_2 equiv 1 pmod{11} ,quad
13 cdot y_3 equiv 1 pmod{15} . $$
Алгоритм решения линейного сравнения даст решения в виде
$$y_1=5, quad y_2=10 , quad y_3=7 . $$
По формуле
1
получаем
$$x_1= underbrace{7cdot 5 cdot 165 + (-1)cdot 10 cdot 120 +
3 cdot 7 cdot 88}_{6423} = 1143+1320times 4 equiv 1143
pmod{1320} .$$
Для
2
решением сравнения $ 7+ 8, z_1 equiv -1 pmod{11} $
очевидно является $ z_1 equiv_{_{11}} -1 equiv_{_{11}} 10 $. Сравнение
$ 7+8 cdot 10 + 8cdot 11 , z_2 equiv 3 pmod{15} $ эквивалентно
$ 13, z_2 equiv 6 pmod{15} $ и имеет решение $ z_2=12 $.
Окончательно
$$x_2= 87 + 8cdot 11 cdot 12 =1143 .$$
Ответ. $ x equiv 1143 pmod{1320} $.
При вычислениях по формуле
1
один из коэффициентов $ y_jM/{M_j} $ можно легко установить, если все остальные уже вычислены:
?
Доказать, что при условиях (и в обозначениях) теоремы имеет место сравнение
$$ frac{M}{M_1} y_1 +frac{M}{M_2} y_2+ dots + frac{M}{M_k} y_k equiv 1 pmod{M} . $$
Какой из алгоритмов теоремы —
1
или
2
— предпочтителен при расчетах
?
Для фиксированной системе сравнений эти
алгоритмы равноэффективны. Однако если идет речь о решении
серии однотипных систем с изменением входящих в них параметров,
то проявляются преимущества каждого из алгоритмов. Рассмотрим сначала
серию систем сравнений
$$
x equiv B_1 pmod{M_1}, x equiv B_2 pmod{M_2}, dots,
x equiv B_k pmod{M_k}
$$
при фиксированном их числе $ k_{} $
и фиксированных же модулях $ M_1,dots,M_{k} $, но варьируемых $ B_1,dots,B_{k} $.
В этом случае имеет смысл использовать представление решения в форме
1
, поскольку для получения решения каждой новой системы серии
нужно будет произвести лишь пересчет суммы при уже вычисленных ранее
величинах $ y_1,dots,y_k $. С другой стороны, если решается серия систем
сравнений, в которой каждая следующая система получается из предыдущей
добавлением одного нового сравнения — т.е., например, система
дополняется сравнением $ xequiv B_{k+1} pmod{M_{k+1}} $ —
то более удобным для вычисления решения становится вариант
2
, так как
при его использовании приходится дополнительно решать лишь одно новое сравнение относительно
$ z_{k} $ и
добавить соответствующее слагаемое в сумму —
т.е. просто прибавить его к решению стартовой системы.
П
Пример 2. Решить системы сравнений
а) $ x equiv 3 pmod{8}, x equiv 1 pmod{11}, x equiv 12 pmod{15} $;
б) $ x equiv 7 pmod{8}, x equiv -1 pmod{11}, x equiv 3 pmod{15},
x equiv 4 pmod{7} $.
Решение. Обе системы могут рассматриваться как
вариации одной и той же системы примера 1, и решение каждой
из этих систем может быть получено модифицированием соответствующего
варианта решения того примера. Так, для системы а) получить решение
не представляет труда, если были заранее вычислены величины $ y_1,y_2 $ и $ y_3 $:
$$x_1= underbrace{3cdot 5 cdot 165 + 1cdot 10 cdot 120 +
12 cdot 7 cdot 88}_{11,067} equiv 507 pmod{1320} .$$
А для системы б) удобнее использовать алгоритм
2
теоремы, тем
более, что решение системы из первых трех сравнений у нас уже имеется.
$$ 1320, z_4 equiv 4 pmod{7} quad Rightarrow quad z_4 =4
quad Rightarrow quad x_2 =1143+1320, z_4 =6423
. $$
Ответ. а) $ x equiv 507 pmod{1320} $; б) $ x equiv 6423 pmod{9240} $.
?
Определить число $ x_{} $ солдат китайской армии, если
а) $ x equiv 3 pmod{7}, x equiv 1 pmod{11}, x equiv 12 pmod{13}, x equiv 10 pmod{17}
$;
б) $ x equiv 3 pmod{7}, x equiv 1 pmod{11}, x equiv 12 pmod{13}, x equiv 11 pmod{17} $.
?
Доказать, что если
$ p_1,p_2,p_3 $ — различные простые числа, то а) решение системы
$$
x equiv B_1 pmod{p_1}, x equiv B_2 pmod{p_2},
$$
можно представить в виде
$$
x equiv p_2^{p_1-1}B_1 + p_1^{p_2-1}B_2 pmod{p_1p_2} ,
$$
а б) решение системы
$$
x equiv B_1 pmod{p_1}, x equiv B_2 pmod{p_2},
x equiv B_3 pmod{p_3}
$$
— в виде
$$
x equiv p_2^{p_1-1}p_3^{p_1-1} B_1 + p_1^{p_2-1} p_3^{p_2-1} B_2 +
p_1^{p_3-1}p_2^{p_3-1} B_3 pmod{p_1p_2p_3} .
$$
Решить эти системы при $ B_1=1,B_2=2,B_3=3 $ и $ p_1=7,p_2=11,p_3=17 $.
Cистема сравнений может иметь решения и при нарушении условий КТО.
?
[Фибоначчи]. Крестьянка несла на базар корзину яиц. Неосторожный
всадник, обгоняя женщину, задел корзину, и все яйца разбились. Желая
возместить ущерб, всадник спросил у крестьянки, сколько яиц было в корзине.
Женщина ответила, что числа яиц не знает, но когда она раскладывала их по
два, по три, по четыре, по пять и по шесть, то каждый раз одно яйцо оставалось
лишним, а когда она разложила по семь, лишних яиц не осталось. Сколько яиц
несла крестьянка на базар?
Т
Теорема. Система
$$
x equiv B_1 pmod{M_1}, x equiv B_2 pmod{M_2}, dots,
x equiv B_k pmod{M_k}
$$
разрешима тогда и только тогда, когда числа
$$
B_j-B_{ell} qquad mbox{ делятся на } qquad operatorname{HOD}(M_j,M_{ell}) quad mbox{ при } quad {j,{ell}} subset {1,dots,k} quad .
$$
Если это условие выполнено, то решение единственно по модулю
$ operatorname{HOK}(M_1,M_2,dots,M_k) $.
§
По поводу КТО см. оригинальный результат
☞
ЗДЕСЬ.
?
Решить систему сравнений
$$
x equiv M_1-1 pmod{M_1}, x equiv M_2-1 pmod{M_2}, dots,
x equiv M_k-1 pmod{M_k} .
$$
Читатель, знакомый с проблемой интерполяции, безусловно
заметит аналогию вариантов
1
и
2
китайской теоремы об остатках с формами соответственно
Лагранжа и Ньютона представления интерполяционного полинома $ y_{}=f(x) $, составляемого по таблице значений
$$
begin{array}{c|ccc}
x & M_1 & dots & M_k \ hline
f(x) & B_1 & dots & B_k
end{array}
$$
Действительно, задачу интерполяции можно «перевести на язык остатков»: найти полином $ f(x)_{} $,
дающий при делении на $ x-M_1 $ в остатке число $ B_{1} $, при делении на $ x-M_2 $ в остатке $ B_{2} $
и т.д.
П
Пример. Верно ли равенство
$$
left| begin{array}{rrrr}
51239 & 79922 & 55538 & 29177 \
46152 & 16596 & 37189 & 82561 \
71489 & 23165 & 26563 & 61372 \
44350 & 42391 & 91185 & 64809
end{array}
right|=0
?
$$
Решение. Фактическое вычисление подобного определителя —
каким бы методом мы не воспользовались —
задача довольно трудоемкая. Однако
вопрос ставится не о фактическом значении, а о равенстве его нулю.
Это обстоятельство может упростить вычисления. Обозначим неизвестное
значение определителя через $ x_{} $; очевидно это число целое. Если $ x=0_{} $,
то и его остаток при делении на любое число $ Min mathbb Z $ тоже должен
быть равным нулю. Если же хоть для
одного $ Min mathbb Z $ выполнится условие $ xnotequiv 0 pmod M $, то и $ xne 0 $.
Вычисление определителя фактически сводится к
умножению элементов определителя. Если же мы ставим задачу определения остатка
от деления этого выражения на $ M_{} $, то имеет смысл
сразу же «сократить» каждый элемент определителя до его остатка от деления
на $ M_{} $.
Возьмем сначала $ M=10 $, т.е. от каждого элемента определителя оставляем
только последнюю цифру:
$$
left| begin{array}{rrrr}
9 & 2 & 8 & 7 \
2 & 6 & 9 & 1 \
9 & 5 & 3 & 2 \
0 & 1 & 5 & 9
end{array}
right| equiv_{_{10}}
left| begin{array}{rrrr}
-1 & 2 & -2 & -3 \
2 & -4 & -1 & 1 \
-1 & 5 & 3 & 2 \
0 & 1 & 5 & -1
end{array}
right| =
left| begin{array}{rrrr}
-1 & 2 & -2 & -3 \
0 & 0 & -5 & -5 \
0 & 3 & 5 & -5 \
0 & 1 & 5 & -1
end{array}
right|=
$$
$$
=-
left| begin{array}{rrr}
0 & -5 & -5 \
3 & 5 & -5 \
1 & 5 & -1
end{array}
right| equiv_{_{10}} 0 .
$$
Итак, полученный ответ является необходимым, но не достаточным условием
равенства определителя нулю. Сделаем еще одну проверку: возьмем $ M=7 $.
$$
left| begin{array}{rrrr}
6 & 3 & 0 & 1 \
1 & 6 & 5 & 3 \
5 & 2 & 5 & 3 \
5 & 6 & 3 & 3
end{array}
right|equiv_{_{7}} 3 ne 0
.
$$
Ответ. Равенство неверно.
Понятно, что если бы определитель был равен нулю, то каждое вычисление
по модулю только «увеличивало бы достоверность» этого события.
Можно ли на основе серии модулярных вычислений установить истинное значение
определителя?
Попробуем это сделать для определителя из примера. Прежде всего,
оценим сверху абсолютную величину определителя. Каждое слагаемое в разложении
определителя по формуле из его определения представляет собой произведение
четырех пятизначных чисел; очевидно, это произведение не превосходит $ 10^{24} $.
Всего таких слагаемых $ 24_{} $, из них половина — с отрицательным знаком.
Поэтому $ |x|<1.2cdot 10^{25} $. Берем теперь все последовательные простые
числа2) $ p_j $, так чтобы их произведение превысило эту оценку:
$$L = underbrace{2cdot 3 cdot 5 times dots times 67 cdot 71}_{20} > 1.2cdot 10^{25}
$$
и вычисляем остатки $ B_{p_j }= x pmod{p_j} $:
$$B_2=0, B_3=0, B_5=0, B_7=3, B_{11}=7,dots, B_{67}=64, B_{71}=39 .$$
Китайская теорема об остатках позволяет однозначно определить
величину $ x_{} $ если она находится в пределах $ 0<x< L $:
$$x=+557940821520864633874788300 . $$
Однако, поскольку мы не знаем знака определителя, то должны предложить
еще один вариант ответа
— из полученного положительного значения следует вычесть величину $ L_{} $:
$$x=-8605834327092627090 . $$
Из двух получившихся вариантов только один — именно последний —
удовлетворяет оценке $ |x|<1.2cdot 10^{25} $. Это и есть величина нашего
определителя.
На самом деле, в только что решенном примере эффективность применения КТО в сравнении с методом вычисления определителя $ 4_{} $-го порядка, основанном на формуле из его определения, не очень очевидна: первый способ из КТО содержит сумму в $ 20 $ слагаемых — по сравнению с $ 24 $ из определения определителя, но каждое из этих слагаемых более громоздко! Можно, однако, слегка уменьшить количество этих слагаемых — скажем, до $ 17 $, если воспользоваться оценкой величины определителя по неравенству Адамара: $ |x|<1.6times 10^{21} $.
Вычислительные эксперименты с определителями порядка $ 16 $ с ОЧЕНЬ БОЛЬШИМИ элементами
☞
ЗДЕСЬ.
?
Остатки от деления числа $ x_{} $ на последовательность целых чисел
$$ x equiv 1 pmod{7}, x equiv 4 pmod{8}, x equiv 4 pmod{9},
$$
$$
x equiv 2 pmod{10}, x equiv 2 pmod{11}, x equiv 5 pmod{13}
$$
вычислены с ошибками; известно, однако, что не более двух остатков ложные. Установите число $ x_{} $.
[1]. Малининъ А., Буренинъ К. Руководство алгебры и собранiе алгебраическихъ задачъ для гимназiй, реальныхъ училищъ и учительскихъ институтовъ. Изданiе седьмое. М. Издание книжнаго магазина наследников бр. Салаевыхъ. 1884.
[2]. Бухштаб А.А. Теория чисел. М. Просвещение. 1966
[3]. LeVeque W.J. Topics in Number Theory. V.1. Addison-Wesley. Mass. 1956.
[4]. Утешев А.Ю., Калинина Е.А. Лекции по высшей алгебре. Часть I.
Учеб. пособие. СПб. «СОЛО». 2007. 246 c.
«Имеются вещи, число их неизвестно. Если считать их тройками, то остаток 2; если считать их пятерками, то остаток 3; если считать их семерками, то остаток 2. Спрашивается, сколько вещей?»
Эта задача — из древнекитайского математического трактата Сунь Цзы (это имя автора; не путать с другим Сунь Цзы, автором «Искусства войны»). Трактат был написан где-то между 3 и 5 веками нашей эры, точнее неизвестно. Требуется найти число, которое при делении на три дает остаток 2, на пять остаток 3, на семь остаток 2. Что такое число существует, и как его найти — есть частный случай теоремы, которую называют «Китайской теоремой об остатках» именно из-за этой задачи. На западе ее открыли на тысячу лет позже, в 13-м веке.
Вот решение задачи, из того же трактата:
«Ответ: 23.
Способ: при счете их тройками и остатке 2 установи 140; при счете их пятерками и остатке 3 установи 63; при счете их семерками и остатке 2 установи 30. Сложи это, получишь 233. Из этого вычти 210 и получишь [искомое]. Вообще [если] при счете их тройками остаток 1, то установи 70; [если] при счете их пятерками остаток 1, то установи 21; [если] при счете их семерками остаток 1, то установи 15. [Если сумма] больше 106, то вычитай 105 и получишь [искомое]».
Сначала не вполне понятно, откуда берутся эти числа, но можно разобраться. Здесь вторая половина решения, начиная со слов «вообще», важнее первой. Объясняется, как поступать в частном случае, когда требуется добиться остатка 1 по модулям 3,5,7. Казалось бы, зачем тогда нужно что-то считать, просто возьми число 1, у него тривиальным образом есть нужные остатки. Но дело в том, что способ решения для этого частного случая потом обобщается на любые желаемые остатки.
Предлагается взять числа 70,21,15 и сложить, и легко проверить, что их сумма 106 дает остаток 1 при делении на 3,5,7. Почему так получилось, и что это за числа? Число 70 дает остаток 1 при делении на 3 и делится без остатка на оба остальных числа, 5 и 7. То же самое с другими: 21 дает остаток 1 при делении на 5, и делится без остатка на 3 и 7, и так далее. Значит, если мы возьмем их сумму, и посмотрим на остаток при делении на 5, например, то первое и третье слагаемое дадут остаток 0, т.к. они делятся на 5, а второе даст остаток 1. И то же самое случится при делении на 3 и 7: одно из слагаемых даст нужный остаток 1, остальные будут делится без остатка.
Теперь предположим, что мы хотим добиться не остатков 1,1 и 1, а остатков 2,3 и 2, как в условии. Просто берем эти «магические» числа 70, 21 и 15 и умножаем вначале на желаемые остатки, перед сложением: 70*2 + 21*3 + 15*2 = 233. Теперь при делении на 3, скажем, первое слагаемое даст остаток 2, а остальные два слагаемых как делились на 3 без остатка, так и продолжают делиться, так что они не мешают. Из этого числа 233 можно вычесть любое кратное 105 (105 = 3*5*7, произведение всех делителей), и это не изменит остатки от деления на 3,5,7, так что можно заменить 233 на 233-210=23. Это и есть то, что написано в первой части решения. Из того, что есть вторая часть, понятно, что в первой части числа 140,63,30 взялись не «от фонаря», а именно по этому методу, хоть это и не сказано прямо.
Откуда же нашлись числа 70,21,15? В тексте это не объясняется никак. Может, так: поскольку мы хотим, чтобы первое число делилось на 5 и 7 без остатка, ясно, что оно должно быть кратным 5*7=35. Поэтому просто будем брать кратные 35: 35,70,105 итд. пока не дойдем до числа, которое дает 1 при делении на 3 (второе требование к этому числу). Это получается 70. С двумя оставшимися «магическими» числами нам повезло: это просто произведения 21=3*7 и 15=3*5, и так удачно получилось, что они уже дают нужный остаток 1 при делении на 5 и 7 соответственно. Если б не давали, мы бы тоже брали их кратные, пока не нашли бы нужное.
Вышеописанное — уже полное описание алгоритма решения китайской теоремы об остатках в общем случае. Его можно применять к любому набору попарно простых делителей, а не только 3,5,7. Но поскольку в трактате это подробно не написано, считается, что Сунь Цзы решил только частный случай. Мне кажется, однако, что он нашел что-то вроде вышеописанного — иначе я не понимаю, откуда он взял числа 70,21,15.
(цитаты из русского перевода Эльвиры Березкиной, который был опубликован ровно полвека назад, в 1963г.)
китайский калькулятор остатков
Первое уравнение
Второе уравнение
Результат
сделано с ❤️
Оглавление
Введение в китайскую теорему об остатках
Вы когда-нибудь слышали о китайской теореме об остатках? Это система, которая имеет дело с конгруэнтностью и одновременными модульными системами и используется для расчета количества элементов, оставшихся в системе, и способов ее решения.
В этой статье мы углубимся в концепцию модуля и сравнений, а также в то, как они соотносятся с китайской теоремой об остатках. Мы также обсудим алгоритм Евклида НОД и тождество Безу — две важные концепции, тесно связанные с китайской теоремой об остатках.
Итак, если вы хотите узнать больше об этой увлекательной области математики, продолжайте читать!
Теорема об остатках в Китае относится к системе, которая содержит сравнения и несколько одновременных модульных систем. Проблема заключается в подсчете количества оставшихся элементов и способах ее решения.
Модуль и сравнения
Вы знакомы с математикой, которая имеет дело с числами? Судя по всему, нет. Большеголовые математики способны находить все больше и больше способов описания и анализа объектов, исходя из их самых смелых фантазий. Чаще всего в формулах, которые они доказывают, нет цифр.
Теория чисел — последняя из этого моря неузнаваемых символов. Это область математики, которая имеет дело только с целыми числами. Например, такие числа, как 0, 1, 42 или 273. Правильно, не заморачивайтесь с дробями. Похоже на узкое поле, не так ли? Должно быть, они уже все нашли.
Остаток от целого числа, деленного на b, который представляет собой целое число r между нулем и b-1, которое остается в качестве лишней «неделимой» или той, которая дает дробь от операции, называется «неделимой». Символически говоря, оно должно удовлетворять уравнению.
a = k * b + r (k — некоторое целое число)
Если мы разделим 17 на 5, то мы знаем, что можем поместить три пятерки в 17. И у нас все равно останется 2. 2 представляет остаток.
Китайская теорема об остатках
Это метод, описывающий набор или систему сравнений, описывающих неизвестную переменную. Заявление будет обнародовано достаточно скоро. Однако сейчас мы просто скажем, что он решает такие проблемы и предоставляет для этого простой алгоритм.
Алгоритм Евклида НОД
Алгоритм Евклида-gcd позволяет найти наибольший общий делитель (иногда называемый наибольшим общим делителем) двух чисел.
Личность Безу
Тождество Безу (также известное как лемма Безу, не путать с теоремой Безу, касающейся деления многочленов) — это небольшая теорема, которая позволяет нам соединить два числа, используя их соответствующие НОД.
Автор статьи
John Cruz
Джон — аспирант, увлеченный математикой и образованием. В свободное время Джон любит ходить в походы и кататься на велосипеде.
Китайский Калькулятор Остатков русский
Опубликовано: Thu Mar 23 2023
В категории Другие калькуляторы
Добавьте Китайский Калькулятор Остатков на свой сайт
Китайский Калькулятор Остатков на других языках
Другие калькуляторы в категории другое
|
Как найти целое, если известна его часть? Например, 3/8 торта весит 300 грамм. Как узнать, сколько весит весь торт? Нахождение целого по его части Если у нас известна какая-либо часть (доля) от целого, то можно всегда «восстановить» целое. При этом нужно помнить, что часть от целого числа может быть выражена либо в виде дроби (обычно обыкновенной), либо в виде процента. Рассмотрим оба случая. 1) Часть числа — это обыкновенная дробь. В этом случае для нахождения целого нужно число, соответствующее данной части, разделить на дробь. Для того, чтобы число разделить на обыкновенную дробь, нужно умножить его на знаменатель дроби и разделить на числитель. _ Пример 1: Специалист отдела кадров получил премию 2000 рублей, что составляет 1/15 часть от его месячной зарплаты. Требуется узнать, сколько составляет зарплата у данного сотрудника. Решение: Зарплата = 2000 / (1/15) = 2000 * 15 = 30000 рублей. Значит, сотрудник получает зарплату 30000 рублей в месяц. _ Пример 2: Было засеяно пшеницей 12 гектаров поля, что составляет 3/5 от его общей площади. Нужно посчитать, чему равна площадь поля. Решение: Площадь поля = 12 / (3/5) = 12 * (5/3) = 20 гектаров. 2) Часть числа представлена в процентах. Если доля от целого является процентом, а не обыкновенной дробью, то подобные задачи можно решать с помощью составления пропорции. _ Пример: Цена апельсинов со скидкой равна 120 рублей, величина скидки равна 20%. Нужно узнать, сколько стоили апельсины изначально. Решение: Так как скидка = 20%, то от исходной цены апельсинов осталось 100% — 20% = 80%. 80% — 120 рублей. 100% — x рублей. 0,8x = 120 рублей. x = 120 / 0,8 = 150 рублей. Таким образом, до скидки апельсины стоили 150 рублей. модератор выбрал этот ответ лучшим Алиса в Стране 3 года назад Часть числа может быть выражена в виде десятичной или простой дроби, в виде процентов, что по сути то же самое, что десятичная дробь, всем понятно, что 0,1 это 10%, например. Если известна часть числа в абсолютном выражении и то, какую часть она составляет от целого, то нет ничего проще, чем определить это целое. Допустим, 20 яблок это 25 % от всех яблок, надо 20 поделить на 0,25, чтобы определить общее количество яблок, 20/0,25 = 80, вот так мы нашли целое по его части. Еще один пример разберем, 12 мест в автобусе это 1/3 от всех мест в автобусе, как найти общее число всех мест в автобусе, делим 12 на 1/3, то есть по правилам деления на дробь умножаем 12 на 3, получается 36. Ну и в итоге решим задачку автора из его вопроса: 300 граммов делим на 3/8 получаем 800 граммов. smile6008 3 года назад В математике и жизни бывают случаи, когда необходимо найти число, зная только его часть. Для этого можно использовать различные способы расчётов, использовать дроби , но удобнее всего рассчитать в процентном соотношении. Итак мы знаем, что 300 грамм составляют 3/8 торта. Нужно узнать сколько же весит торт целиком. Переводим в процентное соотношение, поделим 8 на 3, получим 0,26666 в процентах — это 26,6%. Теперь найдём 100 %, для этого посчитаем пропорцию. 26,6% = 300 ;100 % = x. X = 26,6*300/100.Получаем 799,8 округляем по закону округление в большую сторону, получаем 800 гр весит весь торт. [пользователь заблокирован] 5 лет назад Для лучшего понимания процесса можно делать так (хотя математически это нерационально). Узнайте чему равна ОДНА часть. Для этого заданное число разделите на количество заданных частей в дроби, их 3. 300 делим на 3, получаем 300/3=100 Это одна восьмая часть. Целое — это восемь восьмых, потому предыдущий результат умножаем на 8, получаем 100*8=800 Если же дробь задана, как десятичная, т.е. 0.375, то представляем её, как натуральную (это 375/1000) и поступаем точно так же. Узнаём, чему равна одна тысячная часть 300/375=0.8 Ну, а далее узнаём чему равно само целое 0.8*1000=800 Эл Лепсоид 5 лет назад В общем случае, конечно, следует прибегнуть к составлению пропорции, поставив в соответствие к имеющейся части ее вес, а к целому (т.е. единице) — неизвестную «х». Но, поскольку, у нас во второй части пропорции стоит «1», то решить задачу можно значительно проще: просто разделить на величину известной части. В нашем случае получается: 300/(3/8) = 300*8/3 = 800. Таким образом, весь торт будет весить 800 грамм. СТА 1106 3 года назад 3/8- означает, что на три части из восьми приходится 300 грамм. Требуется узнать вес целого, в данном случае, торта. Для этого нужно узнать, что приходится на одну часть. Можно решить методом пропорции, мой любимый метод. Итак: 3 части — 300 грамм. 8 частей — Х грамм. Решаем пропорцию. 8 × 300 ÷ 3 = 800 грамм. Общий алгоритм решения следующий. Зная, сколько приходится на долю от целого, нужно определить, сколько приходится на единицу измерения ( грамм, килограмм, метр, час и т.д). Затем зная это, просто умножает на все количество долей, на которое поделён данный предмет. В данном случае- это восемь частей. Второй вариант решения задачи. 300 : 3 × 8 = 800 грамм. Ответ. 800 грамм , в обоих вариантах таз решения задачи. Проще не бывает. Надо число означающее часть разделить на количество этих частей и полученный результат умножить на целое. Получим число выражающее целую часть. Пример: Дано 4/15 равняется 40. Делим сорок на четыре и умножаем на 15. Получаем сумму в 150 — это и будет целое. Или 2/10 равняется 40. Делим сорок на два, получаем двадцать. Умножаем двадцать на десять, получаем двести. Целое число двести. Master-Margarita 5 лет назад Чтобы узнать, сколько весит торт в данном случае, надо провести следующие арифметический действия: (300*8)/3=800 грамм. То есть, чтобы найти целое нужно часть умножить на знаменатель дроби и разделить на числитель дроби. В данном случае числитель — 3, а знаменатель — 8. Рина19 5 лет назад Сначала найдём чем у равна 1 часть из всех имеющихся. А затем умножим её на общее число всех частей. На данном примере. Известно, что 3/8 торта весит 300 г, т.е. 3 части из 8 на которые был нарезан торт или, по другому, 3 куска торта из 8 нарезанных кусочков весят 300 г. Тогда 1 кусочек будет весить: 300/3=100 г. Теперь находим чему будет весить все 8 кусков, т.е. весь торт. 100*8=800 г Бекки Шарп 3 года назад Если 3/8 торта весит 300 грамм, то сначала узнаем сколько весит одна часть. 300/3=100 грамм. Теперь умножаем на 8 и получаем, что весь торт весит 800 грамм. Приведем еще пример как найти целое число, если известна часть. В классе присутствует 27 человек и это 3/4 общего количества. Сколько человек в классе? Решить задачу можно так: 27 : 3/4 = 36 человек. Знаете ответ? |



mod(105))
mod(m_1),%20&%20x=(c_2)mod(m_2),....,x=(c_k)mod(m_k))
mod(m_1)\\m_1m_3...m_kx_2=(1)mod(m_2)\\.........\\m_1m_2...m_{k-1}x_k=(1)mod(m_k))
mod%20(m_1m_2...m_k))
mod(3),%20&%20x=(3)mod(5),x=(2)mod(7))
mod(3)=1\\%20&%20(21x_2)mod(5)=1\\(15x_3)mod(7)=1)
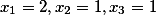
mod(3*5*7)=(233)mod(105))
mod(105)=(233-105-105)mod(105)=23mod(105))

