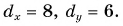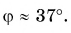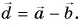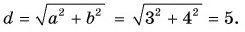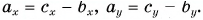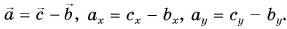Проекция вектора на ось. Проекция вектора на вектор
Навигация по странице:
- Определение проекции вектора на ось
- Определение проекции вектора на вектор
- Формула вычисления проекции вектора на вектор
- Примеры задач на проекцию вектора
- плоские задачи
- пространственные задачи
Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A1B1 оси l, где точки A1 и B1 являются проекциями точек A и B на ось l. (рис. 1).
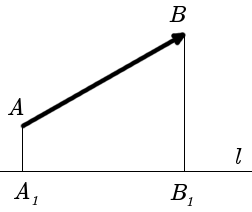 |
| рис. 1 |
Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Пример 1. Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
|b| = √32 + 42 = √9 + 16 = √25 = 5
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 11 | = 2.2 |
| |b| | 5 |
Ответ: Пр ba = 2.2.
Примеры вычисления проекции вектора для пространственных задачи
Пример 2. Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.
Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
|b| = √42 + 22 + 42 = √16 + 4 + 16 = √36 = 6
Найдем проекцию вектора a на вектор b
| Пр ba = | a · b | = | 12 | = 2 |
| |b| | 6 |
Ответ: Пр ba = 2.
Заказать задачи по любым предметам можно здесь от 10 минут
Как найти проекцию вектора на вектор?
Для того, чтобы найти проекцию вектора на вектор ($overline{a}$ на $overline{b}$) нужно разделить скалярное произведение этих векторов на длину последнего вектора $overline{b}$ по формуле: $$text{Пр}_{overline{b}} overline{a} = frac{(overline{a},overline{b})}{|overline{b}|}$$
| Пример 1 |
| Найти проекцию вектора $overline{a} = (1,2)$ на вектор $overline{b} = (-1,2)$ |
| Решение |
|
Вычисляем скалярное произведение векторов. Умножаем соответствующие координаты и складываем $$(overline{a},overline{b}) = 1 cdot (-1) + 2 cdot 2 = -1 + 4 = 3$$ Находим модуль вектора, на который ищем проекцию $$|overline{b}| = sqrt{(-1)^2 + 2^2} = sqrt{5}$$ Подставляя в формулу проекции вектора $overline{a}$ на направляющий вектор $overline{b}$ получаем искомое значение $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$ |
| Пример 2 |
| Вычислить проекцию вектора на вектор, если $overline{a} = (1,2,-3)$ и $overline{b} = (2,1,1)$ |
| Решение |
|
Берем скалярное произведение двух векторов. Перемножаем попарно соответствующие координаты и суммируем полученные значения $$(overline{a},overline{b}) = 1 cdot 2 + 2 cdot 1 + (-3) cdot 1 = 2 + 2 — 3 = 1$$ Так как ищем проекцию на вектор $overline{b}$, то вычисляем его модуль (длину) $$|overline{b}| = sqrt{2^2 + 1^2 + 1^2} = sqrt{6}$$ По главной формуле получаем ответ к задаче $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
| Ответ |
| $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$ |
В математике существуют два определения:
1) геометрическая проекция вектора — вектор;
2) проекция вектора на ось — число.
Геометрическая проекция вектора — это вектор, который можно получить, если провести перпендикуляры от концов вектора до выбранной оси. Проекция начала вектора соответствует началу геометрической проекции, а проекция конца вектора соответствует концу геометрической проекции.
Ваш браузер не поддерживает HTML5 видео
Для вектора
v→
геометрическая проекция на оси (t) — это вектор
vt→
.
Для вектора
n→
геометрическая проекция на оси (y) — это вектор
ny→
.
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
ax=4bx=−3
Если длина вектора
a→
равна
a→
и
α
— это острый угол, созданный вектором и осью (x), то скалярная проекция вектора вычисляется по формуле:
ax=a→⋅cosα
.
Знак проекции вектора выбирается в зависимости от направления оси.
На рисунке видно, что эту формулу можно получить из соотношения в прямоугольном треугольнике:
.
Обрати внимание!
Если вектор и ось проекций параллельны, то скалярная проекция на этой оси — число, которое равно длине вектора, если направления вектора и оси совпадают, или число, противоположное длине вектора, если направления вектора и оси — противоположные.
Если вектор и ось проекций перпендикулярны, то проекция вектора на этой оси равна (0).
at=3bt=−5ct=0dt=0
Проекцией вектора
на заданную осьl называется численное
значение векторана осиl(рис. 1.5а).
Проекцией вектора
на вектор
называется проекция вектора
на ось, имеющую с вектором
одинаковое направление (рис. 1.5б).
Рис. 1.5а Рис. 1.5б
,
где—
угол между вектороми осьюl.
Свойство проекций:
1) Проекция суммы векторов на ось равна
сумме проекций этих векторов, т.е.
Пр.Пр.
+
Пр.;
2) проекция произведения вектора
на число
равна произведению числа на проекцию
вектора,
т.е. ПрlПрl
.
1.3. Декартовы прямоугольные координаты
Положение точки в пространстве будем
определять относительно пространственной
декартовой прямоугольной системы
координат, состоящей из трех взаимно
перпендикулярных осей координат,
пересекающихся в одной точке О,
называемой началом координат.
Ось Oxназывают осьюабсцисс,
осьOy— осьюординат и осьOz — осьюаппликат.
Координатные оси Ox,Oy,Oz,
взятые попарно, определяют три взаимно
перпендикулярные плоскостиxOy,yOz,xOz, называемыекоординатными
плоскостями.
Декартова система координат позволяет
связать с каждой точкой Pпространства,
в котором выбраны три не лежащие в одной
плоскости направленные прямые Ox,
Oy, Oz(оси координат), пересекающиеся
в начале O, три вполне определенных
действительных числа (декартовы
координаты) x, y, z; при этом пишутP(x,y,z).
Оси Ox, Oy, Ozмогут образовывать
правую или левую систему. Дляправой
системы поворот от осиOxк оси Oyна угол, меньший,
совершается в направлении против часовой
стрелки, если смотреть на плоскостьxOyиз какой-либо точки положительной
полуоси Oz (положительная сторона
плоскостиxOy). рис.1.6.
Правая система Левая система
Рис. 1.6
Замечание.Когда мы изучали комплексные
числа, то, наряду с декартовой системой
координат, рассматривали полярную
систему координат на плоскости, которая
задается точкойО (полюсом) и
полярной осью — лучом, выходящим из
полюса. Связь прямоугольных и полярных
координат задается формулами:
, где
(1.3.1)
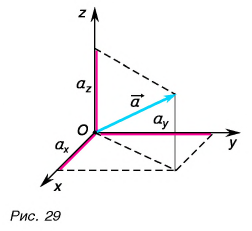
1.4. Координатное представление векторов
Пусть мы имеем прямоугольную систему
координат в пространстве.
Если вместе с вектором
,
имеющим произвольную длину, рассмотреть
вектор, имеющий единичную длину, но
направленный так же, как вектор,
то этот вектор называетсяортом
вектораи обозначается, например,
.
Отсюда следует, что.
Обозначим единичные векторы (орты)
осейOx, Oy, Ozсоответственно
черезпричем
.
Разложим произвольный вектор
трехмерного пространства по ортам. Для
этого построим вектор,
равный вектору.
Из точкиМ опустим перпендикуляр
на плоскость хOу. Из основания
этого перпендикуляра (точкаА)
опустим перпендикуляры на оси координатОхиОу и соединим точкуАс
началомО. На векторахи
построим прямоугольникОАММ3,
диагональю которого будет вектор.
Из рис. 1.7 видно, чтоили
.
Рис. 1.7
Векторы
,
,
называютсясоставляющимивектора
.
Координаты точек
являются координатами вектора.
Можно сказать, что координатами вектора
являются
его проекции на оси координат.
Составляющие вектора можно выразить
через его проекции (координаты):
Подставляя эти значения в равенство
и обозначив
через
получим:
(1.4.1)
Равенство (1.4.1) можно записать в виде:
(1.4.2)
Замечание 1. Равные векторы имеют
одинаковые координаты.
Замечание 2. Разложение векторав виде (1.4.1) возможно только единственным
способом.
Из единственности разложения (1.4.1)
вектора
по ортам, следует, что если координаты
любых двух векторови
равны, т.е.
,
то эти векторы тоже равны .
Вектор
,
идущий от начала точкиОк точкеназываетсярадиус — векторомэтой
точки, и его координаты совпадают с
соответствующими координатами точки(рис. 1.8)
Рис. 1.8
Поэтому
,
или.
Пусть— вектор, координаты начала и конца
которого известныи
.
Тогда координаты векторавыражаются по формулам :
(1.4.3)
Из рис. 1.9 видно, что
(1.4.4)
x
Рис. 1.9
Используя свойства проекций (п.1.2.),
имеем:
,
и аналогичным образом находим.
Разложение вектора
по ортам будет иметь следующий вид:
(1.4.5)
Тройка векторов
называетсякоординатным базисом,
а разложение (1.4.1) вектораназывается разложением вектора
по базису
.
Замечание. Разложение векторана плоскости по базису
имеет вид
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
09.02.201544.66 Mб51Введение в электронику практический подход.pdf
- #
- #
- #
- #
- #
- #
- #
- #
- #
Преподаватель который помогает студентам и школьникам в учёбе.
Проекция вектора на ось в физике — формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
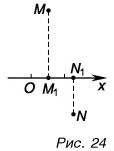
Начнем с понятия проекция точки на ось.
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Как определяют проекцию вектора на ось
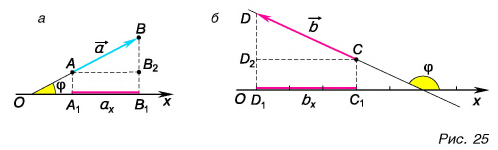
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 
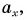
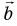
Проекция 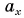
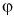
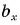
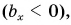
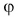
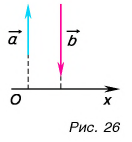
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 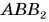
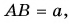
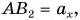
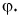
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
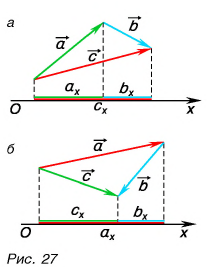
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 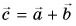
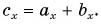
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
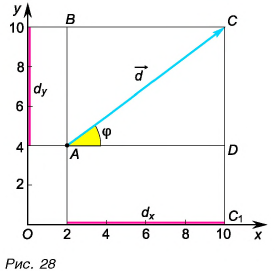
Рассмотрим вектор 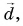
Модуль вектора 
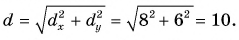
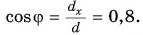
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
Вектор в пространстве определяется тремя проекциями: 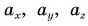
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
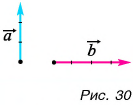
Пример №1
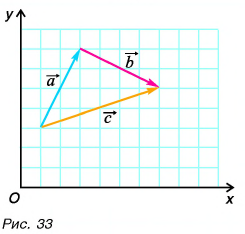
1. Определите сумму и разность взаимно перпендикулярных векторов 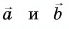
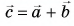
Решение
Сумму векторов 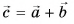
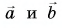
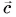
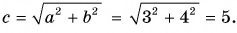
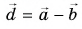
Модуль вектора 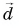
Ответ:
- Заказать решение задач по физике
Пример №2
Выразите вектор 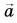
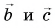
Решение
По правилу треугольника находим: 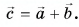
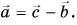
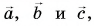
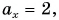
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними