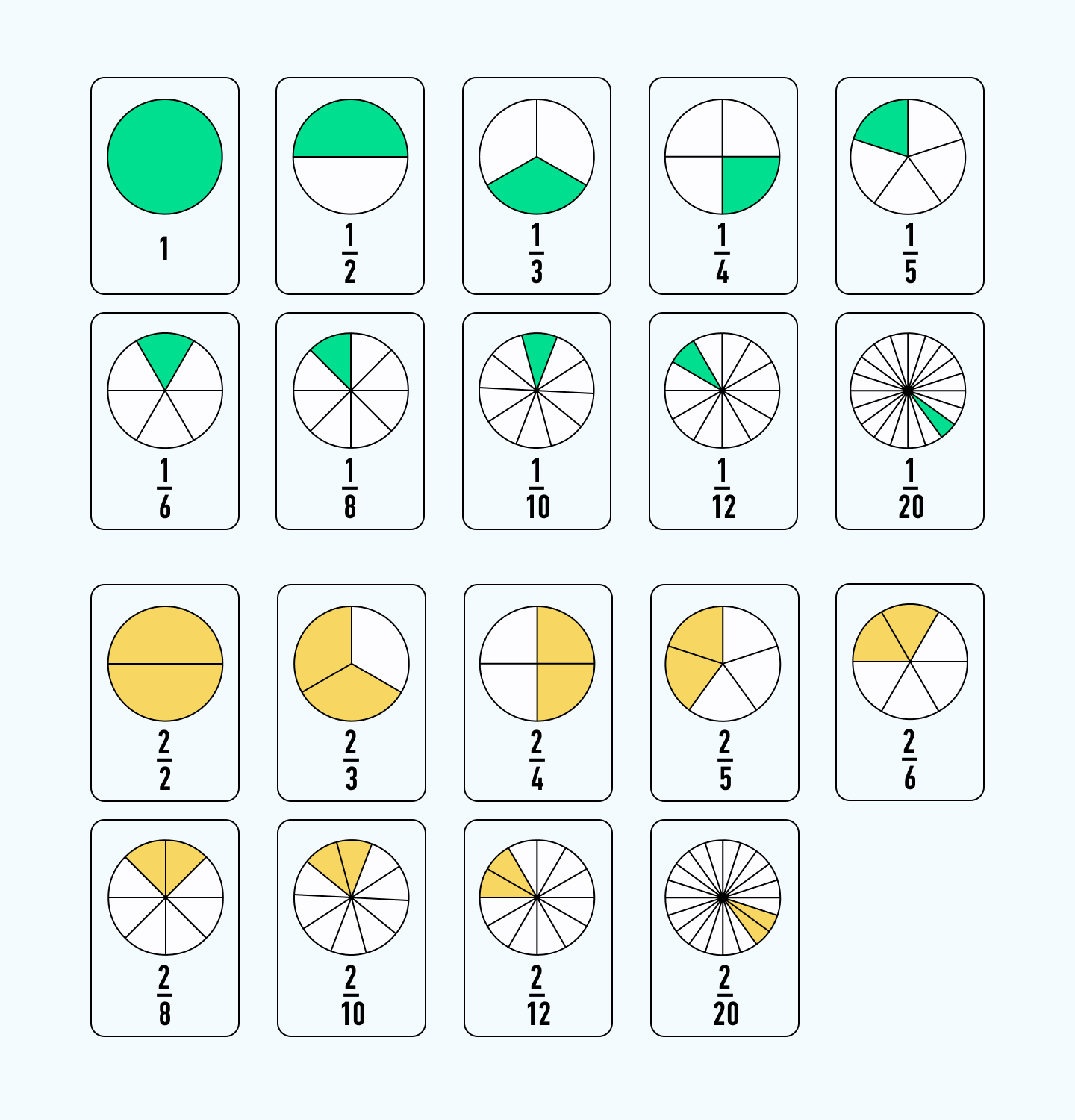
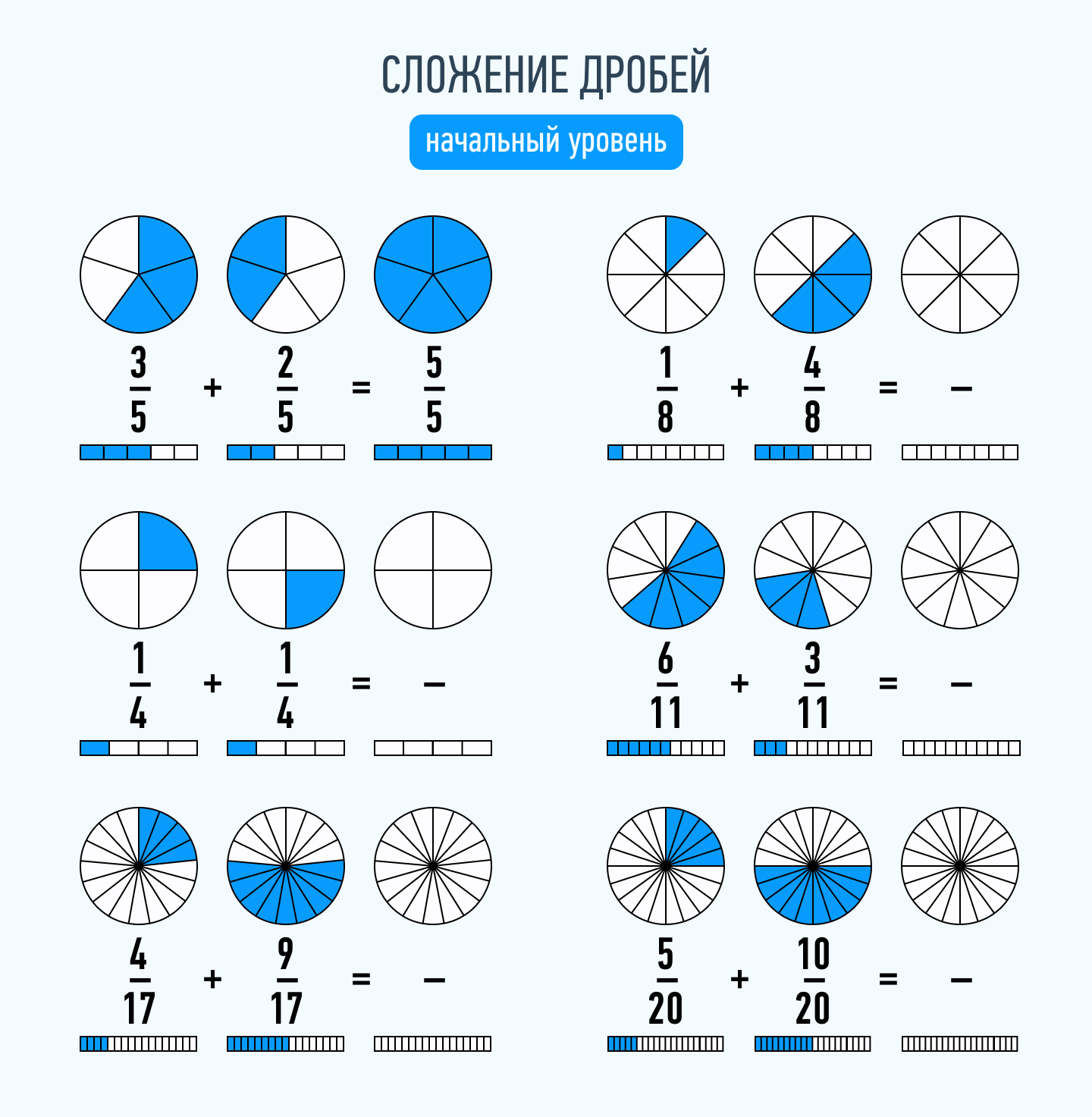
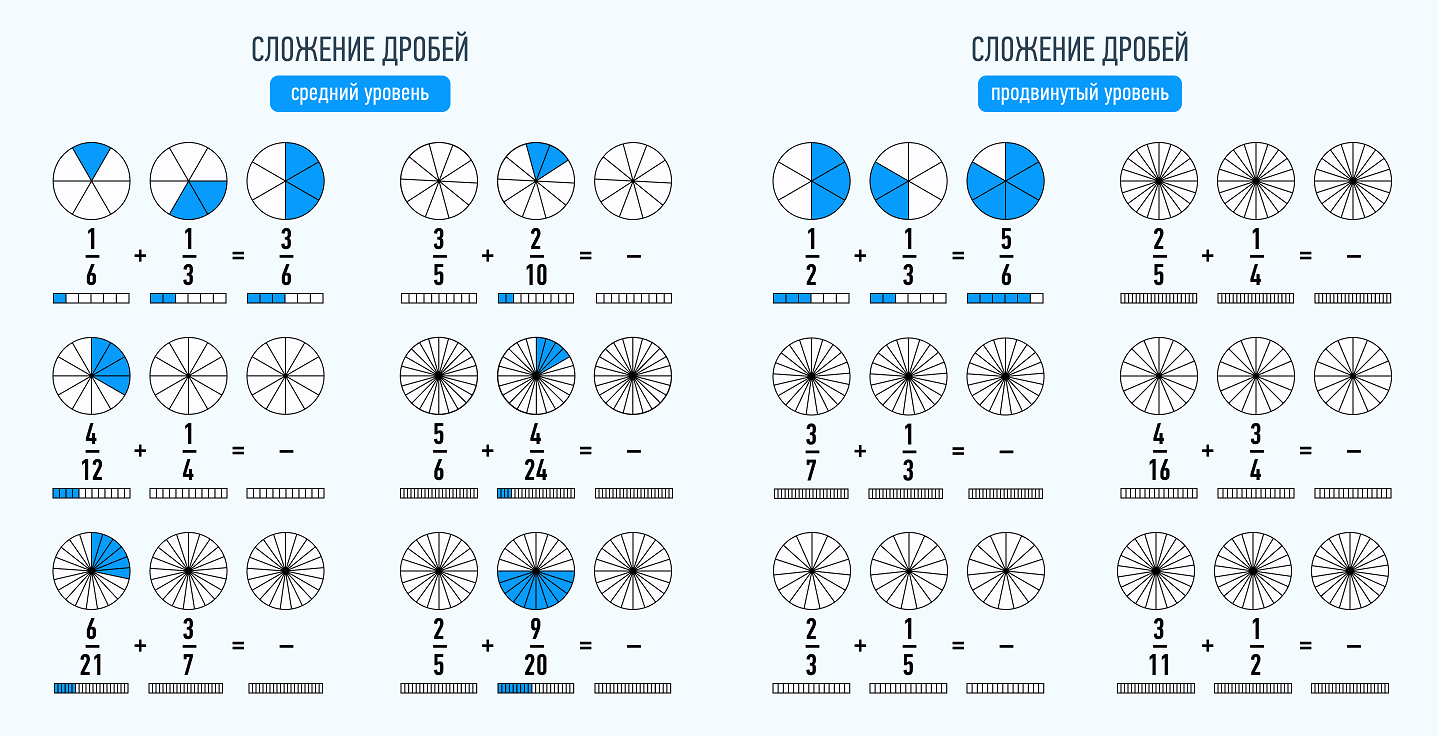
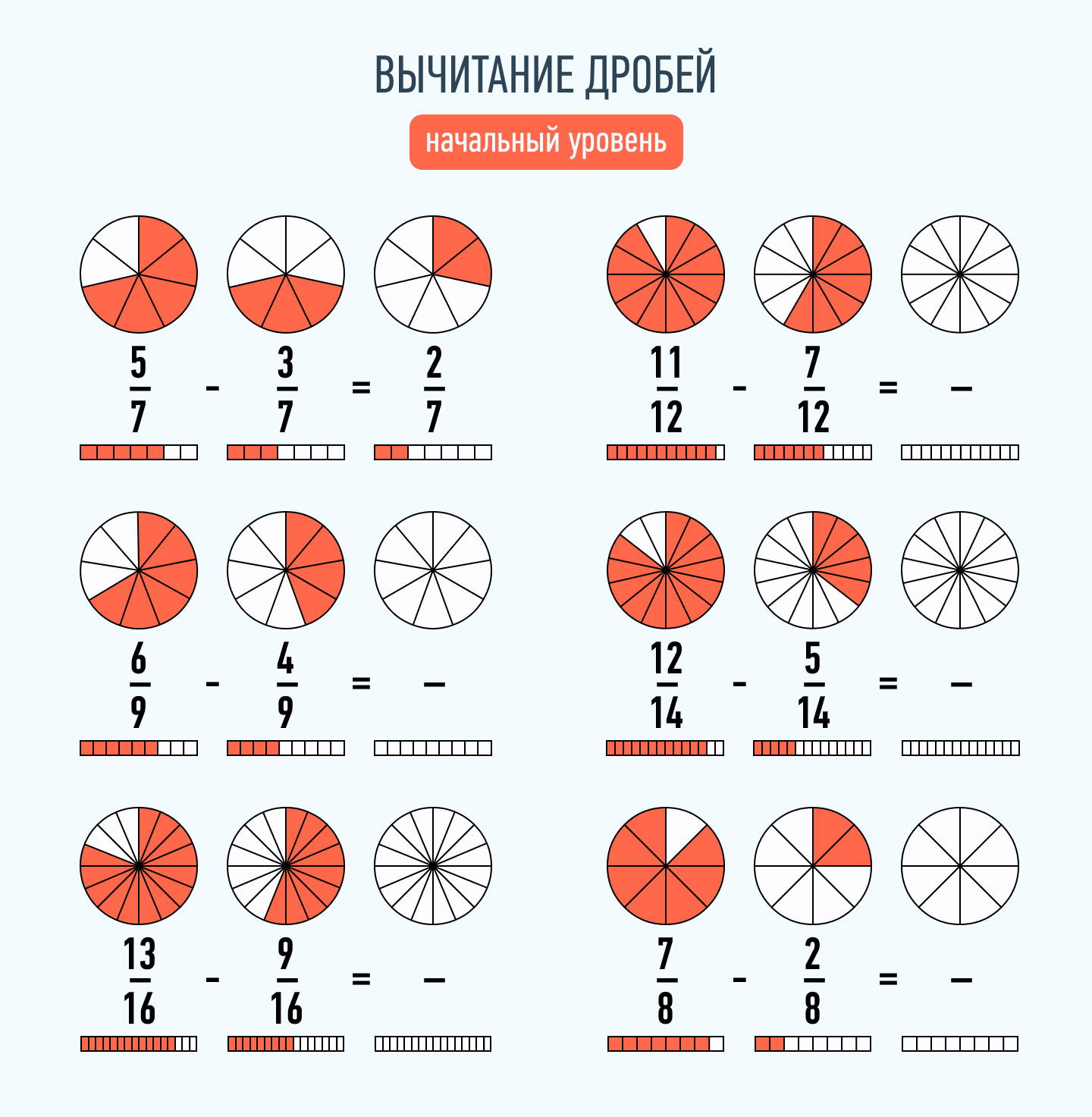
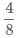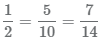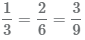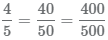В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Как объяснить суть дробей ребенку?
Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.
Что нужно знать о дробях?
1. Дробь — число нецелое, оно обозначает количество долей целого.
2. Дробь меньше целого.
3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.
Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.
Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.
Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.
Что такое смешанные дроби?
В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.
Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.
Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.
Примеры:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Задание:
Выделите целую часть из неправильных дробей:
- 15/4,
- 22/12,
- 30/7.
Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.
Примеры:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Задание:
1. Преобразовать в смешанное число неправильную дробь:
- 27/4,
- 18/5,
- 45/7.
2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:
- 3 4/5;
- 12 7/11.
Десятичные дроби
Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.
Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».
Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления применяется человечеством с самых древних времен. Она интуитивна понятна и проста.
Задание:
Преобразовать следующие дроби в десятичные:
- 8/10,
- 4/100,
- 7/1000.
Сокращение дробей
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Пример 1. Сократить дробь 8/12
Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:
8/12 = 8:4 / 12:4 = 2/3
Пример 2. Сократить дробь 10/25
Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:
10/25 = 10:5 / 25:5 = 2/5
Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.
Задание:
Сократите следующие дроби:
- 6/18,
- 20/40;
- 7/21.
Сложение дробей
Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
Примеры:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Задание:
Выполни сложение дробей с одинаковыми знаменателями:
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.
Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:
- 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
- 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.
Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.
Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:
- 18/42 + 14/42 = 32/42
Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.
Задание:
Выполни сложение дробей с разными знаменателями:
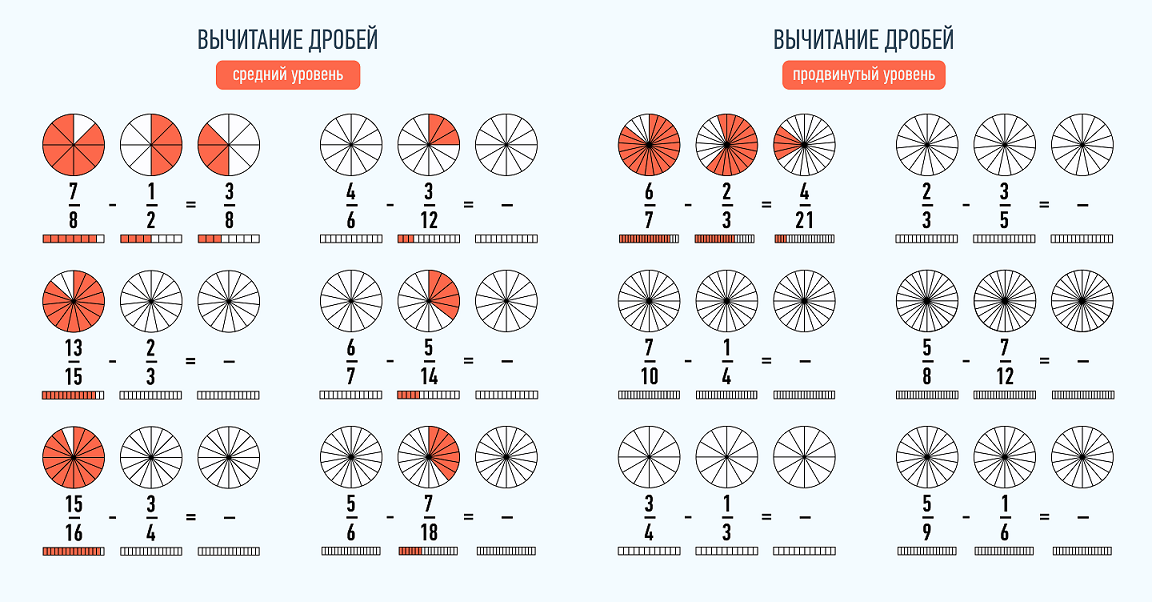
Вычитание дробей
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
7/9 — 2/9 = (7-2) / 9 = 5/9
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Умножение дробей
Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.
Умножение обыкновенных дробей
В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.
Пример:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.
Пример:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Умножение смешанных дробей
Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.
Пример:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Задание:
Выполните умножение дробей:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Деление дробей
Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Пример:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
Пример:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Задание:
Выполните деление дробей:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
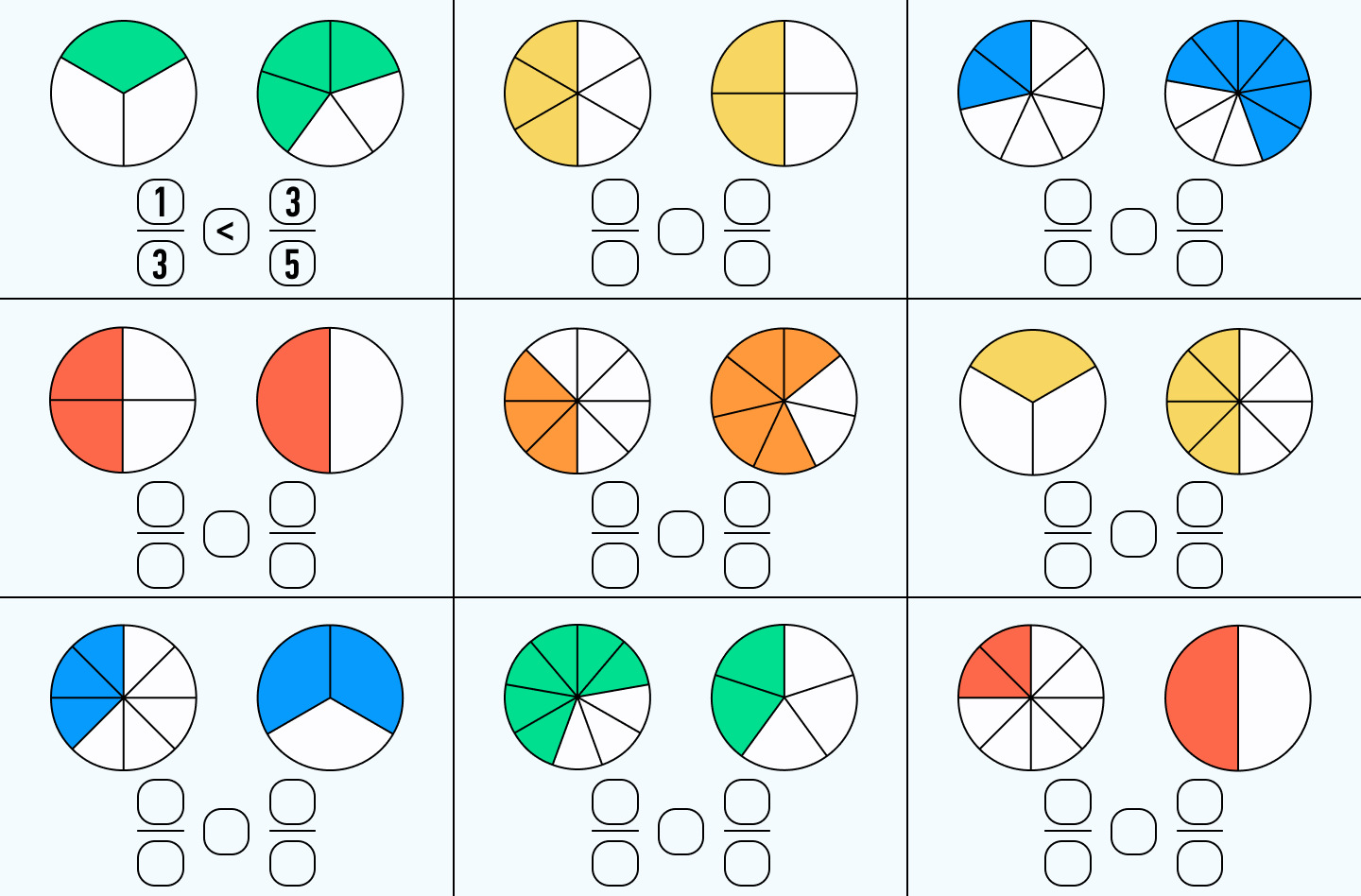
Сравнение дробей
Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.
Пример:
1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.
Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.
Пример:
1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.
Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Пример:
Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.
Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
Задание:
Определите, какие дроби изображены на рисунке, и сравните их:
Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.


Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Читайте также:
- Таблица умножения для детей
- Как объяснить ребенку состав числа?
Математика
5 класс
Урок № 47
Понятие дроби
Перечень рассматриваемых вопросов:
- обыкновенная дробь;
- числитель и знаменатель обыкновенной дроби;
- правильная, неправильная дробь.
Тезаурус
Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы.
Правильные дроби – это дроби, в которых числитель меньше знаменателя
Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя.
Обязательная литература:
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Очень часто в жизни мы слышим такие выражения: «Прошел половину пути», «Купил четвертинку хлеба», «Сделал третью часть от работы». Все эти выражения связаны с новым понятием «дробь». О ней сегодня и пойдёт речь.
Чтобы ввести понятие дроби, выполним следующее задание.
Две части будут весить две третьих килограмма.
Если на отрезке АС укладывается ровно 3 раза отрезок длиной одна пятая сантиметра, то говорят, что длина отрезка равна три пятых сантиметра.
Такие записи называются обыкновенными дробями или просто дробями.
Дробь показывает какую-то часть от целого или единицы. Например, дробь семь восьмых показывает семь восьмых части от единицы.
Обозначенное таким образом число называют рациональным числом. При этом p называется числителем дроби (он всегда находится над чертой), а q – знаменателем дроби (он всегда находится под чертой).
Рассмотрим виды обыкновенных дробей. Обыкновенные дроби можно разделить на следующие виды – правильные, когда числитель меньше знаменателя, и неправильные, когда числитель равен или больше знаменателя.
Сколько часов содержится в четверти суток?
Так как в сутках 24 часа, то нам по условию надо найти четвёртую часть, т. е. разделить двадцать четыре часа на четыре части.
Решим задачу, используя понятие обыкновенной дроби.
В коробке находилось два вида конфет: 5 шоколадных и 6 карамелек. Какую часть всех конфет занимают карамель и шоколад?
Решение: для начала найдём общее количество конфет в коробке, для этого сложим все виды конфет.
5 + 6 = 11 – конфет в коробке.
Теперь можно найти, какую часть от общего количества конфет занимает карамель, а какую шоколадные конфеты. Для этого запишем результат в виде обыкновенной дроби, где в знаменателе укажем общее число конфет. Пять одиннадцатых – часть шоколадных конфет, а шесть одиннадцатых – часть карамели.
Тренировочные задания
№ 1. Сколько минут содержится в одной трети часа?
Решение: для решения этой задачи достаточно вспомнить, что 1 ч = 60 мин.
Найдём третью часть от 60 минут, для этого:
60 мин : 3 = 20 мин
Ответ: 20 мин.
№ 2. Длина отрезка АВ равна 10 см. Чему равен отрезок, длина которого составляет две пятых от длины отрезка АВ?
Решение: сначала найдём, чему равна одна часть из 5 отрезков.
10 см : 5 = 2 см – одна часть.
По условию задачи нужно найти 2 части из пяти, поэтому: 2 см · 2 = 4 см
Ответ: 4 см.
Доли введение
Доли
Круг состоит из 4 разноцветных равных частей. Учащиеся разрезали круг на 4 равные части. Эти равные части называются долями.
Каждому досталась «одна четвертая доля круга», или, короче, «одна четвертая круга». Записывают 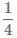
Разноцветный круг
1
1/4
1/4
1/4
1/4
Долю 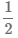
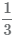
долю 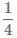
Половина, треть, четверть
1/2
1/3
1/4
Дроби
Обыкновенные дроби
Записи вида 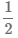
В дроби 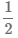
На примере круга: знаменатель — общее количество долей на которые разделили, числитель — количество долей полученных вами.
Пример: Красным цветом отмечена половина отрезка. Можно сказать что красным выделена 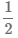
Вы должна запомнить расположение и названия числителя и знаменателя.
Равенство дробей
Равные дроби
Дроби могут различаться по записи, но при этом быть равными. Имеются 3 равных половинки круга, первая половина закрашена красным цветом,
вторая половина разделена на 2 части и закрашена, 3 половина разделена на 3 части.
Каждую из этих половинок круга можно представить в виде дроби 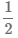
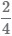
которые равны между собой 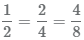
Равные дроби, состоящие из разного количества долей.
1/2
2/4
4/8
Примеры равных дробей:
Сложение дробей
Сложение дробей
Вы можете легко складывать дроби с одинаковыми знаменателями, для этого достаточно сложить их числители, а знаменатель останется тем же.
Ниже представлены примеры сложения частей 2 кругов.
Смотрите также
Другие страницы
В 5 классе на уроках математики ученики знакомятся с дробями и процентами. В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.

Число под чертой (знаменатель), показывает, на сколько частей разделили целое.
Число над чертой (числитель) показывает, сколько этих частей выбрано.
То есть дробь $frac{3}{8}$ (три восьмых) означает, что целое было разделено на 8 частей, а взято из них три.
Существуют три класса задач на дроби: нахождение дроби от числа, нахождение числа по его дроби и выражение отношения чисел в виде дроби.
Как найти дробь от числа
В задачах на дробь от числа известно само число и дробь, которая от него взята. А найти требуется, какую величину составит эта дробь. Рассмотрим такую задачу
Пример 1.1.
В самолёте 120 пассажиров. $frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?
Это задача на нахождение дроби от числа.
Есть число: 120.
Есть дробь: $frac{2}{5}$
Нужно найти, чему равны две пятых от 120.
Решаются задачи на нахождение дроби от числа так.
Решение
Задаём себе два вопроса:
1. Чему равна $frac{1}{5}$ (одна пятая) от 120?
Для этого 120 делим на 5, получаем 24.
2. Чему равны $frac{2}{5}$ (две пятых) от 120?
Результат 24, корый мы получили, нужно умножить на 2.
Получаем 48.
Значит, $frac{2}{5}$ от 120 составляет 48.
Ответ: 48 пассажиров летят впервые.
Попробуем решить ещё одну задачу на нахождение дроби от числа.
Пример 1.2.
В городе живут 1 500 000 человек. Из них $frac{3}{25}$ — школьники. Сколько в городе школьников?
Решение
1. Чему равна $frac{1}{25}$ от 1 500 000?
1 500 000:25 = 60 000
2. Чему равны $frac{2}{25}$ от 1 500 000?
60 000*3 = 180 000
Ответ: 180 000 школьников.
Когда вы набрались опыта решать такие задачи по вопросам, эти два вопроса можно свести в одно действие и использовать правило:
Чтобы найти дробь от числа, нужно это число умножить на дробь
Или, что то же самое:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на её числитель
Пример 1.3.
В автосалон завезли 14 автомобилей. За месяц продали 2/7 этого количества. Сколько автомобилей продали?
Решение
Умножим 14 на $frac{2}{7}$:
$14cdot frac{2}{7} = frac{14cdot 2}{7} = 2cdot 2 = 4$
Ответ: 4 автомобиля.
Теперь рассмотрим задачи второго типа:
Как найти число по дроби
В задачах этого типа исходное число неизвестно. Зато известна величина некоторой части от этого числа и какую дробь составляет эта часть от исходного числа. Для удобства рассмотрим, как бы выглядели эти же три задачи, если бы в них требовалось найти число по дроби.
Пример 2.1.
В самолёте сидят пассажиры (сколько их неизвестно!). Известно, что 48 пассажиров или $frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?
Решение
Эти 48 пассажиров, которые летят впервые, составляют две пятых ($frac{2}{5}$) от общего количества пассажиров в салоне. Мы можем найти одну пятую?
Да, нужно 48 разделить на 2.
48:2 = 24.
Мы узнали, что одна пятая часть от всех пассажиров — это 24 человека. Сколько всего пассажиров? В пять раз больше, то есть 24х5 = 120.
Ответ: 120 пассажиров всегов самолёте
Понятно? Давайте разберём ещё одну задачу.
Пример 2.2.
Три двадцать пятых ($frac{3}{25}$) населения города составляют школьники. Школьников в городе 180 000. Каково общее население города?
Решение
Опять само число (то есть население города) на неизвестно, зато известно, чему равны $frac{3}{25}$ от него.Значит, можно сначала найти, чему равна $frac{1}{25}$ от населения города. Разделим 180 000 на 3:
180 000:3 = 60 000
Зная одну двадцать пятую, можно найти и целое, умножив 60 000 на 25.
60 000х25 = 1 500 000
Ответ: в городе 1 500 000 жителей
Когда будете уверенно решать задачи на нахождение числа по его дроби по вопросам, можно будет заменить эти вопросы одним действием и использовать правило:
Чтобы найти число по его дроби, известную величину нужно разделить на эту дробь
Или, что то же самое:
Чтобы найти число по его дроби, известную величину нужно разделить на числитель дроби и умножить на её знаменатель
Пример 2.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4, что составляет 2/7 всех автомобилей. Сколько автомобилей завезли в салон?
Решение
Разделим 4 на $frac{2}{7}$:
$4: frac{2}{7} = frac{4cdot 7}{2} = 2cdot 7 = 14$
Ответ: 14 автомобилей завезли в салон.
И перейдём теперь к третьему типу задач на дроби, которые изучаются в математике 5 класса:
Как найти отношение двух чисел и выразить его в виде дроби
В задачах на нахождение отношения оба числа известны, а нужно найти, какую дробь второе число составляет от первого. Решаются они проще всего
Пример 3.1.
В самолёте 120 пассажиров. Из них 48 человек летят в первый раз. Какая часть пассажиров летит в первый раз?
Решение
Чтобы найти, какую дробь 48 составляет от общего количества пассажиров (120), нужно 48 разлелить на 120 и затем скоратить, что возможно.
Доля летящих впервые пассажиров составляет $frac{48}{120}$.
И числитель, и знаменатель делятся на 2, значит, можно сократить на 2.
$frac{48}{120}=frac{24}{60}$
Сократим ещё раз на 2:
$frac{24}{60} = frac{12}{30}$
И ещё раз:
$frac{12}{30} = frac{6}{15}$
Теперь можно сократить на 3:
$frac{6}{15} = frac{2}{5}$
Больше сокращать не на что — это и можно записать как окончательный ответ задачи.
Ответ: $frac{2}{5}$ пассажиров летят впервые.
Так что правило для решения задач на нахождение отношения чисел самое простое:
Чтобы найти, в виде какой дроби выражается отноешние двух чисел, нужно сначала записать дробь, в которой числитель и знаменатель — эти числа, а затем сократить её.
Обратите внимание, что дробь $frac{A}{B}$ обозначает, какую долю величина А составляет от величины В и правильно записывайте величины в числитель и знаменатель.
Разберём ещё два примера.
Пример 3.2.
В городе с населением 1 500 000 жителей живут 180 000 школьников. Какую часть населения города составляют школьники?
Решение
Нужно найти, какую часть 180 000 составляет от 1 500 000?
Записываем дробь и сокращаем:
$frac{180000}{1500000}=frac{18}{150}=frac{9}{75}=frac{3}{25}$
Ответ: школьники составляют $frac{3}{25}$ от общего населения города
Пример 3.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4. Какую часть от всех автомобилей это составляет, если всегов автомалон завезли 14 машин?
Решение
Точно так же, берём дробь $frac{4}{14}$ и сокращаем:
$frac{4}{14}=frac{2}{7}$
Ответ: продали $frac{2}{7}$ от общего количества автомобилей.
Вот как решаются задачи на дроби. Вы найдёте справочники по формулам математики 5, 6 и других классов в разделе «Математика в школе».