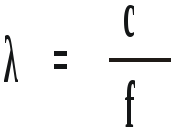Как найти частоту звуковых колебаний
Звуком называют волны механических деформаций, распространяющиеся в любой достаточно упругой среде (жидкостях, твердых телах, газах). Как и другие волны, звук характеризуется, в частности, частотой колебаний. В зависимости от начальных условий найти частоту звука можно разными способами.

Вам понадобится
- — калькулятор;
- — физический справочник;
- — тахометр;
- — звуковой датчик;
- — осциллограф.
Инструкция
Найдите частоту звуковых колебаний, если известна длина их волн и скорость звука в среде, где они распространяются. Вычисления следует производить по формуле F=V/L. Здесь V — скорость звука в среде, а L — длина волны (известная величина). Значения скоростей звука для разных сред можно узнать из физических справочников. Так, для воздуха при нормальных условиях (температуре в районе 20°C и давлении, близком к атмосферному) это значение составляет 341 м/с. Поэтому, например, звуковые колебания в воздухе с длиной волны в 0,25 м будут иметь частоту 341/0,25=1364 Гц.
Найти частоту звуковых колебаний, зная их период, можно по простой формуле: F=1/T. Обратите внимание на то, что для получения корректных значений частоты, представленных в герцах, период T должен быть выражен системе СИ, то есть иметь размерность в секундах.
Для получения частоты звуковых колебаний, распространяющихся в реальной среде, осуществите физический эксперимент. Примените специализированное устройство — тахометр. Сегодня тахометры, как правило, имеют высокую точность измерений и отображают информацию в готовом виде на цифровом индикаторе.
При отсутствии тахометра для нахождения частоты звука можно воспользоваться микрофоном или другим звуковым датчиком с достаточной чувствительностью, а также осциллографом. Подключите датчик к осциллографу и создайте условия для получения сигнала (например, поместите датчик в исследуемую среду). Подберите чувствительность осциллографа так, чтобы колебания на экране отображались с достаточной амплитудой. Путем подстройки частоты развертки добейтесь отображения устойчивой картинки. Узнайте период звуковых колебаний, ориентируясь на шкалу прибора. Найдите частоту, используя способ, описанный во втором шаге.
Обратите внимание
При вычислениях, связанных с получением значений частоты звука, всегда переводите все известные значения в систему СИ.
Полезный совет
Если дополнительно требуется найти циклическую частоту звуковых колебаний, рассчитайте ее по формуле w=2*PI*F, где F — частота, выраженная в герцах, полученная одним из описанных способов.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Загрузить PDF
Загрузить PDF
Частота (или частота волны) — это число полных колебаний или циклов волны, совершенных в единицу времени. Есть несколько различных способов вычислить частоту в зависимости от данной вам информации.
-
1
Формула: f = V / λ[1]
- где f — частота, V — скорость волны, λ — длина волны.
- Пример: вычислите частоту звуковой волны, если длина волны равна 322 нм, а скорость звука равна 320 м/сек.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.[2]
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 322 нм
- 322 нм x (1 м / 10^9 нм) = 3,22 x 10^-7 м = 0,000000322 м
-
3
Разделите скорость волны на ее длину. Для вычисления частоты (f) разделите скорость волны (V) на ее длину (λ), выраженную в метрах.[3]
- Пример: f = V / λ = 320 / 0.000000322 = 993788819,88 = 9,94 x 10^8
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 9,94 х 10^8 Гц.
Реклама
-
1
Формула: f = C / λ. Формула для вычисления частоты волны в вакууме практически идентична формуле для вычисления частоты волны в средах. В вакууме не существует факторов, влияющих на скорость волны, поэтому в формуле используется постоянная величина скорости света, с которой распространяются электромагнитные волны в вакууме.[4]
- В формуле f — частота, С — скорость света, λ — длина волны.
- Пример: вычислите частоту электромагнитной волны, если ее длина равна 573 нм.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 573 нм
- 573 нм х ( 1 м / 10^9 нм) = 5,73 х 10^-7 м = 0,000000573
-
3
Разделите скорость света на длину волны. Скорость света является постоянной величиной, которая равна 3,00 х 10^8 м/с. Разделите эту величину на длину волны (в метрах).[5]
- Пример: f = С / λ = 3,00 х 10^8 / 5,73 х 10^-7 = 5,24 х 10^14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 5,24 х 10^14 Гц.
Реклама
-
1
Формула: f = 1 / T.[6]
Частота обратно пропорциональна времени, которое необходимо для совершения одного колебания волны.- В формуле f — частота, Т — время, которое необходимо для совершения одного колебания волны.
- Пример А: вычислите частоту волны, если ей необходимо 0,32 с для совершения одного колебания.
- Пример B: за 0,57 секунд волна совершает 15 колебаний. Вычислите частоту этой волны.
-
2
Разделите число колебаний на время. Если в задаче дано время, затрачиваемое на 1 колебание, то в этом случае просто разделите 1 на время (Т). Если в задаче дано время, затрачиваемое на несколько колебаний, то в этом случае разделите данное количество колебаний (n) на время (Т).[7]
- Пример А: f = 1 / T = 1 / 0,32 = 3,125
- Пример B : f = n / T = 15 / 0,57 = 26,316
-
3
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример А: частота волны равна 3,125 Гц.
- Пример B: частота волны равна 26,316 Гц.
Реклама
-
1
Формула: f = ω / (2π)[8]
- где f — частота, ω — угловая частота, π — число Пи (математическая константа).
- Пример: волна вращается с угловой частотой 7,17 радиан в секунду. Вычислите частоту этой волны.
-
2
Умножьте Пи на два.
- Пример: 2 * π = 2 * 3,14 = 6,28
-
3
Разделите угловую частоту (в радианах в секунду) на удвоенное число пи (6,28).[9]
- Пример: f = ω / (2π) = 7,17 / (2 * 3,14) = 7,17 / 6,28 = 1,14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота волны равна 1,14 Гц.
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Бумага
Об этой статье
Эту страницу просматривали 113 996 раз.
Была ли эта статья полезной?
Звуковая волна – период, длина, частота и скорость распространения
Калькуляторы онлайн перевода длины звуковой, инфразвуковой или ультразвуковой
волны в частоту и наоборот. Таблица соответствия
нот полного звукоряда частотам.
Звуковая волна – это механические колебания, которые в результате колебаний молекул вещества распространяются в какой-либо
среде (в газе, жидкости или твёрдом теле) и, достигнув органов слуха человека, воспринимаются им как звук. Источник, создающий
возмущение (колебания воздуха), называется источником звука.
Как уже было сказано, для распространения звука необходима какая-либо упругая среда. Поэтому в вакууме ори, не ори – тебя никто не
услышит, по причине того, что звуковые волны распространяться не смогут, так как там нечему колебаться.., да и слушать там, по большому
счёту, тоже некому.
Так же, как и в случае с электромагнитными волнами, соотношение, связывающее длину звуковой волны с частотой колебаний,
в общем случае выглядит следующим образом:
λ (м) = V (м/сек) / F (Гц), где V (м/сек) — это скорость распространения
звука в среде.
Период колебаний также не претерпел никаких изменений и по-прежнему равен:
T(сек) = 1 / F (Гц) = λ (м) / V (м/сек).
Частота колебаний звукового сигнала F (Гц) – это параметр стабильный, практически не зависящий от среды распространения.
А вот скорость звука V (м/сек), а соответственно и длина звуковой волны – это величины, которые зависят
не только от плотности вещества, но и от его упругости, а в случае с жидкостями и газами ещё – и от температуры, и атмосферного
давления.
Зависимость скорости звуковой волны от свойств упругой среды легко прослеживается по следующей формуле:
V (м/сек) = √Eупр (паскаль) / ρ (кг/м3)
,
где Eупр представляет собой модуль объёмной упругости среды, а ρ – плотность среды.
Модуль упругости, так же как и плотность – это справочные величины, прописанные для конкретных материалов.
В качестве примера, ниже приведена таблица величины скорости распространения звука в различных средах:
| Среда | Скорость звука, м/сек |
| Воздух при 0° | 331 |
| Воздух при 30° | 350 |
| Вода | 1450 |
| Медь | 3800 |
| Дерево | 4800 |
| Железо | 4900 |
| Сталь | 5600 |
Для газов параметры модуля объёмной упругости и плотности имеют ярко выраженную зависимость от температуры и атмосферного давления.
Если углубиться, то скорость звука в газах можно вычислить по следующей формуле:
V (м/сек) = √γ*Ратм / ρ ,
где
γ = cp/сv – это отношение удельной теплоёмкости при постоянном давлении
к удельной теплоёмкости при постоянном объёме, а Pатм – атмосферное давление,
которое связано с температурой газообразной среды.
Поэтому, чтобы никого сильно не грузить, приведу и приближённую зависимость скорости звука (при нормальном
атмосферном давлении) от температуры среды:
V (м/сек) = (331 + 0,6 * T°), где 331 м/сек – это скорость звука при 0°С,
а T° – температура в градусах Цельсия.
Теперь можно совместить формулы и получить простое соотношение, связывающее длину звуковой волны с частотой колебаний с учётом
температуры среды:
λ (м) = (331 + 0,6 * T°) / F (Гц).
Всё это без лишнего напряга несложно посчитать при помощи листа бумаги или деревянных счёт, ну а для пущего упрощения жизни человека,
приведу и пару он-лайн считалок для перевода одного из параметров в другой.
Калькуляторы предполагают расчёты длины и частоты звуковой волны для воздушной среды при нормальном атмосферном
давлении (760 мм ртутного столба).
Онлайн калькулятор расчёта длины звуковой волны по частоте
|
Частота звуковых колебаний f |
||
Температура Т(°С) (по умолчанию 20°) |
||
Длина волны |
Онлайн калькулятор расчёта частоты по длине звуковой волны
|
Длина волны λ при заданной Т |
||
Температура Т(°С) (по умолчанию 20°) |
||
Частота колебаний |
Полный диапазон звуковых частот условно находится в пределах:
16…20 000 Гц.
Ниже ( 0,001…16Гц ) – инфразвук.
Выше ( 20…100кГц ) – низкочастотный ультразвук,
ещё выше (100кГц…1МГц) – высокочастотный ультразвук.
А для интересующихся приведу таблицу соответствия нот стандартного музыкального звукоряда частотам.
| Частота (Гц) | ||||||||||||
| Октава | Нота | |||||||||||
| До | До — диез | Ре | Ми — бемоль | Ми | Фа | Фа — диез | Си | Си- диез | Ля | Соль-бемоль | Соль | |
| C | C# | D | Eb | E | F | F# | G | G# | A | Bb | B | |
| 0 | 16.35 | 17.32 | 18.35 | 19.45 | 20.60 | 21.83 | 23.12 | 24.50 | 25.96 | 27.50 | 29.14 | 30.87 |
| 1 | 32.70 | 34.65 | 36.71 | 38.89 | 41.20 | 43.65 | 46.25 | 49.00 | 51.91 | 55.00 | 58.27 | 61.74 |
| 2 | 65.41 | 69.30 | 73.42 | 77.78 | 82.41 | 87.31 | 92.50 | 98.00 | 103.8 | 110.0 | 116.5 | 123.5 |
| 3 | 130.8 | 138.6 | 146.8 | 155.6 | 164.8 | 174.6 | 185.0 | 196.0 | 207.7 | 220.0 | 233.1 | 246.9 |
| 4 | 261.6 | 277.2 | 293.7 | 311.1 | 329.6 | 349.2 | 370.0 | 392.0 | 415.3 | 440.0 | 466.2 | 493.9 |
| 5 | 523.3 | 554.4 | 587.3 | 622.3 | 659.3 | 698.5 | 740.0 | 784.0 | 830.6 | 880.0 | 932.3 | 987.8 |
| 6 | 1047 | 1109 | 1175 | 1245 | 1319 | 1397 | 1480 | 1568 | 1661 | 1760 | 1865 | 1976 |
| 7 | 2093 | 2217 | 2349 | 2489 | 2637 | 2794 | 2960 | 3136 | 3322 | 3520 | 3729 | 3951 |
| 8 | 4186 | 4435 | 4699 | 4978 | 5274 | 5588 | 5920 | 6272 | 6645 | 7040 | 7459 | 7902 |
Физика > Частота звуковых волн
Чему равна частота звуковой волны – частота, длина и скорость звука. Изучите единицу измерения, формулу частоты звуковой волны, что определяет, диапазон.
Частота – количество повторяющихся событий за временную единицу.
Задача обучения
- Объединить частоту, длину и скорость звука.
Основные пункты
- Частота основывается на длине и звуковой скорости:
- Период – длительность цикла повторяющегося события. Выступает обратной частоте.
- Единица измерения – Герц (количество циклов в секунду).
Термины
- Частота – количество периодического события за временную единицу: f = n/t.
- Герц – один период в секунду, единица частоты (Гц).
- Период – длительность цикла в повторяющемся событии.
Звуковые волны обладают частотой, то есть количеством вхождений повторяющегося события за временную единицу.
Частота колебаний звуковой волны основывается на длине волны и скорости звука:
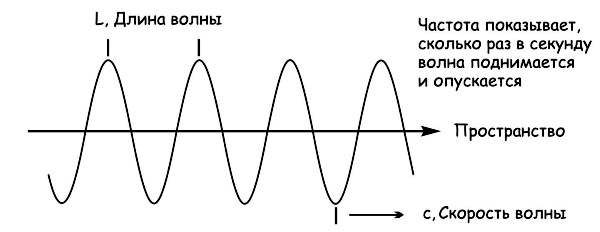
Нижний рисунок демонстрирует связь частоты и длины.
Звуковая волна формируется из источника, вибрирующего на частоте (f), и распространяется при v на длине λ
Частота звуковой волны определяет и другие характеристики. Можно использовать частоту и длину, чтобы отыскать скорость волны. Не забывайте, что она зависит от того, в какой среде перемещается звук. Высокие показатели появляются в твердых веществах. Формула: vs = fλ.
Период – длительность цикла повторяющегося события. В анимации показаны различные частоты и периоды (от наименьшего к наивысшему).
Три мигающих огонька: от самой низкой частоты (сверху) до наивысшей (снизу). F – частота в Герцах. Т – период в секундах
Герц
Единица измерения – Герц (Гц). Это количество циклов в секунду: 100 Гц = 100 циклам.
Различные виды улавливают разные частотные диапазоны. Люди способны услышать 20 – 200000 Гц, а собаки до 60000 Гц. У летучих мышей диапазон вырастает до 120000 Гц. Последние применяют ультразвук, чтобы сориентироваться в пространстве или найти объекты. Звуковые волны отбиваются от предметов. Животное улавливает, сколько времени нужно на возврат, и понимает, какая дистанция образовалась. Это эхолокация.
2.1. Частота звука.
Мы
сталкиваемся со звуком каждый день. По
сути, наши уши ни когда не слышали тишины,
потому как в естественных условиях её
практически не существует (примеры
тишины и источников громких звуков).
Однако, что такое звук?
З
– это колебательный процесс, возникающий
в воздухе (или другой упругой среде) под
действием каких либо колеблющихся
предметов.
Источниками
звука могут быть, например, голосовые
связки человека, струны музыкальных
инструментов или любой другой вибрирующий
предмет, заставляющий колебаться
окружающие его частицы. При этом плотность
воздуха (или другой среды) начинает то
увеличиваться, то уменьшаться в
соответствии с этими колебаниями. Воздух
является упругой средой и оказывает
некоторое обратное сопротивление
колебательному процессу, именно таким
образом происходит сжатие и разряжение
воздушного пространства.
Звуки
образованные синусоидальными сигналами
называются простыми, «чистыми», к ним
можно отнести камертон и флейту. Звуки
других инструментов (голосов, шумов)
имеют более сложные по форме колебания
и могут содержать в себе целое созвучие
простых тонов.
Однако
чтоб понять принцип воздействия звука
на наши слуховые ощущения достаточно
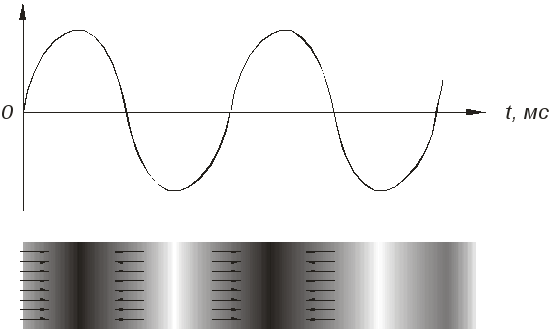
рассмотреть элементарный звук. Его
можно описать графиком изменения во
времени давления воздуха в определенной
точке. При
этом в фазу сжатия среды принято называть
положительной, а фазу разряжения –
отрицательной.
Распределяясь
в стороны со скоростью ~340 м/сек. звуковые
колебания образуют звуковую волну.
Эта
волна воздействует на барабанную
перепонку уха, приводит её в движение,
которые передаются далее по внутреннему
уху, вызывая слуховые ощущения.
Звук
ограничен рамками пространства –
стенами, преградами. Воздух состоит из
частиц, которые тоже являются преградой
на пути следования звука. Энергия,
передаваемая этими частицами со временем
угасает, таким образом, ограничивая
пространство в котором звучит тот или
иной объект. Чтобы достичь наибольшего
пространства звучания необходима
бо́льшая энергия его источника. Таким
образом появляется некое «звуковое
поле» звучания того или иного источника
(гром, комар)
Звуковое
поле – это область распределения
звуковых волн.
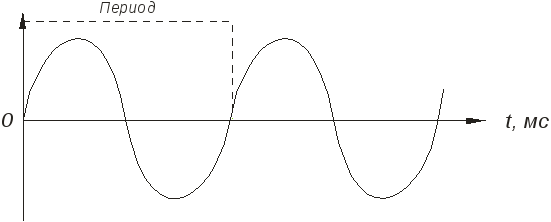
Полный
цикл изменения звукового давления
называется периодом. Количество этих
периодов в одну секунду определяет
частоту звука, которая измеряется в
Герцах (Гц).
Другими
словами это наименьшее расстояние между
точками с одинаковыми фазами колебания,
длину которого можно измерить в метрах
на условной оси распределения звука.
В
акустике, принято считать длины волн в
метрах, это необходимая норма для
произведения ряда расчетов. Чтобы
определить длину волны (λ) необходимо
знать её частоту (f)
и скорость распределения звука (с).
Формула
длины звуковой волны: ,(м.)
(пример
применения значений длин волн,
λ=340/100=3,4 м.)
Понятие
о длине звуковой волны поможет в
дальнейшем объяснить закономерности
интерференции (сложении) и дифракции
(распределении) звуковых волн в
пространстве, помещении студий залов
и т.д. Так же необходимо понимать каким
размером должен обладать источник
звука, что бы создавать, достаточное
для восприятия, звуковое давление.
Однако
стоит помнить том, что звук в воздушной
среде совершенно отличается от звука
в воде, в разряженном воздухе. Частицы
окружающего пространства передают
энергию, строго подчиняясь законам
физики. Чем плотнее среда, тем лучше
происходит передача звука, чем разреженней
пространство, тем меньше передается
энергия. Например, в вакууме звук не
распространяется, в воде передается со
скоростью 1485 м/сек., а в твердых телах
скорость звука составляет 2000—6500 м/с.
Источники
звука.
Наиболее
простым источником звука является
камертон
– небольшой
источник точно и ясно издающий звук
определённой высоты.
Его усы, колеблясь, в пространстве
вызывают простые, синусоидальные
колебания. Обычно частота издаваемого
камертоном звука 440 Гц, что соответствует
ноте «ля» первой октавы.
Струна
– весьма распространенный источник
звука, однако следует учесть, что звук
изданный струной почти не слышим нашими
ушами, это объясняется её толщиной.
Плоскость струны настолько мала, что
колебаний воздушной среды не достаточно,
чтобы возникло возбуждение барабанной
перепонки и слуховых ощущений. Для того
что бы звук струны был слышим необходим
значительный по размерам резонатор,
который предоставляет струне большую
плоскость, тем самым усиливая громкость
звучания. Частота звука струны определяется
её длиной, это её собственная частота
возбуждения. При наличии механизмов и
устройств, способных сократить струну
(лады на гитаре, кулачки в арфе) на
определенный отрезок, появляется
возможность изменить частоту её
возбуждения (примеры).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #