Загрузить PDF
Загрузить PDF
Частота (или частота волны) — это число полных колебаний или циклов волны, совершенных в единицу времени. Есть несколько различных способов вычислить частоту в зависимости от данной вам информации.
-
1
Формула: f = V / λ[1]
- где f — частота, V — скорость волны, λ — длина волны.
- Пример: вычислите частоту звуковой волны, если длина волны равна 322 нм, а скорость звука равна 320 м/сек.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.[2]
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 322 нм
- 322 нм x (1 м / 10^9 нм) = 3,22 x 10^-7 м = 0,000000322 м
-
3
Разделите скорость волны на ее длину. Для вычисления частоты (f) разделите скорость волны (V) на ее длину (λ), выраженную в метрах.[3]
- Пример: f = V / λ = 320 / 0.000000322 = 993788819,88 = 9,94 x 10^8
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 9,94 х 10^8 Гц.
Реклама
-
1
Формула: f = C / λ. Формула для вычисления частоты волны в вакууме практически идентична формуле для вычисления частоты волны в средах. В вакууме не существует факторов, влияющих на скорость волны, поэтому в формуле используется постоянная величина скорости света, с которой распространяются электромагнитные волны в вакууме.[4]
- В формуле f — частота, С — скорость света, λ — длина волны.
- Пример: вычислите частоту электромагнитной волны, если ее длина равна 573 нм.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 573 нм
- 573 нм х ( 1 м / 10^9 нм) = 5,73 х 10^-7 м = 0,000000573
-
3
Разделите скорость света на длину волны. Скорость света является постоянной величиной, которая равна 3,00 х 10^8 м/с. Разделите эту величину на длину волны (в метрах).[5]
- Пример: f = С / λ = 3,00 х 10^8 / 5,73 х 10^-7 = 5,24 х 10^14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 5,24 х 10^14 Гц.
Реклама
-
1
Формула: f = 1 / T.[6]
Частота обратно пропорциональна времени, которое необходимо для совершения одного колебания волны.- В формуле f — частота, Т — время, которое необходимо для совершения одного колебания волны.
- Пример А: вычислите частоту волны, если ей необходимо 0,32 с для совершения одного колебания.
- Пример B: за 0,57 секунд волна совершает 15 колебаний. Вычислите частоту этой волны.
-
2
Разделите число колебаний на время. Если в задаче дано время, затрачиваемое на 1 колебание, то в этом случае просто разделите 1 на время (Т). Если в задаче дано время, затрачиваемое на несколько колебаний, то в этом случае разделите данное количество колебаний (n) на время (Т).[7]
- Пример А: f = 1 / T = 1 / 0,32 = 3,125
- Пример B : f = n / T = 15 / 0,57 = 26,316
-
3
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример А: частота волны равна 3,125 Гц.
- Пример B: частота волны равна 26,316 Гц.
Реклама
-
1
Формула: f = ω / (2π)[8]
- где f — частота, ω — угловая частота, π — число Пи (математическая константа).
- Пример: волна вращается с угловой частотой 7,17 радиан в секунду. Вычислите частоту этой волны.
-
2
Умножьте Пи на два.
- Пример: 2 * π = 2 * 3,14 = 6,28
-
3
Разделите угловую частоту (в радианах в секунду) на удвоенное число пи (6,28).[9]
- Пример: f = ω / (2π) = 7,17 / (2 * 3,14) = 7,17 / 6,28 = 1,14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота волны равна 1,14 Гц.
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Бумага
Об этой статье
Эту страницу просматривали 113 996 раз.
Была ли эта статья полезной?
Длина волны

4.1
Средняя оценка: 4.1
Всего получено оценок: 226.
4.1
Средняя оценка: 4.1
Всего получено оценок: 226.
Для описания волновых процессов в Природе используется ряд специальных величин, специфичных для распространения волн. Важнейшим среди них является длина волны. Рассмотрим это понятие, а также его связь с другими понятиями волновых процессов.
Волна и ее распространение
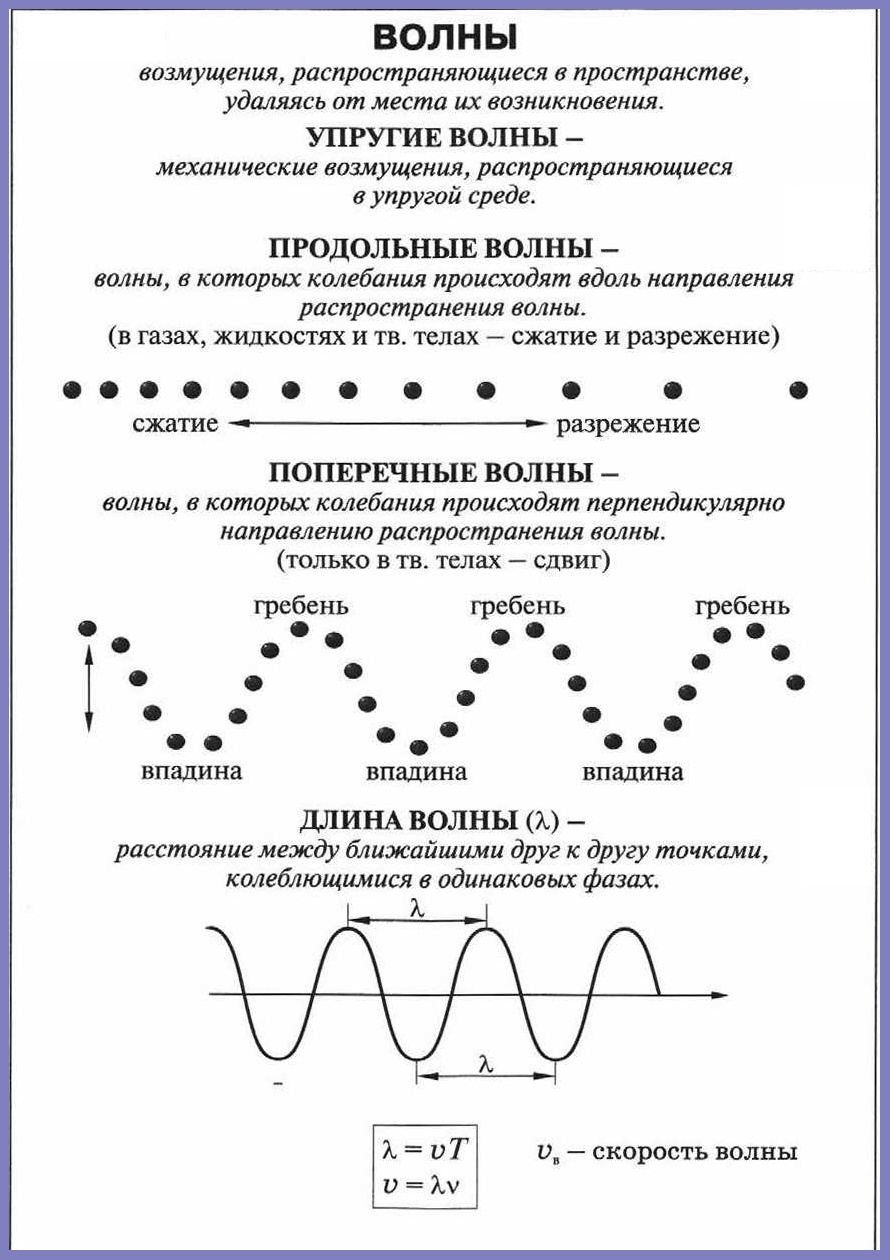
Движение – форма существования материи. Одним из широко распространенных в природе движений является колебательное движение, при котором измеряемая величина изменяется не монотонно, а циклически увеличивая и уменьшая свое значение.
В протяженных объектах любые изменения (и в том числе колебательные процессы), как правило, происходят не сразу во всем объекте, а сперва начинаются в одной его части, а потом распространяются на остальной объект.
Для наблюдения распространения колебательных движений удобно использовать поверхность воды. В первый момент колеблются только частицы воды непосредственно в месте возникновения волны. Далее происходит распространение колебательного движения. При этом сами частицы воды в горизонтальном направлении не движутся, движется лишь само колебание водной глади.
Волна – это колебания среды, распространяющиеся в ней с течением времени.
Параметры волны
Фаза, период и частота
Для распространяющейся волны можно ввести параметр, который называется фазой. Фаза – это одинаковое состояние среды распространения. Для поверхности воды фаза – это величина отклонения от спокойного состояния (от нулевого уровня). Точки волны, находящиеся в одинаковом состоянии, будут находиться в одинаковых фазах. Если записывать в таблицу время, проходящее между одинаковыми фазами какой-то точки, то можно заметить, что это время будет кратно некоторому минимальному значению. Это значение, минимальное время, за которое волна оказывается в одной и той же фазе, называется периодом колебаний $T$ волны. Число периодов за одну секунду называется частотой волны $nu$ (для обозначения используется греческая буква «ню»):
$$nu={1over T}$$
Фазу можно сопоставить с углом на координатной плоскости. Полная волна соответствует углу $2pi$, все фазы повторяются с этим периодом точно так же, как повторяется значение круговых функций (синуса, косинуса и других).
Одному значению отклонения от нулевого значения соответствуют две фазы – одна в момент возрастания, другая – в момент спадания волны (исключение – самый «пик» или самое «дно» волны). Это разные фазы, путать их не следует.
Скорость распространения и длина волны
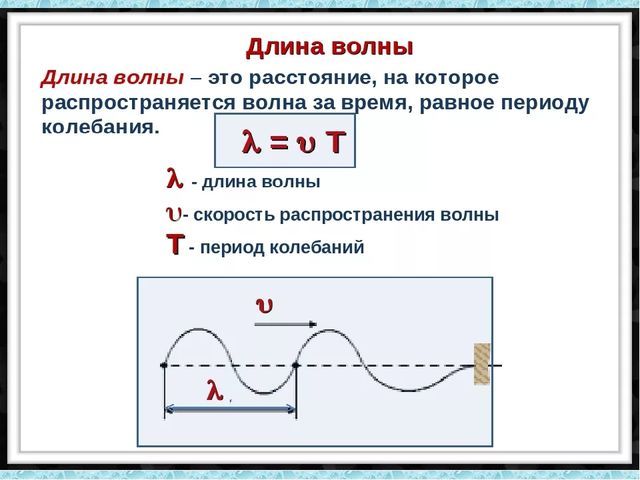
Поскольку волна распространяется не мгновенно, то, отметив одинаковую фазу волны (движущийся гребень), можно определить скорость этого распространения $v$ относительно неподвижных предметов (например, относительно берега, в случае, когда волна распространяется вдоль него). Для вычисления используется обычная формула скорости – отношение пройденного расстояния к прошедшему времени. Кроме того, можно ввести понятие «длина волны».
Расстояние, которое проходит волна за один период колебания, называется длиной волны, для обозначения используется греческая буква $lambda$ (лямбда). Формула длины волны:
$$lambda=vT$$
Если известна частота колебаний, для расчета удобнее пользоваться другой формулой (она вытекает из определения частоты):
$$lambda={vover nu}$$
Слышимый звук представляет из себя колебания плотности воздуха. Распространяется он в нормальных условиях со скоростью, имеющей значения порядка 300-350м/с, и имеет длину волны от ~15мм (самые высокие частоты) до ~15м (самые низкие частоты)
Что мы узнали?
Волна – это колебания среды, распространяющиеся в ней с течением времени. Волна характеризуется рядом параметров, среди которых фаза, период, скорость распространения, длина.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Егор Князев
7/10
Оценка доклада
4.1
Средняя оценка: 4.1
Всего получено оценок: 226.
А какая ваша оценка?
Каждая волна имеет свои параметры движения.
Скорость волны — скорость распространения возмущения.
Пример:
воздействуя на стальной стержень с одного конца, можно вызвать волны сжатия и разрежения со скоростью (5000 frac{м}{с}).
Скорость волны зависит от строения вещества и взаимодействия между её молекулами (атомами). Поэтому в различных средах скорость одной и той же волны будет отличаться.
Помимо скорости, важной характеристикой волны является длина волны.
Длина волны — расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Рассмотрим процесс передачи колебаний от точки к точке при распространении поперечной волны.
Используется модель, в которой частицы среды заменяют шариками. Для удобства их можно пронумеровать (рис. (1)).
Частицы среды связаны между собой межмолекулярными силами взаимодействия, поэтому волна передаётся от одной частицы к другой.
Рис. (1). Модель упругой среды для демонстрации колебаний
Отклоним первый шарик от положения равновесия. Силы притяжения передадут движение второму, третьему шарику. Каждый элемент вещества (молекула, атом) повторит движение первой частицы с запаздыванием, которые называют сдвигом фазы. Это запаздывание зависит от расстояния, на котором находится рассматриваемый шарик по отношению к первому шарику.
Предположим, что первый шарик достиг максимального смещения от положения равновесия (рис. (2)). В этот момент четвёртый шарик только начнет движение, следовательно, он отстаёт от первого на (1/4) колебания.
Рис. (2). Изображение максимального смещения от положения равновесия первого шарика
В момент времени, когда смещение четвертого шарика будет наибольшим (рис. (3)), седьмой шарик будет отставать от него на (1/4) колебания. А если рассмотреть отставание седьмого шарика от первого, то оно составляет (1/2) колебания.
Рис. (3). Изображение максимального смещения от положения равновесия четвёртого шарика
Между седьмым и четвёртым шариком, а также седьмым и десятым (1/4) часть колебания (рис. (4)).
Рис. (4). Изображение максимального смещения от положения равновесия седьмого шарика
Первый и тринадцатый шарик совершают одно колебание, то есть двигаются в одной фазе (рис. (5)). Это значит, что между ними все шарики с первого по двенадцатый проходят полный колебательный процесс или составляют одну волну.
Рис. (5). Изображение максимального смещения от положения равновесия десятого шарика
Начиная с тринадцатого шарика, мы можем отсчитывать новую волну (рис. (6)).
Рис. (6). Изображение модели новой волны
Длину волны измеряют расстоянием, на которое перемещается волновая поверхность за один период колебания источника волн;
Длиной волны является расстояние между двумя ближайшими точками бегущей волны на одном луче, который колеблется в одинаковой фазе:
, где (λ) («лямбда») — длина волны, (upsilon) — скорость волны, (T) — период колебания.
Период колебаний можно выразить как величину, обратную частоте колебаний:
T=1ν
.
Тогда выразим длину волны как отношение скорости и частоты:
λ=υν
.
Длина волны прямо пропорциональна скорости волны и обратно пропорциональна частоте колебаний (прямо пропорциональна периоду колебаний).
Поперечные и продольные волны описываются одними и теми же законами.
Выразим скорость волны:
как отношение длины волны к периоду колебаний:
υ=λT
;
как произведение длины волны на частоту колебаний:
υ=λν
.
За длину волны (λ) примем расстояние между шариками, колеблющимися в одинаковых фазах. Например (см. рис. (6)), между четвёртым и шестнадцатым, третьим и пятнадцатым.
Колебания проходят шарики, начиная с первого и заканчивая двенадцатым, проходят все фазы колебания. Новая волна начинается с тринадцатого шарика. Каждый шарик совершает одно полное колебание за время, которое называют периодом колебаний (T). За это время колебательный процесс проходит расстояние, называемое длиной волны (λ.)
Модель распространения продольных волн представлена на рисунке (7).
Длиной волны будет расстояние между соседними центрами сжатия пружины.
Рис. (7). Распространение продольных волн в упругой пружине
Источником колебаний генерируется волна той же частоты, поэтому вынужденные колебания совпадают по частоте с осциллятором и не зависит от плотности среды, в которой движется волна.
Если в ходе движения волна переходит в среду другой плотности, то скорость движения волны изменяется, а частота колебаний остаётся прежней.
Источники:
Рис. 1. Модель упругой среды для демонстрации колебаний. © ЯКласс.
Рис. 2. Изображение максимального смещения от положения равновесия первого шарика. © ЯКласс.
Рис. 3. Изображение максимального смещения от положения равновесия четвёртого шарика. © ЯКласс.
Рис. 4. Изображение максимального смещения от положения равновесия седьмого шарика. © ЯКласс.
Рис. 5. Изображение максимального смещения от положения равновесия десятого шарика. © ЯКласс.
Рис. 6. Изображение модели новой волны. © ЯКласс.
Рис. 7. Распространение продольных волн в упругой пружине. © ЯКласс.
Основные формулы по физике — КОЛЕБАНИЯ И ВОЛНЫ
При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.
Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.
Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.
Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна — это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
Смотрите также основные формулы квантовой физики
Таблица формул: колебания и волны
|
Физические законы, формулы, переменные |
Формулы колебания и волны |
||||
|
Уравнение гармонических колебаний: где х — смещение (отклонение) колеблющейся величины от положения равновесия; А — амплитуда; ω — круговая (циклическая) частота; t — время; α — начальная фаза; (ωt+α ) — фаза. |
|
||||
|
Связь между периодом и круговой частотой: |
|
||||
|
Частота: |
|
||||
|
Связь круговой частоты с частотой: |
|
||||
|
Периоды собственных колебаний 1) пружинного маятника: где k — жесткость пружины; 2) математического маятника: где l — длина маятника, g — ускорение свободного падения; 3) колебательного контура: где L — индуктивность контура, С — емкость конденсатора. |
|||||
|
Частота собственных колебаний: |
|
||||
|
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А1 и А2 — амплитуды составляющих колебаний, α1 и α2 — начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания |
|
||||
|
Уравнение затухающих колебаний: е = 2,71… — основание натуральных логарифмов. |
|
||||
|
Амплитуда затухающих колебаний: где А0 — амплитуда в начальный момент времени; β — коэффициент затухания; t — время. |
|
||||
|
Коэффициент затухания: колеблющегося тела где r — коэффициент сопротивления среды, m — масса тела; колебательного контура где R — активное сопротивление, L — индуктивность контура. |
|
||||
|
Частота затухающих колебаний ω: |
|
||||
|
Период затухающих колебаний Т: |
|
||||
|
Логарифмический декремент затухания: |
|
||||
|
Связь логарифмического декремента χ и коэффициента затухания β: |
|
||||
|
Амплитуда вынужденных колебаний где ω — частота вынужденных колебаний, fо — приведенная амплитуда вынуждающей силы, при механических колебаниях: при электромагнитных колебаниях: |
|
||||
|
Резонансная частота |
|
||||
|
Резонансная амплитуда |
|
||||
|
Полная энергия колебаний: |
|
||||
|
Уравнение плоской волны: где ξ — смещение точек среды с координатой х в момент времени t; k — волновое число: |
|
||||
|
Длина волны: где v скорость распространения колебаний в среде, Т — период колебаний. |
|
||||
|
Связь разности фаз Δφ колебаний двух точек среды с расстоянием Δх между точками среды: |
|
Поделитесь ссылкой с друзьями:
Похожие таблицы
Комментарии:
Задачи на Механические волны с решениями
Формулы, используемые на уроках «Задачи на Механические волны».
Название величины |
Обозначение |
Единица измерения |
Формула |
Длина волны |
λ |
м |
λ = vT ;λ = v / v |
Скорость волны |
v |
м/с |
v = λ / T ;v = λv |
Период колебаний |
T |
с |
T = λ / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = v / λ ;v = N / t |
Число колебаний |
N |
N = t / T ;N = vt |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Лодка качается на волнах, распространяющихся со скоростью 4 м/с, и за 10 с совершает 20 колебаний. Каково расстояние между соседними гребнями волн?
Задача № 2.
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Задача № 3.
Скорость звука в эбоните 2400 м/с, а в кирпиче — 3600 м/с. В каком веществе звуковому сигналу требуется большее время для распространения? Во сколько раз?
Задача № 4.
Расстояние между ближайшими гребнями волн в море 6 м. Лодка качается на волнах, распространяющихся со скоростью 2 м/с. Какова частота ударов волн о корпус лодки?
Задача № 5.
Наблюдатель, находящийся на расстоянии 2 км 150 м от источника звука, слышит звук, пришедший по воздуху, на 4,8 с позднее, чем звук от того же источника, пришедший по воде. Определите скорость звука в воде, если скорость звука в воздухе равна 345 м/с.
Задача № 6.
Охотник выстрелил, находясь на расстоянии 170 м от лесного массива. Через сколько времени после выстрела охотник услышит эхо?
Задача № 7.
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача № 8.
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача № 9.
Длина волны в воздухе 17 см (при скорости 340 м/с). Найти скорость распространения звука в теле, в котором при той же частоте колебаний длина волны равна 1,02 м.
Задача № 10.
ОГЭ
Расстояние между гребнями волн в море λ = 5 м. При встречном движении катера волна за t = 1 с ударяет о корпус катера N1 = 4 раза, а при попутном — N2 = 2 раза. Найти скорость катера и волны.
Задача № 11.
ОГЭ
Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду А = 0,25 мм, распространяются в воздухе. Длина волны λ = 70 см. Найти скорость распространения колебаний v и максимальную скорость частиц среды.
Краткая теория для решения Задачи на Механические волны.
Это конспект по теме «ЗАДАЧИ на Механические волны». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.