Как найти частоту водорода формула

Изучение спектра атома водорода

Цель
работы:
Исследовать спектр атомарного водорода,
вычислить постоянную Ридберга.

Приборы
и принадлежности:
Монохроматор, газосветные трубки с
водородом.

Введение

Спектр
испускания возникает при переходе атома
из более возбуждённого состояния в
менее возбуждённое. Величина испущенного
кванта энергии определяется разностью
энергетических уровней начального и
конечного состояний.

В
простейшем случае (атом водорода)
сказанное можно проиллюстрировать
небольшим расчётом с использованием
постулатов Бора и второго закона Ньютона
(сила кулоновского притяжения ядром
электрона сообщает ему нормальное
ускорение).

Постулаты Бора

Первый постулат

Существуют
стационарные состоянии, находясь в
которых, атом не излучает и не поглощает
энергию.

Стационарными
являются такие состояния, для которых
выполняется условие:

mr

n_iħ
(n_i

1, 2, 3,…),

где
m
– масса электрона, 
– скорость электрона,
r
– радиус его орбиты, ħ

h/(2)

1,0310^34
Дж/с – постоянная Планка.

Второй постулат

При
переходе атома из состояния с энергией
W_j
в состояние с энергией W_i
испускается или поглощается один фотон
частотой _Ф,
энергия которого рассчитывается по
формуле

E_Ф

h_Ф

W_j

W_i.

Если
W_i

W_j,
происходит излучение фотона, если W_i

W_j,
– поглощение фотона.

Для
атома водорода уравнения, описывающие
поведение электрона, имеют вид:

mr

n_iħ,
(1)

.
(2)

Решая
систему, можно получить значения r
и 
на соответствующей орбите.

Полная энергия
электрона:

W

W_К

W_П



.
(3)

Подставив
r
и 
из уравнений (1) – (2) в уравнение (3),
получим:

W

.

Отсюда:

_Ф

.

Множитель
обозначается буквойR
и называется постоянной Ридберга; R

3,2910¹⁵
c^1.

Линейчатые
спектры обусловлены испусканием
электромагнитного излучения свободными
или слабо связанными атомами. Одним из
источников такого излучения является
возбужденный газ или пар. В данной работе
используются газосветные трубки,
наполненные водородом и неоном.

Установлено,
что спектральные линии атомарного
водорода обнаруживают несложные
закономерности. Частоты соответствующих
линий могут быть определены по формуле

ν

R

(4)

где
ν – частота, ν 
c/,
с
–
скорость
света в вакууме, λ
– длина
волны,
R

постоянная Ридберга, n_i
и n_j
–
целые числа, причем n_j
может принимать значения (n_i

1),(n_i

2),(n_i

3), ….

Рассмотрим
переход атома из различных возбужденных
состояний на один и тот же энергетический
уровень, определяемый квантовым числом
n_i.
Совокупность спектральных линий,
отвечающая таким переходам, образует
серию. Таким образом, n_i
определяет серию. Соответственно
квантовое число n_j
определяет
энергетический уровень, с которого имел
место данный переход, то есть линию в
серии.

Различным
сериям атома водорода: Лаймана, Бальмера,
Пашена, Брэккета, Пфунда отвечают
соответственно значения n_i

1, 2, 3, 4, 5.

Рассмотрим,
как определить частоты спектральных
линий атома водорода, принадлежащих
серии Бальмера, используя комбинационный
принцип, математическое выражение
которого представлено равенством (2).
Для серии Бальмера n_i

2, n_j

3, 4, 5… Следовательно,

ν

Rc(5)

Если
приписать n_j
значения
соответственно 3, 4, 5, 6, то из уравнения
(5) получим значения частот спектральных
линий, лежащих в видимой области и
обозначаемых в спектроскопии H_
H_
H_γ,
H_.
По мере увеличения n_j
разность частот соседних линий
уменьшается, и
при n_j

→ 
сами
частоты
стремятся к пределу

_ГР

R

где
_ГР
–
частота,
соответствующая границе серии Бальмера.
У каждой серии есть своя граница,
соответствующая ей частота определяется
соотношением:

_ГР

R

Рассмотрим
физический смысл _ГР.
Согласно Бору, при переходе атома с
более высокого j-го
энергетического уровня на менее высокий
i-й
уровень излучается квант энергии

hν

E_j

E_i
(6)

Соответственно,
чтобы перевести электрон с уровня i
на уровень j,
необходимо сообщить ему такую же энергию.

Частота
ν_гр
определяет
энергию (Е

h_ГР),
которую
надо сообщить электрону, чтобы удалить
его
с уровня, определяемого числом и, в
пространство за пределы атома, где его
полная
энергия должна быть равна нулю.

Описанный
процесс называется процессом ионизации,
а Е
h_ГР
является
энергией ионизации атома в данном
состоянии.

Эта
величина связана с потенциалом ионизации
простым соотношением:


h_ГР/e,
где
e
– элементарный
заряд, равный 1,610^19
Кл.

Процесс обратный
ионизации: захват электрона атомом
будет сопровождаться излучением света.

Поскольку
электрон, отделенный от атома, может
обладать произвольной кинетической
энергией
W_К,
то
при его захвате ионом должна освобождаться
энергия (h_ГР

W_К).Следовательно,
согласно
второму постулату Бора (1) в этом случае
будет испускаться электромагнитное
излучение
с частотой

ν




_ГР


Таким
образом, возможно излучение с частотой,
большей нежели частота границы серии,
на любую величину W_К/h.
Это означает, что к границе серии со
стороны высоких частот прилегает
сплошной спектр. Излучение спектров
испускания позволяет исследовать
строение атома.

          Частоты всех
спектральных линий атома водорода можно представить одной формулой, которая
была получена экспериментально и называется обобщенной формулой Бальмера:

                                                      
,                                             (1.1)

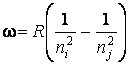
где  –
циклическая (круговая) частота;

       – постоянная Ридберга. Она равна  с^-1;

       – целые числа, которые для различных
серий и различных линий спектра принимают следующие значения:

–   – для серии Лаймана;

–   – для серии Бальмера;

–   – для серии Пашена и т.д.

Таким образом, частоты
спектральных линий в серии Бальмера опишутся формулой:

                                                            ,                                        (1.2)

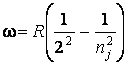
где  ….

          В спектроскопе
принято характеризовать спектральные линии не частотой, а обратной длине волны
величиной:

                                                                   .                                              (1.3)

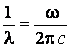
Формула Бальмера в этом случае имеет вид:

                                                               
.                                    (1.4)

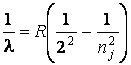
Постоянная Ридберга  в формуле (1.4) имеет значение  и измеряется в м^-1.

          В таблице 1.1 приведены
значения длин волн  серии Бальмера,
рассчитанные по формуле (1.4).

          При возрастании  длина волны  стремится
к предельному значению , которое называется
границей серии. Для серии Бальмера () граница серии
обозначается символом .

Таблица 1.1

Теория Бора это попытка объяснить модель атома пользуясь идеями Планка , о дискретности электромагнитного излучения.

В соответствии с ними Н. Бор предположил, что процессы, происходящие при этом внутри атома, также подчиняются квантовым закономерностям.

Что такое теория Бора

Модель атома, предложенная Резерфордом, не могла удовлетворительно объяснить механизм излучения атомом электромагнитных волн, так как по мере излучения энергия электрона, а вместе с ней и скорость его движения вокруг ядра должны убывать и в конце концов электрон должен упасть на ядро.

В 1913 г. Н. Бор предложил новую теорию излучения света атомами, в основу которой были положены идеи М. Планка. Теория Н. Бора основывается на двух постулатах.

1. Внутренняя энергия атома дискретна, т. е. может принимать только определенные дозволенные значения или уровни, кратные некоторым характерным для данного атома количествам или квантам энергии. Состояния, соответствующие этим уровням энергии, являются стационарными (равновесными): находясь в таком состоянии, атом не излучает электромагнитных волн несмотря на происходящее в нем движение электронов.
2. Испускание (или поглощение) атомом электромагнитного излучения происходит при переходе из одного стационарного состояния в другое. При этом испускается (или поглощается) фотон монохроматического излучения с энергией E_ф, равной разности энергетических уровней Е₂ и Е₁ соответствующих этим состояниям:

Е_ф = Е ₂ — Е₁.

Частота излучения v соответствует энергии фотона:

v = E_ф/h = (E₂ —E₁)/h

где h — постоянная Планка.

Для согласования выдвинутых им положений с Резерфордовской моделью атома Н. Бор предложил считать, что стационарным состояниям или дозволенным энергетическим уровням атома соответствует движение электронов по орбитам определенного радиуса. Эти орбиты должны удовлетворять условию, чтобы момент количества движения l_э электрона был кратен постоянной Планка, деленной на 2π, т. е. где п — есть целое число, называемое квантовым числом атома, которое соответствует порядковому номеру орбиты. Число п может принимать значения: п — 1,2,3 …

Из этого условия можно определить радиусы дозволенных орбит электрона. В общем виде:

r = (h²/(4π²me²))(n²/Z)

где т — масса, е — заряд электрона, п — квантовое число или порядковый номер орбиты, Z — порядковый номер элемента.

Таким образом, радиусы дозволенных орбит прямо пропорциональны квадрату квантового числа и обратно пропорциональны порядковому номеру элемента. Например, для атома водорода (Z = 1) радиус наименьшей (п =1) орбиты r = 0,53•10^-8 см. Эта величина и характеризует порядок размеров атома.

Энергия электрона в атоме состоит из кинетической энергии движения по орбите (скорость порядка 10⁸ см/сек) и потенциальной энергии в поле ядра. Обе величины зависят от радиуса орбиты. Следовательно, определенным радиусам орбит соответствуют определенные энергетические уровни.

Изменение энергии электрона

Как изменяется энергия электрона и энергетический уровень атома при изменении радиуса орбиты.

1. При увеличении радиуса орбиты скорость движения электрона уменьшается, соответственно уменьшается и его кинетическая энергия.
2. Для того чтобы удалить электрон от ядра, надо совершить работу против сил притяжения, следовательно, потенциальная энергия электрона с увеличением радиуса орбиты увеличивается.

При этом потенциальная энергия возрастает на большую величину, чем уменьшается кинетическая, поэтому общая энергия электрона по мере увеличения радиуса орбиты увеличивается. Соответственно возрастают и энергетические уровни атома (рис. 2):

E₁ < Е₂ < Е₃ < …

Разность энергии между двумя соседними стационарными уровнями по мере увеличения радиуса орбит, наоборот, уменьшается:

∆E‘ > ∆E» > ∆E»’ > где ∆E‘ = E₂ — E₁; ∆E »= E₃ — E₂, …

Стационарный уровень с наименьшей энергией называется основным, он характерен для атома в обычном состоянии (т. е. атома, не подвергающегося никаким внешним воздействиям). Остальные стационарные уровни называются возбужденными.

Возбуждение атома

Возбуждение атома требует сообщения ему дополнительной энергии и, следовательно, происходит в результате какого-либо внешнего воздействия на атом.

Это может быть соударение частиц в процессе теплового движения или при электрическом разряде в газах, поглощение фотона электромагнитного излучения и т. п. Возбужденное состояние может возникнуть также при рекомбинации ионов в газе, под действием частиц радиоактивного излучения и т. д.

Возбужденное состояние атома неустойчиво (метастабильно). Как правило, примерно через 10^-8 сек электрон возвращается на основную орбиту, при чем излучает фотон, уносящий дополнительную энергию, полученную электроном при возбуждении атома (рис. , а). 

При этом атом возвращается в основное состояние. Электрон может возвращаться на основную орбиту не сразу, а ступеньками через промежуточные уровни, В этом случае будет излучаться несколько фотонов с частотой, соответствующей разности энергетических уровней ступеней перехода (рис. , б).

При люминесценции возбуждение атомов происходит в результате поглощения энергии фотонов падающего на вещество излучения.

Если энергия фотона достаточно велика (ультрафиолетовое и еще более коротковолновое рентгеновское излучение), то при этом происходит возбуждение атома с последующим излучением (рис. , в).

Для того чтобы перевести внешний электрон на одну из возбужденных орбит, требуется в зависимости от природы атома энергия порядка нескольких электрон-вольт.

При возвращении электрона на основную орбиту будут излучаться фотоны с такой же энергией, что соответствует частоте видимого или близкого к нему ультрафиолетового излучения.

При переходах электрона с одной возбужденной орбиты на другую излучаются фотоны с еще меньшей энергией, относящиеся к инфракрасному излучению.

Таким образом, оптическое излучение связано преимущественно с переходом внешних электронов.

Спектр излучения атомов водорода

Пример спектра излучения атомов водорода в теории атома водорода по бору В зависимости от энергии, сообщенной атому при возбуждении, электрон может перейти на различные возбужденные орбиты.

При возвращении его на основную орбиту будут излучаться фотоны различной энергии, т. е. с различной частотой или длиной волны.

Каждой длине волны излучения соответствует линия в спектре, поэтому в спектре излучения атома водорода должно быть значительное число линий, расположение которых отражает энергетические уровни атома.

В спектре же газа, когда свет излучается громадным количеством атомов, будут присутствовать все возможные линии.

Еще до создания теории Н. Бора было установлено, что в спектре водорода имеются группы (серии) линий, расположение которых подчинено определенным закономерностям.

Например, четыре линии в видимой части спектра вместе с линиями в близкой ультрафиолетовой части составляют серию Бальмера. Частоты всех линий этой серии можно выразить общей формулой: 

v = R ((1/2²) — (1/n²))

где R — постоянная, равная 3,29•10¹⁵ сек^-1, а п — переменное число, которое может принимать значение 3, 4, 5 и т. д.

Имеются и другие серии, например серия Лаймана в ультрафиолетовой части спектра, серии Пашена, Брекета и другие — в инфракрасной, частоты которых также могут быть выражены соответствующими формулами.

Расчеты частоты колебаний атомов водорода

Н. Бор произвел расчеты, в которых связал частоту колебаний, соответствующую длинам волн линий этих серий, с возможными в атоме водорода переходами между энергетическими уровнями.

На рис. 3 приведена диаграмма, в которой сопоставлены график распределения энергетических уровней (в), схема возможных переходов электрона (а), а также расположение линий в спектре (б). 

При переходе электрона с любой возбужденной орбиты на основную разность энергетических уровней наибольшая, фотоны имеют наиболее короткую длину волны и излучение лежит в ультрафиолетовой области (серия Лаймана).

При аналогичном переходе электрона на первую возбужденную орбиту разность энергетических уровней меньше, спектральные линии относятся к видимой части спектра (серия Бальмера).

При переходе электрона на вторую возбужденную орбиту энергия фотонов еще меньше и излучение лежит в инфракрасной области (серия Пашена и др.).

Таким образом, теория Бора получила полное подтверждение в установленных экспериментально спектральных закономерностях.

Статья на тему Теория Бора

Первая попытка создать квантовую теорию атома была сделана Н. Бором в $1913$ г. Он использовал планетарную модель атома, предложенную Резерфордом. Кроме того, в основу своей теории Бор положил два постулата:

1. Постулат стационарных состояний. Согласно нему в атоме существуют стационарные состояния. В данных состояниях атом не излучает энергии. Данным состояниям соответствуют стационарные орбиты. Движение электронов по таким орбитам происходит без излучения электромагнитных волн.

   Если электрон движется по стационарным круговым орбитам, то его момент импульса имеет дискретные квантованные значения, которые подчиняются условию:

   [m_evr_n=nhbar left(n=1,2,3,dots right)left(1right),]

   где $m_e$ — масса электрона, $v$- скорость электрона при движении по орбите радиуса $r_n$, $hbar =frac{h}{2pi }$.

2. Правило частот. Если электрон осуществляет переход с одной стационарной орбиты на другую, то излучается (поглощается) один фотон, имеющий энергию:

   [hnu =E_n-E_mleft(2right),]

   где $E_n и E_m$- энергии стационарных состояний атома до и после излучения (поглощения). Если $E_n > E_m$, то фотон излучается, при $E_n
   [nu =frac{E_n-E_m}{h}(3)]

   составляет линейчатый спектр атома.

Правила квантования

Энергии стационарных состояний электрона в атоме по Бору определяются правилом квантования. Если рассматривать круговые орбиты электронов в атоме, то стационарными являются только те орбиты, двигаясь по которым момент импульса электрона ($L$) равен целому числу постоянных Планка ($hbar $):

Целое число $n$ — квантовое число. Правило квантования определяет некоторое дискретное число орбит, выделяя из всего множества, которое допускает классическая механика.

Используя правило квантования, легко найти круговые стационарные орбиты водородоподобного атома. В водородоподобном атоме электрон, имеющий заряд $q_e$ ядра, заряд которого равен $Zq_e$. Масса электрона много меньше, чем масса ядра. Значит, ядро можно считать неподвижным, при этом электрон вращается по окружности ($r_n$ — радиус окружности) около ядра.

Сила, c которой электрон притягивается к ядру, равна:

Она же равна произведению центростремительного ускорения электрона на его массу, то есть:

Потенциальная энергия электрона, находящегося в поле ядра равна:

При этом полная энергия электрона:

Применяя правила квантования имеем:

Используем выражения (6) и (9) исключаем из них скорость, выражаем радиус стационарной орбиты:

В атоме водорода $Z=1$, радиус первой орбиты равен:

Параметр $r_0$ является первым Боровским радиусом.

Энергия электрона, который движется по орбите номер $n$, определена формулой (8), в которой под $r$ понимают радиус $r_n$. Получаем, что $E_n$ равна:

Формула (11) представляет уровни энергии стационарных состояний электрона в атоме водорода. Состояния атома при $n=1$ называют основным.

Круговые орбиты — частный случай орбиты электрона, который движется в поле ядра. В общем случае электрон должен перемещаться по эллиптическим орбитам. Обобщение правил квантования для такого случая выполнили Ч. Вильсон и А. Зоммерфельд. Квантовые условия (их количество j), которые накладываются в данном случае, с помощью квантовых условий, имеют вид:

В выражении (12) механическая система имеет $j$ степеней свободы. Ее описывают обобщение координаты $q_i$ ($i=1,2,dots ,j$) и обобщенные импульсы $p_i$, определенные как:

где $E_k$ — кинетическая энергия системы, ${dot{q}}_i$ — производные по времени от обобщенных координат. В выражении (12) используются координаты, которые разделяются, то есть в которых импульс является функцией от соответствующей обобщенной координаты.

Выражение для энергии стационарных состояний в случае эллиптических орбит имеет вид:

где ${n=n}_r+n_{varphi }$- главное квантовое число (азимутальное и радиальное квантовые числа).