Как найти частоту среза полосового фильтра

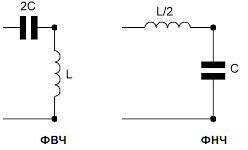
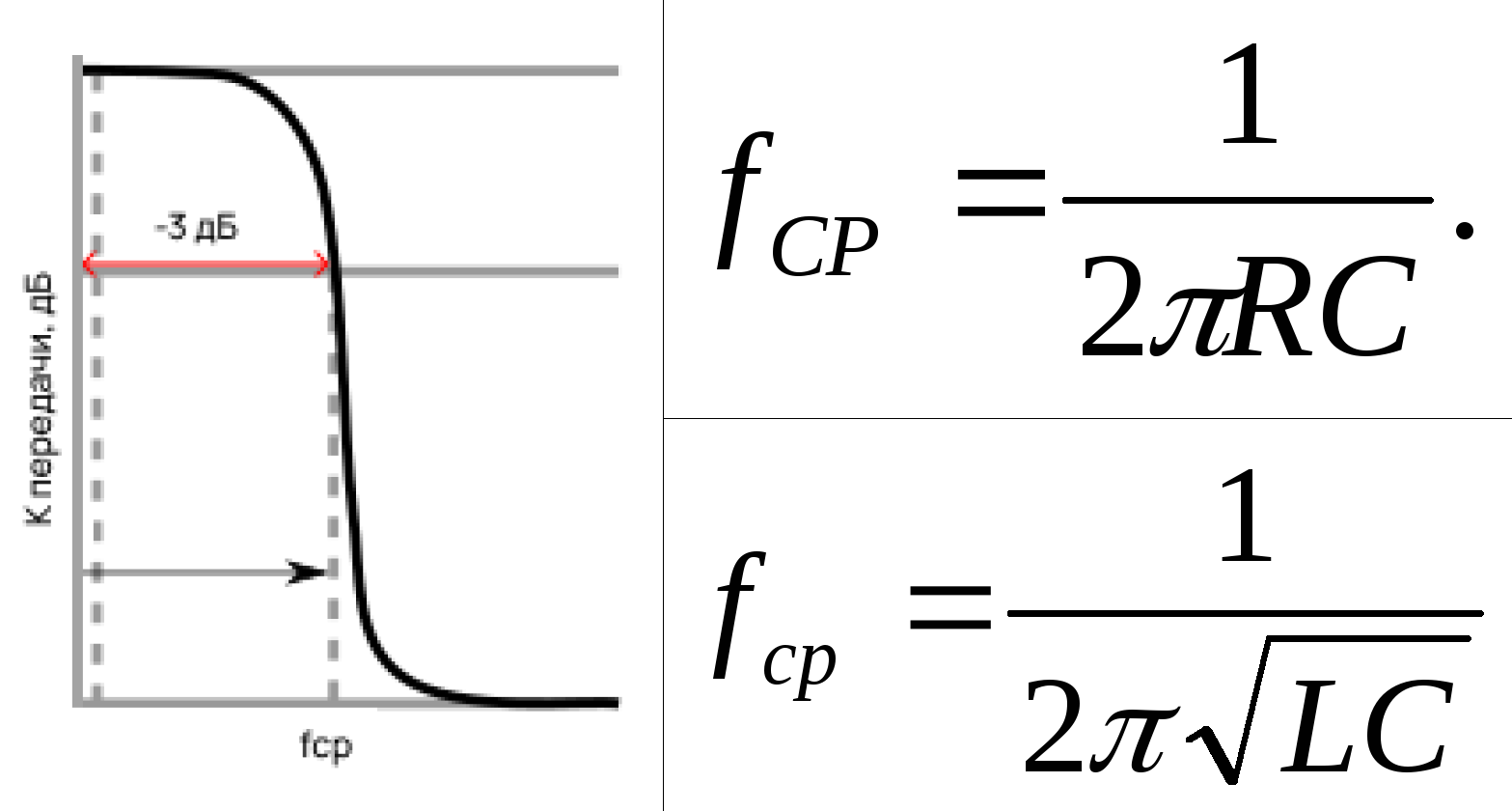Уровень сложности
Средний

Время на прочтение
7 мин

Количество просмотров 11K

Представьте: вы принимаете аналоговый сигнал, смотрите на результаты показаний и видите, что синусоиду «перекосило». Все из-за плохой селективности вашего приемника и шумов, которые он принимает. Чтобы выделить и выровнять полезный сигнал и не слушать бесконечное шипение, в радиоприемнике должны быть качественные фильтры. Но что это такое, как они работают и какими бывают? Давайте разбираться.

Используйте навигацию, если не хотите читать текст полностью:

→ Что такое частотный фильтр
→ Очередной резистивный делитель, или из чего состоят фильтры
→ Немного о параметрах частотных фильтров
→ Рассчитывать фильтры — это сложно
→ Собираем фильтр Чебышева

Что такое частотный фильтр

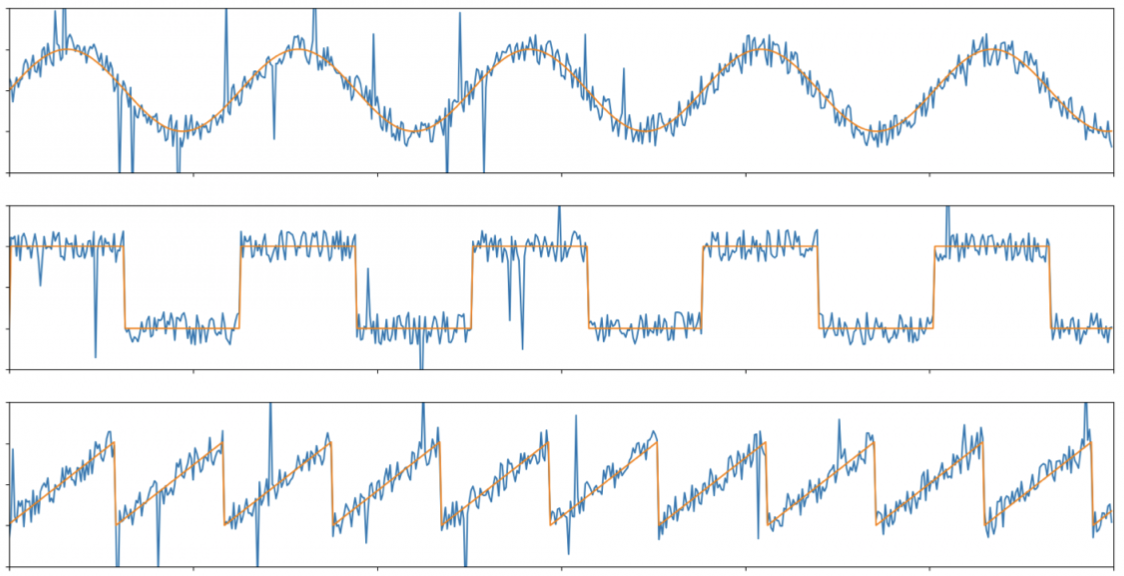
Синий сигнал — с шумами, оранжевый — идеальный, абсолютно чистый. Фильтр не может на 100% выпрямить сигнал, флуктуации все равно будут (см. пример, зеленый — отфильтрованный сигнал).

Частотный фильтр — это электрическая цепь, которая эффективно пропускает только одну область частот. Устройство позволяет «игнорировать» лишние частоты. Тем самым выделять и выравнивать сигналы любой формы — квадратные, синусоидальные, треугольные и другие.

Пример диапазона частот усиливаемого сигнала. Зависимость коэффициента пропускания по напряжению от частоты сигнала.

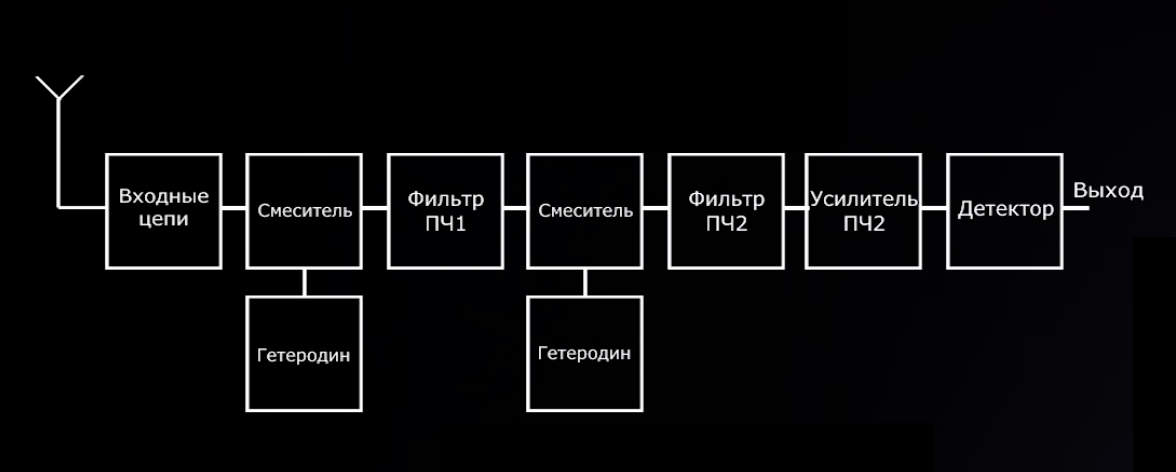
Фильтры широко применяют в измерительной, электронно вычислительной и радиотехнике. Яркий пример из схемотехники приемно-передающих устройств — ФНЧ/ ФПЧ в супергетеродинах и приемниках прямого преобразования, которые помогают выделить определенную частоту из диапазона.

Типичная схема супергетеродина.

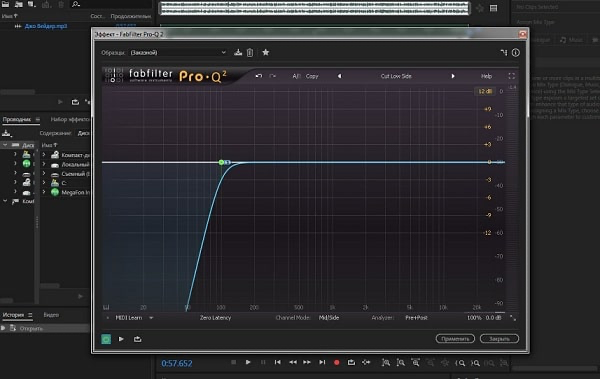
Фильтры используют не только в радиостанциях, усилителях и другой профессиональной технике. Их можно встретить в любом приемно-передающем устройстве — например, в смартфоне или роутере. Если говорить о более «прекрасном», то фильтры используют в эквалайзерах для обработки аудиосигналов.

Эквалайзер FabFilter Pro-Q2.

Какие бывают фильтры

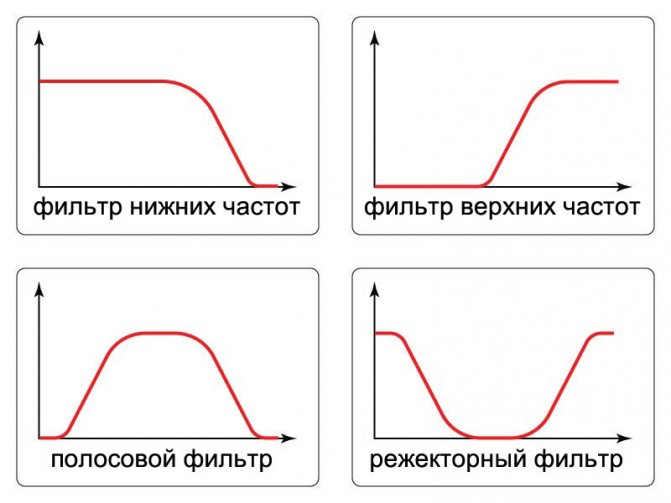
Чаще всего можно встретить фильтры нижних частот (ФНЧ) и верхних (ФВЧ), а также полосовые и заградительные.

Фильтр верхних частот — пропускает частоты выше частоты среза.

Фильтр нижних частот — пропускает частоты ниже частоты среза.

Полосовой фильтр — пропускает определенную полосу.

Заградительный фильтр — не пропускает частоты определенной полосы, но пропускает колебания, выходящие за ее пределы.

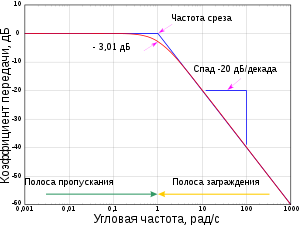
Частота среза — это такая частота, после которой идет фронт (спад) с полосы пропускания на полосу заграждения. Посмотрим, как это выглядит на АЧХ ФНЧ:

Видно, что с увеличением частоты падает коэффициент передачи.

И вот простое правило: чем круче спад, тем круче фильтр.

Соответственно, для названных видов фильтров АЧХ будут следующими:

АЧХ для ФНЧ, ФВЧ, полосового и режекторного (заградительного) фильтров.

Согласитесь — красивые рисунки! Но как получить это на

плате

практике?

Очередной резистивный делитель, или из чего состоят фильтры

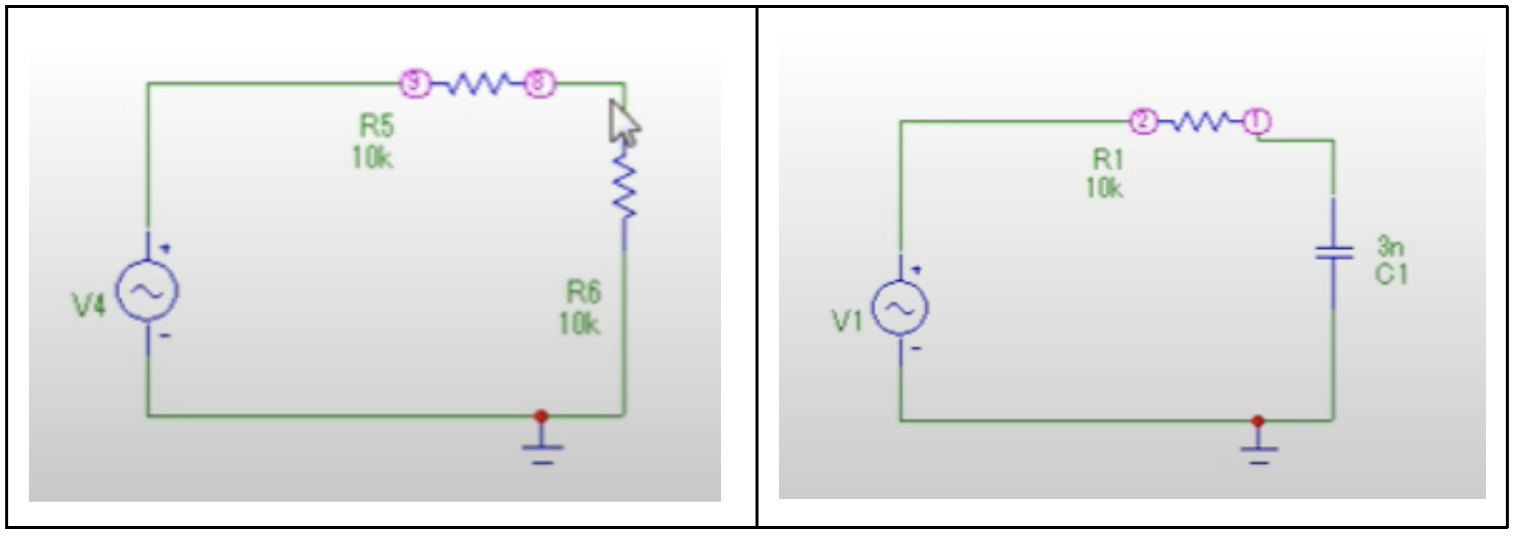
На самом деле, схема фильтра напоминает резистивный делитель (делитель напряжения на резисторах). Посмотрите сами:

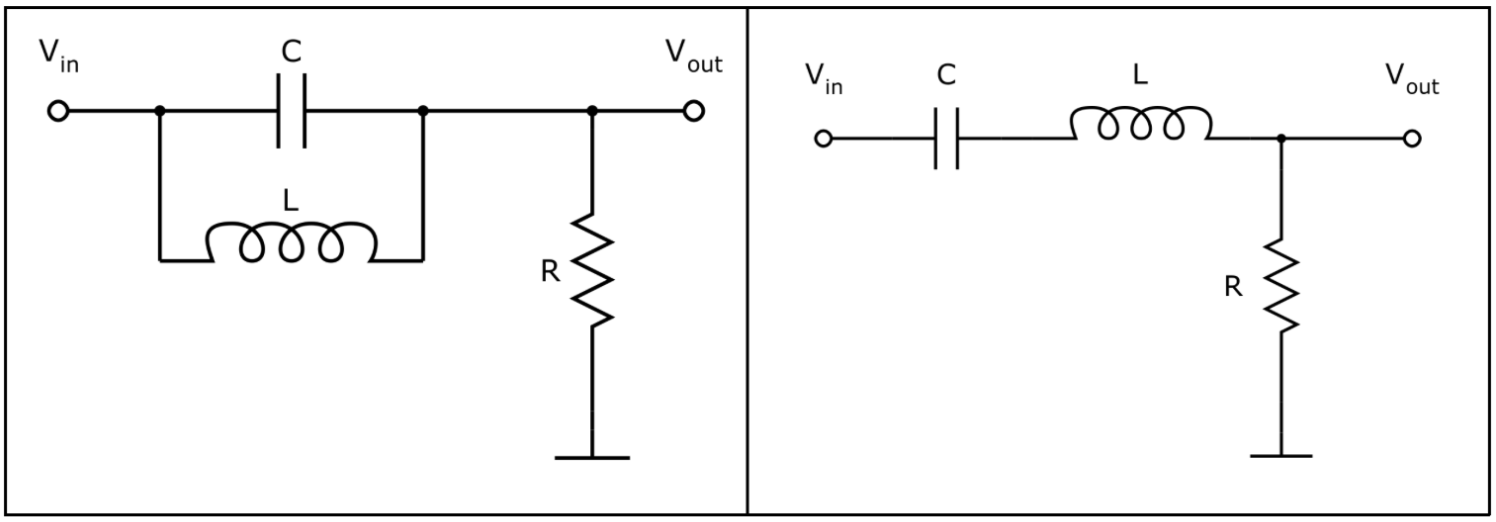
Слева — резистивный делитель, справа — электрический фильтр.

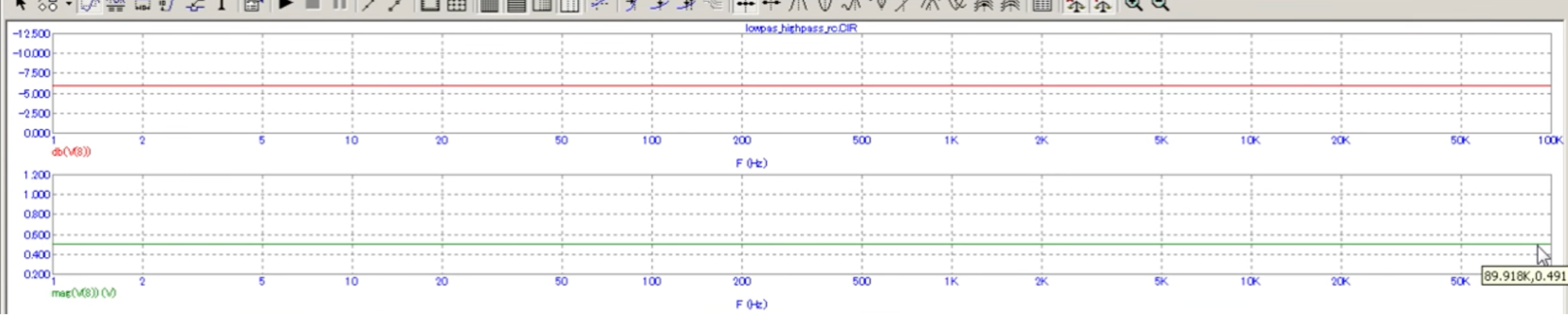
Разница буквально в одном элементе: вместо резистора стоит конденсатор. Но на АЧХ это влияет очень сильно. При включении делителя АЧХ будет стабильна, то есть частота источника на выходную амплитуду никак влиять не будет. Другая ситуация с фильтром: на определенной частоте появляется явный срез.

АЧХ резистивного делителя.

АЧХ ФНЧ.

Это связано с тем, что при увеличении частоты тока сопротивление на конденсаторе уменьшается и напряжение падает — по такому принципу работают ФНЧ.

Запомните правило. Емкостное сопротивление обратно пропорционально частоте тока и емкости конденсатора — чем больше их величины, тем меньше емкостное сопротивление.

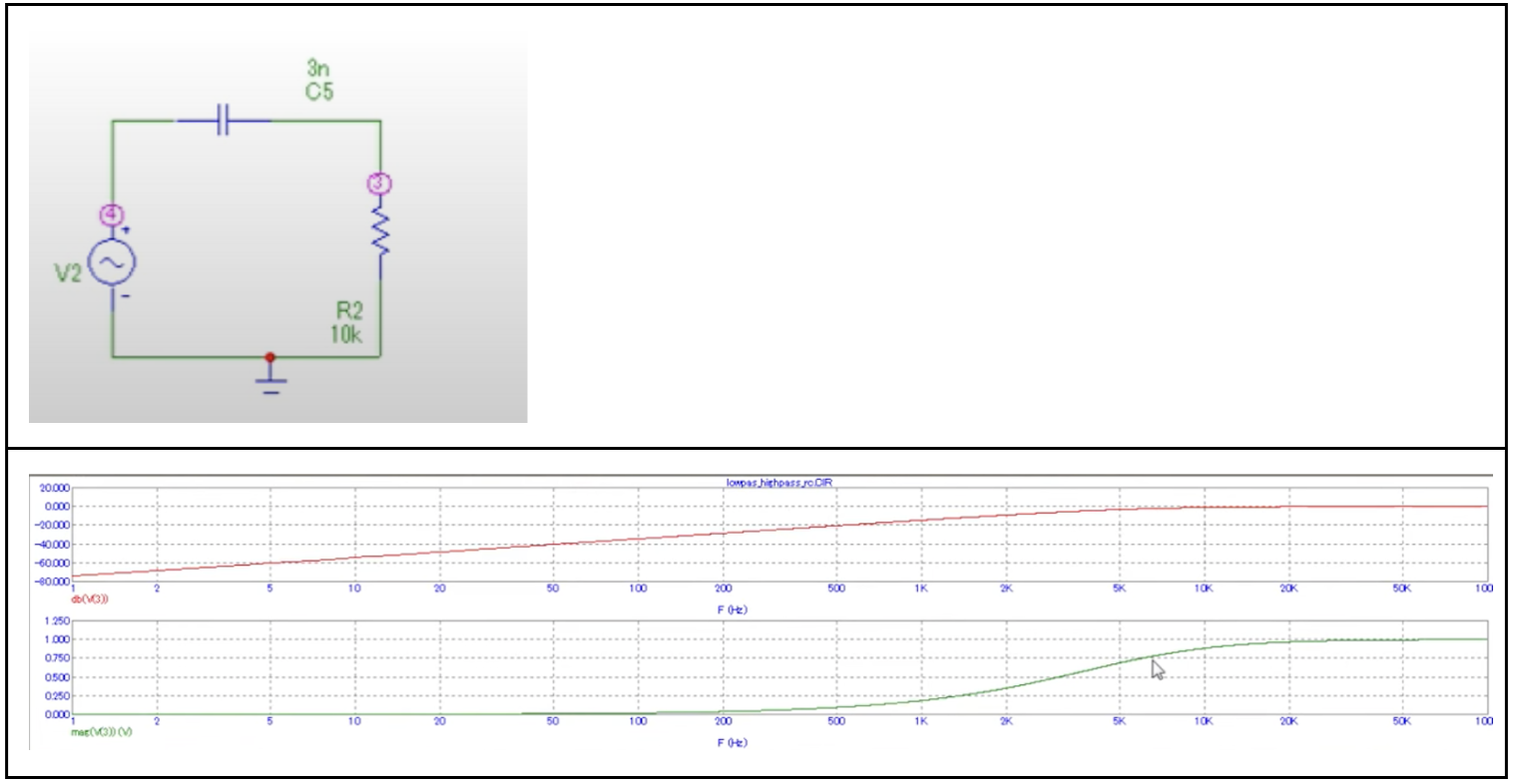
АЧХ можно «отразить», если поменять емкость и резистор местами — превратить ФНЧ в ФВЧ. Но это не все варианты схемотехнического многообразия

Схема и АЧХ для RC-ФВЧ.

LC-фильтры

Вместо резистора можно поставить индуктивность, и тогда вместо привычного ФНЧ (RC-ФНЧ) получим LC-ФНЧ. Суть та же: у него будет своя частота среза и так далее. Но добротность фильтра будет выше — соответственно, область частот, которую пропускает фильтр (она же полоса пропускания), будет меньше, а спад АЧХ — круче. Именно LC-контуры используются в фильтрах для работы с высокочастотным диапазоном.

LC-фильтры.

Принцип построения LC-фильтров основан на свойствах емкостей и индуктивностей по-разному вести себя в цепях переменного тока.

Индуктивное сопротивление катушки прямо пропорционально частоте тока, проходящего через нее. Следовательно, чем выше частота тока на катушке, тем большее реактивное сопротивление она этому току оказывает — сильнее задерживает переменные токи на более высоких частотах и легче пропускает на более низких.

У конденсатора наоборот: чем выше частота тока, тем легче протекает переменный ток. А чем ниже его частота, тем большим препятствием для тока оказывается этот конденсатор.

Схемы режекторного и полосового фильтров чуть сложней. Режекторный фильтр — это цепь с параллельно соединенными индуктивностью и емкостью, а полосовой — с последовательно соединенными.

Слева — режекторный фильтр, справа — полосовой.

Г-, Т- и П-образные фильтры

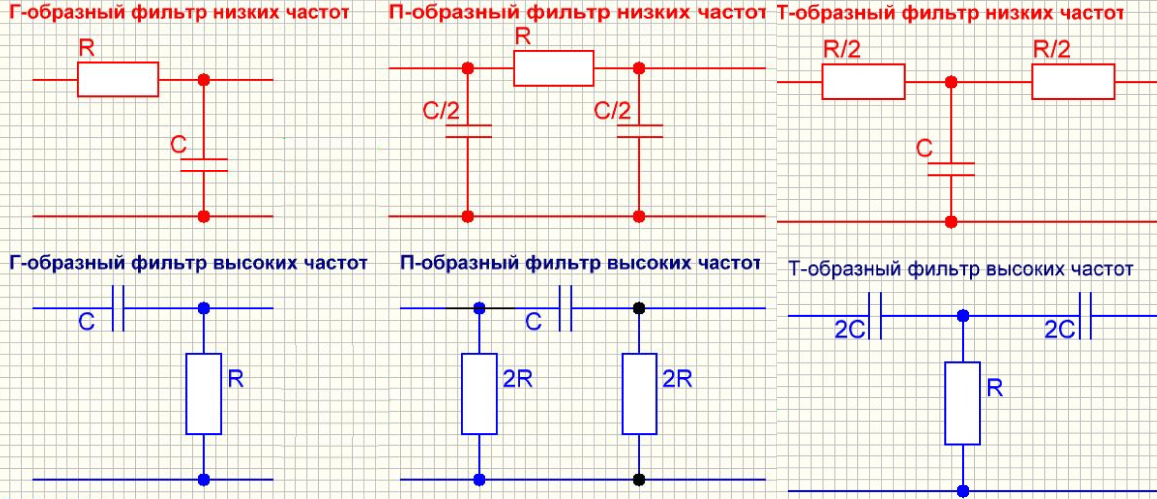
Схематически ФНЧ и ФВЧ бывают Г-образными, Т-образными и П-образными (многозвенными).

Г-образные — это схемы ФНЧ и ФВЧ, которые мы рассмотрели выше. Их входные сопротивления всегда меньше выходных. Г-образные фильтры часто применяют в качестве трансформаторных сопротивлений. В качестве фильтров обычно используют П- и Т-образные схемы.

Г-, П- и Т-образные RC-фильтры.

Тип схемы обычно выбирают из экономических соображений. Например, для сборки LC-ФНЧ лучше использовать П-образную схему, чтобы сэкономить катушки индуктивности, а для LC-ФВЧ — Т-образную.

Немного о параметрах частотных фильтров

Вот мы упомянули, что у фильтров есть ширина полосы пропускания, добротность, частота среза. Но все ли это параметры и как они связаны? Давайте разбираться.

Ключевые параметры

При проектировании частотных фильтров учитывают следующие параметры:

• наклон АЧХ — чем круче, тем лучше,
• частота среза — выбирается разработчиком,
• неравномерность АЧХ — чем меньше, тем лучше,
• отношение входного и выходного сопротивлений — особенно важный параметр для ВЧ-фильтров,
• ослабление в полосе задержания — оно же ослабление в полосе заграждения, но без учета переходного участка (длительности фронта).

Самый важный параметр — это частота среза. С помощью нее мы можем регулировать, какую долю частотного диапазона «проигнорировать», а какую — оставить. Поговорим о ней чуть подробнее.

Подробнее о частоте среза

Частота среза — это такая частота, на которой ослабление фильтра равно -3 дБ в логарифмическом масштабе (в линейном это 0,707).

Важно отметить, что частота среза для ФНЧ и ФВЧ вычисляется по одному выражению:

Зная сопротивление/ индуктивность и емкость, можно определить, на какой частоте случится ослабление на -3 дБ. То есть, опираясь на нужную частоту среза, мы можем рассчитать и спроектировать фильтр. Или не все так просто?

Что такое порядок фильтра

Допустим, вы знаете частоту среза и хотите спроектировать фильтр. Но что такое R, C и L? Обычные номиналы для сопротивления, емкости и индуктивности? Вы можете ответить «да» и будете правы: для ФНЧ и ФВЧ второго порядка (самых обычных Г-образных RC- и LC-фильтров) достаточно подобрать резистор, конденсатор и катушку с нужными параметрами. Но для фильтров больших порядков ответ неоднозначный.

Наклон АЧХ удовлетворяет не всегда: если он сильно пологий, то радиоприемное устройство может поймать лишние частоты. Чтобы избавиться от такого эффекта, разработчики стараются делать фильтры с крутым наклоном АЧХ.

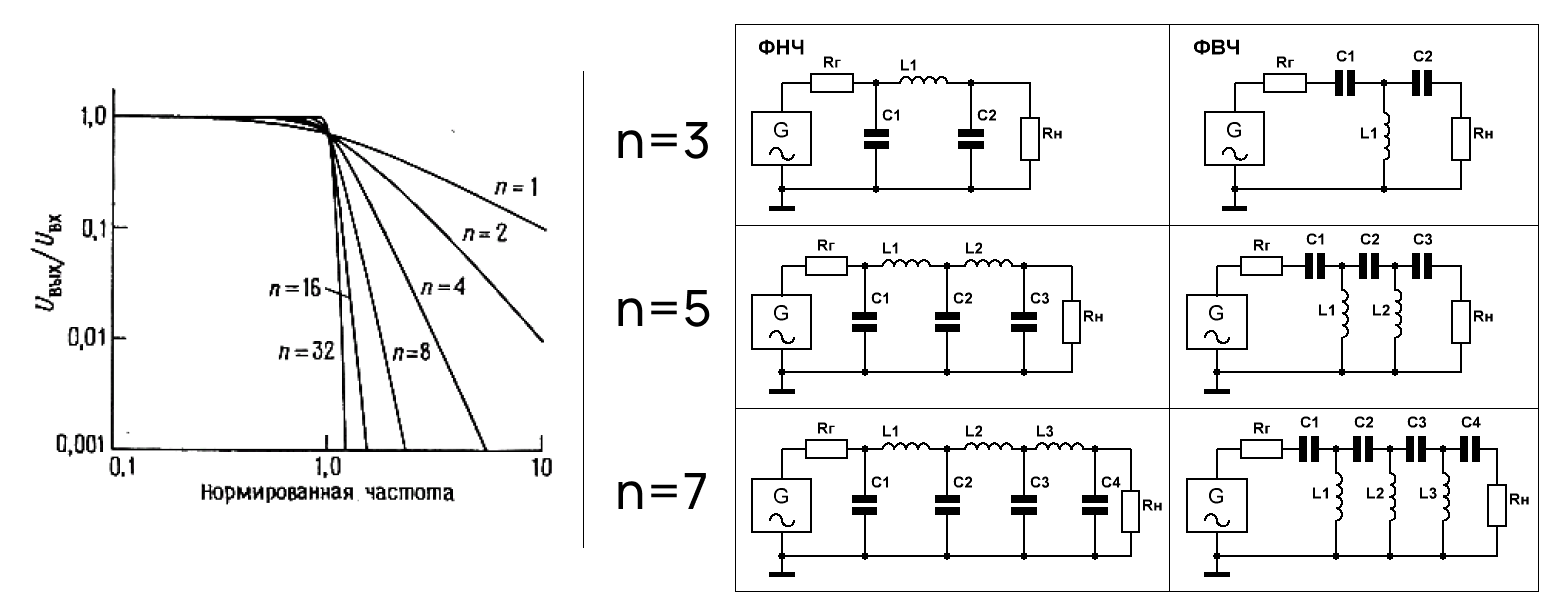
Наклон АЧХ тем круче, чем больше ослабление в полосе задержания и выше порядок фильтра. Последнее указывает на количество L- и C- элементов: в фильтре пятого порядка будет, например, три емкости и две индуктивности.

Зависимость крутизны наклона АЧХ от количества порядков (n).

Можно сказать, что каждый LC-элемент — индуктивность или емкость — дает уклонение АЧХ на 12 дБ на октаву, тогда как RC — всего 6 дБ на октаву.

Октава — это область частотного диапазона, на которой значение частоты увеличивается в два раза. Иногда в литературе предпочитают измерять в декадах, которые обозначают область с увеличением частоты в десять раз.

Рассчитывать фильтры — это сложно

Теперь вы знаете, что означают те самые R, C и L в формулах для частоты среза: это «суммы» номиналов для элементов фильтра. Стало ли от этого проще рассчитывать фильтры под определенную частоту среза? Не особо.

Расчет фильтров — это отдельная наука, объединяющая теорию электрических цепей, электротехнику и математические методы.

Чтобы рассчитать фильтр большого порядка по заданным условиям, применяют специальные методики. Среди них — формулы на базе полиномов Баттерворта и Чебышева, функций Бесселя.

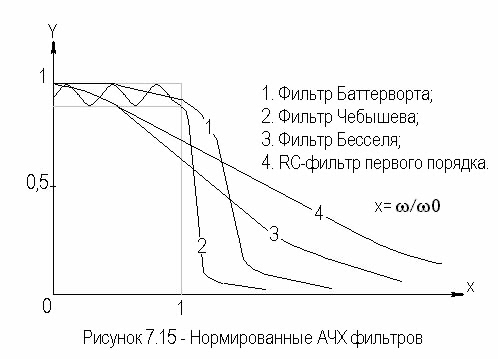
Нормированные АЧХ фильтров.

По сути, выбирая конкретную методику, вы выбираете фильтр:

• Фильтр Баттерворта — обладает самой плоской характеристикой затухания в полосе пропускания, за счет этого имеет плавный спад.
• Фильтр Чебышева — обладает самым крутым спадом, но у него самые неравномерные характеристики в полосе пропускания.
• Фильтр Бесселя — имеет хорошую фазочастотную характеристику и крутой спад.

Чтобы понять теорию расчета фильтров, рекомендую почитать книгу «Аналоговые и цифровые фильтры». Если хотите утонуть в полиномах, аналитических вычислениях комплексных расчетах, сохраняйте в закладки.

Но рассчитать фильтр можно проще, если «схитрить» и использовать онлайн-калькулятор. Так можно узнать, например, номиналы для фильтра Чебышева пятого порядка с частотой среза 4 МГц. Проверим, работает ли он на практике.

Возможно, эти тексты тоже вас заинтересуют:

→ Как геймифицировать аренду серверов со скидкой, связав сайт с внутренней панелью администрирования
→ Первая «зеркалка» от Polaroid, робот-пылесос iRobot, гомеопатия начала XX века и кое-что еще: новые находки на барахолке
→ Проблемы безопасности SNMP на практике: имитация атак и меры профилактики

Собираем фильтр Чебышева

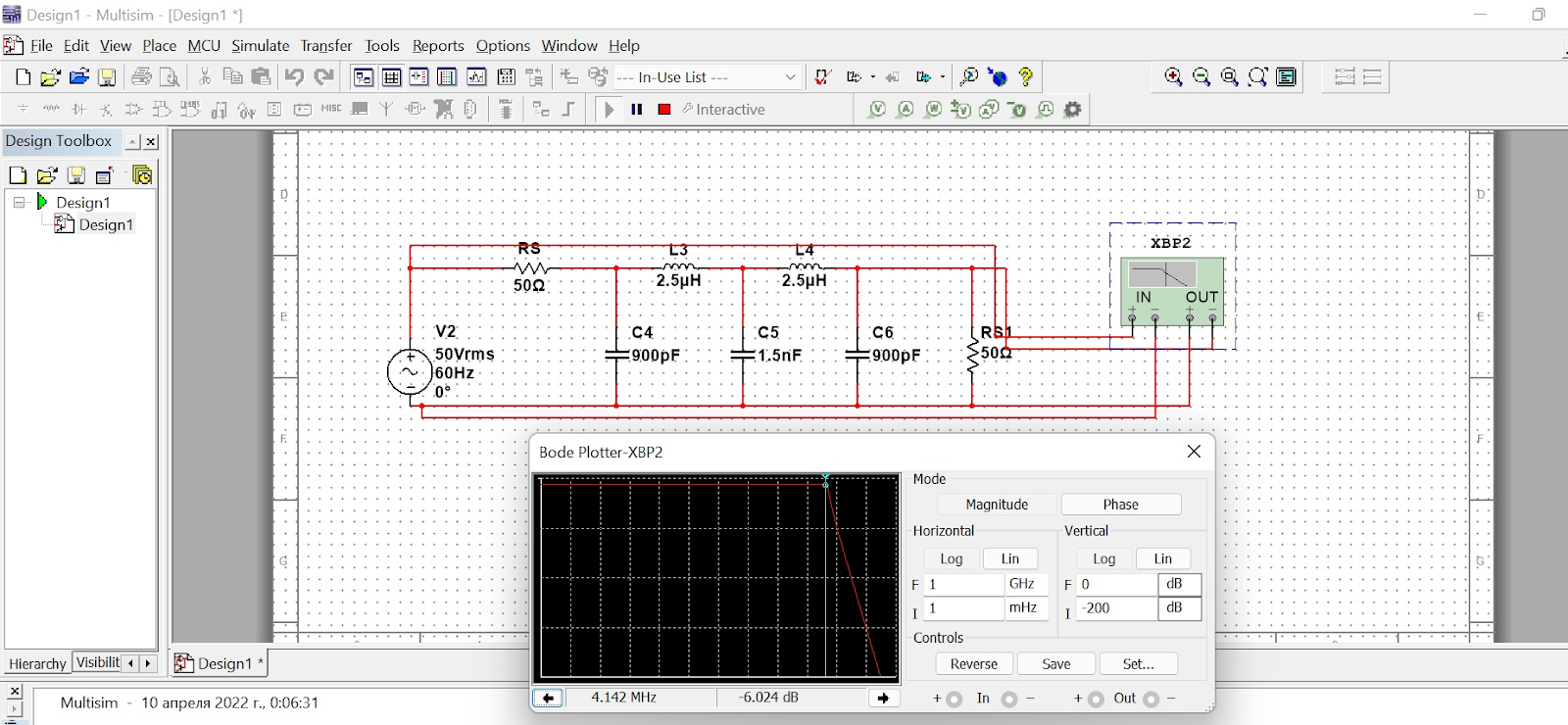
Предварительно я узнал номиналы через онлайн-калькулятор и проверил фильтр в Multisim. Если подключить параллельно Bode Plotter и правильно установить масштабы, программа покажет идеальную АЧХ фильтра Чебышева.

Multisim, схема ФНЧ Чебышева пятого порядка.

Супер — схему можно «перенести» на макетную плату.

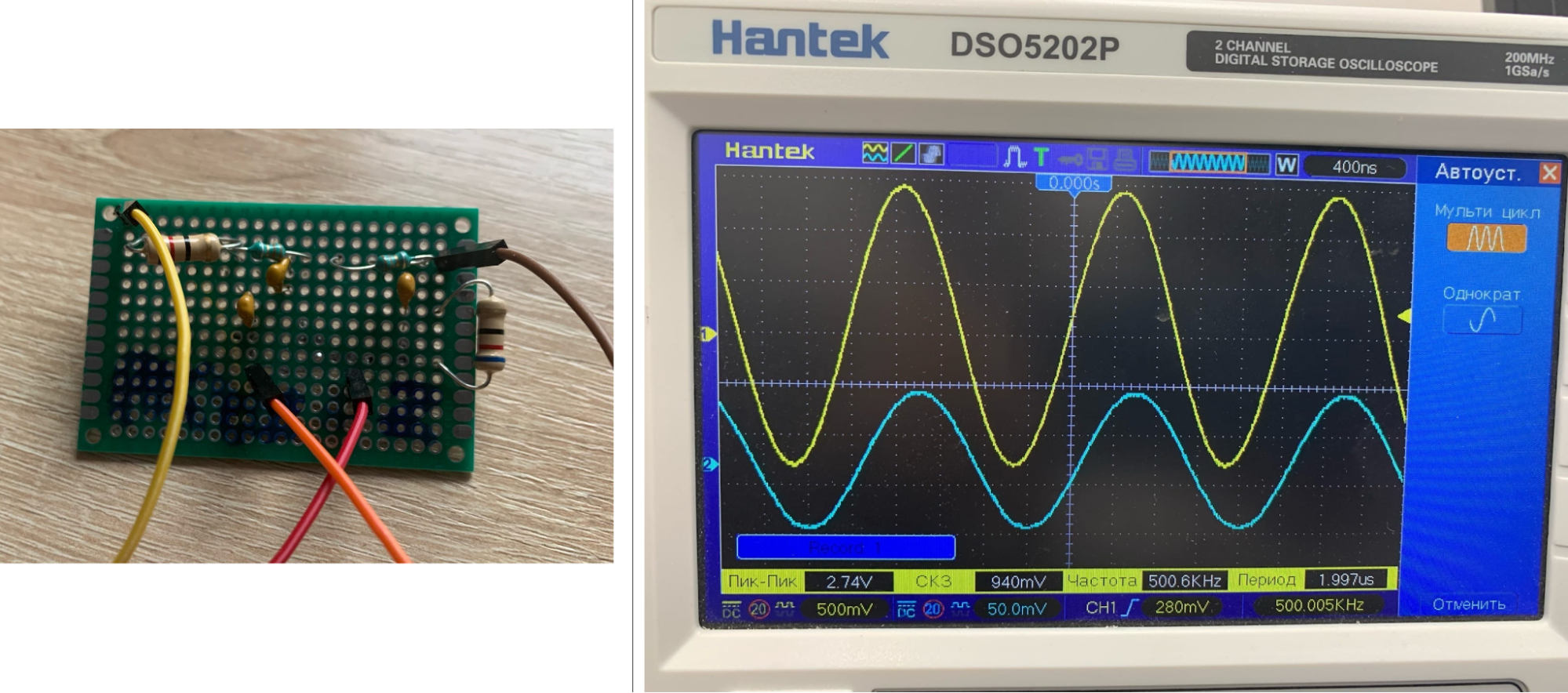
Понадобится генератор гармонических колебаний и осциллограф, подключенный к выходам фильтра. Если у вас есть анализатор цепей, можно использовать его.

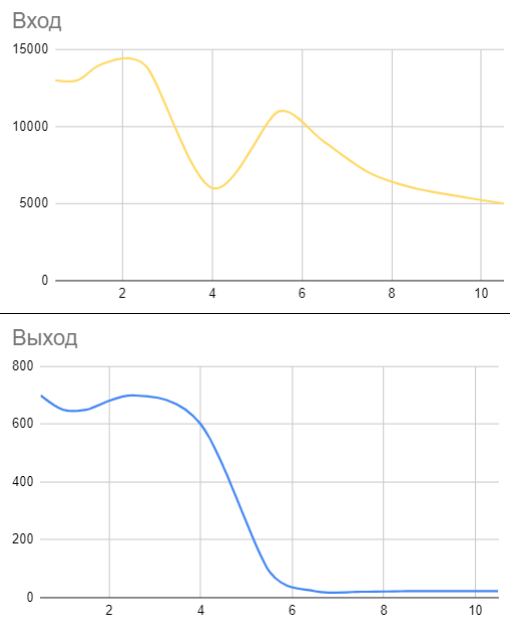
Синусоида синего цвета — выходной сигнал, желтого — входной.

Обратите внимание. Электрическая схема может отличаться по номиналам от идеальной, которую вы рассчитали под свою частоту среза. Не всегда возможно точно повторить значения емкостей и индуктивностей, потому что элементов с такими номиналами может просто и не быть.

Постепенно увеличивая частоту входного сигнала, можно составить таблицу для построения графика.

Если отразить значения на системе координат, получится график для фильтра Чебышева.

Готово — у нас получилось добиться вполне крутого спада на частоте 4 МГц, ФНЧ Чебышева работает.

В статье рассмотрена лишь малая часть теоретических и практических аспектов. Фильтров гораздо больше: есть активные на базе операционных усилителей, микроконтроллеров, рассчитанные топологии Саллена-Ки и программные фильтры. Обо всем этом — в следующей статье.

Лабораторная
работа № 5

ИССЛЕДОВАНИЕ
ПРОСТЕЙШИХ ФИЛЬТРОВ

Цель
работы: изучение
свойств, приобретение практических
навыков по расчету и моделированию
простейших фильтров.

Работа выполняется
в системе моделирования MicroCAP.

В работе необходимо определить частотные
характеристики простейших пассивных
фильтров.

Теоретическая
часть

Простейшие электрические фильтры

Электрические
фильтры — это устройства, которые
пропускают на выход сигналы одних частот
и не пропускают сигналы других частот.
По виду АЧХ фильтры разделяются на
фильтры нижних частот (НЧ), верхних
частот (ВЧ), полосовые фильтры (ПЧ) и др.

Фильтры
нижних частот (НЧ). Фильтр нижних
частот без изменения передает сигнал
нижних частот, включая и нулевую частоту
(постоянный сигнал), а на высоких частотах
обеспечивает затухание сигналов. На
рис.3,а изображена схема простого фильтра
НЧ. Сопротивление емкости С зависит от
частоты входного сигнала и равно Х_С
= 1 / ωC . Емкость С вместе
с резистором R образуют
делитель напряжения. Для частоты ω = 0
сопротивление емкости равно бесконечности.
И весь сигнал со входа схемы поступает
на выход. С увеличением частоты
сопротивление емкости уменьшается и
все большая его часть будет замыкаться
на землю. И в пределе, когда ω = ∞,
сопротивление емкости будет равно 0,
напряжение на выходе также будет равно
0. Таким образом, схема обладает свойствами
фильтра НЧ.

Для расчета частотной характеристики
схемы воспользуемся методом комплексных
амплитуд. По схеме рис.3,б, используя
формулу для делителя напряжения, найдем
выходной сигнал

.

Отсюда найдем комплексный коэффициент
передачи

,

где Т = RC – постоянная
времени RC – цепочки.

АЧХ представляет
собой модуль комплексного коэффициента
передачи
,

а ФЧХ аргумент
комплексного коэффициента передачи
..

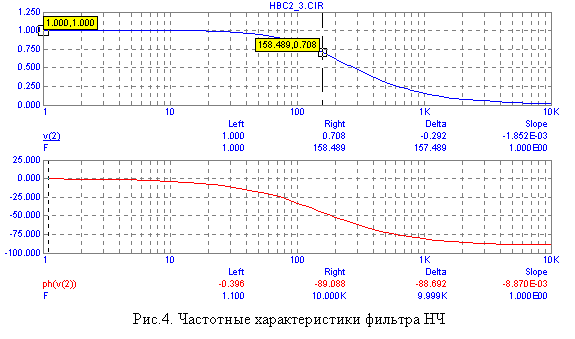
На рис.4 показаны
частотные характеристики ФНЧ для R
= 1 кОм, и С = 1 мкФ.

На
АЧХ фильтра можно выделить три области
частот: полосу пропускания, переходную
область, и полосу подавления сигнала.
В полосе пропускания допускается
снижение коэффициента передачи в

раза. На АЧХ такое уменьшение коэффициента
передачи происходит на частое 158,489 ≈
159 Гц. Частота, на которой коэффициент
передачи уменьшается в

раз, называется частотой
среза.
Частота среза разделяет область
пропускания фильтра от переходной
области. Полоса пропускания фильтра НЧ
лежит от 0 Гц до частоты среза f_c.
Частота среза RC
–фильтра НЧ равна f_c.=
1/ 2πRC
или круговая частота среза ω_с
= 1/RC
= 1 / T.
В этом легко убедиться, если в формулу
АЧХ фильтра вместо ω подставить ω_с
= 1/RC,
то получим
,
что означает, что на частоте ω_с
= 1/RC
коэффициент передачи уменьшился в

раз.

Частота, которая
разделяет переходную область фильтра
от полосы подавления сигнала, не
нормируется. Она определяется в
зависимости от требований, предъявляемых
к АЧХ фильтра в конкретном применении.
Для сравнения различных фильтров эта
частота иногда определяется на уровне
0,01 от коэффициента передачи на нулевой
частоте.

Обычно АЧХ необходимо анализировать
в широком диапазоне частот, например
для операционного усилителя широкого
применения, от единиц Гц до десятков
МГц. В этом случае удобно ось частот
представлять в логарифмическом масштабе
lag f или
lag, как показано на графике
на рис. 4. Коэффициент передачи при этом
измеряется в обычном линейном масштабе.
Однако, если коэффициент передачи
(усиления) изменяется в очень широких
пределах, как, например, в операционном
усилителе, то его удобно выражать в
логарифмическом масштабе:

L(ω) =
20lg A.

Единицы измерения – децибелы (дБ),
десятая часть бела. Зависимость
коэффициента усиления от частоты
входного сигнала в логарифмическом
масштабе называется логарифмической
амплитудно-частотной характеристикой
(ЛАЧХ).

Что собой представляет единица измерения
бел, и почему коэффициент перед логарифмом
равен 20, а не 10 как следовало бы ожидать.
Единица измерения 1 бел соответствует
отношению мощностей в 10 раз:

1 Б = P₂
/ P₁ =
10.

Так как 1 Белл – это очень большая
величина, то на практике используют
более мелкие величины децибелы (в одном
беле содержится 10 дБ). Поэтому в
коэффициенте усиления по мощности
коэффициент пропорциональности равен
10:

L_ap
= 10 lag P₂ /
P₁.

Но у нас
коэффициент усиления, это отношение
амплитуд токов или напряжений. А для
токов и напряжений мощность пропорциональна
квадрату токов или напряжений

P = UI = U²/R
= I²R.

При отношении амплитуд в 10 раз мощность
увеличивается в 100 раз, т.е. на 2 бела или
на 20 децибел:

U₂/U₁
= 10, P₂/P₁
= (U₂/U₁)²
= (10)²
= 100.

Поэтому в формуле для логарифмического
коэффициента усиления появился множитель
20 , а не 10.

Логарифмические единицы удобны еще
тем, что если известны коэффициенты
усиления отдельных каскадов или узлов
усилителя и общий коэффициент усиления
равен произведению этих коэффициентов,
то в логарифмическом масштабе коэффициент
усиления находят как алгебраическую
сумму логарифмических коэффициентов
усиления отдельных каскадов.

На рис.5 представлена ЛАЧХ RC
фильтра НЧ, которая была рассмотрена
ранее.

Частота
среза фильтра определяется на уровне
-3 дБ от максимального значения коэффициента
усиления в полосе пропускания. Это видно
из показаний слайдера правого курсора.
Величина – 3 дБ в логарифмическом
масштабе соответствует коэффициенту
усиления

в линейном масштабе, то есть L
= 20lg 0,707 = -3 дБ. Из ЛАЧХ
хорошо видно как подавляется сигнал на
высоких частотах. Так на частоте 10 кГц
логарифмический коэффициент усиления
почти равен – 40 дБ, что соответствует
значению 0,01 в линейном масштабе.
Попробуйте определить коэффициент
усиления на этой частоте по АЧХ на рис.4.

Фазочастотные
характеристики в обоих случаях строятся
в линейном масштабе. Из фазочастотных
характеристик видно, что наибольшее
изменение фазы происходит на частоте
среза фильтра.

Фильтры верхних частот (ВЧ). Фильтр
верхних частот без изменения передает
сигнал верхних частот, а на низких
частотах обеспечивает затухание сигнала.
Схема простого RC фильтра
верхних частот представлена на рис. 6.
Аналогично, как и для фильтра нижних
частот найдем выходной сигнал

.

Отсюда найдем комплексный коэффициент
передачи

,

где Т = RC – постоянная
времени RC – цепочки.

АЧХ представляет
собой модуль комплексного коэффициента
передачи
,

а ФЧХ аргумент
комплексного коэффициента передачи
.

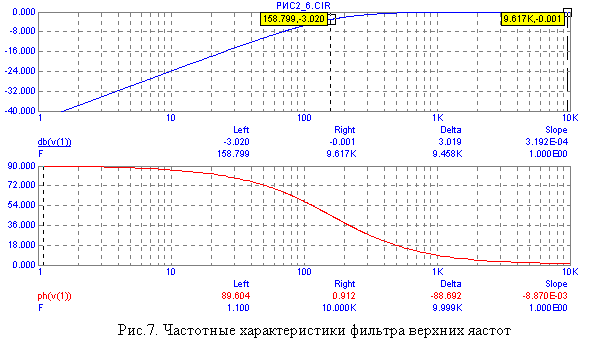
На рис. 7. Показаны
частотные характеристики фильтра ВЧ (
R = 1 кОм, и С = 1 мкФ)в
логарифмическом масштабе.

Частота среза
фильтра определяется также, как и для
фильтра НЧ и равна
ω_с = 1/RC
= 1 / T или f_c.=
1/ 2πRC = 1/( 6,28 ּ1
кОм ּ1 мкФ ) = 159 Гц. На
графике АЧХ частота среза определяется
на уровне – 3 дБ от максимального значения
коэффициента усиления. Положение левого
курсора определяет частоту среза, так
как разность между показаниями
коэффициента усиления правого и левого
курсора равна 3,019 ≈ 3 дБ.

Полосовой
фильтр. Соединяя последовательно
фильтр верхних и низких частот с
перекрывающимися амплитудно-частотными
характеристиками можно получить
полосовой фильтр. Полосовой фильтр
пропускает сигнал в некоторой полосе
частот и подавляет сигнал на низких и
высоких частотах. На рис 8. показана
схема полосового фильтра.

Найдем комплексный коэффициент усиления
схемы.

.

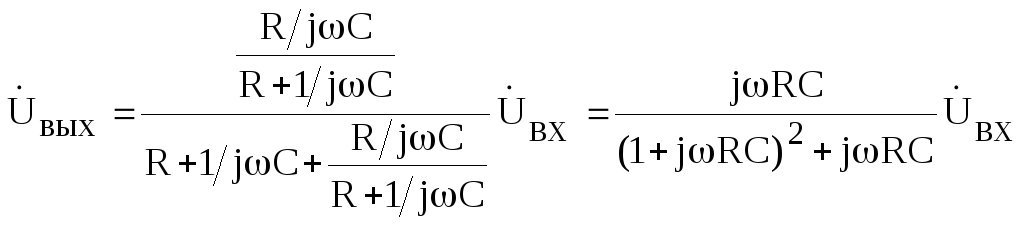
Введем обозначение
ωRC = Ω. Раскрывая скобки,
получим

Комплексный
коэффициент усиления равен

.

АЧХ представляет
собой модуль комплексного коэффициента
передачи
,

ФЧХ определяется из
выражения
.

Коэффициент
максимальный при Ω = 1. Следовательно,
резонансная частота f₀
= 1/ 2πRC. Коэффициент усиления
на резонансной частоте равен A(f₀)
= 1/3, а фазовый сдвиг равен 0.

На рис.9 приведены
частотные характеристики полосового
фильтра при R=1 кОм и С = 1
мкФ.

Резонансная
частота фильтра равна 159,591 Гц. АЧХ
полосового фильтра имеет две частоты
среза, которые располагаются слева и
справа от резонансной частоты f₀,
и также определяются на уровне – 3 дБ
относительно максимального значения
коэффициента усиления.

2. Задание
и порядок выполнения

Согласно вашего
варианта, рассчитайте фильтры нижних,
верхних частот и полосовой фильтр.
Расчет заключается в определении величин
конденсаторов и сопротивлений при
заданной частоте среза для фильтров
нижних и верхних частот и центральной
частоты для полосового фильтра. При
расчете необходимо задаться величиной
емкости конденсатора и из соответствующих
формул для частот среза и центральной
частоты найти величины сопротивлений.
Величины емкостей и сопротивлений
должны быть физически реализуемыми.

Для расчета
фильтров нижних и верхних частот
используйте формулу f_c.=
1/ 2πRC, а для полосового
фильтра f₀ = 1/ 2πRC.
Варианты заданий возьмите из таблицы.

В системе
моделирования MicroCAP
определите частотные характеристики
фильтров.

В режиме Scope
определите частоты среза фильтров
верхних и нижних частот, для полосового
фильтра определите центральную частоту,
частоты среза и добротность. Сравните
полученные частоты среза и центральную
частоту фильтров с заданными значениями
и сделайте выводы о правильности расчета.

1. Содержание
   отчета

• привести
  схемы проведения экспериментов;

• привести
  формулы и результаты расчетов;

• привести
  необходимые графики, полученные при
  моделировании;

• ответить
  на поставленные вопросы;

• сделать
  выводы.

1. Контрольные
   вопросы

1. Что такое
   электрический фильтр?

2. Что такое
   комплексный коэффициент усиления и
   как его получить

3. Нарисуйте
   схему простейшего фильтра нижних
   частот.

4. Как определить
   частоту среза фильтра?

5. Нарисуйте
   АЧХ фильтра ВЧ.

6. Нарисуйте
   схему простейшего фильтра верхних
   частот.

7. Как определить
   частоту среза фильтра?

8. Нарисуйте
   АЧХ фильтра ВЧ.

9. Приведите
   формулы для определения частоты среза
   фильтров НЧ и ВЧ.

10. Нарисуйте
    схему простейшего полосового фильтра.

11. Как определить
    частоту среза полосового фильтра?

12. Нарисуйте
    АЧХ полосового фильтра. Чему равен
    коэффициент передачи полосового фильтра
    на частоте f₀?

13. Приведите
    формулы для определения центральной
    частоты полосового фильтра.

14. Что такое
    добротность полосового фильтра и как
    ее определить?

15. Что такое
    полоса пропускания, переходная область
    и полоса подавления фильтра?

16. Как выражается
    амплитудночастотная характеристика
    в логарифмическом масштабе?

17. Нарисуйте
    ЛАЧХ фильтров НЧ, ВЧ и полосового
    фильтра.

18. Как определить
    частоту среза фильтров по АЧХ в
    логарифмическом масштабе?

Соседние файлы в папке Lab_rab_12_13

• #
• #
• #
• #
• #

Фильтры нижних и высших частот

Фильтр нижних частот (ФНЧ) — электрическая цепь, эффективно пропускающая частотный спектр сигнала ниже определённой частоты, называемой частотой среза, и подавляющая сигнал выше этой частоты.

Фильтр высших частот (ФВЧ) — электрическая цепь, эффективно пропускающая частотный спектр сигнала выше частоты среза, и подавляющая сигнал ниже этой частоты.

Рассмотрим в качестве фильтра простейшую цепь RC, принцип работы которой основан на зависимости реактивного сопротивления конденсатора от частоты сигнала.

Если к источнику переменного синусоидального напряжения U частотой f подключить последовательно резистор сопротивлением
R и конденсатор ёмкостью C, падение напряжения на каждом из элементов можно вычислить
исходя из коэффициента деления с импедансом Z.

Импеданс — комплексное (полное) сопротивление цепи для гармонического сигнала.
Z² = R² + X² ;    Z = √(R² + X²) , где Х — реактивное сопротивление.

Тогда на выводах резистора напряжение U_R будет составлять:

X_C – реактивное сопротивление конденсатора, равное 1/2πfC

При равенстве R = X_C на частоте f, выражение упростится сокращением R и примет вид:

Следовательно, на частоте f равенство активного и реактивного сопротивлений цепочки RC обеспечит
одинаковую амплитуду переменного синусоидального напряжения на каждом из элементов в √2 раз меньше входного напряжения,
что составляет приблизительно 0.7 от его значения.
В этом случае частота f определится исходя из сопротивления R и ёмкости С выражением:

τ — постоянная времени цепи RC равна произведению RC

Повышение частоты уменьшит реактивное сопротивление конденсатора и падение напряжение на нём, тогда напряжение на выводах резистора возрастёт.
Соответственно, понижение частоты увеличит напряжение на конденсаторе и уменьшит на резисторе.

Зависимость амплитуды переменного напряжения от его частоты называют амплитудно-частотной характеристикой (АЧХ).

Если рассмотреть АЧХ напряжения на выводах конденсатора или резистора в RC цепи, можно наблюдать на частоте f = 1/(2π τ)
спад уровня до значения 0.7, что соответствует -3db по логарифмической шкале.

Следовательно, цепь RC может быть использована как фильтр нижних частот (ФНЧ) — красная линия на рисунке, или фильтр высших частот (ФВЧ) — синяя линия.

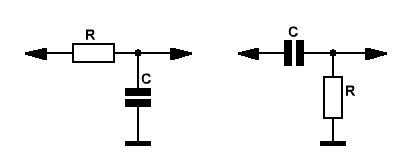
Ниже представлены схемы включения RC-цепочек в качестве фильтров соответственно ФНЧ и ФВЧ.

Частоту f = 1/(2π τ) называют граничной частотой f_гр или частотой среза f_ср фильтра.

Частоту среза фильтра можно посчитать с помощью онлайн калькулятора

Достаточно вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

В предыдущих статьях мы рассказали вам о фильтрах низких и высоких частот. В этой же статье речь пойдет о другой категории фильтров, их называют полосовые фильтры, мы представим их базовую схему, расскажем о функциональных возможностях, частотной характеристике и их применениях.

Можно сказать, что полосовой фильтр представляет собой комбинацию фильтра низких частот и фильтра высоких частот. Само название фильтра говорит о том, что он пропускает только определенную полосу частот и блокирует все остальные частоты.

В звуковых аппаратурах иногда необходимо передать только определенный диапазон частот, этот диапазон частот не начинается с 0 Гц или не заканчивается на очень высокой частоте, но эти частоты находятся в определенном диапазоне, широком или узком. Эти полосы частот обычно называют полосой пропускания.

Пассивный полосовой фильтр

Полосовой фильтр получается путем каскадирования пассивных фильтров низких частот и пассивных фильтров высоких частот. Такое расположение обеспечит избирательный фильтр, который пропускает только определенные частоты. Эта новая схема RC-фильтра может пропускать как узкий диапазон частот, так и широкий диапазон частот.

Этот диапазон прохождения частот, который является либо узким, либо широким диапазоном, будет зависеть от того, как каскадируются пассивные фильтры низких и высоких частот. Высокая и низкая частоты среза зависят от конструкции фильтра. Этот полосовой фильтр выглядит просто как частотно-селективный фильтр.

На приведенной выше схеме показан полосовой фильтр. На вход подается синусоидальный сигнал. Свойства комбинаций низких и высоких частот дают нам полосовой фильтр. При расположении одного набора RC-элементов последовательно и другого набора RC-элементов параллельно схема ведет себя как полосовой фильтр.

Это дает нам фильтр второго порядка, т.к. схема имеет два реактивных компонента. Один конденсатор относится к фильтру низких частот, а другой конденсатор относится к фильтру высоких частот. Без каких-либо изменений входного сигнала этот полосовой фильтр пропускает определенный диапазон частот. Этот фильтр не создает дополнительных шумов в сигнале.

Частоту среза цепи можно рассчитать следующим образом:

f_C = 1/(2πRC)​

Регулируя частоты среза фильтров высоких и низких частот, мы можем получить соответствующую ширину полосы пропускания для полосового фильтра.

Этот фильтр содержит две частоты среза: низкую частоту среза ‘f_L ‘ и высокую частоту среза ‘f_H ‘. При этом диапазон частот, пропущенных через фильтр, называется полосой пропускания фильтра. В общем, ширина полосы канала может быть рассчитана по частотам ‘f_H  и f_L ‘.

BW = f_H – f_L

Где ‘f_H‘ — частота среза фильтра высоких частот, а ‘f_L‘ — частота среза фильтра низких частот. «BW» — это полоса пропускания фильтра. Полосовой фильтр пропускает частоты выше частоты среза фильтра высоких частот и ниже частоты среза фильтра низких частот.

Получается, что частота среза фильтра низких частот должна быть выше, чем частота среза фильтра высоких частот.

Полосовой фильтр с использованием компонентов R, L и C

Схема полосового фильтра с использованием катушки индуктивности, конденсатора и резистора приведена ниже:

Центральную частоту полосового фильтра, также называемую «резонансным пиком», можно определить с помощью приведенного ниже уравнения:

f_c = 1/2π√(LC)​

Где L = индуктивность катушки индуктивности, единицы измерения которой выражены в Генри (Гн).

C = емкость конденсатора в фарадах (Ф).

Мы также можем разработать полосовой фильтр с индукторами, но мы знаем, что из-за высокого реактивного сопротивления конденсаторов конструкция полосового фильтра с RC-элементами имеет больше преимуществ, чем RL-схемы.

Частотная характеристика полосового фильтра

Частота полюсов примерно равна частоте максимального усиления.

Кривая частотной характеристики полосового фильтра показана ниже. Идеальные характеристики и практические характеристики полосовых фильтров различаются из-за входного реактивного сопротивления схемы.

Усиление входного сигнала можно рассчитать, взяв логарифм 20 (V out / V in ). Диапазон может быть довольно большим в зависимости от внутренних характеристик схемы. Сигнал ослабляется на низких частотах, выходной сигнал увеличивается с наклоном +20 дБ или 6 дБ, пока частота не достигнет нижней граничной частоты «fL».

На этой частоте коэффициент усиления сигнала достигает значения 1/√2 = 70,7 %.

После частоты среза f L выходной сигнал будет увеличиваться с увеличением частоты со скоростью -20 дБ и достигает максимального усиления, и это усиление будет постоянным, пока не достигнет более высокой частоты среза ‘f_H’. После более высокой частоты среза выходной сигнал снижается с наклоном -20 дБ или -6 дБ.

Ранее мы говорили, что фазовый сдвиг фильтра первого порядка составляет 90°. Мы знаем, что полосовой фильтр является фильтром второго порядка, поэтому фазовый сдвиг в два раза больше, чем у фильтра первого порядка, то есть 180°. Фазовый угол будет меняться с увеличением частоты. На центральной частоте выходные и входные сигналы синфазны друг с другом.

Ниже резонансной частоты выходной сигнал опережает входной сигнал, а выше резонансной частоты выходной сигнал отстает от входного сигнала. Амплитуда входного сигнала всегда больше выходного сигнала. Для увеличения коэффициента усиления схемы значение сопротивления R1 должно быть больше, чем сопротивление R2.

Центральная частота полосового фильтра

«Центральную частоту» или «резонансную частоту», при которой выходное усиление максимально, можно получить, вычислив среднее геометрическое низкой и высокой частот среза.

f _r ² = f _H xf _L

fr = √(f _H xf _L )

Где fr — резонансная частота или центральная частота.

f _H  – верхняя граничная частота -3 дБ

f _L  – нижняя частота среза -3 дБ

Пример полосового фильтра

Предположим, что полосовой фильтр пропускает частоты от 1 кГц до 30 кГц и содержит резистор 10 кОм. Учитывая эти значения, мы можем рассчитать емкость конденсатора.

Вы уже знаете, что значение частоты среза фильтра низких частот должно быть выше, чем у фильтра высоких частот. Таким образом, частота среза фильтра высоких частот составляет 1 кГц, а частота среза фильтра низких частот — 30 кГц.

На этапе фильтра высоких частот:

f L = 1 кГц и сопротивление R = 10 кОм

C = 1/(2πf L R) = 1/(2*π*1000*1000) = 15,8 нФ

На этапе фильтра низких частот:

f H = 30 кГц и сопротивление R = 10 кОм

C = 1/(2πf H R) = 1/(2*π*30000*10000) = 510 пФ

Из приведенных выше расчетов емкость конденсатора, необходимая для фильтра высоких частот, составляет 15,8 нФ, а емкость конденсатора фильтра низких частот составляет 510 пФ.

Описание пассивного полосового фильтра

Полосовой фильтр получается путем каскадирования фильтра низких и высоких частот. Это фильтр второго порядка, поскольку он содержит два реактивных элемента. Порядок фильтра зависит от количества каскадных цепей, используемых в схеме.

Усиление выходного сигнала всегда меньше, чем входного сигнала. На центральной частоте выходной сигнал находится в фазе, но ниже центральной частоты выходной сигнал опережает фазу со сдвигом на +90°, а выше центральной частоты выходной сигнал будет отставание по фазе со сдвигом фазы -90°.

Практические характеристики полосового фильтра немного отличаются от идеальных характеристик. Это изменение в основном связано с каскадным фильтром высоких частот с фильтром низких частот.

Выходное усиление всегда меньше единицы. Когда мы обеспечиваем электрическую изоляцию между фильтрами высоких и низких частот, мы можем добиться лучшей производительности фильтра.

Полосовой фильтр оптимизирует чувствительность приемника. Сначала в конструкцию добавляется фильтр высоких частот, а затем добавляется фильтр низких частот. Даже если мы сначала добавим фильтр низких частот, а затем фильтр высоких частот, он никогда не изменит выходной сигнал.

От номинала резистора R1 будет зависеть добротность фильтра. Если R1 низкий, то добротность низкая, а если значение R1 высокое, то добротность высокая.

Итог

Полосовые фильтры используются в среде беспроводной связи в цепях передатчика и приемника. В секции передатчика этот фильтр пропускает только необходимые сигналы и уменьшает помехи сигналов от других станций. В секции приемника фильтр не дает проникать нежелательному сигналу в каналы.

Данные фильтры используются для оптимизации отношения сигнал/шум приемника, используются в области оптической связи, такой как LIDARS, в некоторых методах цветовой фильтрации, а также используются в медицинском оборудовании, таком как ЭЭГ.

В следующей статье мы поговорим о полосно-заградительном фильтре.

С Уважением, МониторБанк

А не фильтрануть ли нам широким махом входной сигнал на предмет подавления помехи относительно единичного уровня
на требуемой частоте, в заданное число раз отличающейся от границы полосы пропускания?

А как насчёт расчёта активных полиномиальных фильтров второго порядка на
звеньях Рауха, Сален-Ки и биквадратного звена?

А кривую изменения реактивного сопротивления ёмкости в зависимости от частоты — не изобразить ли?

«Хватит умничать, пальцем покажи!», — предвижу я законное роптание посетителя, впавшего в соблазн от заголовка страницы.

И действительно. Здесь мне не тут! Базар надо фильтровать, а не безобразия нарушать!

Итак, приступим.
Для начала мы рассмотрим активные и пассивные ФНЧ, ФВЧ, ПФ без использования катушек индуктивности.

Определимся с терминологией.

— Фильтр нижних частот (ФНЧ) представляет собой устройство, которое пропускает сигналы низких частот и задерживает сигналы
высоких частот.
— Фильтр верхних частот (ФВЧ) соответственно пропускает сигналы высоких частот и задерживает сигналы низких.
— Полосовой фильтр (ПФ) пропускает сигналы в некоторой полосе частот и подавляет сигналы и на низких частотах, и на высоких.

— Полоса пропускания определяется как диапазон частот, в котором АЧХ фильтра не выходит за пределы заданной неравномерности
(обычно — 3дБ).

— Частотой среза фильтра называют частоту, ослабление сигнала на которой достигает -3дБ по логарифмической шкале,
или 1/√2 ≈ 0.71 по линейной.
— Неравномерность АЧХ в полосе пропускания — размер флуктуации АЧХ от пика до пика в полосе пропускания.
— Крутизна частотной характеристики фильтра – скорость спада АЧХ в полосе подавления (дБ/октаву или дБ/декаду).

А начнём мы с простейших RC фильтров первого порядка. Слева фильтр нижних частот (ФНЧ), справа фильтр верхних частот (ФВЧ).

Рис.1

Крутизна спада АЧХ таких фильтров в полосе подавления — 6 дБ/октаву.
Частота среза рассчитывается по формуле:  

Теперь надо определиться — из каких соображений выбирать номиналы R и С.
Ёмкость посчитается нашей табличкой, а к выбору сопротивления резистора, для достижения заявленной крутизны, надо подойти со всей
ответственностью.
Номинал этого резистора должен быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного
сопротивления последующего.

РИСУЕМ ТАБЛИЧКУ ДЛЯ ФИЛЬТРОВ ПЕРВОГО ПОРЯДКА

ТЕПЕРЬ ТО ЖЕ САМОЕ С ДРУГИМИ ВВОДНЫМИ

Для получения простейшего полосового фильтра первого порядка, нужно последовательно соединить ФНЧ и ФВЧ с Рис.1,
не забывая, что значение сопротивления R второго фильтра должно быть на порядок (в 10 раз) выше сопротивления
первого.

Важно понимать, что хорошей крутизны спада АЧХ от таких простейших фильтров добиться не удастся. Тут нам прямая
дорога к активным фильтрам, или к фильтрам на LC цепях.

Именно активные фильтры мы и рассмотрим на следующей странице.