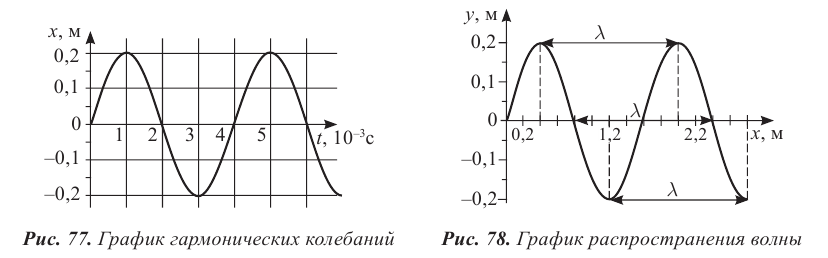
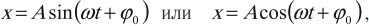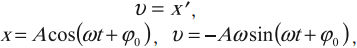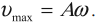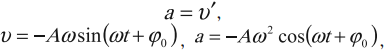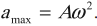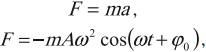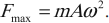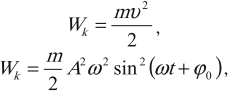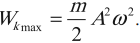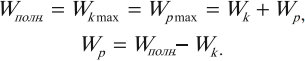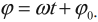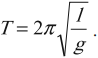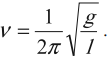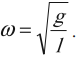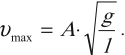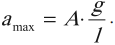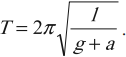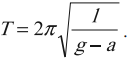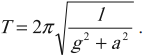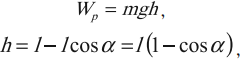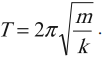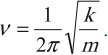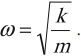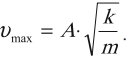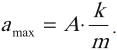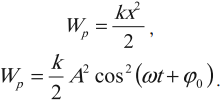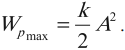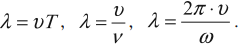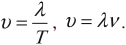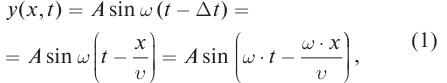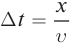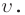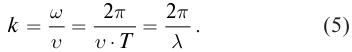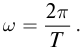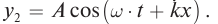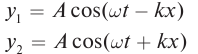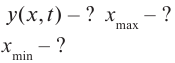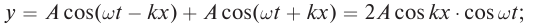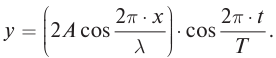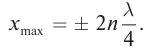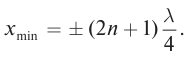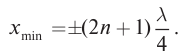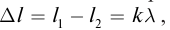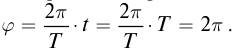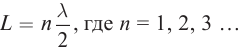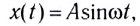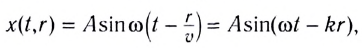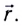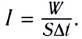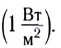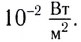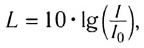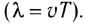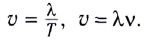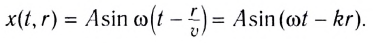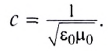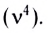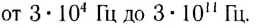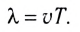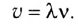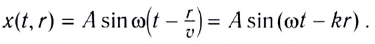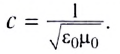Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
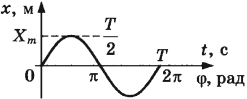
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
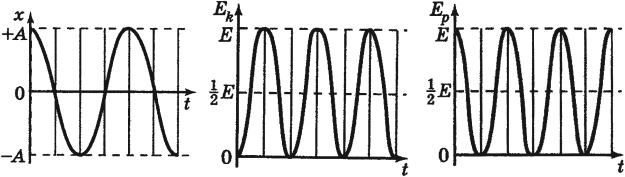
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
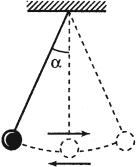
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
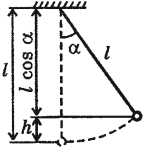
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
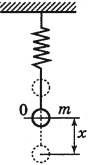
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
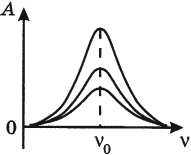
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
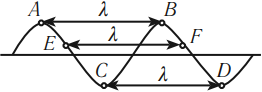
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Механические колебания и волны
2.9 (58.66%) 149 votes
Частота колебаний, теория и онлайн калькуляторы
Частота колебаний
Гармонические колебания, частота и др их характеристики
Определение
Колебаниями называют такие движения или процессы, которые повторяются.
По своей природе колебания делят на механические, электромагнитные и др. Разные виды колебаний описывают при помощи одинаковых уравнений и при этом используют одинаковые характеристики.
Колебания являются свободными (собственными), если они происходят за счет энергии, которая получена колебательной системой один раз и в дальнейшем внешние воздействия на эту систему отсутствуют.
Самым простым видом колебаний являются гармонические колебания. Гармоническими колебаниями называют такие колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса. Пусть происходят гармонические колебания никоторого параметра $s$, тогда они описываются как:
[s=A{cos ({omega }_0t+varphi ) } left(1right),]
где $A=s_{max}$ — амплитуда колебаний; ${omega }_0$ — циклическая (круговая) частота колебаний; $varphi $ — начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ — фаза колебаний. Величина $s$ лежит в пределах $-Ale sle $+A.
Промежуток времени через который повторяются определенные состояния системы (T) называют периодом. За время равное периоду колебаний фаза изменяется на величину равную $2pi $, поэтому:
[T=frac{2pi }{{omega }_0}left(2right).]
Разные процессы, повторяющиеся через равные промежутки времени (периодические процессы) можно представить в виде совокупности наложенных гармонических колебаний.
Определение частоты колебаний
Определение
Физическая величина обратная периоду колебаний называется частотой колебаний ($nu $). Частота колебаний — это количество полных колебаний, которые совершаются за единицу времени.
[nu =frac{1}{T}left(3right).]
Из (2) и (3) следует, что циклическая частота равна:
[{omega }_0=2pi nu left(4right).]
Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:
[left[nu right]=с^{-1}=Гц.]
Герц — единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса. Единица измерения частоты периодического процесса называется в честь немецкого ученого Г. Герца.
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Частота дискретных событий, частота вращения
Определение
Частотой дискретных колебаний ($n$) — называют физическую величину, которая равна количеству действий (событий) в единицу времени.
Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(5right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(6right).]
Примеры задач с решением
Пример 1
Задание. Каковы: циклическая частота колебаний и частота колебаний величины $r$, если ее гармонические колебания заданы уравнением:
[r=0,5{cos left(3pi t+frac{pi }{4}right)(м) . }]
Решение.Рассмотрим уравнение колебаний параметра $r$:
[r=0,5{cos left(3pi t+frac{pi }{4}right)left(мright)(1.1) . }]
Из этого уравнения мы видим, что амплитуда колебаний равна $r_{max}=0,5 (м)$; ${omega }_0=3pi $ ($frac{рад}{с}$). Частоту колебаний ($nu $) найдем, используя формулу:
[{omega }_0=2pi nu left(1.2right).]
Выразим $nu $, имеем:
[nu =frac{{omega }_0}{2pi } left(1.3right).]
Подставляя ${omega }_0=3pi $textit{ }($frac{{rm рад}}{{rm с}}$) получаем:
[nu =frac{3pi }{2pi }=frac{3}{2}left(Гцright).]
Ответ. ${omega }_0=3pi $ $frac{рад}{с};;$ $nu $=1,5 Гц
Пример 2
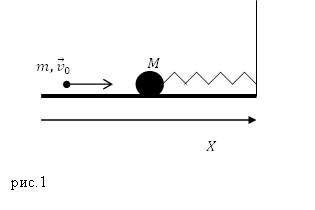
Задание. Шар массой $M$ закреплен на пружине коэффициент упругости, которой равен $k$. Шар лежит на гладкой горизонтальной поверхности (рис.1). Горизонтально летела пуля, ее скорость составляла $v_0 $, была направлена в сторону шара и в момент удара была параллельна оси пружины, масса пули $m$. После удара о шар пуля застряла в нем. Какова частота колебаний шара, вызванных ударом пули. Шар может скользить по столу без трения. Массу пружины и сопротивление воздуха не учитывать.
Решение. После того, как пуля ударила по шарику и застряла в нем, данная система будет совершать колебания. Так как по условию задачи колебания можно считать свободными (трения нет), то колебания шарика (с пулей) на пружине являются свободными и гармоническими, их можно описать как, например изменение координаты шарика, который примем за материальную точку:
[x=x_m{sin left({omega }_0t+varphi right)left(2.1right). }]
В таких колебаниях кинетическая энергия переходит в потенциальную энергию и наоборот, поэтому можно записать закон сохранения энергии в виде:
[frac{(m+M)v^2_m}{2}=frac{kx^2_m}{2} left(2.2right),]
где $frac{(m+M)v^2_m}{2}$ — кинетическая энергия системы в момент, сразу следующий за ударом, скорость шарика с пулей максимальна; $frac{kx^2_m}{2}$ — потенциальная энергия сжатой пружины в момент максимального ее сжатия, когда шарик с пулей перестаёт двигаться.
Амплитуду скорости колебаний найдем как:
[v_x=frac{dx}{dt}=frac{d}{dt}(x_m{sin left({omega }_0t+varphi right)=x_m{omega }_0{cos left({omega }_0t+varphi right)to v_m= }x_m{omega }_0(2.3). }]
Подставим $v_m$ в (2.2), имеем:
[frac{(m+M){x_m}^2{{omega }_0}^2}{2}=frac{kx^2_m}{2}to {omega }_0=sqrt{frac{k}{m+M}}left(2.4right).]
Применим выражение:
[nu =frac{{omega }_0}{2pi } left(2.5right).]
Найдем частоту колебаний системы:
[nu =frac{1}{2pi }sqrt{frac{k}{m+M}}.]
Ответ. $nu =frac{1}{2pi }sqrt{frac{k}{m+M}}$
Читать дальше: частота.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Условие задачи:
Волны распространяются в упругой среде со скоростью 100 м/с. Наименьшее расстояние между точками среды, фазы колебаний которых противоположны, равно 1 м. Определить частоту колебаний.
Задача №9.6.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(upsilon=100) м/с, (Delta l=1) м, (nu-?)
Решение задачи:
Скорость распространения колебаний (upsilon) можно определить через длину волны (lambda) и частоту колебаний (nu) следующим образом:
[upsilon = lambda nu]
Откуда частота колебаний (nu) равна:
[nu = frac{upsilon }{lambda };;;;(1)]
Точки, фазы колебаний которых противоположны, колеблются с разностью фаз, равной (pi). Если точки, находящиеся на расстоянии (l), колеблются с разностью фаз (pi), а точки, находящиеся на расстоянии (lambda) – c разностью фаз (2pi), то справедливо записать следующее соотношение:
[frac{l}{pi } = frac{lambda }{{2pi }}]
Выразим отсюда длину волны (lambda):
[lambda = 2l;;;;(2)]
Подставим выражение (2) в формулу (1), тогда получим:
[nu = frac{upsilon }{{2l}}]
Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:
[nu = frac{{100}}{{2 cdot 1}} = 50;Гц]
Ответ: 50 Гц.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.6.8 Волна с частотой 5 Гц распространяется в пространстве со скоростью 3 м/с
9.6.10 На озере в безветренную погоду с лодки бросили тяжелый якорь. От места бросания
9.6.11 Рассчитать длину звуковой волны в воде, если частота колебаний 440 Гц
Содержание:
Волновое движение:
Процесс распространения колебаний в упругой среде называют механической волной. Для механических волн нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию, она должна обладать инертными и упругими свойствами.
Различают поперечные и продольные волны. Продольные волны могут распространяться в любых средах: твердых, жидких и газообразных; поперечные – только в твердых средах.
Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. Волны переносят энергию колебаний.
Изучив страницу, вы сможете:
- исследовать образование стоячих звуковых волн в воздухе;
- объяснять механизм образования стоячих волн, определять узлы и пучности, используя графический метод;
- исследовать интерференцию от двух источников на поверхности воды;
- объяснять принцип Гюйгенса и условия наблюдения дифракционной картины механических волн.
Уравнение бегущей волны
Колебательное движение тела в упругой среде является источником механической волны.
Волну, переносящую энергию, называют бегущей волной.
В однородной среде скорость распространения волны остается величиной постоянной. Смещение y (x, t) от положения равновесия частиц среды при распространении волны зависит от координаты x на оси 0х, вдоль которой распространяется волна, и от времени t по закону:
где
Введем волновое число 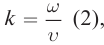
Смещение точек упругой среды в волне, бегущей в противоположном направлении выбранной оси 0х, можно определить по формуле:
Вспомните! Основные характеристики волн. Волны, созданные источником, совершающим гармонические колебания, характеризуются амплитудой колебания частиц среды A, частотой 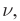
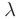
Длиной волны 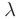
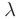
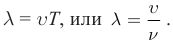
Физический смысл волнового числа
Запишем формулу (2), выразив циклическую частоту через период 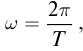
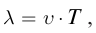
Бегущая волна обладает двойной периодичностью – во времени и в пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны 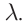
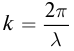
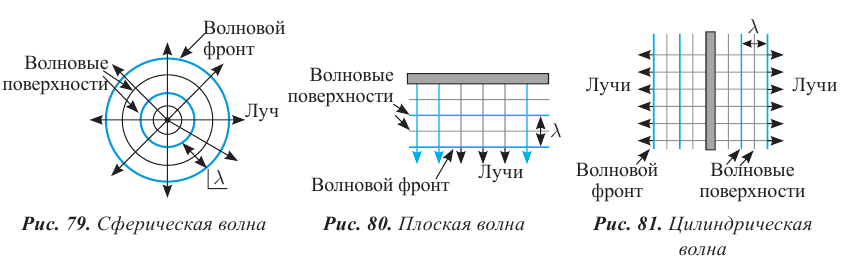
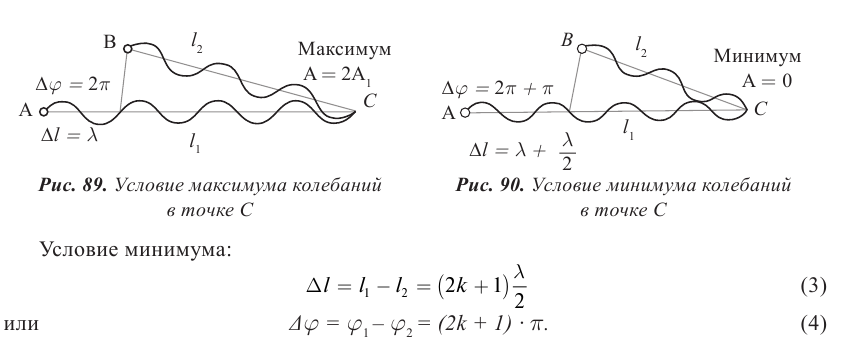
Фронт волны и волновая поверхность
Волна за время, равное периоду колебаний, достигает точек пространства, расположенных от источника на расстоянии длины волны. Совокупность этих точек представляет собой фронт волны, который отделяет колеблющиеся точки среды от точек, не вовлеченных в колебательное движение. Фронт волны от точечного источника представляет собой сферу, от плоской пластины – плоскость, от струны – форму цилиндра (рис. 79–81).
Фронт волны – это геометрическое место точек пространства, до которых дошли колебания в данный момент времени t.
Направление распространения волны указывает луч, который перпендикулярен фронту волны.
В волне можно рассмотреть множество поверхностей, все точки которых совершают колебания синфазно, их называют волновыми поверхностями. При множестве волновых поверхностей, фронт волны только один.
Геометрическое место точек пространства, которые совершают колебания в одинаковой фазе в данный момент времени, называют волновой поверхностью.
Стоячие волны
Уравнение стоячей волны При отражении от более плотной среды волна, изменив свое направление на обратное, меняет фазу на 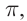
Получим уравнение стоячей волны путем сложения уравнений бегущих волн:
Заменив волновое число его значением 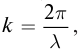
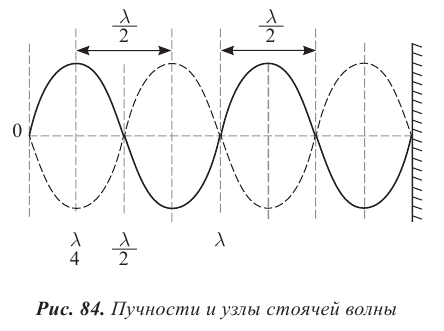
Координаты точек пучностей и узлов определяются из условий наибольшего и наименьшего значений амплитуды. При 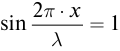
При 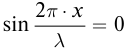
Расстояния между двумя соседними пучностями или двумя соседними узлами равны:
В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не переносится в другие части струны. В каждом таком отрезке происходит дважды за период превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Отсутствие переноса энергии является отличительной особенностью стоячей волны.
Пример:
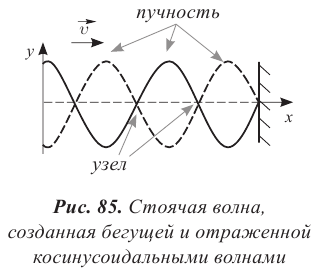
Уравнение бегущей волны, изображенной на рисунке (рис. 85): 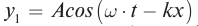
А. Получите уравнение стоячей волны как сумму падающей и отраженной волн.
В. Полученное выражение запишите, заменив волновое число и циклическую частоту через длину волны и период.
С. Определите положение узлов и пучностей.
Дано:
Решение: А. Уравнение стоячей волны определятся сложением уравнений бегущих волн: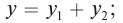
В.
С. При 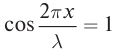
С. Расстояние от узлов определим из условия 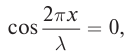
Ответ: 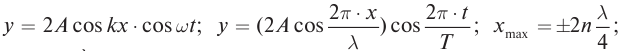
Интерференция волн
Если в некоторой среде несколько источников возбуждают механические волны, то они распространяются независимо друг от друга. Все точки среды принимают участие в колебаниях, вызванных каждой волной в отдельности. Наложение волн, в результате которой появляется устойчивая картина чередующихся максимумов и минимумов колебаний частиц среды, называют интерференцией.
Интерферировать могут только волны, имеющие одинаковую частоту и постоянный сдвиг фаз. Такие волны называют когерентными, их создают источники, колеблющиеся с одинаковой частотой и постоянным значением сдвига фаз.
Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.
Интерференция бывает стационарной и нестационарной. Стационарную интерференционную картину могут давать только когерентные волны: например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников (рис. 87).
Запомните! Волны называют когерентными, если их источники совершают колебания одной частоты с постоянным сдвигом фаз.
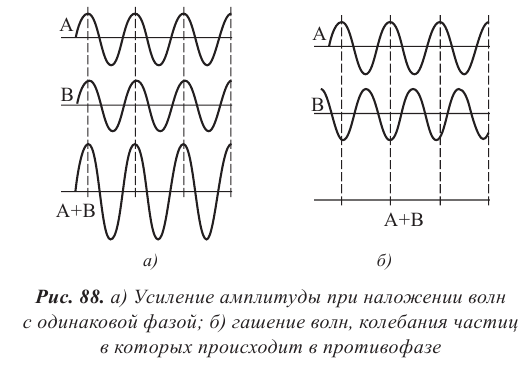
Условие максимума и минимума при интерференции двух волн
Амплитуда колебаний при наложении волн определяется в соответствии с принципом суперпозиции (рис. 88). Если в некоторой точке среды накладываются гребни когерентных волн, то происходит усиление колебаний, амплитуда принимает значение, равное сумме амплитуд. Если накладывается гребень одной волны с впадиной другой волны, то при равенстве амплитуд отдельно взятых волн данная точка пространства не совершает колебания. Если амплитуды отличаются, то колебания в этой точке совершаются с амплитудой равной разности амплитуд распространяющихся волн.
Для определения результата интерференции волн, распространяющихся от двух источников А и В, находящихся на расстоянии 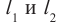
где 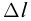
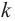
так как волна за период пробегает расстояние равное длине волны 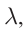
Минимум колебаний в рассматриваемой точке среды наблюдается в том случае, если от двух когерентных источников распространяются волны со сдвигом фаз, равным нечетному числу p, а разность хода лучей кратна нечетному числу полуволн. В этом случае колебания происходят в противофазе (рис. 90).
Возьмите на заметку:
Интерференция волн приводит к перераспределению энергии колебаний между частицами среды. Это не противоречит закону сохранения энергии, так как в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.
Распространение волн. Принцип Гюйгенса – Френеля
На основе принципа Х. Гюйгенса: каждая точка среды, до которой дошло возмущение, является источником вторичных волн, невозможно объяснить, почему источники вторичных волн создают фронт только по направлению распространения волны. Для объяснения явлений распространения волны французский физик О. Френель в 1815 г. дополнил принцип Х. Гюйгенса представлениями о когерентности и интерференции вторичных волн. При наложении вторичных когерентных волн происходит интерференция, в результате которой амплитуда колебаний в различных точках пространства становится разной: по направлению распространения волны усиливается, в обратном направлении – уменьшается. Огибающая фронты вторичных волн является фронтом результирующей волны (рис. 92).
Дифракция механических волн
Вторичные волны, созданные точками среды, которые находятся на краю отверстия или препятствия, искривляются и волна огибает препятствие (рис. 93 а–г).
Дифракция – это явление огибания волнами препятствий.
Все волны способны огибать препятствия, если длина волны соизмерима с размерами препятствия. Дифракция становится заметной, если размеры препятствия меньше длины волны.
Физика в нашей жизни:
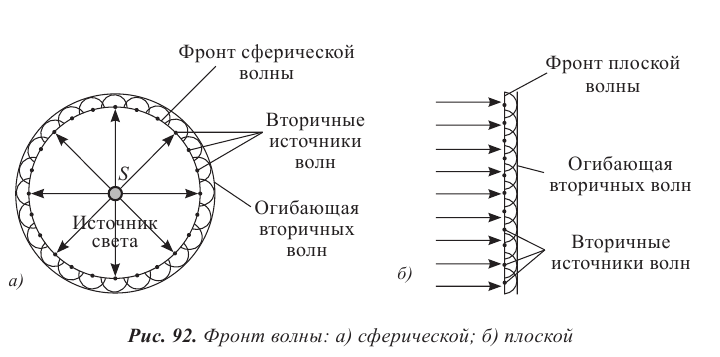
Струнные музыкальные инструменты
Интересно знать! Адырна (рис. 96 а) – один из древнейших казахских струнных инструментов. В его форме отобразилась воинственность кочевников-казахов: он напоминает изогнутый лук воина. Деревянный корпус инструмента легкий, так как он пустотелый. Струны изготавливают из кусков специально выделанной кожи или сплетенных из верблюжьей шерсти нитей. Музыкант играет, перебирая струны. Их в инструменте 13. Жетыген (рис. 96 б) – семиструнный музыкальный инструмент. Он имеет прямоугольную форму, изготовлен из дерева, струны – из конского волоса. Легенда о жетыгене раскрывает причину использования именно семи струн. Старик, потерявший семерых сыновей, вылил свое горе, исполняя кюи о них. Вспоминая каждого из сыновей, он натягивал новую струну на музыкальном инструменте.
Условие возникновения стоячей волны в струне
Стоячая волна в струне возникает только в том случае, если длина 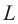
Набору значений 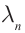
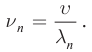
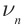
В отличие от груза на пружине или маятника, у которых имеется единственная собственная частота, струна обладает бесконечным числом собственных резонансных частот. На рисунке 96 в изображены несколько типов стоячих волн в струне. Стоячие волны различных типов могут одновременно присутствовать в колебаниях струны.
Визуализация звуковых волн
Существует несколько способов демонстрации стоячей волны, один из них – фигуры Хладни (рис. 97). Немецкий физик Эрнст Хладни получал узор, посыпая пластинку песком и проводя по краю смычком. Движения смычка заставляли пластинку колебаться на некоторой резонансной частоте. Песок скапливался и лежал неподвижно в узлах, а на участках, где отраженная волна усиливала бегущую, песок смещался.
Интересно знать! В Шотландии есть рослинская капелла св. Матвея, на одной из арок которой есть 213 резных каменных кубов, с вырезанным на них геометрическим рисунком. Многие исследователи пытались понять, что зашифровано в рисунках на кубах. Отставной генерал ВВС Томас Митчел со своим сыном, пианистом Стюартом Митчелом предложили оригинальный способ расшифровки послания. Они сопоставили геометрические рисунки с фигурами Хладни и пришли к выводу, что на кубах записаны ноты. Собрав ноты воедино и творчески обработав их, они представили миру произведение «Рослинский Мотет».
Итоги:
Глоссарий
Волновая поверхность – геометрическое место точек, имеющих одинаковую фазу колебаний.
Дифракция – явление огибания волнами препятствий.
Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.
Когерентные волны – волны, имеющие одинаковую частоту и постоянный сдвиг фаз.
Механическая волна – процесс распространения колебаний в упругой среде.
Фронт волны – геометрическое место точек пространства, до которых дошли колебания в данный момент времени t.
Распространение колебаний в упругих средах. Продольные и поперечные волны
Опыт показывает, что колебания, возбужденные в какой-либо точке упругой среды, с течением времени передаются в ее другие точки. В качестве примера достаточно вспомнить, что измерение пульса осуществляется на запястье, хотя сердце расположено внутри грудной клетки. Такие явления связаны с распространением механических волн.
Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.
Механические волны не могут распространяться в вакууме.
Источником механических волн является колеблющееся тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в ней с определенной скоростью, зависящей от плотности и упругих свойств среды.
Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы колеблются вблизи положений равновесия. Среднее смещение частиц за большой промежуток времени равно нулю.
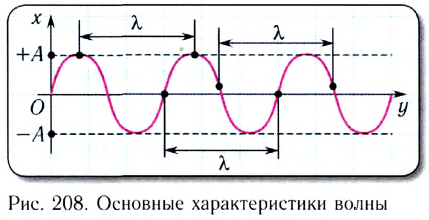
Рассмотрим основные характеристики волны.
Волновой фронт — это воображаемая поверхность, до которой дошло волновое возмущение в данный момент времени.
Линия, проведенная перпендикулярно волновому фронту в направлении распространения волны, называется лучом. Луч указывает направление распространения волны.
Основными характеристиками волны являются (рис. 208):
Рассмотрим колебания источника волны, происходящие с циклической частотой 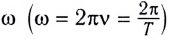
где x(t) — смещение источника от положения равновесия.
В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна v, то зависимость от времени t координаты (смещения) х колеблющейся точки, находящейся на расстоянии r от источника, описывается функцией
где k — волновое число 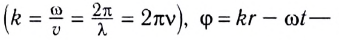
Выражение х(t, r) называется уравнением плоской волны, распространяющейся (бегущей) вдоль направления радиус-вектора
Бегущую волну можно наблюдать, проведя следующий опыт: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна, описываемая уравнением плоской волны.
Рассмотрим классификацию бегущих волн по направлению колебаний частиц среды, в которой они распространяются.
Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волн. Продольную волну легко получить с помощью длинной пружины, которая лежит на гладкой горизонтальной поверхности и один конец ее закреплен. Легким ударом по свободному концу В пружины мы вызовем появление волны (рис. 209).
При этом каждый виток пружины будет колебаться вдоль направления распространения волны ВС. Примерами продольных волн являются звуковые волны в воздухе и жидкости.
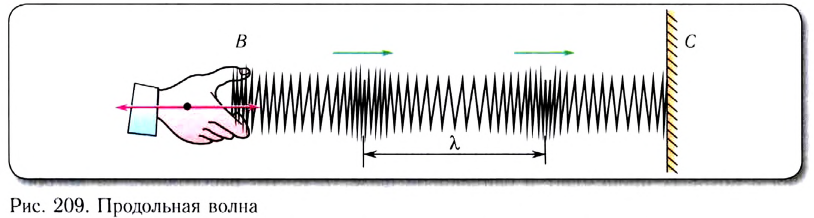
Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны. С помощью длинной пружины можно продемонстрировать распространение поперечных волн, если совершать колебания незакрепленного конца перпендикулярно пружине (рис. 210).
Поперечные волны вызывают звучание струн музыкальных инструментов при их возбуждении.
Продольные колебания симметричны относительно линии распространения ВС, и их действие на любой регистрирующий прибор не изменяется, если прибор будет поворачиваться вокруг направления распространения.
Действие поперечных волн на регистрирующий прибор зависит от того, в какой плоскости, проходящей через линию распространения, происходит колебание. Эта особенность поперечных волн носит название поляризации. Если колебания происходят в одной плоскости, то волну называют плоско или линейно поляризованной. Если конец вектора колебаний, например вектора смещения, скорости, напряженности электрического поля, описывает эллипс или окружность, то волну называют эллиптически или циркулярно-поляризованной.
До сих пор мы рассматривали волны, распространяющиеся в какой-либо среде. Волны, которые распространяются на границе раздела двух сред, называются поверхностными волнами. Примером данного типа волн служат волны на поверхности воды.
Звуковые волны. Скорость звука. Ультразвук
Звуком называются колебания среды, воспринимаемые органами слуха.
Раздел физики, в котором изучаются звуковые явления, называется акустикой.
Звуковая волна — упругая продольная волна, представляющая собой зоны сжатия и разрежения упругой среды (например, воздуха), распространяющиеся в пространстве с течением времени. Таким образом, в процессе распространения звуковой волны меняются такие характеристики среды, как давление и плотность.
Звуковые волны классифицируются по частоте следующим образом:
Многие животные могут воспринимать ультразвуковые частоты. Например, собаки могут слышать звуки до 50 000 Гц, а летучие мыши — до 100 000 Гц. Инфразвук, распространяясь в воде на сотни километров, помогает китам и многим другим морским животным ориентироваться в толще воды.
Звуковые волны приносят человеку жизненно важную информацию — с их помощью мы общаемся, наслаждаемся мелодиями, узнаем по голосу знакомых людей. Мир окружающих нас звуков разнообразен и сложен, однако мы достаточно легко ориентируемся в нем и безошибочно можем отличить пение птиц от шума городской улицы.
Одной из важнейших характеристик звуковых волн является спектр. Спектром называется набор различных частот, образующих данный звуковой сигнал. Спектр может быть сплошным или дискретным.
В сплошном спектре присутствуют волны, частоты которых заполняют весь заданный спектральный диапазон.
В
дискретном спектре — конечное число волн с определенными частотами и амплитудами, которые образуют рассматриваемый сигнал.
По типу спектра звуки разделяются на шумы и музыкальные тона.
Шум — совокупность множества разнообразных кратковременных звуков (хруст, шелест, шорох, стук и т.п.) — представляет собой наложение большого числа колебаний с близкими амплитудами, но различными частотами (имеет сплошной спектр).
Музыкальный тон создается периодическими колебаниями звучащего тела (камертон, струна) и представляет собой гармоническое колебание одной частоты. На основе музыкальных тонов создана музыкальная азбука — ноты (до, ре, ми, фа, соль, ля, си), которые позволяют воспроизводить одну и ту же мелодию па различных музыкальных инструментах.
Музыкальный звук (созвучие) — результат наложения нескольких одновременно звучащих музыкальных тонов, из которых можно выделить
основной тон, соответствующий наименьшей частоте. Основной тон называется также первой гармоникой. Все остальные тоны называются обертонами. Обертоны называются гармоническими, если частоты обертонов кратны частоте основного тона. Таким образом, музыкальный звук имеет дискретный спектр.
Любой звук, помимо частоты, характеризуется интенсивностью.
Интенсивность I — это энергия 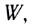
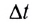
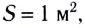
Другими словами, интенсивность любой волны — мощность, переносимая волной через единичную площадку, расположенную перпендикулярно к направлению распространения волны.
Единицей интенсивности в СИ является ватт на метр в квадрате
Чтобы вызвать звуковые ощущения, волна должна обладать некоторой минимальной интенсивностью, называемой порогом слышимости.
С возрастом порог слышимости человека возрастает.
Интенсивность звуковых волн, при которой возникает ощущение боли, называют порогом болевого ощущения или болевым порогом. Интенсивность звука, улавливаемого ухом человека, лежит в широких пределах: от 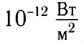
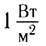
Реактивный самолет может создать звук интенсивностью 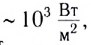
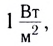
Уровни интенсивности звука L определяют обычно, используя шкалу, единицей которой является бел (Б) или, что гораздо чаще, децибел (дБ) (одна десятая бела). 1 Б самый слабый звук, который воспринимает наше ухо. Единица названа в честь изобретателя телефона А. Г. Белла. Измерение уровня интенсивности в децибелах проще, поэтому принято в физике и технике.
Уровень интенсивности L любого звука в децибелах вычисляется через интенсивность звука по формуле
где I — интенсивность данного звука, 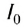
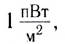
Так, поезд метро создает уровень интенсивности звука 100 дБ, мощные усилители — 120 дБ, а реактивный самолет — 150 дБ. Тем, кто при работе подвергается воздействию шума свыше 100 дБ, следует пользоваться наушниками.
Физическим характеристикам звука соответствуют определенные (субъективные) характеристики, связанные с восприятием его конкретным человеком. Это связано с тем, что восприятие звука — процесс не только
физический, но и физиологический. Действительно, человеческое ухо воспринимает звуковые колебания определенных частот и интенсивностей (это объективные, не зависящие от человека характеристики звука) по-разному, в зависимости от «характеристик приемника» (здесь влияют субъективные индивидуальные черты каждого человека).
Основными физиологическими характеристиками звука являются громкость, высота и тембр.
Громкость (степень слышимости звука) определяется как интенсивностью звука (амплитудой колебаний в звуковой волне), так и различной чувствительностью человеческого уха на разных частотах, т. е. его способностью улавливать звуки различных частот. Наибольшей чувствительностью человеческое ухо обладает в диапазоне частот от 1000 Гц до <5000 Гц. Порог слышимости зависит от частоты звука: при частоте 1000 Гц он примерно 120—130 дБ, а при частоте 50 Гц — примерно 50 дБ. С частотой изменяется также и кажущаяся громкость звука. Звук, имеющий уровень интенсивности 20 дБ на частоте 1000 Гц, вследствие особенностей восприятия будет иметь такую же громкость, как и звук в 50 дБ на частоте 100 Гц. Следует отметить, что болевой порог в зависимости от частоты изменяется не столь существенно, как порог слышимости.
При увеличении интенсивности в 10 раз уровень громкости увеличивается на . 20 дБ. Вследствие этого звук в 50 дБ оказывается в 100 раз интенсивнее звука в 30 дБ.
Высота звука определяется частотой звуковых колебаний, обладающих наибольшей интенсивностью в спектре.
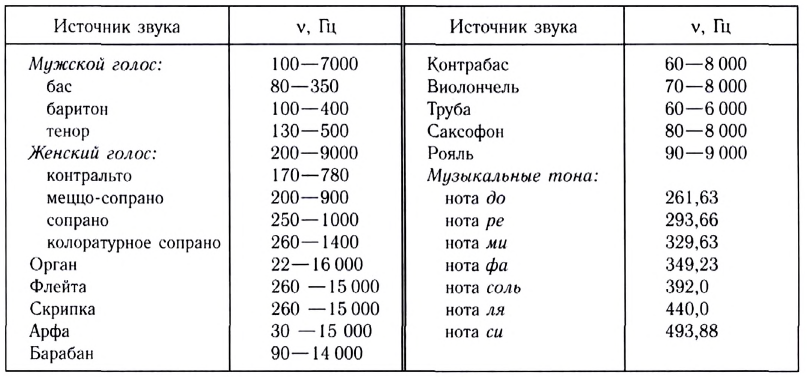
Тембр (оттенок звука) зависит от того, сколько обертонов присоединяется к основному тону и какова их интенсивность и частота. По тембру мы легко отличаем звуки скрипки и рояля, флейты и гитары, голоса людей (табл. 6) и т. д.
Скорость звука зависит от упругих свойств, плотности и температуры среды. Чем больше упругие силы, тем быстрее передаются колебания частиц соседним частицам и тем быстрее распространяется волна. Поэтому скорость звука в газах меньше, чем в жидкостях, а в жидкостях, как правило, меньше, чем в твердых телах (табл. 7).
Скорость звука в идеальных газах с ростом температуры растет пропорционально 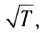
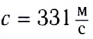
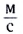
Таблица 6
Частота колебаний различных источников звука
Таблица 7
Скорость звука с в различных средах
Впервые скорость распространения звука в воздухе была определена в 1640 г. французским физиком Мареном Мерсенном. Он измерял промежуток времени между моментами появления вспышки и звука при ружейном выстреле. Мерсенн определил, что скорость звука в воздухе равна
Способ ориентации или исследования окружающих объектов, основанный на излучении ультразвуковых импульсов с последующим восприятием отраженных импульсов (эха) от различных объектов, называется эхолокацией, а соответствующие приборы — эхолокаторами. Наиболее известные животные, обладающие способностью к эхолокации, — летучие мыши и дельфины. По своему совершенству эхолокаторы этих животных не уступают, а во многом и превосходят (по надежности, точности, энергетической экономичности) современные эхолокаторы, созданные человеком.
Эхолокацию используют различные китообразные, а также птицы гуахаро, V. гнездящиеся в глубоких пещерах Венесуэлы и на острове Тринидад, стрижи-салаганы, живущие в пещерах Юго-Восточной Азии.
Эхолокаторы, используемые под водой, называются гидролокаторами или сонарами (название sonar образовано из начальных букв трех английских слов: sound — звук, navigation — навигация, range — дальность). Сонары незаменимы при исследованиях морского дна (его профиля, глубины), для обнаружения и исследования различных объектов, движущихся глубоко под водой. При их помощи могут быть легко обнаружены как отдельные большие предметы или животные, так и стаи небольших рыб или моллюсков.
Волны ультразвуковых частот широко используются в медицине в диагностических целях. УЗИ-сканеры позволяют исследовать внутренние органы человека. Ультразвуковое излучение, в отличие от рентгеновского, безвредно для человека.
Электромагнитные волны. Скорость электромагнитных волн
Основные характеристики механических волн:
Бегущая волна
Длина волны 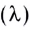
Скорость распространения волны:
Уравнение бегущей волны:
Продольная волна
Волна называется продольной, если колебания происходят вдоль направления распространения волн.
Поперечная волна
Волна называется поперечной, если колебания происходят в направлениях, перпендикулярных к направлению распространения волны.
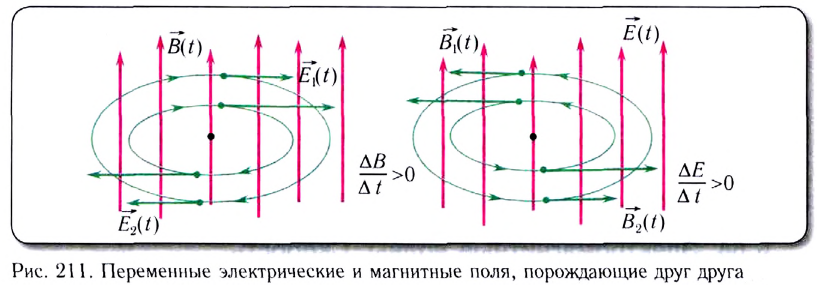
Впервые гипотезу о существовании электромагнитных волн высказал в 1864 г. Максвелл. Он показал, что источниками электрического поля могут быть либо электрические заряды, либо магнитные поля, меняющиеся во времени. Магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическим током), либо переменными электрическими полями. Изменение индукции магнитного поля с течением времени вызывает появление в окружающем пространстве вихревого электрического поля. Силовые линии этого поля замкнуты, а вектор его напряженности 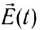
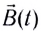
Максвелл предположил, что любое изменение напряженности электрического поля сопровождается возникновением вихревого магнитного поля.
Совокупность связанных друг с другом периодически изменяющихся электрического и магнитного полей называют электромагнитным полем. Согласно теории Максвелла переменное электромагнитное поле распространяется в пространстве в виде электромагнитных волн.
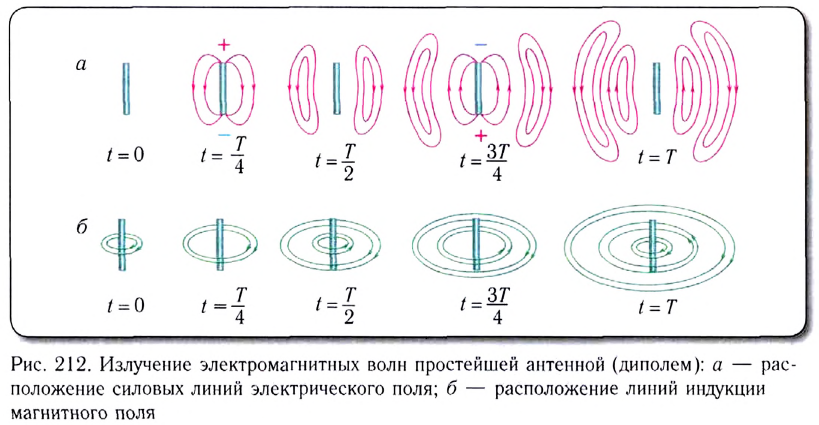
При ускоренном движении зарядов в проводнике создается переменное электрическое поле, которое порождает переменное магнитное поле, а последнее, в свою очередь, вызывает появление вихревого электрического поля уже на большем расстоянии от заряда и т.д. (рис. 212, а, б). Таким образом, попеременно порождая друг друга, в пространстве распространяется электромагнитное поле.
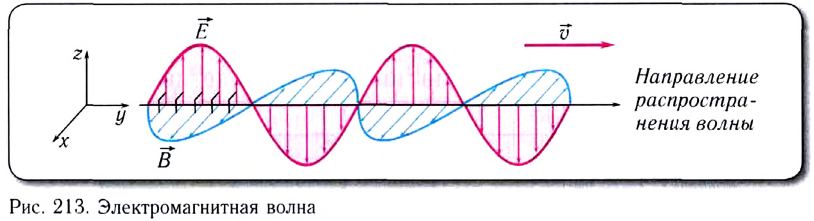
Электромагнитное поле, распространяющееся в вакууме или в какой-либо среде с течением времени с конечной скоростью, называется электромагнитной волной (рис. 213). Электромагнитные волны являются поперечными — вектор скорости 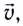
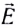
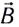
Одним из важнейших результатов теории Максвелла было теоретическое определение скорости электромагнитных волн. Согласно этой теории скорость с электромагнитной волны в вакууме связана с электрической постоянной 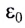
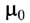
Скорость распространения волны с в вакууме является предельной. В веществе скорость распространения меньше с и зависит от его электрических и магнитных свойств.
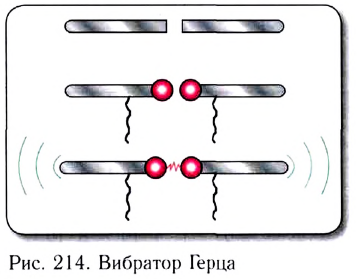
Экспериментально электромагнитные волны были открыты в 1887 г. немецким физиком Генрихом Рудольфом Герцем. Для их генерации он использовал специальное устройство (рис. 214).
Длина волны, возникавшей при проскакивании искры между электродами устройства, была 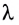
получило название вибратора Герца.
Герц считал, что такие волны невозможно использовать для передачи информации. Однако 7 мая 1905 г. русский ученый Александр Степанович Попов осуществил первую в мире передачу информации электромагнитными волнами — радиопередачу и положил начало эры радиовещания.
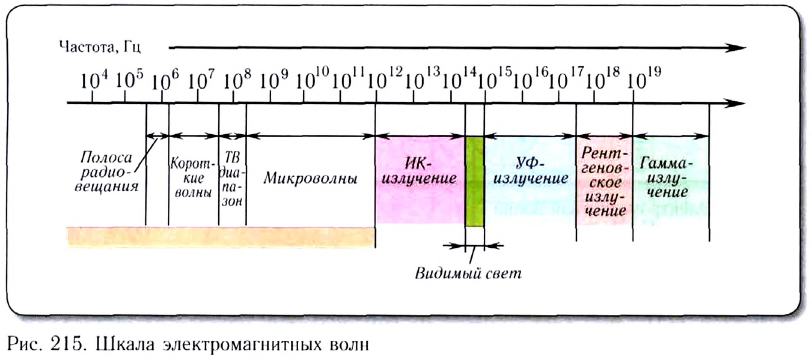
Свойства электромагнитных волн очень сильно зависят от их частоты. Спектр электромагнитного излучения удобно изображать в виде шкалы электромагнитных волн, приведенной на рисунке 215, а их классификация в зависимости от частот (длин волн) дается в таблице 8.
Таблица 8
Классификация электромагнитных волн
В настоящее время электромагнитные волны находят широкое применение в науке и технике:
- плавка и закалка металлов в электротехнической промышленности, изготовление постоянных магнитов (низкочастотные волны);
- телевидение, радиосвязь, радиолокация (радиоволны);
- мобильная связь, радиолокация (микроволны);
- сварка, резка, плавка металлов лазерами, приборы ночного видения (инфракрасное излучение);
- освещение, голография, лазеры (видимое излучение);
- люминесценция в газоразрядных лампах, закаливание живых организмов, лазеры (ультрафиолетовое излучение);
- рентгенотерапия, рентгеноструктурный анализ, лазеры (рентгеновское излучение);
- дефектоскопия, диагностика и терапия в медицине, исследование внутренней структуры атомов, лазеры, военное дело (гамма-излучение).
Изобретение радио. Принципы радиосвязи
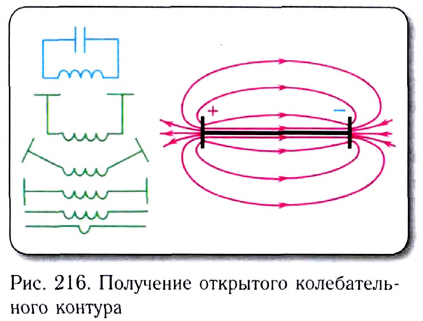
Вспомним колебательный контур, состоящий из конденсатора и катушки индуктивности, в котором возникают электромагнитные колебания (рис. 216).
Он называется закрытым, так как в нем происходит лишь обмен энергией между конденсатором, в котором сосредоточена энергия электрического поля, и катушкой, в которой сосредоточена энергия магнитного поля.
Потери энергии при электромагнитных колебаниях в контуре на излучение в окружающее пространство настолько малы, что можно считать: контур не создает электромагнитного излучения. Таким образом, вследствие изменения электрического и магнитного полей в закрытом пространстве внутри конденсатора и катушки закрытый колебательный контур не может служить источником электромагнитного излучения.
Для эффективного излучения контур нужно «открыть», раздвинув обкладки конденсатора, т. е. создать условия для того, чтобы поля «уходили» в пространство (см. рис. 216). Однако мощность электромагнитного излучения в этом случае невелика. И в таком виде его невозможно использовать на практике.
Исследования по передаче информации электромагнитными волнами, проведенные Поповым, показали, что колебательный контур можно использовать для радиосвязи, если одну обкладку конденсатора заземлить, а к другой присоединить вертикально натянутый провод, оставив его верхний конец свободным. Это устройство называется антенной. Антенна — незамкнутый провод или система проводов, подвешенных высоко над поверхностью Земли, по которым проходят переменные токи.
Применение антенны позволяет значительно увеличить мощность электромагнитного излучения. Колебательный контур, снабженный антенной, называется открытым, причем мощность излучения пропорциональна частоте излучения в четвертой степени
Рассмотрим устройство открытого колебательного контура. Основными его элементами являются конденсатор определенной емкости и катушка индуктивности. Отметим, что любой проводник имеет индуктивность, хоть и очень малую. Любые два проводника, разделенные изолятором, могут рассматриваться как конденсатор, имеющий определенную емкость контура (см. рис. 216). Эта система называется открытым колебательным контуром (вибратором Герца). Радиосвязью называется передача информации электромагнитными волнами, частоты которых охватывают диапазон
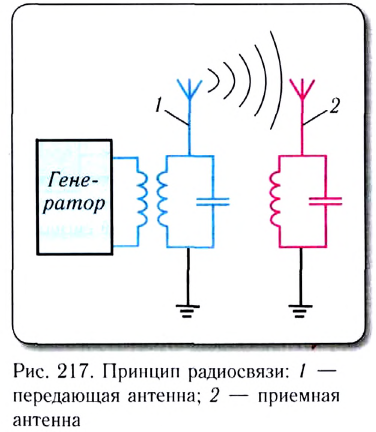
Рассмотрим принцип радиосвязи. В передающей антенне, настроенной в резонанс с генератором (рис. 217), возбуждаются высокочастотные токи, которые, в свою очередь, возбуждают электромагнитные волны в окружающем антенну пространстве. Эти волны, достигая приемной антенны, настроенной в резонанс с генератором, возбуждают токи той же частоты, которые могут быть усилены и использованы.
Токи звуковых частот, а также низкочастотные поля, применяемые в электротехнике, не годятся для радиосвязи по двум причинам:
- электромагнитные волны, возбуждаемые такими токами, обладают очень малой энергией и поэтому не могут распространяться па большие расстояния;
- для эффективного излучения таких волн размеры антенн должны быть очень большими (например, при частоте 1000 Гц длина антенны должна быть 150км).
С учетом этих причин для радиосвязи используются электромагнитные волны высоких частот (от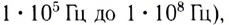
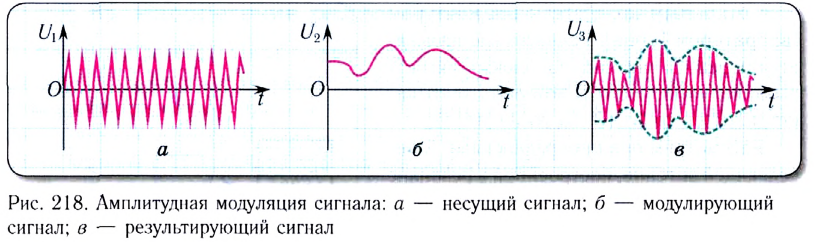
Инженеры нашли выход в специальном «смешивании» высокочастотных и низкочастотных сигналов. Поэтому радиопередачи осуществляются электромагнитными волнами высокой частоты (рис. 218, а), измененными низкочастотными сигналами (рис. 218, б, в). Этот прием получил название модуляции.
Модуляцией электромагнитной волны называется изменение ее параметров (амплитуды, частоты, фазы) по заданному закону. При этом модулируемые величины изменяются с частотой, намного меньшей частоты волны. Модулируемая волна (высокочастотная) называется несущей волной, а ее частота — несущей частотой.
В зависимости от того, какой параметр подвергается изменению, модуляция подразделяется на амплитудную, частотную и фазовую. Простейшей является амплитудная модуляция (см. рис. 218). При амплитудной модуляции в цепь высокочастотного генератора включается устройство, изменяющее ток в ней с частотой звукового сигнала, несущего информацию. При этом амплитуда несущей волны изменяется в соответствии с частотой низкочастотного сигнала.
Обратный процесс — процесс выделения низкочастотного звукового сигнала из модулированного высокочастотного — называется детектированием.
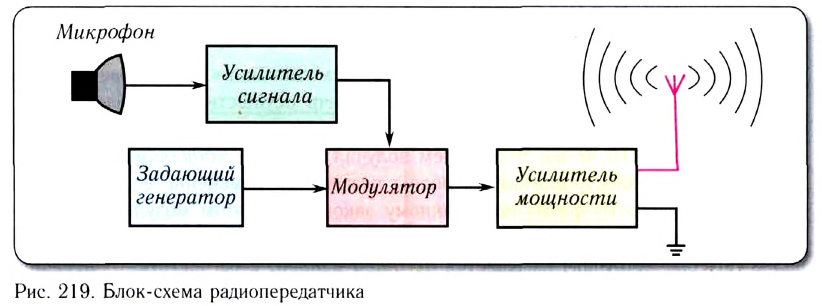
Любая радиосвязь включает работу радиопередатчика и радиоприемника.
Радиопередатчиком называется устройство, передающее информацию электромагнитными волнами радиочастотного диапазона.
Основные элементы радиопередатчика:
- генератор незатухающих колебаний несущей частоты;
- блок модуляции;
- усилитель и передающая антенна.
Блок-схема радиопередатчика приведена на рисунке 219.
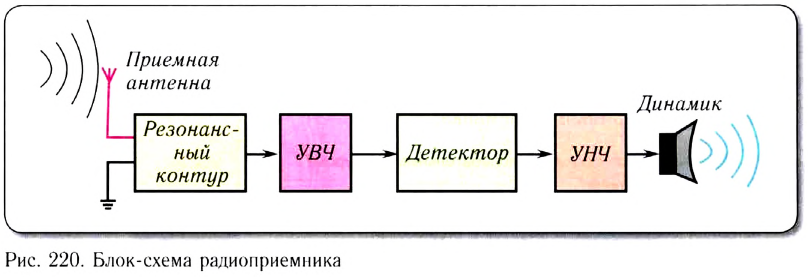
Радиоприемником называется устройство, принимающее информацию, кото рая передается электромагнитными волнами радиочастотного диапазона от радиопередатчика.
Основные элементы радиоприемника:
- приемная антенна с резонансным контуром, преобразующая энергию радио волн в энергию высокочастотных колебаний;
- блок детектирования, который выделяет модулированные колебания, усиливает и демодулирует их;
- воспроизводящее устройство (телефон, громкоговоритель), на которое подается низкочастотный модулирующий сигнал после его усиления.
Блок-схема радиоприемника приведена на рисунке 220.
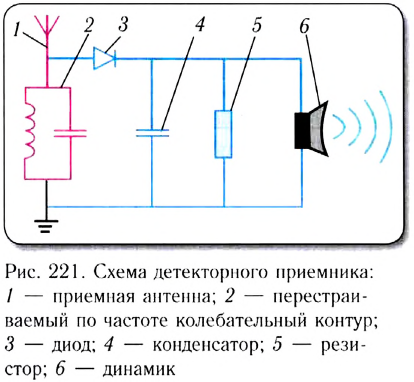
Простейшим радиоприемником является так называемый детекторный приемник (рис. 221). Он состоит из приемной антенны, соединенной с перестраиваемым по частоте колебательным контуром, детектора (полупроводниковый диод — устройство, пропускающее ток только в одном направлении), конденсатора (конденсатор обладает малым сопротивлением для высокочастотного сигнала и большим для низкочастотного, поэтому высокочастотный сигнал идет через конденсатор, а низкочастотный — через динамик) и динамика.
Соединенные параллельно конденсатор емкостью С и резистор сопротивлением R являются сглаживающей цепочкой. Их емкость и сопротивление подбираются таким образом, что 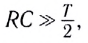
- Заказать решение задач по физике
Радиовещание. Принципы телевидения
В современной технике используются радиоволны различных частот. Классификация радиоволн по длинам волн и частотам приведена в таблице 9.
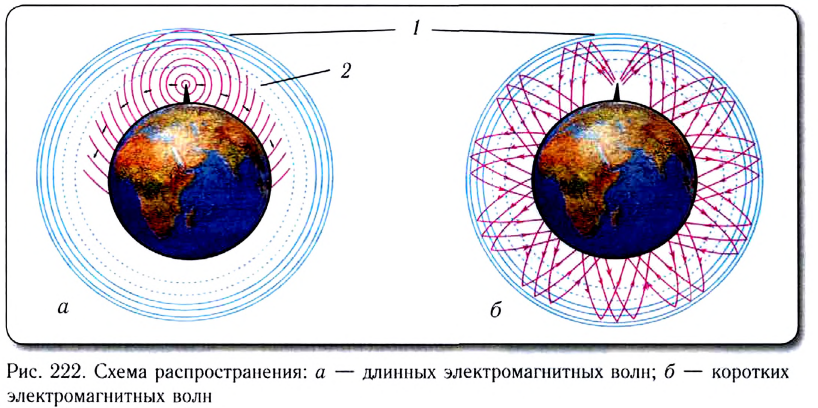
Радиоволны сильно отличаются по своим свойствам. Например, длинные и средние волны хорошо огибают естественные препятствия. Но на средних волнах дальность приема резко отличается днем и ночью. Это связано с тем, что средние волны сильно поглощаются нижним слоем ионосферы 2 и отражаются от более отдаленного слоя 1 (рис. 222, а). Дальность их приема сильно возрастает ночью, так как из-за отсутствия солнечного излучения нижний слой ионосферы 2 пропадает.
Таблица 9
Классификация радиоволн но длинам волн и частотам
Короткие волны отражаются от ионосферы и, таким образом, многократно отражаясь от поверхности Земли и ионосферы 1 (рис. 222, б), могут распространяться на очень большие расстояния.
Советский радист Э. Кренкель, находясь в северной полярной экспедиции в » У» 30-е годы XX в., с помощью маломощной радиостанции установил связь с австралийскими радистами.
Ультракороткие волны пропускаются ионосферой и не огибают препятствия. Осуществление связи такими волнами возможно только в пределах прямой видимости. Это привело к сооружению гигантских (400—500 м высотой) телевизионных башен, электромагнитные волны с которых Moгут попадать в приемники, находящиеся от них на расстоянии порядка 70—80 км. Только использование спутников на различных орбитах решило вопрос с приемом теле- и радиопередач и телефонных сообщений в любых уголках Земли.
Останкинская телебашня имеет высоту 535 м и позволяет вести прием теле-визионных передач на расстоянии до 120 км от Москвы.
Области использования радиоволн:
- радиовещание — передача речи, музыки на длинных, средних, коротких, ультракоротких волнах метрового диапазона;
- радиосвязь — передача на расстояние телеграфных сигналов и телефонных разговоров на ультракоротких волнах метрового и дециметрового диапазонов;
- телевидение — передача на расстояние изображения (аудио- и видеосигналов) на ультракоротких волнах метрового и дециметрового диапазонов;
- радиолокация — обнаружение и определение положения различных объектов на волнах метровых, дециметровых, сантиметровых и миллиметровых диапазонов;
- радиоастрономия — исследование с помощью радиотелескопов (рис. 223) космических объектов по их ультракоротковолновому излучению.
Для радиолокации используются ультракороткие радиоволны, длина которых лежит в метровом, дециметровом, сантиметровом и миллиметровом диапазонах, вследствие того, что:
- необходимы приемлемые размеры антенн радиолокатора;
- размеры исследуемых объектов больше или сравнимы с длинами радиоволн;
- чем меньше длина волны, тем легче обеспечить формирование достаточно короткого импульса;
- ультразвуковые волны слабо поглощаются атмосферой независимо от погодных условий.
Радар (радиолокатор) — прибор, представляющий собой комбинацию ультракоротковолнового радиопередатчика и приемника. С помощью общей антенны для приема и передачи создастся остронаправленный радиолуч. Излучение осуществляется короткими импульсами длительностью порядка 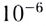
Важнейшим преимуществом радиолокации является независимость работы радаров от погодных условий и времени суток.
Радиоволнами осуществляется передача на расстояние изображений предметов. На телевизионной станции производится преобразование передаваемого изображения в последовательность электрических сигналов.
Сигнал изображения модулирует несущие высокочастотные колебания. Эти колебания излучаются антенной в виде радиоволн и передаются на большое расстояние. Они принимаются антенной телевизора. В результате детектирования снова получается электрический сигнал изображения. Он преобразуется в видимое изображение на экране кинескопа телевизора. Вместе с сигналом изображения передаются и звуковые сигналы.
Телевизионные передачи ведутся в диапазоне от 50 Мгц до 230 Мгц, в котором волны распространяются только в пределах прямой видимости.
Мобильная сотовая связь
В течение полутора веков, прошедших с момента изобретения телефона, телефонная связь настолько прочно вошла в быт современного человека, что отсутствие телефона в квартире практически стало исключением. К достоинствам проводных телефонных сетей следует отнести надежность связи и развитую систему абонентских сетей, позволяющую пользователю связаться с абонентом практически в любой стране мира.
Однако «жесткая привязка» абонента к стационарному телефонному аппарату, «ограниченная» к тому же длиной провода телефонной трубки, не позволяла пользователю быть мобильным, т. е, свободно перемещаться в пространстве во время разговоров или между ними.
Во второй половине прошлого века по мере совершенствования техники и технологии стала развиваться идея создания всемирной (глобальной) сети мобильной (сотовой) телефонной связи, позволяющей пользователю иметь доступ к развитой абонентской сети при помощи портативной переносной (мобильной) трубки-телефона значительного (десятки километров) радиуса действия.
Реализация этой идеи позволила бы вывести телефонную связь на новый уровень популярности и доступности с точки зрения пользователя, который имел бы свой индивидуальный телефонный номер и практически неограниченную свободу передвижения (мобильности) во время разговоров или между ними.
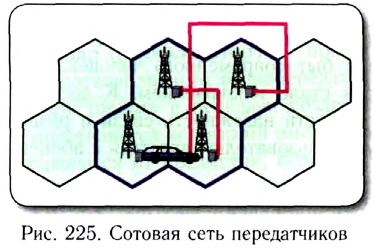
Предлагаемый принцип действия мобильной телефонной связи достаточно прост: при помощи трубки-телефона (мобильного телефона) абонент связывается с ближайшей базовой станцией (передатчиком) сети (рис. 224).
Эта базовая станция, в свою очередь, связывается со следующим передатчиком сети и т. д. по мере требования абонента (рис. 225).
Описанный принцип создания развитой абонентской сети называется сотовым принципом, поскольку по такому же принципу пчелы выстраивают соты внутри улья. При этом каждая созданная ячейка служит основой для создания следующей точно такой же ячейки и т. д.
В силу этого обстоятельства мобильную телефонную связь принято называть также сотовой телефонной связью. При движении абонента (например, на автомобиле) (см. рис. 225) базовые станции самостоятельно следят за ним и «передают» друг другу, что происходит практически без потери качества связи, быстро и совершенно незаметно для пользователя.
Самая простая часть структурной схемы сотовой связи — мобильный (переносной) телефон, состоит из двух частей: собственно «трубки» или ME (Mobile Equipment) и модуля идентификации абонента, или смарт-карты SIM (Subscriber Identity Module), получаемой при заключении контракта с тем или иным оператором.
Каждому сотовому телефону при производстве присваивается собственный номер или международный идентификатор мобильного устройства IMEI (International Mobile Equipment Identity), позволяющий отличить его от второго точно такого же.
В нашей стране используется стандарт сетей второго поколения GSM (Global System for Mobile Communications), который был разработан в 1990 г. Данный стандарт использует рабочую частоту v = 900 МГц, позволяющую значительно улучшить качество связи по сравнению со стандартами первого поколения.
Первый оператор GSM принял абонентов в 1991 году, а уже к началу 1994 г. мировые сети, основанные на данном стандарте, имели 1,3 миллиона абонентов. К концу 1995 г. их число увеличилось до 10 миллионов!
При включении мобильного телефона с активированной смарт-картой он «сам» находит ближайшую базовую станцию соответствующей сотовой сети, после чего весь пакет телефонных услуг данной сети становится доступным абоненту.
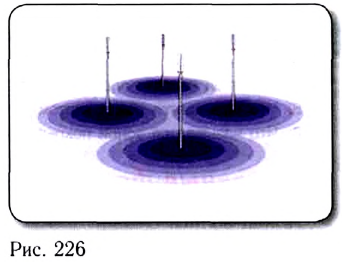
Каждый передатчик обеспечивает радиопокрытие в среднем на расстоянии до двух десятков километров от него (рис. 226).
Для рационального использования сотовой сети передатчиков разрабатываются оптимальные схемы их взаиморасположения на местности с учетом ее рельефа.
Важнейшей характеристикой для выбора того или иного оператора сотовой сети является зона покрытия различных населенных пунктов нашей страны базовыми станциями данной сети.
Современные технологии позволяют в метро или других труднодоступных для электромагнитных волн местах устанавливать микробазовые станции или пикосоты (рис. 227), которые позволяют значительно разгружать мобильный трафик на напряженных направлениях.
Основные формулы
Длина волны:
Скорость волны:
Уравнение бегущей волны:
Скорость распространения электромагнитных волн в вакууме:
- Продольные и поперечные волны в физике
- Звуковые волны в физике
- Электрическое поле в физике
- Работа по перемещению заряда в электростатическом поле
- Электромагнитные волны и их свойства
- Магнитные явления в физике
- Магнитный поток
- Волны в физике
google.com/+ВикторЦекунов
Репетитор по математике, физике (Минск): Виктор Иванович.
Высшая математика и физика для студентов.
Профессиональный репетитор окажет помощь в решении задач, подготовит к экзаменам. Занятия в Серебрянке, индивидуально. (90 мин)
= 20 $.
Тел: +375(29) 127 61 86.
___________________________________________________________________________________
Оказываю
платные услуги: решение задач по физике. Оплата WebMoney.
Заказы направляйте сюда: Платные услуги
___________________________________________________________________________________
4.1.
Механические колебания.
4.1.1. Гармонические колебания.
4.1.2. Свободные затухающие колебания.
4.1.3. Вынужденные колебания. Резонанс.
4.2. Электрические колебания.
4.3. Упругие волны. Акустика.
4.4. Электромагнитные волны. Излучение.
_______________________________________________________________________________________________
4.1. Механические колебания. 4.1.1. Гармонические колебания.
4.1.1-1.
Частица совершает гармоническое колебание с амплитудой А и периодом Т = 12 с.
Найти время t₁ , за
которое смещение частицы изменяется от 0 до А/2.
Решение:
Т = 12 с
х(0) = 0
х(t₁) =
А/2 (1)
t₁ – ?
Так как начальное положение частицы х(0) = 0, то частица колеблется по закону
синуса с начальной фазой ϕ₀ = 0:
x = Asin(ωt + ϕ₀) или
x = Asinωt, (2)
где ω = 2π/T –
круговая частота.
С учётом условия (1), запишем (2) в виде:
х(t₁) = Asin(ωt₁);
А/2 = Asin( (2π/T)t₁ );
1/2 = sin(2πt₁/T); 2πt₁/T = π/6. Отсюда
t₁ = T/12.
t₁
= 12/12 = 1 с.
Ответ: t₁ = T/12 = 1 c.
4.1.1-2.
Определить период Т простых гармонических колебаний диска радиусом R = 40
см около горизонтальной оси, проходящей через образующую диска.
Решение:
R = 0,4
м
T − ?
В данном случае диск − это физический маятник, период колебаний которого
определим по формуле:
, (1)
где −
I
момент инерции диска относительно оси вращения, проходящей через точку подвеса
А (см. рис.); x = AO = R −
расстояние от точки подвеса до центра тяжести О диска; m −
масса диска; g = 9,8
м/с² − ускорение свободного падения.
Момент инерции I₀ диска относительно оси симметрии диска:
I₀ = mR²/2.
По
теореме Штейнера:
I = I₀ + mR². Имеем
I = mR²/2 + mR² = 3mR²/2. Тогда по (1)
4.1.1-3.
Материальная точка движется согласно уравнению r(t) = A(icosωt + jsinωt), где
A = 0,5
м, ω = 5
с⁻¹. Изобразите на рисунке траекторию движения. Определите модуль скорости и
модуль нормального ускорения.
Решение:
r(t) = A(icosωt + jsinωt) (1)
A = 0,5
м
ω = 5
с⁻¹
v − ?
an − ?
Представим (1) в виде:
r(t) = iAcosωt + jAsinωt (1*)
Радиус вектор r(t)
точки: r(t) = ix + jy, где x, y −
проекции радиус вектора соответственно на оси OX и OY; i, j −
единичные векторы (орты), направленные соответственно по оси OX и OY.
Тогда (1*) примет вид
ix + jy = iAcosωt + jAsinωt,
отсюда получим два уравнения
x = Acosωt, (*)
y = Asinωt. (**)
Возведём их в квадрат
x² = A²cos²ωt,
y² = A²sin²ωt.
Сложим эти уравнения
x² + y² = A²cos²ωt + A²sin²ωt или x² + y² = A²(cos²ωt + sin²ωt).
Отсюда, т.к. cos²ωt + sin²ωt = 1,
получим уравнение траектории движения точки
x² + y² = A². (2)
Уравнение (2) − это уравнение окружности радиусом R = A = 0,5
м с центром в начале координат (см. рис.).
Найдём проекции скорости vx и vy. Для этого продифференцируем x и y из
(*) и (**) по времени t:
vx = xtʹ = (Acosωt)tʹ = — Aωsinωt;
vy = ytʹ = (Asinωt)tʹ = Aωcosωt.
Тогда квадрат скорости
v² = vx² + vy² или v² = (-
Aωsinωt)² + (Aωcosωt)² или
v² = A²ω²(sin²ωt + cos²ωt) или v² = A²ω².
Отсюда модуль скорости v:
v = Aω. (3)
v =
0,5·5 = 2,5 м/с².
Модуль нормального ускорения an: an = v²/R или, с учётом (3) и R = A, получим an = A²ω²/A или
an = Aω².
an =
0,5·5² = 12,5 м/с².
Ответ: траектория − окружность радиусом R = A = 0,5
м с центром в начале координат, v = Aω = 2,5 м/с², an = Aω² = 12,5 м/с².
_______________________________________________________________________________________________
4.1.2. Свободные затухающие колебания.
4.1.2-1.
Амплитуда затухающих колебаний уменьшилась в n = 100
за 15 с. Чему равен коэффициент затухания β?
Решение:
t = 15 c
n = 100
A = A₀/n (*)
β – ?
Зависимость амплитуды А затухающих колебаний от времени t:
A = A₀e—βt, (1)
где A₀ –
начальная амплитуда; β – коэффициент затухания.
Имеем из (1) и (*):
A₀/n = A₀e—βt; 1/n = e—βt; eβt = n; βt = ln(n)
отсюда
β = ln(n)/t.
β =
ln(100)/15 = 0,307 1/c.
Ответ: β = ln(n)/t = 0,307 1/c.
4.1.2-2. Найти
логарифмический декремент затухания тонкого стержня, подвешенного за один из
его концов, если за промежуток времени t = 5
мин его полная механическая энергия уменьшилась в n = 4·10² раз. Длина
стержня L = 50 см.Решение:
t = 5 мин = 300 с
n = 400
L = 0,5
м
λ − ?
В данном случае стержень − это физический маятник.
Логарифмический декремент затухания λ
λ = βT, (1)
где β –
коэффициент затухания, T− период колебаний стержня.
1. Найдём коэффициент затухания
β.
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
ω –
частота затухающих колебаний; ω₀ – собственная частота колебаний.
Зависимость от времени t полной механической энергии Е физического маятника:
Е = E₀e-2βt,
где E₀ – начальная (при t = 0) полная механическая энергия.
Отсюда имеем
n = Е₀/Е = Е₀/(E₀e-2βt) = 1/(e-2βt) =
e2βt.
Получили n = e2βt.
Прологарифмируем это равенство Ln(n) = 2βt. Отсюда
β = Ln(n)/(2t). (3)
2. Найдём период Т затухающих колебаний.
Оценим коэффициент
β2 по (3).
β = Ln(400)/(2·300)
= 0,009986, отсюда
β² = (0,009986)² ≈ 0,0000997.
Собственная частота колебаний физического маятника:

где J = mL²/3 –
момент инерции стержня относительно оси вращения, m –
масса стержня, g – ускорение свободного падения, d = L/2 –
расстояние от точки подвеса до центра тяжести стержня.
Подставим всё в (4) и, после упрощения, получим

По (4*) оценим ω₀2:
ω₀2 = 3·9,8/(2·0,5) = 29,9.
Так как β² << ω₀2,
то, пренебрегая β², из (2) следует ω ≈ ω₀ , поэтому период затухающих колебаний T
T = 2π/ω = 2π/ω₀ или
. (4**)
Подставим в (1) найденные β из (3) и Т из (4**) и, после упрощения, получим
.
= 0,01157.
4.1.2-3. Логарифмический
декремент затухания тела, колеблющегося с частотой 50 Гц, равен 0,02.
Определите: время, за которое амплитуда колебаний тела уменьшится в 20
раз; число колебаний тела, чтобы произошло подобное уменьшение амплитуды.Решение:
ν = 50 Гц
λ =
0,02
n = 20
t − ?
N − ?
1. Пусть β –
коэффициент затухания; T = 1/ν – период, ν – частота колебаний. Логарифмический декремент
затухания λ:
λ = βT или λ = β/ν,
отсюда
β = λν. (1)
Амплитуда А затухающих колебаний
A = A₀·e—βt,
где A₀ −
начальная амплитуда (при t = 0).
Подставим сюда из условия задачи A = A₀/n:
A₀/n = A₀·e—βt,
отсюда eβt = n и,
после логарифмирования, βt = Ln(n), отсюда
t = ( Ln(n) )/β и, с
учётом (1),
t = ( Ln(n) )/(λν). (2)
2. Число колебаний N за время t:
N = t/T = tν = (
и, с учётом (2), ) = ν( Ln(n) )/(λν) или
N = ( Ln(n) )/λ. (3)
3. Вычисления по формулам (2) и (3):
t = ( Ln(20)
)/(0,02·50) ≈ 3 с.
N = ( Ln(20)
)/0,02 ≈ 150.
Ответ: t = ( Ln(n) )/(λν) ≈ 3
с; N =( Ln(n) )/λ ≈
150.
4.1.2-4. Составьте
дифференциальное уравнение гармонических свободных затухающих крутильных
колебаний механической системы.Решение:
Пусть
система (например, тонкий однородный диск, подвешенный в горизонтальном
положении к упругой нити) совершает крутильные колебания относительно
закреплённой оси Z (ось нити). Пусть на диск действует упругая сила,
проекция момента которой на ось Z равна
Mz = — kϕ, (1)
где k −
постоянная, ϕ −
угол поворота из положения равновесия. Знак “минус” указывает на то, что при
отклонении системы на угол ϕ, момент упругой силы возвращает систему к положению
равновесия. Поместим диск в вязкую среду ( например, жидкость ). Момент силы
сопротивления Mc,
действующий на диск, пропорционален угловой скорости ϕʹ:
Mc = — ηϕʹ,
(2)
где η −
постоянная.
Уравнение динамики вращательного движения диска имеет вид
Iϕʹʹ = Mz + Mc,
(3)
где I –
момент инерции диска относительно оси вращения.
С учётом (1) и (2), уравнение (3) примет вид Iϕʹʹ = —
kϕ — ηϕʹ,
отсюда
ϕʹʹ + (η/I)ϕʹ + (k/I)ϕ = 0.
Применив обозначения 2β = η/I, ω₀² = k/I, перепишем последнее уравнение:
ϕʹʹ + 2βϕʹ + ω₀²ϕ = 0.
Это дифференциальное уравнение описывает затухающие крутильные колебания
механической системы.
Ответ: ϕʹʹ + 2βϕʹ + ω₀²ϕ = 0.
4.1.2-5.
Найти добротность Q осциллятора, у которого отношение резонансной частоты ωрез
к частоте затухающих колебаний ω равно η.
Решение:
ωрез/ω = η (*)
Q − ?
Пусть β − коэффициент затухания, ω₀ − собственная частота колебаний, T = 2π/ω −
период затухающих колебаний, λ = βT = 2πβ/ω − логарифмический декремент
затухания. Тогда добротность Q:
Q = π/λ = π/(2πβ/ω), или
Q = ω/(2β). (1)
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
Формула для резонансной частоты ωрез:
ωрез² = ω₀² — 2β². (3)
Из (2) вычтем (3)
ω² — ωрез² = (ω₀² — β²) — (ω₀² — 2β²), или
ω² — ωрез² = ω₀² — β² — ω₀² + 2β², или
ω² — ωрез² = β². (**)
С учётом условия (*) имеем ωрез = ωη. Тогда (**) примет вид
ω² — ω²η² = β², или
ω²(1 — η²) = β², отсюда
Подставляя полученное выражение ω в (1), окончательно получим:
___________________________________________________________________________________
4.1.3. Вынужденные колебания. Резонанс.
4.1.3-1.
Осциллятор массы m движется по закону x = Asinωt под действием вынуждающей силы
Fₓ = F₀cosωt. Найти коэффициент затухания β осциллятора.
Решение:
m,
x = Asinωt,
Fₓ = F₀cosωt,
β − ?
Установившееся смещение х(t) осциллятора при вынужденных колебаниях:
x = Acos(ωt — ϕ), (1)
где амплитуда А колебаний
(2)

ω₀ − собственная частота колебаний осциллятора,
f₀ = F₀/m. (*)
Так как по условию смещение х(t) осциллятора x = Asinωt, то из (1) следует: ϕ =
π/2
(т. к. cos(ωt — π/2) = sinωt). Тогда из (3) имеем:



4.1.3-2.
При неизменной амплитуде вынуждающей силы амплитуда вынужденных колебаний при
частотах ω₁ = 100 с⁻¹ и ω₂ = 300 с⁻¹ оказывается одинаковой. Найти резонансную
частоту ωрез.
Решение:
F₀ = const (амплитуда
вынуждающей
силы)
ω₁ = 100 с⁻¹
ω₂ = 300 с⁻¹
А₁ = А₂
ωрез − ?
Амплитуда А вынужденных колебаний:
(*)
где f₀ =
F₀/m, m − масса
осциллятора, β − коэффициент затухания, ω₀ −
собственная частота колебаний, ω − частота вынужденных колебаний.
При постоянной
амплитуде вынуждающей силы F₀ (и,
следовательно, постоянной f₀) из (*) при двух разных частотах ω₁
и ω₂ получаем две амплитуды А₁ и А₂ вынужденных колебаний:
С учётом условия А₁ = А₂ , получим
Отсюда, приравнивая знаменатели и, возводя полученное равенство в квадрат,
получим
(ω₀² — ω₁²)² + 4β²ω₁² = (ω₀² — ω₂²)² + 4β²ω₂² или
ω₀⁴ — 2ω₀²ω₁²+ ω₁⁴ + 4β²ω₁² = ω₀⁴ — 2ω₀²ω₂² + ω₂⁴ + 4β²ω₂² или
— 2ω₀²ω₁²+ ω₁⁴ + 4β²ω₁² = — 2ω₀²ω₂² + ω₂⁴ + 4β²ω₂² или
2ω₀²(ω₂² — ω₁²) + (ω₁⁴ — ω₂⁴) + 4β²(ω₁² — ω₂²) = 0 или
— 2ω₀²(ω₁² — ω₂²) + (ω₁² — ω₂²)(ω₁² + ω₂²) + 4β²(ω₁² — ω₂²) = 0 и, после
деления на (ω₁² — ω₂²) ≠ 0:
— 2ω₀² + ω₁² + ω₂² + 4β² = 0. (1)
Формула для резонансной частоты ωрез:
отсюда ω₀² = ωрез² + 2β² и подставим в (1)
— 2(ωрез² + 2β²) + ω₁² + ω₂² + 4β² = 0 или
— 2ωрез² + ω₁² + ω₂² = 0, отсюда
_______________________________________________________________________________________________ 4.2. Электрические колебания.4.2-1.
Небольшая магнитная стрелка совершает малые колебания вокруг оси,
перпендикулярной направлению внешнего магнитного поля. При изменении индукции
этого поля период колебаний стрелки уменьшился в η = 5
раз. Во сколько раз и как изменилась индукция поля? Затухание колебаний
пренебрежимо мало.
Решение:
T₁/T₂ = η = 5
B₂/B₁ − ?
Момент сил М, действующий на стрелку со стороны магнитного
поля
М = [B·Pm],
где Pm −
вектор магнитного момента стрелки.
Модуль момента сил
М = B·Pm·sinϕ, где ϕ –
угол между векторами B и Pm.
При малых колебаниях угол ϕ очень мал и sinϕ ≈ ϕ. Тогда
М = B·Pm·ϕ.
При повороте стрелки на угол ϕ возникает момент сил М, стремящийся вернуть стрелку в
положение равновесия, т.е. М = — B·Pm·ϕ. Если J – момент инерции стрелки относительно оси вращения,
то основное уравнение динамики вращательного движения примет вид
Jϕ’’ = M или Jϕ’’ = —
B·Pm·ϕ отсюда
ϕ’’ + (B·Pm/J)·ϕ = 0. (1)
Если ω – циклическая
частота колебаний, то сравнивая (1) с уравнением гармонических колебаний
ϕ’’ + ω²ϕ = 0,
получим
ω² = B·Pm/J,
отсюда
ω = √(B·Pm/J).
Тогда период T
колебаний
T = 2π/ω или
T = 2π√( J/(B·Pm) ). (2)
На основе (2) для разных B₁ и B₂ получим соответствующие T₁ и T₂
T₁ = 2π√( J/(B₁·Pm) )
T₂ = 2π√( J/(B₂·Pm) ).
Отсюда
T₁/T₂ = √(B₂/B₁) и
отсюда
B₂/B₁ = (T₁/T₂)² = η² =
25. Итак
B₂/B₁ = η² =
25.
Ответ: индукция магнитного поля увеличится в η² = 25
раз.
4.2-2. Индуктивность
катушки равна 0,125 Гн. Уравнение колебаний силы ток в ней имеет вид:
i = 0,4cos(1000t), где
все величины выражены в системе СИ. Определить амплитуду напряжения на катушке.
Решение:
L = 0,125 Гн
i = 0,4cos(1000t). (1)
Um − ?
Уравнение колебаний силы тока в катушке имеет вид:
i = Imcos(ωt). (2)
Из (1) и (2) имеем
Im = 0,4
А − амплитуда силы тока в катушке; ω = 1000 с⁻¹− частота.
Индуктивное сопротивление катушки: XL = ωL .
По закону Ома
Im = Um/XL,
отсюда
Um= XL·Im или
Um = ωL·Im.
Um
= 1000·0,125·0,4 = 50 В.
Ответ: Um = 50 В.4.2-3. Электрический
колебательный контур состоял из последовательно соединенных катушки с
индуктивностью L = 0,8
Гн и конденсатора емкостью С. Сопротивление катушки и соединительных проводов
было равно R =
2000 Ом. После того, как часть витков в катушке замкнулась накоротко,
индуктивность ее уменьшилась в n = 7 раз, частота собственных колебаний в контуре
возросла в k = 3
раза, а коэффициент затухания этих колебаний не изменился. Определить емкость
конденсатора.Решение:
L = 0,8 Гн
R =
2000 Ом
L₂ = L/n
n = 7
ω₂ = kω
k = 3
β = const
C − ?
Коэффициент затуханий β = R/(2L).
ω и ω₂ −
начальная и конечная частоты собственных колебаний в контуре, где
ω = √(
1/(LC) — β² ) =
√( 1/(LC) — R²/(4L²) );
ω₂ = √(
1/(L₂C) — β² ) =
√( n/(LC) — R²/(4L²) ).
Возведём в квадрат равенство ω₂ = kω, получим ω₂² = k²ω² или
n/(LC) — R²/(4L²) = k²( 1/(LC) — R²/(4L²) ),
отсюда
C = 4L(k² — n)/( R²(k² — 1)
).
C =
4·0,8·(3² — 7)/( 2000²·(3² — 1) ) = 2·10⁻⁷ Ф.
Ответ: C = 4L(k² — n)/( R²(k² — 1) ) = 2·10⁻⁷ Ф.
4.2-4.
Ток в колебательном контуре зависит от времени как I = Imsinω₀t, где Im = 9,0
мА, ω₀ = 4,5·10⁴ с⁻¹. Ёмкость конденсатора С = 0,50 мкФ. Найти индуктивность
контура и напряжение на конденсаторе в момент t = 0.
Решение:
I = Imsinω₀t (*)
Im = 9·10⁻³ А
ω₀ = 4,5·10⁴ с⁻¹
С = 0,5·10⁻⁶ Ф
L − ?
U(0) − ?
1). Собственная частота ω₀ колебательного контура
, отсюда
1
L = ––––– . (1)
ω₀²C
2). Закон сохранения энергии в колебательном контуре:
LI²/2 + CU²/2 = LIm²/2
или, с учётом (*),
L(Imsinω₀t)²/2 + CU²/2 = LIm²/2.
Отсюда при t = 0 (т.к. sinω₀0 = 0) получим напряжение U(0) = Um на конденсаторе
в момент времени t = 0 (
Um − максимальное напряжение):
CU²(0) = LIm²
и, подставляя сюда L из (1), получим
Im²
CU²(0) = ––––– или
ω₀²C
Im
U(0) = Um = –––– . (2)
ω₀C
Вычисления по формулам (1) и (2 ):
1
L = –––––––––––––––– = 0,001 Гн = 1 мГн.
(4,5·10⁴)²·0,5·10⁻⁶
9·10⁻³
U(0) = Um = –––––––––––––– = 0,4 В.
4,5·10⁴·0,5·10⁻⁶
_______________________________________________________________________________________________
4.3. Упругие волны. Акустика.
4.3-1.
По шнуру слева направо бежит со скоростью v
незатухающая гармоническая волна. При этом поперечное смещение точки О шнура
изменяется по закону y = Acos(ωt). Как зависит от времени смещение точки шнура,
находящейся правее точки О на расстоянии x от
нее?
Решение:
y = Acos( ω(t — x/v) ).
Ответ: y = Acos( ω(t – x/v) ).
4.3-2.
Уравнение плоской звуковой волны имеет вид ξ = 60cos(1800t — 5,3x). где ξ – в мкм, t – в секундах, х – в метрах.
Найти:
а) отношение амплитуды смещения частиц среды к длине волны;
б) амплитуду
колебаний скорости частиц среды и ее отношение к скорости распространения
волны;
в) амплитуду колебаний относительной деформации среды и её связь с амплитудой колебаний скорости частиц среды.
Решение:
ξ = 60·10⁻⁶cos(1800t – 5,3x)
(1)
a) A/λ – ?
б) Vm – ? Vm/v – ?
в) (∂ξ/∂x)m – ? (∂ξ/∂x)m = f(Vm) – ?
а) Уравнение плоской синусоидальной волны
ξ = Acos(ωt – kx).
(2)
Из (1) и (2) следует
A = 60·10⁻⁶ м – амплитуда колебаний частиц среды,
ω = 1800 1/с – циклическая частота,
k = 5,3 1/м – волновое число.
k = 2π/λ, отсюда λ = 2π/k. Тогда
A/λ = A/(2π/k) или
A/λ = Ak/(2π).
A/λ =
60·10⁻⁶·5,3/(2·3,14) = 5,1·10⁻⁵.
б)
Амплитуда
колебаний скорости частиц среды
Vm = Aω. (*)
Vm =
60·10⁻⁶·1800 = 0,11 м/с. = 11 см/с.
Скорость
распространения волны
v = ω/k. (3)
Тогда ( см. (*) )
Vm/v = Aω/(ω/k) = Ak.
Vm/v = Ak.
Vm/v = 60·10⁻⁶·5,3 = 3,2·10⁻⁴.в) Относительную деформацию среды найдём дифференцируя (2) по х:
∂ξ/∂x = ( Acos(ωt – kx) )xʹ = — Aksin(ωt – kx).
Отсюда амплитуда колебаний относительной деформации среды:
(∂ξ/∂x)m = Ak. (**)
(∂ξ/∂x)m = 60·10⁻⁶·5,3 = 3,2·10⁻⁴.
Связь между амплитудой колебаний относительной деформации среды (dξ/dx)m и амплитудой колебаний скорости частиц среды Vm найдем по (*) и (**). Имеем
(dξ/dx)m = Ak = (Vm/ω)k = Vmk/ω = ( с учётом (3) ) = Vm/v. Получили
(dξ/dx)m = Vm/v или
Vm = v·(dξ/dx)m ,
где v = ω/k = 1800/5,3 = 340 м/с – скорость волны.
Ответ: a) A/λ = 5,1·10⁻⁵;
б) Vm = 0,11 м/с, Vm/v = 3,2·10⁻⁴;
в) (∂ξ/∂x)m = 3,2·10⁻⁴, Vm = v·(dξ/dx)m , где v = 340 м/с – скорость волны.
4.3-3.
Что такое амплитуда колебаний скорости частиц среды?
Решение:
Объясню
на простом примере. В озере на воде поплавок. Бросьте в воду камешек,
от него во все стороны пойдут волны. Поплавок колеблется на волнах.
Скорость колебаний поплавка − это скорость колебаний частиц среды (воды). Максимальная скорость колебаний поплавка − это амплитуда колебаний скорости частиц среды.
Амплитуда
колебаний скорости частиц среды
Vm = Aω (A —
амплитуда, ω —
циклическая частота).
Скорость распространения волны
v = ω/k (k —
волновое число).
A, ω, k
определяют из общего вида уравнения бегущей плоской синусоидальной волны
ξ = Acos(ωt – kx).
4.3-4.
Точечный изотропный источник испускает звуковые колебания с частотой ν = 1,45
кГц. На расстоянии r₁ = 5 м от источника амплитуда смещения частиц среды А₁ =
50 мкм, а в точке А, находящейся на расстоянии r₂ = 10 м от источника,
амплитуда смещения в η = 3 раза меньше А₁. Найти:
а) коэффициент затухания волны γ;
б) амплитуду колебаний скорости частиц среды в точке А.
Решение:
ν = 1450 Гц
r₁ = 5 м
А₁ = 50·10⁻⁶ м
r₂ = 10 м
А₂ = А₁/η (η = 3) (*)
а) γ − ?
б) Vm − ? (в точке А)
От данного точечного источника распространяются сферические волны. Для
однородной поглощающей среды уравнение сферической волны:
(1)
где ξ − смещение частиц среды; ω = 2πν − циклическая частота; k − волновое
число.
а). Из (1) выпишем амплитуду A смещения частиц среды (множитель перед
косинусом):
A =
(A₀/r)·e⁻ᵞʳ.
Отсюда для r = r₁ и r = r₂ получаем амплитуды смещения частиц среды A₁ и A₂
соответственно
A₁ = (A₀/r₁)·e⁻ᵞr₁ , (**)
A₂ = (A₀/r₂)·e⁻ᵞr₂ . (***)
Делим (**) на (***) и, с учётом (*), получаем:
·η = (r₂/r₁)·eᵞ⁽r₂⁻r₁⁾ отсюда ηr₁/r₂ = eᵞ⁽r₂⁻r₁⁾ , отсюда, по определению логарифма, имеем
ln(ηr₁/r₂) = γ(r₂ — r₁), отсюда
γ = ln(3·5/10)/(10 — 5) ≈
0,08 м⁻¹.
б). Для нахождения скорости смещения частиц среды V найдём частную производную
по времени t от (1):
V = ∂ξ/∂t = (A₀/r)·e⁻ᵞʳ·( — ωsin(ωt—kr) ).
С учётом ω = 2πν, имеем
V =
— (2πνA₀/r)·e⁻ᵞʳ·sin(ωt-kr).
Отсюда амплитуда колебаний скорости частиц среды Vm (множитель перед синусом):
Отсюда в точке А (r = r₂) амплитуда колебаний скорости частиц среды
Vm = (2πνA₀/r₂)·e⁻ᵞr₂
и, с учётом (***), получим Vm = 2πνA₂. Тогда, учтя (*), окончательно получим:
Vm = 2πνA₁/η.
Vm = 2·3,14·1450·50·10⁻⁶/3 ≈ 0,15 м.
4.3-5. Плоская
звуковая волна, частота которой 100 Гц и амплитуда 5 мкм, распространяется со
скоростью 300 мс в воздухе, плотность которого равна 1,2 кгм³.
Определить интенсивность волны.Решение:
ν = 100 Гц
а = 5·10⁻⁶ м
V = 300
мс
ρ = 1,2
кгм³
I − ?
Интенсивность I
звуковой волны
I = ρа²ω²V/2 и
т.к. ω = 2πν, то
I = ρа²(2πν)²V/2.
I =
1,2·(5·10⁻⁶)²·(2·3,14·100)²·300/2 = 1,77·10⁻³ Вт/м².
Ответ: I = 1,77·10⁻³ Вт/м².
4.3-6.
Стальная струна длины l = 100 см и диаметра d = 0,50 мм даёт основной тон
частоты ν = 256 Гц. Найти силу её натяжения.
Решение:
l = 1 м
d = 0,5·10⁻³ м
ν = 256 Гц
ρ = 7800 кг/м³ (плотность стали)
F − ?
В закреплённой с обоих концов натянутой струне при возбуждении поперечных
колебаний устанавливаются стоячие волны. Основной тон частоты ν колебаний
струны:
ν = V/2l, отсюда
V = 2lν, (1)
где
− фазовая скорость поперечных волн в струне.
Отсюда
F = V²ρ₁ , (2)
где ρ₁ = m/l − линейная плотность струны, m = ρV₀ − масса струны, V₀ = (πd²/4)l
= πd²l/4 − объём струны.
Имеем: ρ₁ = ρV₀/l = ρ(πd²l/4)/l = ρπd²/4. Получили
ρ₁ = ρπd²/4. (3)
Подставляя в (2) V из (1) и ρ₁ из (3), получим силу натяжения F струны
F = (2lν)²ρπd²/4, или
F = πρ(lνd)².
F = 3,14·7800· (1·256·0,5·10⁻³)² ≈ 401,3 Н.
Ответ: F = πρ(lνd)² ≈ 401,3 Н.
_______________________________________________________________________________________________
4.4. Электромагнитные волны. Излучение.
4.4-1.
Электромагнитная волна с частотой 6·10¹⁴ Гц распространяется в
стекле, показатель преломления которого 1,5. Какова скорость волны в стекле и
значение волнового числа?
Решение:
ν = 6·10¹⁴
Гц
n = 1,5
c = 3·10⁸
м/с (скорость света в вакууме)
V – ? k – ?
Скорость V волны
в стекле:
V = c/n . (1)
Длина волны в стекле:
λ = V/ν = c/(nν). (*)
Волновое число k:
k = 2π/λ или с
учётом (*)
k = 2πnν/с.
(2)
Вычисления по (1), (2)
V = 3·10⁸/1,5
= 2·10⁸ м/с.
k = 2·3,14·1,5·6·10¹⁴/(3·10⁸) =
1,88·10⁷ (1/м).
Ответ: V = 2·10⁸
м/с; k =
1,88·10⁷ (1/м).
4.4-2. Определить
показатель преломления призмы из парафина , если его диэлектрическая
проницаемость Ԑ = 2 и магнитная проницаемость μ = 1.
Решение:
Ԑ = 2
μ = 1
n – ?
Показатель преломления среды
n = C/V. (1)
С – скорость света в вакууме.
Скорость света в среде
V = C/√(Ԑμ). (2)
Из (1) и (2) имеем
n = √(Ԑμ).
n =
√(2·1) = 1,41.
Ответ: n = 1,41.
___________________________________________________________________________________