Простое объяснение принципов решения частных производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения частных производных
Вычисление частной производной функции из нескольких переменных осуществляется по тем же правилам, что и функций с одной переменной. Разница лишь той, что другие переменные не участвуют дифференцировании (вычислении производной).
Проще говоря, чтобы найти частную производную функции по переменной
,переменную
будем считать константой (производная константы равна нулю), после чего находим производную функции по
с помощью таблицы производных элементарных функций –
. Готово!
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Примеры решения частных производных
Задача
Найти частные производные функции .
Решение
Частная производная функции по независимой переменной :
Производная суммы равна сумме производных. Производная от вычисляется по правилам вычислений производных функций одного аргумента, производная от слагаемого
вычисляется как производная от функции двух аргументов. При этом аргумент
считается константой. Производная от слагаемого
вычисляется как производная от константы.
.
Частная производная функции по независимой переменной :
Здесь вычисления также происходят по правилам вычисления производной суммы. Производная от вычисляется как производная от константы (независимым аргументом при этом считается
). Производная от слагаемого
вычисляется как производная от функции двух аргументов. При этом аргумент
считается константой, а
– независимым аргументом. Вычисление производной от слагаемого
осуществляется по правилам вычисления производных функций с одним аргументом.
.
Ответ
.
Задача
Найти частные производные функции .
Решение
Найдём частную производную функции по независимой переменной :
Функция является сложной. Производной показательной функции с основанием
является сама функция. Производная показателя степени вычисляется в при условии, что
является константой и равна
. Производная функции
равна произведению
и
. В результате получаем:
.
Найдём частную производную функции по независимой переменной :
По аналогии с предыдущим случаем производная функции будет равна произведению производных от функции и показателя её степени
:
Считая постоянной величиной, находим производную по независимому аргументу
:
.
Ответ
.
Задача
Найти частные производные функции .
Решение
Частная производная функции по независимой переменной будет равна производной от
. Производная от слагаемого
при этом будет равна нулю как производная от константы.
Частная производная функции по независимой переменной находится аналогичным образом, при этом предполагается, что
является константой.
Ответ
Задача
Найти частные производные функции .
Решение
Частная производная функции по независимой переменной
определяется слагаемым
. Производная второго слагаемого –
равна нулю, как производная от константы.
В свою очередь, частная производная функции по независимой переменной
будет определяться обоими слагаемым:
Таким образом, окончательно получаем:
Ответ
Задача
Найти частные производные функции .
Решение
При нахождении производной по независимой переменной , функцию
следует рассматривать как степенную. По правилу нахождения производной степенной функции получаем:
Производная по независимой переменной находится по правилу вычисления производной показательной функции, которая, в свою очередь, определяется по правилам нахождения производных сложных функций, т.к. переменная
входит в показатель степени виде функции
.
Производная показательной функции равна:
Производная показателя степени равна:
В результате получаем:
Ответ
Задача
Найти частные производные функции .
Решение
Частная производная по независимой переменной находится как сумма слагаемых:
Частная производная по независимой переменной находится как сумма слагаемых:
Ответ
Задача
Найти частные производные функции .
Решение
По правилу нахождения производной квадратного корня получаем, рассматривая как независимый аргумент:
Т.к. функция является сложной, то результат вычисления производной от квадратного корня – следует домножить на производную подкоренного выражения:
.
Рассматривая в качестве независимого аргумента, получаем:
По аналогии с предыдущим случаем, результат вычисления производной от квадратного корня – следует домножить на производную подкоренного выражения:
.
Ответ
Задача
Найти частные производные функции .
Решение
Данная функция является сложной, поэтому процесс нахождения производной данной функции целесообразно производить в несколько этапов.
Производная показательной функции с основанием равна самой себе. Далее необходимо найти производную показателя степени:
. В свою очередь аргумент функции арктангенс в данном случае также представляет собой сложную функцию:
. Результирующая производная будет равна произведению производных трёх функций:
и
.
Нахождение частной производной функции по аргументу :
Нахождение частной производной функции по аргументу :
Ответ
Задача
Найти частные производные первого и второго порядков функции .
Решение
Найдём частную производную первого порядка по аргументу :
Найдём частную производную второго порядка по аргументу :
Найдём частную производную первого порядка по аргументу :
Найдём частную производную второго порядка по аргументу :
Ответ
Задача
Найти частные производные первого и второго порядков функции .
Решение
Найдём частную производную первого порядка по аргументу :
Найдём частную производную второго порядка по аргументу :
Найдём частную производную первого порядка по аргументу :
Найдём частную производную второго порядка по аргументу :
Ответ
Частные производные для функции от нескольких переменных
21 сентября 2015
Рассмотрим функцию от двух переменных:
[f=fleft( x,y right)]
Поскольку переменные $x$ и $y$ являются независимыми, для такой функции можно ввести понятие частной производной:
Частная производная функции $f$ в точке $M=left( {{x}_{0}};{{y}_{0}} right)$ по переменной $x$ — это предел
[{{{f}’}_{x}}=underset{Delta xto 0}{mathop{lim }},frac{fleft( {{x}_{0}}+Delta x;{{y}_{0}} right)}{Delta x}]
Аналогично можно определить частную производную по переменной $y$ :
[{{{f}’}_{y}}=underset{Delta yto 0}{mathop{lim }},frac{fleft( {{x}_{0}};{{y}_{0}}+Delta y right)}{Delta y}]
Другими словами, чтобы найти частную производную функции нескольких переменных, нужно зафиксировать все остальные переменные, кроме искомой, а затем найти обычную производную по этой искомой переменной.
Отсюда вытекает основной приём для вычисления таких производных: просто считайте, что все переменные, кроме данной, являются константой, после чего дифференцируйте функцию так, как дифференцировали бы «обычную» — с одной переменной. Например:
$begin{align}& {{left( {{x}^{2}}+10xy right)}_{x}}^{prime }={{left( {{x}^{2}} right)}^{prime }}_{x}+10ycdot {{left( x right)}^{prime }}_{x}=2x+10y, \& {{left( {{x}^{2}}+10xy right)}_{y}}^{prime }={{left( {{x}^{2}} right)}^{prime }}_{y}+10xcdot {{left( y right)}^{prime }}_{y}=0+10x=10x. \end{align}$
Очевидно, что частные производные по разным переменным дают разные ответы — это нормально. Куда важнее понимать, почему, скажем, в первом случае мы спокойно вынесли $10y$ из-под знака производной, а во втором — вовсе обнулили первое слагаемое. Всё это происходит из-за того, что все буквы, кроме переменной, по которой идёт дифференцирование, считаются константами: их можно выносить, «сжигать» и т.д.
Что такое «частная производная»?
Сегодня мы поговорим о функциях нескольких переменных и о частных производных от них. Во-первых, что такое функция нескольких переменных? До сих пор мы привыкли считать функцию как $yleft( x right)$ или $tleft( x right)$, или любую переменную и одну-единственную функцию от нее. Теперь же функция у нас будет одна, а переменных несколько. При изменении $y$ и $x$ значение функции будет меняться. Например, если $x$ увеличится в два раза, значение функции поменяется, при этом если $x$ поменяется, а $y$ не изменится, значение функции точно так же изменится.
Разумеется, функцию от нескольких переменных, точно так же как и от одной переменной, можно дифференцировать. Однако поскольку переменных несколько, то и дифференцировать можно по разным переменным. При этом возникают специфические правила, которых не было при дифференцировании одной переменной.
Прежде всего, когда мы считаем производную функции от какой-либо переменной, то обязаны указывать, по какой именно переменной мы считаем производную — это и называется частной производной. Например, у нас функция от двух переменных, и мы можем посчитать ее как по $x$, так и по $y$ — две частных производных у каждой из переменных.
Во-вторых, как только мы зафиксировали одну из переменных и начинаем считать частную производную именно по ней, то все остальные, входящие в эту функцию, считаются константами. Например, в $zleft( xy right)$, если мы считаем частную производную по $x$, то везде, где мы встречаем $y$, мы считаем ее константой и обращаемся с ней именно как с константой. В частности при вычислении производной произведения мы можем выносить $y$ за скобку (у нас же константа), а при вычислении производной суммы, если у нас где-то получается производная от выражения, содержащего $y$ и не содержащего $x$, то производная этого выражения будет равна «нулю» как производная константы.
На первый взгляд может показаться, что я рассказываю о чем-то сложном, и многие ученики по началу путаются. Однако ничего сверхъестественного в частных производных нет, и сейчас мы убедимся в этом на примере конкретных задач.
Задачи с радикалами и многочленами
Задача № 1
Чтобы не терять время зря, с самого начала начнем с серьезных примеров.
[zleft( x,y right)=sqrt{frac{y}{x}}]
Для начала напомню такую формулу:
[{{left( sqrt{x} right)}^{prime }}_{x}=frac{1}{2sqrt{x}}]
Это стандартное табличное значение, которое мы знаем из стандартного курса.
В этом случае производная $z$ считается следующим образом:
[{{{z}’}_{x}}={{left( sqrt{frac{y}{x}} right)}^{prime }}_{x}=frac{1}{2sqrt{frac{y}{x}}}{{left( frac{y}{x} right)}^{prime }}_{x}]
Давайте еще раз, поскольку под корнем стоит не $x$, а некое другое выражение, в данном случае $frac{y}{x}$, то сначала мы воспользуемся стандартным табличным значением, а затем, поскольку под корнем стоит не $x$, а другое выражение, нам необходимо домножить нашу производную на еще одну из этого выражения по той же самой переменной. Давайте для начала посчитаем следующее:
[{{left( frac{y}{x} right)}^{prime }}_{x}=frac{{{{{y}’}}_{x}}cdot x-ycdot {{{{x}’}}_{x}}}{{{x}^{2}}}=frac{0cdot x-ycdot 1}{{{x}^{2}}}=-frac{y}{{{x}^{2}}}]
Возвращаемся к нашему выражению и записываем:
[{{{z}’}_{x}}={{left( sqrt{frac{y}{x}} right)}^{prime }}_{x}=frac{1}{2sqrt{frac{y}{x}}}{{left( frac{y}{x} right)}^{prime }}_{x}=frac{1}{2sqrt{frac{y}{x}}}cdot left( -frac{y}{{{x}^{2}}} right)]
В принципе, это все. Однако оставлять ее в таком виде неправильно: такую конструкцию неудобно использовать для дальнейших вычислений, поэтому давайте ее немного преобразуем:
[frac{1}{2sqrt{frac{y}{x}}}cdot left( -frac{y}{{{x}^{2}}} right)=frac{1}{2}cdot sqrt{frac{x}{y}}cdot frac{y}{{{x}^{2}}}=]
[=-frac{1}{2}cdot sqrt{frac{x}{y}}cdot sqrt{frac{{{y}^{2}}}{{{x}^{4}}}}=-frac{1}{2}sqrt{frac{xcdot {{y}^{2}}}{ycdot {{x}^{4}}}}=-frac{1}{2}sqrt{frac{y}{{{x}^{3}}}}]
Ответ найден. Теперь займемся $y$:
[{{{z}’}_{y}}={{left( sqrt{frac{y}{x}} right)}^{prime }}_{y}=frac{1}{2sqrt{frac{y}{x}}}cdot {{left( frac{y}{x} right)}^{prime }}_{y}]
Выпишем отдельно:
[{{left( frac{y}{x} right)}^{prime }}_{y}=frac{{{{{y}’}}_{y}}cdot x-ycdot {{{{x}’}}_{y}}}{{{x}^{2}}}=frac{1cdot x-ycdot 0}{{{x}^{2}}}=frac{1}{x}]
Теперь записываем:
[{{{z}’}_{y}}={{left( sqrt{frac{y}{x}} right)}^{prime }}_{y}=frac{1}{2sqrt{frac{y}{x}}}cdot {{left( frac{y}{x} right)}^{prime }}_{y}=frac{1}{2sqrt{frac{y}{x}}}cdot frac{1}{x}=]
[=frac{1}{2}cdot sqrt{frac{x}{y}}cdot sqrt{frac{1}{{{x}^{2}}}}=frac{1}{2}sqrt{frac{x}{ycdot {{x}^{2}}}}=frac{1}{2sqrt{xy}}]
Все сделано.
Задача № 2
[zleft( x,y right)=frac{xy}{{{x}^{2}}+{{y}^{2}}+1}]
Этот пример одновременно и проще, и сложней, чем предыдущий. Сложнее, потому что здесь больше действий, а проще, потому что здесь нет корня и, кроме того, функция симметрична относительно $x$ и $y$, т.е. если мы поменяем $x$ и $y$ местами, формула от этого не изменится. Это замечание в дальнейшем упростит нам вычисление частной производной, т.е. достаточно посчитать одну из них, а во второй просто поменять местами $x$ и $y$.
Приступаем к делу:
[{{{z}’}_{x}}={{left( frac{xy}{{{x}^{2}}+{{y}^{2}}+1} right)}^{prime }}_{x}=frac{{{left( xy right)}^{prime }}_{x}left( {{x}^{2}}+{{y}^{2}}+1 right)-xy{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{prime }}_{x}}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}]
Давайте посчитаем:
[{{left( xy right)}^{prime }}_{x}=ycdot {{left( x right)}^{prime }}=ycdot 1=y]
Однако многим ученикам такая запись непонятна, поэтому запишем вот так:
[{{left( xy right)}^{prime }}_{x}={{left( x right)}^{prime }}_{x}cdot y+xcdot {{left( y right)}^{prime }}_{x}=1cdot y+xcdot 0=y]
Таким образом, мы еще раз убеждаемся в универсальности алгоритма частных производных: каким бы мы образом их не считали, если все правила применяются верно, ответ будет один и тот же.
Теперь давайте разберемся еще с одной частной производной из нашей большой формулы:
[{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{prime }}_{x}={{left( {{x}^{2}} right)}^{prime }}_{x}+{{left( {{y}^{2}} right)}^{prime }}_{x}+{{{1}’}_{x}}=2x+0+0]
Подставим полученные выражения в нашу формулу и получим:
[frac{{{left( xy right)}^{prime }}_{x}left( {{x}^{2}}+{{y}^{2}}+1 right)-xy{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{prime }}_{x}}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}=]
[=frac{ycdot left( {{x}^{2}}+{{y}^{2}}+1 right)-xycdot 2x}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}=]
[=frac{yleft( {{x}^{2}}+{{y}^{2}}+1-2{{x}^{2}} right)}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}=frac{yleft( {{y}^{2}}-{{x}^{2}}+1 right)}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}]
По $x$ посчитано. А чтобы посчитать $y$ от того же самого выражения, давайте не будем выполнять всю ту же последовательность действий, а воспользуемся симметрией нашего исходного выражения — мы просто заменим в нашем исходном выражении все $y$ на $x$ и наоборот:
[{{{z}’}_{y}}=frac{xleft( {{x}^{2}}-{{y}^{2}}+1 right)}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}]
За счет симметрии мы посчитали это выражение гораздо быстрее.
Нюансы решения
Для частных производных работают все стандартные формулы, которые мы используем для обычных, а именно, производная частного. При этом, однако, возникают свои специфические особенности: если мы считаем частную производную $x$, то когда мы получаем ее по $x$, то рассматриваем ее как константу, и поэтому ее производная будет равна «нулю».
Как и в случае с обычными производными, частную (одну и ту же) можно посчитать несколькими различными способами. Например, ту же конструкцию, которую мы только что посчитали, можно переписать следующим образом:
[{{left( frac{y}{x} right)}^{prime }}_{x}=ycdot {{left( frac{1}{x} right)}^{prime }}_{x}=-yfrac{1}{{{x}^{2}}}]
Далее мы точно таким же образом считаем еще две конструкции, а именно:
[{{left( xy right)}^{prime }}_{x}=ycdot {{{x}’}_{x}}=ycdot 1=y]
Вместе с тем, с другой стороны, можно использовать формулу от производной суммы. Как мы знаем, она равна сумме производных. Например, запишем следующее:
[{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{prime }}_{x}=2x+0+0=2x]
Теперь, зная все это, давайте попробуем поработать с более серьезными выражениями, поскольку настоящие частные производные не ограничиваются одними лишь многочленами и корнями: там встречаются и тригонометрия, и логарифмы, и показательная функция. Сейчас этим и займемся.
Задачи с тригонометрическими функциями и логарифмами
Задача № 1
[zleft( x,y right)=sqrt{x}cos frac{x}{y}]
Запишем следующие стандартные формулы:
[{{left( sqrt{x} right)}^{prime }}_{x}=frac{1}{2sqrt{x}}]
[{{left( cos x right)}^{prime }}_{x}=-sin x]
Вооружившись этими знаниями, попробуем решить:
[{{{z}’}_{x}}={{left( sqrt{x}cdot cos frac{x}{y} right)}^{prime }}_{x}={{left( sqrt{x} right)}^{prime }}_{x}cdot cos frac{x}{y}+sqrt{x}cdot {{left( cos frac{x}{y} right)}^{prime }}_{x}=]
Отдельно выпишем одну переменную:
[{{left( cos frac{x}{y} right)}^{prime }}_{x}=-sin frac{x}{y}cdot {{left( frac{x}{y} right)}^{prime }}_{x}=-frac{1}{y}cdot sin frac{x}{y}]
Возвращаемся к нашей конструкции:
[=frac{1}{2sqrt{x}}cdot cos frac{x}{y}+sqrt{x}cdot left( -frac{1}{y}cdot sin frac{x}{y} right)=frac{1}{2sqrt{x}}cdot cos frac{x}{y}-frac{sqrt{x}}{y}cdot sin frac{x}{y}]
Все, по $x$ мы нашли, теперь давайте займемся вычислениями по $y$:
[{{{z}’}_{y}}={{left( sqrt{x}cdot cos frac{x}{y} right)}^{prime }}_{y}={{left( sqrt{x} right)}^{prime }}_{y}cdot cos frac{x}{y}+sqrt{x}cdot {{left( cos frac{x}{y} right)}^{prime }}_{y}=]
Опять же посчитаем одно выражение:
[{{left( cos frac{x}{y} right)}^{prime }}_{y}=-sin frac{x}{y}cdot {{left( frac{x}{y} right)}^{prime }}_{y}=-sin frac{x}{y}cdot xcdot left( -frac{1}{{{y}^{2}}} right)]
Возвращаемся к исходному выражению и продолжаем решение:
[=0cdot cos frac{x}{y}+sqrt{x}cdot frac{x}{{{y}^{2}}}sin frac{x}{y}=frac{xsqrt{x}}{{{y}^{2}}}cdot sin frac{x}{y}]
Все сделано.
Задача № 2
[zleft( x,y right)=ln left( x+ln y right)]
Запишем необходимую нам формулу:
[{{left( ln x right)}^{prime }}_{x}=frac{1}{x}]
Теперь посчитаем по $x$:
[{{{z}’}_{x}}={{left( ln left( x+ln y right) right)}^{prime }}_{x}=frac{1}{x+ln y}.{{left( x+ln y right)}^{prime }}_{x}=]
[=frac{1}{x+ln y}cdot left( 1+0 right)=frac{1}{x+ln y}]
По $x$ найдено. Считаем по $y$:
[{{{z}’}_{y}}={{left( ln left( x+ln y right) right)}^{prime }}_{y}=frac{1}{x+ln y}.{{left( x+ln y right)}^{prime }}_{y}=]
[=frac{1}{x+ln y}left( 0+frac{1}{y} right)=frac{1}{yleft( x+ln y right)}]
Задача решена.
Нюансы решения
Итак, от какой бы функции мы не брали частную производную, правила остаются одними и теми же, независимо от того, работаем ли мы с тригонометрией, с корнями или с логарифмами.
Неизменными остаются классические правила работы со стандартными производными, а именно, производная суммы и разности, частного и сложной функции.
Последняя формула чаще всего и встречается при решении задач с частными производными. Мы встречаемся с ними практически везде. Ни одной задачи еще не было, чтобы там нам она не попадалась. Но какой бы мы формулой не воспользовались, нам все равно добавляется еще одно требование, а именно, особенность работы с частными производными. Как только мы фиксируем одну переменную, все остальные оказываются константами. В частности, если мы считаем частную производную выражения $cos frac{x}{y}$ по $y$, то именно $y$ и является переменной, а $x$ везде остается константой. То же самое работает и наоборот. Ее можно выносить за знак производной, а производная от самой константы будет равна «нулю».
Все это приводит к тому, что частные производные от одного и того же выражения, но по разным переменным могут выглядеть совершенно по-разному. Например, посмотрим такие выражения:
[{{left( x+ln y right)}^{prime }}_{x}=1+0=1]
[{{left( x+ln y right)}^{prime }}_{y}=0+frac{1}{y}=frac{1}{y}]
Задачи с показательными функциями и логарифмами
Задача № 1
[zleft( x,y right)={{e}^{x}}{{e}^{frac{x}{y}}}]
Для начала запишем такую формулу:
[{{left( {{e}^{x}} right)}^{prime }}_{x}={{e}^{x}}]
Зная этот факт, а также производную сложной функции, давайте попробуем посчитать. Я сейчас решу двумя различными способами. Первый и самый очевидный — это производная произведения:
[{{{z}’}_{x}}={{left( {{e}^{x}}cdot {{e}^{frac{x}{y}}} right)}^{prime }}_{x}={{left( {{e}^{x}} right)}^{prime }}_{x}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{left( {{e}^{frac{x}{y}}} right)}^{prime }}_{x}=]
[={{e}^{x}}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot {{left( frac{x}{y} right)}^{prime }}_{x}=]
Давайте решим отдельно следующее выражение:
[{{left( frac{x}{y} right)}^{prime }}_{x}=frac{{{{{x}’}}_{x}}cdot y-x.{{{{y}’}}_{x}}}{{{y}^{2}}}=frac{1cdot y-xcdot 0}{{{y}^{2}}}=frac{y}{{{y}^{2}}}=frac{1}{y}]
Возвращаемся к нашей исходной конструкции и продолжаем решение:
[={{e}^{x}}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot frac{1}{y}={{e}^{x}}cdot {{e}^{frac{x}{y}}}left( 1+frac{1}{y} right)]
Все, по $x$ посчитано.
Однако как я и обещал, сейчас постараемся посчитать эту же частную производную другим способом. Для этого заметим следующее:
[{{e}^{x}}cdot {{e}^{frac{x}{y}}}={{e}^{x+frac{x}{y}}}]
В этом запишем так:
[{{left( {{e}^{x}}cdot {{e}^{frac{x}{y}}} right)}^{prime }}_{x}={{left( {{e}^{x+frac{x}{y}}} right)}^{prime }}_{x}={{e}^{x+frac{x}{y}}}cdot {{left( x+frac{x}{y} right)}^{prime }}_{x}={{e}^{x+frac{x}{y}}}cdot left( 1+frac{1}{y} right)]
В результате мы получили точно такой же ответ, однако объем вычислений оказался меньшим. Для этого достаточно было заметить, что при произведении показатели можно складывать.
Теперь посчитаем по $y$:
[{{{z}’}_{y}}={{left( {{e}^{x}}cdot {{e}^{frac{x}{y}}} right)}^{prime }}_{y}={{left( {{e}^{x}} right)}^{prime }}_{y}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{left( {{e}^{frac{x}{y}}} right)}^{prime }}_{y}=]
[=0cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot {{left( frac{x}{y} right)}^{prime }}_{y}=]
Давайте решим одно выражение отдельно:
[{{left( frac{x}{y} right)}^{prime }}_{y}=frac{{{{{x}’}}_{y}}cdot y-xcdot {{{{y}’}}_{y}}}{{{y}^{2}}}=frac{0-xcdot 1}{{{y}^{2}}}=-frac{1}{{{y}^{2}}}=-frac{x}{{{y}^{2}}}]
Продолжим решение нашей исходной конструкции:
[={{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot left( -frac{x}{{{y}^{2}}} right)=-frac{x}{{{y}^{2}}}cdot {{e}^{x}}cdot {{e}^{frac{x}{y}}}]
Разумеется, эту же производную можно было бы посчитать вторым способом, ответ получился бы таким же.
Задача № 2
[zleft( x,y right)=xln left( {{x}^{2}}+y right)]
Посчитаем по $x$:
[{{{z}’}_{x}}={{left( x right)}_{x}}cdot ln left( {{x}^{2}}+y right)+xcdot {{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{x}=]
Давайте посчитаем одно выражение отдельно:
[{{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{x}=frac{1}{{{x}^{2}}+y}cdot {{left( {{x}^{2}}+y right)}^{prime }}_{x}=frac{2x}{{{x}^{2}}+y}]
Продолжим решение исходной конструкции: $$
[1cdot ln left( {{x}^{2}}+y right)+xcdot frac{2x}{{{x}^{2}}+y}=ln left( {{x}^{2}}+y right)+frac{2{{x}^{2}}}{{{x}^{2}}+y}]
Вот такой ответ.
Осталось по аналогии найти по $y$:
[{{{z}’}_{y}}={{left( x right)}^{prime }}_{y}.ln left( {{x}^{2}}+y right)+xcdot {{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{y}=]
Одно выражение посчитаем как всегда отдельно:
[{{left( {{x}^{2}}+y right)}^{prime }}_{y}={{left( {{x}^{2}} right)}^{prime }}_{y}+{{{y}’}_{y}}=0+1=1]
Продолжаем решение основной конструкции:
[xcdot frac{1}{{{x}^{2}}+y}cdot 1=frac{x}{{{x}^{2}}+y}]
Все посчитано. Как видите, в зависимости от того, какая переменная берется для дифференцирования, ответы получаются совершенно разные.
Нюансы решения
Вот яркий пример того, как производную одной и той же функции можно посчитать двумя различными способами. Вот смотрите:
[{{{z}’}_{x}}=left( {{e}^{x}}cdot {{e}^{frac{x}{y}}} right)={{left( {{e}^{x}} right)}^{prime }}_{x}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{left( {{e}^{frac{x}{y}}} right)}^{prime }}_{x}=]
[={{e}^{x}}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot frac{1}{y}={{e}^{x}}cdot {{e}^{^{frac{x}{y}}}}left( 1+frac{1}{y} right)]
[{{{z}’}_{x}}={{left( {{e}^{x}}.{{e}^{frac{x}{y}}} right)}^{prime }}_{x}={{left( {{e}^{x+frac{x}{y}}} right)}^{prime }}_{x}={{e}^{x+frac{x}{y}}}.{{left( x+frac{x}{y} right)}^{prime }}_{x}=]
[={{e}^{x}}cdot {{e}^{^{frac{x}{y}}}}left( 1+frac{1}{y} right)]
При выборе разных путей, объем вычислений может быть разный, но ответ, если все выполнено верно, получится одним и тем же. Это касается как классических, так и частных производных. При этом еще раз напоминаю: в зависимости от того, по какой переменной идет взятие производной, т.е. дифференцирование, ответ может получиться совершенно разный. Посмотрите:
[{{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{x}=frac{1}{{{x}^{2}}+y}cdot {{left( {{x}^{2}}+y right)}^{prime }}_{x}=frac{1}{{{x}^{2}}+y}cdot 2x]
[{{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{y}=frac{1}{{{x}^{2}}+y}cdot {{left( {{x}^{2}}+y right)}^{prime }}_{y}=frac{1}{{{x}^{2}}+y}cdot 1]
В заключение для закрепления всего этого материала давайте попробуем посчитать еще два примера.
Задачи с тригонометрической функция и функцией с тремя переменными
Задача № 1
[zleft( x,y right)={{3}^{xsin y}}]
Давайте запишем такие формулы:
[{{left( {{a}^{x}} right)}^{prime }}={{a}^{x}}cdot ln a]
[{{left( {{e}^{x}} right)}^{prime }}={{e}^{x}}]
Давайте теперь решать наше выражение:
[{{{z}’}_{x}}={{left( {{3}^{xsin y}} right)}^{prime }}_{x}={{3}^{x.sin y}}cdot ln 3cdot {{left( xcdot sin y right)}^{prime }}_{x}=]
Отдельно посчитаем такую конструкцию:
[{{left( xcdot sin y right)}^{prime }}_{x}={{{x}’}_{x}}cdot sin y+x{{left( sin y right)}^{prime }}_{x}=1cdot sin y+xcdot 0=sin y]
Продолжаем решать исходное выражение:
[={{3}^{xsin y}}cdot ln 3cdot sin y]
Это окончательный ответ частной переменной по $x$. Теперь посчитаем по $y$:
[{{{z}’}_{y}}={{left( {{3}^{xsin y}} right)}^{prime }}_{y}={{3}^{xsin y}}cdot ln 3cdot {{left( xsin y right)}^{prime }}_{y}=]
Решим одно выражение отдельно:
[{{left( xcdot sin y right)}^{prime }}_{y}={{{x}’}_{y}}cdot sin y+x{{left( sin y right)}^{prime }}_{y}=0cdot sin y+xcdot cos y=xcdot cos y]
Решаем до конца нашу конструкцию:
[={{3}^{xcdot sin y}}cdot ln 3cdot xcos y]
Задача № 2
[tleft( x,y,z right)=x{{e}^{y}}+y{{e}^{z}}]
На первый взгляд этот пример может показаться достаточно сложным, потому что здесь три переменных. На самом деле, это одна из самых простых задач в сегодняшнем видеоуроке.
Находим по $x$:
[{{{t}’}_{x}}={{left( x{{e}^{y}}+y{{e}^{z}} right)}^{prime }}_{x}={{left( xcdot {{e}^{y}} right)}^{prime }}_{x}+{{left( ycdot {{e}^{z}} right)}^{prime }}_{x}=]
[={{left( x right)}^{prime }}_{x}cdot {{e}^{y}}+xcdot {{left( {{e}^{y}} right)}^{prime }}_{x}=1cdot {{e}^{y}}+xcdot o={{e}^{y}}]
Теперь разберемся с $y$:
[{{{t}’}_{y}}={{left( xcdot {{e}^{y}}+ycdot {{e}^{z}} right)}^{prime }}_{y}={{left( xcdot {{e}^{y}} right)}^{prime }}_{y}+{{left( ycdot {{e}^{z}} right)}^{prime }}_{y}=]
[=xcdot {{left( {{e}^{y}} right)}^{prime }}_{y}+{{e}^{z}}cdot {{left( y right)}^{prime }}_{y}=xcdot {{e}^{y}}+{{e}^{z}}]
Мы нашли ответ.
Теперь остается найти по $z$:
[{{{t}’}_{z}}={{left( xcdot {{e}^{y}}+{{y}^{z}} right)}^{prime }}_{z}={{left( xcdot {{e}^{y}} right)}^{prime }}_{z}+{{left( ycdot {{e}^{z}} right)}^{prime }}_{z}=0+ycdot {{left( {{e}^{z}} right)}^{prime }}_{z}=ycdot {{e}^{z}}]
Мы посчитали третью производную, на чем решение второй задачи полностью завершено.
Нюансы решения
Как видите, ничего сложного в этих двух примерах нет. Единственное, в чем мы убедились, так это в том, что производная сложной функции применяется часто и в зависимости от того, какую частную производную мы считаем, мы получаем разные ответы.
В последней задаче нам было предложено разобраться с функцией сразу от трех переменных. Ничего страшного в этом нет, однако в самом конце мы убедились, что все они друг от друга существенно отличаются.
Ключевые моменты
Окончательные выводы из сегодняшнего видеоурока следующие:
- Частные производные считаются так же, как и обычные, при этом, чтобы считать частную производную по одной переменной, все остальные переменные, входящие в данную функцию, мы принимаем за константы.
- При работе с частными производными мы используем все те же стандартные формулы, что и с обычными производными: сумму, разность, производную произведения и частного и, разумеется, производную сложной функции.
Конечно, просмотра одного этого видеоурока недостаточно, чтобы полностью разобраться в этой теме, поэтому прямо сейчас на моем сайте именно к этому видео есть комплект задач, посвященных именно сегодняшней теме — заходите, скачивайте, решайте эти задачи и сверяйтесь с ответом. И после этого никаких проблем с частными производными ни на экзаменах, ни на самостоятельных работах у вас не будет. Конечно, это далеко не последний урок по высшей математике, поэтому заходите на наш сайт, добавляйтесь ВКонтакте, подписывайтесь на YouTube, ставьте лайки и оставайтесь с нами!
Смотрите также:
- Производная параметрической функции
- Системы линейных уравнений: основные понятия
- Сравнение дробей
- Четырехугольная пирамида в задаче C2
- Задача B5: вычисление площади методом обводки
- Задача B4: вклад в банке и проценты
Чтобы понять частные производные, сначала нужно разобраться с обычными. И не нужно ничего искать: в нашей отдельной статье мы уже подготовили все для того, чтобы у вас это получилось. А сейчас речь пойдет о частных производных.
Добро пожаловать на наш телеграм-канал за полезной рассылкой и актуальными студенческими новостями.
Функция двух и более переменных
Прежде чем говорить о частных производных, нужно затронуть понятие функции нескольких переменных, без которого нет смысла в частной производной. В школе мы привыкли иметь дело с функциями одной переменной:
Производными таких функций мы и считали раньше. График функции одной переменной представляет собой линию на плоскости: прямую, параболу, гиперболу и т.д.
А что, если добавить еще одну переменную? Получится такая функция:
Это – функция двух независимых переменных x и y. График такой функции представляет собой поверхность в трехмерном пространстве: шар, гиперболоид, параболоид или еще какой-нибудь сферический конь в вакууме. Частные производные функции z по иксу и игреку соответственно записываются так:
Существуют также функции трех и более переменных. Правда, график такой функции нарисовать невозможно: для этого понадобилось бы как минимум четырехмерное пространство, которое невозможно изобразить.
Частная производная первого порядка
Запоминаем главное правило:
При вычислении частной производной по одной из переменных, вторая переменная принимается за константу. В остальном правила вычисления производной не меняются.
То есть, частная производная по сути ничем не отличается от обычной. Так что, держите перед глазами таблицу производных элементарных функций и правила вычисления обычных производных. Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции:
Сначала возьмем частную производную по иксу, считая игрек обычным числом:
Теперь считаем частную производную по игреку, принимая икс за константу:
Как видите, ничего сложного в этом нет, а успех с более сложными примерами – лишь дело практики.
Частная производная второго порядка
Как находится частная производная второго порядка? Так же, как и первого. Чтобы найти частные производные второго порядка, нужно просто взять производную от производной первого порядка. Вернемся к примеру выше и посчитаем частные производные второго порядка.
По иксу:
По игреку:
Частные производные третьего и высших порядков не отличаются по принципу вычисления. Систематизируем правила:
- При дифференцировании по одной независимой переменной, вторая принимается за константу.
- Производная второго порядка – это производная от производной первого порядка. Третьего порядка – производная от производной второго порядка и т.д.
Частные производные и полный дифференциал функции
Частый вопрос в практических заданиях – нахождение полного дифференциала функции. Для функции нескольких переменных полный дифференциал определяется, как главная линейная часть малого полного приращения функции относительно приращений аргументов.
Определение звучит громоздко, но с буквами все проще. Полный дифференциал первого порядка функции нескольких переменных выглядит так:
Зная, как считаются частные производные, нет никакой проблемы вычислить и полный дифференциал.
Частные производные – не такая уж и бесполезная тема. Например, дифференциальные уравнения в частных производных второго порядка широко используются для математического описания реальных физических процессов.
Здесь мы дали лишь общее, поверхностное представление о частных производных первого и второго порядка. Вас интересует эта тема или остались конкретные вопросы? Задавайте их в комментариях и обращайтесь к экспертам профессионального студенческого сервиса за квалифицированной и скорой помощью в учебе. С нами вы не останетесь один на один с проблемой!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Частные производные
Частной производной по x функции z = f(x,y) в точке A(x0,y0) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.
Частные производные функции z(x,y) находятся по следующим формулам:
Вторые частные производные функции z(x,y) находятся по формулам:
Смешанные частные производные функции z(x,y) находятся по формулам:
Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
x2+xy ≡ x^2+x*y.
cos2(2x+y) ≡ (cos(2*x+y))^2
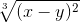
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
Примеры
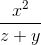
cos2(2x+zy) ≡ (cos(2*x+z*y))^2
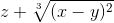
Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.
Частные производные функции нескольких переменных
Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δxz=f(x+Δx,y)-f(x,y) – это частное приращение функции z по аргументу x; Δyz=f(x,y+Δy)-f(x,y) – это частное приращение функции z по аргументу у.
Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:
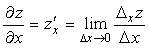
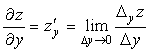
Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.
Пример 1. z=2x5+3x2y+y2–4x+5y-1
Пример 2. Найти частные производные функции z = f(x;y) в точке A(x0;y0).
Находим частные производные:
Найдем частные производные в точке А(1;1)
Находим вторые частные производные:

Найдем смешанные частные производные:
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Данный онлайн калькулятор предназначен для решения частных производных первого и второго порядков.
Частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Следовательно, частные производные находятся так же, как и производные функций одной переменной. Частная производная это обобщенное понятие производной, когда в функции содержится несколько переменных.
Калькулятор поможет найти частные производные функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
: x^a
модуль x: abs(x)
Для того, чтобы найти производную функции
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции 
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где 
Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.
- Примеры
- x*E^x, x;
- x^3*E^x, {x,17};
- x^3*y^2*Sin[x+y], x;
- x^3*y^2*Sin[x+y], y,
- x/(x+y^4), {x,6}.

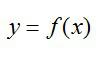
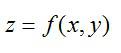
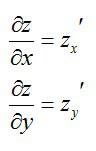
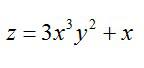
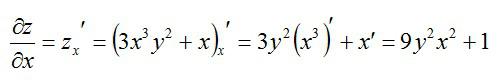
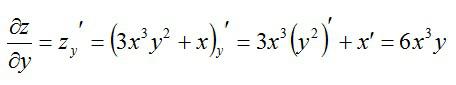
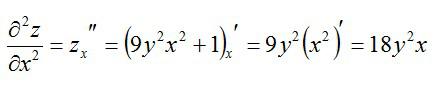
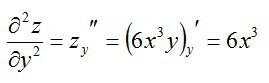
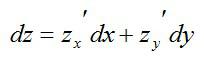
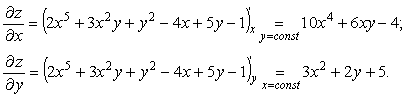

 : x^a
: x^a