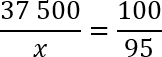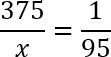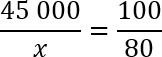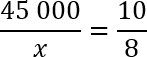Помощь родителям: «целое» и «части».
Тема «Целое и части» — одна из важных в математике 1 классе.
Познакомить с этими понятиями очень легко на самом простом примере: возьмите яблоко.
Что можно рассказать о нем? (На самом деле ответов очень много – это цвет, размер, форма).
Что мы видим теперь? Сколько кусков получилось?
Кусок в математике называется – частью.
Сколько получилось частей? А можно по-другому разрезать?
Что больше: целое или его часть?
Если мы соединим эти части, то получим целое яблоко.
Часть всегда меньше целого, а целое всегда больше части.
Целое равно сумме частей.
Чтобы найти часть, надо из целого вычесть другую часть.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 67
ГДЗ учебник по математике 2 класс Петерсон. Часть 2. Урок 28. Решение задач. Номер №9
Как найти целое? Как найти часть? Определи в равенствах части и целое и найди x.
x − a = p
x + b = c
d − x = k
Решение
Чтобы найти целое нужно сложить части.
Чтобы найти часть нужно из целого вычесть другую часть.
x − a = p
x − целое;
a, p − части.
x = a + p
x + b = c
c − целое;
x, b − части.
x = c − b
d − x = k
d − целое;
x, k − части.
x = d − k
Решение уравнений с опорой на отношение «части и целое»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Урок математики в 1 классе
УМК «Классическая программа»
Решение уравнений с опорой на отношение «части и целое»
Автор: Шишкалова Нина Петровна
учитель начальных классов
МБОУ «СОШ№6»
Г. Сосновый Бор
Цель:
учить решать уравнения, используя графические модели (схемы) и отношение «части и целое».
Подготовительный этап к восприятию нового материала.
Задание 1. У данных фигур покажите части и целое.
Задание 2. Найдите лишнюю фигуру.
а)
б)
в)
г)
д)
е)
Задание 2. По данной модели составьте из частей целое. Запишите формулу, применяя правило.
А
М
В
К
А = _____________
Если сложить части, то получится целое.
М
В
К
По этой же модели запишите формулы, как из целого найти части.
А
М = ____________
В = _____________
К = _____________
Если из целого вычесть часть, то останется другая часть.
К = А – М – В
Проверьте правильность выполненного вами задания.
А = М + В + К
М = А – В – К
В = А – М – К
Задание 3. (выполняется устно)
— Вычислить целое по его частям.
+
=
5 и 2 4 и 5
3 и 7 8 и 1
6 и 2 9 и 2
— Вычислить часть по целому и другой части.
=
—
8 и 2 5 и 4
7 и 1 6 и 2
7 и 4 3 и 2
Задание 4.
Обозначьте задуманное число буквой Х, У или Z. Запишите предложения формулами.
К задуманному числу прибавили 2 и получили 4.
Из задуманного числа вычли 3 и получили 2.
Из числа 7 вычли задуманное число и получили 6.
Равенства имеют вид: (проверка)
Х + 2 =4 У – 3 = 2 7 – Z = 6
Равенство, в котором есть неизвестная величина, называется уравнением.
Чтобы решить уравнение, нужно определить, что неизвестно — часть или целое. В этом помогут модели и схемы.
Задание 5.
— Обозначьте в каждом уравнении части и целое и найдите неизвестное число.
Х + 2 = 4 У – 3 = 2 7 – Z = 6
Х = У = Z =
Алгоритм.
Определите, частью или целым является неизвестная величина.
Примените правило и выберите действие.
Проверка выполненного задания.
x + 2 = 4 y — 3 = 2
x = 4 — 2 y = 3 + 2
7 — z = 6
z = 7 — 6
Проблемные и практические задачи по теме.
Задание 1.
Найдите и прочитайте те выражения, которые являются уравнениями.
c = a – b 5 = 6 – x
7 + x = 10 6 + 2 = 9
6 = 4 + 2 x – 4 = 3
Задание 2.
Составьте модели к найденным уравнениям и найдите неизвестное число.
Проверка выполненного задания.
7 + x = 10 5 = 6 — x
10
7
X
6
5
X
x – 4 = 3
x
4
3
Задание 3.
Составьте всевозможные уравнения по данной схеме.
x
c
a
Возможные варианты ответов.
x + c = a
a – x = c
c + x = a
a – c = x
Задание 4. Дано уравнение. x = d – a
— Определите, по какой из схем составлено уравнение.
Задание 5.
Решите задачу, используя модели или схему.
Мама испекла 16 пирожков. Когда несколько пирожков съели, их осталось 10. Сколько пирожков съели?
Проверьте схему и объясните свой выбор решения.
?
10
16
16
?
10
Выводы по теме.
Уравнение – это равенство с одним неизвестным.
Если неизвестна часть, то от целого отнимают другую часть.
Если неизвестно целое, то части складывают.
Уравнение – один из способов решения задачи.
Курс повышения квалификации
Охрана труда
- Сейчас обучается 114 человек из 42 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 233 человека из 54 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 352 человека из 64 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 586 282 материала в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 27.12.2020
- 1548
- 44
- 27.12.2020
- 1592
- 6
- 27.12.2020
- 574
- 4
- 27.12.2020
- 486
- 0
- 27.12.2020
- 449
- 0
- 27.12.2020
- 356
- 1
- 27.12.2020
- 510
- 3
- 27.12.2020
- 191
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 03.06.2020 618
- PPTX 148 кбайт
- 4 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Софронова Ольга Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 24277
- Всего материалов: 234
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута
Минобрнауки создаст для вузов рекомендации по поддержке молодых семей
Время чтения: 1 минута
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута
Ленобласть распределит в школы прибывающих из Донбасса детей
Время чтения: 1 минута
В школах Хабаровского края введут уроки спортивной борьбы
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Получите новую специальность с дополнительной скидкой 10%
Цена от 4900 740 руб. Промокод (до 23 февраля): Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки
источники:
http://reshalka.com/uchebniki/2-klass/matematika/peterson/753
http://infourok.ru/reshenie-uravnenij-s-oporoj-na-otnoshenie-chasti-i-celoe-4730144.html
Как находить долю от чего-то
Это только вожди мирового пролетариата, выкинув вперед руку и широко улыбаясь, предлагали сделать все ресурсы общими для всего народа, а после пользоваться ими коллективно. Это называется утопией, к тому же бессмысленной. В современном мире все постоянно приходится делить и находить в нем свою долю.
Вам понадобится
- калькулятор, моральные принципы
Инструкция
Чтобы не остаться с носом ни при решении задачи по математики из учебника за шестой класс, ни при разрешении более серьезных проблем, связанных с разделом и получением чего-либо, нужно уметь искать долю. Или, другими словами, часть от целого, тема «проценты».
Возьмем для примера что-нибудь сладкое, например, банки с вареной сгущенкой. Возьмем их много – пусть будет 192 штуки. И попробуем найти долю от целого (количество всех банок) равную 14 процентам. Для этого нам необходимо:
1. Сделать над собой усилие и, скрепя сердцем, смирится с тем, что сгущенкой придется делиться.
2. Произвести следующие математические действия – разделить наше целое 192 на 100. Таким образом, мы ищем, сколько сгущенки мы можем принять за один процент, в нашем примере это 1,92 банки сладкого лакомства.
3. Теперь вспомним, какую долю нам нужно отдать – 14 процентов, и найти непосредственно ее. Берем полученные выше 1,92 и умножаем на 14. Получаем 26,88 банок.
4. Но, поскольку в результате расчетов оказалось дробное число, округляем его в большую строну, так как десятая после запятой больше 5.
5. Итого, 27 банок и есть наша искомая нами доля.
6. Еще раз, чтобы закрепить и уже без манипуляций с едой. Берем целое, делим его на сто и умножаем на х (икс) процентов, где х (икс) – доля, которую нужно найти.
Предлагаем сделать плавный переход от сухой математики к прозаичной лирике. При разделе имущества, доставшегося по наследству указанным в завещании людям крайне редки случаи, когда принятые решения по определению искомых долей устраивают всех участников юридического процесса. Даже в сплоченных семьях и родовых кланах есть место зависти и остро развитому, но абсолютно субъективному чувству псевдо-справедливости. Поэтому в некоторых жизненных ситуациях, где велика роль личностного фактора, подобной этой, схема с процентами работает плохо. В этом случае руководствуйтесь своим уровнем морального развития и потребностями.
Полезный совет
На этикетках продуктов питания рядом с количеством калорий часто указывают их суточную долю от дневной нормы потребления для человека.
Источники:
- Урок математики в 3-м классе по теме «Нахождение доли числа»
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
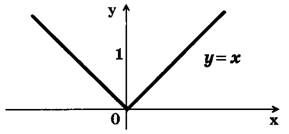
Функция у = |х| и ее график
|х| — модуль х (абсолютная величина х). Эта функция определяется так:
График функции у = |х| изображен на рис. 1.
Рис. 1
Функция у = |х| определена при хє R, принимает только неотрицательные значения. Таким образом, D(y)=(-∞;+∞); Е (у) = [0;+∞); функция у = |х| обращается в нуль при х=0. При х є (-∞;0) функция убывает, при х є (0;+∞) функция у = |х| возрастает.
Поскольку y(-x)= |-х| = |х| = y(x), то функция у = |х| четная.
Замечание. В общем случае можно рассмотреть модуль функции:
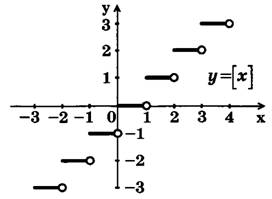
Функция у=[х] и ее график
[х] — целая часть х. [х] — наибольшее целое число, не превосходящее х. Если хє [0,+1), то у=[х]=0; если хє [1;2), то у=[х]=1; если хє |-1;0), то у=[х]=-1; если хє [-2;-1), то у=[х]=-2 и так далее.
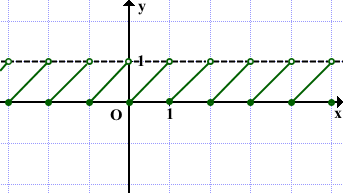
График функции у=[х] изображен на рис. 2. Белыми кружочками (белыми точками) изображены выколотые значения (т. е. те значения, которые функция не принимает в этих точках). Так, для функции у=[х] у(1)≠0, у(1)=1; у(2)≠1, у(2)=2 и т.д.
Рис. 2
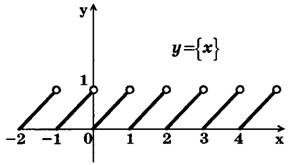
Функция у={х} и ее график
{х} — дробная часть х, {х}=х-[х]. Функция у={х} является периодической, основной период Т=1, {х+1}={х}, поэтому достаточно сначала построить ветвь графика на любом промежутке длиной 1, например при х є[0;1).
Если х є[0;1), то [х]=0 => {х}=х. На рис. 3 изображен график функции y={х}.
Рис. 3
Функция дробная часть числа
Определение
Дробной частью действительного числа называется разность между этим числом и его целой частью.
Дробную часть числа x обозначают {x}.
По определению, {x}=x-[x].
Для любого x∈R 0≤{x}<1.
В частности, если n — целое число (n∈Ζ), {n}=0.
Примеры.
Вычислить дробную часть {x} числа x, если x принимает значения:
9,43; 0,3; -0,56; 12 3/7; 2/9; -4/15; 20; -11.
Решение:
{9,43}=9,43-[9,43]=9,43-9=0,43;
{0,3}=0,3-[0,3]=0,3-0=0,3;
{-0,56}=-0,56-[-0,56]=-0,56-(-1)=-0,56+1=0,44.
{20}=0;
{-11}=0.
Определение
Функцию, ставящую в соответствие каждому значению x дробную часть этого числа — число {x}, называют функцией дробной части числа и обозначают y={x}.
Функция дробная часть числа определена на множестве действительных чисел: x∈R.
Область значений функции — полуинтервал y∈[0;1).
Утверждение.
Если k∈Ζ, то {x+k}={x}.
Доказательство:
По определению дробной части числа {x+k}=x+k-[x+k].
По свойству целой части числа [x+k]=[x]+k.
Следовательно, {x+k}=x+k-[x+k]=x+k-[x]-k=x-[x]={x}.
Что и требовалось доказать.
Из утверждения следует, что на каждом промежутке вида [k; k+1), где k∈Z, график функции y={x} имеет одинаковый вид.
При k=0 x∈ [0; 1), [x]=0.
Отсюда y={x}=x-[x]=x-0=x.
То есть при x∈ [0; 1) y=x.
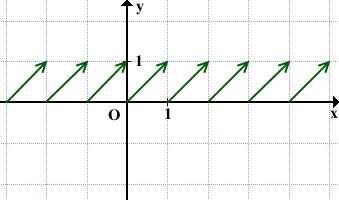
График функции y={x}
Стрелки на графике показывают, что правые концы отрезков не принадлежат графику.
Другой вариант показать, что левые концы отрезков принадлежат графику, а правые — не принадлежат, изобразить их, соответственно, закрашенными и выколотыми точками.
Поскольку {x+k}= {x}, функция дробная часть числа является периодической. Её период T=k — любое целое число, отличное от нуля.
Наименьший положительный период (главный период) T=1.
Метод решения задач с процентами
Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции
Данные задачи на проценты можно записать в виде следующих соотношений:
все — 100% часть — часть в %
которые можно записать в виде пропорции
| все | = | 100% |
| часть | часть в % |
Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.
Примеры решения задач на проценты
30 соответствует 100% x соответствует 15%
решим полученное уравнение
Ответ: 15% от 30 равно 4.5.
20 соответствует 100% 35 соответствует x
решим полученное уравнение
Ответ: 35 составляет 175% от 20.
x соответствует 100% 20 соответствует 5%
решим полученное уравнение
Ответ: 400.
При изучении процентов вам также будут полезны:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как решать задачи с процентами
О чем эта статья:
Основные определения
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».
Процент — это одна сотая часть от любого числа. Обозначается вот так: %.
Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18.
А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:
Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а потом используем предыдущее правило и переведем десятичную дробь в проценты:
Типы задач на проценты
В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.
Тип 1. Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?
Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).
Ответ: из общего количества изготовленных стульев контроль не прошли 100 штук.
Тип 2. Нахождение числа по его проценту
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.
Задача. Школьник решил 40 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?
Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 40 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.
40 : 0,16 = 40 · 100 : 16 = 250
Ответ: 250 задач собрано в этом учебнике.
Тип 3. Нахождение процентного отношения двух чисел
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?
Как решаем: поделим 10 на 25, полученную дробь переведем в проценты.
10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%
Ответ: в классе 40% девочек.
Тип 4. Увеличение числа на процент
Чтобы увеличить число на некоторое количество процентов, можно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.
А можно воспользоваться формулой:
a = b · (1 + с : 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом месяце стикерпак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикерпак?
Как решаем: можно найти 12% от 110:
Прибавить к исходному числу:
110 + 13,2 = 123,2 рубля.
Или можно воспользоваться формулой, тогда:
110 · (1 + 12 : 100) = 110 · 1,12 = 123,2.
Ответ: стоимость стикерпака в этом месяце — 123 рубля 20 копеек.
Тип 5. Уменьшение числа на процент
Чтобы уменьшить число на несколько процентов, можно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.
А можно воспользоваться формулой:
a = b · (1 − с : 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом году школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?
Как решаем: можно найти 25% от 100:
Вычесть из исходного числа 100 − 25 = 75 человек.
Или можно воспользоваться формулой, тогда:
100 · (1 − 25 : 100) = 75/p>
Ответ: 75 выпускников в этом году.
Тип 6. Задачи на простые проценты
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.
Формула расчета выглядит так:
S = а · (1 + у · х : 100),
где a — исходная сумма,
S — сумма, которая наращивается,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Марии срочно понадобились деньги и она взяла на один год в долг 70 000 рублей под 8% ежемесячно. Сколько денег она вернет через год?
Как решаем: подставим в формулу данные из условий задачи.
70 000 · (1 + 12 · 8 : 100) = 137 200
Ответ: 137 200 рублей вернет Мария через год.
Тип 7. Задачи на сложные проценты
Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.
Формула расчета выглядит так:
S = а · (1 + х : 100) y ,
где S — наращиваемая сумма,
a — исходная,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Антон хочет оформить вклад 10 000 рублей на 5 лет в банке, который дает 10% годовых. Какую сумму снимет Антон через 5 лет хранения денег в этом банке?
Как решаем: просто подставим в формулу данные из условий задачи:
10000 · (1 + 10 : 100)3 = 13 310
Ответ: 13 310 рублей снимет Антон через год.
Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!
Есть случаи, когда найти процент от числа проще, если представить проценты в виде простых дробей. В таком случае будем искать часть числа.
- 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
- 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
- 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
- 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
- 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
- 100 — 25 = 75,
значит нужно заплатить 75% от первоначальной цены. - Используем правило соотношения чисел:
8500 : 4 * 3 = 6375.
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Задачи на проценты с решением
Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.
Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
Ответ: масса воды 53,2 кг
Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?
Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.
Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:
0,6х — 0,25 * 0,6x = 0,45x
После двух понижений изменение цены составит:
Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.
Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?
По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто
Получается, что стоимость одной пары брюк — это 23% стоимости пальто.
Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.
Ответ: пять пар брюк на 15% дороже, чем одно пальто.
Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.
По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.
Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.
Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.
А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.
Ответ: заработок жены составляет 27%.
Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.
Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.
Значит, 19 килограммов питательного вещества в абрикосах — это 10% веса свежих абрикосов. Найдем число по проценту.
Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.
Задачи на проценты: стандартный расчет с помощью пропорций
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
37 500 — 100%
X — 95%
Нужно составить пропорцию и найти x . Получаем:
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
45 000 — 100%
x — 80%
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
45 000 · 8 = x · 10
Это простейшее линейное уравнение. Выразим из него переменную x :
x = 45 000 · 8 : 10
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
http://skysmart.ru/articles/mathematic/kak-reshat-zadachi-s-procentami
http://www.berdov.com/ege/percent/standartnii-metod-proporcii/