|
t*ГР= SГP– α* |
(100) |
|
t*М=tГР± λWOst |
где SГР и α* вычислены по формулам (96) и (99).
Приведенные приемы расчета эфемерид Солнца и звезд дают достаточно точные для мореходной астрономии координаты в течение 15—20 лет от начальной эпохи, и их сравнительно легко реализовать на ЭВМ. Существуют и другие алгоритмы получения эфемерид, зависящие от поставленных задач и типа ЭВМ.
На судовых ЭВМ данного поколения нет смысла вычислять различные частные задачи, например кульминации, восходы светил, элементы освещенности и другие, поэтому, независимо от наличия машины, на судне требуется МАЕ.
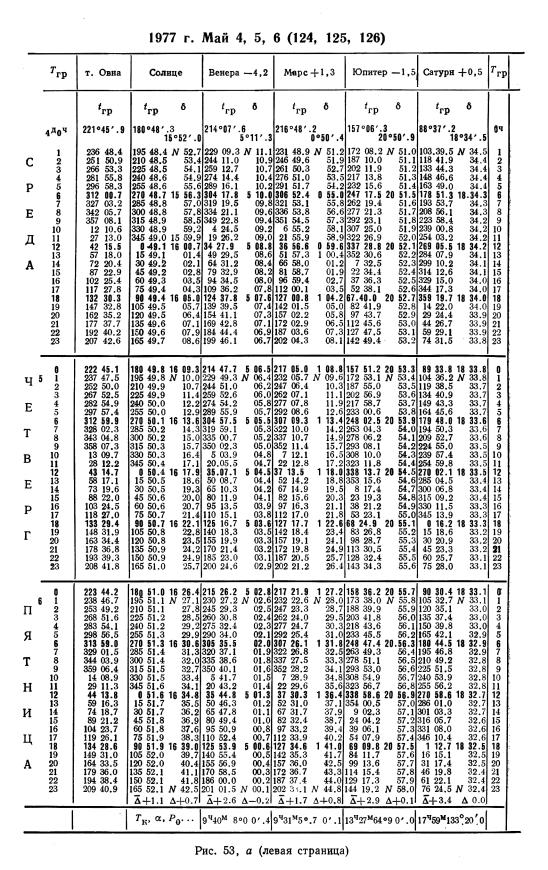
Основные данные помещены в ежедневных таблицах МАЕ, занимающих большую его часть. На каждом развернутом листе МАЕ приведены данные для трех суток: на левой странице — часовые углы точки Овна (звездное время), часовые углы и склонения Солнца, Венеры, Марса, Юпитера и Сатурна; на правой странице — часовые углы и склонения Луны, время ее восхода и захода на каждый день, время восхода, захода Солнца и сумерек на среднюю дату листа (рис. 53). Внизу страниц приведены дополнительные данные: время кульминации, параллаксы, радиусы и др. Рассмотрим принцип устройства таблиц МАЕ для часовых углов и склонений светил.
136
137

138
Получение звездного времени. Аргументами для входа в МАЕ являются гринвичская дата, Тгр и название светила, поэтому найдем зависимость, связывающую часовой угол точки Овна с Тгр. Применяя основную формулу времени к среднему Солнцу, получим:
SГР=tГР9+α9
или
так как
SГР= tГРE, а tГР9=TГР±12ч
По формуле (101) для значений Тгр через 1Ч предвычислены и помещены в МАЕ табличные значения tт точки Овна (помечены tгр). Поправка за избыток ∆T сверх часа получается дифференцированием формулы (101) по Т. Переходя к конечным приращениям и взяв величину ∆α9 за 60м, получим
∆tГРE/∆Т=1+ ∆α9/60м
откуда
∆tГРE=∆Т+(∆α9/60м) ∆Т
|
или |
||||
|
∆tГРE=(∆Т+µ ∆Т)о |
(102) |
|||
|
где µ= |
∆α |
=0,0027379 — |
коэффициент |
перевода единиц среднего |
|
60м |
||||
|
времени в звездные. |
||||
|
Очевидно, |
формула (102) |
представляет |
перевод промежутка ∆T в |
звездные единицы и в градусную меру.
Поправки, рассчитанные по формуле (102), помещены в конце МАЕ в «Основных интерполяционных таблицах» (ОИТ) на каждую минуту и секунду часа. В таблицу входят с минутами ∆Т (сверху) и секундами (слева) в графу «Точка Овна». Выбрав ∆tE, придают ее к часовому «табличному» значению tT и далее получают местное звездное время
|
Ost |
(103) |
|
tME=tT+ ∆tE± λW |
Вычисления производят по схеме, показанной в примере 25. Величину SM
139

определяют при подборе звезд по звездному глобусу или таблицам, а также как промежуточную величину при определении tM* .
Пример 25. 5 мая 1977 г. в Тc=5ч53м (№=8Оst); λ=103°50′, 2Оst; Txр=9ч52м47с; u=+28′. Определить tME (SM).
Решение
Получение часовых углов и склонений звезд. Формула для часового угла звезды получается из основной формулы времени решением ее относительно tM* :
tM* =SM–α*= tME+τ*
где τ*=360°—α*
Подставляя в эту формулу значение tME из формулы (103), получим tM* =tM+∆tE±λ+τ* (104)
Величины τ*, а также δ* приведены в разделе МАЕ, озаглавленном «Звезды. Видимые места» (с. 270 МАЕ), для 159 наиболее ярких звезд в порядке возрастания их α. На левой странице по прямому восхождению, номеру и месту звезды в созвездии приведены τ* — градусы на год, минуты по месяцам. На правой странице по номеру и собственному имени звезды (если оно есть) приведены δ*. Так как минуты τ* и δ даны на первое число месяца, на промежуточные даты приходится интерполировать их между колонок. На вкладыше к МАЕ (приложение IV) величины τ и δ для 50 наиболее ярких звезд
140

приведены через 10 дней, поэтому интерполировать их не нужно, так как их значения точнее, чем в основных таблицах. Названия созвездий и звезд, их номера в МАЕ отыскиваются при необходимости на обратной стороне карты звездного неба, прилагаемой к Ежегоднику (приложение V к МАЕ).
Пример 26. 5 мая 1977 г. около Тс=19Ч52М (№=7W); λ=95°47,0′ W
наблюдали α Волопаса; Тхр=2Ч50М38С; и=+1М48С,0. Определить t*M и δ*. Решение.
Получение часовых углов и склонений Солнца, планет и Луны.
Формулу, выражающую часовой угол через аргумент Тгр, можно получить из основной формулы времени, записав ее два раза — для среднего Солнца и для данного светила:
SГР=t9ГР+α9
SГР=tСВГР+αСВ
В один и тот же момент левые части равны, поэтому
tГРСВ +αСВ = tГР +α
или
tГРСВ = tГР +α −αСВ
но по формуле (72) имеем: tГРСВ =ТГР±12ч
Подставляя значение tГР , получим формулу для часового угла светила:
141

∆αСВМАКС
|
tГРСВ =Тгр±12ч+α −αСВ |
(105) |
По этой формуле для Тгр через интервал в 1Ч предвычислены табличные значения tT часовых углов Солнца, четырех планет и Луны, помещенные в ежедневных таблицах МАЕ в колонке tГР. Приращение часового угла за промежуток ∆Т сверх целого часа ТГР получается следующим путем. Дифференцируя выражение (105) по Т и переходя к конечным приращениям, получим
∆∆Tt =1 + ∆∆αT − ∆α∆ТСВ
Принимая изменения прямых восхождений за 1Ч=60м и прибавив и отняв
|
постоянную величину |
∆α |
МАКС |
||||||||||
|
СВ |
, получим |
|||||||||||
|
60М |
||||||||||||
|
∆α |
− ∆α |
МАКС |
∆α МАКС − ∆α |
СВ |
||||||||
|
∆t = |
∆T + |
СВ |
∆T |
+ |
СВ |
∆Т (106) |
||||||
|
60М |
60М |
|||||||||||
|
Таким путем |
изменение часового |
угла светила за |
промежуток ∆ТМ,С |
разделено на две части: равномерную ∆t1 (в первых скобках), не зависящую от даты, и неравномерную ∆t2, меняющуюся по датам. В величину ∆t1 входят: ∆α — изменение прямого восхождения среднего Солнца за час, равное 2,5′;
— наибольшее возможное изменение α данного светила за час: для Солнца 2,8′; для Венеры 3,5′; для Луны 43,5′. Величина ∆t1 представляет перевод промежутка ∆ТМ,С в равномерное изменение t, т.е. как бы во время,
считаемое по данному светилу. Для Солнца и планет величина ∆α — ∆αСВМАКС ,
представляющая как бы переводной коэффициент, принята в МАЕ одинаковой по наибольшему ∆ для Венеры, равному 3,5′, поэтому второй член в скобках равен 1,0′, а ∆t1 за час составит 14°59′ и доли его за меньшие промежутки. Для Луны величина ∆α — ∆αСВМАКС составит 41,0′, поэтому ∆t1 за час равна 14°19′.
Значения ∆t1 для Солнца (планет) и Луны вычислены для каждой минуты и секунды часа и приведены в ОИТ в отдельных колонках.
Вторая поправка ∆t2 учитывает неравномерность изменения α Луны,
142

Солнца и планет:
|
∆t2 |
= |
∆αМАКС − ∆α |
СВ |
∆ТГРМ |
(107) |
|
СВ |
|||||
|
60М |
|||||
|
где ∆αСВ — изменение α светила в данное время; |
|||||
|
∆αСВМАКС – ∆αСВ =∆ — |
квазиразность |
(искусственная |
разность), |
предвычислена для Луны на каждый час, а для Солнца и планет — на среднюю дату листа (приведена внизу колонок).
Квазиразностью ∆ в МАЕ называется разность между наибольшим возможным изменение α светила за 1Ч и фактическим изменением его за данный час. Квазиразность в нашем МАЕ всегда положительна, так как взято
∆αМАКС (в английском — для Венеры бывает отрицательна). Например, для
Солнца наибольшая ∆=3,5’—2,3’=1,2′; для Луны =18,0′; для планет ∆=6,0′. Квазиразность интерполируется на данную минуту, для чего надо войти с
выбранной ∆ и минутой ∆ТГР в две крайние колонки ОИТ. Полученная поправка ∆t2 дает отклонение изменения tCB данного светила от равномерного в данный час.
|
Следовательно, tГР на данный момент Tгр получается по формуле |
|||||||
|
tгр=tT+ ∆t1+ ∆t2 |
(108) |
||||||
|
Для получения местного часового угла светила имеем формулу |
|||||||
|
t |
M |
= t |
T |
+ ∆t + ∆t |
2 |
± λOst |
(109) |
|
1 |
W |
Вычисления производят по схеме, приведенной в примере 27. Склонение Солнца, Луны и планет приводится также через час, поэтому на промежуточное время его следует интерполировать в соответствии с формулой
|
δ =δ‘+ |
∆ |
∆TГРМ |
(110) |
|
|
60 |
||||
где δ’ — значение склонения на ближайший меньший час TГР, выбранное из ежедневных таблиц;
∆ — часовая разность склонений со своим знаком, выбираемая внизу колонки для Солнца и планет и рядом с δ — для Луны (иногда для Венеры и
143

Солнца ∆ следует образовать самому). Интерполирование производят по двум крайним колонкам ОИТ, входя в них с минутой ∆Т и ∆.
Пример 27. 4 мая 1977 г. в Тс=14ч30м (№=11W); λ=160°26′ W, секундомер пущен в ТГРП =1Ч30М00С; наблюдали Солнце Тскм=2*48с. Определить t М и δ
Решение
Пример 28. 5 мая 1977 г. в Тс=543″ (№=12 Оst); λс=166°25’Ost наблюдали Луну: Tхр=5Ч39М48С; u=+3М43С.
Определить tMe и δ. Решение.
144
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Скачать PDF
- Детская площадка
- Здоровье
- Инженерное дело
- математика
- физика
- финансовый
- Химия
Часовой угол Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Системы солнечной энергии ↺ | |
| Системы солнечной энергии | Основы ↺ |
|
✖Солнечное время — это расчет течения времени, основанный на положении Солнца на небе. Снято в 24-часовом формате. Например, 18:00 — это 18:00.ⓘ Солнечное время [ST] |
+10% -10% |
|
✖Часовой угол в любой момент — это угол, на который должна повернуться Земля, чтобы меридиан наблюдателя оказался точно на одной линии с солнечными лучами.ⓘ Часовой угол [ω] |
⎘ копия |
Формула
✖
Часовой угол
Формула
`»ω» = («ST»/3600-12)*15*0.0175`
Пример
`»-3.004167rad»=(«2000s»/3600-12)*15*0.0175`
Калькулятор
👍
Часовой угол Решение
ШАГ 0: Сводка предварительного расчета
Используемая формула
Часовой угол = (Солнечное время/3600-12)*15*0.0175
ω = (ST/3600-12)*15*0.0175
В этой формуле используются 2 Переменные
Используемые переменные
Часовой угол — (Измеряется в Радиан) — Часовой угол в любой момент — это угол, на который должна повернуться Земля, чтобы меридиан наблюдателя оказался точно на одной линии с солнечными лучами.
Солнечное время — (Измеряется в Второй) — Солнечное время — это расчет течения времени, основанный на положении Солнца на небе. Снято в 24-часовом формате. Например, 18:00 — это 18:00.
ШАГ 1. Преобразование входов в базовый блок
Солнечное время: 2000 Второй —> 2000 Второй Конверсия не требуется
ШАГ 2: Оцените формулу
Подстановка входных значений в формулу
ω = (ST/3600-12)*15*0.0175 —> (2000/3600-12)*15*0.0175
Оценка … …
ω = -3.00416666666667
ШАГ 3: Преобразуйте результат в единицу вывода
-3.00416666666667 Радиан —> Конверсия не требуется
ОКОНЧАТЕЛЬНЫЙ ОТВЕТ
-3.00416666666667 ≈ -3.004167 Радиан <— Часовой угол
(Расчет завершен через 00.003 секунд)
Кредиты

ДИТ УНИВЕРСИТЕТ
(ДИТУ),
Дехрадун
АДИТЬЯ РАВАТ создал этот калькулятор и еще 50+!

Институт информационных технологий Вишвакармы, Пуна
(VIIT Пуна),
Пуна
Абхишек Дхармендра Бансиле проверил этот калькулятор и еще 10+!
8 Основы Калькуляторы
Угол падения солнечных лучей
Идти
Угол падения = acos(sin(Угол широты)*(sin(Угол склонения)*cos(Угол наклона)+cos(Угол склонения)*cos(Азимутальный угол поверхности)*cos(Часовой угол)*sin(Угол наклона))+cos(Угол широты)*(cos(Угол склонения)*cos(Часовой угол)*cos(Угол наклона)-sin(Угол склонения)*cos(Азимутальный угол поверхности)*sin(Угол наклона))+cos(Угол склонения)*sin(Азимутальный угол поверхности)*sin(Часовой угол)*sin(Угол наклона))
Часовой угол на восходе и закате
Идти
Часовой угол = acos(-tan(Угол широты—Угол наклона)*tan(Угол склонения))
Световой день
Идти
Световой день = 3600*acos(-tan(Угол широты)*tan(Угол склонения))
Коэффициент наклона для отраженного излучения
Идти
Коэффициент наклона для отраженного излучения = (Отражательная способность*(1-cos(Угол наклона)))/2
Эффективность преобразования энергии солнечного дымохода
Идти
Максимальная эффективность солнечного дымохода = 9.81*Высота дымохода/(1005*Температура окружающего воздуха)
Коэффициент наклона для рассеянного излучения
Идти
Коэффициент наклона для рассеянного излучения = (1+cos(Угол наклона))/2
Угол склонения
Идти
Угол склонения = 23.45*sin(0.9863*(284+Количество дней))
Часовой угол
Идти
Часовой угол = (Солнечное время/3600-12)*15*0.0175
Часовой угол формула
Часовой угол = (Солнечное время/3600-12)*15*0.0175
ω = (ST/3600-12)*15*0.0175
-
English
Spanish
French
German
Italian
Portuguese
Polish
Dutch
Copied!
Часовая и минутная стрелка онлайн.Угол между ними.
| Час и минута разделенные пробелом |
| Угол между стрелками (градусы) |
Обратимся опять к школьным задачам и задачам на сообразительность. Одной из таких задач является узнать, какой угол образуют между собой минутная и часовая стрелка на механических часах в 16 часов 38 минут, или одна из вариаций — сколько времени будет после начала первых суток, когда часовая и минутная стрелка будут образовывать угол в 70 градусов.
Или в самом общем виде «найдите угол между часовой и минутной стрелкой»(с)
Самый простой вопрос, на который много людей умудряются давать неправильный ответ. Какой угол между часовой и минутной стрелкой на часах в 15 часов 15 минут?
Ответ ноль градусов не является правильным ответом 
Давайте разбираться.
Минутная стрелка за 60 минут совершает полный оборот по циферблату, то есть совершит оборот на 360 градусов. За это же самое время (60 минут) часовая стрелка пройдет путь всего одну двенадцатую часть от окружности, то есть сдвинется на 360/12 = 30 градусов
Давайте считать подробно, какой же угол проходит каждая стрелка от 0 часов и нуля минут?
Насчет минутной все очень просто. Составляем пропорцию минуты относятся к пройденному углу как полный оборот(60 минут) к 360 градусам.
Таким образом пройденный угол минутной стрелкой составит минуты/60*360 = минуты*6
Как результат вывод каждая пройденная минута смещает минутную стрелку на 6 градусов
Отлично! Теперь что насчет часовой. А принцип тот же самый, только надо время (часы и минуты) привести к долям часа.
Например 2 часа 30 минут — это 2.5 часа ( 2 часа и его половинка), 8 часов и 15 минут — это 8.25 ( 8 часов и одна четвертинка часа), 11 часов 45 минут — это 11 часов и три четвертинки часа то есть 8.75)
А дальше все просто такая же пропорция: Час(в виде долей часа) относится пройденному углу как 12 часов ( за 12 часов ведь часовая стрелка опишет весь циферблат) к 360 градусам.
Таким образом пройденный угол часовой стрелкой составит часы( в долях часа)*360.12 = часы*30
И как следствие вывод каждая пройденный час смещает часовую стрелку на 30 градусов
Теперь очень легко посчитать угол между стрелками вычислив разницу между углом минутной и часовой стрелки
угол между стрелками = (час+(минуты /60))*30 -минуты*6
где час+(минуты /60) — это положение часовой стрелки
Таким образом ответ к задаче: какой же угол составят стрелки когда на часах 15 часов 15 минут, будет следующим:
15 часов 15 минут это равноценно положению стрелок в 3 часа и 15 минут и таким образом угол составит (3+15/60)*30-15*6=7.5 градуса
В принцие можно считать и так 15.25*30-15*6=367.5 градуса, просто отсюда убираете полные обороты (360 градусов) и получаем тот же самый результат в 7.5 градуса.
Если же у вас есть потребность перевести время в текст то пожалуйста ознаомтесь с материалом Время (часы, минуты, секунды) прописью, а кому часто приходится работать с временными отрезками, складывать минуты и часы, высчитывая простой или наработку на отказ то стоит перейти сюда Суммирование временных отрезков
По углу между стрелками определить время
| Угол, между минутной и часовой стрелкой |
| Время на циферблате когда будет заданный угол |
Это задача сложнее, так как мы решать будем в общем виде, то есть определять все пары (час и минута) когда они будут образовывать заданный угол.
Итак, напомним. Если время выражено в виде HH:MM (час:минута) то угол между стрелками выражается формулой
((HH+cfrac{MM}{60})30-6MM)
Теперь, если обозначим угол буквой U и перевести все в альтернативный вид, то получим следующую формулу
(U=30HH-cfrac{11MM}{2})
Или избавшись от знаменателя, получаем основную формулу связывающая угол между двумя стрелками, и позициями этих стрелок на циферблате.
(2U=60HH-11MM)
заметьте, что угол может быть и отрицательным, то есть в пределах часа у нас может два раза встречаться один и тот же угол, например угол в 7.5 градуса может быть и в 15 часов 15 минут и 15 часов и 17.72727272 минут
Если нам, как в первой задаче был задан угол, то получаем уравнение с двумя переменными. В принципе оно не решается, если не принять условие что час и минута могут быть только целыми числами.
При таком условии мы получаем классическое диофантово уравнение. Решение которого очень простое. Рассматривать мы их пока не будем, а приведем сразу окончательные формулы
где k — произвольное целое число.
Результат часов естественно берем по модулю 24, а результат минут по модулю 60
Посчитаем все варианты когда часовая и минутная стрелка совпадают? То есть когда угол между ними равен 0 градусов.
Как минимум мы знаем две таких точки 0 часов и 0 минут и 12 часов дня 0 минут. А остальные??
Создадим таблицу, положений стрелок когда угол между ними ноль градусов
| k | Часовая стрелка | Минутная стрелка | Пояснения |
|---|---|---|---|
| 0 | 0 | 0 | то есть ровно полночь |
| 1 | 11 | 60 | то есть 12 часов |
| 2 | 22 | 0 | ОШИБКА!! |
Упс! на третьей строке у нас ошибка в 10 часов никак стрелки не совпадают.Это можно убедится взглянув на циферблат. В чём же дело?? Вроде все правильно считали.
А все дело в том, что в промежутке между 10 и 11 часами, для того что бы минутная и часовая стрелка совпадала, минутная стрелка должна находится где то в дробной части какой то минуты.
Это легко проверить по формуле 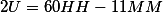
получим, что минутная стрелка будет находится между(!!) делениями 54 и 55 ( совсем точно на позиции 54.545454 минут).
Именно поэтому наши последние формулы не сработали, так как мы подразумевали что часы и минуты числа целые(!).
Задачи, которые встречаются на ЕГЭ
Мы рассмотрим задачи, решения которых есть в интернете, но пойдем другим путем. Возможно это облегчить той части школьников, которые ищут простой и необременительный способ решать задачи.
Ведь чем больше разных вариантов решения задач тем лучше.
Итак, мы знаем только одну формулу 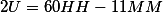
Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?
Рассуждения «решателей» на других интернет-ресурсах меня немного утомили и запутали . Вот для таких «утомленных» как я, мы решаем эту задачу по другому.
Определим когда в первом (1) часу минутная и часовая стрелка совпадет (угол 0 градусов)? Подставляем в уравнение изветные числа и получаем
(MM=cfrac{60}{11}=5.45454545)
то есть в 1 час и почти в 5.5 минут. это раньше чем 1 час 35 минут? Да! Отлично, значит этот час мы не учитываем в дальнейших расчетах.
Нам надо найти 10-ое совпадение минутной и часовой стрелки, начинаем анализировать:
в первый раз часовая стрелка будет в 2 часа и сколько то минут,
во второй раз в 3 часа и сколько минут
…
в восьмой раз в 9 часов и сколько то минут
в девятый раз в 10 часов и сколько то минут
в девятый раз в 11 часов и сколько то минут
Теперь осталось найти где будет находится минутная стрелка в 11 часов, так что бы стрелки совпадали
(MM=cfrac{660}{11}=60)
А теперь умножает 10 раз оборота( а это каждый час) на 60 (перведя в минуты) получим 600 минут. и высчитываем разницу между 60 минутами и 35 минутами ( которые были заданы)
Окончательный ответ получили 625 минут.
Что и требовалось доказать. Не надо никаких уравнений, пропорций, ни какая из стрелок с какой скоростью двигалась. Всё это мишура. Достаточно знать одну формулу.
Более интересная и сложная задача звучит так. В 8 часов вечера, угол между часовой и минутной стрелкой составялет 31 градуса . Сколько будет показывать время стрелки, после того как минутная и часовая стрелка образуют прямой угол 5 раз?
Итак в нашей формуле опять известны два из трех параметров 8 и 31 градус. Определяем миунтную стрелку по формуле получим 38 минут.
Когда ближайшее время когда стрелки будут образовывать прямой (90 градусов) угол?
(MM=cfrac{480-180}{11}=27.272727)
(MM=cfrac{480+180}{11}=60)
То есть в 8 часов 27.27272727 минут это первый прямой угол в этом часе и в 8 часов и 60 минут это второй угол в этом часе.
Первый прямой угол уже прошел относительно заданного времени, поэтому его не считаем.
Первый 90 градусов в 8 часов 60 минут ( можно сказать что ровно в 9-00) — раз
в 9 часов и сколько то минут — это два
в 10 часов и сколько минут — это три
еще раз в 10 и сколько минут — это 4-ре, так совпадений в 10 часу два
и в 11 часов и сколько минут это пять.
то есть нам надо посчитать в 11 часу два положения минутной стрелки когда угол равен +90 и -90 градусов. Какое время из этих раньше наступит то и является правильным ответом
Еще проще если мы воспользуемся ботом. Введем 90 градусов и получим следующую таблицу
| Время на циферблате когда будет заданный угол | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
то есть в 11 часо 10.90 минут будет как раз пятый раз когда между часовой и минутной стрелкой вновь образуется прямой угол.
Надеемся данный разбор, поможет Вам как формулировать задачи для учеников, так и легко решать подобные тесты на сообразительность и в ЕГЭ.
Удачи в расчетах!
|
From Wikipedia, the free encyclopedia
In astronomy and celestial navigation, the hour angle is the angle between two planes: one containing Earth’s axis and the zenith (the meridian plane), and the other containing Earth’s axis and a given point of interest (the hour circle).[1]
It may be given in degrees, time, or rotations depending on the application.
The angle may be expressed as negative east of the meridian plane and positive west of the meridian plane, or as positive westward from 0° to 360°. The angle may be measured in degrees or in time, with 24h = 360° exactly.
In celestial navigation, the convention is to measure in degrees westward from the prime meridian (Greenwich hour angle, GHA), from the local meridian (local hour angle, LHA) or from the first point of Aries (sidereal hour angle, SHA).
The hour angle is paired with the declination to fully specify the location of a point on the celestial sphere in the equatorial coordinate system.[2]
Relation with right ascension[edit]
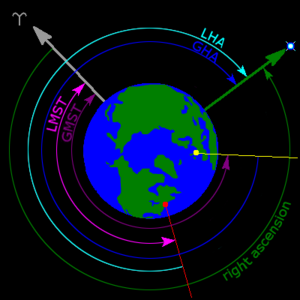
As seen from above the Earth’s north pole, a star’s local hour angle (LHA) for an observer near New York (red dot). Also depicted are the star’s right ascension and Greenwich hour angle (GHA), the local mean sidereal time (LMST) and Greenwich mean sidereal time (GMST). The symbol ʏ identifies the vernal equinox direction.
Assuming in this example the day of the year is the March equinox so the sun lies in the direction of the grey arrow then this star will rise about midnight. Just after the observer reaches the green arrow dawn comes and overwhelms with light the visibility of the star about six hours before it sets on the western horizon. The Right Ascension of the star is about 18h
The local hour angle (LHA) of an object in the observer’s sky is
or
where LHAobject is the local hour angle of the object, LST is the local sidereal time, 

Negative hour angles (−180° < LHAobject < 0°) indicate the object is approaching the meridian, positive hour angles (0° < LHAobject < 180°) indicate the object is moving away from the meridian; an hour angle of zero means the object is on the meridian.
Solar hour angle[edit]
Observing the Sun from Earth, the solar hour angle is an expression of time, expressed in angular measurement, usually degrees, from solar noon. At solar noon the hour angle is zero degrees, with the time before solar noon expressed as negative degrees, and the local time after solar noon expressed as positive degrees. For example, at 10:30 AM local apparent time the hour angle is −22.5° (15° per hour times 1.5 hours before noon).[4]
The cosine of the hour angle (cos(h)) is used to calculate the solar zenith angle. At solar noon, h = 0.000 so cos(h) = 1, and before and after solar noon the cos(± h) term = the same value for morning (negative hour angle) or afternoon (positive hour angle), so that the Sun is at the same altitude in the sky at 11:00AM and 1:00PM solar time.[5]
Sidereal hour angle[edit]
The sidereal hour angle (SHA) of a body on the celestial sphere is its angular distance west of the vernal equinox generally measured in degrees. The SHA of a star varies by less than a minute of arc per year, due to precession, while the SHA of a planet varies significantly from night to night. SHA is often used in celestial navigation and navigational astronomy, and values are published in astronomical almanacs.[citation needed]
See also[edit]
- Clock position
- List of orbits
Notes and references[edit]
- ^ U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. Mill Valley, CA: University Science Books. p. 729. ISBN 0-935702-68-7.
- ^ Explanatory Supplement (1992), p. 724.
- ^ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. p. 88. ISBN 0-943396-35-2.
- ^ Kreider, J. F. (2007). «Solar Energy Applications». Environmentally Conscious Alternative Energy Production. pp. 13–92. doi:10.1002/9780470209738.ch2. ISBN 9780470209738.
- ^ Schowengerdt, R. A. (2007). «Optical radiation models». Remote Sensing. pp. 45–88. doi:10.1016/B978-012369407-2/50005-X. ISBN 9780123694072.
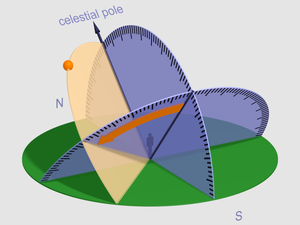
Небесной сферой называется сфера произвольного радиуса, с центром в произвольной точке пространства, на которую спроектированы светила и параллельно перенесены в ее центр основные направления и плоскости Земли и наблюдателя на ней.
В зависимости от расположения центра сферы она называется: геоцентрической – центр совпадает с центром Земли; гелиоцентрической – центр находится в центре Солнца; топоцентрической – центр находится на поверхности Земли.
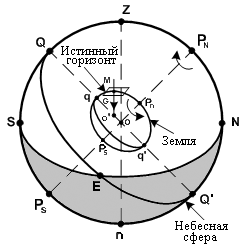
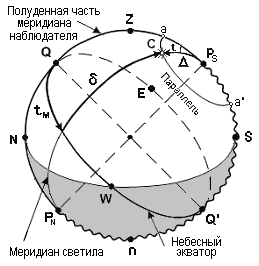
Для Земли основным направлением является ее ось, а основной плоскостью – экватор. Для места наблюдателя на Земле основным направлением является направление силы тяжести в точке М, которое называют отвесной линией. Основной плоскостью места наблюдателя является истинный горизонт – плоскость касательная к поверхности Земли в точке М, т. е. плоскость перпендикулярная отвесной линии. Долгота точки (М) λм определяет основную плоскость, которая называется меридианом наблюдателя.
Параллельный перенос отвесной линии точки М из точки О1 в точку О (центр небесной сферы) определяет отвесную линию Zn небесной сферы. Точка Z называется зенитом наблюдателя (место наблюдателя на сфере), точка n – надиром. Линия параллельная оси Земли pnps называется осью мира PNPS , причем точки PN и PS называются полюсами мира.
Плоскость истинного горизонта в точке М на Земле, принесенная в центр сферы дает в сечении со сферой большой круг NESW, который называется истинным горизонтом и он делит сферу на надгоризонтную с точкой Z и подгоризонтную с точкой n части.
Плоскость экватора Земли qq, принесенная в центр сферы, дает в сечении со сферой большой круг QQ, который называется небесным экватором. Он делит сферу на северную с точкой PN и южную – PS части.
Плоскость географического меридиана наблюдателя pnMqps, перенесенная в центр сферы, дает в сечении со сферой большой круг ZPNNQnPSSQ, который называется меридианом наблюдателя. Он делит сферу на восточную с точкой Е и западную с точкой W части.
Ось мира PNPS делит меридиан наблюдателя на полуденную часть, включающую точку Z (PNZPS) и полуночную часть, включающую точку n (PNnPS волнистая линия).
Полюс мира, находящийся в надгоризонтной части сферы называется повышенным полюсом. Его наименование всегда одноименно с широтой места М на Земле.
Если из центра сферы провести направления на светила, то на ее поверхности получим точки С называемые видимыми местами светил.
В мореходной астрономии применяются следующие системы сферических прямоугольных координат небесной сферы: горизонтная, 1-ая экваториальная, 2-ая экваториальная и эклиптическая. Осями координат являются основные круги.
Горизонтная система координат. Эта система необходима для выполнения измерений навигационных параметров (высота светила или азимут на светило) на Земле. Координаты светила зависят от видимого суточного вращения небесной сферы (времени) и координат места наблюдателя на Земле.
Основное направление – отвесная линия.
Основные круги – меридиан наблюдателя и истинный горизонт.
Меридианом наблюдателя называется большой круг на небесной сфере, плоскость которого параллельна плоскости земного меридиана места наблюдателя.
Истинным горизонтом называется большой круг, плоскость которого перпендикулярна отвесной линии.
Вспомогательные круги – вертикал и альмукантарат.
Вертикалом называется половина большого круга, проходящая через точки зенит (Z,) надир(n) и светило (заданную точку).
Альмукантаратом называется малый круг, плоскость которого параллельна плоскости истинного горизонта.
Координаты – высота и азимут.
Высотой (h) называется дуга вертикала светила от истинного горизонта до светила в пределах от –90° до +90°. Знак минус для светил находящихся в подгоризонтной части сферы.
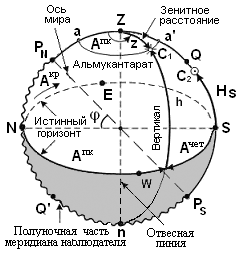
Высота светил, находящихся на меридиане наблюдателя, называется меридиональной высотой. Она обозначается буквой H и имеет наименование точки истинного горизонта, над которой находится светило N или S (рис. 2, светило С2).
В мореходной астрономии используются три системы счета азимута:
Круговым азимутом (А кр ) называется дуга истинного горизонта от точки N до вертикала светила, отсчитываемая в сторону Е, в пределах от 0° до 360°.
Полукруговым азимутом (А пк ) называется дуга истинного горизонта от полуночной части меридиана наблюдателя (N или S) до вертикала светила, отсчитываемая в сторону Е или W, в пределах от 0° до 180° и имеет наименование: первая буква совпадает с наименованием широты места наблюдателя, вторая с направлением отсчета или с наименованием полусферы, где находится светило.
Четвертным азимутом (А чет ) называется дуга истинного горизонта от точки N или S до вертикала светила, отсчитываемая в сторону Е или W, в пределах от 0° до 90° и имеет наименование: первая буква совпадает с наименованием точки начала отсчета, вторая с направлением отсчета.
Кроме сферических координат светило может быть задано в полярных координатах относительно точки Z (зенита). Координатами являются зенитное расстояние и азимут.
Зенитным расстоянием называется дуга вертикала светила от точки зенит до светила в пределах от 0° до 180°.
Зенитное расстояние связано с высотой соотношением
Азимут определяется как угол при зените в полукруговом счете.
Первая экваториальная система координат. В этой системе одна координата светила не зависит от координат места наблюдателя, а вторая зависит от долготы места и времени.
Примечание. Следует помнить, что меридиан наблюдателя непосредственно связан с меридианом места наблюдателя, т. е. долготой места.
Основное направление – ось мира.
Основные круги – меридиан наблюдателя и небесный экватор.
Небесным экватором называется большой круг, плоскость которого перпендикулярна оси мира.
Вспомогательные круги – небесные меридианы и параллели.
Небесным меридианом называются половина большого круга, проходящего через полюса мира и заданное светило или точку на небесной сфере.
Небесными параллелями называются малые круги, плоскость которых параллельна плоскости небесного экватора.
Координаты – местный часовой угол и склонение.
Местным часовым углом (tм) называется дуга небесного экватора от полуденной точки меридиана наблюдателя до меридиана светила, отсчитываемая в сторону W в пределах от 0° до 360°.
Так как отсчет часового угла ведется от меридиана наблюдателя, а он связан с меридианом места, то все часовые углы являются местными
Такой счет часовых углов называют астрономическим, и он имеет наименование W. Обычно для этого счета часовых углов наименование не пишут (в МАЕ все часовые углы W). При решении параллактического треугольника с помощью таблиц, используют часовые углы в практическом счете.
Практическим местным часовым углом называется дуга небесного экватора от полуденной точки меридиана наблюдателя до меридиана светила, отсчитываемая в сторону W или Е в пределах от 0° до 180°. Наименование часового угла одноименно с направлением отсчета.
Из всех местных часовых углов выделяется часовые углы для наблюдателя, находящегося на меридиане Гринвича ( TМ=0°), которые называют гринвичскими часовыми углами.
Склонением () называется дуга меридиана светила от небесного экватора до светила в пределах от 0° до 90°.Наименование склонения одноименно с полюсом мира, к которому производится отсчет.
Кроме сферических координат светило может быть задано в полярных координатах относительно точки повышенного полюса мира. Координатами являются полярное расстояние и часовой угол.
Полярным расстоянием () называется дуга меридиана светила от повышенного полюса мира до светила в пределах от 0° до 180° с наименованием полюса мира, к которому производится отсчет (разноименно с наименованием повышенного полюса мира).
Часовой угол определяется как угол при повышенном полюсе мира в астрономическом или практическом счете.
Вторая экваториальная система координат. В этой системе координаты светила не зависят от суточного движения светил (времени) и места наблюдателя на Земле. Поэтому 2-ая экваториальная система координат подобна географической системе координат.
Основным направлением является ось мира.
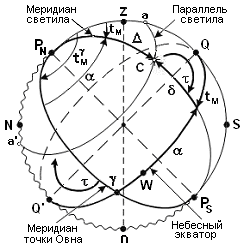
Основные круги – небесный экватор и меридиан точки Овна ().
Точкой Овна () называется точка на небесном экваторе, в момент перехода центра Солнца из южной в северную полусферу при его видимом годовом движении.
Положение точки Овна не зависит от суточного вращения небесной сферы. Поэтому в 1-ой экваториальной системе координат положение точки Овна определяется местным часовым углом точки Овна (t м).
Вспомогательные круги те же, что в 1-ой экваториальной системе – небесные меридианы и небесные параллели.
Координатами являются – прямое восхождение и склонение
Прямым восхождением () называется дуга небесного экватора от точки Овна до меридиана светила, отсчитываемая в сторону обратную W часовым углам (или в сторону видимого годового движения Солнца) в пределах от 0° до 360°.
При расчете местных часовых углов светил с помощью МАЕ вместо прямого восхождения используется координата звездное дополнение.
Звездным дополнением () называется дуга небесного экватора от точки Овна до меридиана светила, отсчитываемая в сторону противоположную W часовых углов в пределах от 0° до 360°.
Склонение () то же, что в 1-ой экваториальной системе.
Так как 1-ая и 2-ая экваториальные системы отличаются только в одной координате (см. рис. 4), то переход от одной системе к другой выражается формулой
Эта формула называется основной формулой времени.
(2-4). Параллактический треугольник и его решение, Графическое решение задач на небесной сфере, Таблицы ТВА-52 , Вычислительная схема и правила вычисления h и А.
Параллактическим треугольником называется сферический треугольник, в вершинах которого находятся точки повышенного полюс мира, зенита и светила.
Элементами этого треугольника являются:
сторона ZC равная 90°–h;
угол в точке Z равный азимуту светила в полукруговом счете;
угол в точке повышенного полюса мира PN равный tм светила в практическом счете;
параллактический угол q.
При использовании основных формул сферической тригонометрии элементы треугольника должны быть всегда меньше 180°.
Основное достоинство параллактического треугольника заключается в том, что он связывает координаты светила с географическими координатами места наблюдателя.
Для решения сферического треугольника должны быть заданы 3 из 6 его элементов. Это сторона равная 90°– φ, сторона равная 90°– и угол между ними равный tм в практическом счете.
Для получения значения высоты светила (h) применим формулу косинусов к стороне ZC
sinh= sinφ sin + cosφ cos costм (3)
Для получения значения азимута светила (А) применим формулу котангесов (4-х рядом лежащих элементов) к углу А
Можно получить другие формулы расчета азимута, используя в качестве аргумента высоту светила (h) полученную по формуле (3).
Расчет азимута по аргументам φ, и h.
Для получения значения азимута светила используем формулу косинусов к углу А.
Расчет азимута по аргументам , tм и h.
Для получения значения азимута светила используем формулу синусов
Азимут получим в пределах от 0° до 90°, т. е. в четвертном счете. Правила определения наименования азимута, приведенные в МТ, достаточно сложные. Формулу обычно используют при фактических наблюдениях с одновременной фиксацией (с помощью гирокомпаса) наименования четверти горизонта, в которой измерена высота светила .
Решение параллактического треугольника выполняется по формулам сферической тригонометрии на калькуляторе или с помощью таблиц.
В настоящее время основным способом решения параллактического треугольника является его решение по формулам с помощью калькулятора, а вспомогательным – с помощью таблиц.
Теперь можно рассчитать кажущееся положение Солнца: высотаh и азимут А — в любой точке на широте φ в любое время суток в соответствии с углом τ и в любое время года в соответствии с углом склонения δ.
Мы же приведем результат в простейшем виде:
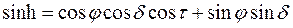
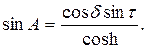
где φ — географическая широта ;
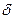
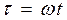
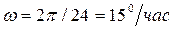
где 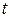
Очевидно, в полдень высота Солнца h максимальна, h = 90° -φ +δ.
Во время летнего солнцестояния высота Солнца в нашей местности в момент кульминации составляет: h = 90˚- φ + δ☼ = 90˚ — 56,5˚ +23,5˚=57˚, во время зимнего солнцестояния h = 90˚- φ + δ☼= 90˚ — 56,5˚ — 23,5˚=10˚, а в дни равноденствий, когда Солнце находится на небесном экваторе- δ☼=0, h = 33,5˚.
Часовой угол захода(восхода) Солнца
При восходе и заходе Солнца h = 0. Из уравнения (3.4) видно, что это произойдет при углах τ в каждом из двух случаев, близких к полудню, для которых при h = 0 из уравнение имеем:
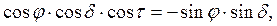
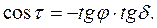
Тогда часовой угол захода (восхода) Солнца для горизонтальной поверхности
τ=arccos(-tg 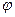
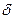
ЛЕКЦИЯ 5
Тема: Фотоэлектрические преобразование солнечной энергии
В этой системе основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.
Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.
Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.
Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии азимуты отсчитываются от точки севера.)
Первая экваториальная система координат
В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.
Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.
Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.
Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0 h до +12 h ) к западу и от 0° до −180° (от 0 h до −12 h ) к востоку.
Вторая экваториальная система координат
В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение β (реже — полярное расстояние p). Другой координатой является прямое восхождение α.
Прямым восхождением (RA,α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере).
RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор в весеннее равноденствие.
Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу.
- Объект на небесном экваторе имеет склонение 0°
- Склонение северного полюса небесной сферы равно +90°
- Склонение южного −90°
У склонения всегда указывается знак, даже если склонение положительно.
Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > 90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ [1]
Эклиптическая система координат
В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.
Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.
Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.
Галактическая система координат
В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.
Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.
Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу.
Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.
Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).
Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:
Изменения координат при вращении небесной сферы
Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.
История и применение
Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.
Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.
Использование различных систем координат
Горизонтальная система координат используется для определения направления на светило с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.
Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.
Вторая экваториальная система координат является общепринятой в астрометрии. В этой системе составляются звёздные карты и описываются положения светил в каталогах.
Эклиптическая система координат используется в теоретической астрономии при определении орбит небесных тел.

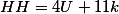
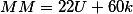
mod24)
mod60)
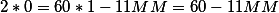
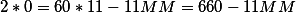
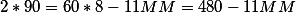
=60*8-11MM=480-11MM)