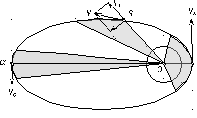
Сегодня речь пойдет о конфигурации планет.
Конфигурация — характерное взаимное положение Солнца, планет, других небесных тел Солнечной системы на небесной сфере.
Будем называть планеты нижними, если они расположены ближе к Солнцу, чем Земля. Остальные планеты будут верхними – они расположены дальше нашей планеты от Солнца.
Планета может расположиться так, что Земля, Солнце и указанная планета находятся на одной линии. При этом может оказаться, что Солнце расположилось между Землей и рассматриваемой планетой. Такое расположение будем называть верхним соединением. Если же планета оказалась между Землей и Солнцем – то это уже нижнее соединение. Также может быть, что Земля находится между верхней планетой и Солнцем – тогда речь пойдет о противостоянии, или оппозиции.
Элонгация — одна из конфигураций планет, такое положение планеты, при котором её угловое расстояние от Солнца максимально для земного наблюдателя. Различают восточную и западную элонгацию (планета находится, соответственно, к востоку и к западу от Солнца). Об элонгации имеет смысл говорить только для Венеры и Меркурия; наилучшие условия для наблюдения этих планет наступают именно вблизи элонгаций. Из-за того, что орбиты планет не вполне круговые, угловое расстояние от Солнца в момент элонгации может быть разным, для Меркурия — от до
, для Венеры — около
.
Квадратура — в астрономии такая конфигурация Луны или верхней планеты (то есть планеты, более удалённой от Солнца, чем Земля) относительно Земли и Солнца, когда угол планета-Земля-Солнце равен . Если светило при этом находится к востоку от Солнца, конфигурация называется восточной квадратурой, к западу — западной квадратурой.
Сидерический период — это время совершения полного оборота какого-либо тела (планеты, кометы, астероида или искусственного спутника) вокруг главного тела (Солнца или др. планеты для спутника планеты) относительно неподвижных звёзд. Сидерический период также называют годом. Например, Меркурианский год, Юпитерианский год, и т. п.
Синодический же период — это время наблюдения с Земли совершения полного оборота планеты вокруг Солнца или Луны (искусственного спутника) вокруг Земли относительно Солнца ; промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.
Будем помнить также и о том, что орбиты планет не круговые. Это эллипсы, причем Солнце находится в одном из главных фокусов орбиты планеты.
Перигелий — ближайшая к Солнцу точка орбиты планеты или иного небесного тела Солнечной системы.
Антонимом перигелия является афелий (апогелий) — наиболее удалённая от Солнца точка орбиты. Воображаемую линию между афелием и перигелием называют линией апсид.
Названия апоцентров меняются: эти точки получают конкретные наименования но названию центрального тела, и некоторые из них приведены в нижеследующей таблице:
Задача 9.
| Центральное тело | Греческое название | Наименование перицентра | Наименование апоцентра |
| Солнце | Гелиос | перигелий | афелий |
| Земля | Гея | перигей | апогей |
| Венера | Геспер | перигесперий | апогесперий |
| Марс | Арес | периарий | апоарий |
| Сатурн | Кронос | перикроний | апокроний |
| Луна | Селена | периселений | апоселений |
Теперь обратимся к математике и разберемся, что же такое эксцентрисистет. Будем говорить об эксцентриситете эллипса, поскольку нас пока больше интересуют орбиты планет.
Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси; обозначив эксцентриситет буквой , получаем:
Так как , то
, т. е. эксцентриситет каждого эллипса меньше единицы. Заметим, что
, поэтому
Или
И
Следовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к единице, тем меньше , тем меньше, следовательно, отношение
; значит, чем больше эксцентриситет, тем более эллипс вытянут. В случае окружности
и
.
Радиус перигелия рассчитывается по формуле:
где:
— большая полуось;
— эксцентриситет орбиты.
Скорость в перигелии рассчитывается по формуле:
где:
— гравитационная постоянная;
— масса Солнца;
— большая полуось;
— эксцентриситет орбиты.
Афелийное расстояние рассчитывается по формуле
Следовательно, большая полуось орбиты планеты является средним ее расстоянием от Солнца
Cидерические периоды обращения и
двух планет связаны с их средними расстояниями
и
от Солнца третьим законом Кеплера
Если дается в годах и
— в астрономических единицах, то, принимая для Земли
год и
а. е., получим для любой планеты
Средняя орбитальная, или круговая, скорость планеты
всегда выражается в км/с. Так как обычно задается в астрономических единицах (1 а. е.=
км) и T— в годах (1 год=
с), то
Подставляя , получим:
Где скорость планеты теперь выражена в км/с.
Средняя продолжительность синодического периода обращения планеты связана с сидерическим периодом
уравнением синодического движения: для верхних планет
для нижних планет
где — сидерический период обращения Земли, равный 1 звездному году.
Задача 1.
Найти перигельное и афелийное расстояния, сидерический и синодический периоды обращения, а также круговую скорость малой планеты Поэзии, если большая полуось и эксцентриситет ее орбиты равны 3,12 а. е. и 0,144.
Перигельное расстояние, а.е.
афелийное расстояние, а.е.
Сидерический период обращения
а так как а. е., то планета верхняя и поэтому ее синодический период обращения
вычисляется по формуле
при году:
Круговая скорость, км/с:
Задача 2.
Вычислить перигельное и афелийное расстояния планет Сатурна и Нептуна, если их средние расстояния от Солнца равны 9,54 а. е. и 30,07 а. е., а эксцентриситеты орбит— 0,054 и 0,008.
Перигельное расстояние Сатурна, а.е.
афелийное расстояние Сатурна, а.е.
Перигельное расстояние Нептуна, а.е.
афелийное расстояние Нептуна, а.е.
Ответ: а.е.,
а.е.,
а.е.,
а.е.
Задача 3.
Какая из двух планет — Нептун (а = 30,07 а.е., ) или Плутон (а = 39,52 а. е.,
) — подходит ближе к Солнцу? В скобках даны большая полуось и эксцентриситет орбиты планеты.
Нужно сравнить перигельные расстояния, причем для Нептуна мы его уже вычислили: а.е. Вычислим для Плутона:
Таким образом, Плутон ближе подходит к Солнцу.
Задача 4.
Найти эксцентриситет орбиты и перигельное расстояние планеты Марса и астероида Адониса, если у Марса большая полуось орбиты равна 1,52 а. е. и наибольшее расстояние от Солнца 1,66 а. е., а у Адониса соответственно 1,97 а. е. и 3,50 а. е. Указать, какая из этих двух планет подходит ближе к Солнцу.
Опять определим перигельные расстояния. Наибольшие расстояния от Солнца нам известны – афелийные. Тогда для Марса
Следовательно, перигельное расстояние Марса равно
Для Адониса
Следовательно, перигельное расстояние Адониса равно
Таким образом, Адонис подходит ближе к Солнцу.
Ответ: ,
а.е. ,
,
а.е.
Задача 5.
На каком среднем и наибольшем гелиоцентрическом расстоянии движутся малые планеты Икар и Симеиза, если у Икара перигельное расстояние и эксцентриситет орбиты равны 0,187 а. е. и 0,827, а у Симеизы — 3,219 а. е. и 0,181? У какой из этих планет радиус-вектор изменяется в больших пределах, абсолютно и относительно?
Так как афелийное расстояние у Симеизы больше, то радиус-вектор ее длиннее (абсолютно). Но, так как , то относительно радиус-вектор Икара больше изменяется.
Задача 6.
Вычислить периоды обращения вокруг Солнца планеты Венеры и астероида Европы, у которых средние гелиоцентрические расстояния соответственно равны 0,723 а. е. и 3,10 а. е.
Сидерический период Венеры равен:
Или 224,5 суток.
Сидерический период астероида Европы равен:
Ответ: сидерический период Венеры равен 0,615 года или 224,5 суток, а у Европы 5,458 года.
Задача 7.
Определить периоды обращения вокруг Солнца малой планеты Аполлона и кометы Икейи, если обе они проходят вблизи Солнца почти на одинаковых расстояниях, равных у Аполлона 0,645 а. е., а у кометы 0,633 а. е., но их орбиты имеют эксцентриситеты 0,566 и 0,9933 соответственно.
Определим большие полуоси орбит Аполлона и кометы Икейи:
Тогда сидерический период Аполлона
Тогда сидерический период Икейи
Ответ: года,
лет.
Задача 8.
Первый спутник планеты Юпитера — Ио обращается вокруг нее за 42ч28м на среднем расстоянии в 421 800 км. С какими периодами обращаются вокруг Юпитера его спутники Европа и Ганимед, большие полуоси орбит которых равны 671,1 тыс. км и 1070 тыс. км?
Для спутников справедлив закон Кеплера. Применим его для Европы:
Период 42ч28м= ч.
А теперь то же самое для Ганимеда:
Ответ: Период Европы 85,23 ч, или 3д 55, период Ганимеда 171,59 ч, или 7д 15
Задача 9.
Найти средние расстояние от Сатурна его спутников Мимаса и Реи, обращающихся вокруг планеты с периодами в 22ч37м и 4д,518. Самый крупный спутник планеты — Титан, обращается за 15д,945 по орбите с большой полуосью в 1221 тыс. км.
Переведем периоды в часы: период Мимаса 22,62 ч, период Реи 108,43 ч, период Титана 382, 68 ч.
Применяем закон Кеплера для Титана и Мимаса:
То же для Реи:
Ответ: большая полуось Мимаса 185,27 тыс. км, Реи 526,7 тыс. км.
Как рассчитать большую полуось?
Таким образом, большая полуось, обозначенная а, определяется выражением a=12(r1+r2) a = 1 2 ( r 1 + r 2 ) . Рис. 13.19 Эллипс перелета имеет перигелий на орбите Земли и афелий на орбите Марса.
Как найти большую полуось?
Большая полуось составляет половину большой оси. Чтобы найти длину большой полуоси, мы можем использовать следующую формулу: Длина большой полуоси = (AF + AG) / 2, где A — любая точка эллипса, а F и G — фокусы эллипса.
Что такое большая полуось орбиты?
Большая полуось —половина большой оси и равна расстоянию от центра эллипса до одного конца эллипса. Это также среднее расстояние планеты от Солнца в одном фокусе.
Как найти большую и малую полуоси?
(х/а)**2 +(у/б)**2 = 1, a — большая полуось, b — малая полуось, и a ≥ b без ограничения общности, поскольку можно просто поменять местами имена, если a < b. Если a = b, то эллипс специализируется на круге с радиусом a = b. Два фокуса эллипса имеют особое геометрическое значение.
Смотрите также, почему малайский тигр находится под угрозой исчезновения
Как найти большую и малую полуоси эллипса?
Что такое большая полуось в физике?
Большая полуось это среднее значение максимального и минимального расстояний и. эллипса из фокуса — то есть расстояний от фокуса до концов большой оси: В астрономии эти крайние точки называются апсидами.
Как найти большую полуось по заданному перигелию?
Учитывая, что орбита представляет собой эллипс с большой полуосью a и эксцентриситетом e, тогда расстояние в афелии равно a(1−e), а расстояние в афелии равно a(1+e). Сложение двух вместе дает 2a . Следовательно, расстояние по большой полуоси равно половина суммы перигелийного и афелиевого расстояний.
Как найти малую полуось большой полуоси?
Большая и малая полуоси составляют половину длины большой и малой осей. Для вычисления их длин используйте один из формулы на большой / малой оси эллипса и разделить на два.
Что такое большая полуось МКС?
Международная космическая станция имеет период обращения 91,74 минуты, следовательно, большая полуось 6738 км [1].
Какова большая полуось SO 2 в AU?
0,99892124 AU 2015 SO 2
| Открытие | |
|---|---|
| перигелий | 0,890962 AU (133,2860 Гм) |
| Большая полуось | 0,99892124 а.е. (149,436491 Гм) |
| Эксцентриситет | 0.108076 |
| Орбитальный период | 1,00 года (364,66602 дн.) |
Что такое большая полуось эллипса викторины?
Каждый эллипс имеет значение эксцентриситета от 0 (окружность) до 1 (по сути, плоская линия, называемая параболой). Самая длинная ось эллипса называется большой осью. Самая короткая ось называется малой осью. Половина майора ось называется большой полуосью.
Как найти эксцентриситет большой полуоси?
Эксцентриситет e можно рассчитать по формуле взяв расстояние от центра до фокуса и разделив его на расстояние по большой полуоси. Предельными случаями являются окружность (e=0) и отрезок прямой (e=1).
Какая формула для орбитального периода?
Формула: Р2=ка3 где: P = период обращения, измеренный в единицах времени. a = среднее расстояние до объекта, измеренное в единицах расстояния.
Какова большая полуось Земли в астрономических единицах?
Орбитальные данные планет и карликовых планет
| планета | Большая полуось (AU) | Наклонение экватора к орбите (°) |
|---|---|---|
| земной шар | 1.000 | 23.4 |
| Марс | 1.5273 | 25.2 |
| Юпитер | 5.2028 | 3.1 |
| Сатурн | 9.5388 | 26.7 |
Что такое большая полуось в науке?
половина большой оси эллипса, которую одно небесное тело описывает вокруг другого, как планета вокруг солнца или спутник вокруг планеты, что эквивалентно среднему расстоянию между двумя телами. …
Как найти период обращения в АС?
Если размер орбиты (а) выразить в астрономических единицах (1 а.е. равна среднему расстоянию между Землей и Солнцем), а период (Р) измерять в годах, то Третий закон Кеплера гласит, что P2 = a3. где P — в земных годах, a — в а.е., а M — масса центрального объекта в единицах массы Солнца.
Как вы решаете для Aphelions?
Расстояние перигелия P=a(1−e) и расстояние афелия А=а(1+е) где e=0,875 — эксцентриситет. Это дает перигелийное расстояние 2,375 а.е. и афелийное расстояние 35,625 а.е.
Что такое малая полуось в астрономии?
Малая полуось b равна половина наименьшего диаметра эллипса. Вместе с большой полуосью а и эксцентриситетом е он образует набор связанных величин, полностью описывающих форму эллипса: b2 = a2(1-e2)
См. также, чем занимается эколог водно-болотных угодий.
Что такое малая полуось Меркурия?
Параметры орбиты
| Меркурий | Соотношение (Меркурий/Земля) | |
|---|---|---|
| Большая полуось (106 км) | 57.909 | 0.387 |
| Звездный период обращения (дни) | 87.969 | 0.241 |
| Тропический орбитальный период (дни) | 87.968 | 0.241 |
| Перигелий (106 км) | 46.002 | 0.313 |
Чему равен его малый радиус или малая полуось?
Малая полуось это длина кратчайшего радиуса эллипса, то есть наименьшее расстояние между центром эллипса и периметром эллипса. при b≤a малая полуось равна b.
Что понимают под большой полуосью эллипса?
Большая полуось а равна половина наибольшего диаметра эллипса. Вместе с малой полуосью b и эксцентриситетом e он образует набор связанных величин, полностью описывающих форму эллипса: b2 = a2(1-e2)
Каково значение большой полуоси?
Таким образом, большая полуось, обозначенная а, определяется выражением a=12(r1+r2) a = 1 2 ( r 1 + r 2 ) . Рис. 13.19 Эллипс перелета имеет перигелий на орбите Земли и афелий на орбите Марса.
Где приземлился CZ 5B?
Изображение Индийского океана с камеры видеонаблюдения/SpaceNews. Итог: китайская ракета «Великий поход 5B», которая успешно запустила модуль космической станции «Тяньхэ» 29 апреля 2021 года, совершила неконтролируемый повторный вход обратно в атмосферу Земли и в конечном итоге приземлилась 8 мая. в Индийском океане к западу от Мальдивских островов.
Орбита МКС эллиптическая?
МКС вращается вокруг Земли в среднем на высоте 400 км (248 миль) над поверхностью, перемещаясь со скоростью примерно 8 км в секунду (17 900 миль в час). … Орбиты имеют эллиптическую (овальную) форму., но большинство космических аппаратов, вращающихся вокруг Земли, движутся по орбитам, максимально приближенным к окружности, чтобы поддерживать постоянную высоту (высоту) над Землей.
Какова большая полуось SO 102 в AU?
После поправки на так называемый «эффект наклона» большие полуоси оказываются равными 960 а.е. для S2 и 815 а.е. для С0-102.
Смотрите также, каковы два основных компонента клеточных мембран?
Как рассчитывается P2 a3?
P2(в годах) = a3(в а.е.)/М(в солнечных массах), где P — период обращения, a — большая полуось орбиты, а M — сумма масс двух объектов.
Как рассчитать АУ?
Для общего сведения можно сказать, что одна астрономическая единица (а.е.) представляет собой среднее расстояние между Землей и нашим Солнцем. AU составляет примерно 93 миллиона миль (150 миллионов км). Это примерно 8 световых минут. Точнее, одна астрономическая единица (AU) = 92 955 807 миль (149 597 871 км).
Что такое викторина по большой полуоси?
Большая полуось. Расстояние от центра до края эллипса по большая ось. Малая полуось. Расстояние от центра до края эллипса по малой оси.
Что такое перигелий в астрономии?
: точка, ближайшая к в солнце на пути вращающегося небесного тела (например, планеты) — ср. афелий. Другие слова из слова перигелий Примеры предложений Узнайте больше о перигелии.
Что такое эксцентриситет в астрономии?
Эксцентриситет эллиптической орбиты равен мера величины, на которую он отклоняется от окружности; его находят путем деления расстояния между фокальными точками эллипса на длину большой оси.
Какова формула эксцентриситета?
Эксцентриситет — это в основном отношение расстояний точки эллипса от фокуса и директрисы. Если расстояние фокуса от центра эллипса равно «с», а расстояние от конца эллипса до центра равно «а», то эксцентриситет e = c/a.
Как рассчитать эксцентриситет орбиты?
Формула для определения эксцентриситета эллипса: расстояние между фокусами, деленное на длину большой оси.
Как рассчитать перигелий и афелий с эксцентриситетом?
a = большая полуось и e = эксцентриситет. Афелий = а(1 + е); перигелий = а(1 – е). Сумма дает большую ось 2а, а разница составляет 2ае. Итак, e = сумма/разность.
Как найти орбиту спутника?
Как видно из уравнения v = SQRT(G * Mцентральный / Р), масса центрального тела (земли) и радиус орбиты влияют на орбитальную скорость. Радиус орбиты, в свою очередь, зависит от высоты спутника над землей. 2.
Связь между эксцентриситетом, большой и малой полуосью
Эллипс: как вычислить большую полуось, малую полуось и эксцентриситет в геодезической съемке.
Основы эллипса — взаимосвязь между большой полуосью, малой полуосью, математический класс 11
Третий закон Кеплера, перигелийное расстояние Комета Галлея
1. Теоретическая разрешающая способность телескопа:
, где λ – средняя длина световой волны (5,5·10-7 м), D – диаметр объектива телескопа, или
, где D – диаметр объектива телескопа в миллиметрах.
2. Увеличение телескопа:
, где F – фокусное расстояние объектива, f – фокусное расстояние окуляра.
3. Высота светил в кульминации:
высота светил в верхней кульминации, кульминирующих к югу от зенита ( ):
, где – широта места наблюдения, – склонение светила;
высота светил в верхней кульминации, кульминирующих к северу от зенита ( ):
, где – широта места наблюдения, – склонение светила;
высота светил в нижней кульминации:
, где – широта места наблюдения, – склонение светила.
4. Астрономическая рефракция:
приближенная формула для вычисления угла рефракции, выраженного в секундах дуги (при температуре +10°C и атмосферном давлении 760 мм. рт. ст.):
, где z – зенитное расстояние светила (для z
5. Время:
звездное время:
, где – прямое восхождение какого-либо светила, t – его часовой угол;
среднее солнечное время (местное среднее время):
Tm=T+, где T – истинное солнечное время, – уравнение времени;
всемирное время:
, где – долгота пункта с местным средним временем Tm, выраженная в часовой мере, T0 – всемирное время в этот момент;
поясное время:
, где T0 – всемирное время; n – номер часового пояса (для Гринвича n=0, для Москвы n=2, для Красноярска n=6);
декретное время:
или
6. Формулы, связывающие сидерический (звездный) период обращения планеты T с синодическим периодом ее обращения S:
для верхних планет:
;
для нижних планет:
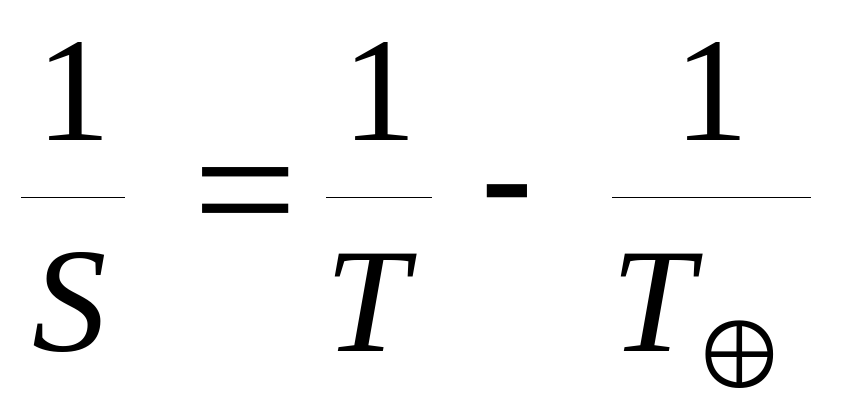
7. Третий закон Кеплера:
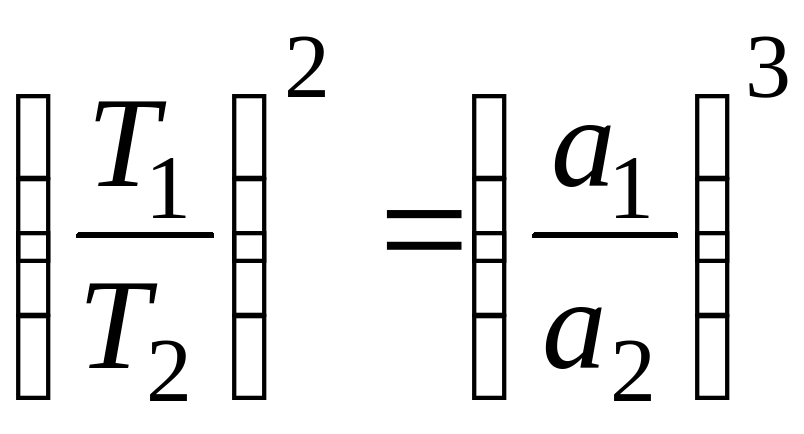
8. Закон всемирного тяготения:
, где m1 и m2 – массы притягивающихся материальных точек, r – расстояние между ними, G – гравитационная постоянная.
9. Третий обобщенный закон Кеплера:
, где m1 и m2 – массы двух взаимно притягивающихся тел, r – расстояние между их центрами, Т – период обращения этих тел вокруг общего центра масс, G – гравитационная постоянная;
для системы Солнце и две планеты:
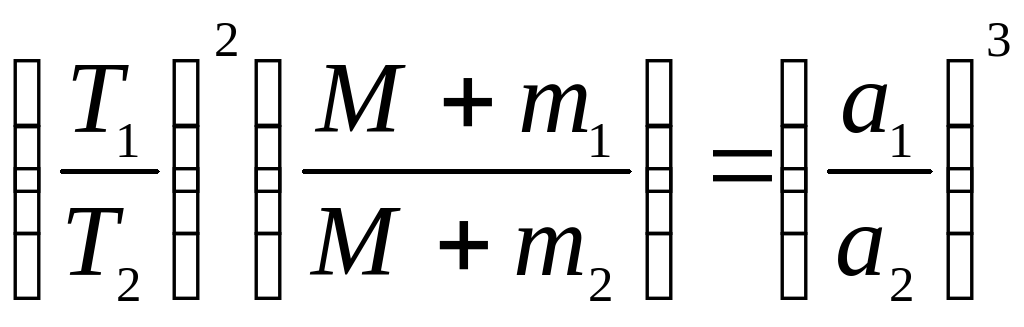
для систем Солнце и планета, планета и спутник:
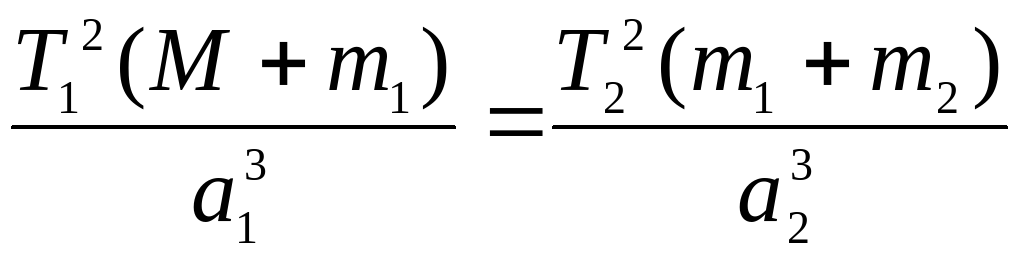
при M m1, а m1 m2,
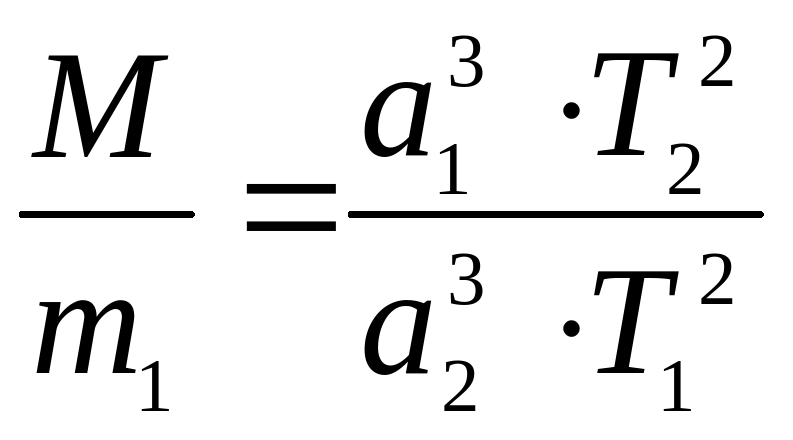
10. Линейная скорость движения тела по параболической орбите (параболическая скорость):
, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки параболической орбиты.
11. Линейная скорость движения тела по эллиптической орбите в избранной точке:
, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки эллиптической орбиты, a – большая полуось эллиптической орбиты.
12. Линейная скорость движения тела по круговой орбите (круговая скорость):
, где G – гравитационная постоянная, M – масса центрального тела, R – радиус орбиты, vp – параболическая скорость.
13. Эксцентриситет эллиптической орбиты, характеризующий степень отклонение эллипса от окружности:
, где c – расстояние от фокуса до центра орбиты, a – большая полуось орбиты, b – малая полуось орбиты.
14. Связь расстояний перицентра и апоцентра с большой полуосью и эксцентриситетом эллиптической орбиты:
, , , где rП – расстояния от фокуса, в котором находится центральное небесное тело, до перицентра, rА – расстояния от фокуса, в котором находится центральное небесное тело, до апоцентра, a – большая полуось орбиты, e – эксцентриситет орбиты.
15. Расстояние до светила (в пределах Солнечной системы):
, где R – экваториальный радиус Земли, ρ0– горизонтальный параллакс светила, выраженный в секундах дуги,
или , где D1 и D2 – расстояния до светил, ρ1 и ρ2 – их горизонтальные параллаксы.
16. Радиус светила:
, где ρ – угол, под которым с Земли виден радиус диска светила (угловой радиус), R – экваториальный радиус Земли, ρ0– горизонтальный параллакс светила.
17. Расстояние до звезд:
в парсеках: , где – годичный параллакс звезды, выраженный в радианах;
в астрономических единицах: , где – годичный параллакс звезды, выраженный в секундах дуги;
в километрах: , где – годичный параллакс звезды, выраженный в секундах дуги, a – средний радиус (большая полуось) земной орбиты.
18. Связь блеска звезды и ее звездной величины (формула Погсона):
, где I1 – освещенность, создаваемая звездой, звездная величина которой равна m1, и I2 – освещенность, создаваемая другой звездой, звездная величина которой равна m2.
19. Абсолютная звездная величина:
, где m – видимая звездная величина, R – расстояние до звезды в парсеках.
20. Закон Стефана–Больцмана:
ε=σT4, где ε – энергия, излучаемая в единицу времени с единицы поверхности, Т – температура (в кельвинах), а σ – постоянная Стефана–Больцмана.
21. Закон Вина:
, где λmax – длина волны, на которую приходится максимум излучения абсолютно черного тела (в сантиметрах), Т – абсолютная температура в кельвинах.
22. Закон Хаббла:
, где v – лучевая скорость удаления галактики, c – скорость света, Δλ – доплеровское смещение линий в спектре, λ – длина волны источника излучения, z – красное смещение, r – расстояние до галактики в мегапарсеках, H – постоянная Хаббла, равная 75 км / (сМпк).
4

В геометрии большая ось эллипса — это его самый длинный диаметр : отрезок линии, который проходит через центр и оба фокусы с концами в самых широких точках периметра .
Большая полуось составляет половину большой оси и, таким образом, проходит от центра через фокус и по периметру. Малая полуось эллипса или гиперболы — это отрезок прямой, который находится под прямым углом с большой полуосью и имеет один конец в центре конического участка. В частном случае окружности длины обеих полуосей равны радиусу окружности.
Длина большой полуоси a эллипса связана с длиной малой полуоси b через эксцентриситет e и прямую полуось ℓ { displaystyle ell}
b = a 1 — e 2, ℓ = a (1 — e 2), a ℓ = b 2. { displaystyle { begin {align} b = a { sqrt {1-e ^ {2}}}, \ ell = a left (1-e ^ {2} right), , a ell = b ^ {2}. end {align}}}
Большая полуось гиперболы , в зависимости от соглашения, составляет плюс или минус половина расстояние между двумя ветвями. Таким образом, это расстояние от центра до любой вершины гиперболы.
A парабола может быть получена как предел последовательности эллипсов, в которой один фокус фиксируется, а другой может перемещаться произвольно далеко в одном направлении, сохраняя ℓ { displaystyle ell}
Большая и малая оси — это оси симметрии кривой: в эллипсе малая ось является более короткой; в гиперболе это тот, который не пересекает гиперболу.
Содержание
- 1 Эллипс
- 2 Гипербола
- 3 Астрономия
- 3,1 Период обращения
- 3,2 Среднее расстояние
- 3,3 Энергия; вычисление большой полуоси из векторов состояния
- 3.4 Большая и малая полуоси планет
- 4 См. также
- 5 Ссылки
- 6 Внешние ссылки
Эллипс
Уравнение эллипса:
(x — h) 2 a 2 + (y — k) 2 b 2 = 1. { displaystyle { frac { left (xh right) ^ {2}} {a ^ {2}}} + { frac { left (yk right) ^ {2}} {b ^ {2}}} = 1.}
где (h, k) — центр эллипс в декартовых координатах, в котором произвольная точка задается как (x, y).
Большая полуось — это среднее значение максимального и минимального расстояний r max { displaystyle r _ { max}}

a = r max + r min 2. { displaystyle a = { frac {r _ { max} + r _ { min}} {2}}.}
Малая полуось эллипса — это среднее геометрическое этих расстояния:
b = r max r min. { displaystyle b = { sqrt {r _ { max} r _ { min}}}.}
эксцентриситет эллипса определяется как
e = 1 — b 2 a 2 { displaystyle e = { sqrt {1 — { frac {b ^ {2}} {a ^ {2}}}}}}

r min = a (1 — e), r max = a (1 + e) { displaystyle r _ { min} = a (1-e), r _ { max} = a (1 + e)}

Теперь рассмотрим уравнение в полярные координаты, с одним фокусом в начале координат, а другой в направлении (θ = π) — { displaystyle ( theta = pi) -}
г (1 + е соз θ) = ℓ. { displaystyle r (1 + e cos theta) = ell. ,}
Среднее значение r = ℓ / (1 — e) { displaystyle r = ell / (1- e)}



a = ℓ 1 — e 2. { displaystyle a = { ell over 1-e ^ {2}}. ,}
В эллипсе большая полуось — это среднее геометрическое расстояния от центра для фокусировки и расстояния от центра до любой директрисы.
Малая полуось эллипса проходит от центра эллипса (точка на полпути между фокусами и на линии между ними) до края эллипса. Малая полуось — это половина малой оси. Малая ось — это самый длинный отрезок прямой, перпендикулярный большой оси, который соединяет две точки на краю эллипса.
Малая полуось b связана с большой полуосью a через эксцентриситет e и прямую полуось ℓ { displaystyle ell}
b = a 1 — e 2 a ℓ = b 2. { displaystyle { begin {align} b = a { sqrt {1-e ^ {2}}} , ! \ a ell = b ^ {2}. , ! end {выровнено }}}
A парабола может быть получена как предел последовательности эллипсов, в которой один фокус фиксируется, а другой может перемещаться произвольно далеко в одном направлении, сохраняя ℓ { displaystyle ell}
Длину малой полуоси можно также найти с помощью следующей формулы:
2 b = (p + q) 2 — f 2 { displaystyle 2b = { sqrt {(p + q) ^ {2} -f ^ {2}}}}
где f — расстояние между фокусами, p и q — расстояния от каждого фокуса до любой точки эллипса.
Гипербола
Большая полуось гиперболы находится, в зависимости от соглашения, плюс или минус половина расстояния между двумя ветвями; если это a в направлении x, уравнение будет следующим:
(x — h) 2 a 2 — (y — k) 2 b 2 = 1. { displaystyle { frac { left (xh right) ^ {2}} {a ^ {2}}} — { frac { left (yk right) ^ {2}} {b ^ {2}}} = 1.}
В терминах полу -latus rectum и эксцентриситет мы имеем
a = ℓ e 2 — 1. { displaystyle a = { ell over e ^ {2} -1}.}
Поперечная ось гиперболы совпадает с большой осью.
В гиперболе — сопряженная ось или малая ось Ось длины 2 b { displaystyle 2b}

x 2 a 2 — y 2 b 2 = 1. { displaystyle { frac {x ^ {2}} {a ^ {2}}} — { frac {y ^ {2}} {b ^ {2}}} = 1.}
Малая полуось — это также расстояние от одного из фокусов гиперболы до асимптоты. Часто называемый параметром удара, он важен в физике и астрономии и позволяет измерить расстояние, на которое частица не попадет в фокус, если ее путешествие не будет нарушено телом в фокусе.
Малая полуось и большая полуось связаны через эксцентриситет следующим образом:
b = ae 2 — 1. { displaystyle b = a { sqrt {e ^ {2} -1}}.}
Обратите внимание, что в гиперболе b может быть больше a.
Астрономия
Орбитальная период
В астродинамике период обращения T малого тела, вращающегося вокруг центрального тела по круговой или эллиптической орбите, равен:
T = 2 π a 3 μ { displaystyle T = 2 pi { sqrt {a ^ {3} over mu}}}
где:
a — длина большой полуоси орбиты
μ { displaystyle mu}

. Обратите внимание, что для всех эллипсов с данной большой полуосью период обращения то же самое, несмотря на их эксцентричность.
удельный угловой момент h небольшого тела, вращающегося вокруг центрального тела по круговой или эллиптической орбите:
h = a μ (1 — e 2) { displaystyle h = { sqrt {a mu left (1-e ^ {2} right)}}}
где:
a и
μ { displaystyle mu}

В астрономии большая полуось является одной из наиболее важных орбитальных элементы орбиты вместе с его периодом обращения. Для объектов Солнечной системы большая полуось связана с периодом орбиты третьим законом Кеплера (первоначально эмпирически получено),
T 2 ∝ a 3 { displaystyle T ^ {2} propto a ^ {3} ,}
где T — период, а a — большая полуось. Эта форма оказывается упрощением общей формы для задачи двух тел, как определено Ньютоном :
T 2 = 4 π 2 G (M + m) a 3 { displaystyle T ^ {2} = { frac {4 pi ^ {2}} {G (M + m)}} a ^ {3} ,}
где G — гравитационная постоянная, M — масса центрального тела, а m — масса движущегося по орбите тела. Обычно масса центрального тела настолько больше, чем масса вращающегося тела, что m можно не принимать во внимание. Это предположение и использование типичных астрономических единиц приводит к более простой форме, которую открыл Кеплер.
Путь движущегося по орбите тела вокруг барицентра и его путь относительно его первичного элемента являются эллипсами. Большая полуось иногда используется в астрономии как расстояние между первичными и вторичными объектами, когда отношение масс первичного элемента к вторичному значительно велико (M ≫ m { displaystyle M gg m}
Среднее расстояние
Часто говорят, что большая полуось — это «среднее» расстояние между основными фокус эллипса и вращающееся тело. Это не совсем точно, потому что это зависит от того, какое среднее значение берется за основу.
Усредненное по времени значение обратной величины радиуса, r — 1 { displaystyle r ^ {- 1}}

Энергия; вычисление большой полуоси из векторов состояния
В астродинамике большая полуось a может быть вычислена из векторов орбитального состояния :
a = — μ 2 ε { displaystyle a = — { mu over {2 varepsilon}} ,}
для эллиптической орбиты и, в зависимости от соглашения, то же самое или
a = μ 2 ε { displaystyle a = { mu over {2 varepsilon}} ,}
для гиперболической траектории и
ε = v 2 2 — μ | г | { displaystyle varepsilon = {v ^ {2} over {2}} — { mu over left | mathbf {r} right |}}
(удельная орбитальная энергия ) и
μ = GM { displaystyle mu = GM ,}
(стандартный гравитационный параметр ), где:
- v — орбитальная скорость от вектора скорости движущегося по орбите объекта,
- rявляется декартовым вектором положения орбитального объекта в координатах системы отсчета, относительно которой должны быть вычислены элементы орбиты (например, геоцентрическая экваториальная для орбиты вокруг Земли или гелиоцентрическая эклиптика для орбиты вокруг Солнца),
- G — гравитационная постоянная,,
- M — масса гравитирующего тела, и
- ε { displaystyle varepsilon}
— это удельная энергия движущегося по орбите тела.
Обратите внимание, что для данного количества общей массы удельная энергия и большая полуось всегда одинаковы, независимо от эксцентриситета. или соотношение масс. И наоборот, для данной общей массы и большой полуоси общая удельная орбитальная энергия всегда одинакова. Это утверждение всегда будет верным при любых данных условиях.
Большая и полу-малая оси планет
Орбиты планет всегда приводятся в качестве ярких примеров эллипсов (первый пример Кеплера закон ). Однако минимальная разница между большой и малой полуосями показывает, что они практически круглые по внешнему виду. Эта разница (или соотношение) основывается на эксцентриситете и рассчитывается как ab = 1 1 — e 2 { displaystyle {{a} over {b}} = {1 over { sqrt {1-e ^ {2}}}}}
Причина предположения о выдающихся эллиптических орбитах, вероятно, кроется в гораздо большей разнице между афелием и перигелием. Эта разница (или соотношение) также зависит от эксцентриситета и рассчитывается как rarp = 1 + e 1 — e { displaystyle {{r _ { text {a}}} over {r _ { text {p }}}} = {{1 + e} over {1-e}}}
| Имя | Эксцентриситет | Большая полуось a (AU ) | Малая полуось b (AU ) | разница (%) | Перигелий (AU ) | Афелий (AU ) | разница (%) |
|---|---|---|---|---|---|---|---|
| Меркурий | 0,206 | 0,38700 | 0,37870 | 2,2 | 0,307 | 0,467 | 52 |
| Венера | 0,007 | 0,72300 | 0,72298 | 0,002 | 0,718 | 0,728 | 1,4 |
| Земля | 0,017 | 1,00000 | 0,99986 | 0,014 | 0,983 | 1,017 | 3,5 |
| Марс | 0,093 | 1,52400 | 1,51740 | 0,44 | 1,382 | 1,666 | 21 |
| Юпитер | 0,049 | 5,20440 | 5,19820 | 0,12 | 4,950 | 5,459 | 10 |
| Сатурн | 0,057 | 9,58260 | 9,56730 | 0,16 | 9,041 | 10,124 | 12 |
| Уран | 0,046 | 19,21840 | 19,19770 | 0,11 | 18,330 | 20,110 | 9,7 |
| Нептун | 0,010 | 30.11000 | 30.10870 | 0.004 | 29.820 | 30.400 | 1.9 |
См. Также
Ссылки
Внешние ссылки
-
Элементы орбиты и законы Кеплера. Основные формулы невозмущённого движения.
От постоянных интегрирования
обычно переходят к другим параметрам,
по которым можно вычислять координаты
и скорости спутника на любой момент
времени в инерциальной системе отсчёта.
Их называют элементами орбиты. По своему
назначению элементы орбиты делятся на
три группы. К первой группе относят
элементы, характеризующие размеры и
форму орбиты. Это большая полуосьи эксцентриситет обиты е:
К этой же группе элементов относятся:
фокальный параметр
,
малая полуось,
радиусы орбиты в перигееи
апогее:
а так же период обращения и среднее
движение:
Периодом обращения спутника
вокруг центрального тела называется
промежуток времени между моментами
двух последовательных прохождений
через произвольную точку орбиты. Среднее
движениеинтерпретируется
как средняя угловая скорость движения
спутника.
Элементы второй группы задают ориентировку
орбиты в пространстве. Они связаны с
векторными интегралами площадей и
Лапласа. К этим элементам относятся:
наклонение
,
долготаи аргумент перигея
.
Наклонениемназывают угол между
плоскостью экватора и плоскостью орбиты.
Его можно вычислить по формуле:
Очевидно, что
.
Орбиты с наклонением, равным 0º или 180º
называют экваториальными, а с наклонением
90º– полярными. Орбиты сназывают с прямым движением спутника,
а с– орбиты с обратным движением спутника
( по отношению к направлению вращения
Земли).
Долготой орбитыназывается угол,
отсчитываемый в плоскости экватора от
направления на точку весеннего
равноденствия

до направления на восходящий узел орбиты

Долготу определяют по формуле:
Аргументом перигеяназывается уголмежду направлениями на восходящий узел
и на перигей, отсчитываемый по направлению
движения спутника:
.
Для долготы и аргумента перигея
справедливо:
,
.
Элементы третьей группы задают положение
спутника на орбите. Оно устанавливается
с помощью момента прохождения перигея
или любой из аномалий (обычно истинной
или средней) с указанием эпохи.Истинной аномалией
называется угол между направлениями
на перигей и на спутник, отсчитываемый
в сторону движения спутника:
Средняя аномалияпредставляет
собой угол от направления на перигей
до направления на некоторое фиктивное
положение спутника, движущегося
равномерно по орбите:
.
Уравнение для средней аномалии иногда
называют динамическим интегралом, в
котором содержится шестая независимая
постоянная интегрирования – момент
проходжения перигея
.
Для связи истинной и средней аномалии
вводится эксцентрическая аномалия.
Чтобы её показать, вокруг орбитального
эллипса описывается окружность с центром
в точке С – геометрическом центре
эллипса, с радиусом, равным его большей
полуоси.
Через положение спутника – точку–
проводится перпендикуляр к большей
полуосидо
пересечения с окружностью в точке.
Соединяются точки С и.
Угол,
отсчитываемый при центре эллипса от
направления на перигей до направления
на точку,
называетсяэксцентрической аномалией.
Истинная и эксцентрическая аномалии
связаны соотношением:
,
а средняя и эксцентрическая аномалии
связаны уравнением Кеплера:
.
Часто используется угол от направления
на восходящий узел до направления на
спутник, называемый аргументом широты:
.
Существует множество других систем
элементов. Приведенные здесь параметры
называют Кеплеровыми элементами орбиты.
Законы движения спутника вокруг
центрального тела были открыты И.Кеплером
в начале XVIIв. Выведенные
вначале для вращающихся вокруг Солнца
планет, они оказались пригодными для
всех других тел, поскольку в их основе
лежит закон всемирного тяготения.
1-й закон Кеплера. Движение спутника
вокруг притягивающего тела всегда
происходит по коническому сечению
(окружности, эллипсу, параболе, гиперболе,
прямой), в одном из фокусов которого
находится притягивающий центр. Закон
выражается с помощью уравнения орбиты,
имеющей вид:
.
В зависимости от величины эксцентриситета
различают отбиты в виде окружности
(е=0), эллипса (0 < е < 1), параболы (е = 1),
гиперболы (е > 1) и прямой (е = ∞). В
дальнейшем мы будем рассматривать
только эллиптические орбиты.
Для описания 2-го закона Кеплера
потребуется ввести понятие секториальной
скорости
.
Это площадь, описываемая радиусом-вектором
спутника за единицу времени. Она связана
со скалярной константой площадей С:
.
Площадь, описываемую радиусом-вектором
спутника за промежуток времени
,
можно получить в виде определённого
интеграла:

что является математической записью
2-го закона Кеплера: за равные
промежутки времени радиус-вектор
спутника описывает равные площади.
Вследствии этого, линейная скорость
движения спутника по орбите в перигеебольше,
чем скорость в апогее.
3-й закон Кеплераформулируется
следующим образом: квадраты периодов
обращения спутников пропорциональны
кубам больших полуосей. Математическое
выражение для него получается из формулыЕсли у центрального тела (Земли) имеется
два спутника, соответственно, с периодамиР1 иР2и с большими полуосями
и
,
то для квадратов их периодов можно
записать:
А отношение этих выражение даёт формулу
3-го закона Кеплера:
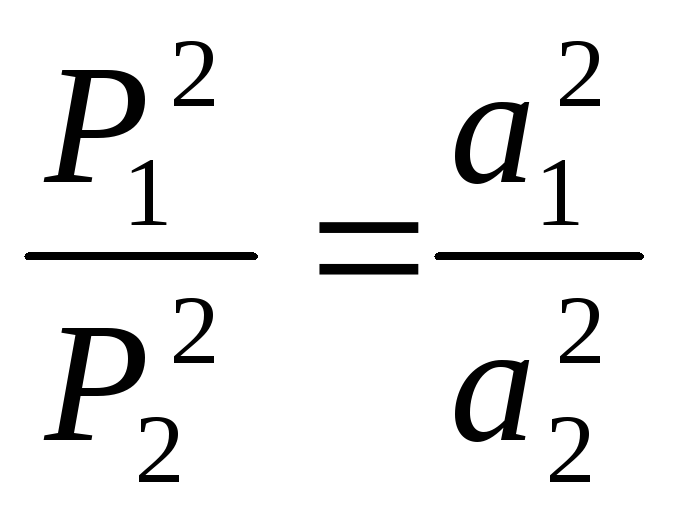
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #






















 — это удельная энергия движущегося по орбите тела.
— это удельная энергия движущегося по орбите тела.