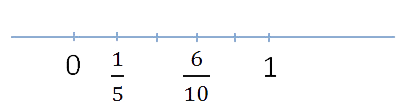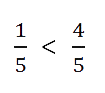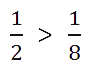Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.
Сравнение дробей с одинаковыми знаменателями.
Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.
Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.
Рассмотрим пример:
Сравните дроби (frac{7}{26}) и (frac{13}{26}).
Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:
(frac{7}{26} < frac{13}{26})
Сравнение дробей с равными числителями.
Если у дроби одинаковые числители, то больше та дробь, у которой знаменатель меньше.
Понять это правило можно, если привести пример из жизни. У нас есть торт. К нам в гости могут прийти 5 или 11 гостей. Если придут 5 гостей, то мы разрежем торт на 5 равных кусков, а если придут 11 гостей, то разделим на 11 равных кусков. А теперь подумайте в каком случаем на одного гостя придется кусок торта большего размера? Конечно, когда придут 5 гостей, кусок торта будет больше.
Или еще пример. У нас есть 20 конфет. Мы можем поровну раздать конфеты 4 друзьям или поровну поделить конфеты между 10 друзьями. В каком случае у каждого друга будет конфет больше? Конечно, когда мы разделим только на 4 друзей, количество конфет у каждого друга будет больше. Проверим эту задачу математически.
(frac{20}{4} > frac{20}{10})
Если мы до решаем эти дроби, то получим числа (frac{20}{4} = 5) и (frac{20}{10} = 2). Получаем, что 5 > 2
В этом и заключается правило сравнения дробей с одинаковыми числителями.
Рассмотрим еще пример.
Сравните дроби с одинаковым числителем (frac{1}{17}) и (frac{1}{15}) .
Так как числители одинаковые, больше та дробь, где знаменатель меньше.
(frac{1}{17} < frac{1}{15})
Сравнение дробей с разными знаменателями и числителями.
Чтобы сравнить дроби с разными знаменателями, необходимо дроби привести к общему знаменателю, а потом сравнить числители.
Пример:
Сравните дроби (frac{2}{3}) и (frac{5}{7}).
Сначала найдем общий знаменатель дробей. Он будет равен числу 21.
(begin{align}&frac{2}{3} = frac{2 times 7}{3 times 7} = frac{14}{21}\\&frac{5}{7} = frac{5 times 3}{7 times 3} = frac{15}{21}\\ end{align})
Потом переходим к сравнению числителей. Правило сравнения дробей с одинаковыми знаменателями.
(begin{align}&frac{14}{21} < frac{15}{21}\\&frac{2}{3} < frac{5}{7}\\ end{align})
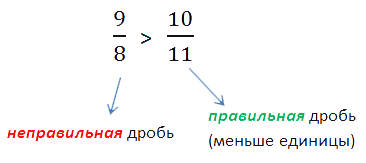
Сравнение неправильной и правильной дроби.
Неправильная дробь всегда больше правильной. Потому что неправильная дробь больше 1, а правильная дробь меньше 1.
Пример:
Сравните дроби (frac{11}{13}) и (frac{8}{7}).
Дробь (frac{8}{7}) неправильная и она больше 1.
(1 < frac{8}{7})
Дробь (frac{11}{13}) правильная и она меньше 1. Сравниваем:
(1 > frac{11}{13})
Получаем, (frac{11}{13} < frac{8}{7})
Вопросы по теме:
Как сравнить дроби с разными знаменателями?
Ответ: надо привести к общему знаменателю дроби и потом сравнить их числители.
Как сравнивать дроби?
Ответ: сначала нужно определиться к какой категории относятся дроби: у них есть общий знаменатель, у них есть общий числитель, у них нет общего знаменателя и числителя или у вас правильная и неправильная дробь. После классификации дробей применить соответствующее правило сравнения.
Что такое сравнение дробей с одинаковыми числителями?
Ответ: если у дробей одинаковые числители, та дробь больше у которой знаменатель меньше.
Пример №1:
Сравните дроби (frac{11}{12}) и (frac{13}{16}).
Решение:
Так как нет одинаковых числителей или знаменателей, применяем правило сравнения с разными знаменателями. Нужно найти общий знаменатель. Общий знаменатель будет равен 96. Приведем дроби к общему знаменателю. Первую дробь (frac{11}{12}) умножим на дополнительный множитель 8, а вторую дробь (frac{13}{16}) умножим на 6.
( begin{align}&frac{11}{12} = frac{11 times 8}{12 times 8} = frac{88}{96}\\&frac{13}{16} = frac{13 times 6}{16 times 6} = frac{78}{96}\\ end{align})
Сравниваем дроби числителями, та дробь больше у которой числитель больше.
( begin{align}&frac{88}{96} > frac{78}{96}\\&frac{11}{12} > frac{13}{16}\\ end{align})
Пример №2:
Сравните правильную дробь с единицей?
Решение:
Любая правильная дробь всегда меньше 1.
Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?
Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби (frac{5}{10} ).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби (frac{3}{5} ).
Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.
(begin{align}&frac{3}{5} = frac{3 times 2}{5 times 2} = frac{6}{10}\\&frac{5}{10} < frac{6}{10}\\&frac{5}{10} < frac{3}{5}\\ end{align})
Ответ: у папы результат лучше.
Основная суть сравнения дробей, заключается в том, чтобы узнать какая дробь больше, а какая меньше. На конкретных примерах разберем, как сравнивать обыкновенные дроби с одинаковыми и разными числителями и знаменателями, как сравнивать дроби с целыми числами и другие случаи.
Как сравнивать обыкновенные дроби?
Существует несколько способов сравнения дробей. Сегодня поговорим о наиболее распространенных. О перекрестном сравнении дробей и сравнении дробей с промежуточным числом — смотрите на соответствующих страницах.
Как сравнить дроби с одинаковыми знаменателями?
Сравнение дробей с одинаковыми знаменателями считается самым простым. Для этого необходимо лишь сравнить числители дроби. В общем виде правило выглядит так:
При сравнении двух дробей с одинаковыми знаменателями, больше будет та дробь — числитель которой больше.
Пример 1: сравнить дроби
4 8
и
2 8
Числитель первой дроби — 4, второй — 2. Т.к. знаменатели одинаковые — сравниваем числители: 4 > 2, соответственно:
Пример 2: сравнить дроби
84 50
и
47 50
Аналогично — сравниваем числители: 84 > 47, соответственно:
Сравнение дробей с одинаковыми числителями
Сравнить дроби с одинаковыми числителями не труднее, чем с одинаковыми знаменателями. Для этого сравнить придётся знаменатели двух дробей. Правило гласит:
При сравнении двух дробей с одинаковыми числителями, больше будет та дробь — знаменатель которой меньше.
Пример 3: сравнить дроби
5 6
и
5 10
Числители дробей — одинаковые. Соответственно сравниваем знаменатели 6 и 10. 6 < 10, отсюда:
Как сравнить дроби с разными знаменателями?
Сравнение дробей с одинаковыми числителями, как и с одинаковыми знаменателями — труда не составляет. А вот, сравнить дроби с разными знаменателями потребует чуть больше усилий. Итак:
Сравнение дробей с разными знаменателями сводится к тому, что необходимо привести дроби к одинаковому знаменателю, а затем сравнить числители.
Пример 4: сравнить дроби
2 5
и
3 6
Чтобы привести дроби к общему знаменателю, необходимо найти такое число, которое будет без остатка делиться и на знаменатель первой дроби и на знаменатель второй, т.е. число кратно обоим знаменателям. Ищем такое число для наших знаменателей 5 и 6 — это 30. Теперь найдем дополнительные множители для каждой дроби. Для этого общий знаменатель разделим на знаменатель каждой дроби:
30 : 5 = 6
30 : 6 = 5
Полученные множители перемножаем с числителями:
2 5
?
3 6
=
2 ∙ 6 30
?
3 ∙ 5 30
=
12 30
?
15 30
Осталось просто сравнить числители. 12 < 15, соответственно:
Отсюда следует, что:
Бывают ситуации когда необходимо сравнить правильную дробь с неправильной. Для подобных случаев существует правило:
При сравнении неправильной дроби с правильной — большая всегда будет неправильная дробь.
Правила сравнения дробей
Резюмируя вышесказанное, выведем общий алгоритм сокращения дробей:
- Если знаменатели одинаковые — сравниваем числители. Большей будет та дробь — числитель которой больше.
- Если числители одинаковые — сравниваем знаменатели. Большей будет та дробь — знаменатель, которой меньше.
- Если знаменатели разные — приводим дроби к общему знаменателю и сравниваем числители. Большей будет та дробь — числитель которой больше.
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Калькулятор сравнения дробей
Оцените материал:
Загрузка…
Содержание:
- Равные дроби
- Принципы сравнения дробей
- Сравнение дробей с разными знаменателями
Равные дроби
Пример
Задание. Найти при каком значении $x$ и $y$ дроби $frac{x}{3}$ и $frac{4}{y}$ будут равны.
Решение. Заданные дроби равны, то есть $frac{x}{3}=frac{4}{y}$ , если равны их числители и знаменатели
соответственно. А тогда имеют место следующие равенства:
$x=4$ $3=y$ или $x=4$ $y=3$
Ответ. $x=4, y=3$
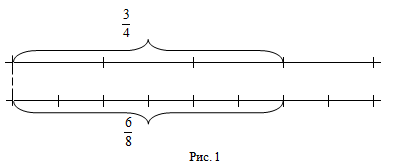
Две дроби считаются равным, если величины, выражаемые этими числами при одной и той же единице измерения, равны между собой.
Например. Дроби $frac{3}{4}$ и
$frac{6}{8}$ равны, так как две длины, из которых одна составляет $frac{3}{4}$ м, а вторая — $frac{6}{8}$ м, равны (рис 1).
Принципы сравнения дробей
Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше.
Например. $frac{7}{18}>frac{5}{18}$ , так как $7>5$
Из двух дробей с одинаковыми числителями больше та, знаменатель которой меньше.
Например. $frac{7}{3}>frac{7}{6}$, так как $3<6$ .
Любая правильная дробь меньше 1.
Например. $frac{4}{5} < 1$
Неправильная дробь, числитель которой равен знаменателю, равна 1.
Например. $frac{3}{3}=1, frac{7}{7}=1$
Неправильная дробь, у которой числитель больше знаменателя, больше 1.
Например. $frac{7}{6}>1$
Любая правильная дробь меньше произвольной неправильной дроби.
Например. $frac{4}{5}<frac{5}{4}$
В общем случае дроби по величине сравниваются следующим образом. Умножают числитель первой дроби на
знаменатель второй, а знаменатель первой на числитель второй. И сравнивают полученные произведения. Если первое
из этих произведений больше/равно/меньше второго, то соответственно и первая дробь больше/равно/меньше второй.
Например. $frac{5}{6}>frac{7}{9}$ , так как $5 cdot 9>6 cdot 7 Leftrightarrow 45>42$
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями, их нужно вначале привести к одинаковому (одному) знаменателю. Для этого
приводят либо к общему знаменателю, либо числитель и знаменатель первой дроби домножают на знаменатель второй и наоборот,
числитель и знаменатель второй дроби на знаменатель первой. И далее дроби сравнивать как дроби с одинаковым знаменателем
(описано выше).

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Сравнить дроби
$frac{3}{4}$ и $frac{5}{7}$
Решение. Приведем дроби к общему знаменателю, для этого
числитель и знаменатель
первой дроби домножим на 7 (знаменатель второй дроби); а числитель и знаменатель второй дроби — на 4, будем иметь:
$frac{3 cdot 7}{4 cdot 7}$ и $frac{5 cdot 4}{7 cdot 4}$
$frac{21}{28}$ и $frac{20}{28}$
Первая дробь больше: $frac{21}{28}>frac{20}{28} Leftrightarrow frac{3}{4}>frac{5}{7}$ , так как ее числитель $21 > 20$
Ответ. $frac{3}{4}>frac{5}{7}$
Читать следующую тему: основное свойство дроби.
Сравнение дробей онлайн
Сравнить дроби это значит понять какая из них больше.
Сравнение дробей с одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями больше та у которой числитель больше
Как понять это правило: знаменатель — это насколько мы делим число, а числитель — сколько частей взять.
Рассмотрим пример
Сравним дроби 5/7 и 6/7
В первой дроби мы берём 5 частей из 7 а во второй 6 частей из 7. Соответственно 6 частей больше чем 5.
5/7 < 6/7
Рассмотрим ещё один пример
Предположим у нас есть яблоко. Мы разрезали его на 4 части. Каждая часть яблока зто 1/4. К примеру Вите мы дали 3 части а Маше 1 часть. Получается Вите мы дали 1/4+1/4+1/4 = 3/4, а Маше 1/4. Отсюда вытекает следующее 3/4 > 1/4
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби с разными знаменателями нужно привести дроби к общему знаменателю а потом сравнить числители.
Рассмотрим пример
Сравним дроби 3/4 и 2/3
Для начала нужно найти наименьшее общее кратное знаменателей. НОК(4,3) = 12
Домножим первую дробь на 3, а вторую на 4.
Получится 9/12 > 8/12
Сравнение дробей с одинаковыми числителями
Из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот
Рассмотрим пример
К примеру у нас есть яблоко. Пол яблока это 1/2. Треть яблока это 1/3. Лучше съесть пол яблока чем треть.
1/2 > 1/3
Сравнение смешанных дробей
Для сравнения смешанных дробей нужно преобразовать смешанную дробь в неправильную. Если знаменатели будут разными то привести дроби к общему знаменателю. Если одинаковыми то сравнить числители.
Похожие калькуляторы
Также как и натуральные числа обыкновенные дроби можно сравнивать.
Рассмотрим две неравные дроби на числовой оси. Меньшая дробь будет располагаться левее, а большая — правее.
Равные дроби соответствует одной и той же точке на числовой оси.
На рисунке хорошо видно, что
<
.
Но необязательно пользоваться числовой осью, чтобы
сравнивать дроби.
Сравнение дробей с одинаковыми знаменателями
Запомните!
Из двух дробей с одинаковыми знаменателями больше та, у которой
числитель больше.
Пример. Сравним
и
.
В обеих дробях одинаковый знаменатель равный 5.
В первой дроби числитель равен 1 и он меньше числителя второй дроби,
который равен 4.
Поэтому первая дробь
меньше второй
.
Сравнение дробей с одинаковыми числителями
Запомните!
Из двух дробей с одинаковыми числителями больше та, у которой
знаменатель меньше.
Пример. Сравним
и
. Ответ:
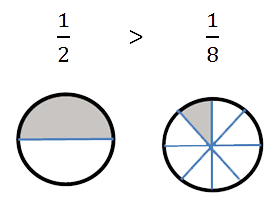
Правило выше легче понять, если представить, что у вас в руках куски торта. В первом случае
торт разделили на 2 части (знаменатель дроби равен 2), и у вас в руках
половина торта, а во втором — торт поделили на
8 частей, и у вас в руках маленькая часть торта.
Сравнение дробей с разными знаменателями
Запомните!
Чтобы сравнить дроби с разными знаменателями, нужно привести
дроби к общему знаменателю.
После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей
с одинаковыми знаменателями.
Пример. Сравним
и
.
Это объясняется тем, что неправильная дробь всегда больше или равна 1, а правильная дробь
всегда меньше 1.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
24 августа 2016 в 14:24
Альбина Королева
Профиль
Благодарили: 0
Сообщений: 2
Альбина Королева
Профиль
Благодарили: 0
Сообщений: 2
и 0.21
как сравнить это и пожалусто объясните
0
Спасибо
Ответить
25 августа 2016 в 10:08
Ответ для Альбина Королева
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Переведите десятичную дробь 0,21 в обыкновенную и далее сравните дроби по правилам сравнения обыкновенных дробей.
Правила сравнения обыкновенных дробей есть в этом уроке.
0
Спасибо
Ответить
25 августа 2016 в 10:28
Ответ для Альбина Королева
Альбина Королева
Профиль
Благодарили: 0
Сообщений: 2
Альбина Королева
Профиль
Благодарили: 0
Сообщений: 2
спасибо за объяснение
0
Спасибо
Ответить
3 августа 2016 в 14:09
Карина Терентьева
Профиль
Благодарили: 0
Сообщений: 1
Карина Терентьева
Профиль
Благодарили: 0
Сообщений: 1
Найдите две дроби, каждаяиз которых меньше
и больше
0
Спасибо
Ответить
5 августа 2016 в 2:11
Ответ для Карина Терентьева
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
и .
0
Спасибо
Ответить
30 сентября 2016 в 14:53
Ответ для Карина Терентьева
Ольга Чикалова-Елисеева
Профиль
Благодарили: 0
Сообщений: 2
Ольга Чикалова-Елисеева
Профиль
Благодарили: 0
Сообщений: 2
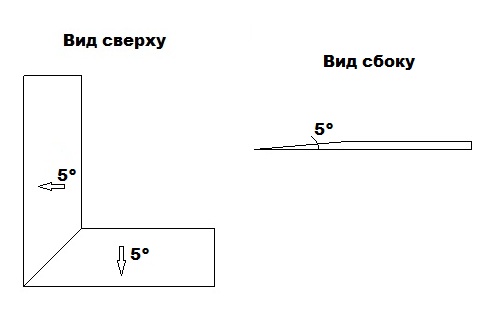
Доброго времени суток. Помогите пожалуйста, я в тупике.
Суть вопроса: плоскости примыкают друг другу под углом 45 градусов. Сами плоскости имеют наклон 5 градусов от внутреннего угла к внешнему. При таком условии градус примыкания должен измениться. Как рассчитать точный градус примыкания?
0
Спасибо
Ответить