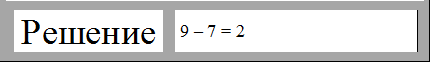Как найти большее число в задаче

Урок 29

    

    Тип урока: Р

    Авторы: Никологорская Н.В. (МОУ СОШ №16 г.    Щелково), А.И. Шушковская (АПК и ППРО РФ, ЦСДП «Школа 2000…»).

    Тема урока: «Задачи на нахождение большего    числа».

    Основные цели:

1) тренировать умение решать задачи на разностноесравнение: нахождение большего числа по известному меньшему числу иразнице (в прямой и косвенной форме), составлению соответствующихграфических схем;

2) тренировать умение учащихся к исправлению допущенныхошибок на основе рефлексии собственной деятельности;

3) тренировать вычислительные навыки в пределах 9.

Тренировать мыслительные операции: аналогия,сравнение, анализ.

Демонстрационный материал:

    

    1) пословица:

Красна птица пером, а человек знаниями.

2) текст задачи 1 для этапа 2 (записан на    доске):

    
Ира прочитала 3 книги, а Миша – на 2
больше. Сколько книг прочитал Миша?
    

3) эталон решения задачи на разностное сравнение    (нахождение большего числа):

    
    

4) текст задачи 2 для этапа 2 (записан на    доске):

Ира прочитала 3 книги. Это на 2 меньше,
чем прочитал Миша. Сколько книг прочитал
Миша?

5) образец для самопроверки самостоятельной    работы № 1:

    

Раздаточный материал:

    1) карточка с заданием 1 для этапа 2:

    
 

2) карточка с заданием 2 для этапа 2:

     

3) алгоритм исправления ошибок (см. урок 27,    часть 1, М-1);

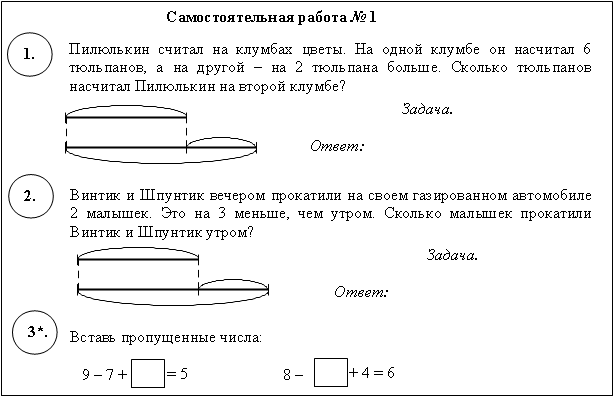
    4) самостоятельная работа № 1:

    
    

5) эталон для самопроверки самостоятельной    работы № 1:

    

6) карточки с заданиями для тренировки:

    

7) подробный образец для самопроверки задания    для тренировки:

    

самостоятельная работа № 2:

    

9) эталон для самопроверки самостоятельной    работы № 2:

    

10) образец для самопроверки дополнительных    заданий:

    № 6, стр. 57

    
    

№ 7, стр. 57

    
    

11) лестница «успеха» для    самооценивания на этапе 9.

Ход урока:

1. Мотивация к учебной деятельности.

Цель:

1) создать условия для возникновения внутреннейпотребности включения в деятельность посредством обращения к опытупрошлого урока;

2) сформулировать образовательную цель урока;

3) установить тематические рамки урока: решение задач наразностное сравнение.

Организация учебного процесса наэтапе 1:

Учитель открывает пословицу Д-1:

Красна птица пером, а человек знаниями.

• Как понимаете эту пословицу?    (Человека красят знания.)

• Что нужно делать, чтобы не потерять знания? (Надо    тренироваться.)

• Правильно, ребята. Вот и у вас сегодня урок    закрепления. По какой теме вы будете закреплять свои знания?    (Решение задач на разностное сравнение.)

• Как будет построен ход урока? (Мы должны сначала    повторить, потом выполнить самостоятельную работу, а если в ней    будут ошибки, то мы должны их исправить.)

• Тогда пожелайте друг другу успехов и приступите к    работе.

    

2. Актуализация и фиксация затруднений в    индивидуальной деятельности.

Цель:

1) актуализировать учебное содержание: решение задач наразностное сравнение;

2) активизировать мыслительные операции: сравнение,анализ, аналогию;

3) организовать мотивацию к выполнению учащимисясамостоятельной работы № 1 на применение способов действий,запланированных для рефлексивного анализа;

4)зафиксировать повторяемые понятия и правила в виде эталонов;

5) организовать самопроверку самостоятельной работы пообразцу с фиксацией учащимися своих результатов (без исправленияошибок);

6) организовать мотивацию учащихся к сопоставлению работпо эталону для самопроверки.

Организация учебного процесса на этапе 2:

1) Решение задачи на нахождение большего числа.

Учитель открывает на доске текстзадачи (Д-2), у учащихся карточки с заданием Р-1:

Ира прочитала 3 книги, а Миша – на 2
больше. Сколько книг прочитал Миша?

• Прочитайте задачу.

• Заполните схему.

Учитель заранее выносит надоску схему к этой задаче. Один учащийся выходит к доске и заполняетсхему с комментированием. Остальные учащиеся работают на карточкахР-1.

    

• Что требуется узнать? (Количество    книг, которое прочитал Миша.)

•     Какого типа задача? (Задача на разностное сравнение, в    которой нужно узнать большее число.)

•     Как найти большее число? (Чтобы узнать большее число,    надо к меньшему числу прибавить разность.)

Учитель открываетна доске эталон Д-3.

    

• Ответьте на вопрос задачи.

Один из учащихсязаписывает решение на доске без комментирования, остальные учащиесяработают на карточках Р-1. Проверка организуется фронтально.

2) Решение задачи на нахождениебольшего числа в косвенной форме.

Учитель открывает на доске текстзадачи Д-4, у учащихся карточки Р-2:

Ира прочитала 3 книги. Это на 2 меньше,
чем прочитал Миша. Сколько книг прочитал
Миша?

• Прочитайте задачу.

•     Сравните условия этих задач, что вы заметили? (В обеих    задачах одни герои, числа, но предложения построены по разному.)

Учитель заранеевыносит схему на доску.

    
• Прочитайте условие задачи еще раз и назовите у кого    книг больше – у Иры или у Миши. (У Иры меньше.)
•     Как вы это определили? (В условии говорится, что    количество книг у Маши меньше с помощью слова это.)

Учитель подчеркивает в условиизадачи слово «ЭТО» и ставит стрелку, учащиеся делают тоже самое на карточках Р-2:

    
• Какой отрезок будет соответствовать ее количеству?    (Меньший.)
•     Итак, с чего мы начали решение этой задачи? (Мы    определили, чего меньше.)
•     Заполним схему до конца.

Один учащийся работает у доскис комментированием, остальные на карточках Р-2.

    
• Сравните схемы этих двух задач. Что заметили?    (Схемы одинаковые.)
•     Какой можете сделать вывод? (Решение этих задач будет    одинаковое.)
•     Итак, это «хитрая» задача. Какое слово    нужно выделить в условии? (Слово «ЭТО».)
•     Что необходимо сделать при решении этой задачи сначала?    (Определить, чего больше, а чего меньше.)

3) Самостоятельная работа №1.

•     Что вы повторили? (Решение задачи на нахождение    большего числа.)

•     Какой ваш следующий шаг? (Написание самостоятельной    работы.)

•     С какой целью? (Проверить себя, допускаем ли мы    ошибки.)

•     А если вы допустите ошибку? (Мы будем над ней    работать.)

•     Вспомните, как вы работали над ошибками. Что вам    помогает в этом? (Алгоритм исправления ошибок.)

•     На данном уроке вы будете использовать алгоритм    исправления ошибок с предыдущих уроков, без изменений.

Учитель раздаетучащимся бланки с самостоятельной работой №1 (Р-4).

Время выполнения ≈ 8–10минут. Включить таймер.

    
• Проверьте свои работы по образцу.

Учитель открывает на доскеобразец для самопроверки Д-5.

    
• Как вы зафиксируете правильность выполнения каждого    задания? (Поставим «+» рядом с верно выполненным    заданием, «?» – если ответ не совпал.)
•     Что вы выяснили для себя, проверив работы по образцу?    (Где есть трудности, а где всё получилось.)
•     Поднимите руку, кто допустил ошибки в задании №    1 (№ 2).

    

Учитель фиксирует на доске    количество человек, допустивших ошибки в каждом из заданий.

                №    1 – … чел.

                №    2 – … чел.

    
•     Что сейчас вы должны сделать? (Проверить свои работы по    эталону для самопроверки.)
•     А, зачем, если вы уже проверили свои работы? (Те, у    кого все плюсы должны проверить ход решения, правильность    определения эталонов, а те, кто выявил, что есть затруднения, должны    определить место ошибки и определить на какое правило допущена    ошибка.)

3. Локализация затруднений.

Цель:

    

    организовать пошаговое сопоставление работ по эталону    для самопроверки (фронтально, с проговариванием во внешней речи):

    а) организовать выявление учащимися места затруднения;

    б) организовать выявление учащимися причины    затруднения;

в) организовать фиксацию отсутствия затруднений в ходерешения и его обосновании.

Организация учебного процесса на этапе 3:

Учитель раздает учащимся эталоны для самопроверки Р-6.

    

• Что вам поможет при проверке    самостоятельной работы? (Алгоритм исправления ошибок.)

•     Что сначала необходимо проверить? (Правильность записи    условий заданий.)

•     Что будете делать, если неправильно? (Запишу правильно    и решу повторно.)

•     Проверьте первое задание? Какой эталон вы применяли при    выполнении задания?

•     У кого возникли затруднения в задании № 1?

•     В каком месте вы допустили ошибку?

•     Проверьте второе задание? Какой эталон вы применяли при    выполнении задания?

•     У кого возникли затруднения в задании № 2?

•     В каком месте вы допустили ошибку?

•     У кого всё верно? Что, это означает? (У нас нет    затруднений.)

4. Коррекциивыявленных затруднений.

Цель:

1) уточнить индивидуальные цели будущихдействий;

2) на основе алгоритма исправления ошибок, организоватьсогласование плана достижения поставленной цели;

3) организовать реализацию согласованного планадействий;

4) для учащихся, допустивших ошибки, организоватьисправление ошибок и выполнение учащимися заданий на те способыдействий, в которых были допущены ошибки;

5) для учащихся, не допустивших ошибки, организоватьвыполнение дополнительных заданий.

Организация учебного процесса на этапе 4:

•     Те, у кого не возникло затруднений в самостоятельной    работе, сформулируйте цель вашей дальнейшей деятельности.    (Тренироваться в выполнении дополнительных заданий.)

•     Выполните дополнительные задания, номера которых    записаны на доске.

Учитель открывает на доске номера дополнительных заданий: №6, 7, стр.57.

    

• Какова же дальнейшая цель работы у    тех, кто выявил затруднения? (Исправить решение, используя эталон    для самопроверки, выполнить задание для выбора.)

•     Какой инструмент вам поможет при работе над ошибками?    (Алгоритм исправления ошибок.)

•     Посмотрите на алгоритм исправления ошибок, есть ли у    вас вопросы по работе с ним? (…)

    
• Перед выполнением работы над ошибками проговорите,    какие правила вам нужно ещё раз осмыслить, понять? (…)
•     Как вы будете это делать? (Будем пошагово применять    правила)

Учащиеся самостоятельно исправляют свои ошибки. В случае возникновения затруднений учащиеся могут исправить свои ошибки, пользуясь эталоном для самопроверки. В случае затруднений учитель организует работу фронтально.

    

• Что теперь нужно сделать, чтобы не    допускать ошибок в подобных заданиях? (Потренироваться в их    выполнении.)

С целью тренировки учитель предлагает учащимся выполнить задания накарточках. Учащиеся выполняют аналогичные задания тем, в которых былидопущены ошибки.

В зависимости от количества ошибившихся учащихся на данные задания, работу можноорганизовать фронтально у доски или самостоятельно.

В случае самостоятельного выполнения заданий на тренировку проверкаорганизуется по образцу.

Результатом работы на данном этапе должно быть выполнение детьми работы надошибками и закрепление способов действий, вызвавших затруднения, привыполнении заданий для тренировки.

5. Обобщение затруднений во внешнейречи.

Цель:

    

    1) организовать обсуждение типовых затруднений;

    2) организовать проговаривание формулировок способов    действий, которые вызвали затруднения.

Организация учебного процесса на этапе 5:

•     Посмотрите на результаты выполнения самостоятельной    работы. В каких заданиях возникло наибольшее количество затруднений?    (…)

•     Повторите, как надо действовать, чтобы эти затруднения    снять? (Найти ошибки, вспомнить правило (алгоритм) и применить их,    чтобы исправить ошибки.)

•     Проговорите еще раз для всех соответствующие способы    действий. (…)

Учащиесяпроговаривают в громкой речи те способы действий, в которых былодопущено наибольшее количество ошибок.

    

• Что дальше делать тем, у кого при    выполнении самостоятельной работы № 1 были трудности?    (Выполнить ещё одну самостоятельную работу.)

6. Самостоятельнаяработа с самопроверкой по эталону.

Цель:

1) организовать выполнение самостоятельной работы №2, аналогичной первой;

2) организовать самопроверку учащимися своих работ поэталону для самопроверки и фиксацию результатов;

3) зафиксировать достижение индивидуальной цели.

Организация учебного процесса на этапе 6:

Учащиеся выполняют задания изсамостоятельной работы №2, которые вызвали у них затруднения, и самостоятельно сопоставляютполученное решение с эталоном для самопроверки. В это время дети, недопустившие ошибок, проверяют дополнительное задание по подробномуобразцу.

    

• Какие задания вы будете выполнять?    (Подобные тем, в которых были допущены ошибки.)

•     Как будете проверять вашу работу? (По эталону,    результат отметим «+» или «?».)

После самостоятельной работы организуется самопроверка по эталону для самопроверки.

    

• Кто допустил ошибки в    самостоятельной работе № 2?

•     В чем их причина?

•     Вы молодцы, что нашли ошибки и поняли их причину. Но    какой вывод вы должны сделать? (Мы не справились с затруднением,    нужно еще тренироваться.)

•     Где вы можете это сделать? (При выполнении домашнего    задания.)

•     Кто не допустил ошибки в самостоятельной работе №2?

•     Сделайте вывод. (Нам удалось справиться с    затруднением.)

7. Включение всистему знаний и повторение.

Цель:

тренировать составлять выражение по рисунку.

Организация учебного процесса на этапе 7:

№ 5, стр. 57

•     Найдите №5 на странице 57.

•     Прочитайте задание.

•     Рассмотрите рисунок под буквой а.

•     По какому признаку разбиты фигуры? (По размеру.)

•     Какое выражение подходит к этому рисунку? (4 + 3.)

•     Почему действие сложение? (Ищем целое.)

•     Что обозначает число 4? (Число маленьких шаров.)

•     Что обозначает число 3? (Число больших шаров.)

•     Запишите выражение.

Далее работаорганизуется аналогично.

8. Рефлексиядеятельности на уроке.

Цель:

1) зафиксировать способы действий взаданиях, где были допущены ошибки;

3) зафиксировать степень соответствия поставленной целии результатов деятельности;

4) оценить собственную деятельность на уроке;

5) наметить цели дальнейшей деятельности;

6) согласовать домашнее задание.

Организация учебного процесса на этапе 8:

•     Чему был посвящён сегодняшний урок? (Повторению и    работе над ошибками.)

•     Какой инструмент помогает вам правильно работать над    ошибками? (Алгоритм исправления ошибок.)

•     Какие цели вы ставили перед собой на уроке? (Выяснить,    есть ли трудности. Понять причину ошибок и устранить её.)

•     Какие результаты вы получили? (…)

•     В каком месте у вас были затруднения? (В решении    задачи, в сравнении выражений, …)

•     Удалось ли их преодолеть? Как?

•     Оцените свою работу по лестнице «успеха».    Если вы не допустили ошибок в первой самостоятельной работе,    поставьте себя на верхнюю ступень. Если вы допустили ошибки в первой    самостоятельной работе, но справились с ошибками, то поставьте себя    на вторую ступень, а если вам не удалось справиться с затруднениями,    поставьте себя на нижнюю ступень.

Учитель проводит рефлексию оценивания учащихся.

    

• Какие трудности остались на конец    урока?

• Где  можно над ними поработать?

Задачи на разностное сравнение

Рассмотрим задачи, в которых речь идёт о разностном сравнении. В таких задачах обычно требуется найти разницу между двумя количествами и ответить на вопросы: на сколько больше? или на сколько меньше?.

Задачи на разностное сравнение решаются с помощью вычитания, то есть:

Чтобы узнать, на сколько одно число больше (или меньше) другого, надо из большего числа вычесть меньшее.

Изучая в школе математику, некоторые  дети сталкиваются с трудностью понятий: на сколько больше или меньше и во сколько больше или меньше. Эту разницу нужно чётко понимать, чтобы избежать ошибок при решении задач. С задачами на разностное сравнение ребенок сталкивается уже в 1 классе, а с задачами на кратное сравнение во 2 или 3 классе при изучении таблицы умножения. Вот тогда и начинается путаница. Где умножить, а где сложить, когда вычитать, а когда делить?

Разностное сравнение чисел

На сколько единиц одно число больше или меньше другого — это разностное сравнение. Для разносного сравнения необходимо  из большего числа вычесть меньшее.

Задача

Арбуз весит 12 кг, а дыня 4 кг. На сколько килограмм арбуз тяжелее дыни?

12-4=8 (кг) — арбуз тяжелее дыни.

Ответ: на 8 кг.

Кратное сравнение чисел

Во сколько раз одно число больше или меньше другого — это кратное сравнение. Для кратного сравнения необходимо большее число разделить на меньшее.

Что такое краты? Это разы. Как говорят  в сказках? Во сто крат лучше, красивее. Это означает во сто раз лучше, красивее.

Задача

Арбуз весит 12 кг, а дыня 4 кг. Во сколько раз арбуз тяжелее дыни?

12:4=3 (раза)— арбуз тяжелее дыни.

Ответ: в 3 раза.

Для того, чтобы в голове ребенка закрепились эти два понятия, нужно прорешать определенное количество задач. Начинать следует с простых задач на разностное и кратное сравнение, а потом можно переходить к составным задачам,  т.е. к задачам, в условие которых может быть включено и разностное, и кратное сравнение одновременно.

Пример составной задачи на разностное и кратное сравнение:

В магазин привезли 300 кг апельсинов. В первый день продали 46 кг апельсинов. Во второй день в 2 раза меньше, чем в первый, а в третий день на 17 кг больше, чем в первый и второй день вместе. Сколько кг апельсинов было продано за 3 дня?

Решение:

1. 46:2=23 (кг) — апельсинов продали во второй день.
2. 23+46=69 (кг) — апельсинов продали за первый и второй день вместе.
3. 69+17=86 (кг) — апельсинов продали в третий день.
4. 69+86=155 (кг) — апельсинов было продано за 3 дня.

Ответ: 155 кг апельсинов.

Задачи на разностное сравнение

• На сколько 5 меньше 8? На сколько 10 больше 3?
• На клумбе распустилось 7 жёлтых цветов, а голубых на 2 больше. Сколько голубых цветов распустилось на клумбе?
• В оркестре играют 13 скрипок, а флейт на 4 меньше. Сколько флейт в оркестре?
• На первой яблоне созрело 24 яблока, а на второй на 9 яблок больше. Сколько яблок созрело на второй яблоне?
• Для ремонта купили 15 банок зелёной краски, а белой на 9 банок больше. Сколько всего банок краски купили?
• Купили 31 шуруп, а болтов на 6 меньше. Сколько всего болтов и шурупов купили?
• Одна книга стоит 77 рублей, а другая на 49 рублей меньше. Сколько стоят обе книги?
• Бабушка купила 18 метров широкой тесьмы, а узкой на 7 метров больше. Сколько всего метров тесьмы купила бабушка?
• В пруду плавали 23 гуся, а уток на 9 меньше. Сколько всего птиц плавало в пруду?
• Собрали 45 кг чёрной смородины, а красной на 7 кг меньше. Сколько всего кг смородины собрали?
• К кормушке прилетело 17 синичек, а воробьёв на 14 больше. Сколько всего птичек прилетело к кормушке?
• У Светы 2 десятка конфет, а у Пети на 17 конфет больше? Сколько всего конфет у Пети и Светы?
• В магазине продавались 25 попугаев, а канареек на 7 больше. Сколько всего птичек продавалось в магазине?
• В коробке 54 кусочка белого мела, а цветного на 14 меньше. Сколько всего кусочков мела было в пакете?
• Около школы росло 37 берёз, а тополей на 8 больше. Сколько всего деревьев росло около школы?
• В пакете 43 шоколадные конфетки, а мятных на 12 меньше. Сколько всего конфет в пакете?
• С одного участка собрали 24 кг помидор, а с другого на 19 кг больше. Сколько всего кг огурцов собрали?
• В вагоне 56 верхних полок, а нижних на 12 меньше. Сколько всего полок в вагоне?
• На пристани 15 катамаранов, а лодок на 17 больше. Сколько всего лодок и катамаранов было на пристани?
• У мальчика 58 орешков, а у девочки на 3 десятка меньше. Сколько всего орешков у девочки и мальчика?

Задачи на кратное сравнение

• Во сколько раз 12 больше, чем 3? Во сколько раз 8 меньше 24?
• Коля собрал 36 орехов, а Даша — 18 орехов. Во сколько раз Даша собрала орехов меньше, чем Коля?
• На первой грядке выросло 12 морковок, а на второй в 2 раза больше. Сколько морковок выросло на второй грядке?
• Бабушке 56 лет, а внучке 8. Во сколько раз внучка моложе бабушки?
• У Светы 12 тетрадей, а у Вали 4 тетради. Во сколько раз больше тетрадей у Светы, чем у Вали?
• У продавца воздушных шаров 14 красных шариков, а зелёных в 2 раза меньше. Сколько зелёных воздушных шариков у продавца?
• Маша съела 24 вишни, а Лиза 12 вишен. Во сколько раз меньше вишен съела Лиза, чем Маша?
• Мама нашла 49 грибов, а сын 7 грибов. Во сколько раз больше грибов нашла мама, чем сын?
• В третьем классе учится 9 девочек и 18 мальчиков. Во сколько раз меньше в третьем классе девочек, чем мальчиков?
• Мама испекла 2 торта и 14 пирожных. Во сколько раз больше пирожных, чем тортов, испекла мама?
• В зоопарке 3 слона и 15 обезьян. Во сколько раз меньше слонов, чем обезьян?
• Мама вымыла 8 тарелок и 4 чашки. Во сколько раз больше мама вымыла тарелок, чем чашек?
• У причала стояло 9 катамаранов и 3 лодки. Во сколько раз меньше у причала лодок, чем катамаранов?
• В магазин привезли 48 кг яблок и 24 кг груш. Во сколько раз груш привезли меньше, чем яблок?
• Длина стороны прямоугольника 12 см, а ширина в 3 раза меньше. Чему равна ширина прямоугольника?
• Периметр квадрата 16 см, а прямоугольника 8 см. Во сколько раз периметр квадрата больше?
• Во сколько раз 8 см меньше 8 м?
• Во сколько раз 1 час больше 15 минут?
• Во сколько раз 2 кг больше, чем 400 грамм?

Составные задачи на разностное и кратное сравнение

• Машинка стоит 120 рублей, а кукла в три раза дешевле. На сколько дороже стоит машинка, чем кукла?
• 5 ящиков с апельсинами весят 40 кг, а ящик с хурмой 4 кг. На сколько легче ящик с хурмой?
• Мишка стоит 20 рублей, а солдатик в 2 раза дешевле. На сколько дороже мишка, чем солдатик?
• В столовой за 5 дней расходуется 180 кг хлеба. На сколько килограммов больше расходуется хлеба за 5 дней, чем за один?
• В саду 5 рядов вишен по 8 деревьев и 4 ряда яблонь по 5 деревьев. Во сколько раз меньше в саду растёт яблонь, чем вишен?
• При изготовлении раствора для укладки кирпича требуется 60 кг песка, а цемента на 40 кг меньше. Во сколько раз меньше требуется цемента, чем песка?
• С бахчи собрали 55 арбузов, а дынь на 44 меньше. Во сколько раз больше собрали арбузов, чем дынь?
• 2 утки снесли по 8 яиц, а курица снесла 72 яйца. На сколько яиц больше снесла курица, чем 2 утки?
• В первом тайме футболисты забили 3 гола, а во втором в 2 раза больше. На сколько больше голов забили во втором тайме, чем в первом?
• 6 ящиков апельсинов весят 48 кг, а 4 ящика мандаринов 16 кг. Во сколько раз ящик апельсинов весит больше, чем ящик мандаринов?
• 7 банок равного веса клубничного варенья весят 14 кг, а 5 банок равного веса земляничного варенья весят 20 кг. Во сколько раз банка с клубничным вареньем легче банки с земляничным вареньем?
• Глубина колодца 30 метров, а глубина оврага на 20 метров меньше. Во сколько раз глубина оврага меньше, чем колодца?
• 5 ящиков со сливами весят 35 кг, а 4 ящика с виноградом 48 кг. На сколько килограммов легче ящик со сливами?
• В парке 3 аллеи по 12 берёз в каждой, а лип в 4 раза меньше, чем берёз. На сколько берёз больше, чем лип?
• В автосалоне продается 24 машины серебристого цвета, а красных в 3 раза меньше. Черных машин в автосалоне на 5 больше, чем красных. Сколько всего машин в автосалоне?
• В магазин привезли 200 кг яблок, апельсинов в 2 раза больше, чем яблок, а бананов — на 50 кг меньше, чем апельсинов. Сколько всего килограммов фруктов привезли в магазин?
• Из 26 оконных стёкол, привезённых в магазин, цветных оказалось на 18 штук меньше, чем обычных. Сколько цветных стёкол привезли в магазин?
• В первой коробке 65 скрепок, а в другой – на 35 скрепок больше, чем в первой. В третьей коробке в 5 раз меньше скрепок, чем во второй. Сколько скрепок в трех коробках?
• На первой полке 75 книг, а на второй – в 5 раз меньше книг, чем в первой. На третьей полке на 35 книг больше, чем на второй. Сколько книг на трех полках?

Что тренируется, то развивается. Прорешав хотя бы часть этих задач, ваш ребёнок уже закрепит понятия разностного и кратного сравнения чисел и перестанет путаться.

В качестве игрового момента можно предложить ребенку математические фокусы с загадыванием чисел. Там эти знания ему тоже очень пригодятся.

С уважением, Ольга Наумова

МАТЕМАТИЧЕСКИЕ НЕЙРОТРЕНАЖЕРЫ

Авторская методика!

Ольга Наумова НЕЙРОСЧЕТ Сложение и вычитание до 10

Уникальный прогрессивный нейротренажер, в котором отработка навыков устного счета объединена с упражнениями для мозга в единую гармоничную систему. Результат не заставит себя ждать!

Эффективный фитнес для мозга и тела не только для дошкольников и младших школьников, но и для взрослых.
Дети с удовольствием включаются в эту подвижную, но непростую игру!

Кому необходим этот тренажер?

• Любому ребенку, испытывающему какие-либо затруднения в учебе;
• Ребенку, у которого проблемы с устным счетом;
• Ребенку, который отстает в развитии;
• Ребенку, который не хочет учиться;
• Человеку, который хочет улучшить внимание и память;
• Любому ребенку, который хочет развить свои способности;
• Любому взрослому, который хочет стать более энергичным и успешным.

В тренажере вы найдете:

• 60 различных таблиц устных вычислений для занятий;
• 9 уровней сложности + усложнения внутри каждого уровня;
• Четкие и удобные инструкции;
• Авторскую методику, разработанную и усовершенствованную во время практических занятий с детьми.

Регулярные занятия позволят:

• научиться быстро и правильно считать в пределах 10;
• улучшить навыки устного счета;
• развить мышление и память;
• сделать работу полушарий более слаженной;
• развить внимание;
• развить математические способности;
• развить скорость реакции;
• облегчить процесс чтения и письма;
• повысить работоспособность;
• выработать устойчивость к отвлекающим факторам;
• улучшить показания в учебе.

Регулярные занятия очень быстро дадут видимый результат!
Рекомендуемый возраст от 4 лет.
Максимальная польза для тела и интеллекта!

Ольга Наумова НЕЙРОСЧЕТ Сложение и вычитание до 20

В тренажере вы найдете:

• 60 различных таблиц устных вычислений для занятий;
• 9 уровней сложности + усложнения внутри каждого уровня;
• Четкие и удобные инструкции;
• Авторскую методику, разработанную и усовершенствованную во время практических занятий с детьми.

Регулярные занятия позволят:

• научиться быстро и правильно считать в пределах 20;
• улучшить навыки устного счета;
• развить мышление и память;
• сделать работу полушарий более слаженной;
• развить внимание;
• развить математические способности;
• развить скорость реакции;
• облегчить процесс чтения и письма;
• повысить работоспособность;
• выработать устойчивость к отвлекающим факторам;
• улучшить показания в учебе.

Регулярные занятия очень быстро дадут видимый результат!
Рекомендуемый возраст от 6 лет.

Ольга Наумова НЕЙРОСЧЕТ Табличное умножение и деление

Это непросто, но дети с удовольствием включаются в эту подвижную игру!

Кому необходим этот тренажер?

• Любому ребенку, испытывающему какие-либо затруднения в учебе;
• Ребенку, у которого проблемы с устным счетом;
• Ребенку, который не может или не хочет запоминать таблицу умножения;
• Ребенку, который не хочет учиться;
• Человеку, который хочет улучшить внимание и память;
• Любому ребенку, который хочет развить свои способности;
• Любому взрослому, который хочет стать более энергичным и успешным.

В тренажере вы найдете:

• 60 различных таблиц устных вычислений для занятий;
• 9 уровней сложности + усложнения внутри каждого уровня;
• Четкие и удобные инструкции;
• Авторскую методику, разработанную и усовершенствованную во время практических занятий с детьми.

Регулярные занятия позволят:

• быстро запомнить таблицу умножения;
• улучшить навыки устного счета;
• развить мышление и память;
• сделать работу полушарий более слаженной;
• развить внимание;
• развить математические способности;
• развить скорость реакции;
• облегчить процесс чтения и письма;
• повысить работоспособность;
• выработать устойчивость к отвлекающим факторам;
• улучшить показания в учебе.

Регулярные занятия очень быстро дадут видимый результат!
Рекомендуемый возраст от 8 лет.
Максимальная польза для тела и интеллекта!

Ольга Наумова НЕЙРОСЧЕТ Сложение и вычитание до 100

В тренажере вы найдете:

• 60 различных таблиц устных вычислений для занятий;
• 9 уровней сложности + усложнения внутри каждого уровня;
• Четкие и удобные инструкции;
• Авторскую методику, разработанную и усовершенствованную во время практических занятий с детьми.

Регулярные занятия позволят:

• научиться быстро и правильно считать в пределах 100;
• улучшить навыки устного счета;
• развить мышление и память;
• сделать работу полушарий более слаженной;
• развить внимание;
• развить математические способности;
• развить скорость реакции;
• облегчить процесс чтения и письма;
• повысить работоспособность;
• выработать устойчивость к отвлекающим факторам;
• улучшить показания в учебе.

Методика прекрасно зарекомендовала себя во время практических занятий с детьми!

О. Наумова НЕЙРОТРЕНИНГ Безударные гласные

Большой полноценный ТРЕНИНГ с выстроенной системой упражнений.
НЕЙРОТРЕНИНГ позволит продуктивно отработать самую распространенную и трудную орфограмму в русском языке — безударные гласные в корне слова, проверяемые ударением.

Что даст прохождение ТРЕНИНГА:

• повышение уровня грамотности;
• развитие внимания;
• активацию работы мозга;
• умение применять полученные знания на практике;
• увеличение скорости обработки информации;
• развитие речи;
• развитие памяти;
• улучшение успеваемости в школе и т.д.

Кому нужен этот ТРЕНИНГ?

• Ребенку, который делает ошибки на письме;
• Родителям, которые хотят разобраться в теме и помочь своему ребенку;
• Учителю, который использует нестандартные и действенные приёмы в обучении;
• Репетитору желающему в разы увеличить результативность своих занятий.

Что найдете в ТРЕНИНГЕ:

• Продуманную и проверенную на практике систему упражнений;
• 200 страниц результативных заданий;
• 9 уровней сложности нейроупражнений;
• Нестандартные и наиболее эффективные задания по основной теме;
• Упражнения для развития речи;
• Дополнительные задания к упражнениям на отработку знаний частей речи, состава слова, деления на слоги, умения составлять предложения и др.

В результате прохождения ТРЕНИНГА ребенок получит:

• умение видеть в текстах и слышать слова с безударными гласными;
• умение быстро и без ошибок подбирать проверочные слова;
• повышение грамотности в целом;
• развитие «орфографического чутья»;
• уменьшение количества ошибок;
• активацию работы мозга;
• развитие мышления;
• увеличение скорости мысли;
• улучшение показателей в учёбе.

ПОДХОДИТ ДЛЯ ИНДИВИДУАЛЬНОЙ И ГРУППОВОЙ РАБОТЫ.

Заходите также в Книжную лавку  за полезными книгами!

Благодарю, что поделились статьей в социальных сетях!

План урока:

Понятие «задача». Составные части задачи

Задачи на нахождение целого

Задачи на увеличение числа на несколько единиц

Задачи на нахождение части

Задачи на уменьшение числа на несколько единиц

Задачи на разностное сравнение

Привет! По пути на наше занятие я встретила свою очень хорошую подружку. Ее зовут Даша – следопыт.

Она очень любознательная и стремиться находить ответы на все вопросы, даже самые сложные. Ей стало очень интересно, чем мы будем заниматься на сегодняшнем уроке. Я рассказала Даше, что тема у нас довольно непростая, мы будем разбираться в типах задач, искать способы их решения.

Даша подумала, что это будет очень увлекательно и попросила разрешить ей поприсутствовать у нас на уроке. Конечно же, я с радостью согласилась. Итак, сегодня наше занятие мы проведем втроем.

Понятие «задача». Составные части задачи

Послушай, какую историю рассказала мне Даша. Ее друг бычок Борька попросил помочь и провести расследование.

Утром у него на столе в вазочке лежало 9 шоколадных конфет.

А когда бычок вернулся с прогулки, то увидел в вазочке всего 6 конфет.

Борька обратился к Даше с просьбой разобраться с исчезновением конфет и узнать, куда они делись.

Даша определила, что конфет стало меньше. Она задумалась, почему это могло случиться. Например, конфеты могли выпасть из вазочки. Но конфет ни на столе, ни под столом не оказалось.

Тогда Даша решила, что конфеты кто-то забрал. Она внимательно присмотрелась к друзьям бычка, которые собрались в комнате, и заметила, что у лисенка Жулика щеки испачканы шоколадом.

Даша все поняла и нашла правильный ответ: это лисенок съел конфеты. И Жулик сразу же в этом сознался, а затем попросил прощение за свой поступок. Все были очень рады, что проблема решилась.

Я тоже очень обрадовалась, ведь история Даши поможет объяснить новый материал на сегодняшнем уроке. Давай по порядку проанализируем последовательность расследования.

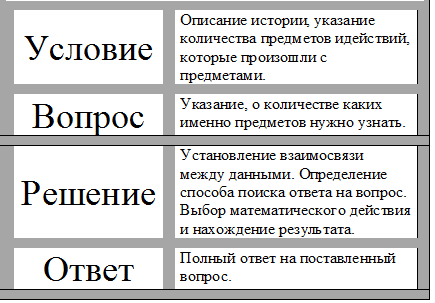
1. Бычок Борька рассказал, что произошло.
2. Он задал вопрос и попросил найти ответ.
3. Даша подумала, порассуждала и нашла правильное решение.
4. Она дала ответ на вопрос бычка.

Это же и есть порядок работы над задачей! Вот определение понятия задача – это проблемная ситуация, которую нужно решить путем логических рассуждений, математических вычислений. В результате решения задачи нужно найти правильный ответ на поставленный вопрос.

Вот составные части задачи.

Давай мы Дашину историю превратим в задачу и решим ее.

Итак, приступим. Сначала разберемся с условием.Для математической задачи важно иметь необходимые числовые данные.

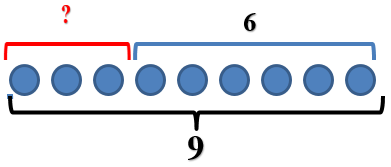
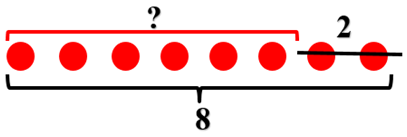
Чтобы лучше понять условие задачи, мы будем рисовать. Не обязательно рисовать именно конфеты. Можно их обозначить просто кружочками. Изобразим 9 кружочков–конфет.

Из этих конфет часть забрали и часть осталась. Мы знаем, что осталось 6 конфет. Отметим их.

Итак, мы проанализировали и изобразили условие нашей задачи. Идем дальше.

Теперь нам нужно определить вопрос задачи. Ее вопрос почти всегда включает слово «сколько».Даше нужно было узнать, куда исчезли конфеты. А мы узнаем, сколько исчезло конфет.

Для этого нам нужно определить количество конфет в той части, которую мы еще не выделили.

Пока все ясно? Тогда переходим к следующему этапу. Нам нужно понять, как найти решение задачи. Для этого давай подумаем. Нас интересуют конфеты в подмножестве, которое является частью множества из 9 конфет, лежавших в вазочке сначала. Мы с тобой выучили на прошлом уроке, что найти часть из целого можно с помощью действия вычитания. Осталось составить пример. Мы должны из общего количества конфет (число 9) вычесть количество конфет, которые остались (число 6). 9 минус 6 будет 3.

Ну вот, мы посчитали конфеты в подмножестве, которое забрали. Давай вспомним вопрос: «Сколько конфет исчезло?» Мы это только что установили, значит можно переходить к последнему этапу и дать ответ на вопрос.

Мы закончили работу над задачей.

1. Разобрались с ее условием.
2. Определили вопрос.
3. Подумали над решением.
4. И дали ответ.

Теперь ты сможешь решить любую задачу. Их очень много. Мы рассмотрим решение простых задач.

Задачи на нахождение целого

Вот наша первая задача. Ее составила для нас Даша.

У обезьянки Башмачок было 5 бананов. А Даша принесла ей еще 3 банана. 

Какой вопрос мы можем задать по условию этой задачи? Правильно, мы можем спросить, сколько всего бананов стало у обезьянки?

Итак, начнем работать. Сначала проанализируем первую составную часть задачи– условие.

О ком говорится в задаче? Правильно, об обезьянке. О том, что у нее было 5 бананов.

Что случилось потом? Верно, ей дали еще 3 банана. Запишем это в нашу таблицу

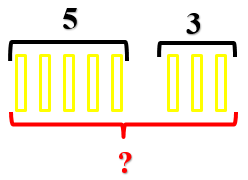
Теперь обозначим условие задачи схематически. Вместо бананов будем рисовать прямоугольники. Сначала нарисуем 5 бананов, которые были у обезьянки.

Поскольку обезьянке дали еще бананы, то нарисуем их рядом.

Вспомним вопрос задачи и запишем его в таблицу

Значит, нам нужно вместе посчитать бананы, которые были, и бананы, которые ей еще дали

Теперь приступим к решению задачи.

Получается, что теперь у обезьянки все бананы лежат вместе, т.е. подмножество бананов, которые были у нее раньше, объединилось с подмножеством бананов, которые она получила потом.

Давай вспомним материал прошлого урока. Какое математическое действие мы используем при объединении подмножеств в одно общее?

Правильно, это действие сложение. Значит, для решения нашей задачи мы должны составить выражение на сложение. К 5 бананам, которые были у обезьянки, прибавим 3 банана, которые ей дала Даша. Что получится?

Сумма чисел 5 и 3 равна 8. Вот мы и посчитали все бананы. Теперь у обезьянки всего стало 8 бананов.

Обрати внимание, мы нашли ответ на вопрос нашей задачи! Можно заканчивать

Вот мы и разобрались с нашей задачей.

С помощью какого действия мы нашли ответ? Да, это было действие сложение.

Почему мы использовали именно это действие? Совершенно точно, потому что по условию предметы добавлялись. Два подмножества предметов объединяются в одно целое. Такой тип задач называется задачи на нахождение целого.

Один из главных вопросов в задачах на нахождение целого «Сколько всего?»  Потому что именно после объединения двух подмножеств надо пересчитать все предметы вместе.

В нашей задаче предметов прибавилось, потому что Даша дала еще бананы. Подумай, в каком еще случае предметов добавится?

Правильно, если:

• что-то подарят;
• что-то положат;
• сделают еще несколько предметов;
• кто-то придет или приедет;
• объединить две группы предметов (например, посчитать вместе мальчиков и девочек).

Во всех указанных случаях мы получим задачи на нахождение целого. Такие задачи нужно решать с помощью действия сложения.

Задачи на увеличение числа на несколько единиц

А вот другая задача. Она немного не похожа на предыдущие. Давай рассмотрим, в чем ее особенности.

У Даши было 4 воздушных шарика, а у игуаны Иса – на 5 шариков больше. Сколько шариков было у игуаны?

Сначала проанализируем условия задачи. Что нам известно?

Правильно, мы знаем о Даше. У нее 4 шарика.

Но мы не знаем, сколько шариков у игуаны! Однако у нас есть подсказка о их количестве. В задаче сказано, что у игуаны на 5 шариков больше.

Запишем это условие и вопрос.

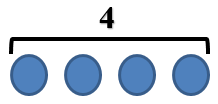
Попробуем изобразить. Вот 4 шарика Даши

А как показать шарики игуаны? У нее их на 5 больше, чем у Даши. Значит их столько же (т.е. 4) и еще 5. Покажем это.

Давай подумаем над решением этой задачи. Выбор действия подсказан в самом условии. Помнишь, в результате какого действия становится больше?

Правильно, это действие сложения. Значит, для решения задачи нам нужно составить пример на сложение

Мы посчитали, сколько шариков у игуаны, а это и есть вопрос нашей задачи. Ура! Мы нашли нужный ответ! 

Задача решена!

Теперь давай разберемся, в чем ее особенность. В условии задачи содержалась подсказка, которая указала на выбор математического действия. Помнишь?

Было сказано, что у игуаны на несколько шариков больше. Больше становиться в результате действия сложения. Поэтому, чтобы посчитать шарики игуаны, нужно прибавлять.

Это задача на увеличение числа на несколько единиц. Их решать очень легко, если внимательно прочитать условие. Как только ты заметишь указание, что предметов, которые нужно посчитать, на несколько единиц больше, то сразу выбирай действие сложения. 

Задачи на нахождение части

А сейчас еще одна задача.

На кусте росло 8 ягод. Лис жулик сорвал 2 ягоды. Сколько ягод осталось?

Довольно простое и понятное условие. Попробуй сам записать все, что нам известно.

Давай проверим. Мы знаем, сколько было ягод, и знаем, сколько ягод сорвал Жулик. Поэтому запись такая

Что нужно узнать? Запиши вопрос

Кажется, все понятно. Теперь давай порассуждаем. Из тех ягод, что были на кусте, часть ягод сорвали. Изобразим это на схеме

Подумай, что произойдет, если убрать часть предметов?

Правильно, их останется меньше.

А теперь вспомни, какое математическое действие используется при удалении из множества предметов одного его подмножества?

Конечно же, это действие вычитание. Значит нам нужно из числа 8, которое обозначает количество всех ягод вычесть число 2, которое обозначает количество сорванных ягод.

Запишем решение. 

Мы узнали, что на кусте осталось 6 ягод. Можем записать ответ.

Вот как просто! Когда мы что-то убираем, то остается только часть от всего, что было. Это задачи на нахождение части. Они решаются с помощью действия вычитания.

Давай подумаем, в каких еще ситуациях будет оставаться только часть предметов.

Например:

• что-то съели;
• забрали;
• продали;
• ушли;
• увезли;
• отрезали;
• прочитали.

Можно еще продолжать, но главное, ты должен запомнить, что в результате таких действий часть предметов убирается и их остается меньше. Поэтому в задачах на нахождение части всегда используется действие вычитания.

Задачи на уменьшение числа на несколько единиц

Давай разбираться со следующей задачей. Ее придумала Даша.

Даша собралась в поход. Она положила себе в рюкзак 5 пар носков, а футболок взяла на 3 меньше. 

Прочитай внимательно условие. Какие вещи взяла Даша? Что о них известно?

Правильно, мы знаем, что Даша взяла 5 пар носков.

А для каких вещей не указано точное количество?

Верно, мы не знаем точно, сколько Даша взяла футболок. Сказано, что их на 3 меньше, чем носков. Давай это запишем.

Можешь сказать, какой будет вопрос? Что нам нужно узнать?

Правильно, мы будем узнавать, сколько же футболок взяла с собой Даша

Это тоже задача с подсказкой. Мы можем даже не рисовать носки и футболки, чтобы понять, как ее решать. Ты уже догадался, что за подсказка?

Ну, конечно же, это указание, что футболок меньше! А мы уже знаем, какое математическое действие нужно применять, если предметов меньше. Это действие вычитание. 

Все очень просто. Нам нужно из числа 5, которое обозначает количество носков, вычесть число 3, которое показывает, на сколько футболок меньше

Вот и все! Теперь нам известно, что Даша взяла в поход 2 футболки. Можем писать ответ

И задача решена!

Это мой любимый тип задачи. Он называется задачи на уменьшение числа на несколько единиц. При их решении невозможно ошибиться. Раз сказано, что предметов на несколько единиц меньше, значит, будем вычитать, и получим правильный ответ.

Задачи на разностное сравнение

А вот еще одна задача от Даши и о ее друге Паровозике.

В первый день Паровозик перевез 9 пассажиров, а во второй день – 7 пассажиров. 

Очень простое и понятное условие. Все известно – и сколько в первый день перевез, и сколько во второй.

Можем это записать.

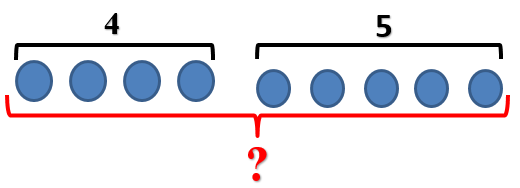
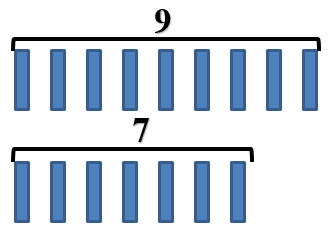
И нарисовать это можем. Пассажиров обозначим палочками. Сначала нарисуем пассажиров, которые ехал в первый день, а ниже тех, кто ехал во второй.

А вот вопрос Даша придумала очень необычный. Она решила, что мы слишком легко со всеми задачами справляемся и нужно немного усложнить. Вот вопрос.

Итак, нужно для начала определить в какой день он перевез пассажиров больше, а в какой меньше. Это довольно легко. Ты уже умеешь сравнивать числа. Скажи, что получиться?

Правильно, 9 > 7. Это можно прочитать, как «9 больше, чем 7» или «7 меньше, чем 9».

Но в задаче недостаточно только сравнить числа. Нужно узнать, какая между ними разница, т.е. выполнить разностное сравнение. Давай еще раз посмотрим на рисунок. Что ты заметил?

Видишь, в первый день изобразили палочек столько же, сколько и во второй день, и остались еще «лишние» палочки. Их можно отгородить. Для этого отделим одинаковое количество палочек. Во множестве с меньшим количеством элементов 7 палочек, значит, и во множестве с большим количеством элементов мы отсчитаем 7 палочек. 

Чтобы найти ответ на вопрос задачи, нужно узнать количество «лишних» палочек.

 То есть нам надо найти часть из множества, в котором 9 палочек.

А вот это уже просто! Вспомни, с помощью какого математического действия можно найти часть множества. Конечно же, это вычитание.

Получается, мы должны из большего числа вычесть меньшее число. 

Мы провели не только сравнение чисел, но и нашли их разность. Это называется разностное сравнение чисел. Можно записывать ответ. 

Вот мы и познакомились еще с одним типом задач – задачи на разностное сравнение. Их главная особенность в том, что вопрос начинается со слов «На сколько …?». Для решения этих задач нужно следовать такому алгоритму.

1. Определить, какое число больше.
2. Из большего числа вычесть меньшее.

Ты еще не устал? Мы выучили 5 разных типов задач:

• задачи на нахождение целого;
• задачи на увеличение числа на несколько единиц;
• задачи на нахождение части;
• задачи на уменьшение числа на несколько единиц;
• задачи на разностное сравнение.

Каждая из них имеет один единственно правильный вариант решения. Поэтому нужно очень хорошо подумать и разобраться. Всегда будь внимательным к вопросу задачи. Поиск правильного решения зависит именно от того, количество каких предметов нужно узнать. 

Чтобы потренироваться в решении разных задач, попроси родителей приобрести сборник задач для 1 класса.

А сейчас давай проверим, как ты научился анализировать условие задачи и правильно определять ее тип. Выполни тестовые задания. 

Для материалов урока взяты кадры из обучающего м/с «Даша-путешественница», 2004