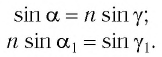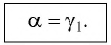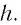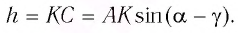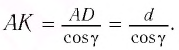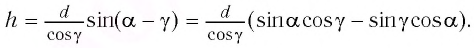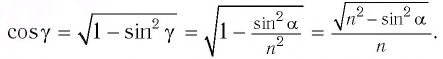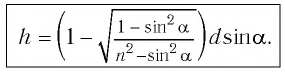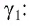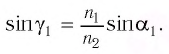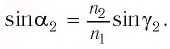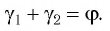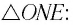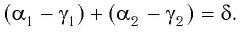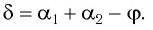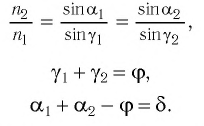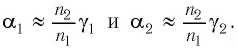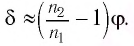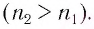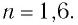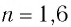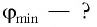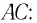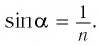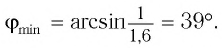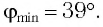2017-11-04
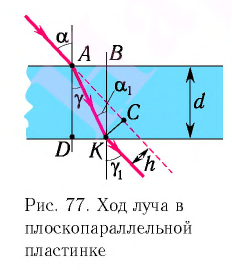
Определить боковое смещение луча после прохождения через плоскопараллельную стеклянную пластинку толщиной 6 см, имеющую показатель преломления 1,6. Угол падения луча света на пластинку $40^{ circ}$.
Решение:
Расстояние между лучами найдем из треугольника ABD (рис.):
$d = AB sin ( alpha — beta)$,
где $AB = frac{h}{ cos beta}$ ($h$ — толщина пластинки, $beta$ — угол преломления). Окончательно имеем
$d = h frac{ sin ( alpha — beta)}{ cos beta}$.
Угол преломления $beta$ определим из выражения $frac{ sin alpha}{ sin beta} = n:$
$sin beta = frac{ sin alpha}{n}, sin beta = frac{0,643}{1,6} = 0,402; beta = 23^{ circ}40^{ prime}$.
Зная угол преломления $beta$, можно определить смещение луча:
$d = frac{6 см cdot 0,2812}{0,9159} approx 1,84 см$.
|
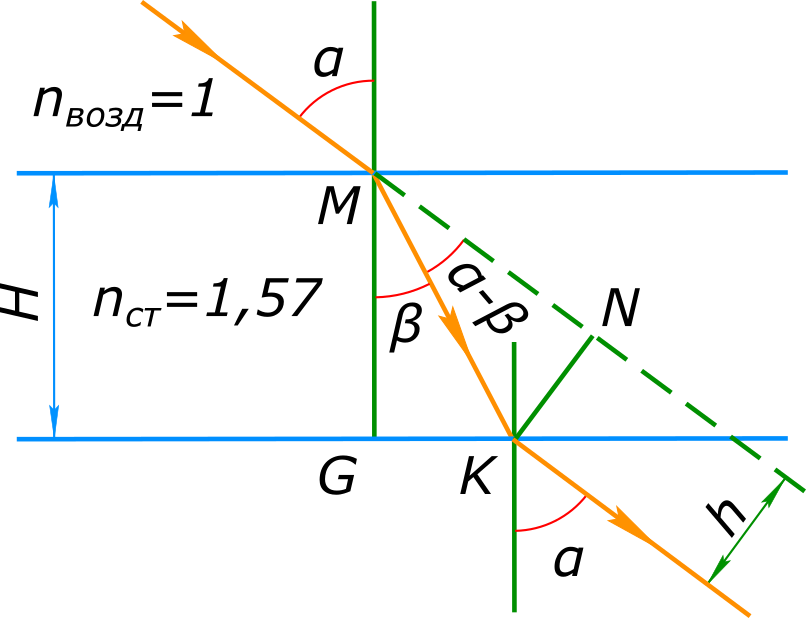
Луч света падает на плоскопараллельную стеклянную пластину толщиной 6 см. Угол падения 60 градусов. Найти величину бокового смещения луча, прошедшего через эту пластину. Оцените сложность задачи: 0 голосов, средняя сложность: 0.0000 Решения задачиДано: H=6 см; α=60°=π/3; $n_{возд}$=1; $n_{ст}$=1,57 h=? Изобразим графически условие задачи Решение: Согласно закону преломления света $frac{sinα}{sinβ}=frac{n_{ст}}{n_{возд}}$, откуда $sinβ=frac{n_{возд}sinα}{n_{ст}}=frac{1×0,866}{1,57}$=0,5516, откуда $β=arcsin0,5516$=0,5843 Из треугольника MGK находим $cosβ=frac{MG}{MK}$, откуда $MK=frac{MG}{cosβ}$ Из треугольника MKN находим $sin(α-β)=frac{KN}{MK}$, откуда $h=KN=MKsin(α-β)=frac{MGsin(α-β)}{cosβ}=frac{6sin(frac{π}{3}-0,5843)}{cos0,5843}=frac{6×0,4465}{0,834}$=3,2 см. Ответ: величина бокового смещения луча составит 3,2 см. Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь |
Записать новую задачу Все задачи Все темы Все физики |
Содержание:
Прохождение света через плоскопараллельные пластинки и призмы:
Законы отражения и преломления света широко используются для управления ходом световых пучков. Для отражения света в приборах применяются зеркала и призмы, для преломления — призмы, плоскопараллельные пластинки, линзы.
Зеркала, призмы, пластинки и линзы являются элементами, комбинируя которые, создают различные оптические приборы. Рассмотрим отдельные элементы оптических приборов.
Плоскопараллельная пластинка
Рассмотрим ход луча в плоскопараллельной пластинке. На рисунке 77 показан ход светового луча в плоскопараллельной пластинке толщиной
Согласно закону преломления на первой и второй границах раздела для луча, падающего под углом 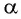
Здесь 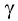
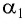
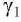
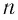
Накрест лежащие углы 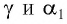
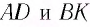

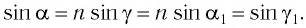
Таким образом, луч света, проходя через плоскопараллельную пластинку, с обеих сторон которой находится одна и та же среда, смещается параллельно своему начальному направлению на некоторое расстояние
Соответственно, все предметы, если смотреть на них сквозь прозрачную плоскопараллельную пластинку под углом, не равным нулю, будут также казаться смещенными.
Найдем, от каких параметров пластинки зависит смещение 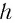
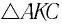
Из 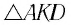
Отсюда:
С учетом закона преломления 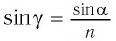
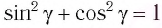
Расстояние 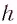
Как видно из соотношения (2), смещение 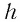
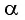
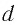
Трехгранная призма
Рассмотрим ход луча в трехгранной призме. Пусть световой луч 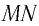
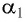
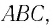
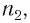
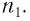
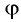
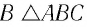
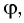
Пусть луч 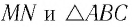
Если показатель призмы 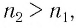
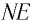
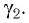
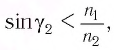
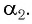
Отклонение от начального направления луча 
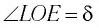
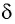
Рассмотрим 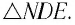
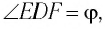
Применим эту же теорему к
Из формул (5) и (6) определим связь угла падения 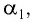
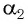
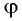
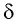
В результате получим систему уравнений (3), (4), (5), (7):
Система уравнений (8) позволяет решить задачу на прохождение луча света через трехгранную призму без полного отражения на ее гранях.
- Заказать решение задач по физике
Если угол падения 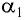
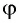
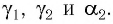
Подставляя полученные выражения для 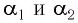
Из соотношения (9) следует, что, во-первых: чем больше преломляющий угол 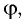
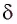
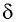
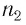
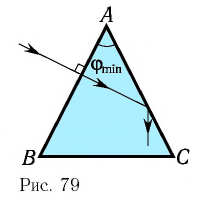
Пример решения задачи
Определите наименьший преломляющий угол 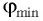
Дано:
Решение:
Запишем условие полного отражения на боковой грани
Вследствие того, что 
Ответ:
- Поляризация света
- Линзы в физике
- Глаз как оптическая система
- Звук в физике и его характеристики
- Электромагнитная природа света
- Интерференция света
- Дифракция света
- Принцип Гюйгенса — Френеля
Условие задачи:
Определить смещение светового луча при прохождении его через стеклянную пластинку с параллельными гранями, если толщина пластинки 4 см и угол падения 70°.
Задача №10.3.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(d=4) см, (alpha=70^circ), (l-?)
Решение задачи:
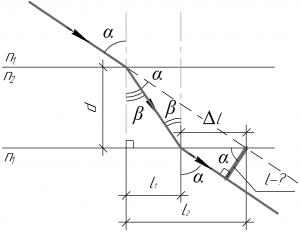
[l = Delta lcos alpha;;;;(1)]
Расстояние (Delta l) можно определить следующим образом:
[Delta l = {l_2} – {l_1}]
Расстояния (l_1) и (l_2) можно найти из соответствующих прямоугольных треугольников (да, опять) по следующим формулам:
[left{ begin{gathered}
{l_1} = d cdot tgbeta hfill \
{l_2} = d cdot tgalpha hfill \
end{gathered} right.]
Учитывая все вышесказанное, формула (1) примет вид:
[l = dcos alpha left( {tgalpha – tgbeta } right);;;;(2)]
Чтобы найти угол преломления (beta), запишем закон преломления света (также известен как закон преломления Снеллиуса):
[{n_1}sin alpha = {n_2}sin beta]
Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_1) равен 1, показатель преломления стекла (n_2) равен 1,5.
Тогда:
[sin beta = frac{{{n_1}sin alpha }}{{{n_2}}}]
[beta = arcsin left( {frac{{{n_1}sin alpha }}{{{n_2}}}} right);;;;(3)]
Подставим выражение (3) в формулу (2):
[l = dcos alpha left( {tgalpha – tgleft( {arcsin left( {frac{{{n_1}sin alpha }}{{{n_2}}}} right)} right)} right)]
Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:
[l = 0,04 cdot cos 70^circ left( {tg70^circ – tgleft( {arcsin left( {frac{{1 cdot sin 70^circ }}{{1,5}}} right)} right)} right) = 0,0266;м = 26,6;мм]
Ответ: 26,6 мм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.3.32 На какое расстояние сместится луч, пройдя плоскопараллельную стеклянную пластинку
10.3.34 Луч света падает под углом 30° на плоскопараллельную стеклянную пластинку
10.3.35 Луч света падает перпендикулярно на вертикальную грань прозрачной призмы