Боковое ребро правильной пирамиды, формула
 |
Боковое ребро правильной пирамиды находится по формуле [ b = sqrt{ h^2 + Big( frac{a}{2sin(frac{180°}{n})} Big) ^2 } ] |
b — Боковое ребро правильной пирамиды (SA или SB или SC или SD или SE)
n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника (AB или BC или CD или DE или EA) — основания правильной пирамиды
h — высота правильной пирамиды (OS)
Боковое ребро правильной пирамиды выводится из следующих формул
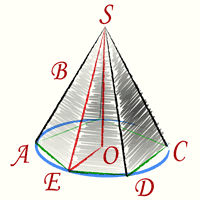
Синим цветом на рисунке изображена описанная вокруг основания правильной пирамиды окружность. Треугольник SOE прямоугольный.
Его стороны: OS — высота правильной пирамиды (h), OE —
радиус описанной окружности вокруг правильного многоугольника (основание правильной пирамиды (R)),
SE — Боковое ребро правильной пирамиды (b).
По теореме Пифагора
[ SE = b = sqrt{ h^2 + R^2 } ]
подставив сюда только радиус описанной окружности получается формула (1).
Вычислить, найти боковое ребро правильной пирамиды по формуле(1)
Боковое ребро правильной пирамиды |
стр. 277 |
|---|
Правильная пирамида – это геометрическое тело, образованное правильным многоугольником, лежащим в основании и боковыми ребрами, подымающимися в одну вершину из всех углов основания. Такая пирамида является типовой, поскольку обладает множеством свойств за счет своего основания. Помимо того, что все боковые грани представляют собой конгруэнтные треугольники, а все боковые ребра равны (также как и ребра в основании между собой), высота правильной пирамиды опускается ровно в центр вписанной и описанной окружностей для заданного многоугольника. Поэтому в такой пирамиде возникает сразу два прямоугольных треугольника во внутреннем пространстве, один из них соединяет высоту с апофемой радиусом вписанной окружности, а второй соединяет высоту с боковым ребром радиусом описанной окружности.
Таким образом, для того, чтобы найти боковое ребро пирамиды, необходимо знать лишь сторону основания, общее количество сторон этого же многоугольника и высоту. По теореме Пифагора, боковое ребро является гипотенузой и, следовательно, находится сложением:
Подставив в формулу значение радиуса описанной окружности для правильного многоугольника, получаем окончательный ее вид:
Как найти ребро четырехугольной пирамиды
Четырехугольная пирамида — это пятигранник с четырехугольным основанием и боковой поверхностью из четырех треугольных граней. Боковые ребра многогранника пересекаются в одной точке — вершине пирамиды.

Инструкция
Четырехугольная пирамида может быть правильной, прямоугольной или произвольной. Правильная пирамида имеет в основании правильный четырехугольник, а ее вершина проецируется в центр основания. Расстояние от вершины пирамиды до ее основания называется высотой пирамиды. Боковые грани правильной пирамиды являются равнобедренными треугольниками, а все ребра равны.
В основании правильной четырехугольной пирамиды может лежать квадрат или прямоугольник. Высота H такой пирамиды проецируется в точку пересечения диагоналей основания. В квадрате и прямоугольнике диагонали d одинаковы. Все боковые ребра L пирамиды с квадратным или прямоугольным основанием равны между собой.
Для нахождения ребра пирамиды рассмотрите прямоугольный треугольник со сторонами: гипотенуза — искомое ребро L, катеты — высота пирамиды H и половина диагонали основания d. Вычислите ребро по теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов: L²=H²+(d/2)². В пирамиде с ромбом или параллелограммом в основании противоположные ребра попарно равны и определяются по формулам: L₁²=H²+(d₁/2)² и L₂²=H²+(d₂/2)², где d₁ и d₂ — диагонали основания.
В прямоугольной четырехугольной пирамиде ее вершина проецируется в одну из вершин основания, плоскости двух из четырех боковых граней перпендикулярны плоскости основания. Одно из ребер такой пирамиды совпадает с ее высотой H, а две боковые грани являются прямоугольными треугольниками. Рассмотрите эти прямоугольные треугольники: в них один из катетов — ребро пирамиды, совпадающее с ее высотой H, вторые катеты — стороны основания a и b , а гипотенузы — неизвестные ребра пирамиды L₁ и L₂. Следовательно, два ребра пирамиды найдите по теореме Пифагора, как гипотенузы прямоугольных треугольников: L₁²=H²+a² и L₂²=H²+b².
Оставшееся неизвестным четвертое ребро L₃ прямоугольной пирамиды найдите по теореме Пифагора как гипотенузу прямоугольного треугольника с катетами Н и d, где d — диагональ основания, проведенная от основания ребра, совпадающего с высотой пирамиды Н к основанию искомого ребра L₃: L₃²= H²+d².
В произвольной пирамиде ее вершина проецируется в случайную точку на основании. Для нахождения ребер такой пирамиды рассмотрите последовательно каждый из прямоугольных треугольников, в которых гипотенуза — искомое ребро, один из катетов — высота пирамиды, а второй катет — отрезок, соединяющий соответствующую вершину основания с основанием высоты. Для нахождения величин этих отрезков необходимо рассмотреть треугольники, образованные в основании при соединении точки проекции вершины пирамиды и углов четырехугольника.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Рассмотрим основание пирамиды — это квадрат, так как пирамида правильная. Диагональ квадрата делит его на два равносторонних прямоугольных треугольника с катетами по 8 см.
c=8 корней из 2 — это длина диагонали. Точка пересечения диагоналей делит их пополам и с/2=4 корня из 2.
Рассмотрим треугольник, сторонами которого являются половина диагонали, высота пирамиды и ее ребро. Этот треугольник прямоугольный, так как присутствует высота. Ищем гипотенузу — ребро пирамиды по теореме Пифагора
с в квадрате = 100 + (4 корня из 2) в квадрате
с в квадрате = 100+32=132
с=2 корня из 33 (см)
Ответ: 2 корня из 33 см длина ребра
Для решения построим рисунок (http://bit.ly/3hotzNb).
Так как, по условию, пирамида правильная, то в ее основании лежит квадрат АВСД с длиной стороны 8 см.
Тогда диагональ АС = ВД = АД * √2 = 8 * √2 см.
Диагонали квадрата равны и в точке пересечения делятся пополам.
Тогда ОА = АС / 2 = 8 * √2 / 2 = 4 * √2 см.
ОЕ высота пирамиды, тогда треугольник АОЕ прямоугольный в котором, по теореме Пифагора, определим длину гипотенузы АЕ.
AE^2 = AO^2 + OE^2 = 32 + 100 = 132.
AE = √132 = 2 * √33 cм.
Ответ: Длина бокового ребра равна 2 * √33 cм.


