Как найти ближайшее значение в массиве - AvtoShod.ru

Here’s the pseudo-code which should be convertible into any procedural language:

array = [2, 42, 82, 122, 162, 202, 242, 282, 322, 362]
number = 112
print closest (number, array)

def closest (num, arr):
    curr = arr[0]
    foreach val in arr:
        if abs (num - val) < abs (num - curr):
            curr = val
    return curr

It simply works out the absolute differences between the given number and each array element and gives you back one of the ones with the minimal difference.

For the example values:

number = 112  112  112  112  112  112  112  112  112  112
array  =   2   42   82  122  162  202  242  282  322  362
diff   = 110   70   30   10   50   90  130  170  210  250
                         |
                         +-- one with minimal absolute difference.

As a proof of concept, here’s the Python code I used to show this in action:

def closest (num, arr):
    curr = arr[0]
    for index in range (len (arr)):
        if abs (num - arr[index]) < abs (num - curr):
            curr = arr[index]
    return curr

array = [2, 42, 82, 122, 162, 202, 242, 282, 322, 362]
number = 112
print closest (number, array)

And, if you really need it in Javascript, see below for a complete HTML file which demonstrates the function in action:

<html>
    <head></head>
    <body>
        <script language="javascript">
            function closest (num, arr) {
                var curr = arr[0];
                var diff = Math.abs (num - curr);
                for (var val = 0; val < arr.length; val++) {
                    var newdiff = Math.abs (num - arr[val]);
                    if (newdiff < diff) {
                        diff = newdiff;
                        curr = arr[val];
                    }
                }
                return curr;
            }
            array = [2, 42, 82, 122, 162, 202, 242, 282, 322, 362];
            number = 112;
            alert (closest (number, array));
        </script>
    </body>
</html>

Now keep in mind there may be scope for improved efficiency if, for example, your data items are sorted (that could be inferred from the sample data but you don’t explicitly state it). You could, for example, use a binary search to find the closest item.

You should also keep in mind that, unless you need to do it many times per second, the efficiency improvements will be mostly unnoticable unless your data sets get much larger.

If you do want to try it that way (and can guarantee the array is sorted in ascending order), this is a good starting point:

<html>
    <head></head>
    <body>
        <script language="javascript">
            function closest (num, arr) {
                var mid;
                var lo = 0;
                var hi = arr.length - 1;
                while (hi - lo > 1) {
                    mid = Math.floor ((lo + hi) / 2);
                    if (arr[mid] < num) {
                        lo = mid;
                    } else {
                        hi = mid;
                    }
                }
                if (num - arr[lo] <= arr[hi] - num) {
                    return arr[lo];
                }
                return arr[hi];
            }
            array = [2, 42, 82, 122, 162, 202, 242, 282, 322, 362];
            number = 112;
            alert (closest (number, array));
        </script>
    </body>
</html>

It basically uses bracketing and checking of the middle value to reduce the solution space by half for each iteration, a classic O(log N) algorithm whereas the sequential search above was O(N):

0  1  2   3   4   5   6   7   8   9  <- indexes
2 42 82 122 162 202 242 282 322 362  <- values
L             M                   H  L=0, H=9, M=4, 162 higher, H<-M
L     M       H                      L=0, H=4, M=2, 82 lower/equal, L<-M
      L   M   H                      L=2, H=4, M=3, 122 higher, H<-M
      L   H                          L=2, H=3, difference of 1 so exit
          ^
          |
          H (122-112=10) is closer than L (112-82=30) so choose H

As stated, that shouldn’t make much of a difference for small datasets or for things that don’t need to be blindingly fast, but it’s an option you may want to consider.

Источник

Для неотсортированного массива. Для отсортированного лучше использовать бинпоиск.

Python 3.4+: tio.run

def f(a, val):
  return min((x for x in a if x > val), default=None)

a = [1, 2, 5, 22, 33, 44, 312]
print(f(a, 3))
print(f(a, 10))
print(f(a, 1000))

Более ранние версии: tio.run

def f(a, val):
  return min([x for x in a if x > val] or [None])

a = [1, 2, 5, 22, 33, 44, 312]
print(f(a, 3))
print(f(a, 10))
print(f(a, 1000))

Вывод в обоих случаях:

5
22
None

Источник

Дан отсортированный массив целых чисел, найти k ближайшие элементы к target в массиве, где k а также target заданы положительные целые числа.

The target может присутствовать или отсутствовать во входном массиве. Если target меньше или равно первому элементу входного массива, вернуть первым k элементы. Точно так же, если target больше или равно последнему элементу входного массива, вернуть последний k элементы. Возвращаемые элементы должны быть в том же порядке, что и во входном массиве.

Например,

Input: [10, 12, 15, 17, 18, 20, 25], k = 4, target = 16
Output: [12, 15, 17, 18]

Input: [2, 3, 4, 5, 6, 7], k = 3, target = 1
Output: [2, 3, 4]

Input: [2, 3, 4, 5, 6, 7], k = 2, target = 8
Output: [6, 7]

Потренируйтесь в этой проблеме

Идея состоит в том, чтобы выполнить линейный поиск, чтобы найти точку вставки. i. Точка вставки определяется как точка, в которой ключ target будет вставлен в массив, т. е. индекс первого элемента больше ключа, или размер массива, если все элементы в массиве меньше указанного ключа. Затем сравните элементы вокруг точки вставки. i чтобы получить первый k ближайшие элементы. Временная сложность этого решения O(n), куда n это размер ввода.

Мы также можем найти точку вставки i с использованием алгоритм бинарного поиска, который работает в O(log(n)) время. С момента обнаружения k ближайший элемент занимает O(k) время, общая временная сложность этого решения равна O(log(n) + k). Ниже приведена реализация на C, C++, Java и Python, основанная на этой идее:

C

#include <stdio.h>

#include <stdlib.h>

// Функция для поиска в указанном массиве `nums` ключа `target`

// используя алгоритм бинарного поиска

int binarySearch(int nums[], int n, int target)

{

int low = 0;

int high = n — 1;

while (low <= high)

{

int mid = low + (high — low) / 2;

if (nums[mid] < target) {

low = mid + 1;

}

else if (nums[mid] > target) {

high = mid — 1;

}

else {

return mid; // ключ найден

}

return low; // ключ не найден

}

// Функция для поиска `k` элементов, ближайших к `target`, в отсортированном целочисленном массиве `nums`

void findKClosestElements(int nums[], int target, int k, int n)

{

// найти точку вставки с помощью алгоритма бинарного поиска

int i = binarySearch(nums, n, target);

int left = i — 1;

int right = i;

// запустить `k` раз

while (k— > 0)

{

// сравниваем элементы по обе стороны от точки вставки `i`

// чтобы получить первые `k` ближайших элементов

if (left < 0 || (right < n &&

abs(nums[left] — target) > abs(nums[right] — target))) {

right++;

}

else {

left—;

}

// вывести `k` ближайших элементов

left++;

while (left < right)

{

printf(«%d «, nums[left]);

left++;

}

int main(void)

{

int nums[] = { 10, 12, 15, 17, 18, 20, 25 };

int n = sizeof(nums) / sizeof(nums[0]);

int target = 16, k = 4;

findKClosestElements(nums, target, k, n);

return 0;

}

Скачать Выполнить код

результат:

12 15 17 18

C++

#include <iostream>

#include <vector>

#include <algorithm>

using namespace std;

// Функция для поиска `k` ближайших элементов к `target` в отсортированном целочисленном векторе `input`

vector<int> findKClosestElements(vector<int> const &input, int target, int k)

{

// найти точку вставки с помощью алгоритма бинарного поиска

int i = lower_bound(input.begin(), input.end(), target) — input.begin();

int left = i — 1;

int right = i;

// запустить `k` раз

while (k— > 0)

{

// сравниваем элементы по обе стороны от точки вставки `i`

// чтобы получить первые `k` ближайших элементов

if (left < 0 || (right < input.size() &&

abs(input[left] — target) > abs(input[right] — target))) {

right++;

}

else {

left—;

}

// вернуть `k` ближайших элементов

return vector<int>(input.begin() + left + 1, input.begin() + right);

}

int main()

{

vector<int> input = { 10, 12, 15, 17, 18, 20, 25 };

int target = 16, k = 4;

vector<int> result = findKClosestElements(input, target, k);

for (int i: result) {

cout << i << » «;

}

return 0;

}

Скачать Выполнить код

результат:

12 15 17 18

Java

import java.util.Arrays;

import java.util.Collections;

import java.util.List;

class Main

{

// Функция для поиска `k` элементов, ближайших к `target`, в отсортированном списке `input`

public static List<Integer> findKClosestElements(List<Integer> input, int k, int target)

{

// найти точку вставки с помощью алгоритма бинарного поиска

int i = Collections.binarySearch(input, target);

// Collections.binarySearch() возвращает `-(точка вставки) — 1`

// если ключ не содержится в списке

if (i < 0) {

i = —(i + 1);

}

int left = i — 1;

int right = i;

// запустить `k` раз

while (k— > 0)

{

// сравниваем элементы по обе стороны от точки вставки `i`

// чтобы получить первые `k` ближайших элементов

if (left < 0 || (right < input.size() &&

Math.abs(input.get(left) — target) > Math.abs(input.get(right) — target))) {

right++;

}

else {

left—;

}

// вернуть `k` ближайших элементов

return input.subList(left + 1, right);

}

public static void main(String[] args)

{

List<Integer> input = Arrays.asList(10, 12, 15, 17, 18, 20, 25);

int target = 16, k = 4;

System.out.println(findKClosestElements(input, k, target));

}

Скачать Выполнить код

результат:

[12, 15, 17, 18]

Python

# Функция для поиска в указанном массиве `nums` ключа `target`

# с использованием алгоритма бинарного поиска

def binarySearch(nums, target):

low = 0

high = len(nums) — 1

while low <= high:

mid = low + (high — low) // 2

if nums[mid] < target:

low = mid + 1

elif nums[mid] > target:

high = mid — 1

else:

return mid # Ключ # найден

return low # Ключ # не найден

# Функция для поиска `k` элементов, ближайших к `target`, в отсортированном массиве целых чисел `nums`

def findKClosestElements(nums, target, k):

# найти точку вставки с помощью алгоритма бинарного поиска

i = binarySearch(nums, target)

left = i — 1

right = i

# запускается `k` раз

while k > 0:

# сравнить элементы по обе стороны от точки вставки `i`

#, чтобы получить первые `k` ближайших элементов

if left < 0 or (right < len(nums) and abs(nums[left] — target) > abs(nums[right] — target)):

right = right + 1

else:

left = left — 1

k = k — 1

# возвращает `k` ближайших элементов

return nums[left+1: right]

if __name__ == ‘__main__’:

nums = [10, 12, 15, 17, 18, 20, 25]

target = 16

k = 4

print(findKClosestElements(nums, target, k))

Скачать Выполнить код

результат:

[12, 15, 17, 18]

Приведенное выше решение для выполнения двоичного поиска, чтобы найти точку вставки, а затем пытается найти k ближайшие элементы. Однако мы можем объединить всю логику в одну процедуру бинарного поиска. Вот как алгоритм будет выглядеть в C, Java и Python:

C

#include <stdio.h>

#include <stdlib.h>

// Функция для поиска `k` элементов, ближайших к `target`, в отсортированном целочисленном массиве `nums`

void findKClosestElements(int nums[], int target, int k, int n)

{

int left = 0;

int right = n;

while (right — left >= k)

{

if (abs(nums[left] — target) > abs(nums[right] — target)) {

left++;

}

else {

right—;

}

// вывести `k` ближайших элементов

while (left <= right)

{

printf(«%d «, nums[left]);

left++;

}

int main(void)

{

int nums[] = { 10, 12, 15, 17, 18, 20, 25 };

int n = sizeof(nums) / sizeof(nums[0]);

int target = 16, k = 4;

findKClosestElements(nums, target, k, n);

return 0;

}

Скачать Выполнить код

результат:

12 15 17 18

Java

import java.util.Arrays;

import java.util.List;

import java.util.stream.Collectors;

class Main

{

// Функция для поиска `k` элементов, ближайших к `target`, в отсортированном целочисленном массиве `nums`

public static List<Integer> findKClosestElements(int[] nums, int k, int target)

{

int left = 0;

int right = nums.length — 1;

while (right — left >= k)

{

if (Math.abs(nums[left] — target) > Math.abs(nums[right] — target)) {

left++;

}

else {

right—;

}

return Arrays.stream(nums, left, right + 1).boxed()

.collect(Collectors.toList());

}

public static void main(String[] args)

{

int[] nums = {10, 12, 15, 17, 18, 20, 25 };

int target = 16, k = 4;

System.out.println(findKClosestElements(nums, k, target));

}

Скачать Выполнить код

результат:

[12, 15, 17, 18]

Python

# Функция для поиска `k` элементов, ближайших к `target`, в отсортированном массиве целых чисел `nums`

def findKClosestElements(nums, k, target):

left = 0

right = len(nums) — 1

while right — left >= k:

if abs(nums[left] — target) > abs(nums[right] — target):

left = left + 1

else:

right = right — 1

return nums[left:left + k]

if __name__ == ‘__main__’:

nums = [10, 12, 15, 17, 18, 20, 25]

target = 16

k = 4

print(findKClosestElements(nums, k, target))

Скачать Выполнить код

результат:

[12, 15, 17, 18]

Временная сложность приведенного выше решения равна O(n) и не требует дополнительного места.

Источник

Remove From My Forums

Поиск ближайшего значения в массиве

Вопрос
Здравствуйте. Как найти ближайшее значение в float массиве к тому, которое введет пользователь?

Например, дан массив: 1,1;1,2;1,3 и т.д. до 2.

Пользователь ввел число 1,34, значит вывести должно 1,3.

Если 1,35 то 1,4(ну вообщем все по правилам округления в математике) .

Как это все сделать на C#?
- Изменено
  
  9 января 2018 г. 21:19

Ответы

Более подробно? Организуете перебор, где ищете минимальное значение, которое вычисляется, как модуль числа от разности между текущим элементом массива и введенным числом. При нахождении минимального
отклонения обновляете значение минимального отклонения и номер элемента при котором произошло изменение.
- Помечено в качестве ответа
  afomin31
  10 января 2018 г. 15:28

Источник

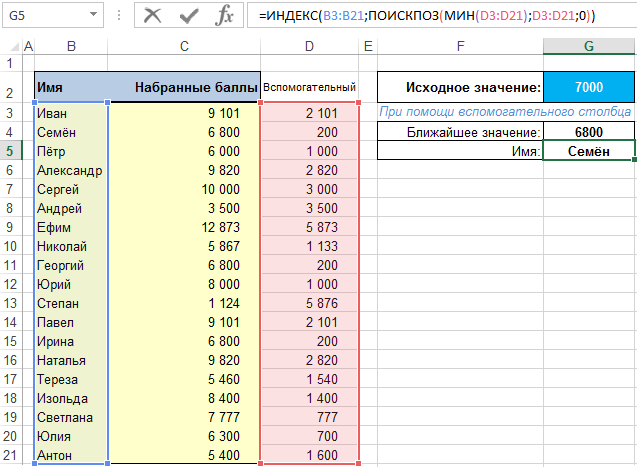
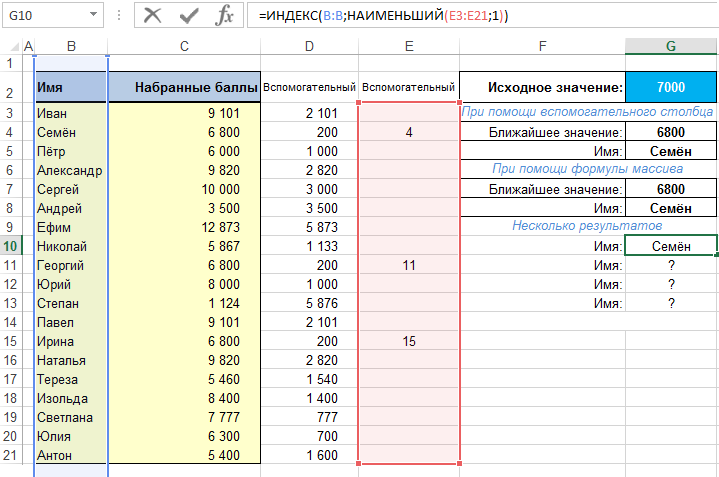
В данном примере Excel будем искать ячейки с наиболее близкими значениями к какому-то числу, выбранному пользователем (меньшими, большими, равными — без разницы. Важно, чтобы они были как можно ближе к искомому значению).

Как найти ближайшее большее значение по формуле в Excel

Начнем с простой таблицы, в которой имеется список имен и соответствующие им баллы.

Сразу стоит отметить что для некоторых имен число баллов повторяются.

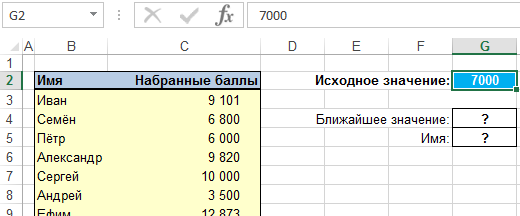
Хотелось бы, чтобы Excel вернул значения баллов, которые являются наиболее близкими к числу, введенному в исходной ячейке G2 рабочего листа, а также и имена, соответствующие тем значениям.

По одному запросу нужно получить ближайшее значение числа баллов и соответствующее ему имя.

Поиск ближайшего значения без массива в Excel

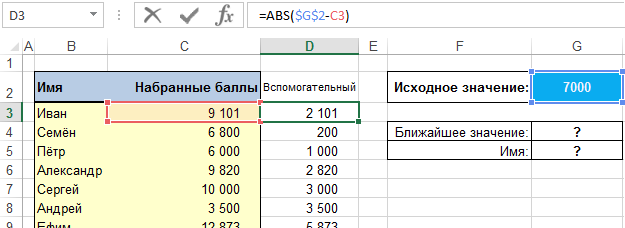
Одним из простых способов решения проблемы является использование вспомогательного столбца. В ячейках этого столбца будут находиться абсолютные значения разности исходного числа и баллов из списка.

Разумеется, решение нашей проблемы будет найдено в строке, в которой это значение является наименьшим.

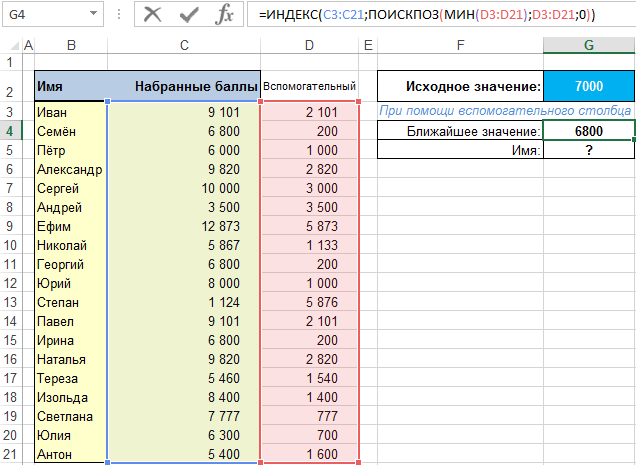
Чтобы выбрать соответствующее значение и соответствующее ему имя, достаточно использовать следующие формулы с использованием функций ИНДЕКС и ПОИСКПОЗ. Для ближайшего значения:

Для имени соответствующему ближайшему значению:

Где столбец «D» — наш вспомогательный столбец, а столбец «B» — столбец с именами. Сразу же добавлю (для ясности), что столбец «C» является столбцом со значениями баллов.

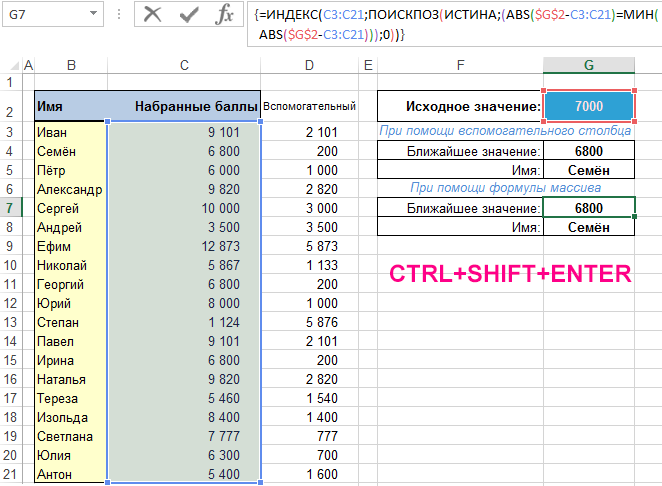
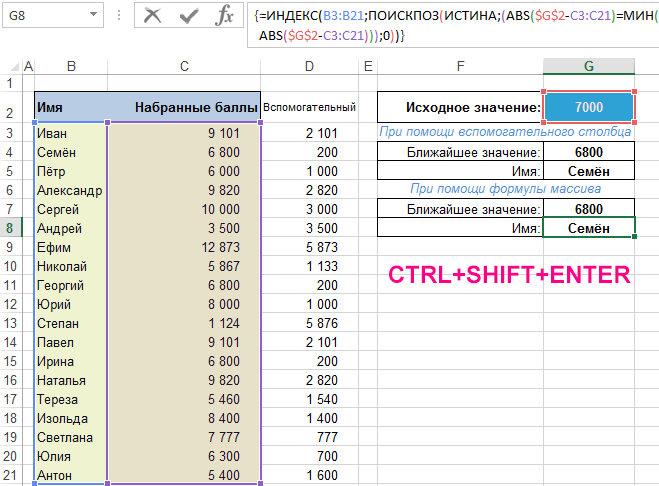
Поиск ближайшего значения в массиве Excel

Решение «хардкор» с использованием формул массива (для любителей и тех, кто просто хочет потренироваться в создании формул массива).

Поиск ближайшего значения в массиве (CTRL+SHIFT+ENTER):

Поиск соответствующего ему имени в массиве (CTRL+SHIFT+ENTER):

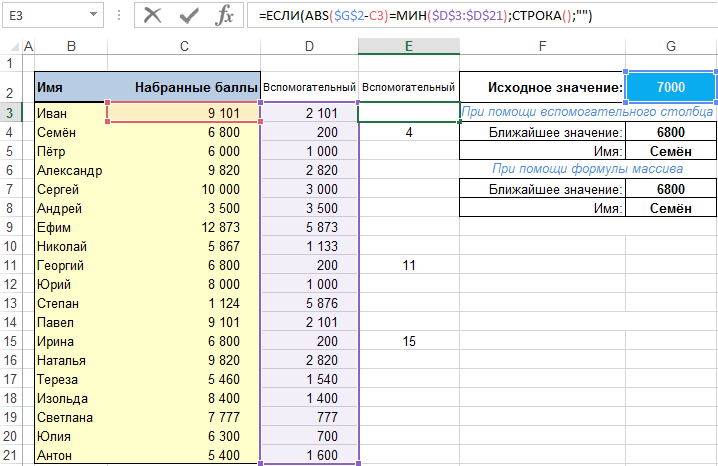
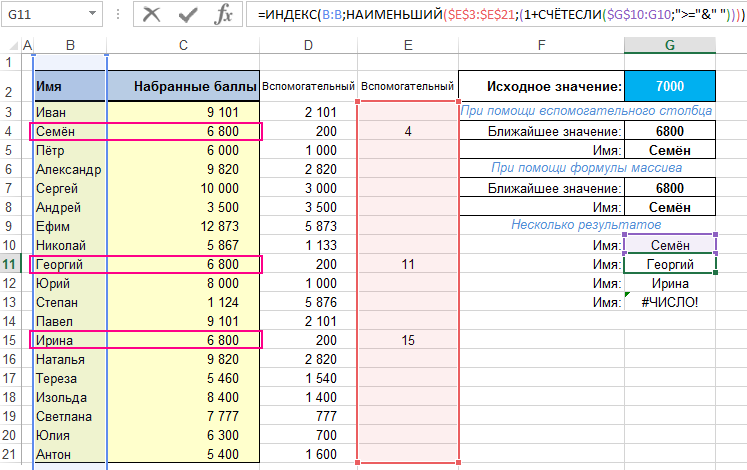
Повторяющиеся ближайшие значения в Excel

Два способа, которые показаны выше, возвращают только одно значение. Поэтому, когда нескольким именам соответствуют равные значения баллов, формула возвращает только первое имя из списка.

Итак, каким же образом можно заставить Excel вернуть список всех имен с интересующими нас значениями баллов при наличии дубликатов ближайших значений?

Есть два решения с использованием вспомогательного столбца. Первое без, а второе с использованием формул массива.

Сначала подготовим для себя вспомогательный столбец. Первая ячейка будет содержать формулу:

которую затем перетягиваем (копируем) в другие ячейки вспомогательного столбца.

Формула должна возвращать номер строки, в которой находится значение, наиболее близкое к искомому. В противном случае возвращает пробел.

Без использования формул массива

Вспомогательный столбец уже готов, мы можем вернуться к нашему поиску.

В первой ячейке диапазона, в котором вы хотите иметь список всех имен, введите следующую формулу:

а в ячейку ниже, которая будет возвращать следующее имя, введите формулу:

которую затем скопируйте еще ниже. В результате все выглядит более или менее так, как показано на рисунке ниже. Как видите, в результате работы указанных формул вы получаете список всех имен, которые соответствуют искомому критерию.

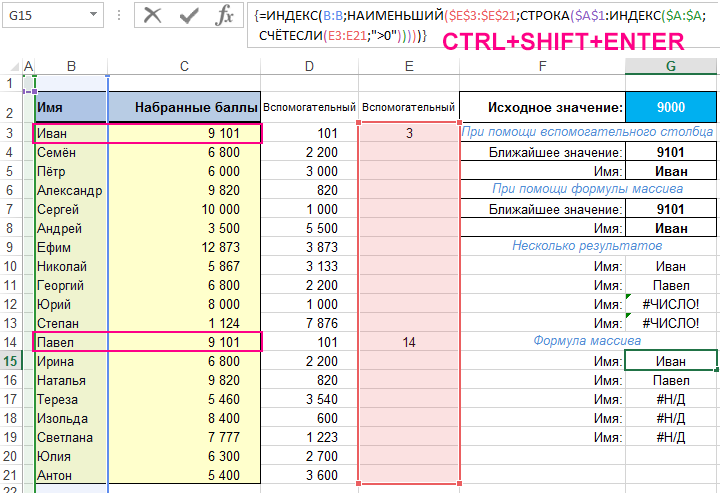
Поиск дублирующийся ближайших значений в массиве Excel

В завершении то же самое, но с использованием формул массива (мы используем вспомогательный столбец, описанный ранее).

Выбираем диапазон ячеек, в которых мы хотим иметь список имен (например, G15:G19) и используем формулу массива:

Формула точно вернет то, что вы ожидаете. Во всех «не соответствующих результатам» ячейках формула вернет код ошибки. При необходимости их легко удалить или поместить в аргументы функции ЕСЛИОШИБКА.

Источник

C

C++

Java

Python

C

Java

Python

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://i1.social.s-msft.com/globalresources/Images/trans.gif?cver=0001" alt=" locked" /> Поиск ближайшего значения в массиве

Вопрос

Ответы

Как найти ближайшее большее значение по формуле в Excel

Поиск ближайшего значения без массива в Excel

Поиск ближайшего значения в массиве Excel

Повторяющиеся ближайшие значения в Excel

Без использования формул массива

Поиск дублирующийся ближайших значений в массиве Excel

Не пропустите также:

Поиск ближайшего значения в массиве