Как найти авых в физике - AvtoShod.ru - решение различных проблем

Вопрос 15 Электрический ток в металлах. Работа выхода.

Металлы в твёрдом состоянии имеют кристаллическую
структуру: расположение атомов в пространстве характеризуется периодической
повторяемостью и образует геометрически правильный рисунок, называемый кристаллической
решёткой.

Проводимость металлов обусловлена наличием свободных
электронов, которые могут перемещаться между ионами, находящимися в узлах
кристаллической решётки.

Газ свободных электронов в кристаллической решетке металла
представляет собой модель, показанную на. рисунке 15.1, где выделена траектория
одного из электронов.

Если
металлический проводник включить в замкнутую цепь, содержащую источник
тока, то

свободные
электроны продолжают Рисунок 15.1

совершать хаотическое тепловое движение, но
теперь — под действием возникшего внешнего электрического поля — они вдобавок
начнут перемещаться упорядоченно. Это направленное течение электронного
газа, накладывающееся на тепловое движение электронов, и есть электрический
ток в металле (поэтому свободные электроны называются также электронами
проводимости). Скорость упорядоченного движения электронов в металлическом
проводнике составляет приблизительно 0,1 мм/с.

О природе электрического тока в металлах было поставлено
множество опытов.

1) Опыт
Рикке

В 1901 году немецкий физик Э. Рикке поставил опыт,
доказывающий проводимость металлов за счёт свободных электронов.

В электрическую цепь были включены три прижатых друг к
другу цилиндра: два медных по краям и один алюминиевый между ними (рисунок
15.2). По этой цепи пропускался электрический ток в течение года.

Рисунок 15.2. Опыт Рикке

За год сквозь цилиндры прошёл заряд более трёх миллионов
кулон. Предположим, что каждый атом металла теряет по одному валентному
электрону, так что заряд иона равен элементарному заряду q_e = 1,6·10^-19
Кл Если ток создаётся движением положительных ионов, то нетрудно подсчитать
(сделайте это сами!), что такая величина прошедшего по цепи заряда
соответствует переносу вдоль цепи около 2кг меди.

Однако после разъединения цилиндров было обнаружено лишь
незначительное проникновение металлов друг в друга, обусловленное естественной
диффузией их атомов (и не более того). Электрический ток в металлах не
сопровождается переносом вещества, поэтому положительные ионы металла не
принимают участия в создании тока.

2) Опыты
Стюарта и Толмена

Прямое экспериментальное доказательство того, что
электрический ток в металлах создаётся движением свободных электронов, было
дано в опыте Т.Стюарта и Р.Толмена (1916 год).

Эксперименту Стюарта–Толмена предшествовали качественные
наблюдения, сделанные четырьмя годами ранее русскими физиками Л.И.Мандельштамом
и Н.Д.Папалекси. Они обратили внимание на так называемый электроинерционный
эффект: если резко затормозить

движущийся проводник, то в
нём возникает кратковременный импульс тока. Эффект объясняется тем, что в
течение небольшого времени после торможения проводника его свободные заряды
продолжают двигаться по инерции.

Однако никаких
количественных результатов Мандельштам и Папалекси не получили, и
наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит
Стюарту и Толмену, которые не только наблюдали указанный электроинерционный
эффект, но и произвели необходимые измерения и расчёты.

Установка Стюарта и Толмена показана
на рисунке

15.3

Рисунок 15.3.

Катушка с большим числом витков металлического провода
приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью
скользящих контактов были подсоединены к специальному прибору — баллистическому
гальванометру, который позволяет измерять проходящий через него заряд.

После резкого торможения катушки в цепи возникал импульс
тока. Направление тока указывало на то, что он вызван движением отрицательных
зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по
цепи, Стюарт и Толмен вычислили отношение заряда одной частицы к её массе q/m.
Оно оказалось равно отношению заряда к массе электрона, которое в то время уже
было хорошо известно:

Так было окончательно выяснено, что носителями свободных
зарядов в металлах являются свободные электроны. Как видите, этот давно и
хорошо знакомый вам факт был установлен сравнительно поздно — учитывая, что
металлические проводники к тому моменту уже более столетия активно
использовались в самых разнообразных экспериментах по электромагнетизму
(сравните, например, с датой открытия закона Ома — 1826 год. Дело, однако,
заключается в том, что сам электрон был открыт лишь в 1897 году).

На этой основе можно объяснить существование работы выхода
электронов из металла. Оказывается между металлом и вакуумом существует
контактная разность потенциалов. Так как в процессе движения электроны могут
покидать его, образуя «электронное облако». Часть электронов снова возвращается
в металл, другие снова его покидают. Явление очень похоже на испарение
жидкости. Толщина этого слоя равна нескольким межатомным расстояниям и
составляет d = (10^-10 – 10^-9) м. По вычислениям
контактная разность потенциалов составляет примерно φ = 1,4 В.

Для выхода электрона из металла тоже совершаться работа,
которая называется работой выхода. В вакууме работа выхода вычисляется по
формуле:

Для всех металлов работу выхода можно определить по
справочнику:

3) Классическая
электронная теория проводимости металлов

В 1900 году П.Друде создал классическую электронную теорию
проводимости металлов, которую затем развил Г. Лоренц. Согласно этой теории ,
электронный газ в металле рассматривается по аналогии с идеальным газом.

Основные положения теории:

1)
Свободные электроны в металлах ведут себя как молекулы идеального
газа и подчиняются его законам.

2)
Движение свободных электронов в металлах подчиняется законам
механики Ньютона.

3)
Свободные электроны в процессе хаотического движения сталкиваются
не между собой, а с ионами кристаллической решётки.

4)
При столкновении электронов с ионами, электроны передают свою
кинетическую энергию полностью.

Теория, построенная учёными является приближенной (грубой),
но объясняет многие законы электрического тока в металлах. Количественная
теория движения электронов в металле строиться на законах квантовой физики.

Решение задач

Задача 1 Сможет ли вылететь электрон из алюминия,
летящий со скоростью 8500 км/с, если работа выхода электрона из алюминия равна
4,25эВ (табличная величина)?

Дано: = 8500 км/с = 85·10⁵
м/с, А_вых = 4,25 эВ

Найти: сможет ли вылететь электрон
из алюминия — ?

Решение: для ответа на вопрос
необходимо сравнить кинетическую энергию электрона с работой выхода электрона
из металла, если Е_кин> А_вых, то электрону хватит этой
кинетической энергии, чтобы вылететь из металла.

Переведём работу
выхода из электрон Вольт в Джоули А_вых = 4,25 эВ = 4,25·1,6·10^-19
= 6,8·10^-19 Дж.

Найдём кинетическую энергию электрона:

Так как Е_кин>
А_вых, значит электрон сможет вылететь из алюминия Ответ:
электрон сможет вылететь из алюминия.

Источник

Все основные формулы по школьной физике, которые помогут для подготовке к ЕГЭ, а также для решения задач в 7, 8, 9, 10 и 11 классах. Все формулы структурированы, что позволит из запомнить гораздо быстрее.

Равномерное движение
S= U∙t, U= S/t, t=S/U	Уравнение движения при равномерном движении? где U-скорость, t-время, S-расстояние
x=x₀+U₀t	Координата при равномерном прямолинейном движении
Равномерное движение по окружности
T=t/N, T=1/v, Т=2π/ω T=2πR/U, T=2π ∙√(R/a)	T – период N – количество оборотов
v=1/T, v=ω/2π, v=U/2πR, v=1/2π ∙√(a/R), v=N/t, v=L/t	v – частота R – радиус окружности
ω=2π/Т, ω=2πv, ω=φ/t ω=U/R, ω=√(a/R)	ω – угловая скорость t – время
υ=2πR/Т, υ=2πvR, U=ωR U=√(a/R), U=L/t	U – линейная скорость тела
a=υ²/R, a=ω²R, a=Uω a=4π²R/T²	a – центростремительное ускорение
L=φR	L – длина дуги окружности (φ – угол поворота (в радианах))
Равноускоренное движение
X=X₀+υ₀∙t+(a∙t²)/2	Уравнение прямолинейного равноускоренного движения
S=U₀t+a∙t²/2 S= (υ²-υ₀²) /2а S= (υ+υ₀) ∙t /2 = U_ср∙t	Расстояние при равноускоренном движении
υ=υ₀+a∙t	Rонечная скорость тела при равноускоренном движении
a=(υ-υ₀)/t	Ускорение
U=√(2gh) t_{падения}=√(2h/g) S=U∙√(2h/g)	— Падение тела с высоты — Горизонтальный бросок (h-высота падения, g – ускорение свободного падения 9,8м/с², t-время падения, S-расстояние)
h_max=U₀²/2g	Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью U₀
t_{подъема}=U₀/g	Время подъема тела на максимальную высоту
t_полета=2U₀/g	Полное время полета (до возвращения в исходную точку)
S_торм=U₀²/2a	Тормозной путь тела двигавшегося до начала торможения со скоростью U₀ , а затем тормозившего с ускорением а
U = √(U₀²+(gt)²) tgβ = U_y/Ux = gt/U₀	Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту
h_max=(U₀∙sinα)²/2g t_{подъема}=(U₀∙sinα)/g	Бросок с земли на землю под углом к горизонту равным α. Время подъема до высшей точки и максимальная высота
S_x=U_x∙t_полетаS=U₀∙cosα∙t_полета S=U₀²∙sin2α/g t_полета=2U₀²∙sinα/g	Полное время и дальность полета при броске под углом к горизонту
Импульс
p=mυ	Импульс тела
Ft=∆p	Импульс силы
F=∆p/∆t	Второй закон Ньютона в импульсной форме
p_k=p_n	Закон сохранения импульса: в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется
Энергия
A=F∙S∙cosα	Механическая работа (F – сила, S – путь,  – угол между направлением движения и силой)
P=A/t=F∙υ	Мощность (если мощность переменная, то рассчитывается средняя мощность)
Eп=mgh	Потенциальная энергия тела, поднятого над землей
Eп=kx²/2	Потенциальная энергия упруго деформированного тела
η=Aп/Аз	Коэффициент полезного действия
Ek=mυ²/2	Кинетическая энергия тела
Молекулярная физика
ρ=m/V	Плотность (ρ – его плотность, m – масса вещества, V – объем)
ν=N/ Na = m/M	Количество вещества (N – число частиц вещества, содержащееся в массе вещества m, Na – число Авогадро, m0 – масса одной молекулы вещества, M – молярная масса)
М=m/ν	Молярная масса
m₀=m/N=M/Na	Масса одной молекулы вещества
P=nkT=1/3nm₀υ²pV=NkT	Основное уравнение молекулярно-кинетической теории идеального газа (p – давление газа, n = N/V – концентрация его молекул, m0 – масса одной молекулы, Uкв – средняя квадратичная скорость)
U_кв=√(3kT/m₀), U_кв=√(3RT/M)	Cредняя квадратичная скорость
Ek=3/2∙kT	Средняя кинетическая энергия поступательного движения одной молекулы (k – постоянная Больцмана, T – абсолютная температура)
kNa=R	Связь универсальной газовой постоянной и постоянной Авогадро
PV=m/M∙RT	Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)
PV=const (m=const и T= const)	Газовые законы. Закон Бойля-Мариотта (изотермический процесс)
V/T=const (m=const и p= const)	Газовые законы. Закон Гей-Люссака (изобарный процесс)
P/T =const (m=const и V= const)	Газовые законы. Закон Шарля (изохорный процесс)
PV/T=const (m=const )	Газовые законы. Универсальный газовый закон (Клапейрона)
V=Vo(1+λt)	Тепловое расширение газов описывается законом Гей-Люссака. (V – объем жидкости при 0 °С, V – при температуре t , λ – коэффициент объемного расширения жидкости)
l=lo(1+αt) S=So(1+2αt) V=Vo(1+3αt)	Изменение линейных размеров, площади и объема тела (lo, So , Vo – соответственно длина, площадь поверхности и объем тела при 0 °С, α – коэффициент линейного расширения тела)
Динамика
Первый закон Ньютона	Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения
F=ma	Второй закон Ньютона (F – сила, m – масса, а – ускорение).
F_1-2= — F_2-1	Третий закон Ньютона (сила действия равна силе противодействия)
F_упр = kx	Сила упругости (k – жесткость пружины, х – величина растяжения (или сжатия) пружины, оно равно разности между конечной и начальной длиной деформируемой пружины)
Fy=-kx	Закон Гука
F_{тр.скольжения}=F_{тр.макс} = μТ	Сила трения скольжения ( μ– коэффициент трения, N – сила реакции опоры.)
F=mg F=G∙M∙m/r²g=G∙M/R_n²	Сила тяжести — Закон Всемирного тяготения (G – гравитационная постоянная, F – сила с которой притягивается тело массой m к телу или планете массой M, r – расстояние между центрами этих тел)
g_h= GM/(R_n+h)² = g_h= gR_n²/(R_n+h)²	Ускорение свободного падения на некоторой высоте от поверхности планеты (h – высота над поверхностью планеты)
U= √(GM/(R_n+h)) U= √(gR_n²/(R_n+h))	Скорость спутника на круговой орбите радиусом r = R_n + h
U=√(gR_n)	Первая космическая скорость (скорость движения спутника по орбите вблизи поверхности планеты)
T₁²/T₂²= R₁³/R₂³	Закон Кеплера для периодов обращение T1 и T2 двух тел, вращающихся вокруг одного притягивающего центра на расстояниях R1 и R2 соответственно
Р=m(g+a) Р=m(g-a)	Вес тела, движущегося с ускорением а↑ Вес тела, движущегося с ускорением а↓
Термодинамика
Q=cm(T₂-T₁) C=cm Q=C(T₂-T₁)	Количество теплоты (энергии) необходимое на нагревания некоторого тела (C-теплоемкость, c-удельная теплоемкость, m- масса, t- температура)
Q=λm	Количество теплоты при плавлении (λ – удельная теплота плавления, m – масса расплавившегося тела или кристаллизовавшейся жидкости)
Q=rm	Количество теплоты при парообразовании (r – удельная теплота парообразования, m – масса испарившейся жидкости или конденсировавшегося пара)
Q=qm	Количество теплоты при сгорании топлива (q – удельная теплота сгорания топлива, m – масса сгоревшего топлива)
A=P∙ΔV = m/M∙ R∙ΔT, p = const	Работа идеального газа
U=3/2∙M/µ∙RT	Внутренняя энергия идеального одноатомного газа
ΔU=A+Q	Первый закон (начало) термодинамики (ЗСЭ) (Q – теплота полученная (отданная) газом)
η= (Q₁— Q₂)/ Q₁	КПД тепловых двигателей
η= (Т₁— Т₂)/ Т₁	КПД идеальных двигателей (цикл Карно)
ρ=pM/RT	Абсолютная влажность (ρ — абсолютная влажность, р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура)
φ=ρ/ρ₀∙100% φ=P/P₀∙100%	Относительная влажность (ρ — абсолютная влажность, ρ₀ -количество водяного пара, которое необходимо для насыщения 1 м3 воздуха при данной температуре) (P — давление водяного пара, Pо — давление насыщенного пара при данной температуре)
E_p = σS	Поверхностное натяжение (σ – коэффициент поверхностного натяжения данной жидкости)
F_н= σL	Сила поверхностного натяжения, действующая на участок границы жидкости длиной L
Статика и Гидростатика
M=F∙ℓ	Момент силы (F – сила, ℓ – плечо силы, т.е. кратчайшее расстояние между точкой опоры, относительно которой происходит вращение и линией действия силы)
Р=F/S	Давление (F – сила, S – площадь на которую распределено действие силы)
P=ρ∙g∙h P=P₀+ρ∙g∙h	Давление на глубине жидкости (p0 – атмосферное давление, ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости)
Fa=ρ_ж∙g∙V	Закон (сила) Архимеда (V – объем погруженной части тела, который иногда также называют объемом вытесненной жидкости)
Электростатика
q = Ne	Электрический заряд (N – количество элементарных зарядов, е – элементарный заряд)
λ=q/L, σ=q/S, ρ=q/V	Линейная, поверхностная и объемная плотность заряда
F=k∙q₁∙q₂/R²F=k∙q₁∙q₂/εr²	Закон Кулона (сила электростатического взаимодействия двух зарядов величиной q1 и q2, находящихся на расстоянии r друг от друга в веществе с диэлектрической проницаемостью ε):
E=1/(4πεε₀)	Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра
E= σ/(2εε₀)	Напряженность электрического поля, которую создает заряженная плоскость
ε=E₀/E	Диэлектрическая проницаемость
E=F/q	Напряженность электрического поля
E=k∙q/R²	Напряженность электрического поля точечного заряда
E=2πkσ	Напряженность электрического поля бесконечной плоскости
W= k∙q₁q₂/R = k∙q₁q₂/εr	Потенциальная энергия взаимодействия двух электрических зарядов
U=Ed, Δφ=E∙ Δl	Cвязь между напряженностью поля и напряжением
A=qU, U=A/q	Работа электрического поля, Напряжение
A= qEd, U=E∙d	Работа электрического поля в однородном поле при перемещении заряда вдоль его силовых линий, Напряжение для однородного электрического поля
φ=W/q	Потенциал
φ=k∙q/R	Потенциал точечного заряда
C=q/U	Электроемкость
C=S∙ε∙ε₀/d	Электроемкость плоского конденсатора
q=CU	Заряд конденсатора
E = U/d = σ/εε₀	Напряженность поля внутри конденсатора
F=qE/2	Сила притяжения пластин конденсатора
W=qU/2=q²/2С=CU²/2	Энергия заряженного конденсатора
Электрический ток
I=q/t	Сила тока (q – заряд, протекший через некоторое поперечное сечение проводника за время t)
R=ρ∙ℓ/S	Сопротивление проводника (l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника)
R=R₀(1+αt)	Сопротивление проводника
I=U/R	Закон Ома для участка цепи (U – электрическое напряжение)
I₁=I₂=I, U₁+U₂=U, R₁+R₂=R	Законы последовательного соединения
U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R	Законы параллельного соединения
ε=A_ст/q	Электродвижущая сила источника тока, ЭДС (Aст – работа сторонних сил по перемещению заряда q)
I=ε/(R+r)	Закон Ома для полной цепи
I=ε/r	Сила тока короткого замыкания (R=0)
Q=A=I²Rt	Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока, протекающего по проводнику, обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике
P=IU=U²/R=I²R	Мощность электрического тока
m = kQ = kIt	Электролиз. Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит
Магнетизм
Fa=IBℓsinα	Сила Ампера (В – индукция магнитного поля, I – сила тока в проводнике, l – его длина, α – угол между направлением силы тока (т.е. самим проводником) и вектором индукции магнитного поля)
M = NBIS∙sinα	Момент сил, действующих на рамку с током (N – количество витков, S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции)
Fл=Bqυ∙sinα	Сила Лоренца (q – электрический заряд частицы, υ – её скорость, α – угол между направлением движения частицы и вектором индукции магнитного поля)
R=mU/qB	Радиус траектории полета заряженной частицы в магнитном поле
B=Fmax/ℓ∙I	Вектор магнитной индукции
Ф=BSсos α Ф=LI	Магнитный поток Φ через площадь S
Ei=ΔФ/Δt	Закон электромагнитной индукции
Ei=Вℓυsinα	ЭДС индукции при движении проводника
Esi=-L∙ΔI/Δt	ЭДС самоиндукции
Wм=LI²/2	Энергия магнитного поля катушки
Колебания
a+ω₀²x=0	Уравнение описывает физические системы способные совершать гармонические колебания с циклической частотой ω0
x = A cos (ωt + φ0)	Уравнением движения для гармонических колебаний (x– координата тела в некоторый момент времени t, A – амплитуда колебаний, ω – циклическая частота колебаний, φ0 –начальная фаза колебаний).
Х=Хmax∙cos ωt	Уравнение гармонических колебаний
T=t/N, v=N/t=1/T ω=2πv=2π/T	Связь некоторых характеристик колебательного процесса (T – период, N – количество полных колебаний, v – частота колебаний, ω – циклическая частота)
υ = x'(t) = –Aω sin (ωt + φ0)	Скорость тела при колебательном движении
υ_m = ωA	Максимальное (амплитудное) значение скорости
a = υ'(t) = x»(t) a = –Aω² cos (ωt + φ0)	Ускорение тела при колебательном движении
a_m = Aω²	Максимальное (амплитудное) значение ускорения
ω₀=√(g/ℓ) T=2π√ℓ/g	Циклическая частота и период колебаний математического маятника (l – длина маятника, g – ускорение свободного падения)
ω₀=√(k/m) T=2 π √m/k	Циклическая частота и период колебаний пружинного маятника (m – масса груза, k – коэффициент жесткости пружины маятника)
W=CU²/2+LI²/2 W=CU_max²/2=LI_max²/2	Электрический контур
T=2π ∙√LC ω=2π/T=1/(√LC)	Период колебаний кол. контура и циклическая частота
I_д=I₀/√2, I_д=I_max/√2 U_д=U₀/√2, U_д=U_max/√2	Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин; Действующее значение силы тока и напряжения
P=U_дI_д=I_д²R=U_д²/R	Мощность в цепи переменного тока
U₁/U₂=n₁/n₂	Трансформатор: если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2
λ= υТ=υ/v	Волны. Длина волны (υ – скорость распространения волны, T – период, v – частота)
X_L=ωL=2πLν	Индуктивное сопротивление
Xc=1/ωC	Емкостное сопротивление
Z=√(Xc-X_L)²+R²	Полное сопротивление
Оптика
L_опт=L_n	Оптическая длина пути (L – геометрическая длина траектории, по которой «идет» луч света, n – показатель преломление среды, в которой это происходит)
x=mλL/d	Интерференционная схема Юнга (L – расстояние между экраном и плоскостью в которой расположены две щели, d – расстояние между этими щелями, λ – длина волны света, которым освещаются щели).
d∙sin φ=k λ	Формула дифракционной решетки (d – период решетки, или расстояние между соседними штрихами, φ – угол под которым наблюдается очередной дифракционный максимум, k – номер (порядок) максимума, λ – длина волны света, падающего на дифракционную решетку)
n₂₁=n₂/n₁= υ₁/ υ₂	Закон преломления света на границе двух прозрачных сред (α – угол падения, β – угол преломления, n1 – показатель преломления первой среды, из которой падает луч, n2 – показатель преломления второй среды, в которую проникает луч)
n₂₁=sinα/sinβ	Показатель преломления
1/F=1/d + 1/f	Формула линзы (d – расстояние от линзы до предмета, f – расстояние от линзы до изображения, F – фокусное расстояние, D – оптическая сила линзы)
D=1/F	Оптическая сила линзы
Δd=kλ, Δd=(2k+1)λ/2	max интерференции, min интерференции
Атомная и ядерная физика
E=hv=hc/λ	Энергия кванта света, т.е. фотона (h – постоянная Планка, λ – длина волны света, v – частота света)
P=mc=h/ λ=Е/с	Импульс фотона
hν=A_вых+(mU²/2)_max hν=A_вых+Ek, Ek=еU_зhν_min=A_вых=hc/λ	Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ) (А_вых – работа выхода, слагаемое в скобках –максимальная кинетическая энергия вылетающих электронов, v – частота падающего света)
(mU²/2)_max=еU_з	Максимальная кинетическая энергия вылетающих электронов
ν_к = A_вых/h	Красная граница фотоэффекта
hν_nm = \|En – Em\|	Второй постулат Бора (правило частот). При переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний
N=N₀∙2^—^t^/^T	Закон радиоактивного распада
E_CB=(Zm_p+Nm_n-Mя)∙c²	Энергия связи атомных ядер
Основы СТО
ℓ=ℓ₀∙√1-υ²/c²	Релятивистское сокращение длины. Длина тела, движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины
t=t₁/√(1-υ²/c²)	Релятивистское удлинение времени события. Время, за которое происходит некоторое событие в движущейся системе отсчета с точки зрения наблюдателя из неподвижной системы отсчета
υ=(υ₁+υ₂)/1+ υ₁∙υ₂/c²	Релятивистский закон сложения скоростей
Е = mс²	Связь энергии и массы тела. Наименьшей энергией Е0 тело обладает в инерциальной системе отсчета относительно которой оно покоится и называется собственной энергией тела (энергия покоя тела)

Источник

Изучение законов фотоэффекта привело ученых к неожиданному выводу: при взаимодействии с веществом (поглощении или излучении) свет ведет себя подобно движущимся частицам (квантам). Что это за частицы? Каковы их свойства и как они связаны с волновыми характеристиками света?

Электронвольт — энергия, которую приобретет частица с зарядом, равным элементарному, при перемещении между двумя точками с ускоряющей разностью потенциалов 1В ().

Развивая идеи Планка, Эйнштейн в 1905 г. для объяснения экспериментальных законов внешнего фотоэффекта выдвинул гипотезу о дискретности самого электромагнитного излучения — свет излучается, поглощается и распространяется в виде отдельных порций (квантов). Он рассмотрел элементарные процессы поглощения и испускания этих квантов.

По гипотезе Эйнштейна, монохроматическое электромагнитное излучение частотой обладает не только волновыми свойствами, но и свойствами характерными для потока частиц. Каждая такая частица движется со скоростью света с и несет квант энергии . Назвать эти частицы фотонами предложил в 1928 г. американский физик Артур Комптон.

Энергия фотона может быть выражена через длину волны λ:

(1)

Из релятивистского определения импульса для фотона следует, что модуль его импульса определяется выражениями:

(1-1)

Следовательно, для фотона:

Исключая скорость из релятивистских выражений импульса и энергии тела:

получаем соотношение:

(1-2)

Для фотона из формулы (1-2) находим, что масса фотона равна нулю (m = 0).

Масса фотона, движущегося со скоростью света в вакууме, равна нулю.

Таким образом, фотон — удивительная частица, которая обладает энергией E = hν, импульсом , но вследствие того, что скорость фотона всегда равна скорости света в вакууме, то масса равна нулю (m = 0). Такие частицы называют безмассовыми.

Фотон является элементарной частицей, только в отличие от других элементарных частиц он не имеет массы, а потому «обречен» всегда двигаться со скоростью распространения света.

Таким образом, фотон обладает следующими свойствами:

— существует только в движении;

— является безмассовой частицей (m = 0);

— электрически нейтрален (q = 0);

—скорость его движения равна скорости распространения света в вакууме во всех ИСО;

— его энергия пропорциональна частоте соответствующего электромагнитного излучения (E = hν);

— модуль импульса фотона равен отношению его энергии к модулю скорости движения ().

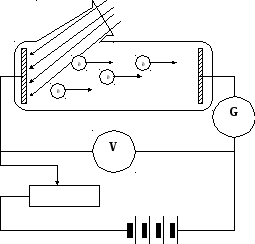
Рассмотрим объяснение экспериментальных законов фотоэффекта, предложенное Эйнштейном на основе квантовых представлений. При освещении электрода электромагнитным излучением (см. рис. 171) происходит взаимодействие фотонов с электронами вещества. Если энергия фотона E = hν достаточно велика, то какой-либо из электронов после поглощения фотона может получить энергию достаточную для того, чтобы покинуть облучаемый образец. Электроны, покинувшие образец, имеют некоторую скорость, поэтому даже при отсутствии напряжения между электродами сила фототока не равна нулю. Именно поэтому, вольтамперная характеристика фотоэффекта при напряжении, равном нулю, не проходит через нуль (см. рис. 172, в).

Для того чтобы покинуть вещество электрон должен совершить работу против сил взаимодействия электрона с атомами вещества. Таким образом, минимальная энергия необходимая для выбывания электрона с поверхности вещества, называется работой выхода и обозначается А_вых(А_вых > 0). Для металлов эта работа связана с преодолением сил взаимодействия электронов с положительно заряженными ионами кристаллической решетки, которые удерживают электрон в веществе. Работа выхода для металлов обычно составляет несколько электронвольт (см. табл 9).

Таблица 9. Фотоэлектрические характеристики некоторых веществ

Вещество			λ_к, нм
Цезий	1,9	4,6	650
Калий	2,2	5,3	560
Натрий	2,3	5,6	540
Кальций	2,7	6,5	460
Цинк	3,7	8,9	340
Серебро	4,3	10	260
Вольфрам	4,5	11	280
Никель	5,0	12	250
Платина	5,3	13	230

Оставшаяся часть энергии поглощенного кванта составляет кинетическую энергию освободившегося электрона. Наибольшей кинетической энергией $begin mathsize 20px style fraction numerator m straight upsilon subscript max superscript 2 over denominator 2 end fraction end style$ будут обладать те электроны, которые поглотят кванты света вблизи поверхности металла и вылетят из него, не успев потерять энергию при столкновениях с другими частицами в металле. На основе закона сохранения энергии можно записать следующее уравнение для фотоэлектрона:

(2)

Это соотношение называют уравнением Эйнштейна для внешнего фотоэффекта.

Отметим, что — это максимальная кинетическая энергия электрона , которой он может обладать, вылетев из вещества. Из-за различных потерь кинетическая энергия электрона будет меньше расчетного значения.

Если энергия фотонов очень велика (рентгеновское или -излучение) для кинетической энергии необходимо использовать релятивистское выражение:

так как скорости фотоэлектронов сравнимы со скоростью света

Используя уравнение Эйнштейна, можно объяснить экспериментальные законы фотоэффекта.

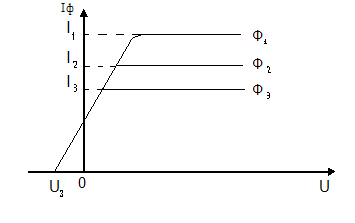
Объяснение первого закона фотоэффекта. Сила фототока насыщения пропорциональна общему числу фотоэлектронов, покидающих поверхность металла за единицу времени. Число таких фотоэлектронов, в свою очередь, пропорционально числу фотонов, падающих на поверхность за это же время. Именно пропорционально, а не равно, так как часть квантов света поглощается кристаллической решеткой, и их энергия переходит во внутреннюю энергию металла. Таким образом, увеличение интенсивности падающего света приводит к росту числа фотоэлектронов, покидающих поверхность металла.

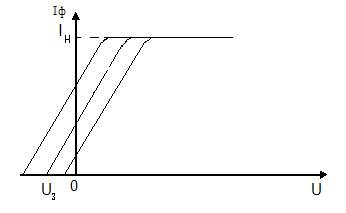
Объяснение второго закона фотоэффекта. Фотоэлектрон вырывается из катода за счет действия одного кванта падающего излучения. Поэтому кинетическая энергия фотоэлектрона зависит не от полной энергии волны, а от энергии одного кванта, т.е. частоты . При увеличении частоты падающего света максимальная кинетическая энергия фотоэлектронов возрастает линейно, как следует из уравнения Эйнштейна для фотоэффекта (3), согласно соотношению:

(3)

Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, «затрудняющее» вылет электронов, то сила тока уменьшится, так как теперь фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.

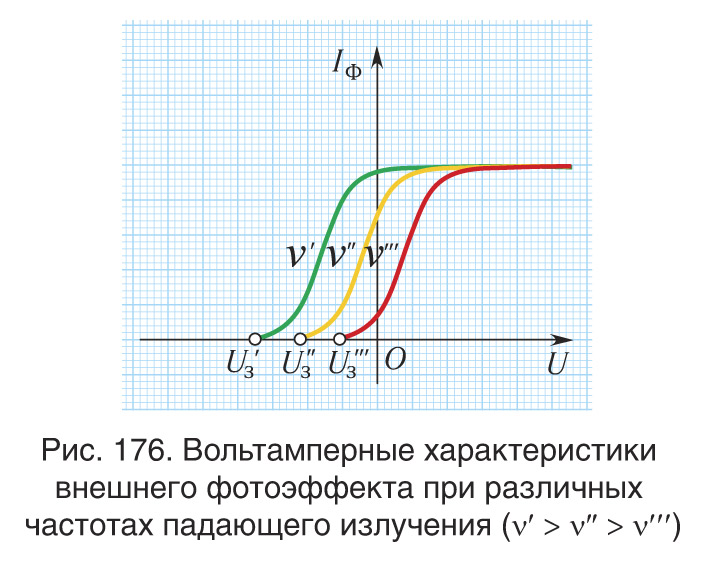
При некотором отрицательном значении напряжения U_з электроны затормаживаются и, не достигнув поверхности анода, возвращаются на катод. Сила тока в цепи при этом будет равна нулю (рис. 176). Величину U_з, при которой сила тока в цепи равна нулю, называют задерживающим напряжением. Следовательно, вся кинетическая энергия электронов затрачивается на работу против сил электрического поля. При этом максимальная кинетическая энергия электронов выражается через задерживающее напряжение следующим образом:

(4)

Объяснение третьего закона фотоэффекта. Если частота ν падающего излучения меньше граничной частоты , при которой , то испускания электронов не происходит . Таким образом, фотоэффект отсутствует, если частота излучения оказывается меньше некоторой характерной для данного вещества величины .

Следовательно, красную границу фотоэффекта можно найти из условия

(5)

Она зависит только от работы выхода электронов, т.е. определяется строением металла и состоянием его поверхности.

Длина волны излучения, соответствующая красной границе фотоэффекта, может быть определена из соотношения

(6)

Из уравнения Эйнштейна для фотоэффекта (2) следует, что, находя тангенс tg α угла наклона прямых линий на рисунке 174, можно вычислить постоянную Планка, так как:

а по точкам пересечения продолжения графиков (см. рис. 175) с осями U_з и — найти работу выхода А_вых и красную границу для данного вещества.

С появлением мощных монохроматических источников света (лазеров) удалось наблюдать процессы многофотонного поглощения. В таких процессах, прежде чем покинуть вещество, электрон может поглотить не один, а с несколько фотонов. Поэтому уравнение Эйнштейна для многофотонного фотоэффекта запишется в виде:

где N — число фотонов, за счет поглощения которых вылетел электрон.

Следовательно, для многофотонного фотоэффекта частота красной границы уменьшается в N раз, а соответствующая ей длина волны в N раз увеличивается:

В настоящее время трудно представить себе современную науку и технику без применения устройств (приемников излучения), преобразующих световые сигналы в электрические. Такие устройства называются фотоэлементами (рис. 177).

Фотоэлементы используются для контроля пассажиропотока в метро, для включения и выключения освещения на улицах, для управления производственными процессами, в военной технике: в самонаводящихся снарядах, для сигнализации и локации. Инфракрасные фотоэлементы широко используются в пультах дистанционного управления различными бытовыми электронными приборами (телевизор, кондиционер и т.д.).

В 1921 г. при присуждении Альберту Эйнштейну Нобелевской премии по физике в решении Нобелевского комитета указывалось, что «премией особенно отмечается объяснение законов фотоэлектрического эффекта».

Первый фотоэлемент на внешнем фотоэффекте был создан Столетовым в 1888 г.

Источник

ЯГМА

Медицинская
физика

Лечебный факультет

1 Курс

2 семестр

Лекция № 9

« Фотоэффект
»

Составил:
Бабенко Н.И..

2011
г.

Фотоэффект.
Законы внешнего фотоэффекта.

Фотоэффект
– группа явлений, связанных с испусканием
электронов возбужденными атомами
вещества за счет энергии поглощенных
фотонов. Открыт немецким ученым Герцем
в 1887 году. Экспериментально изучен
русским ученым А.Г. Столетовым (1888 –
1890г.г.).Теоретически объяснен А. Эйнштейном
(1905 г.).

Виды фотоэффекта.

Внутренний
фотоэффект:

а. Изменение
проводимости среды под действием света,
фоторезистивный
эффект,
характерен для полупроводников.

б. Изменение
диэлектрической проницаемости среды
под действием света, фотодиэлектрический
эффект,
характерен для диэлектриков.

в. Возникновение
фото ЭДС, фотогальванический
эффект,
характерен для неоднородных полупроводников
p
и n
-типа.

Внешний
фотоэффект:

Это явление выхода
(эмиссии ) электронов из вещества в
вакуум за счет энергии поглощенных
фотонов.

Фотоэлектроны
– это электроны вырванные из атомов
вещества за счет фотоэффекта.

Фототок –
это электрический ток, образованный
упорядоченным движением фотоэлектронов
во внешнем электрическом поле.

Свет
(Ф) «К» и «А» —
электроды,

помещенные в вакуум

«V»
— фиксирует напряжение

между электродами

«G» — фиксирует фототок

К(-)

А(+) «П» — потенциометр
для

изменения
напряжения

«Ф»
— световой поток

—
+

Рис. 1. Установка
для изучения законов внешнего фотоэффекта.

Сила
фототока насыщения ( т. е. количество
электронов, испускаемых с катода в
единицу времени ) пропорциональна
световому потоку, падающему на металл
( Рис. 2).

где k
– коэффициент пропорциональности, или
чувствительности металла к фотоэффекту

Рис. 2. Зависимость
фототоков насыщения ( I₁,
I₂,
I₃ ) от
интенсивности световых
потоков: Ф₁>Ф₂> Ф₃.Частота
падающих световых потоков постоянна.

II закон фотоэффекта (закон Эйнштейна — Ленарда).

Если поменять
местами полюса батареи источника ((К(+),
А(-)), то между катодом (К) и анодом (А)
возникает электрическое поле, которое
тормозит движение электронов. При
некотором запирающем значении обратного
напряжения Uз
фототок равен 0 ( Рис. 3 ).

Рис. 3. Зависимость
фототоков насыщения для разных частот
падающего света при постоянной
интенсивности падающего света.

В этом случае
электроны вылетающие с катода, даже с
максимальной скоростью Vmax,
не смогут пройти через запирающее поле.

Измерив значение
запирающего напряжения Uз,
можно определить максимальную кинетическую
энергию E_k_maxвыбиваемых
излучением электронов. При изменении
интенсивности светового потока Ф,
максимальная кинетическая энергия E_k_max
не изменяется, но если увеличить частоту
электромагнитного излучения ( сменить
видимый свет на ультрафиолетовый), то
максимальная кинетическая энергия E_k_max
фотоэлектронов увеличится.

Начальная
кинетическая энергия фотоэлектрона
пропорциональна частоте падающего
излучения и не зависит от его интенсивности.

E_k_max ~ hv

где h
постоянная Планка, v
частота падающего света.

III закон внешнего фотоэффекта (Закон красной границы).

Если последовательно
облучать катод различными монохроматическими
излучениями, можно обнаружить, что с
увеличением длины волны λ,
энергия фотоэлектронов уменьшается и
при некотором значении длины волны λ,
внешний фотоэффект прекращается.

Наибольшее
значение длины волны λ
( или
наименьшее значение частоты v
) при которой внешний фотоэффект еще
имеет место, называется красной
границей фотоэффекта
для данного вещества.

Для серебра λкр
= 260нм

Для цезия λкр
=>620 нм

2. Уравнение Энштейна и его применение к трем законам фотоэффекта.

В1905 году Энштейн дополнил теорию Планка
предположив/, что свет, взаимодействуя
с веществом, поглощается такими же
элементарными порциями (квантами,
фотонами), какими он по теории Планка и
испускается.

Фотон
– это частица, не обладающая массой
покоя (m₀
=0), и движущаяся со скоростью, равной
скорости света в вакууме (c=3·10⁸м/с).

Квант
–- порция энергии фотона.

В основе уравнения
Эйнштейна для фотоэффекта лежат три
постулата:

1. Фотоны
взаимодействуют с электронами атома
вещества и полностью поглощаются ими.

2. Один
фотон взаимодействует только с одним
электроном.

3. Каждый
поглощенный фотон освобождает один
электрон. При этом энергия фотона «ħλ»
расходуется
на работу выхода «ē»
с поверхности вещества А_вых
и на сообщене ему кинетической энергии

ћ·ν
= ћ·
=
— уравнение Эйнштейна

Эта энергия «ħν»
-будет максимальной, если электроны
отрываются от поверхности.

Применение уравнения
к объяснению трех законов фотоэффекта.

К I
закону:

П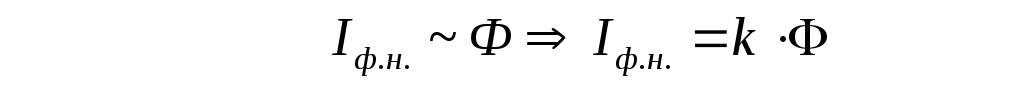ри
увеличении интенсивности монохроматичного
излучения растет число поглощенных
металлом квантов, поэтому растет и число
вылетающих из него электронов и растет
сила фототока:

Ко II закону:

Из
уравнения Эйнштейна:

, т.е. Е_k_maxфотоэлектрона
зависит только от рода металла (А_вых.)
и от частоты ν(λ)
падающего излучения и не зависит от
интенсивности излучения (Ф).

К III закону:

если

ħν<А_вых
– то при любой интенсивности излученя
фотоэффекта не будет, т.к. этой энергии
фотона не хватит, чтобы вырвать ē
из вещества.

ħν>А_вых
– фотоэффект наблюдается, так как
энергии фотона хватит и на работу выхода
А_вых.,
и на сообщение ē
кинетической энергии Е_к_max.

ħν=А_вых
– граница фотоэффекта при которой

и энергии
фотона хватает только на выход ē
с поверхности
металла.

В этом
случае уравнение Эйнштейна имеет вид:

—
красная граница фотоэффекта

Соседние файлы в папке Медицинская физика

Источник

Работа выхода электронов из металлов, не металлов и неорганических соединений (Таблица)

Формула работа выхода электронов

В металлах имеются электроны проводимости, образующие электронный газ и участвующие в тепловом движении. Так как электроны проводимости удерживаются внутри металла, то, следовательно, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. Эта работа, естественно, различна для разных металлов.

Потенциальная энергия электрона внутри металла постоянна и равна:

W_p = -eφ , где j – потенциал электрического поля внутри металла.

При переходе электрона через поверхностный электронный слой потенциальная энергия быстро уменьшается на величину работы выхода и становится вне металла равной нулю. Распределение энергии электрона внутри металла можно представить в виде потенциальной ямы.

В рассмотренной выше трактовке работа выхода электрона равна глубине потенциальной ямы, т.е.

A_вых = eφ

Этот результат соответствует классической электронной теории металлов, в которой предполагается, что скорость электронов в металле подчиняется закону распределения Максвелла и при температуре абсолютного нуля равна нулю. Однако в действительности электроны проводимости подчиняются квантовой статистике Ферми-Дирака, согласно которой при абсолютном нуле скорость электронов и соответственно их энергия отлична от нуля.

Максимальное значение энергии, которой обладают электроны при абсолютном нуле, называется энергией Ферми E_F . Квантовая теория проводимости металлов, основанная на этой статистике, дает иную трактовку работы выхода. Работа выхода электрона из металла равна разности высоты потенциального барьера eφ и энергии Ферми.

A_вых = eφ’ — E_F

где φ’ – среднее значение потенциала электрического поля внутри металла.

Таблица работа выхода электронов из простых веществ

В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.

Вещество	Формула вещества	Работа выхода электронов (W, эВ)
серебро	Ag	4,7
алюминий	Al	4,2
мышьяк	As	4,79 — 5,11
золото	Au	4,8
бор	B	(4,60)
барий	Ba	2,52
бериллий	Be	3,92
висмут	Bi	4,34
углерод (графит)	C	4,45 — 4,81
кальций	Ca	2,76 — 3,20
кадмий	Cd	4,04
церий	Ce	2,6 — 2,88
кобальт	Co	4,40
хром	Cr	4,60
цезий	Cs	1,94
медь	Cu	4,36
железо	Fe	4,40 — 4,71
галлий	Ga	3,96 — 4,16
германий	Ge	4,66
гафний	Hf	(3,53)
ртуть	Hg	4,52
индий	In	(3,60 — 4,09)
иридий	Ir	(4,57)
калий	K	2,25
лантан	La	(3,3)
литий	Li	2,49
магний	Mg	3,67
марганец	Mn	3,76 — 3,95
молибден	Mo	4,20
натрий	Na	2,28
ниобий	Nb	3,99
неодим	Nd	(3,3)
никель	Ni	4,91 — 5,01
осмий	Os	(4,55)
свинец	Pb	4,05
палладий	Pd	(4,98)
празеодим	Pr	(2,7)
платина	Pt	5,30 — 5,55
рубидий	Rb	2,13
рений	Re	4,98
родий	Rh	4,75
рутений	Ru	(4,52)
сурьма	Sb	4,08 — 4,56
скандий	Sc	(3,2 — 3,33)
селен	Se	4,86
кремний	Si	3,59 — 4,67
самарий	Sm	(3,2)
олово (γ-форма)	Sn	4,38
олово (β-форма)	Sn	4,50
стронций	Sr	2,74
тантал	Ta	4,13
теллур	Te	4,73
торий	Th	3,35 — 3,47
титан	Ti	4,14 — 4,50
таллий	Tl	3,68 — 4,05
уран	U	3,27 — 4,32
ванадий	V	3,77 — 4,44
вольфрам	W	4,54
цинк	Zn	4,22 — 4,27
цирконий	Zr	3,96 — 4,16

Таблица работа выхода электронов из неорганических соединений

Вещество	Формула вещества	Работа выхода электронов (W, эВ)
бромистое серебро	AgBr	~3,9
хлористое серебро	AgCl	~4,6
иодистое серебро	AgI	~4,0
сульфид серебра	Ag₂S	~3,8
триоксид бора	B₂O₃	4,7
оксид бария	BaO	1,0 — 1,6
барий вольфрамовокислый	BaWO₄	2,27
окись бериллия	BeO	3,8 — 4,7
окись кальция	CaO	1,8 — 2,4
ортовольфрамат кальция	Ca₃WO₆	2,13
борид хрома	CrB₂	3,36
окись цезия	Cs₂O	1,0 — 1,17
окись меди	CuO	4,35 — 5,34
закись меди	Cu₂O	5,15
окись железа	FeO	3,85
вода	H₂O	6,1
карбид гафния	HfC	2,04
оксид магния	MgO	3,1 — 4,4
диборид марганца	MnB₂	4,14
диборид молибдена	MoB₂	3,38
триоксид молибдена	MoO₃	4,25
силицид молибдена	MoSi₂	5,0 — 6,0
хлористый натрий	NaCl	4,2
борид ниобия	NbB₂	3,65
карбид ниобия	NbC	2,24
окись никеля	NiO	5,55
борид скандия	ScB₂	2,3 — 2,9
кремнезём	SiO₂	5,0
окись стронция	SrO	2,0 — 2,6
карбид тантала	TaC	3,05 — 3,14
пентаоксид тантала	Ta₂O₅	4,65
дикарбид тория	ThC₂	3,5
оксид тория	ThO₂	2,54 — 2,67
сульфид титана	TiS	3,4
диборид титана	TiB₂	3,88 — 3,95
карбид титана	TiC	2,35 — 3,35
нитрид титана	TiN	2,92
окись титана	TiO	2,96 — 3,1
двуокись титана	TiO₂	4,7
карбид урана	UC	2,9 — 4,6
диборид ванадия	VB₂	3,88 — 3,95
диборид вольфрама	WB₂	2,62
диоксид вольфрама	WO₂	4,96
дисилицид вольфрама	WSi₂	5,0 — 6,0
борид циркония	ZrB	4,48
диборид циркония	ZrB₂	3,70
карбид циркония	ZrC	2,2 — 3,8
нитрид циркония	ZrN	2,92

_______________

Источник информации:

1. Landolt-Borstein’s Zahlenwerte und Funktionen aus Phsik, Chemie, Astrunumie, Geophysik, Thechnik, 6-е издание., Берлин, т. I, ч.4, 1955; т. II, ч.6, разд. 1, 1959.

2. В.С. Фоменко. Эмиссионные свойства элементов и химических соединений. Изд. АН УСССР, Киев, 1961.

Источник

1) Опыт Рикке

2) Опыты Стюарта и Толмена

3) Классическая электронная теория проводимости металлов

Решение задач

Равномерное движение

Равномерное движение по окружности

Равноускоренное движение

Импульс

Энергия

Молекулярная физика

Динамика

Термодинамика

Статика и Гидростатика

Электростатика

Электрический ток

Магнетизм

Колебания

Оптика

Атомная и ядерная физика

Основы СТО

II закон фотоэффекта (закон Эйнштейна — Ленарда).

III закон внешнего фотоэффекта (Закон красной границы).

2. Уравнение Энштейна и его применение к трем законам фотоэффекта.

Работа выхода электронов из металлов, не металлов и неорганических соединений (Таблица)

Формула работа выхода электронов

Таблица работа выхода электронов из простых веществ

Таблица работа выхода электронов из неорганических соединений

Не пропустите также:

1) Опыт
Рикке

2) Опыты
Стюарта и Толмена

3) Классическая
электронная теория проводимости металлов