From Wikipedia, the free encyclopedia
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity.
Formally, an automorphism of a graph G = (V, E) is a permutation σ of the vertex set V, such that the pair of vertices (u, v) form an edge if and only if the pair (σ(u), σ(v)) also form an edge. That is, it is a graph isomorphism from G to itself. Automorphisms may be defined in this way both for directed graphs and for undirected graphs.
The composition of two automorphisms is another automorphism, and the set of automorphisms of a given graph, under the composition operation, forms a group, the automorphism group of the graph. In the opposite direction, by Frucht’s theorem, all groups can be represented as the automorphism group of a connected graph – indeed, of a cubic graph.[1][2]
Computational complexity[edit]
Constructing the automorphism group is at least as difficult (in terms of its computational complexity) as solving the graph isomorphism problem, determining whether two given graphs correspond vertex-for-vertex and edge-for-edge. For, G and H are isomorphic if and only if the disconnected graph formed by the disjoint union of graphs G and H has an automorphism that swaps the two components.[3] In fact, just counting the automorphisms is polynomial-time equivalent to graph isomorphism.[4]
This drawing of the Petersen graph displays a subgroup of its symmetries, isomorphic to the dihedral group D5, but the graph has additional symmetries that are not present in the drawing. For example, since the graph is symmetric, all edges are equivalent.
The graph automorphism problem is the problem of testing whether a graph has a nontrivial automorphism. It belongs to the class NP of computational complexity. Similar to the graph isomorphism problem, it is unknown whether it has a polynomial time algorithm or it is NP-complete.[5]
There is a polynomial time algorithm for solving the graph automorphism problem for graphs where vertex degrees are bounded by a constant.[3]
The graph automorphism problem is polynomial-time many-one reducible to the graph isomorphism problem, but the converse reduction is unknown.[4][6][7] By contrast, hardness is known when the automorphisms are constrained in a certain fashion; for instance, determining the existence of a fixed-point-free automorphism (an automorphism that fixes no vertex) is NP-complete, and the problem of counting such automorphisms is ♯P-complete.[5][7]
Algorithms, software and applications[edit]
While no worst-case polynomial-time algorithms are known for the general Graph Automorphism problem, finding the automorphism group (and printing out an irredundant set of generators) for many large graphs arising in applications is rather easy. Several open-source software tools are available for this task, including NAUTY,[8] BLISS[9] and SAUCY.[10][11] SAUCY and BLISS are particularly efficient for sparse graphs, e.g., SAUCY processes some graphs with millions of vertices in mere seconds. However, BLISS and NAUTY can also produce Canonical Labeling, whereas SAUCY is currently optimized for solving Graph Automorphism. An important observation is that for a graph on n vertices, the automorphism group can be specified by no more than 
Practical applications of Graph Automorphism include graph drawing and other visualization tasks, solving structured instances of Boolean Satisfiability arising in the context of Formal verification and Logistics. Molecular symmetry can predict or explain chemical properties.
Symmetry display[edit]
Several graph drawing researchers have investigated algorithms for drawing graphs in such a way that the automorphisms of the graph become visible as symmetries of the drawing. This may be done either by using a method that is not designed around symmetries, but that automatically generates symmetric drawings when possible,[12] or by explicitly identifying symmetries and using them to guide vertex placement in the drawing.[13] It is not always possible to display all symmetries of the graph simultaneously, so it may be necessary to choose which symmetries to display and which to leave unvisualized.
Graph families defined by their automorphisms[edit]
Several families of graphs are defined by having certain types of automorphisms:
- An asymmetric graph is an undirected graph with only the trivial automorphism.
- A vertex-transitive graph is an undirected graph in which every vertex may be mapped by an automorphism into any other vertex.
- An edge-transitive graph is an undirected graph in which every edge may be mapped by an automorphism into any other edge.
- A symmetric graph is a graph such that every pair of adjacent vertices may be mapped by an automorphism into any other pair of adjacent vertices.
- A distance-transitive graph is a graph such that every pair of vertices may be mapped by an automorphism into any other pair of vertices that are the same distance apart.
- A semi-symmetric graph is a graph that is edge-transitive but not vertex-transitive.
- A half-transitive graph is a graph that is vertex-transitive and edge-transitive but not symmetric.
- A skew-symmetric graph is a directed graph together with a permutation σ on the vertices that maps edges to edges but reverses the direction of each edge. Additionally, σ is required to be an involution.
Inclusion relationships between these families are indicated by the following table:
|
|
|
|
|
|
| distance-transitive | distance-regular | strongly regular | ||
|
|
||||
|
|
|
|
||
| symmetric (arc-transitive) | t-transitive, t ≥ 2 | |||
|
(if connected) |
||||
|
|
|
|
|
|
| vertex- and edge-transitive | edge-transitive and regular | edge-transitive | ||
|
|
|
|||
|
|
|
|
||
| vertex-transitive | regular | |||
|
|
||||
|
|
||||
| Cayley graph |
See also[edit]
- Algebraic graph theory
- Distinguishing coloring
References[edit]
- ^ Frucht, R. (1938), «Herstellung von Graphen mit vorgegebener abstrakter Gruppe», Compositio Mathematica (in German), 6: 239–250, ISSN 0010-437X, Zbl 0020.07804.
- ^ Frucht, R. (1949), «Graphs of degree three with a given abstract group», Canadian Journal of Mathematics, 1 (4): 365–378, doi:10.4153/CJM-1949-033-6, ISSN 0008-414X, MR 0032987, S2CID 124723321.
- ^ a b Luks, Eugene M. (1982), «Isomorphism of graphs of bounded valence can be tested in polynomial time», Journal of Computer and System Sciences, 25 (1): 42–65, doi:10.1016/0022-0000(82)90009-5.
- ^ a b Mathon, R. (1979). «A note on the graph isomorphism counting problem». Information Processing Letters. 8 (3): 131–132. doi:10.1016/0020-0190(79)90004-8.
- ^ a b Lubiw, Anna (1981), «Some NP-complete problems similar to graph isomorphism», SIAM Journal on Computing, 10 (1): 11–21, doi:10.1137/0210002, MR 0605600.
- ^ Köbler, Johannes; Schöning, Uwe; Torán, Jacobo (1993), Graph Isomorphism Problem: The Structural Complexity, Birkhäuser Verlag, ISBN 0-8176-3680-3, OCLC 246882287
- ^ a b Torán, Jacobo (2004). «On the hardness of graph isomorphism» (PDF). SIAM Journal on Computing. 33 (5): 1093–1108. doi:10.1137/S009753970241096X.
- ^ McKay, Brendan (1981), «Practical Graph Isomorphism» (PDF), Congressus Numerantium, 30: 45–87, retrieved 14 April 2011.
- ^ Junttila, Tommi; Kaski, Petteri (2007), «Engineering an efficient canonical labeling tool for large and sparse graphs» (PDF), Proceedings of the Ninth Workshop on Algorithm Engineering and Experiments (ALENEX07).
- ^ Darga, Paul; Sakallah, Karem; Markov, Igor L. (June 2008), «Faster Symmetry Discovery using Sparsity of Symmetries» (PDF), Proceedings of the 45th Design Automation Conference: 149–154, doi:10.1145/1391469.1391509, ISBN 978-1-60558-115-6, S2CID 15629172.
- ^
Katebi, Hadi; Sakallah, Karem; Markov, Igor L. (July 2010), «Symmetry and Satisfiability: An Update» (PDF), Proc. Satisfiability Symposium (SAT). - ^ Di Battista, Giuseppe; Tamassia, Roberto; Tollis, Ioannis G. (1992), «Area requirement and symmetry display of planar upward drawings», Discrete and Computational Geometry, 7 (1): 381–401, doi:10.1007/BF02187850; Eades, Peter; Lin, Xuemin (2000), «Spring algorithms and symmetry», Theoretical Computer Science, 240 (2): 379–405, doi:10.1016/S0304-3975(99)00239-X.
- ^ Hong, Seok-Hee (2002), «Drawing graphs symmetrically in three dimensions», Proc. 9th Int. Symp. Graph Drawing (GD 2001), Lecture Notes in Computer Science, vol. 2265, Springer-Verlag, pp. 106–108, doi:10.1007/3-540-45848-4_16, ISBN 978-3-540-43309-5.
External links[edit]
- Weisstein, Eric W. «Graph automorphism». MathWorld.
Изоморфизм, гомоморфизм и автоморфизм графов
Для ориентированного графа множество
дуг можно рассматривать как график бинарного отношения непосредственной достижимости, заданного на множестве вершин.
В неориентированном графе множество
ребер является множеством неупорядоченных пар. Для каждой неупорядоченной пары
можно считать, что вершины
и
связаны симметричным бинарным отношением
, то есть
и
.
Таким образом, с каждым неориентированным и ориентированным графом связано бинарное отношение . Это отношение будем называть отношением смежности.
С алгебраической точки зрения как ориентированный, так и неориентированный граф можно рассматривать как модель, сигнатура которой состоит из одного бинарного отношения: . В классической теории графов изучаются преимущественно конечные модели такого рода.
При указанном подходе различия между ориентированным и неориентированным графами проявляется только в свойствах отношения смежности . Если это отношение симметрично, то граф называют неориентированным, и с этой точки зрения неориентированный граф можно считать частным случаем ориентированного.
Примечание. При таком подходе в неориентированном графе могут быть петли, если отношение содержит некоторые элементы диагонали, в частности является рефлексивным.
Применяя к данному частному случаю моделей общие понятия гомоморфизма и изоморфизма, мы можем сформулировать следующие определения.
Определение 5.14. Отображение множества вершин графа
в множество вершин графа
называют гомоморфизмом графов (графа
в граф
), если для любых двух вершин, смежных в первом графе, их образы при отображении
смежны во втором графе, т.е. если
Биективный гомоморфизм , такой, что любые две вершины смежны в первом графе тогда и только тогда, когда их образы смежны во втором графе, т.е.
называют изоморфизмом графов и
(графа
на граф
), а графы
и
— изоморфными, что записывают в виде
.
Гомоморфизм графов, который является эпиморфизмом, называется также гомоморфизмом одного графа на другой.
Возвращаясь к нашему определению графа посредством двух множеств: множества вершин и множества ребер (дуг)
, получим следующие варианты определений гомоморфизма и изоморфизма.
Гомоморфизм неориентированного графа в неориентированный граф
есть такое отображение
, что для любых двух вершин первого графа, соединенных ребром, их образы при отображении h также соединены ребром, т.е.
Гомоморфизм ориентированного графа в ориентированный граф
есть такое отображение
, что для любых двух вершин
первого графа, таких, что есть дуга, ведущая из
в
, из вершины
тоже ведет дуга в
, т.е.
Изоморфизм неориентированного графа на неориентированный граф
есть такая биекция
, при которой две вершины
и
графа
соединены ребром тогда и только тогда, когда соединены ребром их образы
и
, т.е.
Аналогично изоморфизм ориентированного графа на ориентированный граф
есть такая биекция
, при которой в ориентированном графе
из вершины
ведет дуга в вершину
тогда и только тогда, когда в ориентированном графе
из образа
вершины
ведет дуга в образ
вершины
, т.е.
Пример 5.12. а. На рис. 5.29 отображение , где
есть гомоморфизм ориентированного графа
в ориентированный граф
.
Обратим внимание на петлю : эта петля является образом дуги
, так как
и
. В противоположность этому петля
не имеет прообраза в
.
На этом же рисунке более толстыми стрелками выделен подграф графа
, порожденный подмножеством вершин
, Этот подграф будет гомоморфным образом графа
. Удаляя петлю в вершине
, получим (для того же подмножества вершин) порожденный подграф, являющийся строгим гомоморфным образом графа
. Отметим, что каждая дуга в строгом гомоморфном образе ориентированного графа
имеет прообраз в
.
б. На рис. 5.30 неориентированный граф есть строгий гомоморфный образ графа
(если рассматривать неориентированные графы без петель).
в. На рис. 5.31 отображение h не является гомоморфизмом на
, поскольку
, но
(петли
нет);
, хотя
и т.д. Легко сообразить, что любой двухвершинный гомоморфный образ графа
на рис. 5.31 должен иметь петлю, и, следовательно,
не является гомоморфным образом
ни при каком отображении.
г. На рис. 5.32 изображен один граф из множества двухвершинных гомоморфных образов .
д. Графы, изображенные на рис. 5.33, изоморфны, и изоморфизмом является, например, отображение , такое, что
Дополнения графов
Зачастую для того, чтобы распознать изоморфизм графов, удобно перейти от исходных графов к их дополнениям.
Определение 5.15. Неориентированный (ориентированный) граф называют дополнением неориентированного [ориентированного) графа
, где
— дополнение множества
до множества всех неупорядоченных [упорядоченных пар) на
.
Можно доказать, что графы изоморфны тогда и только тогда, когда изоморфны их дополнения. Например, перейдем к дополнениям графов, изображенных на рис. 5.33. Анализ указанных дополнений (рис. 5.34) позволяет сразу обнаружить их изоморфизм, а следовательно, и изоморфизм исходных графов.
Более сложные случаи распознавания изоморфизма (главным образом, для неориентированных графов) будут рассмотрены в последующей лекции.
Автоморфизм графов
Определение 5.16. Автоморфизм графа — это любая подстановка множества его вершин, являющаяся изоморфизмом
на себя.
Можно показать, что композиция двух любых автоморфизмов графа снова есть автоморфизм этого графа, а подстановка, обратная к автоморфизму, опять-таки есть автоморфизм. Таким образом, множество всех автоморфизмов данного графа образует группу по операции композиции, которая является подгруппой симметрической группы множества вершин графа. Ее называют группой автоморфизмов данного графа.
Рассмотрим некоторые примеры групп автоморфизмов.
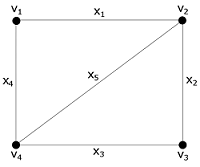
Для графа, изображенного на рис. 5.35,а, группа автоморфизмов порождается транспозициями (1 4) и (2 3), что легко усматривается из анализа дополнения этого графа (рис. 5.35,б). Очевидно, что группа автоморфизмов графа есть подгруппа группы перестановок множества его вершин. Поэтому, согласно теореме 2.13 Лагранжа, порядок группы автоморфизмов графа есть делитель факториала числа его вершин. В частности, для графа на рис. 5.35, а группа автоморфизмов имеет порядок 4 и состоит из тождественной подстановки и подстановок
. Очевидно, что 4! делится на 4.
Можно доказать, что автоморфизмы неориентированного графа сохраняют степени, а ориентированного графа — полустепени исхода и захода всех его вершин. Это свойство позволяет упростить описание автоморфизмов графа.
Пример 5.13. Найдем нетривиальные (т.е. отличные от тождественной подстановки) автоморфизмы неориентированного графа, изображенного на рис. 5.36. Так как среди вершин графа лишь одна вершина имеет степень 1 и лишь одна вершина
имеет степень 2, то при любом изоморфизме эти вершины перейдут в себя. Значит, при изоморфизме возможны лишь перестановки вершин
и
.
Итак, для любого автоморфизма этого графа
. Поскольку
, то
, и, следовательно, поскольку
— единственная вершина, смежная с
, всегда
, т.е. вершина
переходит в себя. Таким образом, единственным нетривиальным автоморфизмом данного графа будет транспозиция
— «отражение» квадрата
относительно диагонали
.
Иногда группу автоморфизмов графа легко найти именно из чисто геометрических соображений при удачном изображении графа. Автоморфизм есть не что иное, как преобразование графа (геометрической фигуры), при котором граф совмещается с самим собой. Поэтому группу автоморфизмов графа можно изучать, анализируя его как геометрическую фигуру.
Пример 5.14. Для графа, изображенного на рис. 5.37, из геометрических соображений вытекает, что автоморфизм сводится к повороту графа на 60° по часовой стрелке вокруг центра тяжести треугольника
.
Следовательно, группа автоморфизмов порождается подстановкой , являющейся композицией трех циклов:
Заметим, что ни один цикл, входящий в , сам по себе не будет автоморфизмом данного графа. Так, если мы рассмотрим цикл
, то
и
, но
.
В заключение сформулируем без доказательства теорему, доказанную Фрухтом в 1938 г. и характеризующую все конечные группы в терминах групп автоморфизмов конечных неориентированных графов.
Теорема 5.5 (теорема Фрухта). Каждая конечная группа изоморфна группе автоморфизмов конечного неориентированного графа.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

существенную помощь. Во-первых, если s(G)≠s(G‘), то отсюда сразу следует неизоморфность графов G и G‘. Во-вторых, если s(G)=s(G‘), то для проверки графов G и G‘ на изоморфизм требуется перебор не всех n! соответствий между вершинами, а лишь тех, при которых сопоставляются вершины одинаковой степени.
Рис. 6.44
Однако имеются случаи, когда при выяснении изоморфизма графов их векторы степеней практически бесполезны: речь идет об регулярных (однородных) графах, в которых степень всех вершин одна и та же. Например, граф, степени всех вершин которого равны трем (рис. 6.45).
|
1 |
6 |
|
|
2 |
5 |
|
|
Рис. 6.45 |
3 |
4 |
Противоположный случай представляют графы, определяемые однозначно с точностью до изоморфизма своим вектором степеней (или, что равносильно, его обращением) и называемые униграфа-
ми.
Два графа гомеоморфны (или тождественны с точностью до вершин степени 2), если они оба могут быть получены из одного и того же графа «включением» в его ребра новых вершин степени 2. Если ребро графа изображено в виде линии, то можно на ней по-
199
ставить точку и считать ее новой вершиной степени 2. Формально эта операция определяется следующим образом.
Пусть G – любой граф и (a,b) – его ребро. Операцией подразделения ребра (a,b) называется удаление из графа G ребра (a,b), добавление новой вершины c и добавление двух новых ребер (a,c) и (c,b).
Граф G1 называется подразделением графа G, если G1 может быть получен из G несколькими подразделениями ребер.
Графы G1 и G2 называются гомеоморфными, если существуют их подразделения, которые изоморфны.
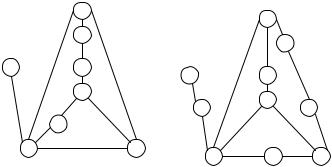
Изображенные на рис. 6.46 графы гомеомофны, и то же самое можно сказать о любых двух циклических графах.
Рис. 6.46
6.8.4. Автоморфизм графов
Автоморфизмом графа G называется изоморфизм графа G на себя, при этом всякий граф G имеет тождественный (или тривиальный) автоморфизм I, такой, что I(x)=x для каждого ребра x и каждой вершины x из G.
Автоморфизм графа есть отображение множества вершин на себя, сохраняющее смежность. Множество таких автоморфизмов, обозначаемое Γ(G), образует группу, называемую группой графа G, или группой автоморфизмов графа G. Таким образом, элементы группы Γ(G) являются подстановками, действующими на множестве вершин графа.
На рис. 6.47 представлен исходный граф и его автоморфизм.
200

v2 v3 v3 v2
Для подстановки в теории графов принята запись
|
1 |
2 |
… |
n |
|||
|
ϕ |
ϕ |
… ϕ |
, |
|||
|
2 |
||||||
|
1 |
n |
|||||
где φ1, φ2,…, φn – те же числа 1, 2,…, n, но записанные, возможно, в каком-либо ином порядке.
Таким образом, вторая строка подстановки образует перестановку φ1, φ2,…, φn из чисел 1, 2,…, n. Различных подстановок вообще из n элементов существует столько же, сколько и перестановок, т.е. n! = 1×2×3×…×n. Однако при построении автоморфизмов требуется сохранение степеней вершин и смежности между ними, что в большинстве случаев существенно сокращает их количество.
Наибольшее количество автоморфизмов в группе автоморфизмов существует у полных и пустых графов – их на n вершинах в обоих случаях будет n!.
Подстановка, оставляющая на месте все элементы, называется
начальной (единичной, тождественной).
|
1 |
2 |
… |
n |
||
|
I = |
, |
||||
|
2 |
… |
n |
|||
|
1 |
|||||
Еe краткая запись α0=(1)(2)…(n).
Для каждой подстановки А существует обратная, т. е. такая, которая переводит φi в i, она обозначается через А-1. Например:
|
1 |
2 |
3 |
4 |
5 |
|||
|
, |
|||||||
|
A = |
3 |
2 |
5 |
1 |
4 |
||
201
|
3 2 5 1 4 |
1 2 3 4 5 |
|||||
|
A |
−1 |
|||||
|
= |
= |
4 2 1 5 3 |
. |
|||
|
1 2 3 4 5 |
||||||
Результат последовательного применения двух подстановок А и
Вснова будет некоторой подстановкой С: если А переводит i в φi, а
Впереводит φi в ψi, то С переводит i в ψi. Подстановка С называется произведением подстановок А и В, что записывается так: С = АВ. Например, если
|
1 2 3 4 5 |
1 2 3 4 5 |
||||||||||
|
, |
B = |
, |
|||||||||
|
A = |
3 2 5 1 4 |
2 5 4 1 3 |
|||||||||
|
то |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
|||||||
|
C = AB = |
4 |
5 |
3 |
2 |
1 |
. |
|||||
При умножении подстановок не выполняется закон коммутативности, т.е., вообще говоря, АВ ≠ ВА, как в том же примере
1 2 3 4 5
BA = .
2 4 1 3 5
Легко видеть, что IA = AI = А, АА-1= А-1А = I, А(ВС) = (АВ)С (ассоциативный закон).
Подстановка, переставляющая местами только два элемента i и j, называется транспозицией:
|
1 |
2 |
3 |
4 |
5 |
||
|
= (2, 4) . |
||||||
|
4 |
3 |
2 |
5 |
|||
|
1 |
||||||
Подстановка, циклически переставляющая данную группу элементов, а остальные элементы оставляющая на месте, называется циклом. Число переставляемых элементов называют длиной цикла. Например, подстановка А есть цикл длины 4: она переводит 1 в
202

3, 3 в 5, 5 в 4, 4 в 1, при этом 2 остается на своем месте. Коротко это записывается так:
|
А = (1, 3, 5, 4)(2). |
||
|
Рассмотрим граф G, изображенный на рис. |
1 |
4 |
|
6.48. |
||
|
Его четыре вершины составляют множество |
||
|
X целых чисел 1, 2, 3, 4. Заметим, что следую- |
|
щий список подстановок: |
2 |
3 |
|
|
α0 = (1)(2)(3)(4), |
α1 = (1)(3)(2,4), |
||
|
α2 = (1,3)(2)(4), |
α3 = (1,3)(2,4) |
Рис. 6.48 |
|
|
включает все подстановки множества X, сохра- |
|||
няющие отношение смежности в графе G. Например, вершины 1 и 4 смежны в G. Подстановка (1,3)(2)(4) преобразует вершины 1 и 4 в вершины 3 и 4, и эти образы 3 и 4, также являются смежными. Таким образом, подстановка (1,3)(2)(4) сохраняет смежность вершин
1 и 4.
В случае если в короткой записи присутствуют только циклы длиной 2, обратная подстановка строится всегда очень просто, так как совпадает с исходной, например, для α1 обратной является α1-1 = =(1)(3)(2,4), а для α3 = (1,3)(2,4) обратной является α3-1 = (1,3)(2,4).
На практике, если граф задан своим изображением, поиск всех автоморфизмов практически осуществляется путем поиска возможных поворотов графа или его «частей» вокруг осей симметрии.
Задача 6.15. Найти группу автоморфизмов данного графа (рис. 6.49) и для каждой подстановки привести обратную.
Решение. В данном графе просматривается несколько условных осей симметрии, относительно которых можно поворачивать граф.
Начальная подстановка:
α0=(1)(2)(3)(4)(5)(6).
203

Если перевернуть граф относительно горизонтальной оси, получим подстановку (рис.6.50):
α1=(1)(2,6)(3,5)(4).
Рис. 6.50
Если перевернуть граф относительно вертикальной оси, получим подстановку (рис.6.51):
α2=(2,3)(6,5)(1,4).
Рис. 6.51
Если сделать эти повороты по очереди, то получим четвертую и последнюю в данном случае подстановку (рис.6.52):
α3=(1,4)(2,5)(3,6).
204
Задача 6.16. Найти все графы, группа подстановок которых содержит подстановку (v1,v2,v3,v4,v5).
Решение. Такого рода задачи решаются переборным методом, причем перебор удобнее всего осуществлять по степеням вершин.
Поскольку, как видно из данной подстановки, в графе пять вершин, максимальная степень вершины равна 4, минимальная в случае пустого графа равна 0. Кроме того, поскольку в цикле участвуют все пять вершин, это значит, что у всех вершин степени одинаковые. Переберем все степени от 0 до 4.
Пусть степень всех вершин равна 0. Эта ситуация наблюдается в пустом графе на пяти вершинах, и он нам по своим свойствам подходит. Итак, первый найденный граф – P5 (отметим, что конкретная нумерация вершин в данном случае не важна).
Пусть степень всех вершин равна 1. Значит, суммарная степень вершин графа равна 5, это число нечетное, следовательно, такого графа не существует.
Пусть степень всех вершин равна 2. Эта ситуация наблюдается в простом цикле на пяти вершинах, по своим свойствам он нам подходит, только важно правильно пронумеровать вершины. Графически можно изобразить найденное решение в виде кольца (рис. 6.53, а) или звезды (рис. 6.53, б). Оба решения эквивалентны.
Обратите внимание на нумерацию вершин: она должна позволять осуществлять переход 1→2→3→4→5→1. Например, вершины в звезде можно было пронумеровать иначе (рис 6.53, в), но ни в коем случае нельзя нарушать циклический порядок (рис. 6.53, г). В последнем случае перестановка (1,2,3,4,5) нарушит смежность вершин (рис. 6.53, д): в исходном графе вершина v1 была смежна с v4 и v5, а после такой перестановки станет смежна с v2 и v3. Итак, второй найденный граф – простой цикл на 5 вершинах (с правильной нумерацией вершин).
Пусть степень всех вершин равна 3. Значит, суммарная степень вершин графа равна 15, следовательно, такого графа не существует.
Пусть степень всех вершин равна 4. Эта ситуация наблюдается в полном графе на пяти вершинах, и он нам по своим свойствам подходит (отметим, что нумерация вершин в данном случае не важна). Следовательно, найдено три возможных графа: P5, Ц5, K5.
205
Содержание
- 1 Вершинная и рёберная группы графов
- 2 Операции на группах подстановок
- 2.1 Сумма подстановок
- 2.2 Произведение групп
- 2.3 Композиция групп
- 2.4 Степенная группа
- 3 См. также
- 4 Источники информации
Вершинная и рёберная группы графов
| Определение: |
| Автоморфизмом (англ. Automorphism) графа называется изоморфизм графа на себя |
Каждый автоморфизм графа есть подстановка множества вершин , сохраняющая смежность. Конечно, подстановка переводит любую вершину графа в вершину той же степени. Очевидно, что последовательное выполнение двух автоморфизмов есть также автоморфизм;
| Определение: |
| Автоморфизмы графа образуют группу подстановок , действующую на множестве вершин . Эту группу называют группой или иногда вершинной группой графа (англ. point-group). |
| Определение: |
| Вершинная группа графа индуцирует другую группу подстановок , называемую реберной группой графа (англ. line-group) — она действует на множестве ребер . |
Для иллюстрации различия групп и рассмотрим граф , показанный на рисунке; его вершины помечены а ребра . Вершинная группа состоит из четырех подстановок
Тождественная подстановка вершинной группы индуцирует тождественную подстановку на множестве ребер, в то время как подстановка индуцирует подстановку на множестве ребер, в которой ребро остается на месте, меняется с , а с . Таким образом, реберная группа состоит из следующих подстановок, индуцируемых указанными выше элементами вершинной группы:
Понятно, что реберная и вершинная группы графа изоморфны. Но они, конечно, не могут быть идентичными, так как степень группы равна , а степень группы равна .
| Теорема: |
|
Реберная и вершинная группы графа изоморфны тогда и только тогда, когда граф имеет не более одной изолированной вершины, а граф не является его компонентой. |
| Доказательство: |
|
Пусть подстановка группы индуцируется подстановкой группы . Из определения операции умножения в группе вытекает, что для . Поэтому отображение является групповым гомоморфизмом группы на . Следовательно, тогда и только тогда, когда ядро этого отображения тривиально.
|
Операции на группах подстановок
Пусть — группа подстановок порядка и степени , действующая на множестве , а — другая группа подстановок порядка и степени , действующая на множестве . Например, пусть — циклическая группа порядка , действующая на множестве . Эта группа состоит из трех подстановок и . Если взять в качестве симметрическую группу порядка , действующую на множестве , то получим две подстановки и . Проиллюстрируем на этих двух группах подстановок действие нескольких бинарных операций.
Сумма подстановок
— это группа подстановок, действующая на объединении непересекающихся множеств и элементы которой записываются в виде и представляют собой упорядоченные пары подстановок из и из . Каждый элемент , принадлежащий множеству преобразуется подстановкой по правилу
Таким образом, группа содержит подстановок, каждую из которых можно записать в виде суммы подстановок и , как, например, . (степень равна .)
Произведение групп
— это группа подстановок, действующая на множестве , элементы которой записываются в виде и представляют собой упорядоченные пары подстановок из и из . Элемент множества преобразуется подстановкой естественным образом:
Подстановкой в группе , которая соответствует подстановке будет , где для краткости символ заменен на . (Порядок и степень равны .)
Композиция групп
группы относительно группы также действует на множестве . Для любой подстановки из и любой последовательности , содержащей (не обязательно различных) подстановок из , существует единственная подстановка из , которая записывается в виде , такая, что для всякой пары из выполняется равенство
Композиция имеет степень и порядок . Любую подстановку из можно записать в таком виде, как она действует на множестве . Вводя опять обозначение для упорядоченной пары и используя формулу выше можно представить подстановку в виде . Заметим, что группа имеет порядок и поэтому не изоморфна группе .
Степенная группа
(обозначается ) действует на множестве всех функций, отображающих в . Будем всегда предполагать, что степенная группа действует на множестве, состоящем более чем из одной функции. Для каждой пары подстановок из и из существует единственная подстановка из (записывается ), которая действует на любую функцию из в соответствии со следующим соотношением, определяющим образ каждого элемента при отображении :
Степенная группа имеет порядок и степень . Применяя формулу выше, видим, что подстановка этой группы, полученная из подстановок и , имеет один цикл длины и один цикл длины .
См. также
- Группа
- Википедия — Автоморфизм_графа
Источники информации
- Харари Ф. Теория графов. М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.)
Раскрываем тему канонической нумерации графов. О деревьях была отдельная заметка, теперь переключим внимание на общий случай.
Допустим, мы храним и поддерживаем базу данных молекул. Или путей метаболизма в биологических клетках, или вовсе абстрактных графов, для какой-либо задачи по комбинаторике. В любом случае, речь идёт о графах с дополнительными свойствами.
При помещении в базу очередной записи необходимо проверить, что аналогичной записи в базе ещё нет. Выражаясь математически, нужно убедиться в отсутствии графов, изоморфных добавляемому. Наиболее грубый (и наименее быстрый) способ выглядит так: мы перебираем всю базу и осуществляем проверку изоморфизма каждого графа из базы с новым образцом.
Проверка изоморфизма двух графов — непростая задача. Она очевидно принадлежит к классу NP, но принадлежность её к классам P или NP-полных до сих пор под вопросом. (В комментариях дана ссылка на алгоритм, возможно решающий эту задачу за полиномиальное время.) Пока что для этой задачи придуман собственный класс сложности в NP, под названием GI. Но пусть даже у нас будет эффективная процедура для проверки изоморфизма графов; в любом случае, если записей в базе — миллион, то на проверку присутствия нового образца уйдут многие минуты.
Возможно, перед лицом этой опасности и были изобретены канонические коды графов. Канонический код — это строковое представление графа, не зависящее от порядка нумерации вершин; своего рода хеш-код без промахов. Имея такой код, никогда не потребуется проверять непосредственно изоморфизм графов, достаточно сравнивать две строки. Коды одинаковы тогда и только тогда, когда графы изоморфны.
Таким образом, перед добавлением графа в базу мы вычислим его канонический код, и затем осуществим поиск этого кода (строки) среди имеющихся. Поиск строк, в отличие от изоморфных графов, осуществляется быстро; проблема решена.
Следует отметить, что канонические коды — не единственное средство. Существует немало кодов (см. комментарии), которые вычисляются за полиномиальное время и не являются «каноническими» в том смысле, что могут совпадать у неизоморфных графов. Однако, если коды разные, то графы неизоморфны. Пользуясь этим, можно осуществить отсеивание (screening) большей части неизоморфных графов, и проверять изоморфизм только для оставшихся.
Очевидно, что задача вычисления канонического кода не проще, чем задача проверки изоморфизма; но она интереснее, и канонические коды удобнее в использовании: на один граф вызывается ровно одна специальная процедура.
Любой канонический код состоит из (i) определённой схемы кодирования графа и (ii) процедуры переупорядочения вершин. Нас не интересует схема кодирования; это может быть обход в глубину, или в ширину, или развёрнутая в строку матрица смежности, или просто списки вершин и рёбер… как бы то ни было, кодирование графа подразумевает какой-то порядок его вершин. Наша задача — упорядочить вершины так, чтобы результат не зависел от изначального порядка. Это называется каноническая нумерация (canonical numbering, canonical labeling).
Похоже, что пионерами этой задачи являются Арлазаров, Зуев, Усков и Фараджев, написавшие в 1973 году статью «Алгоритм приведения неориентированных графов к каноническому виду». Насколько большую роль сыграли их идеи — это отдельная тема, выходящая за рамки данной заметки (более того, в оффлайн); мы же останемся в реалиях нынешней сетевой эпохи.
Реалии, однако, мало изменились за последние 15 лет. Австралийский профессор Брендан МакКей (Brendan McKay) в 1980-х годах написал статью «Practical Graph Isomorphism» и соответствующий программный пакет под названием nauty. Долгое время никому не удалось превзойти nauty по быстродействию; хотя для некоторых частных случаев более эффективные алгоритмы всё же появляются, например вот, вот. Особого упоминания заслуживают библиотеки bliss (2007) и saucy2 (2008), которые на больших разреженных графах уверенно обгоняют nauty. Но эти алгоритмы, фактически, не более чем nauty с модификациями.
Печально другое: мало кто из программистов сумел хотя бы подойти близко к пониманию того, как работает nauty. Если мы посмотрим на современные программные пакеты, то окажется, что они либо напрямую используют эту библиотеку: Magma, MuPAD, GRAPE, Planarity, Cyberaide, igraph (использует bliss), либо используют более примитивные алгоритмы: OpenBabel, Marvin. В любом случае, об осмыслении nauty речи не идёт. Приятным исключением является InChI, в которой присутствует алгоритм, явно сделанный с оглядкой на nauty. Настоящая популярность к алгоритму МакКея придёт тогда, когда в каждом пакете он будет реализован по-своему.
Перестановки и упорядоченные разбиения
Говоря здесь о разбиениях, мы подразумеваем упорядоченные разбиения множества вершин графа, т.е. представления этого множества вершин виде упорядоченного набора его попарно непересекающихся непустых подмножеств. [a b c | d e] и [a c b | e d] — одно и то же разбиение, но [d e | a b c] от него отличается. Подмножества [a b c] и [d e] называются ячейками (cells).
Если каждая ячейка разбиения π1 является подмножеством какой-либо ячейки разбиения π2, то π1 называется подразбиением π2, а π2 — надразбиением π1. Также говорят, что π1 мельче π2, а π2 крупнее π1. Мы подразумеваем, что при подразбиении сохраняется порядок ячеек. Например, [a b | c | d e] является подразбиением [a b c | d e] и [a b | c d e], но не [c | a b d e].
Разбиение, в котором все подмножества состоят из одного элемента, называется дискретным (discrete partition). Дискретное разбиение очевидным образом образует перестановку (permutation) вершин. Например, дискретное разбиение [b | c | a | d | e] образует перестановку (b, c, a, d, e).
Разбиение, состоящее из одной ячейки, называется элементарным (unit partition). Любое разбиение является подразбиением элементарного.
Покажем процедуру перебора всех перестановок вершин, основанную на переборе разбиений. При своей крайней примитивности, она является базой всего алгоритма канонической нумерации. Для получения всех перестановок в процедуру следует передать элементарное разбиение.
function AllPermutations(π = [V0|…|Vk])
if π — дискретное разбиение:
yield π
else:
выбрать Vi ∈ π : |Vi| ≠ 1
for v ∈ Vi:
AllPermutations([V0|…|{v}|Viv|…|Vk])
На этом месте у читателя может возникнуть вопрос: зачем нужны разбиения, если наша цель — перебор перестановок? Да, для перебора всех перестановок не нужно вводить понятие разбиений. Но на самом деле, все перестановки нам не нужны, а нужна одна перестановка — каноническая, которую мы выбираем как «лучшую» среди какого-то класса перестановок (не обязательно всех). Очевидно, что чем меньше этот класс, тем лучше, но есть условие: состав этого класса перестановок не должен зависеть от исходной нумерации вершин. Именно здесь нам поможет идея разбиений: мы будем не отбрасывать перестановки, а уточнять разбиения, участвующие в переборе.
Годные разбиения
Мы называем разбиение π годным (equitable), если для него выполняется следующее свойство: для любых двух ячеек V1, V2 ∈ π (не обязательно различных) и для любых v1, v2 ∈ V1 выполняется равенство d(v1, V2)=d(v2, V2), где d(v,V) — количество вершин в V, смежных с v. Очевидно, что все дискретные разбиения являются годнымы.
В работе МакКея доказано, что для каждого разбиения π существует единственное его наикрупнейшее подразбиение, являющееся годным. Процедура уточнения (refine) разбиения находит это годное подразбиение. В упрощённом виде она выглядит так:
function Refine(π = [V0|…|Vk])
for Vi ∈ π :
for Vj ∈ π:
подразбить Vj, сгруппировав элементы v ∈ Vj по d(v, Vi) и отсортировав по возрастанию d(v, Vi)
заменить Vj в π на результат этого подразбиения, удлиняя цикл по Vi, но не удлиняя цикл по Vj
return π
Следовательно, чтобы перебрать все годные подразбиения и все происходящие от них перестановки, нам нужно всего лишь вставить вызов процедуры Refine в перебор:
function AllEquitablePermutations(π = [V0|…|Vk])
Refine(π)
if π — дискретное разбиение:
yield π
else:
выбрать Vi ∈ π : |Vi| ≠ 1
for v ∈ Vi:
AllPermutations([V0|…|{v}|Viv|…|Vk])
Процесс перебора перестановок можно изобразить как дерево разбиений, которое обходится слева направо. Среди листьев первым при обходе встречается самый левый. Обозначим его ξ.
(Правая половина дерева показана не целиком. Вызовы Refine, которые не уточняют подразбиение, также опущены.)
Сравнения перестановок и автоморфизмы
Наша задача — найти каноническую перестановку множества вершин исходного графа. Для этого нужно обзавестить функцией сравнения перестановок cmp, которая бы определяла, которая из двух «лучше» (или они одинаковые). Функция должна задавать транзитивное отношение, а её результат не должен зависеть от первоначальной нумерации вершин графа. Пример такой функции: по исходному графу G и перестановкам π1 и π2 построить графы G1 и G2, вычислить их матрицы смежности, и в качестве cmp(π1, π2) вернуть результат лексикографического сравнения матриц, развёрнутых в строки. Таким образом, канонической перестановкой будет считаться та, для которой матрица смежности наибольшая; если таких перестановок две и более, то они считаются неразличимыми и в качестве канонической можно взять любую из них.
Какой смысл для нас имеют «неразличимые» перестановки? Пусть cmp(π1, π2)=0. Несложно доказать, что в этом случае перестановка γ=π2-1∘π1 (композиция π1 и перестановки, обратной π2) является автоморфизмом вершин исходного графа.
Использование автоморфизмов позволяет существенно (иногда — на порядки) сократить перебор при нахождении канонической перестановки. Поэтому в nauty и производных алгоритмах обязательно осуществляется нахождение всей группы автоморфизмов графа, тогда как нахождение собственно канонической нумерации сделано опцией.
Есть следующий способ найти генераторы группы автоморфизмов графа: при обработке первого встретившегося дискретного разбиения ξ оно сохраняется. Каждое последующее дискретное разибение π сравнивается с ξ: если перестановка ξ-1∘π является автоморфизмом графа, то эта перестановка записывается в группу генераторов.
Сокращение перебора 1: автоморфизм ξ-1∘π
После обнаружения автоморфизма ξ-1∘π, обход можно «поднять» по дереву до общего предка π и ξ, поскольку поддерево этого предка, в котором находится π, «изоморфно» поддереву, в котором находится ξ, и не содержит новой информации. Строгое доказательство приведено в работе МакКея.
Сокращение перебора 2: автоморфизм ρ-1∘π
Как было сказано, поиск канонической нумерации — только опция в алгоритме нахождения автоморфизмов. Когда эта опция включена, мы храним ещё одну перестановку ρ, которая является «лучшей» на данный момент (best so far, BSF). При обнаружении первой перестановки ξ мы копируем её в ρ. Каждую последующую перестановку π мы сравниваем с ρ. Если cmp(π, ρ) > 0, то мы копируем π в ρ. Если cmp(π, ρ) < 0, то ничего не делаем. Если же cmp(π, ρ) = 0, то ρ-1∘π является новым автоморфизмом, и обход можно «поднять» по дереву до общего предка π и ρ.
Сокращение перебора 3: орбиты
Орбита вершины v — это подмножество вершин, в которые может перейти v в результате действия автоморфизмов. Например, на следующем рисунке показаны орбиты вершин графа:
В начале работы nauty каждая вершина принадлежит своей собственной орбите. По мере открывания новых автоморфизмов орбиты увеличиваются, а их количество — сокращается. Например, если найден автоморфизм (a, b, c, d, e) → (b, a, c, e, d), то список орбит из [a][b][c][d][e] становится [a b] [c] [d e]. Если после этого найден автоморфизм (a, b, c, d, e) → (a, c, b, d, e), то список орбит становится [a b c] [d e]
Рассмотрим «линию предков» первого дискретного разбиения ξ. Предположим, мы в процессе обхода дерева вернулись к какому-либо из предков ξ (назовём его ν), чтобы продолжить обход других потомков ν, перебирая другие элементы ячейки Vi. Если рассматриваемый элемент vk ∈ Vi лежит на одной орбите с уже рассмотренным элементом vj ∈ Vi, то существует автоморфизм, открытый в процессе обхода более ранних узлов, который переводит vj в vk. В работе МакКея доказано, что в этом случае нет смысла рассматривать всё поддерево, произведённое отделением vk: все листья этого поддерева будут изоморфны ранее открытым листьям, и все автоморфизмы, которые будут найдены при обходе этого поддерева, будут повторять предыдущие.
Небольшое замечание: после реализации процедуры Refine может показаться, что уточнение тривиального разбиения как раз и определяет орбиты вершин. Для многих графов это действительно так, но не для всех. На следующем рисунке показан пример графа, на котором это не выполняется:
Для всех графов, однако, верно то, что разбиение по орбитам является подразбиением уточнения тривиального разбиения.
Сокращение перебора 4: fix и mcr
С узлами, которые не являются предками ξ, предыдущее сокращение перебора делать нельзя. Для них есть менее сильный, но тоже действенный критерий отсечения потомков. Для применения этого критерия необходимо сохранять информацию о каждом автоморфизме в отдельности (вместо множества орбит, которое накапливает информацию о всех автоморфизмах в совокупности). Для каждого найденного автоморфизма γ запоминаются два множества: fix(γ) и mcr(γ). fix(γ) — это множество вершин, которое при действиии автоморфизма остаются на своих местах. mcr(γ) — это множество вершин, которые являются минимальными по номеру в своих орбитах. Имеются в виду орбиты, составленные по одному автоморфизму γ, а не те, которые используются в предыдущем способе отсечения.
Рассмотрим множество Vi, элементы которого мы перебираем для продолжения обхода дерева из какого-то узла, глубины l. В процессе пути от корня дерева до этого узла l вершин были «зафиксированы», когда мы отделяли их от их ячеек. Назовём множество этих вершин fixed.
В работе МаКея доказано следующее: если fixed ⊂ fix(γ), то можно присвоить в Vi пересечение Vi ∩ mcr(γ) без ущерба для алгоритма. Фактически, речь идёт об автоморфизмах, которые «не затрагивают» вершины, которые мы зафиксировали. Их орбиты можно эксплуатировать так же, как и в предыдущем разделе, что и делается путём пересечения Vi и mcr(γ). Означенная операция выполняется для всех γ, fix и mcr которых мы успели сохранить на данный момент. Следует отметить, что генераторов группы автоморфизмов графа может быть очень много, и сохранять все fix и mcr не всегда возможно. МакКей рекомендует ограничивать количество сохраняемых fix и mcr числом, пропорциональным количеству вершин в графе, с коэффициентом пропорции больше 1 (у него почему-то 50/32).
Алгоритм целиком
В коде имеются глобальные переменные:
getcanon— опция получения канонической нумерации в ρgca_first— уровень общего предка текущего узла и ξgca_canon— уровень общего предка текущего узла и ρorbits— массив индексов орбит; содержит для каждой вершины номер минимальной вершины в её орбите- Ψ — списов посчитанных множеств fix и mcr для найденных автоморфизмов
function AutomorphismSearch(π)
FirstNode(1, π)
function FirstNode(level, π = [V0|…|Vk])
π ← Refine(π)
if π — дискретное:
ξ ← π
gca_first ← level
if getcanon:
ρ ← π
gca_canon ← level
return level-1
Vi ← первая ячейка π, в которой больше 1 вершины
for v ∈ Vi
if orbits[v] ≠ v:
continue (сокращение 3)
π’←[V0|…|{v}|Viv|…|Vk]
fixed ← fixed ∪ v
if v — первая вершина в Vi:
rtnlevel ← FirstNode(level+1, π')
gca_first ← level
else:
rtnlevel ← OtherNode(level+1, π')
fixed ← fixed v
if rtnlevel < level:
return rtnlevel
if level < gca_canon:
gca_canon ← level
return level-1
function OtherNode(level, π = [V0|…|Vk])
π ← Refine(π)
if π — дискретное:
if cmp(π,ξ)=0:
AddFixMcr(ξ-1∘π)
JoinOrbits(ξ-1∘π)
return gca_first (сокращение 1)
if getcanon:
comp ← cmp(π, ρ)
if comp=0:
AddFixMcr(ρ-1∘π)
JoinOrbits(ρ-1∘π)
return gca_canon (сокращение 2)
if comp>0:
ρ ← π
return level-1
Vi ← первая ячейка π, в которой больше 1 вершины
for (fix, mcr) ∈ Ψ:
if fixed ⊂ fix:
Vi ← Vi ∩ mcr (сокращение 4)
for v ∈ Vi:
π’←[V0|…|{v}|Viv|…|Vk]
fixed ← fixed ∪ v
rtnlevel ← OtherNode(level+1, π')
fixed ← fixed v
if rtnlevel < level:
return rtnlevel
if level < gca_canon:
gca_canon ← level
return level-1
Детали реализации
Авторская имплементация nauty содержит трюки для увеличения быстродействия и уменьшения расхода памяти:
- Для хранения графа и множеств используются битовые массивы
- Вся цепочка подразбиений от корня дерева к текущему узлу кодируется всего двумя массивами (lab и ptn). При возвращении к родительскому узлу разбиение восстанавливается функцией recover
Подробности можно узнать в nauty User’s Guide и в коде самой nauty.
Применение
Прелесть изложенного алгоритма в том, что в нём не много завязок на то, что исходное множество вершин — это вершины простого графа. Фактически, можно находить автоморфизмы и каноническую нумерацию для чего угодно, например:
- Для ориентированных графов. Никаких изменений в алгоритме не требуется. МакКей в статье упоминает ориентированные графы, и в nauty есть соответствующая опция
digraph - Для графов с раскрашенными вершинами. Всё, что требуется — начинать не с элементарного разбиения, а сгруппировать вершины по цветам. Эта опция также описана у МакКея и имеется в nauty
- Для графов с раскрашенными рёбрами. Всё, что требуется — изменить функцию
cmpтак, чтобы она учитывала цвета рёбер. Также, можно более эффективно написать процедуруRefine(уточнение разбиения) - Для молекул со стереохимическими свойствами. Опять же, модификации требуются только в функции
cmp
Модификации алгоритма
Не было упомянуто об огромном количестве дополнительных оптимизаций, имеющихся в коде nauty. МакКей признаёт, что у него самого не все они задокументированы. Вот только некоторые:
- «Даровые» автоморфизмы (cheap automorphisms, implicit automorphisms), для обнаружения которых не требуется доходить до дискретного разбиения. Работают в nauty только для неориентированных графов (цвета вершин допускаются)
- Проверка автоморфизма
cmp(π,ξ) может делаться более эффективно без вызоваcmp, с учётом того, что ξ никогда не меняется и нас интересует только то, есть ли изоморфизм - Псевдо-канонические коды разбиений, благодаря которым можно выявить отсутствие автоморфизма, не проверяя его явно. Они же используются для предварительного определения знака функции
cmp - При выборе ячейки Vi для подразбиения можно применять различные эвристики, с целью сокращения перебора