Как найти апофему неправильной пирамиды

Апофема пирамиды. Формулы для апофемы правильной треугольной пирамиды

Пирамида — это пространственный полиэдр, или многогранник, который встречается в геометрических задачах. Основными свойствами этой фигуры являются ее объем и площадь поверхности, которые вычисляются из знания любых двух ее линейных характеристик. Одной из таких характеристик является апофема пирамиды. О ней пойдет речь в статье.

Фигура пирамида

Прежде чем приводить определение апофемы пирамиды, познакомимся с самой фигурой. Пирамида представляет собой многогранник, который образован одним n-угольным основанием и n треугольниками, составляющими боковую поверхность фигуры.

Всякая пирамида имеет вершину — точку соединения всех треугольников. Перпендикуляр, проведенный из этой вершины к основанию, называется высотой. Если высота пересекает в геометрическом центре основание, то фигура называется прямой. Пирамида прямая, имеющая равностороннее основание, называется правильной. На рисунке показана пирамида с шестиугольным основанием, на которую смотрят со стороны грани и ребра.

Апофема правильной пирамиды

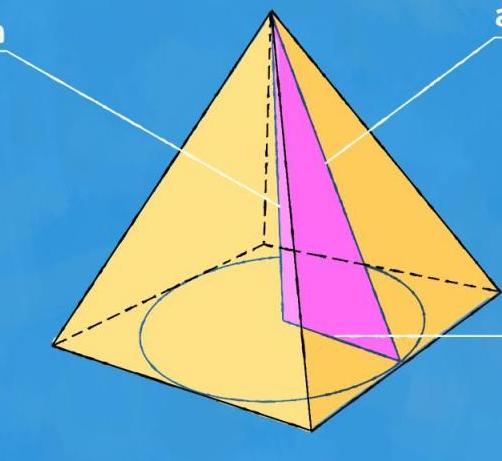
Ее также называют апотемой. Под ней понимают перпендикуляр, проведенный из вершины пирамиды к стороне основания фигуры. По своему определению этот перпендикуляр соответствует высоте треугольника, который образует боковую грань пирамиды.

Поскольку мы рассматриваем пирамиду правильную с n-угольным основанием, то все n апофем для нее будут одинаковыми, поскольку таковыми являются равнобедренные треугольники боковой поверхности фигуры. Заметим, что одинаковые апофемы являются свойством правильной пирамиды. Для фигуры общего типа (наклонной с неправильным n-угольником) все n апофем будут разными.

Еще одним свойством апофемы пирамиды правильной является то, что она одновременно является высотой, медианой и биссектрисой соответствующего треугольника. Это означает, что она делит его на два одинаковых прямоугольных треугольника.

Треугольная пирамида и формулы для определения ее апофемы

В любой правильной пирамиде важными линейными характеристиками являются длина стороны ее основания, ребро боковое b, высота h и апофема h_b. Эти величины друг с другом связаны соответствующими формулами, которые можно получить, если начертить пирамиду и рассмотреть необходимые прямоугольные треугольники.

Правильная треугольная пирамида состоит из 4 треугольных граней, причем одна из них (основание) должна быть обязательно равносторонней. Остальные являются равнобедренными в общем случае. Апофему треугольной пирамиды можно определить через другие величины по следующим формулам:

Первое из этих выражений справедливо для пирамиды с любым правильным основанием. Второе выражение характерно исключительно для треугольной пирамиды. Оно показывает, что апофема всегда больше высоты фигуры.

Не следует путать апофему пирамиды с таковой для многогранника. В последнем случае апофемой называется перпендикулярный отрезок, проведенный к стороне многогранника из его центра. Например, апофема равностороннего треугольника равна √3/6*a.

Задача на вычисление апофемы

Пусть дана правильная пирамида с треугольником в основании. Необходимо вычислить ее апофему, если известно, что площадь этого треугольника равна 34 см 2 , а сама пирамида состоит из 4 одинаковых граней.

В соответствии с условием задачи мы имеем дело с тетраэдром, состоящим из равносторонних треугольников. Формула для площади одной грани имеет вид:

Откуда получаем длину стороны a:

Для определения апофемы h_b воспользуемся формулой, содержащей боковое ребро b. В рассматриваемом случае его длина равна длине основания, имеем:

Подставляя значение a через S, получим конечную формулу:

Мы получили простую формулу, в которой апофема пирамиды зависит только от площади ее основания. Если подставить значение S из условия задачи, то получим ответ: h_b ≈ 7,674 см.

Апофема правильной пирамиды, формула

Апофема правильной пирамиды находится по формуле

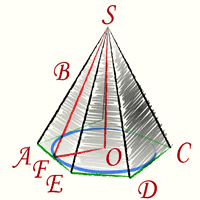
f — апофема правильной пирамиды (SF)
n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника (AB или BC или CD или DE или EA) — основания правильной пирамиды
h — высота правильной пирамиды (OS)

Апофема правильной пирамиды выводится из следующих формул

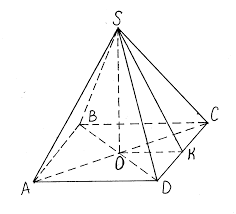
Синим цветом на рисунке изображена вписанная в основание правильной пирамиды окружность. Треугольник SFO прямоугольный. Его стороны: OS — высота правильной пирамиды ( h), OF — радиус вписанной окружности в правильный многоугольник (основание правильной пирамиды ( r)), SF — апофема правильной пирамиды ( f). По теореме Пифагора

подставив сюда только радиус вписанной окружности получается формула (1).

Апофема правильной треугольной пирамиды: формула и пример задачи

При изучении характеристик пространственных фигур в курсе стереометрии большое внимание уделяется таким свойствам, как площадь и объем. В то же время знать линейные параметры фигур важно, чтобы иметь возможность рассчитать указанные свойства. В данной статье ответим на вопрос, как найти апофему пирамиды правильной треугольной.

Какая фигура будет рассмотрена?

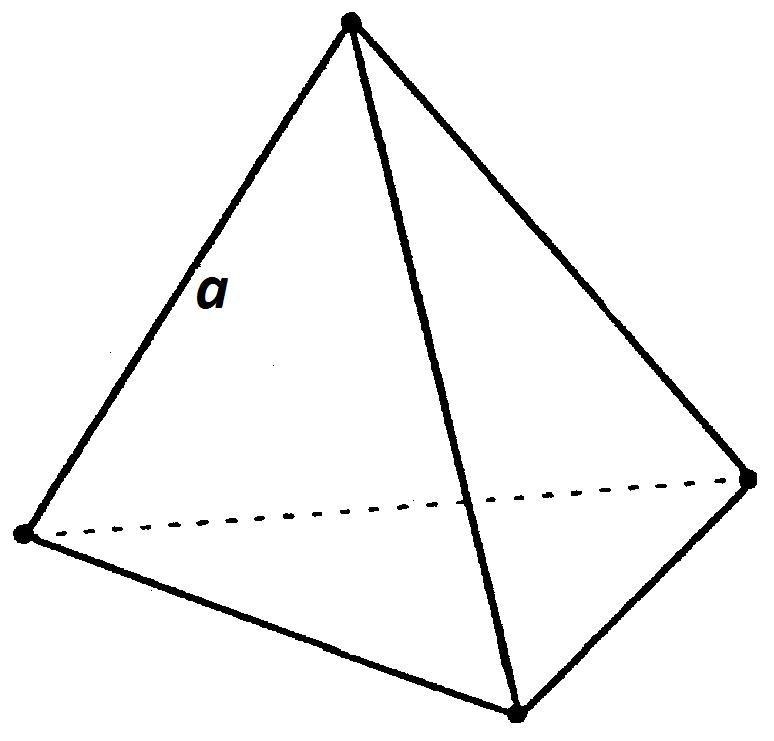
Треугольная пирамида с правильным основанием представляет собой фигуру в пространстве, которая ограничена одним равносторонним треугольником (основание) и тремя равнобедренными треугольниками (боковые стороны). Чтобы иметь возможность более четко представить эту пирамиду, покажем ее на рисунке.

Вам будет интересно: Зазноба — это . Значение слова

Важной точкой любой пирамиды является ее вершина, которая не принадлежит основанию. Если опустить перпендикуляр из нее на основание, то его длина будет высотой фигуры. В дальнейшем будем обозначать высоту буквой h. Высота правильной пирамиды падает точно в геометрический центр треугольника (точка пересечения его медиан, а также биссектрис и высот). Вторым линейным параметром, который следует знать, является длина стороны основания треугольной пирамиды, то есть длина стороны равностороннего треугольника. Обозначим ее буквой a.

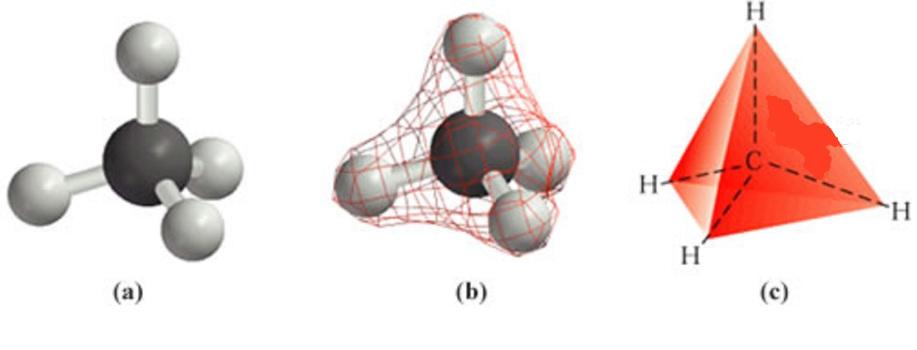
Треугольная пирамида имеет собственное название — тетраэдр. Тетраэдр не является чисто теоретической геометрической фигурой. Она также встречается в некоторых природных структурах. Так, в алмазе атом углерода соединен с четырьмя такими же атомами, которые образуют тетраэдр. Другой пример — это молекула метана, в которой углерод, соединенный с четырьмя атомами водорода, образует правильную треугольную пирамиду.

Формула апофемы пирамиды правильной треугольной

Перейдем непосредственно к вопросу статьи. Для треугольной пирамиды правильной апофемой называется любая из высот боковых треугольников, опущенная из вершины фигуры. Обозначим ее hb. Поскольку рассматриваемая фигура состоит из трех боковых треугольников, которые равны друг другу, то она имеет три одинаковых апофемы hb.

Определение длины апофемы не составляет большого труда. Предположим, что высота h и длина стороны a известны. Проводим высоту фигуры и рассматриваем треугольник прямоугольный, который находится внутри пирамиды и образован следующими сторонами:

• апофемой hb (гипотенуза);
• высотой h (один катет);
• 1/3 медианы m равностороннего треугольника (второй катет).

Длина медианы m треугольника в основании равна:

Пользуясь теоремой Пифагора, получаем формулу для длины апофемы hb:

Эта формула показывает, что длина апофемы hb для любых параметров треугольной пирамиды всегда больше ее высоты h.

Решение задачи на определение значения hb

Решим интересную задачу. Рассчитаем длину апофемы для тетраэдра, у которого все ребра равны друг другу.

Обозначим длину ребра буквой a. Она же является стороной треугольника в основании. Чтобы определить hb, необходимо найти h. Сделать это не сложно, если рассмотреть прямоугольный треугольник, образованный высотой h, ребром a и двумя третями медианы m. Получаем:

h = √(a2 — 4/9*m2) = √(a2 — 4/9*3/4*a2) = a*√(2/3)

Теперь применяем формулу для апофемы, получаем:

hb = √(a2/12 + h2) = √(a2/12 + 2/3*a2) = √3/2*a

Мы получили очевидный результат. Апофема правильной пирамиды треугольной равна длине медианы любого из равносторонних треугольников.

                                                      
Содержание:

1.
Обзор математической и методической литературы по теме, сравнительный анализ
содержания темы в различных школьных учебниках.

2.
Общая характеристика темы

А)
Особенности и роль темы в математике и в школьном курсе математики

Б)
Историческая справка

В)
Программа по математике: инвариантное содержание темы.

3.
Логико-математический анализ содержания темы. Постановка учебных задач.

4.
Тематическое планирование.

Урок
решения ключевых задач по теме «Виды неправильных
пирамид»

Список
литературы

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Обзор математической и методической литературы по теме,
сравнительный анализ содержания темы в различных школьных учебниках.

1.     
Всемирная история (энциклопедия для детей). – М.:
“Аванта+”, 1993.

2.     
Геометрия, 10 – 11: Учеб. для общеобразоват.
учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – 11-е
изд. – М.: Просвещение.

3.     
Геометрия. 10 класс: поурочные планы по учебнику  Л.
С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева и др. / авт.-сост. Г.И.
Ковалева – Волгоград: Учитель. – 125с.

4.     
Методика обучения геометрии: Учеб. пособие для
студ.высш.пед.учеб.заведений /В.А.Гусев, В.В.Орлов, В.А. Панчищина и др.; Под
ред. В.А. Гусева. – М.: Издательский центр «Академия». – 368 с.

5.     
Мулдашев Э. Р. Мировая система пирамид и
монументов древности спасла нас от конца света, но … — М.: “АиФ-Принт”; М.:
“ОЛМА-ПРЕСС”; СПб.: Издательский Дом “Нева”;

6.     
Математический энциклопедический словарь.
А. М. Прохоров и др. – М.: Советская энциклопедия,

7.     
Сверчевская И.А. Устные задачи по теме «Пирамида».
/ И.А. Сверчевская. // Математика в школе. – 2003. — № 7.

8.     
Смирнова И.В., Смирнов В.А. Геометрия. 10 – 11 кл.:
Методические рекомендации для учителя. В двух частях. Ч. 1. – М.: Мнемонзина, .
– 255 с.: ил.

9.     
Современные проблемы теории и практики
общеобразовательной и высшей педагогической школы: Информационный бюллетень
науч.-метод. Отдела. Выпуск 7.-Н.Новгород: НГПУ, 2005.

(1)
В данной книге в занимательной и доступной форме дается исторический материал
для детей разных возрастов.

(2)
Учебник Л. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева и др. для
общеобразовательных учреждений.

(3)
В данном пособии приводятся методические рекомендации к курсу геометрии по
учебнику Л. С. Атанасяна и др. «Геометрия 10-11». Пособие содержит поурочные
планы, составленные в соответствии с программой и «Обязательным минимумом
содержания образовательных программ по математике», снабжено достаточно большим
количеством устных упражнений, задач по готовым чертежам. Описана методика
введения отдельных понятий, даны рекомендации по изучению отдельных теорем.

(4)
Осмысление огромного опыта теории и методики обучения геометрии в школе
является целью данной книги: В ней условно последние десятилетия развития
методики преподавания геометрии в школе разделены на следующие периоды.

1)     
Период использования в школе учебников А.П.
Киселева – продолжался вплоть до начала 60-х годов 20 века.

2)     
Период внедрения в школьную геометрию новых
разделов: элементов теории множеств, геометрических преобразований, векторной
алгебры и т.д. – В.Г. Болтянский,                    А.И. Фетисов, И.М. Яглом и
др.

3)     
«Колмогоровский период» (1965 – 1980) –
характеризуется очень серьезным подходом к осмыслению всей структуры школьной
математики в целом и геометрии в частности.   А.Н. Колмогоров прежде всего
хотел навести порядок с употребляемым в геометрии математическим языком и
системой обозначений, кроме того, он пытался ввести разумную и понятную для
школьников аксиоматику и многое другое. Однако были завышены некоторые
представления о возможностях усвоения геометрических знаний массовым учеником.
Многие очень важные и интересные понятия (конгруэнтность, отображение
пространства на себя, трактовки понятия «вектор» и т. д.), попав в массовую
школу, не приносили никакого эффекта, так как понимать их могли только
учащиеся, имеющие определенный уровень математических способностей, а школа
была массовой и учебник был один.

4)     
«Период традиционных современных учебников» для
массовой школы – авторы             Л.С. Атанасян и др., А.В. Погорелов, И.Ф.
Шарыгин, А.Д. Александров и др. Появление этих учебников было связано с
желанием авторов вернуться к более традиционному (чем у А.Н. Колмогорова)
подходу к изучению школьного курса геометрии. Но перед данными учебниками
появилась новая проблема, связанная с внедрением в систему образования дифференцированных
методов обучения. Оказалось, что для современной школы нужна не только
достаточно четкая и строгая система изложения геометрических знаний, но и
мотивация учения, эстетическое воспитание, связь с окружающим миром, учет
индивидуальных особенностей и способностей учащихся и т. д.

5)     
В течение последних лет ушедшего столетия в разных
регионах России у разных авторов возникло желание изменить отношение к
школьному учебнику вообще, продумать уровни и профили обучения, понять
соотношение влияния математических знаний на развитие личности человека и много
другое. Это привело к появлению достаточно большого количества новых авторских
проектов: А. Л. Вернер и В. И. Рыжик, Т.Г. Ходот,                В. А. Гусев,
Г. А. Клековкин, В. В. Орлов, В. А. Панчищина, Н. С.
Подходова,                   Л. И. Ерганжиева, В. А. Смирнов, И.М. Смирнова.

(5)
В данной книге описываются интересные исторические события, связанные с
пирамидами и другими монументами древности.

(6)
В словаре даются статьи, где даны математические понятия.

(7)
В журнале имеется статья, где приведены устные задачи по теме «Пирамида».

(8)
В  пособии  содержится учебный материал для проведения уроков по геометрии в
старших классах средней школы. Оно рассчитано на учебник геометрии И.М.
Смирновой и В. А. Смирнова, но так же  может быть использовано при обучении по
любому другому учебнику геометрии, входящему в Федеральный перечень учебной
литературы.

В
пособии рассматриваются особенности преподавания геометрии в условиях
модернизации школьного образования, содержатся конспекты уроков по по основным
темам, включены математические диктанты, вопросы для учащихся, индивидуальные
задания по карточкам, задачи для самостоятельной работы, устные упражнения,
контрольные работы, а так же дополнительный учебный материал.

(9)
В данной книге имеется статья Огурцовой О.К. «Методика изучения темы «Виды
неправильных пирамид и наклонных призм» на практических занятиях учебного курса
«Элементарная математика»», где описывается методика изучения данных тем в
курсе математики для общеобразовательных школ.

Тема
«Многогранники» одна из основных в традиционном курсе школьной геометрии. Они
составляют центральный предмет стереометрии. Изучение параллельных и
перпендикулярных прямых и плоскостей, двугранных углов и другое, так же как
введение векторов и координат,- все это только начала стереометрии, подготовка
средств для исследования ее более содержательных объектов – главным образом тел
и поверхностей.

Центральная
роль многогранников определяется прежде всего тем, что многие результаты,
относящиеся к другим телам, получаются исходя из соответствующих результатов
для многогранников.

Многогранники
сами по себе представляют чрезвычайно содержательный предмет исследования,
выделяясь среди всех тел многими интересными свойствами, специально к ним
относящимися теоремами и задачами.

Многогранникам
должно быть уделено в школьном курсе больше внимания еще и потому, что они дают
особенно богатый материал для развития пространственных представлений, для
развития того соединения живого пространственного воображения со строгой
логикой, которое составляет сущность геометрии. Уже самые простые факты,
касающиеся многогранников, требуют такого соединения, которое оказывается при
этом не совсем легким делом.

Использование
многогранников с самого начала изучения стереометрии служит различным
дидактическим целям. На многогранниках удобно демонстрировать взаимное
расположение прямых и плоскостей в пространстве, показывать применение
признаков параллельности и перпендикулярности прямых и плоскостей в
пространстве. Иллюстрация первых теорем стереометрии на конкретных моделях 
повышает интерес учащихся к предмету.

Одной
из основных задач обучения математики является развитие у учащихся абстрактного
мышления. Широкие возможности для реализации этой цели предоставляет тема
«Многогранники».

Более
сложными для школьников оказываются задачи, связанные с наклонными призмами и
неправильными пирамидами. При решении таких задач перед учащимися, как правило,
возникает необходимость самостоятельного выявления связей, существующих между
элементами наклонной призмы и неправильной пирамиды. Анализ учебно-методической
литературы показал, что виды неправильных пирамид и наклонных призм
присутствуют в ней неявно, как определенные задачи. При этом отсутствует их
чёткое описание, не указаны равносильные условия, которые их характеризуют.

Особое
внимание выделению видов таких пространственных фигур, как неправильная
пирамида и наклонная призма, уделила кандидат педагогических наук, старший
преподаватель кафедры теории и методики обучения математике, О.К. Огурцова в
своей работе « Методика изучения темы «Виды неправильных пирамид и наклонных
призм» на практических занятиях учебного курса «Элементарная математика».
Выделение возможных зависимостей между элементами наклонных призм и
неправильных пирамид, а именно рассмотрение видов неправильных пирамид и
наклонных призм, поможет учащимся в школе решать задачи на нахождение объемов
указанных фигур.

Среди неправильных
пирамид выделены следующие виды и условия, характеризующие эти виды:

I. Вершина пирамиды проектируется в центр описанной окружности основания
тогда и только тогда, когда:

1. высота пирамиды проходит через центр
   описанной окружности основания;
2. боковые ребра пирамиды равны;
3. боковые ребра пирамиды равнонаклонены к
   плоскости основания;
4. .боковые ребра пирамиды равнонаклонены к
   высоте пирамиды.

II. Одна боковая грань пирамиды
перпендикулярна к плоскости основания тогда и только тогда, когда:

1. высота пирамиды принадлежит плоскости
   боковой грани;
2. вершина пирамиды проектируется на прямую,
   содержащую сторону основания;
3. двугранный угол при стороне основания
   пирамиды прямой

III. Вершина пирамиды проектируется в центр
вписанной окружности основания тогда и только тогда, когда:

1.     
высота пирамиды проходит через центр вписанной
окружности основания;

2.     
вершина пирамиды равноудалена от сторон основания;

3.     
каждое боковое ребро пирамиды образует равные углы
со смежными сторонами основания;

4.     
боковые грани пирамиды равнонаклонены к основанию;

5.     
боковые грани пирамиды равнонаклонены к высоте
пирамиды.

IV. Две боковые грани пирамиды перпендикулярны
к плоскости основания тогда и только тогда, когда:

1 случай: смежные боковые грани

1.     
боковое ребро пирамиды перпендикулярно к плоскости
основания;

2.     
высота пирамиды совпадает с боковым ребром;

3.     
вершина пирамиды проектируется в вершину основания;

4.     
угол основания является линейным углом двугранного
угла при боковом ребре пирамиды.

2 случай: несмежные боковые грани

1.     
высота пирамиды принадлежит линии пересечения
плоскостей двух несмежных боковых граней

2. Общая характеристика темы

А) Особенности и роль темы в
математике и в школьном курсе математики

Подходы к определению многогранника.

Выделяют
два основных способа введения понятия многогранника в школьном курсе
стереометрии:

1)     
многогранник как поверхность (например, в учебниках
А.Д. Александрова и др. и Погорелова А.В.);

2)     
многогранник как тело.

Чаще
используется второй путь.

Дать
строгое определение понятию многогранника в школе трудно, так как в определение
входят такие понятия как поверхность, ограниченность, внутренние точки и др.
Такая попытка была сделана в книге В.М. Клопского, З.А. Скопеца, М.И.
Ягодовского «Геометрия 9-10».

Наиболее
целесообразно дать описание на основе наглядных представлений школьника. Проще
и короче всего определить многогранник как тело, поверхность которого
состоит из многоугольников. При этом «тело» и «поверхность» можно понимать в
наглядном смысле, как понимают обычно. Тело в отвлечении его от материальности
– это часть пространства. Поэтому данное определение можно пересказать и так:  многогранник
– это часть пространства, ограниченная конечным числом многоугольников.

Например,
у Погорелова А.В.: «Многогранник – это такое тело, поверхность которого состоит
из конечного числа плоских многоугольников»; У Атанасяна Л.С.: «Многогранник –
это поверхность, составленная из многоугольников и ограничивающая некоторое
геометрическое тело».

Рассмотрим
изучение темы «Многогранники» в школьных учебниках. Для примера возьмем
учебники разного уровня изложения материала: предназначенные для
общеобразовательной школы, для гуманитарных классов, для классов с
математическим уклоном.

Сравнительный
анализ содержания темы в различных учебниках.

Учебник
Атанасяна Л.С.

Рассмотрим
изучение темы «Многогранники» по учебнику Атанасяна. Этот учебник предназначен
для общеобразовательной школы. Данная тема изучается в главе 3. На изучение ее
отводится 12 уроков. Ниже приведено поурочное планирование в таблице.

Номер   урока	Содержание учебного материала
1-4	§1. Понятие многогранника. Призма. Понятие многогранника. Призма. Площадь поверхности призмы. ( п.25-27)
5-9	§2. Пирамида. Пирамида. Правильная пирамида. Усеченная пирамида. Площадь поверхности пирамиды. (п.28-30)
10	§3. Правильные многогранники. Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников. (п. 31-33)
11	Контрольная работа.
12	Зачет по теме.

Еще
до изучения темы «Многогранники» учащиеся знакомятся с их простейшими видами в
главе 1 §4 «Тетраэдр и параллелепипед». На их изучение отводится 5 часов.
Понятия тетраэдра и параллелепипеда вводятся в данной главе для того, чтобы
рассмотрение их свойств, построение сечений способствовали углублению понимания
вопросов взаимного расположения прямых и плоскостей, поэтому необходимо, чтобы
решение задач сопровождалось ссылками на аксиомы, определения и теоремы.

Основная
цель темы «Многогранники» — дать учащимся систематические сведения об основных
видах многогранников.

Учащиеся
уже знакомы с такими понятиями, как тетраэдр и параллелепипед, и теперь им
предстоит расширить представления о многогранниках и их свойствах. В учебнике
нет строгого математического определения многогранника, а приводится лишь
некоторое описание, так как строгое определение громоздко и трудно не только
для понимания учащимися, но и для его применения.

Призма А₁ А_2… А_n В₁ В₂ …В_n определяется как многогранник, составленный из двух равных
многоугольников А₁ А_2… А_n и В₁ В₂ …В_n , расположенных в параллельных плоскостях, и n-параллелограммов А₁ А₂ В₂ В₁,
…, А_n А₁ В₁ В_n. Далее вводятся  определения элементов призмы, с помощью моделей
разъясняются понятия прямой призмы, наклонной призмы, правильной призмы.
Необходимо обратить внимание учащихся на то, что четырехугольная призма – это
знакомый им параллелепипед. У произвольного параллелепипеда все шесть граней –
параллелограммы, а боковые грани – прямоугольники, у прямоугольного
параллелепипеда все шесть граней – прямоугольники. При изучении площади
поверхности призмы доказывается теорема о площади боковой поверхности прямой
призмы.

Пирамида определяется как многогранник,
составленный из n-угольника А₁ А₂
… А_n и n-треугольников.
При введении понятия правильной пирамиды следует акцентировать внимание
учащихся на двух моментах: основание пирамиды – правильный многоугольник, и
отрезок, соединяющий вершину пирамиды с центром ее основания, является высотой
пирамиды. Можно устно доказать, что боковые грани правильной пирамиды – равные
равнобедренные треугольники. После этого вводится понятие апофемы правильной
пирамиды (высота боковой грани правильной пирамиды, проведенной из ее вершины),
при этом нужно подчеркнуть, что этот термин употребляется только для правильной
пирамиды, хотя у неправильной пирамиды также могут быть равны высоты боковых
граней.

При
изучении теоремы о площади боковой поверхности правильной пирамиды
полезна символическая запись доказательства. Пусть сторона основания n-угольной пирамиды равна а, апофема равна d, S_∆ — площадь боковой грани. Тогда

S_бок=n∙ S_∆,   S_бок=n∙ad,  S_бок=(n∙a)∙d,   S_бок= Pd,  где P – периметр
основания пирамиды.

Далее
вводится понятие усеченной пирамиды. Плоскость, параллельная основанию
пирамиды, разбивает ее на два многогранника: один из них является пирамидой, а
другой называется усеченной пирамидой. Усеченная пирамида – это часть полной
пирамиды, заключенная между ее основанием и секущей плоскостью, параллельной
основанию данной пирамиды. При выполнении рисунков к задачам на усеченную
пирамиду удобно вначале начертить полную пирамиду, а затем выделить усеченную пирамиду.

При
введении понятия правильной усеченной пирамиды надо отметить, что ее
основания – правильные многоугольники, а боковые грани – равные равнобедренные
трапеции; высоты этих трапеций называются апофемами усеченной пирамиды. Также
выводится  формула площади боковой поверхности правильной усеченной пирамиды.

Последнее,
что изучается в теме «Многогранники» в учебнике, это симметрия в пространстве и
понятие правильного многогранника. Основными понятиями здесь являются понятия
симметричных точек относительно точки, прямой, плоскости; понятия центра, оси,
плоскости симметрии фигуры. Таким образом, в данном учебнике многогранники
изучаются  с опорой на наглядность, предметы окружающей действительности.

Учебник Смирновой И.М.

Данный
учебник предназначен для преподавания геометрии  10-11 классах гуманитарного
профиля. По сравнению с традиционным изложением в учебнике несколько сокращен
теоретический материал, больше внимания уделяется вопросам исторического,
мировоззренческого и прикладного характера.

Особенностью 
учебника является раннее введение пространственных фигур, в том числе
многогранников, в п.3 «Основные пространственные фигуры». Цель – сформировать
представления учащихся об основных понятиях стереометрии, ознакомить с
пространственными фигурами и моделированием многогранников. Вводиться понятие многогранника
как пространственной фигуры, поверхность которой состоит из конечного числа
многоугольников, называемых гранями многогранника. Стороны этих многоугольников
называются ребрами многогранника, а вершины многоугольников – вершинами
многогранника.

Учащимся
демонстрируются следующие многогранники:

 
— куб – многогранник, поверхность которого состоит из шести квадратов;

 
—  параллелепипед – многогранник, поверхность которого состоит из шести
параллелограммов;

 
—  прямоугольный параллелепипед – параллелепипед, у которого грани –
прямоугольники;

 
—  призма – многогранник, поверхность которого состоит из двух равных
многоугольников, называемых основаниями призмы, и параллелограммов, называемых
боковыми гранями (причем у каждого параллелограмма два противоположных ребра
лежат на основаниях призмы);

 
—  прямая призма – призма, боковые грани которой — прямоугольники; правильная
призма – прямая призма, основаниями которой являются правильные многоугольники;

 
—  пирамида – многогранник, поверхность которого состоит из многоугольника,
называемого основанием пирамиды, и треугольников с общей вершиной, называемых
боковыми гранями пирамиды;

 
—  правильная пирамида – пирамида, в основании которой правильный многоугольник,
и все боковые ребра равны.

Показываются
более сложные многогранники, в том числе правильные, полуправильные и
звездчатые многогранники. Рассматривается несколько способов изготовления
моделей многогранников из разверток и геометрического конструктора.
Моделирование многогранников служит важным фактором развития пространственных
представлений учащихся.

Таким
образом, к началу непосредственного изучения темы «Многогранники» учащиеся уже
знакомы (на доступном для них уровне) с традиционным материалом по этой теме.
Появляется возможность расширить представления учащихся о многогранниках,
рассмотрев с ними более подробно правильные, полуправильные и звездчатые
многогранники.

Основная
цель данного раздела – ознакомить учащихся с понятием выпуклости и свойствами
выпуклых многогранников, рассмотреть теорему Эйлера и ее приложения к решению
задач, сформировать представления о правильных, полуправильных и звездчатых
многогранниках.

Можно
привести примерное тематическое планирование данной темы.

Пункт учебника	Содержание	Кол-во часов
18	Выпуклые многогранники	2
19	Теорема Эйлера	2
20*	Приложения теоремы Эйлера	2
21	Правильные многогранники	2
22*	Топологически правильные многогранники	1
23	Полуправильные многогранники	2
23	Звездчатые многогранники	1

Учебник Александрова А.Д.

 Данный
учебник предназначен для классов и школ с математической специализацией, он
дает богатую математическую информацию, развивает ученика, но является
достаточно трудно усваиваемым. В учебнике рассматриваются такие темы, которые в
основной школе  не доступны даже для  «сильных» учеников, например, сферическая
геометрия.

Отметим
особенности изучения многогранников в данном учебнике. Во-первых, многогранники
изучаются после круглых тел. Во-вторых, при изучении многогранника и его элементов
прослеживается связь с многоугольником. Вследствие чего возможны две
последовательности изложения темы: 1) обобщить понятие многоугольника, затем
разобрать аналогичные вопросы в пространстве; 2) пользуясь §21 учебника, дать
сначала определение многогранника, далее обобщить понятие многоугольника.
Особенностью является  введение двух определений призмы (как в учебниках,
рассмотренных выше, и как цилиндр, в основании которого лежит многоугольник),
причем доказывается равносильность этих определений. Аналогично дается другое
определение пирамиде: как конус с многоугольником в основании. Пункт 23.6
содержит раздел о триангулировании многогранника, и в нем дается другое,
конструктивное определение многогранника. §24 «Выпуклые многогранники» впервые
излагается в столь серьезном виде, рассматривается вопрос равносильности  двух
определений выпуклого многогранника. Изложение темы «Правильные многогранники»
также отличается от ее изложения в учебниках по геометрии других авторских
коллективов: сначала показываются пять типов правильных многогранников,
построением доказывается, что все пять типов правильных многогранников
существуют, и только после этого доказывается, что других правильных выпуклых
многогранников быть не может. Обычно же после определения сразу доказывалась
теорема, а существование показывалось позже, что усложняло методику рассказа.

Таким
образом, учебник содержит очень богатый теоретический материал по
многогранникам, которого нет в других учебниках по геометрии, также он может
быть использован как учебник для дополнительного изучения в основной школе.
Ниже в таблице приведено примерное поурочное планирование материала.

№ урока	Содержание учебного материала
1-2	Обобщение понятие многоугольника. Многогранник.
3-5	Призма, параллелепипед. Упражнения.
6-10	Пирамида. Виды пирамид. Упражнения.
11-13	Выпуклые многогранники.
14-16	Теорема Эйлера. Развертка выпуклого многогранника.
17-19	Правильные многогранники.

Во
всех учебниках при изучении многогранников рассматривается практически одни и
те же основные темы: определение многогранника, выпуклые многогранники, призма,
пирамида, правильные многогранники.

Б) Историческая справка

Древнегреческий
математик, автор дошедших до нас теоретических трактатов по математике Евклид,
пирамиду определяет как телесную фигуру, ограниченную плоскостями, которые
от одной плоскости сходятся к одной точке.

Но
это определение подвергалось критике уже в древности. Так Герон предложил
следующее определение пирамиды: “Это фигура, ограниченная треугольниками,
сходящимися в одной точке и основанием которой служит многоугольник”.

Оопределение
Адриена Мари Лежандра, который в 1794 году в своем труде “Элементы геометрии”
пирамиду определяет так: “Пирамида – телесная фигура, образованная
треугольниками, сходящимися в одной точке и заканчивающаяся на различных
сторонах плоского основания”.

В
учебнике 19 века фигурировало еще одно определение пирамиды: “пирамида –
телесный угол, пересеченный плоскостью”.

Пирамидами
называли гробницы древнеегипетских фараонов 3-го – 2-го тысячелетий до
н. э., а так же постаменты храмов в Центральной и Южной Америке, связанные
с космологическими культами.

Первой
пирамидой, построенной в Древнем Египте, является “ступенчатая” пирамида
правителя из III династии — Джосера, которой около 4700 лет. В настоящее время
считается, что приблизительное количество сохранившихся пирамид в Египте
составляет от 70 до 80. И лишь около половины из них — пирамиды фараонов.

Египетские
пирамиды — древнейшие из семи чудес света, незыблемо высятся на фоне
желто-коричневых песков Ливийской пустыни. К изучению пирамид приступили
сравнительно недавно. Два века назад французский ученый Жомар, сопровождавший
армию Наполеона в Египет, составил первое научное описание и провел первые
точные измерения пирамид. Самая высокая пирамида – пирамида Хеопса, или Большая
пирамида. В древности ее высота достигала 148
метров. Сторона квадратного основания равна 233
метрам, а площадь основания превышает 54 000 квадратных метров. Общий
объем всего сооружения – более 2 500 000 кубических метров. Сложена
пирамида из 2 300 000 каменных глыб весом свыше 2-х тонн каждая.
Глыбы со всех сторон гладко отшлифованы. Это значит, что строителям пришлось
обработать около 14 000 000 поверхностей, так как каждый монолит имел
6 граней. Все поверхности отшлифованы с такой математической точностью, что,
соединив их, между ними нельзя просунуть тонкое лезвие ножа.

Пирамиды
строили не только в Египте. Они вырастали и по другую сторону океана, в древних
государствах Центральной Америки. К северу от Мехико ученые открыли обширный
город Теотиукан, ошеломляющий пирамидами гигантских размеров. Самая большая –
пирамида Солнца, периметр ее основания равен 1000
метров, а напротив нее возвышается пирамида Луны.

Вокруг
пирамид в течение многих веков складывалось множество легенд. В средневековье
бытовали легенды, что эти постройки представляли собой нечто вроде камер
хранения для фараонов или житниц, сооружённых библейским Иосифом. Эти
сооружения считали и древними архивами жрецов Египта, и старинными
обсерваториями, и заграждениями, противостоящими пескам.

На
Земле существует целая сеть пирамид. На фоне Гималайского хребта четко
выделяется пирамидальное образование — гора Кайлас; существуют мексиканские
пирамиды. Так вот, расположение г. Кайлас, египетских и мексиканских пирамид
очень интересное, а именно  – если соединить г. Кайлас с мексиканскими
пирамидами, то соединяющая их линия выходит на остров Пасхи. Если соединить г.
Кайлас с египетскими пирамидами, то линия их соединения опять выходит на остров
Пасхи. Очертилась ровно одна четвертая земного шара.

Если
соединить мексиканские пирамиды и египетские, то мы увидим два равных
треугольника. Если найти их площади, то их сумма равна одной четвертой площади
земного шара.

Если
рассмотреть расстояние “Кайлас — египетские пирамиды” и “остров Пасхи –
мексиканские пирамиды”, то мы получим ровно одну четвертую длины линии “Кайлас
– о. Пасхи”. На Земле существует строгая пирамидально-географическая система
пирамид.

Большой
интерес представляет энергия, неразрывно связанная с пирамидами. Как сейчас
установлено, энергия пирамиды впервые была открыта во время Второй Мировой
Войны. Когда немецкие самолёты пролетали над пирамидами, то приборы самолётов
неожиданно отказывались работать. Следует заметить, что египетские лётчики, по
каким-то соображениям культурного характера или из страха, старались никогда не
летать над пирамидами. Между тем указанный феномен никого тогда не
заинтересовал и никто его не стал изучать.

Однако
спустя некоторое время этот феномен принялся исследовать француз Антуан Бови.
Его изучение пирамид началось с того, что однажды он нашёл в царской камере
одной из пирамид трупы кошек, крыс, мышей и других мелких животных, которые
были совершено не подвергнуты гниению! А между тем условия в погребальных
камерах таковы, что они очень способствуют процессу разложения. Действительно,
в этих камерах царят высокие влажность и температура (около 30 градусов по
Цельсию).

Французский
исследователь принялся за разгадку этого явления. В качестве версии он
предположил, что указанный феномен каким-то образом связан с формой пирамиды.
Для подтверждения своей версии сделал точный макет пирамиды Хеопса и расположил
его по оси север-юг. Кроме того, внутрь пирамиды, на уровне трети её высоты он
положил дохлую кошку.

Спустя
некоторое время результаты эксперимента оказались следующими: на трупе не было
зафиксировано ни малейших признаков гниения, более того — не было и никакого
запаха. Создавалось впечатление, что труп кошки неким образом мумифицировался.
Разумеется, радости исследователя не было границ.

Пирамида
способна выставлять защитный барьер против геопатогенных излучений, оказывая
влияние не только на предметы, помещённые вовнутрь её, но и на окружающее
пространство. Причём радиус воздействия прямо пропорционален величине пирамиды.

Можно
провести опыты с семенами: положите их на треть высоты пирамиды в линию
ориентированную на “север — юг”. Очень щепетильным людям можно предположить
расположить их крестом строго на “север-юг” и “запад-восток”. Оставьте семена
на неделю внутри пирамиды. При высевании сажайте семена вперемешку — заряжённые
и обычные, чтобы на росте не отразились дополнительные факторы, такие как
количество солнечного света, воды или характер почвы. Результат не замедлит
сказаться уже на первых стадиях развития растений.

Стеф
Бьеркинс, известный бельгийский радиометрист, также проводил исследования с
энергией пирамид. Учёный положил непосредственно на основание пирамиды два
голубиных яйца. Каждый день он переворачивал яйца. А через 21 день он добавил к
первым яйцам ещё и недавно снесённые. Ещё через 18 дней из первых двух яиц
вылупились 2 птенца. Уникальность этого в том, что голубиные яйца очень недолго
остаются живыми после прекращения инкубации. Таким образом, поместив яйца в
пирамиду, можно сохранять жизнеспособность голубиных эмбрионов, кстати, оба
голубка были здоровыми и сильными в момент рождения. Так древняя пирамида
приходит нам на помощь в совершенно неожиданных областях.

Однако
и с точки зрения архитектуры, и дизайнерского искусства пирамиды представляют
большой интерес. Элементы пирамид применяют в строительстве. Сейчас это очень
модно и придаёт зданию некоторый шик.

Ярким
представителями в этой области являются:

• Торговый центр в
  Илинге (Лондон) – образец постмодернизма. Одна из его башен имеет форму
  пирамиды и придаёт зданию величавый вид;
• Здание книжной
  ярмарки во Франкфурте (Германия) – крыша здания украшена стеклянной
  пирамидой;
• Вход в Лувр
  (Париж) – это не обычная дверь, а пирамида, сделанная из стекла, имеющая
  высоту 21,65 метра.

Арабский
писатель XIII века сказал: “Все на свете боится времени, а время боится
пирамид”. Эти слова, как нельзя, кстати. Дело в том, что пирамиды – это
единственное из семи чудес света чудо, дожившее до нашего времени, до эпохи
телевидения и компьютерных технологий.

В) Программа по математике: инвариантное
содержание темы.

Цель изучения курса
геометрии в 10-11 классах – систематическое изучение свойств геометрических тел
в пространстве, развитие пространственных представлений учащихся, освоение
способов вычисления практически важных геометрических величин и дальнейшее развитие
логического мышления учащихся.

Высокий уровень
абстрактности изучаемого материала, логическая строгость систематического
изложения соединяются с привлечением наглядности на всех этапах учебного
процесса и постоянным обращением к опыту учащегося. Умения изображать важнейшие
геометрические тела, вычислять их объемы имеют большую практическую значимость.

Содержание
действующего школьного курса математики группируется вокруг нескольких
стержневых линий: «Числа и вычисления», «Выражения и их преобразования», «Уравнения»,
«Функции», «Геометрические фигуры. Измерение геометрических величин». Этот
перечень отражает длительный опыт обучения математике и в настоящее время
практически полностью соответствует мировой практике.

Центральными линиями
курса с точки зрения общего образования являются числовая, функциональная и
геометрическая, концентрирующие в себе математические знания, необходимые
прежде всего в повседневной жизни – для решения возникающих на практике
расчетных задач, для ориентации в окружающем пространстве, для коммуникации в
ближайшей среде и в обществе в целом.

Ниже раскрыто
наполнение содержательных линий курса и описано распределение материала по
ступеням обучения.

Геометрические
фигуры. Измерение геометрических величин.

Геометрические
фигуры и их свойства (точки, прямые, плоскости, плоские и пространственные
углы, многоугольники, окружность и круг, многогранники, тела вращения),
геометрические отношения (принадлежность, пересечение, скрещивание, касание,
параллельность и перпендикулярность, равенство и подобие, симметрия),
геометрические величины (длины линий, величины углов, площади и объемы,
применение алгебраического и аналитического аппарата в геометрии.

В начальной школе
учащиеся на опытно-наглядной основе знакомятся с простейшими геометрическими
формами, приобретают начальные навыки изображения геометрических фигур,
овладевают единицами измерения длин и площадей. В среднем звене приобретают
систематизированные сведения об основных геометрических фигурах и связанных с
ними геометрических величинах, об основных геометрических отношениях на
плоскости; приобретают опыт применения аналитического аппарата в решении
геометрических проблем. На старшей ступени обучения расширяются сведения о
планиметрии. Однако основное внимание уделяется изучению пространственных
конфигураций и тел, геометрических величин и отношений в пространстве.

Изучение
программного материала дает возможность учащимся:

·        
получить представления о широте применения
геометрии в различных областях человеческой деятельности;

·        
познакомиться с некоторыми фактами истории
геометрии;

·        
решать задачи на вычисление линейных и угловых
элементов пространственных конфигураций, на нахождение площадей поверхностей и
объемов тел;

·        
решать задачи на доказательство, овладеть набором
приемов, часто применяемых для решения стереометрических задач на вычисление и
доказательство ( вычленение ключевой фигуры или тела, проведение стандартных
дополнительных построений, нахождение геометрических мест точек в пространстве
и др.)

Согласно программам
для общеобразовательных учреждений, уровень обязательной подготовки
определяется следующими требованиями:

ü 
уметь распознавать на моделях и по описанию
основные пространственные тела (призма, пирамида, цилиндр, конус, шар),
указывать их основные элементы, узнавать эти формы в окружающих предметах;

ü 
уметь иллюстрировать чертежом либо моделью условие
стереометрической задачи;

ü 
уметь вычислять значения геометрических величин
(длин, площадей, объемов), применяя изученные формулы;

ü 
уметь решать несложные задачи на вычисление с
использованием изученных свойств и формул.

3. Логико-математический анализ содержания темы. Постановка учебных
задач.

Анализ теоретического материала.

Геометрия, 10,11: учеб.для общеобразоват.
учреждений: базовый и профил. уровни / [Л.С. Атанасян, В.Ф. Бутузов, С.Б.
Кадомцев и др.]  — 15-е изд., доп. -М.: Просвещение. – 256 с.

Глава III Многогранники.

§ 2.

Дидактические
единицы:

 — основная формула для вычисления полной
поверхности пирамиды:

Способ вычисления полной поверхности пирамиды
не является для учащихся новым, т.к. из курса планиметрии они знают свойство
многоугольников: если многоугольник составлен из нескольких многоугольников,
то его площадь равна сумме площадей этих многоугольников.

Это свойство распространяется и на
многогранники, т.к. пирамида – это многогранник, состоящий из многоугольников.
Понятие площадей различных многоугольников  следует повторить из курса планиметрии
на мотивационно-ориентировочном этапе.

Площадь полной поверхности пирамиды равна
сумме площадей всех ее граней (т.е. основания и боковых граней).

Доказательства этой формулы не дается, способ
не является новым, так как учащиеся встречались с аналогичным способом
доказательства при нахождении полной поверхности  призмы. Доказательство
несложное, можно предложить для самостоятельного доказательства учащимся.

Выводы:

1) изучение темы нужно вести на наглядной
основе, необходимо использовать учебные наглядные средства: графические модели,
натуральные модели многогранников.

2) следует повторить из курса планиметрии формулу
нахождения площади треугольника и площади четырехугольника, т.к. с ними связана
основная формула для вычисления площади полной поверхности пирамиды.

3) теоремы о вычисления площади полной
поверхности пирамиды  не очень сложные и учащиеся с помощью наводящих вопросов
сами смогут их доказать

Анализ
задачного материала

Среди задач можно выделить следующие ключевые
задачи.

 №249.

В пирамиде все боковые ребра равны
между собой. Дока­жите, что: а) высота пирамиды проходит через центр окруж­ности,
описанной около основании; б) все боковые ребра пирамиды составляют равные углы
с плоскостью основании.

Дано: ABCS – пирамида,
 SO┴(ABC), SA=SB=SC.

Доказать: а) О — центр описанной  окружности

6)
<SAO=<SBO=<SCO;

Доказательство:

Рассмотрим ∆SAO и ∆SBO  и ∆SCO:   SO   —   общая;    AS=SB=SC   (условие), <SOA=<SOB=<SOC  ∆SAO = ∆SBO  = ∆SCO => <SAO=< SBO= <SCO, т.к.  АО=ВО=СО,
то О – центр окружности описанной около ∆АВС, т.е. что и требовалось доказать.

Пирамида в данной задаче относится к I виду пирамид, вершина которой проектируется в центр описанной
окружности основания. 

   № 251.

Основанием пирамиды DABC является прямоугольный тре­угольник с гипотенузой ВС.
Боковые ребра пирамиды равны друг другу, а ее высота равна 12
см. Найдите боковое ребро пирамиды, если ВС=10 см.

Дано: ABCD – пирамида, ∆ABC, <A=90°, BC=10см, DA=DB=DC, DO┴(ABC), DO=12см.

Найти: AD или DB или DC -?

Решение:
т.к. DA=DB=DC, то O— центр окружности
описанной около  ∆ABC, ∆ABC – прямоугольный, значит OBC, BO=OC=BC=5см в ∆BDO: <O=90°, BO=5см, DO=12см  BD ==13 см

Ответ:
 DA=DB=DC =13 см

            Пирамида в данной задаче относится
к I виду пирамид, вершина которой проектируется в центр описанной
окружности основания. 

 № 246.

Высота треугольной пирамиды равна 40
см. а высота каж­дой боковой грани, проведенная из вершины пирамиды, равна 41
см. а) Докажите, что высота пирамиды проходит через центр окружности,
вписанной в ее основание, б) Най­дите площадь основания пирамиды, если его
периметр ра­вен 42 см.

Дано: ABCS – пирамида,
 SO┴(ABC), SO=40 см, P_ABC = 42 см. SN┴AB, SK┴BC,SM┴AC, SN=SK=SM=41 см.

Доказать: а) О — центр вписанной  окружности в ∆ABC

Найти:
6) S_ABC-?

Доказательство:

а) Рассмотрим ∆SON и  ∆SOM и ∆SOK, SO – общая, SN=SM=SK ∆SON = ∆SOM = ∆SOK (по
катету и гипотенузе) — прямоугольные ON=OK=OM, т.е. O — равноудаленная
от сторон ∆ABC, т.е. лежит на пересечении биссектрис углов ∆ABC, следовательно
О — центр вписанной  окружности,  что и требовалось доказать.

6) S_ABC= Рr, r – радиус окружности
вписанной  в ∆ABC. r = OK ==9 см, S_ABC=*42*9=21*9=189 см²

Ответ:
S_ABC=189 см²

Данная пирамида
относится к III виду пирамид, вершина которой
проектируется в центр вписанной окружности основания.

 № 245.

Основанием пирамиды является
прямоугольник, диагональ которого равна 8
см. Плоскости двух боковых граней пер­пендикулярны к плоскости основания, а
две другие боковые грани образуют с основанием углы 30° и 45°. Найдите пло­щадь
поверхности пирамиды.

Дано: ABCDS – пирамида,
ABCD— прямоугольник, AC=8 см, SO┴(ABC), <BAC = 30°, <BCS = 45°.

 Найти: S_{полн. пов.}-?

Решение:

1)     
AB=a, тогда SB=, т.к. лежит против
угла в 30°,  BC=, т.к. BC= SB в ∆SBC—
прямоугольный, равнобедренный.

С другой стороны AB²+ BC²=AC², т.к. ABCD— прямоугольник.

, , см,
т.е. ABсм, BC = 4 см.

2)     
S_{полн. пов}=S_ABS+S_BCS+S_ADS+S_DCS+S_ABCD.

S_ABS= см²

S_BCS= см²

S_ADS=AС*AD= см²

S_DCS= см²

S_ABCD= см²

S_{полн. пов}=см²

Ответ: S_{полн. пов}= см².

Пирамида в данной задаче относится к IV виду пирамид, две боковые грани которой перпендикулярны к плоскости
основания.

№ 243

 Основанием пирамиды DABC является
треугольник ABC, у которого AB= AC=13 см, BC=10
см, ребро DA перпендикулярно к плоскости основания
и равно 9 см. Найдите пло­щадь боковой поверхности пирамиды.

Дано: ABCD – пирамида,
AB= AC=13 см, BC=10 см, AD┴(ABC), AD = 9 см.

 Найти: S_{бок. пов.}-?

Решение: S_{бок. пов.}=S_ADC+ S_ADB+ S_CDB.

S_ADC = S_ADB т.к. ∆ADC=∆ADB.

S_ADC= см²

Для удобства вычисления S_CDB построим высоту DK к стороне CB и высоту АK к стороне CB. S_CDB=см.

 см.

S_CDB= см² S_{бок.
пов}=58,5*2+75=192 см²

Ответ: S_{бок. пов}=192 см²

Пирамида в данной задаче относится к II
виду пирамид, одна боковая грань которой перпендикулярна к
плоскости основания.

№ 244.

    Основанием
пирамиды DАВС является
прямоугольный треугольник АВС, у которого гипотенуза АВ равна 29
см, катет АС равен 21 см. Ребро DА перпендикулярно
к плоскости основания и равно 20 см. Найдите площадь боковой поверхности
пирамиды.

 Дано:
АВС — пирамида; АВС: С=90°,
АС=21 см,; АВ=29 см, DА(АВС), DА=20 см

Найти: S_бок.
— ?

Решение:

S_бок⁼S_ADC+S_BDA+S_DCB

все грани прямоугольные треугольники =210 см²;

=290 см²;

=290 см²

АDС: DС=см. АВС: СВ=20см

значит S_бок⁼ 210+2*290=790
см².

Пирамида в данной задаче относится к II
виду пирамид, одна боковая грань которой перпендикулярна к
плоскости основания.

№ 247.

Двугранные углы при основании
пирамиды равны. Докажите, что: а) высота пирамиды проходит через центр
окружности, вписанной в основание; б) высоты всех боковых граней, проведенные
из вершины пирамиды, равны; в) площадь боковой поверхности пирамиды равна
половине произведения периметра основания на высоту боковой грани, проведенную
из вершины.

Дано: АВСS — пирамида, SО(АВС), SNО=SКО=SМО; Доказать:

а) О-центр окружности вписанной в АВС

б) NS=SК=SМ;

в) S_бок
= Р_АВС*SN.

Доказательство:

1) Рассмотрим SМО и SNО и SКО; SО — общая;

SNО=SКО=SМО (условие) =>SМО = SNО = SКО

(по катету и острому углу) =>  ОМ=ОN=ОК и МS=NS=КS; т.к. ОМ=ОN=ОК, то О —
равноудалена от сторон АВС, значит О — центр окружности
вписанной в АВС.

2) S_бок
=, ч.т.д.

Данная пирамида относится
к III виду пирамид, вершина которой проектируется в центр
вписанной окружности основания.

№ 248.

    Основанием пирамиды является треугольник со сторонами 12
см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 45°.
Найдите площадь боковой поверхности пирамиды.

Дано: АВСS — пирамида; АВ=АС=10 см, ВС=12 см; SNО=SКО=SМО=45⁰,

Найти:  S_бок
=?;

Решение:

1) т.к. SNО=SКО=SМО=45⁰,
то О — центр окружности вписанной в АВС и ОМ=ОК=ОК=SО. Найдем ОК — ?

2) АСК подобенАОМ (по 2 углам);  ;
АС=10,

СК=ВС=6, АК=8; АО=8-r, ОМ=r; 10r=6*(8-r) 10r+6r=48; r=3, т.е. ОК=ОS=3 см

3) S_бок
=_РABC *SK, SКО: O=90°; ОК=ОS=3;  SК=3отсюда S_бок
= (10+10+12)*3  =16*3=48см²

Данная пирамида
относится к III виду пирамид, вершина которой
проектируется в центр вписанной окружности основания.

№ 250.

    Основанием пирамиды является равнобедренный
треугольник с углом 120°. Боковые ребра образуют с ее высотой, равной 16
см, углы в 45°. Найдите площадь основания пирамиды.

 Дано: АВСD — пирамида, АВ=ВС,
В=120°, DO(АВС),
DО=16
см, ADO=BDO=CDO=45°.

Найти: S_ABC — ?

Решение:

1) т.к. ADO=BDO=CDO=45°, то
АО=ОВ=ОС=ОD — радиус окружности описанной около АВС, а т.к. B=120°, то О — вне
треугольника

2) АВС-вписанный и АВС=120° отсюда АОС=АВС=360°-240°; АОС=120°;
АО=ОС=ОD=16 см по т. синусов в АОС:

  т. к. в АВС АВ=ВС и В=120°, то АВ=ВС=16см, отсюда S_ABC =  S_ABC =  см²

Пирамида в данной задаче относится к I виду пирамид, вершина которой проектируется в центр описанной
окружности основания. 

№ 253.

    Основанием пирамиды является равнобедренная
трапеция с осно­ваниями 6 см и 4 л/6 см и высотой 5
см. Каждое боковое ребро пирамиды равно 13
см. Найдите ее высоту.

 Дано: АВСDS — пирамида, АВСD-равнобедренная трапеция, АD=6 см, ВС=4см, ВНАD, ВН=5 см, АS=ВS=СS^:=DS=13 см

Найти: SО — ?

Решение:

1) т.к. АS=ВS=СS^:=DS, то О — центр
окружности описанной около АВСD и лежит на высоте МN,  ОС=ОD=R — радиус этой окружности;

R²= МС²+МО²; R²=ND²+ОN²; MC²+МО²=ND²+ON²; 3²+
МО²=(2)²+(5- МО)²; 9+ МО²=

24+25-10МО+МО²; МО=4 см, отсюда R= = 5
см

2) SОА: O=90°; АО=5см; АS=13см =>SO=SО = 12 см

Пирамида в данной задаче относится к I виду пирамид, вершина которой проектируется в центр описанной окружности
основания. 

Выводы:

Задачный материал многообразен, отражает все выделенные
дидактические единицы. Особенно часто повторяются задачи с использованием
пирамид 1, 2 и 3 вида. Всего одна задача с использованием пирамиды 4 вида, у
которой две боковые грани перпендикулярны к плоскости основания. Поэтому
приходится давать задачи из различной математической литературы, а не только из
учебника.

Учебные задачи изучения темы

 — формировать у учащихся представление о
способе вычисления полной  и боковой поверхности пирамиды

 — формировать у учащихся умение решать задачи
на доказательство и на нахождение полной  и боковой поверхности пирамиды

Диагностируемые цели:

Ученик должен:

  Знать

• Основную формулу для вычисления полной  и
  боковой поверхности пирамиды
• Основные формулы для вычисления площадей
  геометрических фигур, изучаемых в планиметрии

  Уметь

v 
Выполнять чертеж по условию
стереометрической задачи;

v  Решать задачи на нахождение полной  и боковой поверхности
пирамиды и на вычисление геометриче­ских величин;

v  Использовать
при решении стереометрических задач планиметри­ческие факты и методы;

v  Проводить доказательные рассуждения в ходе решения задач;

  Понимать

ü 
Понимать стереометрические
чертежи;

ü 
Формулы нахождения полной  и боковой поверхности
пирамиды

4. Тематическое планирование.

Отводится примерно 7
часов.

            1. Вводный урок-лекция «Пирамида.
Правильная пирамида. Площадь поверхности пирамиды.»

    Метод обучения: частично-поисковый

    Учебная задача

 — вывести основную формулу для площади
поверхности пирамиды,

 — изучить теорему о нахождении площади
боковой поверхности правильной пирамиды.

            2. Урок усвоения теории

    Тема та же

    Метод обучения: частично-поисковый

    Учебная задача: проверить усвоение теории
по теме

3,
4 Уроки решения ключевых задач по теме: «Площадь поверхности неправильной
пирамиды»

    Метод обучения: частично-поисковый

    Учебная задача: рассмотреть основные виды
задач по теме:  «Площадь поверхности неправильной пирамиды»

            5.  Урок-лекция «Усеченная
пирамида».  

     Метод обучения: частично-поисковый

     Учебная задача:

Вывести основную формулу о нахождении площади
боковой поверхности усеченной пирамиды.

Изучить  теорему о нахождении площади боковой
поверхности усеченной пирамиды.

    6. Урок решения
ключевых задач по теме:

«Площадь поверхности усеченной пирамиды»

    Метод обучения:
частично-поисковый

    Учебная задача: рассмотреть основные виды
задач по теме:

 «Площадь поверхности усеченной пирамиды»

7.    Урок
обобщения и систематизации знаний

     Метод обучения: проблемное изложение,
частично-поисковый

    Учебная задача: обобщить и
систематизировать знания учащихся по данной теме

            8.   Урок контроля

      Метод обучения: частично-поисковый,
репродуктивный

      Учебная задача:  проконтролировать
знания, умения учащихся

Урок решения ключевых задач по теме

«Виды неправильных пирамид»

Учебник
Атанасяна Л.С.

Учебная задача:

1) рассмотреть виды неправильных пирамид;

2) формировать у учащихся умение строить
пирамиды в зависимости от условий задачи;

3) выделить схему решения задач на вычисление площади
поверхности неправильных пирамид

Диагностируемые цели:

Учащиеся
должны знать:

·              
 Виды
неправильных пирамид; формулу нахождения площади боковой и полной поверхности
неправильной пирамиды;

Учащиеся
должны уметь:

·        
Применять
формулу нахождения площади боковой поверхности неправильной пирамиды при
решении основных видов задач по теме:  «Площадь
поверхности неправильной пирамиды».

Учащиеся
должны понимать:

·        
Если вершина пирамиды
равноудалена от сторон основания, то высота пирамиды проходит через центр
вписанной окружности основания

·        
Если высота пирамиды проходит
через центр описанной окружности ос­нования, то  боковые ребра пирамиды равны, равнонаклонены
к плоскости основания и к высоте пирамиды.

·        
Если  высота пирамиды
принадлежит плоскости боковой грани, то  вершина пирамиды проектируется на
прямую, содержащую сторону основания, а  двугранный угол при стороне основания пирамиды
прямой.

·        
Если высота пирамиды совпадает
с боковым ребром, то боковое ребро пирамиды перпендикулярно к плоскости
основания,  вершина пирамиды проектируется в вершину основания, а угол
основания является линейным углом двугранного угла при бо­ковом ребре пирамиды

Метод обучения:  частично-поисковый

Средства обучения: мел, доска, учебник

Форма работы: фронтальная

       Структура урока:

1. Мотивационно-ориентировочная часть (10
   минут)
2. Содержательная часть (30 минут)
3. Рефлексивно-оценочная часть (5 минут)

Ход
урока

I. Мотивационно-ориентировочная часть

1. Среди изображенных тел выберите номера тех фигур,
которые явля­ются пирамидами.

Ответ: 3, 4, 6, 7.

На прошлых уроках вы решали
задачи в которых дана правильная пирамида. Что это такое и какими свойствами
она обладает? (по мере ответов учащихся на доске делается запись):

1.
Определение: (Пирамида называется правильной, если ее  основание– правильный
многоугольник, а  отрезок, соединяющий вершину пирамиды с центром ее основания,
является высотой пирамиды)

2.     
Обозначение: (PA₁A₂…A_n).

3.
Элементы: (основания – правильные многоугольники, боковые грани – равные
равнобедренные треугольники; высота боковой грани, проведенная из вершины – апофема,
точка P  вершина, боковые ребра PA_1, PA_2, … PA_n,,   высота пирамиды — отрезок,
соединяющий вершину пирамиды с центром ее основания)

4. Какие еще свойства есть у правильной
пирамиды? (боковые  ребра  правильной пирамиды равны, боковые грани
правильной пирамиды являются равными равнобедренными треугольниками).

5.
Как построить изображение правильной пирамиды: (При выполнении рисунков к
задачам  вначале начертить основание пирамиды в виде изображения правильного
многоугольника, а затем из центра основания восстановить и на нем выбрать
перпендикуляр к плоскости основания пирамиды, затем соединить ее с каждой
вершиной основания).

6. Формулы (S_бок=n∙ S_∆,  
S_бок=n∙ad,  S_бок=(n∙a)∙d,   S_бок= Pd,  где
P – периметр основания пирамиды)

7. Решить задачу:

Апофема правильной шестиугольной
пирамиды равна h, а двугранный угол при основании равен . Найти полную поверхность пирамиды.

Решение: Так как ,
то .

Основание пирамиды – правильный
шестиугольник, поэтому  и

. Тогда , т.е. ,

. Таким образом, ,

Окончательно находим

Ответ:

— Как вы думаете, для чего мы повторили
свойства правильной пирамиды?

( Для выделения правильной пирамиды из
других геометрических фигур)

А как можно назвать пирамиды у которых в
основании лежит произвольный многоугольник?

(Неправильная пирамида)

Сегодня при решении задач мы увидим,
что существуют разные виды пирамид, поучимся их выделять и познакомимся с их
свойствами.

II.
Содержательная часть.

Задача № 249. В пирамиде все боковые ребра равны между собой. Дока­жите, что: а) высота пирамиды проходит через центр окруж­ности, описанной около основании; б) все боковые ребра пирамиды составляют равные углы с плоскостью основании.
Поиск решения	Оформление задачи
— Что значит боковые ребра равны между собой? ( вершина S равноудалена от вершин основания пирамиды)  — Пусть SO – высота пирамиды. Что можно сказать о треугольниках ∆SAO и ∆SBO  и ∆SCO?  (они равны по гипотенузе и катету:    AS=SB=SC   по условию задачи, SO  – общий катет)  — Что можно сказать о других катетах этих треугольников? (АО=ВО=СО, значит т. O – т. пересечения серединных перпендикуляров, проведенных к сторонам треугольника АВС, т.е. центр описанной около треугольника АВС окружности с радиусом АО=ВО=СО) —  Что можно сказать об углах, которые боковые ребра составляют с плоскостью основания?  (Т. к. ∆SAO,  ∆SBO  и ∆SCO?  равны по гипотенузе и катету:    AS=SB=SC   по условию задачи, SO  – общий катет, то и углы равны между собой <SOA=<SOB=<SOC  ∆SAO = ∆SBO  = ∆SCO => <SAO=< SBO= <SCO)	Дано: ABCS – пирамида,  SO┴(ABC), SA=SB=SC. Доказать: а) О — центр описанной  окружности 6) <SAO=<SBO=<SCO; Доказательство: Рассмотрим ∆SAO и ∆SBO  и ∆SCO:   SO   —   общая;    AS=SB=SC   (условие), <SOA=<SOB=<SOC  ∆SAO = ∆SBO  = ∆SCO => <SAO=< SBO= <SCO, т.к.  АО=ВО=СО, то О – центр окружности описанной около ∆АВС, т.е. что и требовалось доказать.
Выводы: 1) По условию задачи нам известно, что боковые ребра пирамиды равны; 2) Используя данные задачи и полученные из них утверждения, мы получили, что вершина пирамиды проектируется в центр описанной около нижнего основания окружности, а высота пирамиды проходит через центр описанной окружности ос­нования. 3) Далее мы вывели, что боковые ребра равнонаклонены к плоскости основания и к высоте пирамиды. 4) Полученные данные мы использовали для доказательства того, что высота пирамиды проходит через центр окруж­ности, описанной около основании, а все боковые ребра пирамиды составляют равные углы с плоскостью основании. 5) Мы решили задачу вида: «Пирамида, вершина которой проектируется в центр описанной окружности основания».
Задача №  244.     Основанием пирамиды DАВС является прямоугольный треугольник АВС, у которого гипотенуза АВ равна 29 см, катет АС равен 21 см. Ребро DА перпендикулярно к плоскости основания и равно 20 см. Найдите площадь боковой поверхности пирамиды.
— Что значит ребро DА перпендикулярно к плоскости основания? (прямая DА проходит под прямым углом  к плоскости основания, DА– высота пирамиды )  — Что можно сказать о треугольниках АDС, ADB и DBC? ( они  являются прямоугольными , <DАВ=DAС=DCB=900)  — Как вы вычислите площадь боковой поверхности пирамиды? (используя  теорему о том, что площадь многоугольника, составленного из нескольких многоугольников равна сумме площадей этих многоугольников: Sбок=SADC+SBDA+SDCB) — Как вы вычислите площадь прямоугольных треугольников? (она равна половине произведения его катетов) — Как найти катеты прямоугольного треугольника? (по теореме Пифагора)	Дано: АВС — пирамида; АВС: С=90°, АС=21 см,; АВ=29 см, DА(АВС), DА=20 см Найти: Sбок. — ? Решение: Sбок=SADC+SBDA+SDCB все грани прямоугольные треугольники =210 см2; =290 см2; =290 см2 АDС: DС=см. АВС: СВ=20см значит Sбок= 210+2*290=790 см2.
Выводы: 1) Используя данные задачи и полученные из них утверждения, мы получили, что боковое ребро пирамиды перпендикулярно к плоскости основания, а высота пирамиды совпадает с боковым ребром и проектируется в вершину основания. 2) Далее мы вывели, что боковые грани являются прямоугольными треугольниками. 3) Полученные данные, а также формулы для нахождения площади треугольника мы использовали для нахождения боковой поверхности пирамиды. Пирамида в данной задаче относится к II виду пирамид, одна боковая грань которой перпендикулярна к плоскости основания.

      Рефлексивно-оценочный этап

 — Какова была цель урока?

Рассмотреть виды неправильных пирамид и 
выделить схему решения задач на вычисление площади поверхности неправильных
пирамид

 — Мы ее достигли?

Да.

 — Какие виды неправильных пирамид мы узнали?

Пирамида, вершина которой проектируется в
центр описанной окружности основания и пирамида, одна боковая грань которой
перпендикулярна к плоскости основания.

— Какую мы выделили схему решения задач на
вычисление площади поверхности неправильных пирамид ?

 1) Использовать данные задачи для 
указания условия(ий), характеризующего(их) этот вид.

2) вывести равносильные условия,
характеризующие данный вид неправильной пирамиды

3) использовать полученные данные для
решения задачи

На следующем уроке мы продолжим знакомиться с
видами неправильных пирамид и способами решения задач.

— Дома решите №243, № 253, и следующую
тестовую задачу №1:

Задача 1. Основанием пирамиды является прямоугольник со сторонами 3
и 4 м. Каждое боковое ребро пирамиды равно 13
м. Найдите высоту пирамиды и площадь боковой поверхности.

Домашняя работа.

№ 243  Основанием пирамиды DABC является
треугольник ABC, у которого AB= AC=13 см, BC=10
см, ребро DA перпендикулярно к плоскости основания
и равно 9 см. Найдите пло­щадь боковой поверхности пирамиды.

Дано: ABCD – пирамида,
AB= AC=13 см, BC=10 см, AD┴(ABC), AD = 9 см.

 Найти: S_{бок. пов.}-?

Решение: S_{бок. пов.}=S_ADC+ S_ADB+ S_CDB.

S_ADC = S_ADB т.к. ∆ADC=∆ADB.

S_ADC= см²

Для удобства вычисления S_CDB построим высоту DK к стороне CB и высоту АK к стороне CB. S_CDB=см.

 см.

S_CDB= см² S_{бок.
пов}=58,5*2+75=192 см²

Ответ: S_{бок. пов}=192 см²

Пирамида в данной
задаче относится к II виду пирамид, одна боковая грань
которой перпендикулярна к плоскости основания.

№ 253.

    Основанием пирамиды является равнобедренная
трапеция с осно­ваниями 6 см и 4 л/6 см и высотой 5
см. Каждое боковое ребро пирамиды равно 13
см. Найдите ее высоту.

 Дано: АВСDS — пирамида, АВСD-равнобедренная трапеция, АD=6 см, ВС=4см, ВНАD, ВН=5 см, АS=ВS=СS^:=DS=13 см

Найти: SО — ?

Решение:

1) т.к. АS=ВS=СS^:=DS, то О — центр
окружности описанной около АВСD и лежит на высоте МN,  ОС=ОD=R — радиус этой окружности;

R²= МС²+МО²; R²=ND²+ОN²; MC²+МО²=ND²+ON²; 3²+
МО²=(2)²+(5- МО)²; 9+ МО²=

24+25-10МО+МО²; МО=4 см, отсюда R= = 5
см

2) SОА: O=90°; АО=5см; АS=13см =>SO=SО = 12 см

Пирамида в данной задаче относится к I виду пирамид, вершина которой проектируется в центр описанной
окружности основания. 

Задача 1. Основанием пирамиды является прямоугольник со сторонами 3 и 4
м. Каждое боковое ребро пирамиды равно 13
м. Найдите высоту пирамиды и площадь боковой поверхности.

Решение:

1 . Условию задачи удовлетворяет данный рисунок.

2. Так как по условию все боковые ребра равны, то вершина
проектируется в центр описанной около основания окружности, т. е. в точку О пересечения
диагоналей.

3. Следовательно, высота пирамиды равна катету прямоуголь­ного
треугольника OSD, у которого
другой катет равен половине диагонали прямоугольника, а гипотенузой является
боковое ребро.

4. Найдем диагональ прямоугольника ВD=.

5. Высота пирамиды SO = .

6. Для нахождения площади боковой поверхности нужно знать
длины апофем SK и SM:

 из
прямоугольного треугольника SКD найдем

из прямоугольного треугольника SMD найдем

SM=

Найдем площадь боковой поверхности:

S_бок.=2S_∆ASD+2S_∆DSC=.

S_бок.=м².

Пирамида в данной задаче относится к I виду пирамид, вершина которой проектируется в центр описанной
окружности основания. 

Список литературы

1. Березин В. Н. и др.
   Сборник задач для факультативных и внеклассных занятий по математике: Кн.
   для учителя / В. Н. Березин, Л. Ю. Березина, И. Л. Никольская. – М.:
   Просвещение, 1985. – 175 с.
2. Геометрия: Учеб. для
   10-11 кл. общеобразоват. учреждений / Л.С. Атанасян, В.Ф.Бутузов, С.Б.
   Кадомцев и др. – 6-е изд. – М.: Просвещение, 2010. – 207 с.
3. Геометрия: Учеб. Для
   10-11 кл. общеобразоват. учреждений/ А.Д. Александров, А.Л.Вернер, В.И.
   Рыжик. – 3-е изд. – М.: Просвещение, 2010.- 271 с.
4. Математика в школе. –
   2006. — №4.
5. Методика обучения
   геометрии: Учеб. пособие для студ.высш.пед.учеб.заведений /В.А.Гусев,
   В.В.Орлов, В.А. Панчищина и др.; Под ред. В.А. Гусева. – М.: Издательский
   центр «Академия». – 368 с.
6. Прасолов В. В., Шарыгин
   И. Ф. Задачи по стереометрии. – М.: Наука. Гл. ред. физ.-мат. Лит., 1989.
   – 288 с.
7. Программно-методические
   материалы: Математика. 5-11 кл. Тематическое планирование /Сост. Г.М.
   Кузнецова. – 3-е изд., стереотип. – М.: Дрофа, 2008. – 192 с.
8. Программы для общеобразовательных
   учреждений. Математика./ Под ред. Л. М. Котова. – М.: «Просвещение», 1996.
   – 191 с.
9. Современные проблемы
   теории и практики общеобразовательной и высшей педагогической школы:
   Информационный бюллетень научно-методического отдела. Вып.7 / Под. ред.
   проф. В.А. Глуздова, проф. Л.В. Загрековой. – Н.Новгород: НГПУ, 2005. –
   134 с.
10. Теоретические основы
    обучения математике в средней школе: Учебное пособие / Т.А, Иванова, Е.Н.
    Перевощикова, Т.П. Григорьева, Л.И.Кузнецова; Под ред. Проф. Т.А.Ивановой.
    – Н.Новгород: НГПУ, 2003.320 с.
11. Тесты. Математика.
    Варианты и ответы централизованного (абитуриентского) тестирования – М.:
    ООО «РУСТЕСТ», 2006.
12. Углубленное изучение
    геометрии в 10-11 классах: Метод. Рекомендации к преподаванию курса
    геометрии в 10-11 кл. по учеб. Пособию А.Д. Александрова, А.Л.Вернера,
    В.И.Рыжика: книга для учителя. – М.: Просвещение, 1993.-223 с.
13. Экзаменационные билеты по
    математике. Вопросы и ответы. Рекомендации экзаменаторов. – М.: БУКМЭН,
    1996. – 191 с.

Пирамидой в стереометрии называется объёмная фигура, образуемая многоугольником и расположенной вне
его плоскости точкой. Эта точка соединена с точками в вершинах многоугольника отрезками, которые
называются рёбрами пирамиды. Сам многоугольник — это основание пирамиды. При треугольном
основании пирамида будет носить название треугольной, при четырёхугольном – четырёхугольной, и так
далее.

Приведём варианты вычисления апофемы правильной четырёхугольной пирамиды в зависимости от исходных
данных пространственной фигуры. Заданная пирамида обозначена SABCD, где S – вершина, а ABCD –
вершины квадрата в основании.

Вычисление апофемы при известных значениях высоты пирамиды и ребра основания

Апофема пирамиды при известных значениях её высоты SO и стороны квадрата в основании AD=DC=BC=AB
вычисляется по формуле гипотенузы для прямоугольного треугольника SOK. В этом треугольнике одним из
катетов будет высота SO, вторым – половинное значение заданной стороны основания OK=1/2 AD.
Значит: SK²= OK²+ SO² или SK= (1/2 AD) ²+ SO²)
или

L = √ (H² + (a / 2 tan45º)²)

где H — высота, a — ребро основания.

Пример. Пусть высота SO = 4, а сторона основания AD = 6. Тогда апофема L находится
следующим образом: L = √ (( 6 / 2)² + 4²) = 5

Вычисление апофемы при известном значении бокового ребра и ребра основания

При известном значении бокового ребра SD и стороны основания CD для нахождения апофемы SK также
используется теорема Пифагора. В этом случае рассматривается прямоугольный треугольник SKD,
гипотенузой которого выступает боковое ребро SD, одним из катетов – отрезок стороны основания DK, а
вторым – апофема SK. Первый катет равен половине стороны квадрата в основании, поскольку апофема
равнобедренного треугольника, коим является боковая грань пирамиды, является для него и медианой,
делящей основание пополам: DK = 1/2 DC. Отсюда следует, что SD²= DK²+ SK², а SK²= SD²- DK² или, подставляя, получаем выражение:
SK² = SD² — (1/2 DC)², откуда SK = √(SD² — (1/2 DC )²)
или

L = √ (b² — (a / 2)²)

где a — ребро основания, b — боковое ребро.

Пример. Пусть боковое ребро SD равно 5, а сторона основания – 6. Тогда, подставляя
указанные числовые значения, вычисляем значение апофемы: SK =5² – (6 / 2)² ) = 4.

Нахождение апофемы при заданной площади боковых поверхностей и известном ребре основания

Апофема при известной суммарной площади боковых поверхностей Sбок и значении ребра основания CD
вычисляется по следующей схеме. Вначале следует определить площадь каждой из четырёх граней, что
легко сделать, зная, что все они для правильной пирамиды равны между собой. Поэтому общая площадь
делится на четыре равные части: Ssdc = Sбок /4. Затем, при известном
значении площади боковой грани и ребра основания, по формуле площади равнобедренного треугольника
находится его высота, то есть искомая апофема: Ssdc = ½ SK * CD откуда
SK = 2Ssdc / CD. Или, подставляя выведенную площадь грани, SK = 2(Sбок /4) / CD. Преобразив, получаем: SK = Sбок /2CD
или

L = Sбок / 2a

где Sбок — площадь боковых поверхностей, a — ребро основания.

Пример. Допустим, в задаче задана общая площадь боковой поверхности правильной
четырёхугольной пирамиды Sбок = 48 и ребро основания CD = 6. Найдём, используя выведенную формулу,
значение апофемы: SK = 48 / 2 * 6 = 4.

Вычисление апофемы при заданной площади боковых поверхностей и площади основания

Апофема при известных значениях суммарной площади боковых поверхностей Sбок и площади основания Sосн
вычисляется следующим образом. В первую очередь следует найти ребро основания. Площадь основания
пирамиды – квадрата – является произведением двух его сторон либо квадратом стороны. Значит,
значение стороны основания вычисляем по формуле Sосн = CD² или CD = √Sосн. Теперь, зная суммарную площадь боковой поверхности
четырёхугольной пирамиды, делением на 4 находим площадь боковой грани – равнобедренного треугольника
SCD: Ssdc = Sбок / 4. Его площадь также вычисляется, как произведение
основания на высоту, делённое на два: Ssdc =½CD * SK или Sбок/4 =½CD * SK отсюда SK = 2 (Sбок / 4) / CD
или, сократив и подставив выражение для CD: SK = Sбок / 2 Sосн, где SK –
высота грани и искомая апофема.

L = Sбок / (2 * √Sосн)

где Sбок — площадь боковых поверхностей, Sосн — площадь основания.

Пример. Возьмём для примера численные значения, Sбок = 48 и Sосн = 36. Подставляя,
получаем результат: SK = 48 / (2 * √36) = 4.

Вычисление апофемы при заданной площади боковых поверхностей и радиусе описанной вокруг основания
окружности

Найдём апофему при известной площади боковых поверхностей Sбок и радиусе R описанной вокруг основания
ABCD окружности. Рассмотрим прямоугольный треугольник COD, образованный половинами диагоналей этого
квадрата CO и OD, равными заданному радиусу, и гранью в основании CD. Эта сторона в данном
треугольнике выступает гипотенузой. Её можно вывести из теоремы Пифагора: CD² = OD² + OC²,
откуда CD = √(OD²+OC²) или CD = √2R²= R√2.
Теперь определим площадь каждой боковой грани. Она находится путём деления площади полной боковой
поверхности пирамиды на 4: Ssdc = Sбок / 4. По формуле, связывающей
площадь равнобедренного треугольника SDC с его высотой и основанием, выделяем высоту-апофему: Ssdc =½CD * SK Или, подставляя выведенное выше выражение: Sбок/4 = ½CD * SK. Далее преобразовываем для выделения SK: SK=(2 Sбок/4) / CD или, подставляя выведенное для CD выражение и
сокращая, получаем: SK= Sбок / 2R * √2.

L = Sбок / 2R * √2

где Sбок — площадь боковых поверхностей, R — радиус описанной окружности.

Пример. Подставляя для примера числовые значения R = 3√2 и Sбок = 48, получаем в
результате значение апофемы: SK=48 / 2 * (3√2 * √2)=4.

Способ вычисления апофемы при известной площади боковых поверхностей и диагональ основания

Поскольку стороны квадрата ABCD в основании равны и угол между смежными сторонами прямой, значения
этих сторон можно найти, рассматривая прямоугольный треугольник ADC, где заданная диагональ AC
является гипотенузой, а неизвестные стороны AD и CD – равными катетами. Вычисляем их значения по
теореме Пифагора: AC² = AD² + CD² = 2CD² откуда CD = √(AC² / 2)  = AC / √2. Найденное
значение стороны основания позволяет найти апофему — высоту боковой грани SK — при
известной площади этой грани. Суммарная площадь боковой поверхности заданной фигуры Sбок даёт
возможность найти площадь каждой её боковой плоскости. То есть Sscd = Sбок / 4. А теперь Sscd иначе выразим через высоту и основание
грани: Sscd = 1/2 * (SK * CD) или, подставляя ранее выведенную формулу для
CD: Sscd = 1/2 * (SK * ( AC / √2). Теперь все данные кроме искомой апофемы
SK у нас присутствуют, поэтому преобразуем выражение, заменяя SSCD и сокращая: SK= 2 * √2 * Sscd / AC = 2 * √2 (Sбок / 4) / AC = Sбок * √2 / 2АС.

L = Sбок / (2 * √(D² / 2))

где Sбок — площадь боковых поверхностей, D — диагональ основания.

Пример. Допустим, диагональ в основании равна 6√2, а суммарная площадь боковых
граней – 48. Тогда, подставляя числовые значения в полученное выше выражение, вычисляем: SK = 48√2 / 2 * (6√2) = 4

Нахождение апофемы при заданной площади боковых поверхностей и известном периметре основания

Исходными данными, на которые можно опереться при вычислении апофемы для этой задачи, являются Sбок и
Росн. Известное значение периметра квадрата ABCD в основании пирамиды Росн даёт возможность найти
значение его сторон, которые равны между собой как стороны квадрата и находятся путём деления
периметра на 4 равные части: AB = BC = CD = AD = Рabcd / 4. Теперь ребро
CD, одновременно являясь основанием боковой грани SCD, позволяет вычислить её высоту SK – искомую
апофему, при известном значении боковой площади пирамиды. Площадь каждой из 4-х граней найдём путём
деления общей площади на равные части: Sscd= Sбок/4. Далее из формулы
площади равнобедренного треугольника SCD через высоту и основание найдём апофему SK.  Sscd = 1/2 * (SK * CD) или SK = 2* Sscd / CD. Подставляя
выведенные выше через общую площадь и периметр основания значения площади грани и ребро её основания
соответственно, получаем: SK = 2 * (Sбок / 4) / (Рabcd / 4). Или SK = 2Sбок / Рabcd

L = Sбок / (P / 2)

где Sбок — площадь боковых поверхностей, P — периметр основания.

Пример. Предположим, что площадь боковой поверхности Sбок равно 48, периметр
основания – 24. Подставляя данные числовые значения, получаем следующий результат: SK= 2 * (48 / 4) / (24 / 4) = 4.

Вычисление апофемы при заданных значениях площади полной поверхности пирамиды и ребра её
основания

Полная площадь поверхности Sполн в этом случае представляет собой сумму полной площади боковой
поверхности Sбок фигуры и площади квадрата в её основании – Sabcd, сторона которого CD задана
условием задачи. Апофему удобнее всего найти через площадь боковой грани, имея значение её
основания: Sscd = 1/2 * (SK * CD). Преобразуя формулу, получаем: SK = 2* Sscd / CD. Вычтя из площади полной поверхности пирамиды площадь
основания, которую можно найти при его заданном ребре, получаем полную площадь боковой поверхности:
Sполн= Sбок + Sabcd, откуда Sбок= Sполн — Sabcd. Здесь площадь квадрата в основании легко
найти, зная его ребро: Sabcd = CD² и тогда, подставляя: Sбок = Sполн — CD². Разделив Sбок на 4 равные части, получим
площадь боковой грани: Sбок / 4 = (Sполн- CD²) / 4= Sscd. Теперь,
подставив в формулу для вычисления высоты боковой грани найденное выражение, получим: SK = 2* ((Sполн — CD²) /4) / CD или, выполнив сокращение: SK = (Sполн — CD²) /2CD.

L = (Sпол / a — a) / 2

где Sполн — площадь полной поверхности, a — ребро основания.

Пример. Допустим, нам задана общая площадь фигуры S = 84, а ребро её основания – CD
= 6. Тогда, подставляя значения в полученное выражение, находим:
SK = (84 — 62) / (2 * 6) = 4.

Правильной пирамидой называется такая фигура, в основании которой лежит многоугольник с равными
сторонами, то есть правильный. При этом проекция вершины на его плоскость является центром вписанной
в это многоугольное основание и описанной вокруг него окружностей. Отличительными признаками
правильной четырёхугольной пирамиды являются квадрат в основании и лежащая в точке пересечения его
диагоналей проекция вершины на этот квадрат.

Боковые плоскости (грани) правильной пирамиды – равнобедренные треугольники. Основание каждого из них
одновременно является и стороной основания пирамиды.
Проведенная к основанию высота боковых
граней, имеющая для каждой из них одинаковое значение, называется апофемой. Это понятие применяется
при решении множества геометрических задач, в которых фигурирует правильная пирамида с квадратом в
основании. В зависимости от других исходных данных, апофема даёт возможность вычислить площадь
боковой поверхности фигуры, её высоту, длину ребер и сторону основания.

Для решения задач на обширную тему «Стереометрия» нужно выучить и разобрать очень много элементов и тонкостей, полностью изучить все свойства фигур, а также не забывать свойства всех фигур, которые включены в курс «Планиметрии».

Среди задач по объемным фигурам очень часто встречается правильная пирамида, чтобы легко решать их, нужно хорошо с ней познакомиться. Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а ее вершина спроецирована в центр основания. Как раз при изучении этого многоугольника вы услышите об апофеме.

Как вы уже поняли, в геометрии понятие апофемы — это широко распространенное явление. Невозможно узнать некоторые измерения пирамиды без знания этого. Само слово «апофема» — это пришедшее к нам из греческого языка явление, и переводится оно как «откладываю».

Определение

В планиметрии апофема — перпендикуляр (как сам, так и его длина), который проведен к стороне правильного многоугольника из центра. В стереометрии апофема пирамиды — это высота в боковой грани, которая проведена к основанию. Используется только для правильных пирамид. Соответственно, апофема правильной треугольной пирамиды — это высота ее грани, которая представлена равнобедренным треугольником.

Какова роль апофемы

Апофема — это очень важный элемент пирамиды, потому что с ее помощью можно решить огромное количество задач. В частности, боковая поверхность правильной пирамиды равна полупроизведению периметра основания и апофемы грани.

S_бп = (P_осн*h)/2; h — апофема, это ее ключевая роль.

Не путайте с H (высота объемной фигуры в стереометрии).

Также, благодаря знанию апофемы, можно найти площадь грани как равнобедренного треугольника.

Свойства апофемы

Их мало, но все же их нужно помнить. В целом это следствия, вытекающие из определения. Итак, апофема в правильной пирамиде:

1. Опущена на сторону основания под углом 90 градусов.
2. Делит сторону, на которую опущена, пополам, так как является высотой в равнобедренном/равностороннем треугольнике и по совместительству — медианой.

В правильной пирамиде все апофемы равны, так как все ее боковые грани также одинаковые. При нахождении длины апофемы вам придется воспользоваться как свойствами многоугольника, так и свойствами многогранника. Как же найти числовое значение апофемы в правильной пирамиде?

Как найти апофему пирамиды

Ее можно найти, применяя все ранее полученные знания, вот всего лишь несколько примеров:

• Если известны боковое ребро и сторона основания. Так как апофема делит сторону основания пополам и образует с ней угол в 90 градусов, то найти ее из прямоугольного треугольника по теореме Пифагора вам не составит труда. Также можно найти апофему, используя знания соотношений в прямоугольном треугольнике.
• Если известен радиус вписанной окружности в основание правильной пирамиды и высота всей фигуры. Радиус, проведенный к точке касания, перпендикулярен касательной, и апофема перпендикулярна этой стороне основания (которая является касательной к вписанной окружности). Высота фигуры перпендикулярна основанию и попадает в центр окружности, вписанной в основание пирамиды. Следовательно, радиус и высота фигуры являются катетами и образуют прямой угол, а вместе с апофемой — прямоугольный треугольник. И опять же по теореме Пифагора или через соотношения в прямоугольном треугольнике вы легко найдете апофему.

• Также если дана площадь грани и известно основание.

В любом случае при нахождении апофемы вам придется вспоминать все основные законы и правила планиметрии. Если неизвестны какие-то элементы из этого списка, то вы можете оперировать данными параметрами, и, постепенно находя вышеописанные данные, найти апофему вам не составит труда. Надеемся, что наша статья помогла вам в освоении такой интересной темы.