Амплитуда колебаний, теория и онлайн калькуляторы
Амплитуда колебаний
Колебания и их амплитуда
Определение
Повторяющиеся движения или процессы называют колебаниями.
В зависимости от природы колебания могут быть механическими, электромагнитными, звуковыми и др. Разные виды колебаний описывают с помощью одинаковых уравнений и при этом используют одинаковые характеристики.
Колебания называют свободными (иди собственными), если они происходят за счет энергии, которая получена колебательной системой один раз и в дальнейшем внешних воздействий на эту систему нет.
Самым простым видом колебаний являются гармонические колебания.
Определение
Гармоническими колебаниями называют такие колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса..
Пусть происходят гармонические колебания некоторого параметра $s$, тогда эти колебания можно описать при помощи следующего уравнения:
[s=A{cos ({omega }_0t+varphi ) } left(1right),]
где $A=s_{max}$ — амплитуда колебаний; ${omega }_0$ — циклическая (круговая) частота колебаний; $varphi $ — начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ — фаза колебаний.
Амплитудой называют максимальной значение величины, колебания которой рассматривают. Так как косинус (как и синус) изменяется в пределах от единицы до минус единицы, то величина $s$ находится в пределах $-Ale sle $+A.
Метод вращающегося вектора амплитуды колебаний
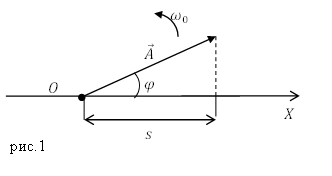
Гармонические колебания можно изображать графически (рис.1), при этом используют метод векторных диаграмм (или метод вращающегося вектора амплитуды). С этой целью, из какой — то произвольно избранной точки оси X, назовем ее точка O, под углом равным начальной фазе (угол $varphi $), откладывают вектор $overline{A}$. Длина этого вектора равна амплитуде ($A$) колебаний. Если этот вектор приводится во вращение с угловой скоростью ${omega }_0$, то проекция конца этого вектора перемещается по оси X и принимает значения от $-A$ до $A$, при этом закон колеблющейся величины будет таким, как представляет уравнение (1). Получается, что гармонические колебания можно изобразить при помощи проекции на некоторую ось вектора амплитуды $overline{A}$, который отложен из произвольной точки этой оси под углом $varphi $, вращающимся с угловой скоростью ${omega }_0$ вокруг избранной точки.
Примеры задач с решением
Пример 1
Задание. Материальная точка совершает гармонические колебания, которые описывает уравнение: $x=0,1{cos ({omega }_0t+varphi )(м) }$. Известно, что период колебаний этой точки равен T=5 c. Какова амплитуда скорости ($v_m$) и амплитуда ускорения ($a_m$) данной точки?
Решение. Прежде всего, найдем циклическую частоту колебаний точки, так как нам известен период колебаний:
[{omega }_0=frac{2pi }{T} left(1.1right).]
Зная закон изменения координаты, определим, как изменяется скорость материальной точки:
[v_x=frac{dx}{dt}=frac{d}{dt}left(x_m{cos left({omega }_0t+varphi right) }right)={-x}_m{omega }_0{sin left({omega }_0t+varphi right) }left(1.2right),]
где $x_m=0,1$ по условию задачи.
Из уравнения (1.2) следует, что амплитуда скорости колебаний точки равна:
[v_m=left|{-x}_m{omega }_0right|=x_m{omega }_0=0,1cdot frac{2pi }{T}=0,04pi left(frac{м}{с}right).]
Используя закон изменения скорости, получим закон изменения ускорения точки:
[a_x=frac{dv_x}{dt}={-x}_m{{omega }_0}^2{cos left({omega }_0t+varphi right) }left(1.3right).]
Из закона (1.3) следует, что амплитуда ускорения точки равна:
[a_m=left|{-x}_m{{omega }_0}^2right|=x_m{{omega }_0}^2=0,1{(frac{2pi }{T})}^2=0,1cdot frac{4{pi }^2}{25}=0,016{pi }^2 left(frac{м}{с^2}right).]
Ответ. $v_m=0,04pi frac{м}{с}$; $a_m=0,016{pi }^2frac{м}{с^2}$
Пример 2
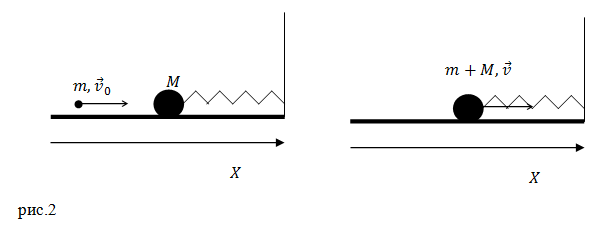
Задание. К горизонтальной пружине, коэффициент упругости которой равен $k,$ прикреплен шар массой $M$. Шар находится на гладком столе, по которому может перемещаться без трения. Пуля летит горизонтально и ударяется о шар, застревает в нем. Скорость пули до удара равна $v_0$, масса пули $m$, скорость ее в момент удара направлена параллельно оси пружины. Какова амплитуда колебаний шара с пулей?
Массу пружины и сопротивление воздуха не учитывать.
Решение. Запишем закон сохранения импульса для системы шар — пуля (до удара) и шар с пулей сразу после удара:
[overline{p}={overline{p}}’left(2.1right).]
Из рис.2 следует, что выражение (2.1) можно преобразовать к виду:
[mv_0=left(m+Mright)vleft(2.2right).]
Из (2.2) выразим скорость шара с пулей сразу после удара:
[v=frac{mv_0}{m+M}left(2.3right).]
Система пуля шар, выведена из состояния равновесия ударом пули. Она совершает свободные гармонические колебания. Кинетическая энергия переходит в потенциальную энергию сжатой пружины. Для двух состояний системы (первое состояние — максимальная скорость движения системы; второе состояние максимальное сжатие пружины) в соответствии с законом сохранения энергии запишем:
[frac{(m+M)v^2}{2}=frac{k{x_m}^2}{2}left(2.4right),]
где $x_m$ — амплитуда колебаний шара с пулей. Подставим величину скорости из (2.3) в (2.4) и выразим амплитуду:
[{left(m+Mright)v^2=k{x_m}^2to x_m=sqrt{frac{left(m+Mright)v^2}{k}}to x}_m=frac{mv_0}{sqrt{(M+m)k}}.]
Ответ. $x_m=frac{mv_0}{sqrt{(M+m)k}}$
Читать дальше: гармонические колебания.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
The maximum distance moved by a point on a vibrating body is called as amplitude. The amplitude is the vertical distance between the peak wave and the equilibrium point. The frequency and the distance traveled by the wave is an important factor to find the amplitude using the amplitude of wave calculator. Enter the required values in the amplitude calculator, it finds the amplitude of wave and prints the output within seconds. The distance can be entered for different units of measurement.
Amplitude of Wave Calculator
The maximum distance moved by a point on a vibrating body is called as amplitude. The amplitude is the vertical distance between the peak wave and the equilibrium point. The frequency and the distance traveled by the wave is an important factor to find the amplitude using the amplitude of wave calculator. Enter the required values in the amplitude calculator, it finds the amplitude of wave and prints the output within seconds. The distance can be entered for different units of measurement.
Code to add this calci to your website 
Formula:
A = D / F
Where,
A = Amplitude of Wave
D = Distance Traveled by the Wave
F = Frequency of the Wave
Example:
Find the amplitude of a sound wave where the distance traveled by the wave is 30cm and the frequency of the wave is 3 Hz.
Solution:
To Convert cm to m,
D = 30 cm
= (30 / 100) m
D = 0.3 m
A = D / F
= 0.3 / 3 = 0.1
A = 0.1dB
Related Calculators:
- Power Consumption Table
- Parallel Circuit Total Inductance Calculator
- Whip Antenna Design Calculator
- Brillouin Function Calculator
- Age Difference Calculator
- Truncated Pyramid Volume Calculator
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
амплитуда:y=2sin(2x)+3
-
амплитуда:f(x)=sin(x)
-
амплитуда:f(x)=2cos(2x-1)+4
-
амплитуда:f(x)=cos(x)-3
-
амплитуда:y=tan(2x-5)
- Показать больше
Описание
Пошаговый поиск амплитуды периодических функций
function-amplitude-calculator
амплитуда y=2sin(2x)+3
ru
Блог-сообщения, имеющие отношение к Symbolab
Functions
A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Скорость движения автомобиля
Идти
Скорость движения автомобиля = (Колесная скорость транспортного средства*Скорость шины)/(Колесная скорость транспортного средства+Скорость шины)
Пройденный путь
Идти
Пройденный путь = Начальная скорость*Время, затраченное на путешествие+(1/2)*Ускорение*(Время, затраченное на путешествие)^2
крутящий момент
Идти
Крутящий момент на колесе = Сила*Длина вектора смещения*sin(Угол между вектором силы и смещения)
Магнитный поток
Идти
Магнитный поток = Магнитное поле*Длина*Толщина плотины*cos(Тета)
Показатель преломления
Идти
Показатель преломления = sin(Угол падения)/sin(Угол преломления)
Тепловая мощность
Идти
Тепловая скорость = Расход пара*Удельная теплоемкость*Разница температур
Pаботай
Идти
Работа = Сила*водоизмещение*cos(Угол А)
Емкость
Идти
Емкость = Диэлектрическая постоянная*Обвинение/вольтаж
Угловая смещение
Идти
Угловая смещение = Расстояние, пройденное на круговой траектории/Радиус кривизны
ускорение
Идти
Ускорение = Изменение скорости/Общее затраченное время
Угловой момент
Идти
Угловой момент = Момент инерции*Угловая скорость
амплитудное
Идти
Амплитуда = Общая пройденная дистанция/Частота
Модуль Юнга
Идти
Модуль для младших = стресс/Напряжение
Штамм
Идти
Напряжение = Изменение длины/Длина
стресс
Идти
стресс = Сила/Площадь
Начиная с седьмого класса в школах начинают преподавать такую тему, как «Механические колебания». Начиная с ОГЭ и заканчивая ЕГЭ, эта тема прослеживается во многих экзаменах и вступительных испытаниях. Важной частью ее является изучение понятия амплитуды колебаний. Поэтому для начала ознакомимся с тем, что такое амплитуда колебаний и как обозначается амплитуда колебаний в физике, ведь со временем многое забывается, а именно данной переменной почему-то во многих школах уделяют меньше всего внимания.
Что такое амплитуда колебаний?
Амплитуда колебаний — это максимально возможное отклонение или смещение величины в большую или меньшую сторону от положения равновесия или от среднего значения. К примеру, для пружинного маятника положение равновесия — это покоящийся на пружине груз, а когда он начинает двигаться, то обретает определенную амплитуду, которая определяется растяжением или сжатием пружины.
Для математического же маятника немного проще — максимальное отклонения груза от положения покоя — это и есть амплитуда колебаний.
В то время как амплитуда колебаний радиоволн считается именно по отклонению от среднего значения.
Теперь перейдем к тому, какой буквой обозначается амплитуда колебаний.
Обозначение
В седьмом классе детей приучают обозначать амплитуду колебаний простой буквой «А». Например: А=4 см, то есть амплитуда равна четырем сантиметрам.
Но уже в восьмом классе ученики изучают такое понятие, как механическая работа, и именно она в физике обозначается буквой «А». Ученики начинают путаться в этих значениях, и к 10-11-у классу не имеют четкого представления о том, как обозначается амплитуда колебаний в физике.
В случае с пружинными и математическими маятниками лучше всего записывать амплитуду через максимальные значения. То есть Хмакс. означает максимальное отклонения от положения равновесия. Например Хмакс.=10 см, то есть пружина, как вариант, растянется максимум на 10 см. Это и будет амплитудой колебаний.
В 11-м классе выпускники изучают электромагнитные колебания. И там встречаются колебания заряда, напряжения и силы тока. Для того чтобы записать амплитуду напряжения, принято обозначать ее как максимальное значение. Для заряда и прочих величин соответственно.
Как найти амплитуду колебаний?
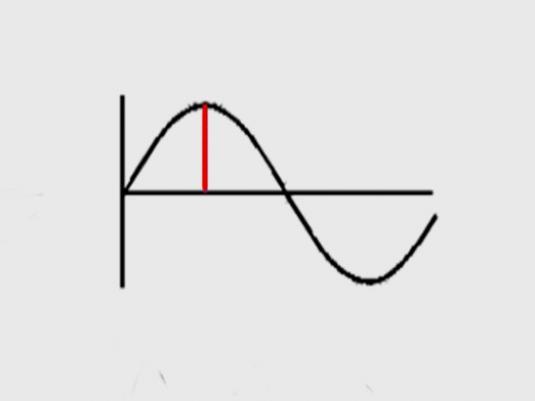
Обычно в задачах на нахождение амплитуды представлен график, подобный тому, что нарисован на картинке выше. В таком случае амплитудой будет являться максимальное значение по вертикальной оси Y. Амплитуда показано красной чертой.
Например, на данном рисунке изображен график колебаний математического маятника.
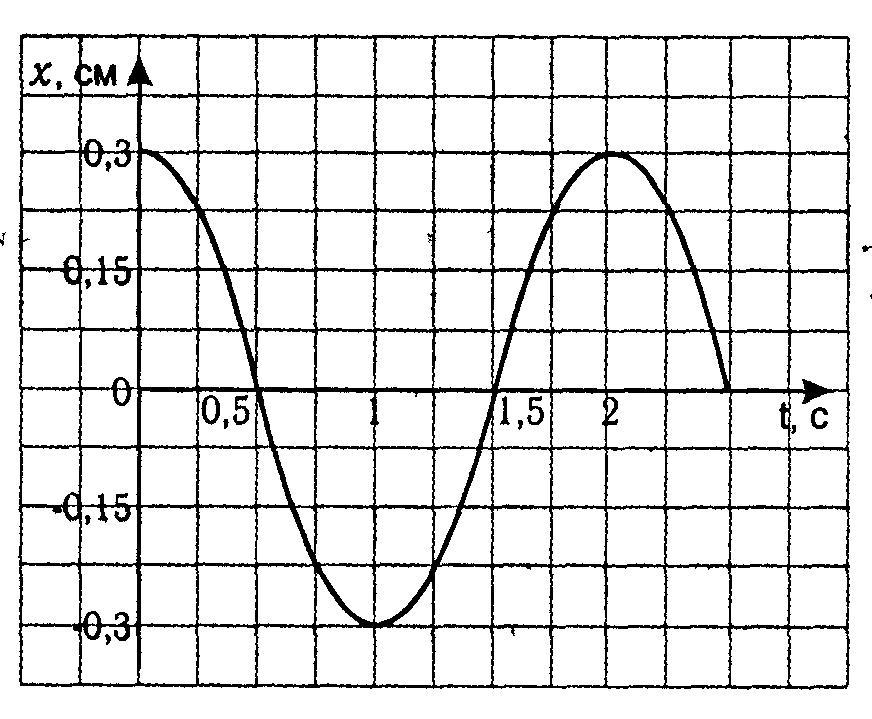
Зная, что амплитуда колебаний математического маятника — это максимальное удаление от положение равновесия, можем определить, что максимальное значение Х=0,3 см.
Найти амплитуду с помощью вычислений можно следующими способами:
1. Если груз совершает гармонические колебания и в задаче известны путь, который проходит тело, и количество колебаний, то амплитуда находится как отношение пути к количеству колебаний, умноженному на 4.
2. Если в задаче дан математический маятник, то при известных максимальной скорости и длине нити можно найти амплитуду, которая будет равна произведению максимальной скорости на квадратный корень из отношения длины к ускорению свободного падения. Эта формула похожа на формулу периода математического маятника.
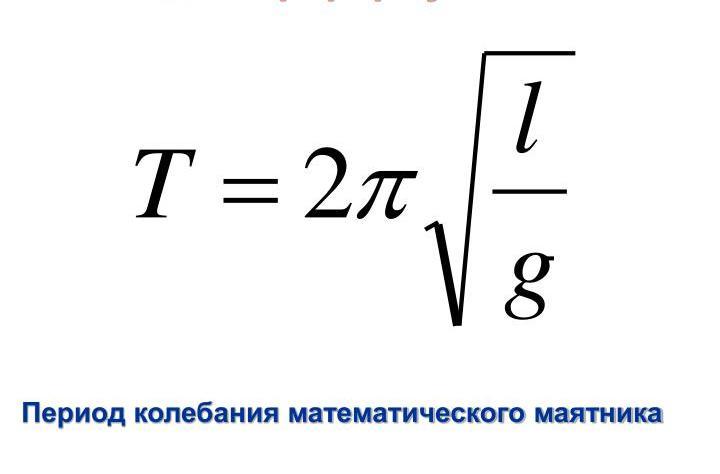
Только вместо 2п используется максимальная скорость.
В уравнениях же амплитудой является все то, что записано до косинуса, синуса или переменной омеги.
Заключение
В этой статье было сказано о том, как обозначается амплитуда колебаний и как она находится. Данная тема является лишь малой долей большого раздела колебательных процессов, но это не снижает ее важности. Ведь не понимая, что такое амплитуда, невозможно работать с графиками правильно и решать уравнения.
Автор:
05-02-2019 22:50
Жду ваши вопросы и мнения в комментариях