Решебник по астрономии 11 класс на урок №8 (рабочая тетрадь) — Законы Кеплера
1. Сформулируйте законы Кеплера.
| Первый закон Кеплера | Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце |
| Второй закон Кеплера | Радиус-вектор планеты в равные промежутки времени описывают равновеликие площади |
| Третий закон Кеплера | Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит |
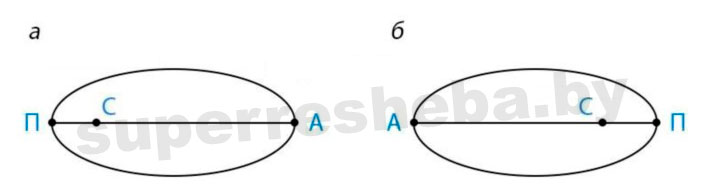
2. На рисунке 8.1 укажите точки афелия и перигелия.
3. Выведите формулы для вычисления перигелийного и афелийного расстояний по известным эксцентриситету и значению большой полуоси.
Перигелийное расстояние ПС = q; афелийное расстояние СА = Q. АП = 2a; ПО = ОА = a. Тогда: q = ОП — СО; e = СО/ОП; СО = e · a; Q = ОА + СО; q = a — ea = a(1 — e); Q = a + ea = a(1 + e).
4. Определите афелийное расстояние астероида Минск, если большая полуось его орбиты а = 2,88 а. е., а эксцентриситете = 0,24.
Решение.
5. Определите перигелийное расстояние астероида Икар, если большая полуось его орбиты а = 160 млн км, а эксцентриситет е = 0,83.
Решение.
6. Выполните задание.
Вариант 1.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
а) скорость планеты максимальна;
б) потенциальная энергия максимальна;
в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
Вариант 2.
1. На рисунке 8.1, б укажите точки орбиты, в которых:
а) скорость планеты минимальна;
б) потенциальная энергия минимальна;
в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
7. Решите задачи.
Вариант 1.
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
Вариант 2.
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,978 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Дано:
a п = 2,77
e = 0,235
a⊕ = 1 а.е.
T⊕ = 1 год
g п = 0,194 м/с²
R п = 512 км = 512000 м
——————————————-
Найти:
q — ?
Q — ?
T п — ?
S п — ?
υ п — ?
Решение:
1) Запишем сначала формулы перигельное и афелийное расстояния:
(1) q = a(1-e) — перигельное расстояние
(2) Q = a(1+e) — афелийное расстояние
Далее мы их находим перигельное и афелийное расстояния:
q = 2,77 а.е. × (1-0,235) = 2,77 а.е. × 0,765 = 2,11905 а.е.
Q = 2,77 а.е. × (1+0,235) = 2,77 а.е. × 1,235 = 3,42095 а.е.
2) Теперь мы находим сидерический период обращения астероида Паллада, по третьему закону Кеплера:
T п²/T⊕² = a п³/a⊕³
Так как a⊕ = 1 а.е. , T⊕ = 1 год , следовательно мы получаем:
T п² = a п³ ⇒ T п = √a п³
Теперь решаем:
T п = √2,77³ = √21,253933 ≈ 4,61 года
3) Дальше мы находим синодеричечкий период обращения астероида Паллада для верхних по такой формуле:
1/S = 1/T⊕ — 1/T п ⇒ 1/S = T п — T⊕/T⊕×Tп
Следовательно мы получим:
S = T⊕×T п/Tп — T⊕
Далее считаем:
S = 1 год × 4,61 года/4,61 года — 1 год = 4,61 года/3,61 года ≈ 1,277 года
4) Теперь мы находим круговую скорость или как говорят первой космической скорости по такой формуле что бы найти скорость астероида Паллада:
υ п = √g п × R п
Теперь считаем:
υ п = √0,194 м/с² × 512000 м = √99328 м²/с² ≈ 315,16 м/с ≈ 0,31516 км/с
Ответ: q = 2,11905 а.е. ; Q = 3,42095 а.е. ; T п = 4,61 года ; S = 1,277 года ; υ п = 315,16 м/с или 0,31516 км/с.
1.
2.
3.
Перигелийное расстояние $ПС = q$; афелийное расстояние $СА = Q$. $АП = 2a$; $ПО = ОА = a$. Тогда: $q = ОП — СО$; $e = dfrac{СО}{ОП}$; $СО = e · a$; $Q = ОА + СО$; $q = a — ea = a(1 — e)$; $Q = a + ea = a(1 + e)$.
4.
Решение.
5.
Решение.
6.
Вариант 1.
1. На рисунке 8.1, а укажите точки орбиты, в которых:
- а) скорость планеты максимальна;
- б) потенциальная энергия максимальна;
- в) кинетическая энергия минимальна.
2. Как изменяется скорость планеты при ее движении от афелия к перигелию? (Увеличится)
Вариант 2.
1. На рисунке 8.1, б укажите точки орбиты, в которых:
- а) скорость планеты минимальна;
- б) потенциальная энергия минимальна;
- в) кинетическая энергия максимальна.
2. Как изменяется скорость Луны при ее движении от перигея к апогею? (Уменьшится)
7.
Вариант 1.
1. Определите период обращения астероида Белоруссия, если большая полуось его орбиты а = 2,40 а. е.
2. Звездный период обращения Юпитера вокруг Солнца Т = 12 лет. Каково среднее расстояние от Юпитера до Солнца?
Вариант 2.
1. Период обращения малой планеты Шагал вокруг Солнца Т = 5,6 года. Определите большую полуось ее орбиты.
2. Большая полуось орбиты астероида Тихов а = 2,71 а. е. За какое время этот астероид обращается вокруг Солнца?
Присоединяйтесь к Telegram-группе @superresheba_11,
делитесь своими решениями и пользуйтесь материалами, которые присылают другие участники группы!
Слайд 1
Решение астрономических задач
полное решение всех
типов задач по

астрономии
Слайд 2
Задачи
Дано:
Тλ =12 ч

Т0=14ч 13 мин
λ – ?
Решение:
Ответ: 2 ч 13 мин з.д.
1. В местный полдень путешественник отметил 14 ч 13 мин по гринвичскому времени. Определите географическую долготу места наблюдения.
Т λ = Т0 + λ
λ=12 ч -14 ч 13 мин = 2 ч 13 мин з.д.
Слайд 3
Задачи
Дано:
Т=1,88 года

Т0=1год
S – ?
Решение:
Ответ: 2,136 года
1. Каков синодический период Марса, если его звездный период равен 1,88 земного года?
Слайд 4
Задачи
Дано:
а=2,88 а.е.

е =0,24
Q – ?
Решение:
Ответ: 3,57 а.е.
1. Определите афелийное расстояние астероида Минск, если большая полуось его орбиты равна 2,88 а.е., а эксцентриситет составляет 0,24.
Слайд 5
Задачи
2. Определите среднее расстояние от Юпитера

до Солнца, если известно, что его звездный период обращения
вокруг Солнца равен 11,86 года.
Дано :
Т= 11,86 года
ТЗ =1 год
аз=1 а.е.
а – ?
Решение:
Ответ: 5,2 а.е.
Слайд 6
Задачи
Дано:
а=1220·103 км

Т=16 суток
ал=384·103 км
Тл=27,3 суток
МЗ=1
МС – ?
Решение:
Ответ:
1. Определите массу Сатурна (в массах Земли), если известно, что спутник Сатурна Титан отстоит от него на расстоянии 1220 тыс. км и обращается с периодом 16 суток.
Слайд 7
Задачи
Дано:
q=363 тыс.км
Q=405

тыс.км
RЗ=6370 км
p1 – ?
p2 –?
Решение:
Ответ: 1°, 54’
1. Расстояние от Земли до Луны в ближайшей к ней точке своей орбиты составляет 363 тыс.км, а в наиболее удаленной точке 405 тыс.км. Определите горизонтальный параллакс Луны в этих положениях.
Слайд 8
Задачи
Дано:
ам=1,52 а.е.

ТЗ=1 год
аз=1 а.е.
t
– ?
Решение:
Ответ: 0,71 года
1. Рассчитайте время полета по полуэллиптической орбите до Марса.
Слайд 9
Задачи
Дано:
D=300 км

α=1′
S=3,84·105 км
d – ?
Решение:
Ответ: да
1. Море Москвы, расположенное на невидимой стороне Луны, имеет поперечник около 300км. Можно ли было бы увидеть его с Земли невооруженным глазом, если бы оно находилось на обращенном к Земле полушарии. Разрешающая способность глаза 1′.
Минимальный размер объекта, видимого глазом определим по формуле:
Так как размеры моря Москвы превышают полученный результат, то его можно было бы увидеть невооруженным глазом.
Слайд 10
Задачи
Дано:
FОБ=800 мм

FОК1=28 мм
FОК2=20 мм
FОК3=10 мм
G – ?
Решение:
Ответ: 28,6; 40; 80
1.Какие увеличения можно получить с помощью школьного телескопа, в котором установлен объектив с фокусным расстоянием 800 мм и имеются сменные окуляры с фокусными расстояниями 28, 10, 20 мм?
Слайд 11
Задачи
2. Определите разрешающую и проницающую способности

школьного телескопа с диаметром объектива, равным 60 мм.
Дано :
D=60 мм
ψ – ?
m – ?
Решение:
Ответ: 2,3» ,11m
Слайд 12
Задачи
Дано:
λ0=434,0 нм

λ=434,12 нм
с=3·105 км/c
– ?
Решение:
Ответ: удаляется, 83 км/с
1. Линия водорода с длиной волны 434,00 нм на спектрограмме звезды оказалась равной 434,12 нм. К нам или от нас движется звезда и с какой скоростью?
Так как >0 ,то звезда удаляется.
Слайд 13
Задачи
2. Поверхность Солнца близка по своим

свойствам к абсолютно черному телу. Определите температуру солнечной поверхности
и мощность излучения единицы поверхности, если максимум лучеиспускательной способности приходится
на длину волны 0,48 мкм.
Дано :
=0,48 мкм
b=2900 К·мкм
Т – ?
– ?
Решение:
Ответ: 6000 К, 7,3·107Вт/м2
Слайд 14
Задачи
1. Вычислите линейный размер солнечного

пятна, если его угловой диаметр равен 17,6». Линейный и
угловой размеры Солнца соответственно равны 13,92·105 км, 32′.
Дано :
DC=13,92·105 км
dc=32′
dп=17,6‘
DП – ?
Решение:
Ответ: 12760 км
Слайд 15
Задачи
2. Определите массу Солнца, если Земля

обращается вокруг Солнца на расстоянии 1 а.е. с периодом
1 год. Орбиту Земли считать круговой.
Дано
:
ТЗ=1год=
=3,156·107 с
аз=1 а.е. =
=1,496·1011 м
MC – ?
Решение:
Ответ: 2·1030 кг
Сила всемирного тяготения является центростремительной
Слайд 16
Задачи
Дано:
m=3,2m
M=-8m

r – ?
Решение:
Ответ:
1700 пк
1. Новая звезда в момент вспышки имела видимую звездную величину 3,2m. Вычислите расстояние до нее, если известно, что большинство новых звезд этого типа имеют абсолютную звездную величину -8m.
Слайд 17
Задачи
Дано:
L=10 LC

T=8400 К
R – ?
Решение:
Ответ:
1. Найдите размеры звезды Альтаир, если ее светимость равна десяти светимостям Солнца, а температура фотосферы 8400К.
Слайд 18
Задачи
Дано:
Т=79 лет

α=17,6”
π=0,75”
d1:d2=3:4
Ek – ?
Решение:
Ответ:
1. У двойной звезды α-Центавра период обращения составляет 79 лет. Большая полуось орбиты 17,6”, а годичный параллакс 0,75”. Определите сумму масс и массы компонентов звезды в отдельности, если они отстоят от центра масс на расстояниях, относящихся как 3:4.
Слайд 19
Задачи
Дано:
МЗ1=0,5 МС

L – ?
M – ?
Решение:
Ответ: L=0,0625 LС, М=8m
1. При изучении масс звезд и их светимостей установлено, что для звезд, принадлежащих к главной последовательности, в интервале от 0,5МС до 10МС светимость пропорциональна четвертой степени ее массы. Проведите необходимые расчеты и укажите на диаграмме местонахождение звезд.
Слайд 20
Задачи
Дано:
D2=300D1
M2=30M1

ρ2 – ?
Решение:
Ответ: 1,6·10-3 кг/м3
2. Какова средняя плотность красного сверхгиганта, если его диаметр в 300 раз больше солнечного, а масса в 30 раз больше, чем масса Солнца?
Слайд 21
Задачи
Дано:
π=0,198”
μ=0,658”

ν=-26,3 км/с
ντ –?
ν
– ?
Решение:
Ответ: 15,8 км/с; 30,7 км/с
1. У звезды Альтаир годичный параллакс равен 0,198”,собственное движение 0,658” и лучевая скорость –26,3 км/с. Определите тангенциальную и пространственную скорости звезды.
Слайд 22
Задачи
Дано:
Т=5· 109лет

Тс=2,5·108 лет
n – ?
Решение:
Ответ: 20 раз
2 Сколько раз за время своего существования Солнце успело обернуться вокруг центра Галактики?
Слайд 23
Задачи
Дано:
α=1°
r=400

пк
ρ=10 -19кг/м3
М –
?
Решение:
Ответ: 240 МС
1. Определите массу Большой газопылевой туманности в Орионе, если ее видимые размеры составляют около 1°, а расстояние до нее 400пк , а плотность газопылевой среды 10-19 кг/м3.
Слайд 24
Задачи
Дано:
d=83’’
r=660пк

D – ?
Решение:
Ответ:
0,27пк, 55691,6 а.е.
2 Планетарная туманность в созвездии Лиры имеет угловой диаметр 83’’ и находится от нас на расстоянии в 660пк. Каковы ее линейные размеры в астрономических единицах?
Слайд 25
Задачи
Дано:
υr=6·103км/с
α=2’=0,033°

D – ?
d –
?
Решение:
Ответ: 80 Мпк, 47 кпк
2. Галактика удаляется от нас со скоростью 6000км/с и имеет видимый угловой размер 2’. Определите расстояние до галактики и ее линейные размеры.
Слайд 26
Задачи
Дано:
m=15,2m
λ0=656,3нм

Δλ=21,9нм
υr – ?
r – ?
L – ?
M
– ?
Ответ: 104км/с; 133 Мпк; 1,2·1010LC; -20,4m
1. В спектре галактики, которая имеет видимую звездную величину 15,2m, линия водорода (λ0=656,3нм) смещена к красному концу спектра на Δλ=21,9нм. Вычислите скорость удаления галактики, расстояние до нее, абсолютную звездную величину и светимость галактики.
Слайд 27
Задачи
Дано:
H=75 км/(с·Мпк)

t – ?
Решение:
Ответ: 13
млрд. лет
2. Величина, обратная постоянной Хаббла, дает примерную оценку времени, которое прошло с момента начала расширения Вселенной. Подсчитайте это время.
Слайд 28
Задачи
Дано:
r=10 Мпк

t – ?
Решение:
Ответ: 65
млн.лет
1. Представьте, что на радиосигнал, принятый от цивилизации из галактики М 106, нами в адрес этой цивилизации отправлена ответная радиограмма. Сколько времени пришлось бы ждать ответа на нее, если расстояние до галактики М 106 составляет 10Мпк?
Слайд 29
Задачи
Дано:
υ=0,9с
tc=1

год
to=25лет
tз – ?
Решение:
Ответ: 42,5 года
2. Какое время (по счету на Земле) отец должен пробыть в космическом полете со скоростью 0,9с, чтобы после возвращения на Землю сравняться по возрасту со своим сыном? Возраст отца при отправке в полет принять равным 25 годам, сына – 1 году.