Как найти абсолютную шероховатость трубы

Шероховатость стенок трубопровода: типы и влияние

Твердые стенки, ограничивающие поток жидкости, всегда в той или иной степени обладают известной шероховатостью. Шероховатость стенок характеризуется величиной и формой различных, порой самых незначительных по размерам, выступов и неровностей, имеющихся на стенках, и зависит от материала стенок и их обработки.

Шероховатость — это совокупность неровностей поверхности с относительно малыми шагами на базовой длине. Измеряется в микрометрах (мкм).

Обычно с течением времени шероховатость изменяется от появления ржавчины, коррозии, отложения осадков и т.д.

В качестве основной характеристики шероховатости служит так называемая абсолютная шероховатость – κ, представляющая собой среднюю величину указанных выступов и неровностей, измеренную в линейных единицах.

Некоторые значения шероховатости стенок трубопровода приведены в таблице ниже

Трубы	κ, мм
Чистые цельнотянутые из латуни, меди и свинца	0,01
Новые цельнотянутые стальные	0,05-0,15
Стальные с незначительной коррозией	0,2-0,3
Новые чугунные	0,3
Асбоцементные	0,03-0,8
Старые стальные	0,5-2,0

В случае когда величина выступов шероховатости стенки трубы меньше, чем толщина вязкого (ламинарного) подслоя неровности стенки полностью погружены в этот слой.

При этом турбулентная часть потока не будет входить в непосредственное соприкосновение со стенками и движение жидкости, а следовательно, и потери энергии не будут зависеть от шероховатости стенок, а будут зависеть только от свойств самой жидкости.

Если величина выступов такова, что они превышают толщину вязкого подслоя, то неровности стенок будут выступать в турбулентную область, увеличивая беспорядочность движения и существенным образом влиять на величину потерь энергии.

В этом случае каждый отдельный выступ можно сравнить с плохо обтекаемой поверхностью, находящейся в окружающем её потоке жидкости и являющейся источников образования вихрей.

В соответствии с написанным выше поверхности условно разделяют на гидравлически гладкие (первый случай) и шероховатые (второй вариант).

На самом деле, толщина вязкого подслоя непостоянна и уменьшается с увеличением числа Рейнольдса. У гидравлически гладких стенок с возрастанием числа Рейнольдса тоже начинает проявляться шероховатость, так как вязкий подслой становиться тоньше и выступы шероховатости, которые первоначально полностью располагались в этом слое, начинают выходить из него, выступая в турбулентную зону.

Следовательно, одна и та же стенка в зависимости от величины числа Рейнольдса может вести себя по разному:

Поэтому абсолютная шероховатость стенок трубопровода не может полностью характеризовать влияние стенок на движение жидкости. Естественно, что стенки с одной и той же абсолютной шероховатостью в потоках небольших поперечных размеров должны будут вносить большие возмущения в поток жидкости и оказывать большее сопротивление движению, чем в потоках большого сечения.

Относительная шероховатость и относительная гладкость.

Для характеристики влияния шероховатости на величину гидравлических сопротивлений, а так же исходя из условий соблюдения подобия, в гидравлике вводится понятие относительная шероховатость – ε.

Под термином относительная шероховатость понимают безразмерное отношение абсолютной шероховатости к некоторому линейному размеру, характеризующему сечение потока(например, к радиусу трубы r, к глубине жидкости в открытом потоке h и т.п.).

Таким образом

ε = κ / r

В некоторых случаях вводят понятие относительной гладкости ε^/ как величины обратной относительной шероховатости

ε^/ = r / κ

В действительно, как показали исследования, на величину гидравлических сопротивлений влияет не только абсолютное значение шероховатости (высота выступов), но также в значительной степени их форма и густота. Учесть влияние этих факторов непосредственными измерениями шероховатости практически невозможно.

Видео о шероховатости

В настоящее время для того, чтобы охарактеризовать шероховатость стенки трубы при гидравлических расчетах обычно пользуются понятием – эквивалентной шероховатости. Этот эквивалент представляет собой такую величину выступов однородной абсолютной шероховатости, которая дает при подсчетах одинаковую с действительной шероховатостью величину потерь напора.

Вместе со статьей «Шероховатость стенок трубопровода: типы и влияние» смотрят:

Кавитация в насосах

Вязкость жидкости

Уравнение неразрывности струи и потока жидкости.

Источник

С
точки зрения инженерных приложений
главными являются следующие задачи: а)
как определить потери напора (энергии);
б)
как распределены скорости по сечению
трубы.

10.1. Абсолютная и относительная шероховатость

На
потери напора по длине при турбулентном
режиме может оказывать влияние
шероховатость стенок. Под шероховатостью
будем понимать присутствие у любой
поверхности неровностей (выступы и
впадины).
При
заводском изготовлении труб шероховатость
их внутренних стенок носит нерегулярный
характер, как по высоте, так и по
расположению, и поэтому одним параметром
охарактеризована быть не может. Несмотря
на это, в технических расчетах выбирают
единственный параметр, а именно среднюю
высоту выступов шероховатости; ее
обозначают k
(или Δ).

Абсолютной
шероховатостью k
называют среднюю высоту выступов
шероховатости.

Опыты
показали, что при одной и той же величине
абсолютной шероховатости влияние ее
на величину гидравлического сопротивления
различно в зависимости от диаметра
трубы. Поэтому вводится величина
относительной шероховатости
.

Относительной
шероховатостью называется отношение
абсолютной шероховатости к диаметру
трубы, т.е.
.

10.2. Закономерности изменения коэффициента гидравлического трения

Потери
напора по длине трубопровода обычно
находят по формуле (9.14). При этом основной
задачей является определение коэффициента

гидравлического
трения
.
В общем случае коэффициент гидравлического
трения может зависеть от двух безразмерных
параметров – числа

Re
=

и k/d,
т.е.
.

На
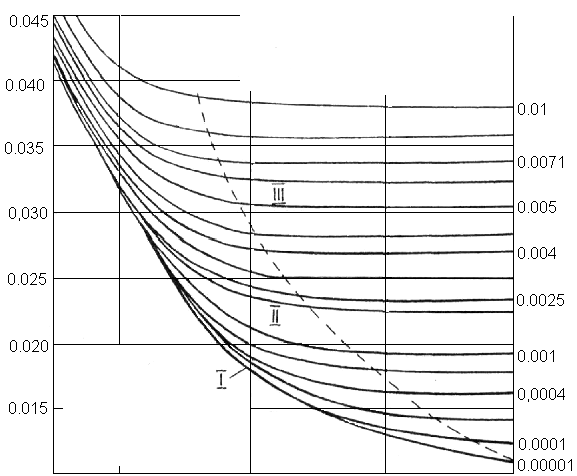
рис. 10.1 представлен экспериментальный
график зависимости коэффициента
от числа Рейнольдса, на нем изменение
коэффициентапредставлено рядом кривых, каждая из
которых соответствует определённой
относительной шероховатости, т.е.
отношениюk/d.

На
графике можно выделить три области: I
— область гидравлически гладких труб,
соответствующую сравнительно малым
числам Рейнольдса, II
— область доквадратичного сопротивления,
III
— область квадратичного сопротивления.
В области гидравлически гладких труб
коэффициент
зависит от числа Рейнольдса, в
доквадратичной области коэффициентзависит от числаRe
и от относительной шероховатости, а в
области квадратичного сопротивления
– только от относительной шероховатости.

10<<500

500<

Re_d<2300

Рис.
10.1. График Мурина – Шевелёва

10.3. Зависимости для коэффициента гидравлического сопротивления и области их применения

Для определения
потерь по длине применяется формула
Дарси-Вейсбаха

h₁
= λ.

Чтобы
выбрать соответствующую зависимость
для λ,
предлагается простой алгоритм. Обычно
заданы: расход Q,
диаметр трубы d,
кинематический коэффициент вязкости
ν
и величина эквивалентной шероховатости
k_э
(из таблиц) для данного материала. В
табл. 10.1 приведены значения k_э
для труб из разных материалов.

Таблица
10.1

Трубы, их материалы и состояние стенок	k, мм
Стальные цельнотянутые новые	0,02 – 0,07
Стальные цельнотянутые, находившиеся в эксплуатации	0,2 – 0,5
Стальные цельнотянутые после продолжительной эксплуатации, сильно заржавленные	До 1,0
Железные оцинкованные	0,15 – 0,18
Чугунные асфальтированные новые	0,13
Чугунные новые	0,25
Чугунные, находившиеся в эксплуатации	1,4

Определяют:

а)
среднюю скорость V==;

б)
число Рейнольдса Rе
=
;

в)
относительную шероховатость
.

1.
Если Rе
< 2300,
то имеет место ламинарный режим и

λ
=
.
(10.1)

2.
Если Rе
> 4000,
то определяют величину параметра

Rе.

3.
Если Rе<10,
то имеет место гладкостенная зона
сопротивления и λ
определяется по формуле Блазиуса

λ
=
.
(10.2)

4.
Если 10 <
Rе<500,
то имеет место доквадратичная зона
сопротивления и λ
определяется по формуле Альтшуля

λ
= 0,11

(10.3)

5.
Если Rе>500,
то имеет место квадратичная зона
сопротивления и λ
определяется по формуле Шифринсона

λ
= 0,11

.
(10.4)

Задача
10.1.
Определить, какой степени средней
скорости пропорциональны потери по
длине в каждой из зон сопротивления.

Решение.
Используется формула Дарси-Вейсбаха
(9.14) и зависимость для
в соответствующей зоне сопротивления.

1.
Для ламинарного режима
64/Rе
и потери h_l
выразятся так

или,
сокращая числитель и знаменатель на V,

В
правой части последней формулы первый
сомножитель не зависит от скорости и
величина h_l
имеет вид h_l=

,
т.е.
потери в ламинарной зоне сопротивления
пропорциональны первой степени скорости.

2. В
зоне квадратичного сопротивления λ
определяется по формуле λ=0,11,
а
потери выразятся так h_l=0,11.

Так
как первый сомножитель в правой части
не зависит от скорости, то потери h_lпропорциональны
скорости в квадрате, откуда и название
зоны – квадратичная зона сопротивления.

Задача
10.2.
Поток в трубе находится в квадратичной
зоне сопротивления. Как изменятся потери
по длине в этой трубе, если расход в ней
увеличить в два раза?

Решение.
Учитывая решение задачи 10.1, заключаем,
что если расход увеличить в два раза,
то и средняя скорость увеличится в два
раза и поэтому (поскольку зона квадратичная)
потери возрастут в 2²,
т.е. в 4 раза.

Задача
10.3.
Отрезок трубы внутренним диаметром
d₁=100
мм был заменен отрезком трубы такой же
длины, но внутренним диаметром d₂,
в 2 раза меньшим: d₂=50
мм.

Определить,
как изменились потери на этом участке
при такой замене. Расход воды остался
таким же; считаем для упрощения решения,
что в обоих случаях квадратичный режим,
изменение λ
не учитываем.

Решение.
Для решения задачи достаточно определить
отношение потерь h₁
в трубе с d₁=100
мм к h₂
в трубе с d₂=50
мм. Выражения для h₁
и h₂
по формуле Дарси-Вейсбаха (9.14)

и
.
Их отношение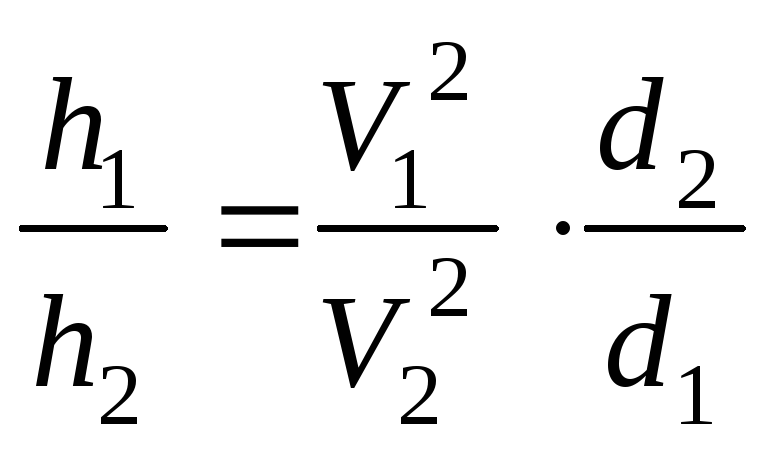.(10.5)

Согласно уравнению
неразрывности

или

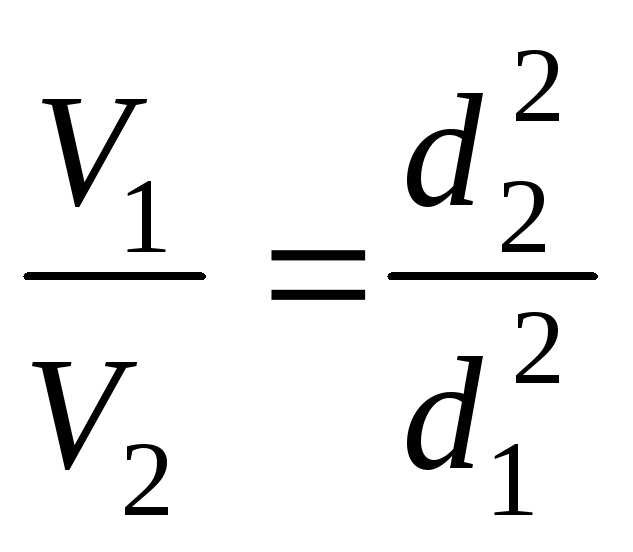
Если возведем обе
части последнего равенства в квадрат,
получим

.
(10.6)

Подставляя
(10.6) в (10.5), имеем окончательно
.

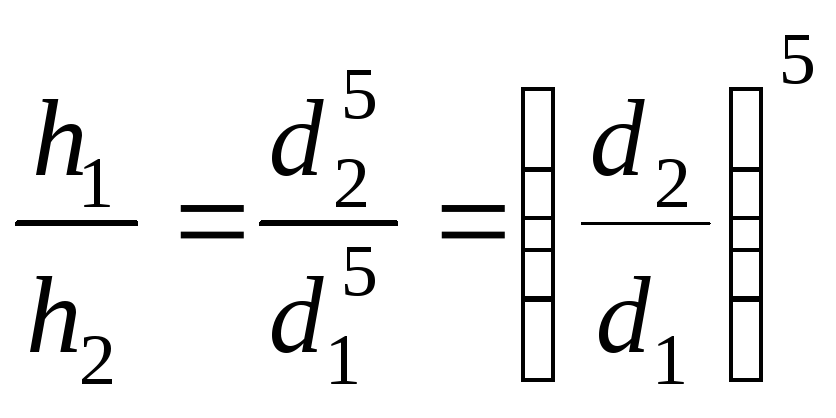
Если
,
то

Таким
образом, потери увеличились в 32 раза!
Если учесть, что
также зависит от диаметра, то получим
несколько меньшее число.

Этот
же результат возможно получить, оценивая
порядок величин, а именно, потери
выражаются зависимостью

или

.(10.7)

Средняя скорость
выражается так

V=Q/S
или V~1/d
²,

т.е.
при
обратно пропорциональна квадрату
диаметра, а средняя скорость в квадрате,
соответственно, обратно пропорциональна
четвертой степени диаметра, т.е.

V²
~1/d
⁴
.
(10.8)

Имея
в виду (10.7) и (10.8), получаем в данном случае

h₁~1/d
⁵,

т.е.
потери обратно пропорциональны диаметру
в пятой степени. Этот результат имеет
большое значение при гидравлических
расчетах водопроводных сетей.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

10-я лекция.

11. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ

11.0. Число Рейнольдса. Характеристика режимов течения вязкой жидкости

11.1 Основные сведения. Эпюры скоростей. Относительная шероховатость

11.2. Коэффициент сопротивления трения по длине трубопровода при турбулентном потоке.

11.3 Гидравлически гладкая труба.

11.4. Относительная шероховатость. Турбулентное течение в шероховатых трубах

11.5 Опыты Никурадзе

11.6. Реальные шероховатые трубы. Опыты Мурина и теплотехнического института.

Рекомендуемые материалы

11.7. Турбулентное течение в некруглых трубах

11.1. Число Рейнольдса. Характеристика режимов течения вязкой жидкости.

Исследования, проведенные Осборном Рейнольсом в лабораторных условиях, позволили установить критерий, характеризующий режим движения вязкой жидкости в трубах и руслах.

Под руслами понимаются трубопроводы и каналы в гидрораспределителях, гидромашинах и других гидравлических устройствах, и каналы с открытой свободной поверхностью жидкости.

Другими исследователями были установлены зависимости, связанные с сопротивлением трения потоку рабочей жидкости.

Использование подобия позволило определить расчетные коэффициенты сопротивлению трения в реальных условиях.

Проблема механического подобия ставится следующим образом.

«Возможно ли прежде, чем создать какое-либо устройство, установить закономерности его действия, произведя опыты на геометрически подобной ему модели меньших размеров?».

При изучении режимов движения жидкости использовалось подобие между явлениями на моделях русел и трубопроводов, проводившимися в лабораторных условиях и явлениями, имевшими место в натуре, то есть в реальных руслах и трубопроводах.

Для адекватности выводов, сделанных на модели в лабораторных условиях, было установлено, что должны соблюдаться следующие условия подобия.

Имеются две подобные системы одинаковой физической природы. Одна система, предназначенная для исследований в лабораторных условиях, будет иметь индекс – м, означающий «модель».

Вторая система, для которой выполняются исследования, реальная конструкция или машина будет иметь индекс – н, означающий «натура».

Однородные части обеих систем должны удовлетворять условиям подобия так, чтобы коэффициенты подобия имели одно и тоже значение при изучении комплекса или отдельных частей машины. Для этого должны соблюдаться следующие условия.

а) Основные коэффициенты подобия.

1.Геометрическо подобие — подобие размеров будет соблюдаться при пропорциональности диаметров, длин трубопроводов, радиусов их закруглений в натуре и на модели:

2. Материальное подобие – подобие масс геометрически соответственных объемных элементов в модели и в натуре:

3. Подобие времени эксперимента в лаборатории и в натуре

Механическое состояние любой системы определяется тремя независимыми физическими величинами: длина , масса и время. Из основных коэффициентов подобия можно образовать производные коэффициенты подобия.

4. Кинематическое подобие – подобие скоростей V₁ и V₂и ускоренийа₁ и а₂:

коэффициент для скоростей

коэффициент для ускорений

За характерные скорости берутся средние скорости на оси.

4. Механическое или силовое подобие соблюдается, если в сравниваемых точках потока отношения сил одинаковы. Используя выражение для второго закона Ньютона, получим, что подобие сил на натуре и моде соблюдается при соотношениях:

коэффициент для сил

4.1 Связь между влиянием сил трения (явление вязкости в жидкости) и действием внешних сил, может быть оценена при использовании закона Ньютона о трении в жидкости

Используя ранее полученное коэффициент для внешних сил по второму закону Ньютона, так как действие силы трения также изменяет ускорение массы жидкости, приравняем, коэффициент для внешних сил коэффициенту, полученному для сил трения

чтобы это равенство соблюдалось,

отношение коэффициентов кинематических вязкостей должно быть равно

Внеся в это равенство дополнительно, вместо λ^-1= λ² λ^-3 и сгруппировав, имеем

(11.1)

Связь сил инерции и сил вязкости при изучении подобных течений на модели и в натуре выражается числом Рейнольдса.

Число Рейнольдса есть отношение сил инерции к силам вязкости в потоках реальной жидкости.

Если число Рейнольдса мало, то в потоке преобладают силы вязкости, если велико – силы инерции.

11.2. Основные сведения о турбулентном режиме течения жидкости. Эпюры скоростей. Относительная шероховатость.

11.2.1. Фиксация скоростей и давлений при турбулентном движении.

Для турбулентного течения в отличии от ламинарного характерны пульсации скоростей и давлений, перемешивание жидкости.

В фиксированной точке потока величина скорости может быть измерена и зафиксирована во времени с помощью трубки полного напора или «трубки Пито» (рис.11.2).

Трубка, повернутая под углом 90°(рис.11.2), устанавливается отверстием навстречу потоку, рядом с ней устанавливается пьезометр. Скорость V частиц жидкости, попадающих в отверстие трубки, тормозится и уменьшается до нуля, а давление увеличивается на величину скоростного напора. Столб жидкости в трубке Пито поднимается над уровнем в пьезометре на высоту равную скоростному напору.

. Измерив, разность высот жидкости в трубке Пито и пьезометре, можно определить скорость жидкости в данной точке.

Запишем уравнение Бернулли для струйки, которая попадает в трубку вдоль ее оси. Для сечений 0-0 имеем Р₀ и V₀, и 1-1 P₁,V₁ =0:

Вокруг трубки давление также близко к Р=Ро, , следовательно, из предыдущего имеем

Скорость во время записи колеблется около среднего значения. Траектории частиц, проходящих через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, (рис.11.1).

11.2.2. Характеристики турбулентного течения.

Турбулентное течение неустановившееся, так как значения скоростей и давлений, а также траектории частиц, изменяются по времени.

Для расчетов, усредняют скорости и давления. Если средние значения скоростей и давлений потока мало изменяются во времени, то по средним значениям принято считать турбулентное течение установившимся.

Средние скорости при турбулентном течении распределены более равномерно по сечению трубопровода в сравнении с ламинарным течением.

Коэффициент (рис.11.3) Кориолиса , учитывающий неравномерность распределения скоростей в уравнении Бернулли, при турбулентном течении меньше, чем при ламинарном течении. При ламинарном течении коэффициент Кориолиса не зависит от Re и равен приблизительно двум, при турбулентном течении близок к единице.

Поскольку при турбулентном течении отсутствует слоистость потока и происходит перемешивание жидкости, касательное напряжение τ на стенке трубы в турбулентном потоке больше, чем при ламинарном при тех же числах Re, благодаря перемешиванию и переносу жидкости в поперечном направлении,

При турбулентном режиме при Re >Re_кр потери энергии на трение по длине значительно больше, чем при ламинарном при тех же размерах трубы, расходе и вязкости жидкости.

При ламинарном режиме потери напора на трение возрастают пропорционально скорости в первой степени, а при переходе к турбулентному течению заметен скачок сопротивления и изменение сопротивления по кривой близкой к параболе (рис.11.4).

Ввиду сложности турбулентного течения и трудностей его аналитического исследования до настоящего времени для него не имеется достаточно строгой и точной его теории.

11.2. Коэффициент сопротивления трения по длине

трубопровода при турбулентном потоке.

Основной расчетной формулой для потерь напора при турбулентном течении в круглых трубах является эмпирическая формула Вейсбаха— Дарси

‚

где λ_т — коэффициент потерь на трение при турбулентном течении, или коэффициент Дарси.

При турбулентном течении потеря напора на трение пропорциональна скорости во второй степени, а коэффициент потерь на трение в формуле для данной трубы можно считать величиной постоянной.

11.3 Турбулентное течение в области гидравлически гладких труб.

Для практических расчетов потерь, связанных с турбулентным течением жидкостей в трубах были проведены экспериментальные исследования, и установлено, что коэффициент λ_т зависит от сочетания двух факторов: неровностей в трубе и числа Рейнольдса.

На графике функциональных зависимостей, связывающих коэффициент λ, неровности в трубе и число Re выделены две области: область гидравлически гладких труб и область гидравлически шероховатых труб.

Труба называется гидравлически гладкой, когда ее шероховатость не влияет на коэффициент λ_т и соответственно на сопротивление потоку.

К гидравлически гладким трубам можно отнести цельнотянутые трубы из цветных металлов, включая и алюминиевые сплавы, а также высококачественные бесшовные стальные трубы. Такие трубы применяются в топливопроводах и гидросистемах. Водопроводные стальные и чугунные трубы гидравлически гладкими не считают.

В области гидравлически гладких труб при турбулентном течении в эмпирические зависимости для коэффициента λ_т , как и для ламинарного движения входит только число Рейнольдса:

λ_т = f(Re).

Основную роль в образовании потерь энергии при турбулентном течении играет перемешивание и рассеивание кинетической энергии завихренных частиц.

Исследования турбулентного течения жидкости при небольших скоростях в области гидравлически гладких труб показали, что на стенке трубы образуется ламинарный подслой (рис.11.5). Это тонкий слой жидкости, движение в котором является слоистым и происходит без перемешивания. В его пределах скорость растет от нуля на стенке до некоторой величины V_л на границе слоя. Толщина δл ламинарного слоя невелика, причем оказывается, что число Re, подсчитанное по толщине δ_л, скорости V_ли кинематической вязкости ν, есть величина постоянная, как постоянно Re_кр для течения в трубах.

Re = V_лδ_л/ν= const

При увеличении скорости потока толщина δ_л ламинарного слоя уменьшается.

11.4. Турбулентное течение в области в шероховатых труб.

Относительная шероховатость.

Труба называется гидравлически шероховатой, когда на ее внутренней поверхности ламинарный подслой мал или отсутствует.

Относительной шероховатостью называется отношение ∆/d, где ∆ — средняя высота бугорков неровностей (шероховатостей) внутри трубы, d — диаметр трубы.

Одинаковая абсолютная шероховатость может совершенно не оказывать влияния на сопротивление трубы большого диаметра, но значительно влияет на сопротивление трубы малого диаметра.

Если все бугорки шероховатости имеют один и тот же размер ∆ и одинаковую форму, такая шероховатость называется равномерно распределенной зернистой шероховатостью.

Область «гидравлически шероховатых труб» состоит из двух частей.

В первой части λ_т зависит от числа Re и от шероховатости внутренней поверхности трубы, выраженной в виде относительной величины

λ_т =f(Re, ∆/d)

Во второй части λ_Т зависит только от шероховатости внутренней поверхности трубы

λ_т= f(∆/d),

11.5 Опыты Никурадзе

Сотрудник Прандтля в Геттингене Никурадзе выполнил опыты по определению сопротивления труб с искусственно созданной равномерно распределенной зернистой шероховатостью на внутренней поверхности.

Шероховатость была получена путем приклейки песчинок определенного размера, полученного просеиванием песка через специальные сита. Сначала внутренние стенки труб покрывались лаком, затем труба заполнялась песком определенной зернистости, с диаметром равным средней неровности ∆, песчинки приклеивались к стенкам однородным слоем, потом опять покрывалась лаком и высушивалась.

Испытания были проведены в диапазоне относительных шероховатостей ∆/r₀ от 1/500 до 1/15) при числах Рейнольдса Re=500 – 10⁶.

На рис.11.6 представлены результаты этих испытаний и построены зависимости lg(1000λ) от lg Re для значений ∆/r₀. ∆ — высота бугорков, r₀– радиус трубы.

1.Область ламинарного режима. Уравнение прямой А, определяющей область ламинарного режима течения, получено из формулы для λл= 64/Re умножением на 1000 и логарифмированием

lg(1000λл) = lg 64000 – lgRe.

От прямой А до осей координат находится область ламинарного режима, в которой коэффициент сопротивления λл зависит только от Re, определяется по формуле для ламинарного режима течения

λ= 64/Re.

2.Область гидравлически гладких труб при турбулентном режиме. Уравнение прямой В, определяющей эту область получено из формулы для Блазиуса λ_тр = 0,316/ умножением на 1000 и логарифмированием

lg(1000λт) = lg 316 – (¼) lgRe.

2.1. Под прямой В до оси абсцисс находится область «гидравлически гладких труб», коэффициент сопротивления λл зависит только от Re и определяется по формуле Блазиуса или Конакова для ламинарного режима течения.

При Re< 10⁵ (сто тысяч) применяется формула Блазиуса

λ_тр = 0,316/ . (11.2)

При Re> 10⁵применяется формула Конакова

λ_тр = 1/(1,8*lgRe-1,5)² (11.3)

Штриховыми линиями показаны зависимости λ_тр для труб с различной относительной шероховатостью ∆/r₀.

2.2. Переходная область. Особенность турбулентного режима течения в этой области в том, что при увеличении числа Re (скорости) толщина ламинарного слоя δ_л уменьшается. Для турбулентного потока при малых числах Re толщина ламинарного слоя больше высоты бугорков шероховатости, бугорки находятся внутри ламинарного слоя, обтекаются плавно (безотрывно) и на сопротивление не влияют. При увеличении Re толщина δ_л уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влияют на сопротивление.

Над областью гидравлически гладких труб начинается переход к режиму шероховатых труб, для труб с шероховатостью ∆/r₀= 1/15, 1/30 и λт yже зависит не только от Re, но и от шероховатости и его значения отклоняются от прямой В сверху.

По числу Рейнольдса нижняя граница переходной области Re_гл ≥ 20d/Δ, верхняя граница – Re_кв < 500 d/Δ.

В переходной области значения λ определяются по графику или по ф-ле Альтшуля

( 11.4)

Следует отметить, что средние значения эквивалентной шероховатости для

— новых цельнотянутых труб Δ =0,1мм,

— для бывших в употреблении Δ = 0,2 мм

3. Область гидравлически шероховатых труб.

Для определения коэффициента λт используются графики или формула Никурадзе

( 11.5 )

или формула Шифринсона

(11.6).

Для старых водопроводных труб (стальных и чугунных) ∆ = 1 мм, применима формула

Область шероховатых труб, где λ зависит только от отношения ∆/r₀называется квадратичной или автомодельной зоной.

При больших Re коэффициент λ_т перестает зависеть от Re и становится постоянным для данной относительной шероховатости. Участки этих штриховых линий параллельны оси абсцисс.

При больших числах Re толщина ламинарного слоя уменьшается, бугорки шероховатости обтекаются турбулентным потоком с вихревыми образованиями, этим объясняется квадратичный закон сопротивления, характерный для данной области.

11.6. Реальные шероховатые трубы. Опыты Мурина

и теплотехнического института.

Опыты Никурадзе проводились на трубах, снабженных искусственной, равномерно распределенной зернистой шероховатостью. Для натуральных шероховатых труб закон изменения λ_т от Re получается иным. На рис.11.7 в полулогарифмических координатах даны результаты опытов, проведенных во Всесоюзном теплотехническом институте Г.А. Муриным.

Коэффициент λ_т для натуральных шероховатых труб на графике указан в зависимости от Re для разных значений d/∆_э.

Отношение названо d/∆_э «относительной гладкостью труб» в отличии от «относительной шероховатости» ∆/d в работе Никурадзе, где ∆_э — абсолютная шероховатость, эквивалентная по сопротивлению зернистой шероховатости в опытах Никурадзе.

Различие в характере кривых, представленных на рис.11.7 и рис.11.6 объясняется тем, что в натурной трубе (см.рис.11.7) бугорки шероховатости имеют различную высоту и при увеличении числа Re начинают выступать за пределы ламинарного слоя при разных Re.

Поэтому переход от линии, соответствующей сопротивлению гладких труб, к горизонтальным прямым соответствующим квадратичному закону, происходит для натурных труб более плавно без провала кривых, характерного для графика Никурадзе.

На этом графике можно выделить также три области.

1.Область гидравлически гладких труб.

При Re < 20 d/∆_э используют формулу Блазиуса для гладких труб

1.2.Переходная зона.

При 20 d/∆_э < Re < 500 d/∆_э используют универсальную формулу А. Д. Альтшуля

(11.7)

1.2. Зона шероховатых труб.

При Re > 500 d/∆_э для режима квадратичного сопротивления (автомодельности):

, (11.8)

где ∆_э — эквивалентная абсолютная шероховатость; d — диаметр трубы.

Таким образом, путем сравнения численного значения отношения d/∆_э с числом Re можно установить границы указанных выше областей (режимов) турбулентного течения в шероховатых трубах.

11.7. Турбулентное течение в некруглых трубах

На практике часто приходится иметь дело с турбулентным течением в некруглых трубах, применяемых, например, в охлаждающих устройствах (радиаторах, теплообменниках, охлаждающих трактах двигателей и др.).

Рассмотрим расчет потерь на трение при турбулентном течении в трубе с поперечным сечением произвольной формы. Суммарная сила трения, действующая на внешнюю поверхность потока длиной l,

Т = П*l*τ₀,

где П — периметр сечения; τ₀ — касательное напряжение на стенке, зависящее в основном от динамического давления, т.е. от средней скорости течения и плотности жидкости .

Расход жидкости и заданная площадь сечения S определяют среднюю скорость. Сила трения пропорциональна периметру сечения.

При некруглом сечении для оценки влияния формы на потерю напора при турбулентном и при ламинарном течении вводят гидравлический радиус Rг, равный отношению площади сечения S некруглой трубы к периметру П его сечения и гидравлический диаметр Dг.

Rг = S/П.

1) Тогда для прямоугольника со сторонами a b получим S=ab, П = 2(a+2b),

Rг = S/П = (ab)/(2(a+b)).

2) Для квадрата Rг = S/П = (a²)/(4a) = a/4.

3) Для зазора а, при а<<b: Rг = S/П = .

16. Сплошные системы разработки — лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Для круглого сечения : Rг = S/П =. Откуда Dг = 4Rг.

Тогда для прямоугольника Dг = 4Rг = 4*(аb)/2(a+b) = 2*(аb)/(a+b), для квадрата Dг = 4*(а/4) = а, для зазора Dг = 4Rг = 4*(а/2)=2а.

Для определения потерь при турбулентном и при ламинарном режиме можно пользоваться формулой Вейсбаха—Дарси. Таким образом, для любой формы сечения

(11.9)

При этом коэффициент λ_т подсчитывают по тем же формулам, а число Рейнольдса выражают через гидравлический диаметр D_г :

Re = (VD_г)/ν.

Источник

Абсолютная шероховатость труб (Таблица)

Шероховатость поверхности — совокупность неровностей поверхности с относительно малыми шагами на базовой длине.

На потери напора по длине при турбулентном режиме может оказывать влияние шероховатость стенок. Под шероховатостью будем понимать присутствие у любой поверхности неровностей (выступы и впадины). При заводском изготовлении труб шероховатость их внутренних стенок носит нерегулярный характер, как по высоте, так и по расположению, и поэтому одним параметром охарактеризована быть не может. Несмотря на это, в технических расчетах выбирают единственный параметр, а именно среднюю высоту выступов шероховатости; ее обозначают k (или Δ).

Абсолютной шероховатостью Δ называют среднюю высоту выступов шероховатости.

Опыты показали, что при одной и той же величине абсолютной шероховатости влияние ее на величину гидравлического сопротивления различно в зависимости от диаметра трубы. Поэтому вводится величина относительной шероховатости Δ/d .

Относительной шероховатостью называется отношение абсолютной шероховатости к диаметру трубы, т.е. Δ/d .

Таблица абсолютная шероховатость поверхности труб

Виды труб и материалов	Состояние поверхности труб, перекачиваемая среда и условия эксплуатации	Шероховатость, Δ, мм
Цельнотянутые из латуни, меди, свинца	Технически гладкие	0,0015—0,0100
Цельнотянутые из алюминия	Технически гладкие	0,015—0,06
Новые	0,02—0,10
Очищенные после многих лет эксплуатации	до 0,04
Цельнотянутые стальные	Битумированные	до 0,04
Теплофикационные для водяного пара и водяные при наличии деаэрации и химической очистки проточной воды	0,10
После одного года эксплуатации на газопроводе	0,12
После нескольких лет эксплуатации в насосно-компрессорных системах газовой скважины при различных условиях	0,04—0,20
Паропроводы насыщенного пара и водяных теплопроводов при незначительных утечках воды (до 0,5%) и деаэрации подпитки	0,20
Трубопроводы систем водяного отопления вне зависимости от источника питания	0,20
Нефтепроводы для средних условий эксплуатации	0,20
Умеренно корродированные	0,4
Наличие небольших отложений накипи	0,4
Паропроводы, работающие периодически (с простоями) и конденсато-проводы с открытой системой конденсата	0,5
Цельнотянутые стальные	Воздухопроводы от поршневых и турбокомпрессоров	0,8
То же, после нескольких лет эксплуатации в других условиях (корродированные или имеющие небольшие отложения)	0,15—1,0
Водопроводные трубы, находившиеся в эксплуатации	1,2—1,5
Наличие больших отложений накипи	3,0
То же, поверхность труб в плохом состоянии	≥5,0
Новые или старые в лучшем состоянии сварные или клепаные соединения	0,04—0,10
Новые битумированные	0,05
Цельнотянутые стальные	Бывшие в эксплуатации, битум частично растворен, корродированные	0,10
Бывшие в эксплуатации, равномерно корродированные	0,15
Цельносварные стальные	Магистральные газопроводы после многих лет эксплуатации	0,5
То же, слоевые отложения	1,1
Наличие значительных отложений	2,0—4,0
После 25 лет эксплуатации на городском газопроводе; наличие неравномерных отложений смолы и нафталина	2,4
Поверхность труб в плохом состоянии; неравномерное покрытие соединений	5,0

Поделитесь ссылкой с друзьями:

Коэффициент шероховатости трубы

Поверхность труб внутри, независимо от материала, из которого она изготовлена, не является абсолютно гладкой. Это вызвано наличием микро бугорков, литьем ППР, сваркой стальных труб, образующимися впадинами и прочими микродефектами, называемыми шероховатостью. Шероховатость может образовываться неравномерно, большими участками, либо иметь равномерное распределение по всей длине или большей части трубопровода.
Коэффициент шероховатости трубы

– это численный показатель, описывающий сопротивление, оказываемое трубой протекающей жидкости. Получаемые значения – эмпирические данные, то есть получаемые в результате опытов, экспериментов, проведения лабораторных исследований. Применяется при проектировании трубопроводов, при строительстве гидротехнических сооружений, проектировании механизмов, систем охлаждения, водоснабжения, фильтрации и прочих.

Выбор характеристик полиэтиленовых труб в зависимости от результатов гидравлического расчета

Selecting Characteristics of Polyethylene Pipes depending on the Hydraulic Calculation Results

Keywords: pressure polyethylene pipes, single-layer pipes, multi-layer pipes, hydraulic calculation of pipelines, flow head losses

Use of pressure polyethylene (PE) pipes for construction of outside networks is becoming more and more popular over the last years. An important stage of outside water supply pipelines’ design is correct selection of pipes. This article describes the main characteristics of pipes, provides an algorithm for hydraulic calculations and recommendations on selection of pipes based on their characteristics.

Использование напорных полиэтиленовых (ПЭ) труб для прокладки наружных сетей получило широкое распространение в последние годы. При проектировании трубопроводов наружного водоснабжения важным этапом является правильный выбор труб. В данной статье описаны основные характеристики труб, дан алгоритм проведения гидравлического расчета и рекомендации по выбору труб в зависимости от их характеристик.

Как получить коэффициент шероховатости?

Наиболее полный документ, описывающий шероховатость поверхности – ГОСТ 2789-73 «Шероховатость поверхностей. Параметры, характеристики, обозначения». Данный стандарт применяется вне зависимости от вида продукции, типа материала, назначения изделий и способа их производства. В то же время, стандарт не описывает частные случаи применения, к примеру, для трубопроводов и прочих систем. Акцент в ГОСТ 2789-73 смещен в сторону описания параметров шероховатости, правил проведения исследований материалов, определения дефектов поверхностей.

Стандартизация современных труб ППР и из других материалов осуществляется по ГОСТ 9378-93, который описывает правила отбора образцов, алгоритм замеров, необходимые технические условия для замера коэффициента шероховатости.

В гидравлических расчетах применяют данные из таблиц для известных материалов. Если же требуется связать коэффициент шероховатости с параметрами объектов (труб, лотков, фитингов, кранов), применяется формула Штриклера:

, где

g – ускорение потока,
k – средняя плотность отложений или шероховатых участков.

Пропорционально увеличению диаметра трубопровода уменьшается и коэффициент шероховатости (чем больше объем проходит по трубе, тем меньше влияние шероховатости на гидравлическое сопротивление). Показатель К также называется средней высотой выступов шероховатой стенки, в гидравлике может также обозначаться как Д или ε.

Если говорить о формулах расчета коэффициента, их применение нецелесообразно ввиду наличия упрощенного варианта – проведения замеров на реальных объектах. Для расчета пропускной способности русел рек и прочих масштабных проектов, формула коэффициента шероховатости также не дает точных результатов, поскольку на его расчет влияет множество неизвестных.

Для удобства сравнения материалов между собой в гидравлике, касающейся трубопроводов и инженерных систем, вводится понятие коэффициент эквивалентной шероховатости. Он рассчитывается в миллиметрах и принимается только для материалов с равномерным образованием шероховатей на внутренней поверхности трубы. В природе такая шероховатость (эквивалентная, равномерная) существует крайне редко, однако для описания технических характеристик удобнее применять именно эквивалентную шероховатость.

Источник

Шероховатость трубы из стали

Рисунок 434. Шероховатость и зарастание трубопровода

Пропускная способность трубопроводов в период эксплуатации снижается, вследствие коррозии и образования отложений на трубах. При этом происходит изменение шероховатости трубопровода и его зарастание (уменьшение поперечного сечения). Увеличение шероховатости и зарастание приводит к уменьшению диаметра трубопровода и как следствие к увеличению потерь напора. Меньше всего этому явлению подвержены асбоцементные, стеклянные и пластмассовые трубы. Сложность физических, химических и биологических явлений, определяющих изменение шероховатости труб и их зарастание, приводит к необходимости ориентироваться на некоторые средние показатели, которые в первом приближении можно оценить по формуле [5]:

Рисунок 435. (19)

— коэффициент эквивалентной шероховатости для новых труб в начале эксплуатации, мм; — коэффициент эквивалентной шероховатости через
t лет эксплуатации, мм; — ежегодный прирост абсолютной шероховатости, мм в год, зависящий от физико-химических свойств подаваемой по ним воды.
По А.Г. Камерштейну, природные воды разбиваются на пять групп, каждая из которых определяет характер и интенсивность снижения пропускной способности трубопровода:

Коррозионное

воздействие

Зарастание трубопровода можно измерять при выполнении реконструкции трубопроводов или ежегодных ремонтах при помощи обычной линейки (рисунок выше), а увеличение шероховатости определять по выше изложенной методике.

Значения коэффициента эквивалентной шероховатости для новых труб приведены в таблице ниже.

Тип трубы	Состояние трубы	Коэффициент эквивалентной шероховатости трубы, мм	Среднее значение коэффициента эквивалентной шероховатости трубы, мм
Бесшовные стальные трубы	Новые и чистые	0.01 – 0.02	0.014
Стальные сварные трубы	Новые и чистые	0.03 – 0.1	0.06
Чугунные трубы	Новые асфальтированные	0 – 0.16	0.12
Чугунные трубы	Новые без покрытия	0.2 – 0.5	0.3
Асбестоцементные	Новые	0.05 – 0.1	0.085
Железобетонные	Новые виброгидропрессованные	0 – 0.05	0.03
Железобетонные	Новые центрифугированные	0.15 – 0.3	0.2
Пластмассовые	Новые, технически гладкие	0 – 0.002	0.001
Стеклянные	Новые, технически гладкие	0 – 0.002	0.001
Алюминиевые	Новые, технически гладкие	0 – 0.002	0.001

Общие потери в трубопроводе, с учетом потерь в местных сопротивлениях могут быть определены по формуле:

Источник

Коэффициент шероховатости новых стальных труб

Рисунок 433. Шероховатость и зарастание трубопровода

Шероховатость стенок трубопровода: типы и влияние

Содержание статьи

Обычно с течением времени шероховатость изменяется от появления ржавчины, коррозии, отложения осадков и т.д.

Абсолютная шероховатость

Некоторые значения шероховатости стенок трубопровода приведены в таблице ниже

Чистые цельнотянутые из латуни, меди и свинца

Новые цельнотянутые стальные

Стальные с незначительной коррозией

Следовательно, одна и та же стенка в зависимости от величины числа Рейнольдса может вести себя по разному:

в одном случае – как гладкая в другом – как шероховатая.

Относительная шероховатость и относительная гладкость.

В некоторых случаях вводят понятие относительной гладкости ε / как величины обратной относительной шероховатости

Выбор характеристик полиэтиленовых труб в зависимости от результатов гидравлического расчета

Использование напорных полиэтиленовых (ПЭ) труб для прокладки наружных сетей получило широкое распространение в последние годы. При проектировании трубопроводов наружного водоснабжения важным этапом является правильный выбор труб. В статье описаны основные характеристики труб, дан алгоритм проведения гидравлического расчета, преставлены рекомендации по выбору труб в зависимости от их характеристик.

Использование труб из полиэтилена для устройства трубопроводов наружного водоснабжения, канализации и технологических трубопроводов обусловлено рядом преимуществ, которыми ПЭ-трубы обладают по сравнению с трубами из традиционных материалов, а именно:

коррозионная стойкость;
срок службы не менее 50 лет * ;
санитарно-гигиеническая и экологическая безопасность;
низкая шероховатость и практическое отсутствие зарастания труб;
высокая стойкость к гидроабразивному износу;
высокая химическая стойкость;
устойчивость к гидравлическим ударам;
устойчивость к воздействию блуждающих токов (не проводят ток);
небольшой вес труб;
легкость транспортирования;
прочность сварных соединений, превосходящая прочность самих труб;
высокая ремонтопригодность.

Шероховатость стенок трубопровода: типы и влияние

Обычно с течением времени шероховатость изменяется от появления ржавчины, коррозии, отложения осадков и т.д.

Абсолютная шероховатость

Некоторые значения шероховатости стенок трубопровода приведены в таблице ниже

Чистые цельнотянутые из латуни, меди и свинца

Новые цельнотянутые стальные

Стальные с незначительной коррозией

Относительная шероховатость и относительная гладкость.

Гидравлически гладкие и шероховатые трубы

В зависимости от соотношения абсолютной высоты выступов шероховатости Δ и толщины вязкого подслоя δ по-разному проявляется влияние вязкостного трения и сил инерции на касательные напряжения и потери энергии в потоке. Толщина вязкого подслоя определяется

Это значение δ следует сравнить с высотой выступов шероховатости. Так как фактическая высота всех выступов не является одинаковой, то вводится понятие эквивалентной шероховатости Δэкв, т.е. такой равномерной шероховатости, которая дает при подсчете одинаковую с заданной шероховатостью величину гидравлического коэффициента трения λ. (Некоторые значения эквивалентной шероховатости приведены в табл. 111.1).

Таблица – Значения эквивалентной шероховатости

Трубы	Δэкв, мм
Стальные цельнотянутые новые	0,02—0,05
То же, неновые (бывшие в эксплуатации)	0,15—0,3
Стальные сварные новые	0,04—0,1
Чугунные новые	0,25—1
Чугунные и стальные сварные неновые	0,8—1,5
Асбестоцементные новые	0,05-0,1
То же, неновые	0,6
Бетонные и железобетонные	0,3—0,8

Схематично можно рассматривать следующие три области гидравлических сопротивлений

1. Область гидравлически гладких труб: выступы шероховатости покрыты вязким подслоем (Δэкв ‹ δ) и не нарушают целостности последнего. Выступы обтекаются без отрывов и вихреобразований. В этом случае шероховатость не влияет на гидравлические сопротивления и гидравлический коэффициент трения, который зависит только от числа Рейнольдса. По данным А. Д. Альтшуля, эта область существует при <10.

Для гидравлически гладких труб наибольшее распространение получила формула Блазиуса

С учетом зависимости и того, что, легко убедиться, что потери напора для гидравлически гладких труб пропорциональны скорости в степени 1,75.

kгл – коэффициент пропорциональности.

2. При > 500 имеет место область гидравлически шероховатых труб: выступы шероховатости выходят за пределы вязкого подслоя (Δэкв>δ). Отрывное обтекание выступов сводит сопротивление трения к сопротивлению обтекания тел с резким изменением конфигурации, которое не зависит от числа Рейнольдса и пропорционально скоростному напору потока и размерам выступов шероховатости. Именно эти факторы связаны с инерционными сопротивлениями перемешивающихся частиц жидкости.

В переходной области сопротивлений гидравлический коэффициент трения может быть определен по формуле А. Д. Альтшуля

3. При 10 <экв в того же порядка, что и толщина вязкого подслоя δ. В этом случае на гидравлическое сопротивление влияют как число Рейнольдса, так и величина выступов шероховатости.

Для гидравлически шероховатых труб формула превращается в формулу Шифринсона

Так как в последнем случае коэффициент гидравлического трения не зависит от скорости движения воды, то из формулы следует, что потери напора пропорциональны квадрату скорости

Гидравлический коэффициент трения (коэффициент Дарси)

Исходя из вышеизложенного, с учетом данных экспериментальных исследований, в общем виде гидравлический коэффициент трения зависит от числа Рейнольдса и относительной шероховатости трубы, т. е.

Одной из наиболее известных работ в этой области являются исследования И. Никурадзе, представленные в виде графика на рис.

На графике показано, что при ламинарном режиме λ зависит только от числа Рейнольдса. При значениях Re = 2320-4000 в зоне периодической смены режимов λ быстро растет. В области гидравлически гладких труб λ зависит только от числа Рейнольдса, уменьшаясь с увеличением последнего.

В переходной области на графике показано семейство кривых для разных относительных шероховатостей. В этой области значения λ в общем возрастают с ростом числа Рейнольдса Rе, но для малых шероховатостей на начальном участке имеет место спад. В области гидравлически шероховатых труб коэффициент λ представлен семейством горизонтальных прямых, разных для различных шероховатостей.

Необходимо отметить, что опыты И. Никурадзе проводились в трубах с искусственной равномерной шероховатостью, наклеенной на стенки трубы в виде песчинок одинаковой крупности. Для практических целей важны результаты опытов К. Кольбрука, Г. А. Мурина, Ф. А. Шевелева и других ученых, проведенные для промышленных труб с естественной неравномерной шероховатостью. Обобщенные результаты этих исследований представлены на графике (рис.), который в отличие от графика Никурадзе показывает, что в переходной области значения λ получаются больше, чем в области квадратичной.

Это важное положение необходимо учитывать при расчете труб, работающих в переходной области. Следует также отметить, что каждая труба не является однозначно гладкой или шероховатой. В зависимости от числа Рейнольдса одна и та же труба может работать в области гидравлически гладких, шероховатых труб или в переходной области. В трубах со сравнительно большой шероховатостью при переходе к турбулентному режиму вязкий подслой не покрывает выступы шероховатости, и область гидравлически гладких труб отсутствует. В зависимости от особенности каждой области имеются различные эмпирические формулы для определения гидравлического коэффициента трения.

Формула Альтшуля применима для всех областей сопротивлений. При малых числах Рейнольдса величина значительно меньше величины и ею можно пренебречь. В этом случае формула превращается в формулу Блазиуса. При больших числах Rе величиной можно пренебречь по сравнению и эта формула превращается в формулу Шифринсона.

Для ряда частных случаев движения жидкости имеются отдельные эмпирические формулы для гидравлического коэффициента трения. Асбестоцементные трубы обычно работают в переходной области сопротивления. Неновые стальные и чугунные трубы при скоростях движения воды V < 1,2 м/с также работают в переходной области сопротивления, а при V > 1,2 м/с — в области гидравлически шероховатых труб. Ф. А. Шевелевым составлены таблицы по определению потерь напора в водопроводных трубах на основании эмпирических формул.

Для расчета движения сточных вод в водоотводных (канализационных) напорных и безнапорных трубах применяется формула Н. Ф. Федорова

D = 4R – гидравлический диаметр;

?2 и a2 – эквивалентная абсолютная шероховатость и безразмерный коэффициент, определяемые по таблице;

Re – число Рейнольдса, при определении которого кинематическая вязкость сточных вод принимается в зависимости от количества взвешенных частиц в них на 5-30% больше, чем вязкость чистой воды.

Таб Коэффициенты ?2 и a2 для формулы Н. Ф. Федорова

Трубы	?2	a2
Асбестоцементные	0,6
Керамические	1.35
Бетонные и железобетонные

Значения гидравлического коэффициента трения для сточных вод получаются большими, чем при движении чистой воды в водопроводных трубах. Н. Ф. Федоровым составлены на основании формулы таблицы пропускной способности и скорости протекания жидкости в водоотводных трубах.

Гидравлический расчет трубопровода.

Гидравлический расчет обычного бытового трубопровода выполняется при помощи уравнения Бернулли:

(z 1 + p 1 /ρg + α 1 u 2 1 /2g) – (z 2 + p 2 /ρg + α 2 u 2 2 /2g) = h 1-2 .

Для гидравлического расчета трубопровода вы можете воспользоваться калькулятором гидравлического расчета трубопровода.

В данном уравнении h1-2 – потери напора (энергии) на преодоление всех видов гидравлического сопротивления, которое приходится на единицу веса перемещающейся жидкости.

h 1-2 = h t + Σh м .

Потери напора на трение по длине потока вы можете рассчитать по формуле Дарси-Вейсбаха

h t = λ(L/d)(v 2 /2g).

где L –длина трубопровода.
d -диаметр участка трубопровода.
v — средняя скорость перемещения жидкости.
λ -коэффициент гидравлического сопротивления, который в общем случае зависит от числа Рейнольдса (Re=v*d/ν), и относительной эквивалентной шероховатости труб (Δ/d).

Значения эквивалентной шероховатости Δ внутренней поверхности труб разных типов и видов указаны в таблице 2. А зависимости коэффициента гидравлического сопротивления λ от числа Re и относительной шероховатости Δ/d указаны в таблице 3.

В случае, когда режим движения ламинарный, то для труб некруглого сечения коэффициент гидравлического сопротивления λ находится по персональным для каждого отдельного случая формулам (табл. 4).

Если турбулентное течение развито и функционирует с достаточной степенью точности, то при определении λ можно использовать формулы для круглой трубы с заменой диаметра d на 4 гидравлических радиуса потока Rг (d=4Rг)

где w– площадь «живого» сечения потока.
c- «смоченный» его периметр (периметр «живого» сечения по контакту жидкость – твердое тело)

Потери напора в местных сопротивлениях можно определить по форм. Вейсбаха

h м = ζ v 2 /2g.

где ζ – коэффициент местного сопротивления, который зависит от конфигурации местного сопротивления и числа Рейнольдса.

При развитом турбулентном режиме ζ = const, что позволяет ввести в расчеты понятие эквивалентной длины местного сопротивления Lэкв. т.е. такой длины прямого трубопровода, для которого ht = hм. В данном случае потери напора в местных сопротивлениях учитываются тем, что к фактической длине трубопровода добавляется сумма их эквивалентных длин

где Lпр – приведенная длина трубопровода.

Зависимость потерь напора h1-2 от расхода называется характеристикой трубопровода.

В случаях когда движение жидкости в трубопроводе обеспечивает центробежный насос, то для определения расхода в системе насос – трубопровод выстраивается характеристика трубопровода h =h(Q) с учетом разности отметок ∆z (h1-2 + ∆z при z1 z2) накладывается на напорную характеристику насоса H=H(Q), которая приведена в паспортных данных насоса (смотреть рисунок). Точка пересечения таких кривых указывает на максимально возможный расход в системе.

10.2. Закономерности изменения коэффициента гидравлического трения

Потери напора по длине трубопровода обычно находят по формуле (9.14). При этом основной задачей является определение коэффициента

гидравлического трения

Re
=

На рис. 10.1 представлен экспериментальный график зависимости коэффициента

и от относительной шероховатости, а в области квадратичного сопротивления – только от относительной шероховатости.

Red

Рис. 10.1. График Мурина – Шевелёва

Влияние шероховатости труб на напор воды

Как поведет себя жидкость в турбулентном потоке, зависит от того, каким является коэффициент шероховатости стальных труб. Различные неровности на внутренней поверхности отражаются на характеристиках коллекторов, их пропускной способности и происходящих внутри процессах. Как и почему это происходит, расскажет данная статья.

Виды шероховатостей в гидравлике

Течение жидкости в ламинарном режиме происходит медленно и плавно, и она спокойно обтекает на своем пути небольшие препятствия. Местное сопротивление в этом случае настолько незначительное, что его величиной можно пренебречь.

На заметку! Турбулентным движением называется движение газа, жидкости или воздуха, при котором кроме средней скорости общего потока, частицы вещества имеют добавочную скорость. Ее направление может не совпадать с направлением средней скорости.

При турбулентном потоке даже мелкие препятствия могут стать источником вихревого движения жидкостей. Они приводят к возрастанию точечных гидравлических сопротивлений, которые в ламинарном потоке настолько малы, что не заслуживают внимания. Препятствиями в данном случае считаются царапины, заусеницы, бугорки и т.п. на стенках трубопровода. В гидравлике они называются выступами шероховатости.

Проблема данного вида может быть абсолютной или относительной:

Абсолютная шероховатость труб зависит от средней высоты бугорков, которые располагаются на внутренних стенках магистрали. Здесь имеет значение качество изготовления, условия эксплуатации и материал конструкции. Данный показатель не оказывает влияния на потерю напора, поскольку не связан с поперечными размерами потока.

Относительная шероховатость труб – это отношение величины абсолютной шероховатости к диаметру трубопровода. Этот показатель сказывается на величине потери напора.

Помимо двух основных видов существует также понятие эквивалентной шероховатости стальных труб, которая искусственно создается бугорками одинаковой высоты по всей длине трубопровода. При ее определении диаметр зерен подбирается так, чтобы в местах квадратичного сопротивления коэффициент по величине был равен коэффициенту при естественной неровности внутренней поверхности сетей.

На заметку! Данный показатель определяется экспериментально, берется из справочных таблиц или вычисляется по приближенной формуле. Как он сказывается на величине гидравлического сопротивления, зависит от диаметра коллектора.

Гидравлически гладкие и шероховатые трубы

У поверхности трубы с внутренней стороны существует относительно статичный слой, рядом с которым все скорости равняются нулю. Этот подвязкий слой называют ламинарным. Если сравнивать с основным потоком, он очень тонкий, но именно из-за него происходят потери напора или удельной энергии.

В случае, когда бугорки на поверхности профиля по высоте меньше толщины ламинарной пленки, они не оказывают влияния на характер движения жидкости. Напор в этом случае может уменьшаться по другим причинам, и такие трубы имеют название – гидравлически гладкие.

Когда высота выступающих зерен больше толщины ламинарной пленки, то напор теряется по причине неровностей внутренней поверхности. Такие конструкции называются гидравлически шероховатыми.

Гидравлические потоки имеют свои особенности, и их следует учитывать при выборе и проектировании транспортирующих магистралей.

В этой статье мы решим задачку на потерю напора в трубопроводе. Данная статья поможет вам понять, как идет сопротивление движению потока. На реальных цифрах, опишу алгоритм как это делать. Используем основные формулы.

Разберем простой пример с трубой, как видно на изображении в начале трубы насос потом идет манометр, который позволяет измерить давление жидкости в начале трубы. Через определенную длину установлен второй манометр, который позволяет измерить давление в конце трубы. Ну и в самом конце стоит кран. Эта схема достаточно проста, и я попытаюсь привести примеры. И так начнем.

Вообще существует не один способ как узнать потерю напора: Способ, когда известно давление вначале и в конце трубы, можно вычислить потерю напора по формуле: М1-М2=Давление

, то есть эта разница между двумя манометрами. Допустим у нас получилось, грубо говоря 0,1 МПа, что составляет одну атмосферу. Это значит у нас потеря напора по длине составляет 0,1 МПа. Обратите внимание, мы можем указывать потерю напора по двум величинам, это по гидростатическому давлению, что составляет 0,1 МПа и по высоте напора водного столба в метрах, что составляет 10 метров. Как я не однократно говорил каждые 10 метров это одна атмосфера давления.

Существует ряд методов, как рассчитать потерю напора не имея манометров на трубах. Ученые исследователи приготовили для нашего пользования замечательные формулы и цифры, которые нам пригодятся.

Существует хорошая формула которая позволяет вычислить потерю напора по длине трубопровода.

Далее находим формулу для нахождения коэффициента гидравлического трения по таблице:

Здесь Δэ

— Эквивалент шероховатости труб. Эта величина в таблицах указывается в милиметрах, но вы когда будете вставлять в формулу обязательно переводите в метры. Вообще не забывайте соблюдать пропорциональность единиц измерения и не смешивайте в формулах разных типа [мм] с [м].

d-внутренний диаметр трубы, то есть диаметр потока жидкости.

Также хочу подметить, что подобные величины по шероховатости бывают абсолютными и относительными или даже есть относительные коэффициенты. Поэтому когда если будете искать таблицы с величинами, то величина эта должа называться «эквивалентом шероховатости труб» и не как иначе, а то результат будет ошибочный. Эквивалент означает — средняя высота шероховатости.

В некоторых ячейках таблицы указаны две формулы, вы можете считать на любой выбранной, они почти дают одинаковый результат.

Вообще в целом, эти формулы показывают и доказывают, что при увеличении скорости или увеличении расхода, всегда увеличивается сопротивление движению потока жидкости, то есть увеличиваются потери напора. Причем увеличиваются не пропорционально, а квадратично. Это говорит о том, что единица увеличения расхода не соответствует затратам на потерю напора. То есть иметь большую скорость потока жидкости в трубе экономически не целесообразно. Поэтому бывает дешевле увеличить диаметр потока. В других статьях обязательно опишу, как посчитать, какой диаметр нам необходим.

Таблица: (Эквивалент шероховатости)

Кому интересно узнать (Эквивалент шероховатости

) для металлопластика, полипропилена и сшитого полиэтилена, то это соответствует и относится к
пластмассам
. То есть в таблице характеристика будет:
Пластмассовые (полиэтилен, винипласт).
Так же хочу обратить внимание, на то, что со временем, на внутренних станках труб, образуется налет, что увеличивает шероховатость труб. Так что имейте ввиду что со временем потери напора только увеличиваются.

Таблица: (Кинематическая вязкость воды

)

График:

Как видно из графика, что при повышении температуры кинематическая вязкость уменьшается, а это значит, что и сопротивление движению воды уменьшается. Это значит, что при потоке горячей воды, «потери напора» будут меньше чем при потоке холодной воды. Кто живет в многоквартирных домах, если обратит внимание, то скорость и напор горячей воды всегда выше чем напор холодной воды. Есть исключения, но в большинстве случаев это так. Теперь вы понимаете, почему это так.

А теперь давайте решим задачу:

Найти потерю напора по длине при движении воды по чугунной новой трубе D=500мм при расходе Q=2 м3/с, длина трубы L=900м, температура t=16°С.

Дано: D=500мм=0.5м Q=2 м3/с L=900м t=16°С Жидкость: H2O Найти: h-?

Видео:

Купить программу

Решение: Для начала найдем скорость потока в трубе по формуле:

V=Q/ω

Сдесь ω

— площадь сечения потока. Находится по формуле:

ω=πR2=π(D2/4)=3.14*(0,52/4)=0,19625 м2

V=Q/ω=2/0,19625=10,19 м/с

Далее находим число Рейнольдса по формуле:

Re=(V*D)/ν=(10,19*0.5)/0,00000116=4 392 241

ν=1,16*10-6=0,00000116. Взято из таблицы. Для воды при температуре 16°С.

Δэ=0,25мм=0,00025м. Взято из таблицы, для новой чугунной трубы.

Далее сверяемся по таблице где находим формулу по нахождению коэффициента гидравлического трения.

λ=0,11(Δэ/D)0,25=0,11*(0,00025/0,5)0,25=0,01645

Далее завершаем формулой:

h=λ*(L*V2)/(D*2*g)=0,01645*(900*10,192)/(0,5*2*9,81)=156,7 м.

Ответ: 156,7 м. = 1,567 МПа.

Также хочу обратить внимание на то, что мы в задаче рассматривали трубу которая на всей своей длине имеет горизонтальное положение.

Давайте рассмотрим пример, когда труба идет вверх под определенным углом.

В этом случае нам к обычной задаче нужно прибавить высоту(в метрах) к потери напора. Если труба будет идти на спуск в низ, то тут необходимо вичитать высоту.

Мы рассмотрели потерю напора по длине трубопровода, также существуют местные сопротивления в виде заужения и поворотов, которые тоже влияют на потерю напора. О них будет описано в других моих статьях. И я обязательно приготовлю статью о том как подобрать насос по напору, чтобы удовлетворить требования расхода жидкости, в зависимости от потерь напора. Если что-то не понятно пишите в комментарии, обязательно отвечу!

Чтобы в ручную не считать всю математику я приготовил специальную программу:

Следующая статья: Местные гидравлические сопротивления

Все о дачном доме Водоснабжение Обучающий курс. Автоматическое водоснабжение своими руками. Для чайников. Неисправности скважинной автоматической системы водоснабжения. Водозаборные скважины Ремонт скважины? Узнайте нужен ли он! Где бурить скважину — снаружи или внутри? В каких случаях очистка скважины не имеет смысла Почему в скважинах застревают насосы и как это предотвратить Прокладка трубопровода от скважины до дома 100% Защита насоса от сухого хода Отопление Обучающий курс. Водяной теплый пол своими руками. Для чайников. Теплый водяной пол под ламинат Обучающий Видеокурс: По ГИДРАВЛИЧЕСКИМ И ТЕПЛОВЫМ РАСЧЕТАМ Водяное отопление Виды отопления Отопительные системы Отопительное оборудование, отопительные батареи Система теплых полов Личная статья теплых полов Принцип работы и схема работы теплого водяного пола Проектирование и монтаж теплого пола Водяной теплый пол своими руками Основные материалы для теплого водяного пола Технология монтажа водяного теплого пола Система теплых полов Шаг укладки и способы укладки теплого пола Типы водных теплых полов Все о теплоносителях Антифриз или вода? Виды теплоносителей (антифризов для отопления) Антифриз для отопления Как правильно разбавлять антифриз для системы отопления? Обнаружение и последствия протечек теплоносителей Как правильно выбрать отопительный котел Тепловой насос Особенности теплового насоса Тепловой насос принцип работы Запас мощности котла. Нужен ли он? Про радиаторы отопления Способы подключения радиаторов. Свойства и параметры. Как рассчитать колличество секций радиатора? Рассчет тепловой мощности и количество радиаторов Виды радиаторов и их особенности Автономное водоснабжение Схема автономного водоснабжения Устройство скважины Очистка скважины своими руками Опыт сантехника Подключение стиральной машины Полезные материалы Редуктор давления воды Гидроаккумулятор. Принцип работы, назначение и настройка. Автоматический клапан для выпуска воздуха Балансировочный клапан Перепускной клапан Трехходовой клапан Трехходовой клапан с сервоприводом ESBE Терморегулятор на радиатор Сервопривод коллекторный. Выбор и правила подключения. Виды водяных фильтров. Как подобрать водяной фильтр для воды. Обратный осмос Фильтр грязевик Обратный клапан Предохранительный клапан Смесительный узел. Принцип работы. Назначение и расчеты. Расчет смесительного узла CombiMix Гидрострелка. Принцип работы, назначение и расчеты. Бойлер косвенного нагрева накопительный. Принцип работы. Расчет пластинчатого теплообменника Рекомендации по подбору ПТО при проектировании объектов теплоснабжения О загрязнение теплообменников Водонагреватель косвенного нагрева воды Магнитный фильтр — защита от накипи Инфракрасные обогреватели Радиаторы. Свойства и виды отопительных приборов. Виды труб и их свойства Незаменимые инструменты сантехника Интересные рассказы Страшная сказка о черном монтажнике Технологии очистки воды Как выбрать фильтр для очистки воды Поразмышляем о канализации Очистные сооружения сельского дома Советы сантехнику Как оценить качество Вашей отопительной и водопроводной системы? Профрекомендации Как подобрать насос для скважины Как правильно оборудовать скважину Водопровод на огород Как выбрать водонагреватель Пример установки оборудования для скважины Рекомендации по комплектации и монтажу погружных насосов Какой тип гидроаккумулятора водоснабжения выбрать? Круговорот воды в квартире фановая труба Удаление воздуха из системы отопления Гидравлика и теплотехника Введение Что такое гидравлический расчет? Невязка гидравлического расчета Физические свойства жидкостей Гидростатическое давление Поговорим о сопротивлениях прохождении жидкости в трубах Режимы движения жидкости (ламинарный и турбулентный) Гидравлический расчет на потерю напора или как рассчитать потери давления в трубе Местные гидравлические сопротивления Профессиональный расчет диаметра трубы по формулам для водоснабжения Как подобрать насос по техническим параметрам Профессиональный расчет систем водяного отопления. Расчет теплопотерь водяного контура. Гидравлические потери в гофрированной трубе Теплотехника. Речь автора. Вступление Процессы теплообмена Тплопроводность материалов и потеря тепла через стену Как мы теряем тепло обычным воздухом? Законы теплового излучения. Лучистое тепло. Законы теплового излучения. Страница 2. Потеря тепла через окно Факторы теплопотерь дома Начни свое дело в сфере систем водоснабжения и отопления Вопрос по расчету гидравлики Конструктор водяного отопления Диаметр трубопроводов, скорость течения и расход теплоносителя. Вычисляем диаметр трубы для отопления Расчет потерь тепла через радиатор Мощность радиатора отопления Расчет мощности радиаторов. Стандарты EN 442 и DIN 4704 Расчет теплопотерь через ограждающие конструкции Найти теплопотери через чердак и узнать температуру на чердаке Подбираем циркуляционный насос для отопления Перенос тепловой энергии по трубам Расчет гидравлического сопротивления в системе отопления Распределение расхода и тепла по трубам. Абсолютные схемы. Расчет сложной попутной системы отопления Расчет отопления. Популярный миф Расчет отопления одной ветки по длине и КМС Расчет отопления. Подбор насоса и диаметров Расчет отопления. Двухтрубная тупиковая Расчет отопления. Однотрубная последовательная Расчет отопления. Двухтрубная попутная Расчет естественной циркуляции. Гравитационный напор Расчет гидравлического удара Сколько выделяется тепла трубами? Собираем котельную от А до Я… Система отопления расчет Онлайн калькулятор Программа расчет Теплопотерь помещения Гидравлический расчет трубопроводов История и возможности программы — введение Как в программе сделать расчет одной ветки Расчет угла КМС отвода Расчет КМС систем отопления и водоснабжения Разветвление трубопровода – расчет Как в программе рассчитать однотрубную систему отопления Как в программе рассчитать двухтрубную систему отопления Как в программе рассчитать расход радиатора в системе отопления Перерасчет мощности радиаторов Как в программе рассчитать двухтрубную попутную систему отопления. Петля Тихельмана Расчет гидравлического разделителя (гидрострелка) в программе Расчет комбинированной цепи систем отопления и водоснабжения Расчет теплопотерь через ограждающие конструкции Гидравлические потери в гофрированной трубе Гидравлический расчет в трехмерном пространстве Интерфейс и управление в программе Три закона/фактора по подбору диаметров и насосов Расчет водоснабжения с самовсасывающим насосом Расчет диаметров от центрального водоснабжения Расчет водоснабжения частного дома Расчет гидрострелки и коллектора Расчет Гидрострелки со множеством соединений Расчет двух котлов в системе отопления Расчет однотрубной системы отопления Расчет двухтрубной системы отопления Расчет петли Тихельмана Расчет двухтрубной лучевой разводки Расчет двухтрубной вертикальной системы отопления Расчет однотрубной вертикальной системы отопления Расчет теплого водяного пола и смесительных узлов Рециркуляция горячего водоснабжения Балансировочная настройка радиаторов Расчет отопления с естественной циркуляцией Лучевая разводка системы отопления Петля Тихельмана – двухтрубная попутная Гидравлический расчет двух котлов с гидрострелкой Система отопления (не Стандарт) — Другая схема обвязки Гидравлический расчет многопатрубковых гидрострелок Радиаторная смешенная система отопления — попутная с тупиков Терморегуляция систем отопления Разветвление трубопровода – расчет Гидравлический расчет по разветвлению трубопровода Расчет насоса для водоснабжения Расчет контуров теплого водяного пола Гидравлический расчет отопления. Однотрубная система Гидравлический расчет отопления. Двухтрубная тупиковая Бюджетный вариант однотрубной системы отопления частного дома Расчет дроссельной шайбы Что такое КМС? Расчет гравитационной системы отопления Конструктор технических проблем Удлинение трубы Требования СНиП ГОСТы Требования к котельному помещению Вопрос слесарю-сантехнику Полезные ссылки сантехнику — Сантехник — ОТВЕЧАЕТ!!! Жилищно коммунальные проблемы Монтажные работы: Проекты, схемы, чертежи, фото, описание. Если надоело читать, можно посмотреть полезный видео сборник по системам водоснабжения и отопления

Источник

Шероховатость стенок трубопровода: типы и влияние

Относительная шероховатость и относительная гладкость.

Видео о шероховатости

10.1. Абсолютная и относительная шероховатость

10.2. Закономерности изменения коэффициента гидравлического трения

10.3. Зависимости для коэффициента гидравлического сопротивления и области их применения

Рекомендуемые материалы

Абсолютная шероховатость труб (Таблица)

Таблица абсолютная шероховатость поверхности труб

Комментарии:

Коэффициент шероховатости трубы

Выбор характеристик полиэтиленовых труб в зависимости от результатов гидравлического расчета

Как получить коэффициент шероховатости?

Шероховатость трубы из стали

Коэффициент шероховатости новых стальных труб

Шероховатость стенок трубопровода: типы и влияние

Абсолютная шероховатость

Относительная шероховатость и относительная гладкость.

Выбор характеристик полиэтиленовых труб в зависимости от результатов гидравлического расчета

Шероховатость стенок трубопровода: типы и влияние

Абсолютная шероховатость

Гидравлически гладкие и шероховатые трубы

Гидравлический расчет трубопровода.

(z 1 + p 1 /ρg + α 1 u 2 1 /2g) – (z 2 + p 2 /ρg + α 2 u 2 2 /2g) = h 1-2 .

h 1-2 = h t + Σh м .

h t = λ(L/d)(v 2 /2g).

h м = ζ v 2 /2g.

10.2. Закономерности изменения коэффициента гидравлического трения

Влияние шероховатости труб на напор воды

Виды шероховатостей в гидравлике

Гидравлически гладкие и шероховатые трубы

Не пропустите также:

Шероховатость стенок трубопровода: типы и влияние

Относительная шероховатость и относительная гладкость.

Видео о шероховатости

10.1. Абсолютная и относительная шероховатость

10.2. Закономерности изменения коэффициента гидравлического трения

10.3. Зависимости для коэффициента гидравлического сопротивления и области их применения

Рекомендуемые материалы

Абсолютная шероховатость труб (Таблица)

Таблица абсолютная шероховатость поверхности труб

Комментарии:

Коэффициент шероховатости трубы

Выбор характеристик полиэтиленовых труб в зависимости от результатов гидравлического расчета

Как получить коэффициент шероховатости?

Шероховатость трубы из стали

Коэффициент шероховатости новых стальных труб

Шероховатость стенок трубопровода: типы и влияние

Абсолютная шероховатость

Относительная шероховатость и относительная гладкость.

Выбор характеристик полиэтиленовых труб в зависимости от результатов гидравлического расчета

Шероховатость стенок трубопровода: типы и влияние

Абсолютная шероховатость

Гидравлически гладкие и шероховатые трубы

Гидравлический расчет трубопровода.

(z 1 + p 1 /ρg + α 1 u 2 1 /2g) – (z 2 + p 2 /ρg + α 2 u 2 2 /2g) = h 1-2 ­.

h 1-2 = h t + Σh м .

h t = λ(L/d)(v 2 /2g).

h м = ζ v 2 /2g.

10.2. Закономерности изменения коэффициента гидравлического трения

Влияние шероховатости труб на напор воды

Виды шероховатостей в гидравлике

Гидравлически гладкие и шероховатые трубы

Не пропустите также:

(z 1 + p 1 /ρg + α 1 u 2 1 /2g) – (z 2 + p 2 /ρg + α 2 u 2 2 /2g) = h 1-2 .