Как найти а по графику функции ах2 - AvtoShod.ru - решение различных проблем

Скачать материал

Сейчас обучается 137 человек из 43 регионов

Сейчас обучается 25 человек из 18 регионов

Сейчас обучается 184 человека из 50 регионов

Краткое описание документа:

В учебнике «Алгебра 9» под редакцией С.А. Теляковского нет заданий на нахождение коэффициентов квадратичной функции с помощью графика параболы, однако такое задание есть в модуле «Алгебра» ОГЭ — 2015 в тренировочных вариантах. Алгоритм нахождения значения коэффициентов a,b, c квадратичной функции позволит ученику научиться определять эти коэффициенты.

I. Нахождение коэффициента a :

1) По графику параболы определяем координаты вершины (m;n).

2) По графику параболы определяем координаты любой точки А (х1;у1).

3) Подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

у=a(х-m)2 +n.

4) Решая полученное уравнение, находим а.

II. нахождение коэффициента b:

1) Сначала находим значение коэффициента a (шаг I, смотри выше).

1) В формулу для абсциссы вершины параболы m= -b/2a подставляем значения m и a.

2) Вычисляем значение коэффициента b.

III. нахождение коэффициента с:

1) Находим ординату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;с) — точка пересечения графика параболы с осью Оу.

Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II (находим коэффициенты a, b).

2) Подставляем найденные значения a, b , А(х1 ;у1) в уравнение у=ax2 +bx+c и находим с.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 267 572 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

07.02.2015
765
2

07.02.2015
911
1

07.02.2015
623
1

07.02.2015
1274
4

07.02.2015
1251
13

07.02.2015
1542
3

Рейтинг:
5 из 5

07.02.2015
3920
71

Источник

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.

— Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

— Аналогично с (a<-1), только график вытянут вниз.

— Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.

— Аналогично (a∈(-1;0)), только ветви направлены вниз.
Парабола пересекает ось y в точке (c).
(b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) — абсциссы (икса) вершины параболы:

(x_в=-frac{b}{2a})
(b=-x_вcdot 2a)

Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).

(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)

Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:

(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1); (x_2=frac{2+4}{2}=3).

Ответ: (3).

2 способ – находим формулу по точкам

Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).

(begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})
Решаем систему.
Пример:

(begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})

Вычтем из второго уравнения первое:

(0=9a-b)
(b=9a)

Подставим (9a) вместо (b):

(begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
(begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

(2=-2a)
(a=-1)

Найдем (b):

(b=-9)

Подставим в первое уравнение (a):

(5=20+c)
(c=-15).

Получается квадратичная функция: (y=-x^2-9x-15).

Пример (ЕГЭ):

Решение:

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})

(begin{cases}8=a-b+4\2=a+b+4 end{cases})

(begin{cases}4=a-b\-2=a+b end{cases})

Сложим 2 уравнения:

(2=2a)
(a=1)

Подставим во второе уравнение:

(-2=1+b)
(b=-3)

Получается:

(g(x)=x^2-3x+4)

Теперь найдем точки пересечения двух функций:

(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)

Теперь можно найти ординату второй точки пересечения:

(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)

Ответ: (22).

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

(y=x^2-10x+25-4)
(y=x^2-10x+21)

Готово.

Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).
(f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)

Смотрите также:
Как найти k и b по графику линейной функции?

Источник

Каталог заданий.
Чтение графиков функций

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Найдите значение a по графику функции изображенному на рисунке.

Найдите значение b по графику функции изображенному на рисунке.

Найдите значение c по графику функции изображенному на рисунке.

Найдите значение k по графику функции изображенному на рисунке.

На рисунке изображён график функции  Какие из утверждений относительно этой функции неверны? Укажите их номера.

1)  функция возрастает на промежутке 

4)  прямая  y=2   пересекает график в точках   и 

Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)

Пройти тестирование по этим заданиям

Источник

Нахождение коэффициентов квадратичной функции y=ax²+ bx +c

I Нахождение коэффициента а :

по графику параболы определяем координаты вершины (m,n)
по графику параболы определяем координаты любой точки A (x;y)
подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

y=а(х-m)²+n

решаем полученное уравнение.

II. нахождение коэффициента b: b= — (х₁+ х₂) это для приведённого уравнения

Сначала находим значение коэффициента a (шаг I, смотри выше)

В формулу для абсциссы параболы m = 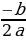подставляем значения m и а

Вычисляем значение коэффициента b.

III. нахождение коэффициента с: с = х₁∙ х₂это для приведённого уравнения

Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,Ь)
Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах² +bх+с и находим с.

I Нахождение коэффициента а :

по графику параболы определяем координаты вершины (m,n)
по графику параболы определяем координаты любой точки A (x;y)
подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

y=а(х-m)²+n

решаем полученное уравнение.

II. нахождение коэффициента b:

Сначала находим значение коэффициента a (шаг I, смотри выше)

В формулу для абсциссы параболы m = 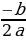подставляем значения m и а

Вычисляем значение коэффициента b.

III. нахождение коэффициента с:

Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II {находим коэффициенты а,b)
Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах² +bх+с и находим с.

Рассмотрим задачу: где невозможно по графику найти точно m и n необходимо найти все коэффициенты уравнения, задающего график:

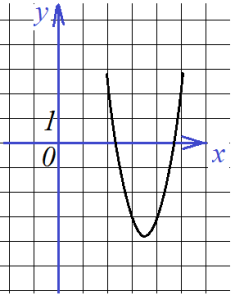
Найти все коэффициенты по графику функции

Подставляем в уравнение: координаты выбранных точек, например, таких: (2;2), (5;2), (4;-3). Получается:

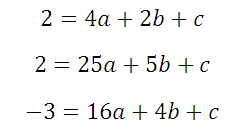
Последние два уравнения вычтем:

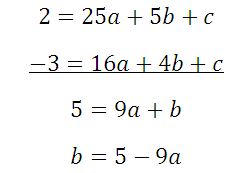
Данное выражение подставим в первое и второе уравнения:

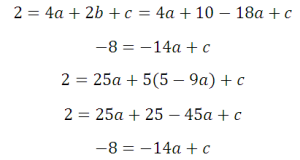
Вычтем два получившихся уравнения:

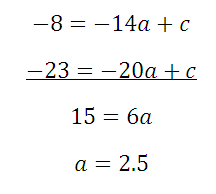
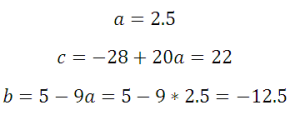
Зная а, можем найти и остальные коэффициенты:

Следующая задача: найти коэффициенты уравнения, задающего график функции, изображенный на рисунке:

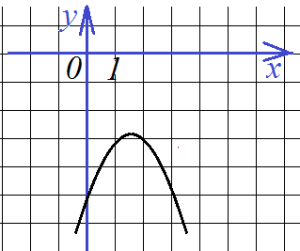
Найти все коэффициенты по графику функции

Здесь будет немного попроще, так как определить коэффициент с можно по рисунку: с=-5. Это значит, что потребуется только две точки, и система будет состоять только из двух уравнений. Возьмем для ее составления точки (1;-3) и (2;-3):

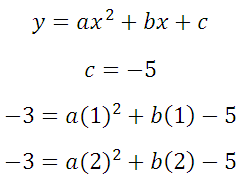
Вычтем получившиеся уравнения (второе – из первого) и определим коэффициенты а и b:

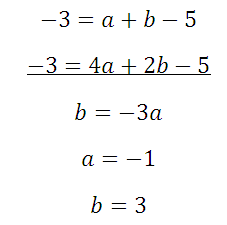
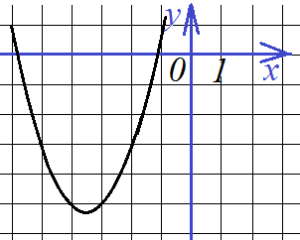
Найти все коэффициенты по графику функции

Наконец, еще одно такое же задание. Снова необходимо определить все коэффициенты функции, график которой представлен на рисунке:

Зададимся точками. Их будет три, уравнений тоже три, так как нам необходимо найти три коэффициента – a, b и c.

Точки будут: (-2; -3),(-5; -3) и (-3; -5) . Тогда уравнения:

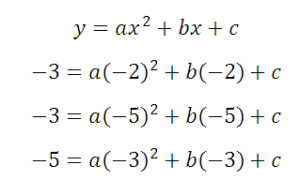
Из первого уравнения вычитаем второе:

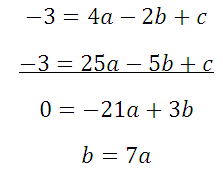
Полученное подставим в первое и третье:

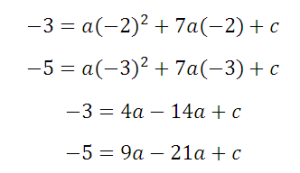
Полученные уравнения вычтем вновь, и найдем искомое:

Источник

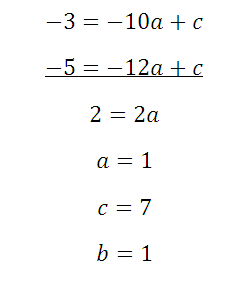
Как определить a, b и c по графику параболы

1 способ – ищем коэффициенты на графике

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим (9a) вместо (b):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение (a):

Получается квадратичная функция: (y=-x^2-9x-15).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

Алгоритм нахождения значения коэффициентов a,b, c квадратичной функции

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

I . Нахождение коэффициента a :

1) По графику параболы определяем координаты вершины ( m;n ).

2) По графику параболы определяем координаты любой точки А ( х _1; у ₁ ).

3) Подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

4) Решая полученное уравнение, находим а.

II . нахождение коэффициента b :

Сначала находим значение коэффициента a (шаг I, смотри выше).

В формулу для абсциссы вершины параболы m= -b/2a подставляем значения m и a.

Вычисляем значение коэффициента b .

III. нахождение коэффициента с :

Находим ординату у точки пересечения графика параболы с осью Оу , это значение равно коэффициенту с , т.е. точка (0; с ) — точка пересечения графика параболы с осью Оу .

Если по графику невозможно найти точку пересечения с осью Оу , то выполняем шаги I , II (находим коэффициенты a, b ).

Подставляем найденные значения a, b , А( х ₁ ;у ₁ ) в уравнение у=ax 2 +bx+c и находим с .

Краткое описание документа:

I . Нахождение коэффициента a :

1) По графику параболы определяем координаты вершины (m;n).

2) По графику параболы определяем координаты любой точки А (х1;у1).

3) Подставляем эти значения в формулу квадратичной функции, заданной в другом виде:

4) Решая полученное уравнение, находим а.

II . нахождение коэффициента b:

1) Сначала находим значение коэффициента a (шаг I, смотри выше).

1) В формулу для абсциссы вершины параболы m= -b/2a подставляем значения m и a.

2) Вычисляем значение коэффициента b.

III. нахождение коэффициента с:

Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II (находим коэффициенты a, b).

2) Подставляем найденные значения a, b , А(х1 ;у1) в уравнение у=ax2 +bx+c и находим с.

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 703 человека из 76 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 857 человек из 77 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

Сейчас обучается 48 человек из 21 региона

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

Для всех учеников 1-11 классов
и дошкольников
Интересные задания
по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 846 424 материала в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

07.02.2015
688
0

07.02.2015
826
1

07.02.2015
575
1

07.02.2015
1220
4

07.02.2015
1128
10

07.02.2015
1385
3

07.02.2015
3686
69

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

07.02.2015 80756
DOCX 58.9 кбайт
348 скачиваний
Рейтинг: 4 из 5
Оцените материал:

Настоящий материал опубликован пользователем Копташкина Альбина Ивановна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 7 лет и 6 месяцев
Подписчики: 1
Всего просмотров: 85342
Всего материалов: 5

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

В России выросло число детей с ОВЗ, поступающих в колледжи

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Роспотребнадзор сообщил об опасности размещения вышек сотовой связи на территории школ

Время чтения: 1 минута

Путин объявил 2022-2031 годы Десятилетием науки и технологий

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Квадратные уравнения. Углубленное изучение свойств квадратных уравнений

Разделы: Математика

Тип урока: урок обобщения и систематизации знаний, углубленное изучение свойств квадратных уравнений.

Образовательные цели урока: обеспечить закрепление теоремы Виета, обратить внимание учащихся на решение квадратных уравнений ах 2 + вх + с = 0, в которых а+в+с=0; привить навыки устного решения таких уравнений.

Воспитательные цели урока: способствовать выработке у школьников желания и потребности обобщения изучаемых фактов, развивать самостоятельность и творчество.

Ход урока

1. Организационный момент.

Учащимся сообщаются задачи урока:

Контроль знаний с помощью тестирования (тест на заполнение пропусков, чтобы получилось верное определение, формулировка, правило)
Решение задач на применение прямой и обратной теорем Виета.
Изучение нового свойства квадратных уравнений.

2. Повторение пройденного материала.

1) Решить уравнение (работа у доски): 7х 2 — 9х + 2 =0

Решение: D = в 2 – 4ас, D = 25, х₁ = , х₂ = 1. Ответ: х₁ = , х₂ = 1.

2) Тест “ Квадратные уравнения”:

Вариант 1

. уравнением называется уравнение ах 2 + вх + с = 0, где а,в,с – заданные числа, а 0, х – переменная.
Уравнение х 2 = а, где а > 0, имеет корни х₁ = . ; х₂ = .
Уравнение ах 2 = 0, где а 0, называется . .
Уравнение ах 2 + вх + с = 0, где а 0, в 0, называется . квадратным уравнением.
Если ах 2 + вх + с = 0 — квадратное уравнение (а 0), то “в” называют . коэффициентом.
Корни квадратного уравнения ах 2 + вх + с = 0 вычисляют по формуле х = . .
Приведенное квадратное уравнение х 2 + рх + q = 0 совпадает с уравнением общего вида, в котором а = . в = . с = . .
Если х₁ и х₂ — корни уравнения х 2 + рх + q = 0, то справедливы формулы х₁ + х₂ =. ; х₁ * х₂ = .

Вариант 2

Если ах 2 + вх + с = 0 — квадратное уравнение, то а называют . коэффициентом, с — . членом.
Уравнение х 2 = а, где а 2 + с = 0, где а 0, с 0, называется . квадратным уравнением.
Корни квадратного уравнения ах 2 + вх + с = 0 вычисляют по формуле х₁ = . ; х₂ = . .
Квадратное уравнение ах 2 + вх + с = 0 имеет два различных действительных корня, если в 2 – 4ас . 0.
Квадратное уравнение вида х 2 + рх + q = 0 называют . .
Сумма корней приведенного квадратного уравнения равна . коэффициенту, взятому с . знаком, а произведение корней равно . числу.
Если числа p, q, х_1, х ₂ таковы, что х₁ + х₂ = — Р; х₁ * х₂ = . то х₁ и х₂ — корни уравнения.

3. Задание на определение вида уравнения (устно).

— Ребята, здесь вы видите уравнения, определенные по какому-то признаку. Как вы думаете, какое из уравнений этой группы является лишним?

источники:

http://infourok.ru/algoritm_nahozhdeniya_znacheniya_koefficientov_ab_c_kvadratichnoy_funkcii-371015.htm

http://urok.1sept.ru/articles/658252

Источник

Краткое описание документа:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

1 способ – ищем коэффициенты на графике

2 способ – находим формулу по точкам

3 способ – используем преобразование графиков функций

Как определить a, b и c по графику параболы

1 способ – ищем коэффициенты на графике

3 способ – используем преобразование графиков функций

Алгоритм нахождения значения коэффициентов a,b, c квадратичной функции

Краткое описание документа:

Математика: теория и методика преподавания в образовательной организации

Дистанционное обучение как современный формат преподавания

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Оставьте свой комментарий

Автор материала

Дистанционные курсы для педагогов

Подарочные сертификаты

Квадратные уравнения. Углубленное изучение свойств квадратных уравнений

Не пропустите также:

Дистанционные курсы
для педагогов