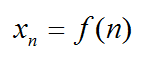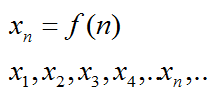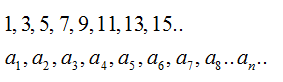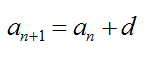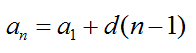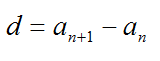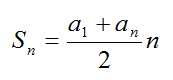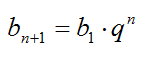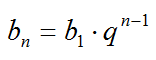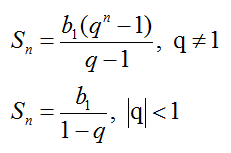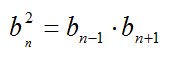Как найти 3 наименьших элемента в последовательности

Собственно вот моё задание:
Дана квадратная матрица А, составьте программу формирования последовательности В, элементами которой являются элементы матрицы А расположенные под главной диагональю. В полученной последовательности найдите 3 наименьших элемента. Если количество между первый и вторым элементом совпадает с количеством между вторым и третьим то поменять их местами сохранив порядок следования(без доп массива) линейный массив вывести в строку

И мне не понятно как в массиве найти 3 наименьших элемента, я могу найти один но 3 хз как + не используя доп.массив, если кто-то делал что-то подобное напишите как делали.
Была идея сортировать методом хоара а потом 3 последних элемента считать минимальными но это доп.массив(

const
n=10; //кол-во элементов в массиве
 
var
  a: array[1..n] of real;  //основной массив
  i: integer;
  
 procedure Out (var a: array[1..n] of real);  //вывод массива
 var i: integer;
 begin
 write('Массив:');
 for i:=1 to n do
 write(' ',a[i]);
     end;
 
procedure Swap(var a,b: real); //меняет 2 числа местами
var temp: real;
begin
 temp:=a; a:=b; b:=temp;
 end;
 
 function MinEl(var b: array[1..n] of real; el: integer): integer;  //ищет в массиве номер минимального элемента, начиная с номера el
 var u: integer;
 begin
 result:=el;
 for u:= el+1 to n do
 if b[u]<b[result] then result:=u;
   end;
   
 procedure Three (b: array[1..n] of real);  //основная процедура по поиску трех минимумов: создает копию массива a (чтобы основной массив не изменялся)
 var i: integer;
 begin
 write('Три наименьших элемента:');
  for i:=1 to 3 do   begin       //на место i-го элемента становится минимальный элемент в промежутке от i до n
  swap(b[i],b[minel(b,i)]);
  write(' ',b[i]);           //и выводится на экран
  end;
 end;
 
begin
  for i := 1 to n do                //создаем массив
      a[i] := random(101) - 50;
      Out(a);                 //выводим на экран
      writeln;
      Three(a);            //ищем три минимума
writeln;
Out(a);                        //показываем, что основной массив не изменился
            writeln;
end.

Вход. Массив
элементов Array[i],
1 
i 
n, принадлежащих
множеству, на котором установлен линейный
порядок, и целое k, 1
 k
 n.

Выход. k-й
наименьший элемент из массива Array.

Метод. В
основе алгоритма лежит рекурсивная
процедура, Selection (Выбор)
заключающаяся в разбиении всей
последовательности по некоторому
элементу m на три
подпоследовательности S₁,
S₂ и S₃
такие, что S₁
содержит все элементы, меньшие m,
S₂ – все элементы,
равные m, а S₃
– все элементы, бóльшие m.
Сосчитав количество элементов, находящееся
в S₁ и S₂,
можно определить, в какой из
последовательностей необходимо далее
искать k-й наименьший
элемент, и, таким образом, свести задачу
к задаче меньшей размерности.

Но чтобы получить
линейный алгоритм, надо уметь за линейное
время находить разбивающий элемент
так, чтобы длина каждой из
подпоследовательностей S₁
и S₂ была бы не
больше фиксированной доли длины исходной
последовательности. Здесь вся хитрость
заключается в способе выбора разбивающего
элемента m.
Последовательность, заданная массивом
разбивается на подпоследовательности
по пять элементов в каждой. Каждая из
подпоследовательностей упорядочивается,
и из медиан этих подпоследовательностей
составляется новая подпоследовательность
M. Ввиду изложенного
способа выбора M она
содержит только n/5
элементов (x
наибольшее целое число, содержащееся
в x), и можно найти её
медиану в пять раз быстрее, чем у
последовательности из n
элементов.

Очевидно, что
не менее четверти всех элементов
последовательности будут меньше или
равны m и соответственно
не менее четверти всех элементов будут
больше или равны m.
Вместо разбиения на подпоследовательности
по пять элементов можно использовать
и другие виды разбиений, но необходимо
помнить, что сумма длин двух
последовательностей, к которым применяется
рекурсивная процедура Selection,
должна быть меньше n.
Иначе время работы алгоритма не будет
линейным.

Основные
составляющие программы нахождения k-го
наименьшего элемента последовательности
с использованием алгоритма 12.1 приведены
ниже.

Программа
12.1 Нахождения k-го
наименьшего элемента

//
Программа использует порядковые
статистики для выбора k-го минимального

//
элемента в последовательности длины
NUM

#include
<stdlib.h>

#include
<stdio.h>

#include
<io.h>

#define
NUM 124

int
Selection(int
array[], unsigned
order, unsigned
init, unsigned
fin);

void
main()

{

unsigned
order, index;

int
result, *array;

//
В этом месте должна стоять программа
ввода массива array и выбора order

result=Selection(array,
order, 0, NUM-1);

if
(result==-32767) printf(«Error:
order вне
границ
массива
n»);

else
printf(«The
%d-й
минимальный
элемент
в
массиве
is %dn», order, result);

delete
[ ]
array;

}
// Конец
main

int
Selection(int
array[], unsigned
order, unsigned
init, unsigned
fin)

{//
Функция выбора k-го
элемента из последовательности, заданной
массивом

//
array, order=k,
массив задаётся своими границами init и
fin.

unsigned
min, max, num_med, indi, indj;

int
*median, mean, temp;

if
(fin<init) printf(«Неправильное
использование:
init > fin n»);

if
((init>(order-1))||(fin<(order-1))) return
-32767;

if
((fin-init+1)<25)

{

//
В этом месте должна стоять функция
сортировки короткого массива с числом

//
элементов, меньшим 25, находящихся в
большом массиве array
между

//
элементами с номерами init
и fin

return
(array[order-1]);

}
else

{

min=init;
max=init+4; indi=0;

//
Отведение динамической памяти под
массив медиан последовательностей из

//
пяти
элементов

median=new
int[(fin-init+1)/5+1];

//
Разбиение на группы по 5 элементов,
сортировка элементов в группах и

//
нахождение медианы в каждой группе

while
(max<=fin)

{

//
В этом месте должна стоять функция
сортировки короткого массива из пяти

//
элементов массива array,
имеющих индексы между min
и max

median[indi++]=array[min+2];

min+=5;
max+=5;

}

num_med=indi;

mean=Selection(median,
(num_med>>1)+1, 0, num_med-1); //


delete
[ ] median;

//
Если разбиение массива array на три части
даёт подмассивы, содержащие

//
элементы меньшие, равные и бóльшие, чем
mean соответственно

indi=init;
indj=fin;

while(indi<=indj)

{

while
((array[indj]>=mean)&&(indj>=init)) indj—;

while
((array[indi]<mean)&&(indi<=fin)) indi++;

if
(indi<indj)

{

//
Поменять
местами
array[indi] и
array[indj]

temp=array[indi];
array[indi++]=array[indj]; array[indj—]=temp;

}

}

if(indi>=order)
return
Selection(array, order, init, indi-1); //


while
(array[indi]==mean) indi++;

for
(indj=indi+1; indj<=fin; indj++)

if(array[indj]==mean)

{

array[indj]=array[indi];
array[indi++]=mean;

}

if(indi>=order)
return mean;

else
return
Selection(array, order, indi, fin); //


}

}
// Конец Selection

Некоторые
пояснения к программе. Если размер
входной последовательности относительно
мал (не более 25 элементов), то гораздо
проще отсортировать данную
последовательность, например, методом
взбалтывания, и выбрать её k-й
элемент.

Основная описанная
в алгоритме процедура применяется
только в случае наличия достаточно
большого количества элементов во входной
последовательности. Тогда производится
выбор разбивающего элемента как медианы
медиан пятёрок элементов, на которые
разбивается входная последовательность.
Элементы внутри пятёрок сортируются,
например, методом взбалтывания, и
выбирается средний элемент их пятёрки
(медиана). Данные медианы хранятся в
динамическом массиве median.
После этого к массиву median
применяется та же процедура Selection,
используемая для нахождения медианы
этого массива m, которая
и выбирается в качестве разбивающего
элемента. Размер массива median
равен n/5.
После разбиения последовательности на
три подпоследовательности S₁
(состоящую из элементов, меньших m),
S₂ (состоящую из
элементов, равных m)
и S₃ (состоящую из
элементов, бóльших m),
программа определяет в какой их данных
подпоследовательностей будет находиться
k-й элемент всей
последовательности. Если он находится
в S₂, то работа
заканчивается и программа возвращает
результат, равный m.
Если же искомый элемент находится в S₁
или S₃, то программа
применяет процедуру Selection
к соответствующей подпоследовательности.
Количество элементов в каждой из
подпоследовательностей S₁
и S₃ находится в
пределах от n/4 до
3n/4 (убедитесь
в этом самостоятельно). Поэтому сумма
длин подпоследовательностей, к которым
применяется процедура Selection
на каждом шаге (массив median
и подпоследовательность S₁
или S₃) будет меньше
n. Поэтому исходный
массив разбивается на пятёрки элементов.
Некоторые другие «магические числа»
(вместо 5) тоже годятся. Попробуйте найти
их самостоятельно.

Теорема
8. Алгоритм 12.1 находит k-й
наименьший элемент в n-элементной
последовательности за время O(n).

Доказательство.
Корректность алгоритма доказывается
непосредственной индукцией по n,
и эта часть доказательства остаётся в
качестве упражнения. Пусть T(n)
– время, затрачиваемое на выбор k-го
наименьшего элемента из последовательности
длины n. Длина
последовательности M
(median) не больше n/5,
и поэтому рекурсивный вызов процедуры
Selection(median,
n/10,
0, n/5)
в строке  для массива
median занимает время, не
большее T(n/5).

Каждая из
последовательностей S₁
и S₃ имеет длину не
более 3n/4.
Поэтому рекурсивный вызов Selection
в строке 
или 
занимает времени не более T(3n/4).
Все остальные операторы тратят не более
O(n)
времени. Таким образом, для некоторых
постоянных c и b

Несложно показать (докажите
самостоятельно), что T(n)
 20bn
удовлетворяет последней системе. 

Теперь целесообразно
рассмотреть среднее время, затрачиваемое
на выбор k-го наименьшего
элемента в последовательности из n
элементов. Для дальнейшего рассмотрения
этого вопроса потребуется определение
транзитивного замыкания.

Определение.
Транзитивным замыканием отношения
R (см. раздел 2.1)
называется такое отношение R⁺,
что cR⁺d
тогда и только тогда, когда существует
последовательность истинных утверждений
вида e₁Re₂,
e₂Re₃,
,
e_m–1Re_m,
где m2,
c=e₁
и d=e_m.

Пусть теперь
S={a₁,
a₂,a_n}
– множество из n
различных элементов, а T
– дерево решений какого-нибудь алгоритма
для нахождения k-го
наименьшего элемента в S.
Каждый путь p в T
определяет такое отношение R_p
на S, что a_i
R_p
a_j,
если два различных элемента a_i
и a_j
сравниваются в некотором узле, лежащем
на p, и в результате этого
сравнения либо a_i
< a_j,
либо a_j
 a_i.
Пусть
–
транзитивное замыкание отношения R_p.
Образно говоря, если a_ia_j,
то последовательность сравнений,
представленная путём p, выясняет, что
a_i
< a_j,
поскольку никакой элемент не сравнивается
сам с собой.

Лемма
2. Если на пути p
выясняется, что a_m
является k-м наименьшим
элементом в S, то для
любого im,
1 i
 n,
либо a_ia_m,
либо a_ma_i.

Доказательство.
Допустим, что некоторый элемент a_u
не связан с a_m
соотношением
.
Докажем, что, поместив a_u
либо перед, либо после a_m
в линейном порядке, заданном на S,
получим противоречие с предположением,
что путь p правильно
установил, что a_m
является k-м наименьшим
элементом в S. Пусть
S₁ ={a_ja_ja_u}
(где подобная запись означает: множество
S₁ состоит из
элементов a_j,
для которых выполняется условие a_ja_u),
S₂={a_ja_ua_j},
и в S₃ входят
остальные элементы из S.
По предположению a_u
и входят в a_m.

Если a_j
– произвольный элемент в S₁
(соответственно в S₂)
и a_ia_j
(соответственно a_ja_i),
то в силу транзитивности a_i
также принадлежит S₁
(соответственно в S₂).
Следовательно, можно построить такой
линейный порядок R,
совместимый с
,что
все элементы множества S₁
предшествуют всем элементам из S₃,
которые в свою очередь предшествуют
всем элементам из S₂.

По предположению
элемент a_u
не связан отношением

ни с одним элементом из S₃.
Допустим, что a_u
предшествует a_m
при линейном порядке R,
т.е. a_ua_m.
Тогда можно построить новый порядок
R,
совпадающий с R во
всём, кроме того, что a_u
следует непосредственно за a_m.
Отношение R
также совместимо с
.
Для каждого порядка R
и R
можно найти различные элементы,
удовлетворяющие соответственно R
или R.
Но a_m
не может быть k-м
наименьшим элементом в обоих случаях,
т.к. в R
элементу a_m
предшествует на один элемент меньше,
чем в R. Поэтому
заключаем, что если какой-то элемент из
S не связан с a_m
отношением
,
то дерево T не может
правильно выбрать k-й
наименьший элемент из S.
Случай a_ma_u
исследуется аналогично. 

Теорема 9.
Если T – дерево решений,
выбирающее k-й наименьший
элемент в множестве S,
║S║=n,
то глубина любого листа дерева T
не меньше n–1.
Следствием данной теоремы будет
утверждение, что для нахождения k-го
наименьшего элемента в S
требуется не меньше n–1 сравнений,
как в среднем, так и в худшем случае.

Доказательство.
Рассмотрим путь p в T
из корня к листу. По лемме 2 либо a_ia_m,
либо a_ma_i
для каждого im,
где a_m
– элемент, выбранный в качестве k-го
наименьшего. Для элемента a_i
im,
определим ключевое сравнение как
первое сравнение не p,
содержащее a_i
и такое, что выполнено одно из условий:

1. a_i
   сравнивается с a_m,

2. a_i
   сравнивается с a_j,
   a_i
   R_p
   a_j,
   и a_ja_m,

3. a_i
   сравнивается с a_j,
   a_j
   R_p
   a_i,
   и a_ma_j.

Интуитивно
ключевое сравнение для a_i
– это первое сравнение, из которого
можно определить, предшествует элемент
a_i
элементу a_m
или следует за ним.

Понятно, что
всякий элемент a_i,
кроме a_m,
обладает сравнением; иначе не выполнилось
бы ни a_ia_m,
ни a_ma_i.
Далее легко видеть, что ни никакое
сравнение не может быть ключевым для
обоих сравниваемых элементов. Так как
в ключевые сравнения должны вовлекаться
n–1 элементов, то
длина пути p должна
быть не меньше n–1.

Поэтому выбирающий
алгоритм 12.1 с точностью до постоянного
множителя оптимален в классе деревьев
решений. Теперь рассмотрим другой
выбирающий алгоритм, который имеет
квадратичную сложность в худшем случае,
но среднее время работы которого
составляет лишь долю времени работы
алгоритма 12.1. Данный алгоритм использует
стратегию, аналогичную той, что применялась
в алгоритме Быстрсорт.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задачи по нахождению минимального и/или максимального элемента в массиве очень часто встречаются в различных учебных пособиях по программированию и, как правило, вызывают трудности у начинающих программистов или просто студентов, получивших такое задание.

В данной статье вы узнаете, как написать реализацию программы на языке C++, которая находит максимальный и минимальный элемент в массиве и выводит на экран. А узнать множество решений других задач можно в разделе с решениями задач по программированию на языке C++.

Что такое максимальный и минимальный элемент массива

Для начала поймем, что же такое максимальный или минимальный элемент в массиве? Всё просто, максимальный элемент массива — это элемент, который имеет самое большое числовое значение, а минимальный элемент массива — это элемент, имеющий самое маленькое значение.

Пример: в массиве, состоящем из таких элементов: 3, 1, 0, -4, 16, 2 — максимальный элемент равен 16, т.к. это число больше других, а минимальный элемент равен -4, т.к. оно меньше остальных.

Поняв это, можно приступить к решению задачи.

Алгоритм решения задачи

— Инициализация массива, переменных, хранящих минимальное и максимальное значение.

— Заполнение массива случайными числами при помощи цикла и функции, возвращающей случайные числа.

— Вывод массива.

— Сравнение каждого элемента массива: Если элемент больше переменной с максимальным значением, то значение записывается в переменную; Если элемент меньше переменной с минимальным значением, то значение записывается в переменную.

— Вывод переменных с максимальным и минимальным элементом.

Алгоритм решения на языке C++

Для начала нужно подключить заголовок ввода/вывода <iostream>, заголовок стандартных функций <cstdlib> в ней имеется функция rand(), которая позволит заполнить массив случайными числами. Заполнение каждого элемента массива вручную требует времени, его можно сэкономить автоматизировав процесс. Подключаем пространство имён std. Создаём константу N, она будет определять количество элементов в массиве.

#include <iostream> 
#include <cstdlib> 

using namespace std; //Пространство имён std

const int N = 10;//Количество элементов в массиве

int main() 
{

	return 0;
}

В теле функции main() инициализируем массив целых чисел из N лементов, целочисленные переменные max и min, они будут хранить значение максимального и минимального элементов массива соответственно.

	int mass[N], max, min;

Теперь заполним массив случайными числами. Для этого используем цикл от 0 до N (не включительно), который пройдется по каждому элементу массива и поместит случайное значение от 0 до 98. Это можно сделать, использовав функцию rand(), которая возвращает случайное число. Поделить возвращаемое значение на 99 и внести в ячейку остаток от деления, таким образом значение ячейки будет иметь значение в диапазоне от 0 до 99(не включая 99, т.к. остаток от деления не может быть кратным делителю).  При этом выведем значения элементов массива на экран.

	cout << "Элементы: |";
	for(int r = 0; r<N; r++) // Цикл от 0 до N
	{
		mass[r] = rand()%99; // Заполнение случайным числом
		cout << mass[r] << "|"; // Вывод значения
	}
	cout << endl;

В результате программа выведет на экран значения элементов массива, разделенное вертикальными чертами:

Элементы: |28|43|72|79|23|70|55|39|69|1|

Обратите внимание! Если вы программируете под Windows и у Вас не отображаются русские символы в консоли, то советую Вам почитать о решении этой проблемы в статье Русские символы(буквы) при вводе/выводе в консоль на C++.

Далее определим максимальный и минимальный элемент в массиве, для этого вновь пройдемся по массиву циклом. При помощи условия определим максимальный и минимальный элемент массива.

Перед циклом нужно будет занести первый элемент массива в переменные min и max, они будут хранить минимальное и максимальное значение изначально, а во время цикла поменяют его, если найдётся значение меньше для min или больше для max.

	max = mass[0];//Помещаем значения 1-го элемента
	min = mass[0];//массива в переменные
	for(int r = 1; r<N; r++)
	{
		if(max < mass[r]) max = mass[r]; //если значение элемента больше значения переменной max, то записываем это значение в переменную
		if(min > mass[r]) min = mass[r]; //аналогично и для min
	}

После цикла выведем значения min и max.

	cout << "Min: " << min << endl;
	cout << "Max: " << max << endl;

После компиляции и запуска прогамма выводит следующее

Элементы: |28|43|72|79|23|70|55|39|69|1|
Min: 1
Max: 79

Пробегаемся по элементам массива глазами и видим, что минимальное значение — 1, а максимальное — 79. Переменные min и max имеют эти же значения соответственно, следовательно алгоритм работает.

Весь листинг программы на C++

#include <iostream>
#include <cstdlib>

using namespace std;

const int N = 10;

int main() 
{
	int mass[N], max, min;

	cout << "Элементы: |";
	for(int r = 0; r<N; r++)
	{
		mass[r] = rand()%99;
		cout << mass[r] << "|";
	}
	cout << endl;
	
	max = mass[0];
	min = mass[0];
	for(int r = 1; r<N; r++)
	{
		if(max < mass[r]) max = mass[r];
		if(min > mass[r]) min = mass[r];
	}
	cout << "Min: " << min << endl;
	cout << "Max: " << max << endl;
	
	return 0;
}

По просьбам читателей возобновляем рубрику «Математика для чайников». Говорим о числовых последовательностях и вычислении их пределов. Выясняем, чем последовательность отличается от простого набора чисел и как ее можно задать.

Нужно больше полезной и интересной информации? Этого добра много не бывает! Присоединяйтесь к нам в телеграм.

Последовательности чисел

Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной. 

Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.

Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.

Что такое числовая последовательность? 

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.

Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N. 

Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.

На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.

Какие бывают последовательности

Различают:

• постоянную, или монотонную последовательность: 1, 1, 1, 1, 1… 
• возрастающую последовательность, в которой каждый следующий элемент больше предыдущего
• убывающую последовательность, в которой каждый следующий элемент меньше предыдущего

Также последовательности делятся на сходящиеся и расходящиеся. Сходящаяся последовательность имеет конечный предел. А предел расходящейся последовательности равен бесконечности, либо последовательность вообще не имеет предела. Но о пределах немного позже.

Рассмотрим самые известные примеры последовательностей. Еще со школы всем знакомы арифметическая и геометрическая прогрессии.

Арифметическая прогрессия

Посмотрим на числа:

Что у них общего? Они все нечетные и каждое следующее можно получить из предыдущего, прибавляя к нему одно и то же число. Назовем его d. В данном случае d=2.

Описанная выше последовательность – арифметическая прогрессия. Приведем основные формулы для нее:

Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.

Сумма первых n членов прогрессии вычисляется по формуле:

Также африфметическая прогрессия обладает характреристическим свойством:

Геометрическая прогрессия

Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии задаются соотношением:

Основные формулы для геометрической прогрессии приведены ниже. Формула n-го члена прогрессии:

Сумма первых n членов прогрессии:

Характеристическое свойство геометрической прогрессии:

Способы задания последовательностей

Последовательность можно задать несколькими способами:

1. Аналитически или, проще говоря, формулой.
2. Реккурентно. Здесь известно несколько первых членов прогрессии и есть формула, которая позволяет вычислить последующие.
3. Описательно, простым перечислением всех элементов последовательности.

Предел последовательности

Мы уже говорили о пределах функций и способах их вычисления. Из определения последовательности следует, что последовательность – это и есть некоторая функция. Так что, вычисление пределов последовательностей будет во многом схоже с вычислением пределов функций. Правда, со своими особенностями.

Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.

Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.

Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел. 

Что нужно помнить, вычисляя пределы последовательностей

Кстати! Также полезно помнить, что для всех наших читателей сейчас действует скидка 10% на любой вид работы.

1. Последовательность может иметь только один предел.
2. Если последовательность имеет предел, то она ограничена. Обратное верно не всегда!
3. Если члены некоторой последовательности zn заключены между соответствующими членами двух последовательностей xn, yn, сходящихся к одному пределу, то и эта последовательность сходится к тому же пределу.
4. Предел постоянной последовательности равен ее постоянному.
5. Если две последовательности x и y равны между собой, то пределы этих последовательностей также равны между собой, если они существуют.
6. Если каждый член сходящейся последовательности не превосходит соответствующего члена другой сходящейся последовательности, то и предел первой не превосходит предела второй.
7. Предел суммы (разности) двух последовательностей равен сумме (разности) их пределов. При условии, что обе последовательности имеют пределы.
8. Предел произведения двух последовательностей, имеющих пределы, существует и равен произведению пределов последовательностей. 
9. Постоянный множитель можно выносить за знак предела.
10. Предел частного двух последовательностей, имеющих пределы, равен частному пределов этих последовательностей, если предел знаменателя не равен нулю.

Для проверки своих решений при вычислении пределов не обязательно нести работу на проверку преподавателю. Достаточно воспользоваться онлайн калькулятором. 

Тема последовательностей разрабатывалась многими математиками на протяжении веков. Охватить ее в одной статье просто невозможно. Здесь мы дали лишь поверхностное представление. Если у вас есть вопросы или нужна консультация – обращайтесь к специалистам студенческого сервиса, которые помогут быстро прийти к понимаю.