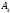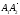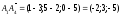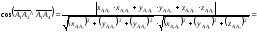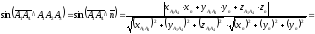Как найди длину ребра по координатам

Онлайн решение Пирамиды по координатам вершин

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

16

Задание
1.1.

Даны
координаты вершин пирамиды
,
,
,
.

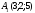
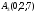
1).
длину ребра
;

2).
угол между ребрами

и
;

3).
угол между ребром

и гранью
;

4).
площадь грани
;

5).
объём пирамиды;

6).
уравнение прямой
;

7).
уравнение плоскости
;

8).
уравнение высоты, опущенной из вершины

на грань
.

Решение.

1).
Используем формулу для нахождения длины
ребра через
координаты его конечных точек:

.

2).
Запишем координаты векторов

и
:

;

Угол
между ребрами
– это угол между векторами

и
,
поэтому используем соответствующую
формулу:

.

Тогда,
получим:

.

3).
Угол между
ребром и гранью
– это угол между вектором

и нормальным вектором плоскости
.

Находим
нормальный вектор

плоскости

как векторное произведение векторов

и
:

.

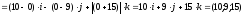
Далее,
используем соответствующую формулу
для вычисления искомого угла:

.

Следовательно,

.

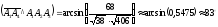
4).
Площадь грани

вычисляется как половина длины векторного
произведения векторов

и
,
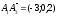
на которых она построена, т.е. половина
длины нормального вектора плоскости
.
Тогда, получим:

Векторное
произведение:

i(5
• 2-0 • (-3)) — j(0 • 2-(-3) • (-3)) + k(0 • 0-(-3) • 5)
= 10i + 9j + 15k

.

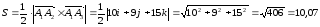
5).
Используем формулу для нахождения
объёма
пирамиды
через координаты векторов
;
;
,
на которых она построена:

.

6).
Запишем симметричные уравнения
прямой

через координаты точки

и направляющего вектора
:

;

.

7).
Запишем уравнение
плоскости

по известному нормальному вектору

и точке плоскости
:

;

;

;

.

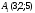
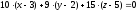
8).
Направляющим вектором искомой высоты
есть нормальный вектор плоскости
:

(поскольку высота перпендикулярна к
этой плоскости).

Запишем
симметричные уравнения
высоты через
координаты точки

и направляющего вектора
:

;

;..

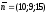
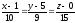
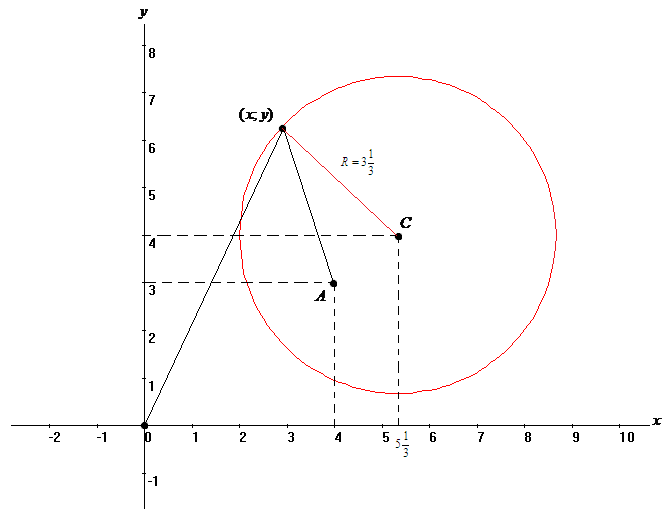
Задание
1.2.

Составить
уравнение и построить линию, расстояния
каждой точки которой от начала координат
и от точки

относятся как 2:1.

Решение.

Пусть

– произвольная точка данной линии.

Находим
расстояние от точки линии к началу
координат по соответствующей формуле
расстояния между двумя точками:

.

Находим
расстояние от точки на линии к точке
:

.

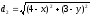
По
условию, найденные расстояния относятся
как 2:1. Следовательно,

;
;

.

Преобразуем
полученное уравнение указанной линии:

;

;

;

;

;

.

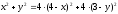
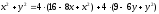
Выделяем
полные квадраты:

;

;

;

;

;

.

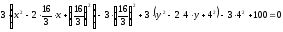
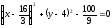
Следовательно,

– каноническое уравнение окружности
с центром в точке

и радиусом
.

Задание
1.3.

Дана
система линейных уравнений. Доказать
её совместность и решить методом Гаусса.

.

Решение.

Теорема
Кронекера-Капелли: для того, чтобы
линейная система уравнений являлась
совместной необходимо и достаточно,
чтобы ранг основной матрицы системы
был равен рангу расширенной матрицы.

Запишем
расширенную матрицу системы:

.

Сводим
расширенную матрицу системы к
трапециевидной форме, используя
эквивалентные преобразования.

Поменяем
местами первую и третью строки расширенной
матрицы:

.

Разделим
первую строку на 2.

.

Умножим
первую строку на (-2) и прибавим ко второй.
Полученные результаты запишем во вторую
строку новой расширенной матрицы.

.

Умножим
первую строку на (-3) и прибавим к третьей.
Полученные результаты запишем в третью
строку новой расширенной матрицы.

.

Прибавим
вторую строку к третьей. Полученные
результаты запишем в третью строку
новой расширенной матрицы.

.

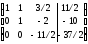
Требуемая
форма расширенной матрицы получена.
Количество ненулевых строк основной и
расширенной матрицы одинаковы, поэтому
ранг основной матрицы равен рангу
расширенной. Это означает, что система
линейных уравнений является
совместной.

Из
последней расширенной матрицы находим
решение системы (обратный ход):

1).
из третьей строки получим:

;
;

2).
из второй строки получим:

;
;
;

3).
из первой строки получим

;
;
.

Таким
образом
,,.

Выполним
проверку полученного решения. Подставляя
найденные значения x₁,x₂,x_3.

Приходим
к тождеству.

Задание
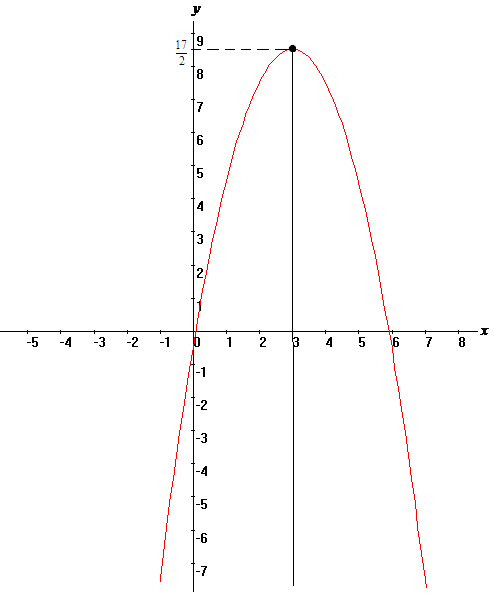
1.4.

Привести
к каноническому виду уравнения линий
второго порядка. Сделать чертежи.

а).
;

б).
;

в).
.

Решение.

а).
.

Разделим
обе части уравнения на 2:

;
;
.

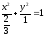
Следовательно,
имеем каноническое уравнение эллипса
с центром в начале координат, с фокусами
на оси ординат (поскольку
),
малой полуосью

и большой полуосью
.

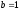
б).
.

Разделим
обе части уравнения на 3:

;
;
.

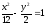
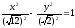
Следовательно,
имеем каноническое уравнение гиперболы
с фокусами на оси абсцисс, действительной
полуосью

и мнимой полуосью
.

в).
.

Выделяем
полный квадрат по переменной
:

;
;

.

Тогда,
получим:

;
;
.

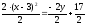
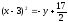
Следовательно,
получили каноническое уравнение параболы
с вершиной в точке
,
с фокусом на отрицательной полупрямой

(парабола опущена ветками вниз)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Пример 1:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти:

1) координаты и модули векторов А₁ А₂и А₁ А₄;  

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) площадь грани А₁ А₂ А₃;         

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂ А₃;

7) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3.

Сделать чертеж.

А₁ (0; 4; -4), А₂ (5; 1; -1), А₃ (-1; -1; 3), А₄ (0; -3; 7).

Решение от преподавателя:

Пример 2:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

1. А₁ (7; 7; 3), А₂ (6; 5; 8), А₃ (3; 5; 8), А₄ (8; 4; 1).

Решение от преподавателя:

Пример 3:

Решение от преподавателя:

 Уравнение плоскости. 
Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

Уравнение плоскости A₁A₂A₃ 

(x-3)(1*2-0*3) — (y-2)((-2)*2-3*3) + (z+2)((-2)*0-3*1) = 2x + 13y — 3z-38 = 0 

Угол между прямой A₁A₄ и плоскостью A₁A₂A₃. 
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.267) = 15.486^o 

Уравнение высоты пирамиды через вершину A₄(0,2,2) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 

Уравнение плоскости через вершину A₄(0,2,2) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением: 
A(x-x₀) + B(y-y₀) + C(z-z₀) = 0 
Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 
2(x-0)+13(y-2)-3(z-2) = 0 
или 
2x+13y-3z-20 = 0

Пример 4:

Решение от преподавателя:

Даны координаты пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 

1. Уравнение плоскости. 
   Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

Уравнение плоскости A₁A₂A₃ 

(x-0)(3*2-8*3) — (y-1)(3*2-(-3)*3) + (z-1)(3*8-(-3)*3) = -18x — 15y + 33z-18 = 0 
Упростим выражение: -6x — 5y + 11z-6 = 0 

2) Угол между прямой A₁A₄ и плоскостью A₁A₂A₃. 
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: -6x — 5y + 11z-6 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.193) = 11.128^o 

3) Уравнение высоты пирамиды через вершину A₄(0,5,4) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: -6x — 5y + 11z-6 = 0 

4) Уравнение плоскости через вершину A₄(0,5,4) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости

5)  Координаты вектора  A₁A₄(0;4;3) 

Уравнение прямой, проходящей через точку А₁(0,1,1) параллельно вектору А₁А₂(0,4,3) имеет вид:

Пример 5:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя:

Пример 6:

Решение от преподавателя:

1) Даны координаты  вершин пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 
Координаты векторов. 
Координаты векторов:       A₁A₂(3;3;3)        A₁A₄(0;4;3) 

 Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   ,    где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
Найдем угол между ребрами A₁A₂(3;3;3) и A₁A₃(0;4;3): 

А₁ = arccos(0,808)

Найдем площадь грани с учётом геометрического смысла векторного произведения: 
S =
Найдем векторное произведение

=i(3*2-8*3) — j(3*2-(-3)*3) + k(3*8-(-3)*3) = -18i — 15j + 33k 

3) Объем пирамиды. 
Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

Координатывекторов:A₁A₂(3;3;3)    A₁A₃(-3;8;2) A₁A₄(0;4;3) :      

Пример 7:

Решение от преподавателя:

1. Угол между ребрами. 
   Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   
   где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   γ = arccos(0) = 90.003⁰ 
2. Площадь грани 
   Площадь грани можно найти по формуле: 
   
   где 
   
   Найдем площадь грани A₁A₂A₃ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   
   Площадь грани A₁A₂A₃ 
3. Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

где определитель матрицы равен: 
∆ = (-2)*(0*4-0*2)-3*(1*4-0*3)+(-3)*(1*2-0*3) = -18 

Пример 8:

Даны координаты вершин пирамиды А₁А₂А₃А₄ . Найти:

1) длину ребра А₁А₂;

2) угол между рёбрами А₁А₂  и А₁А₄ ;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объём пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃;

Сделать чертёж.

А₁(3; 5; 4),        А₂(8; 7; 4),            А₃(5; 10; 4),          А₄(4; 7; 8).

Решение от преподавателя:

1) Длина ребра A₁A₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребрами А₁А₄ и гранью А₁А₂А₃;

Найдем уравнение стороны А₁А₄:

Вектор нормали:  к плоскости А₁А₂А₃.

4) площадь грани А₁А₂А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

Итак: z=4 – уравнение плоскости А₁А₂А₃.

уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

A₄O – высота:

Уравнение A₄O:

Т.к. , то

В результате получаем уравнение высоты:

Пример 9:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя: